Resonance-Based Sparse Signal Decomposition and its Application in Mechanical Fault Diagnosis: A Review
Abstract
:1. Introduction
2. Theoretical Foundation of Wavelet Bases
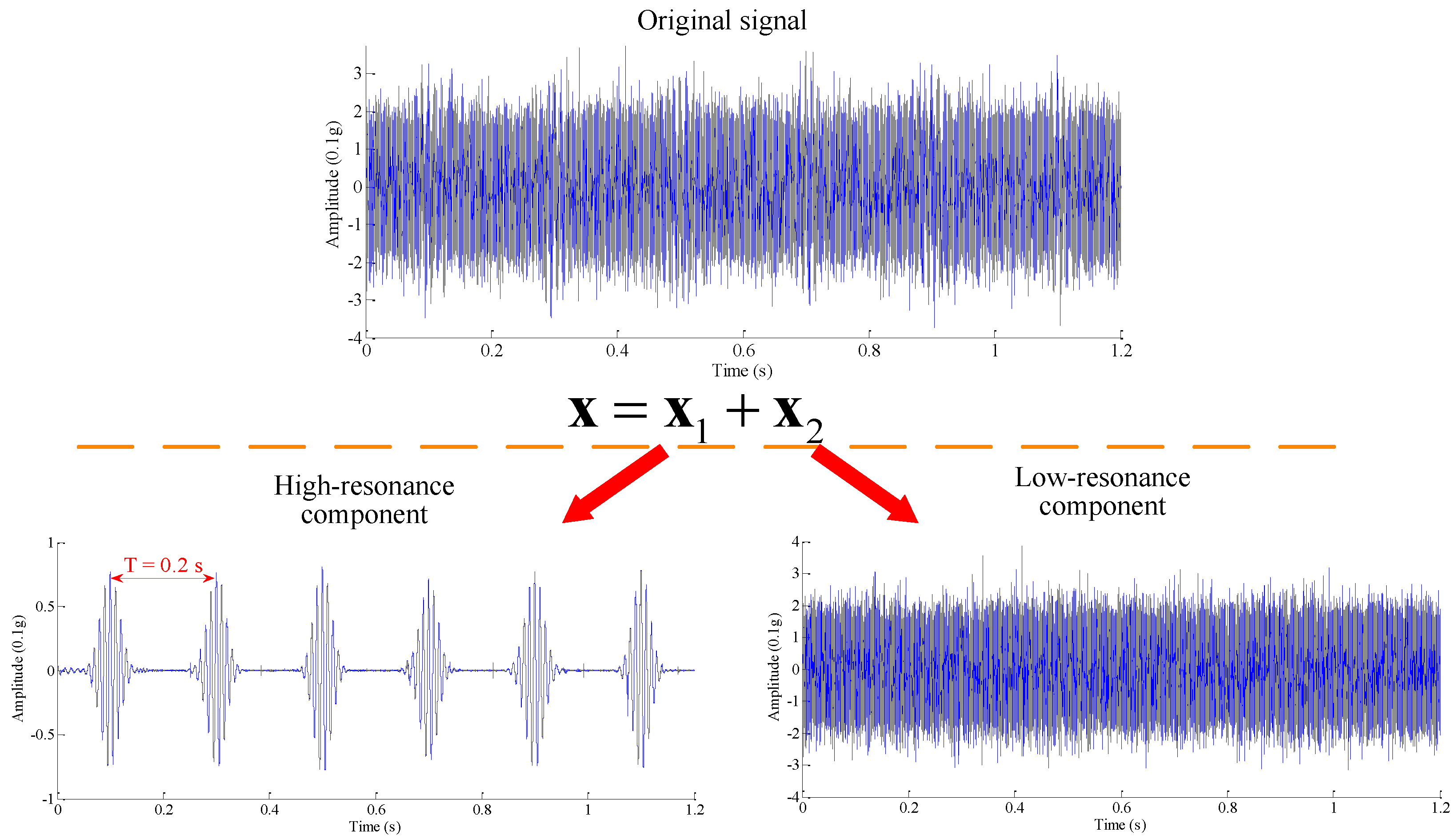
2.1. Signal Resonance
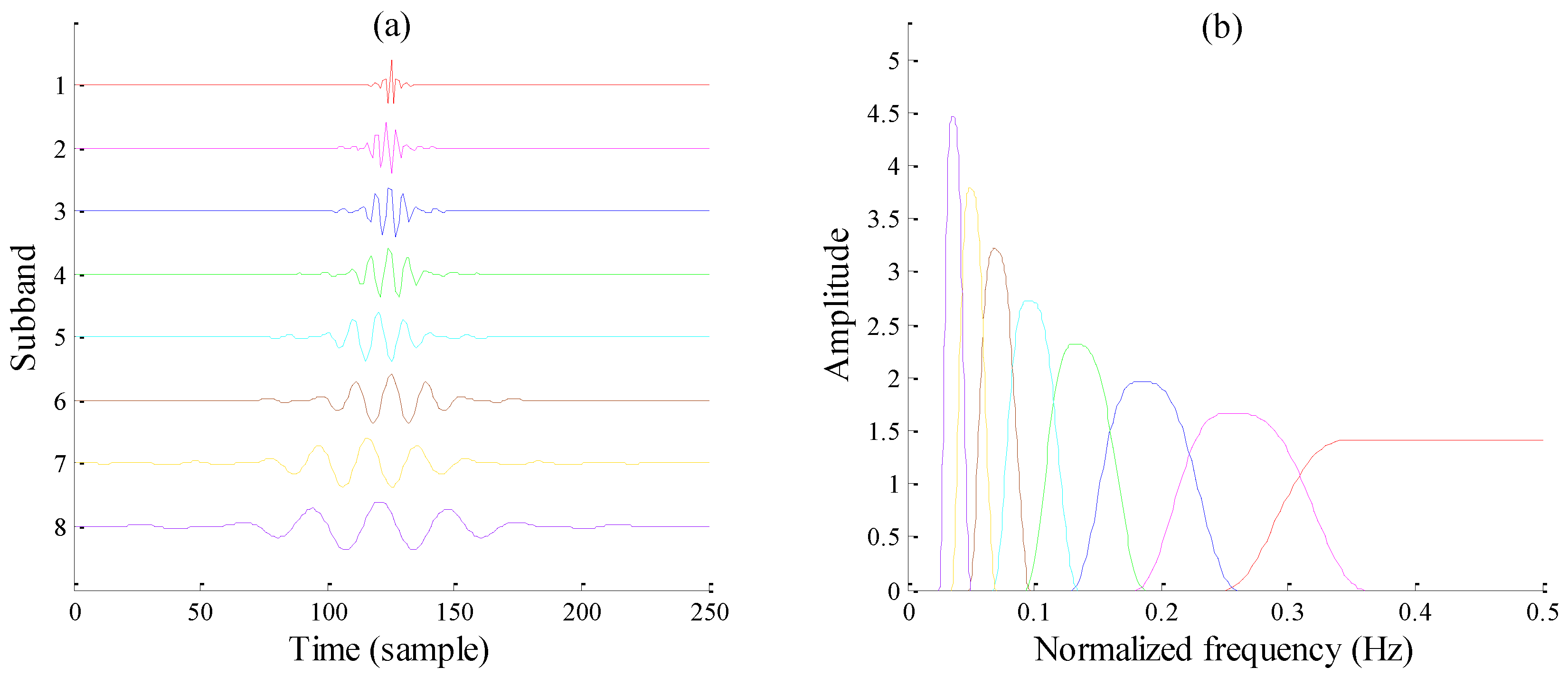
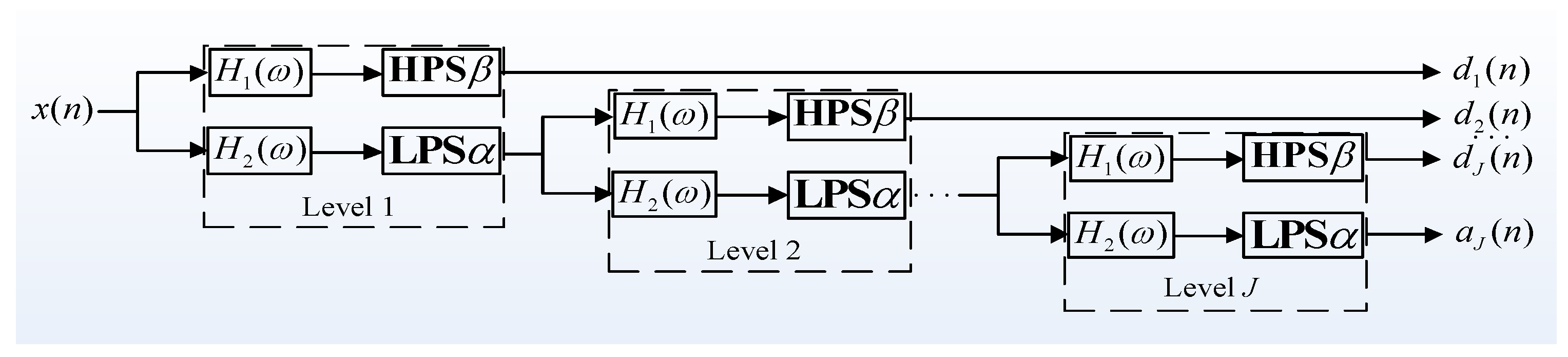
2.2. Basic Theory of RADWT
2.3. Basic Theory of TQWT
3. Resonance-Based Sparse Signal Decomposition
3.1. RSSD Implementation Algorithm
- Step 1
- Input a signal x for decomposition;
- Step 2
- Assisted with a priori information, select suitable Q-factors Q1, and Q2, redundancy factors r1, and r2, and decomposition levels J1, and J2 to construct corresponding wavelet bases S1, S2 via TQWT;
- Step 3
- According to the observation signal noise level, determine suitable weight coefficients and establish Equation (10);
- Step 4
- Solve the optimization problem with SALSA and obtain the optimal coefficient matrixes ;
- Step 5
- Utilize to represent the estimates of high- and low-resonance components with .
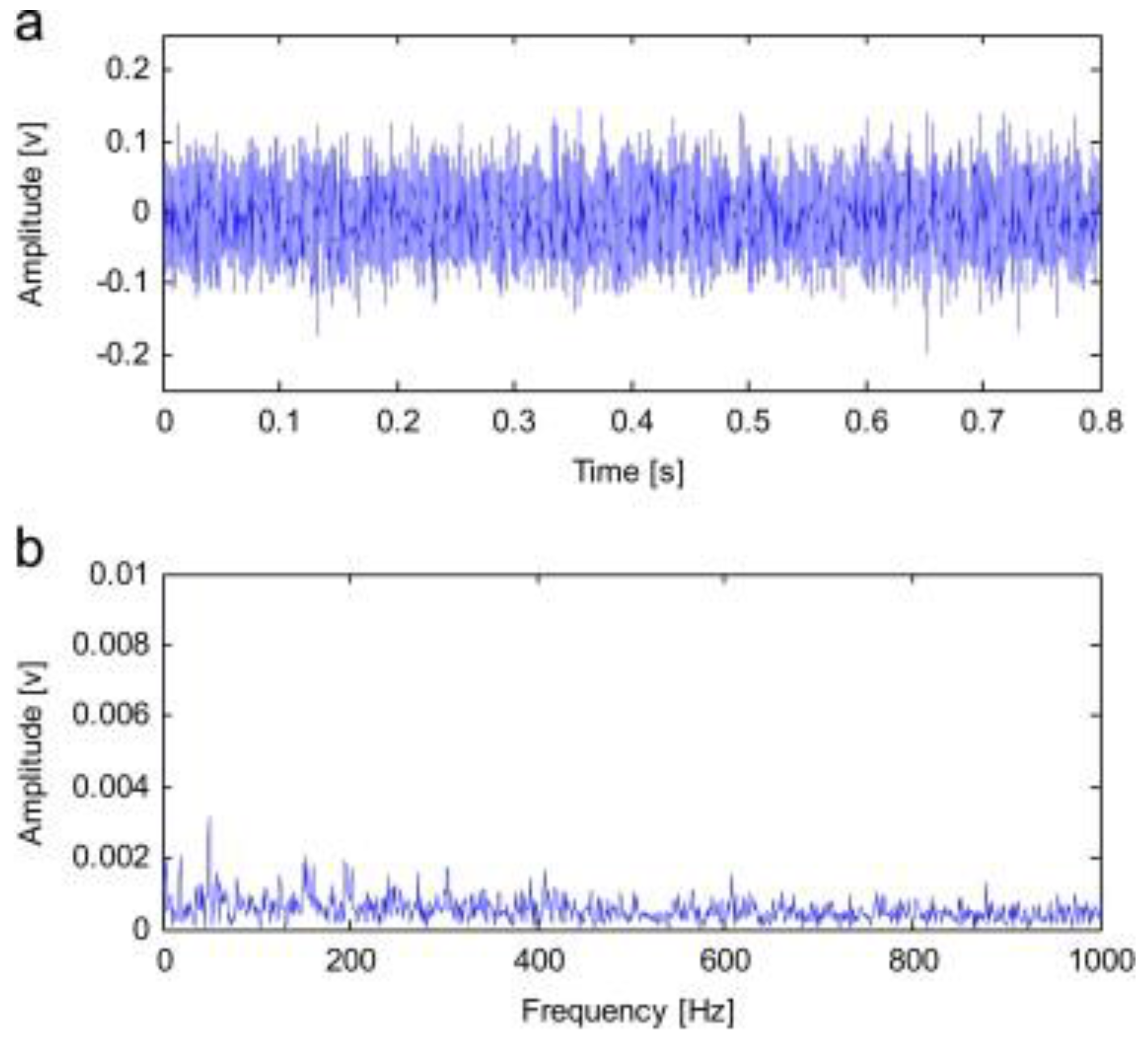
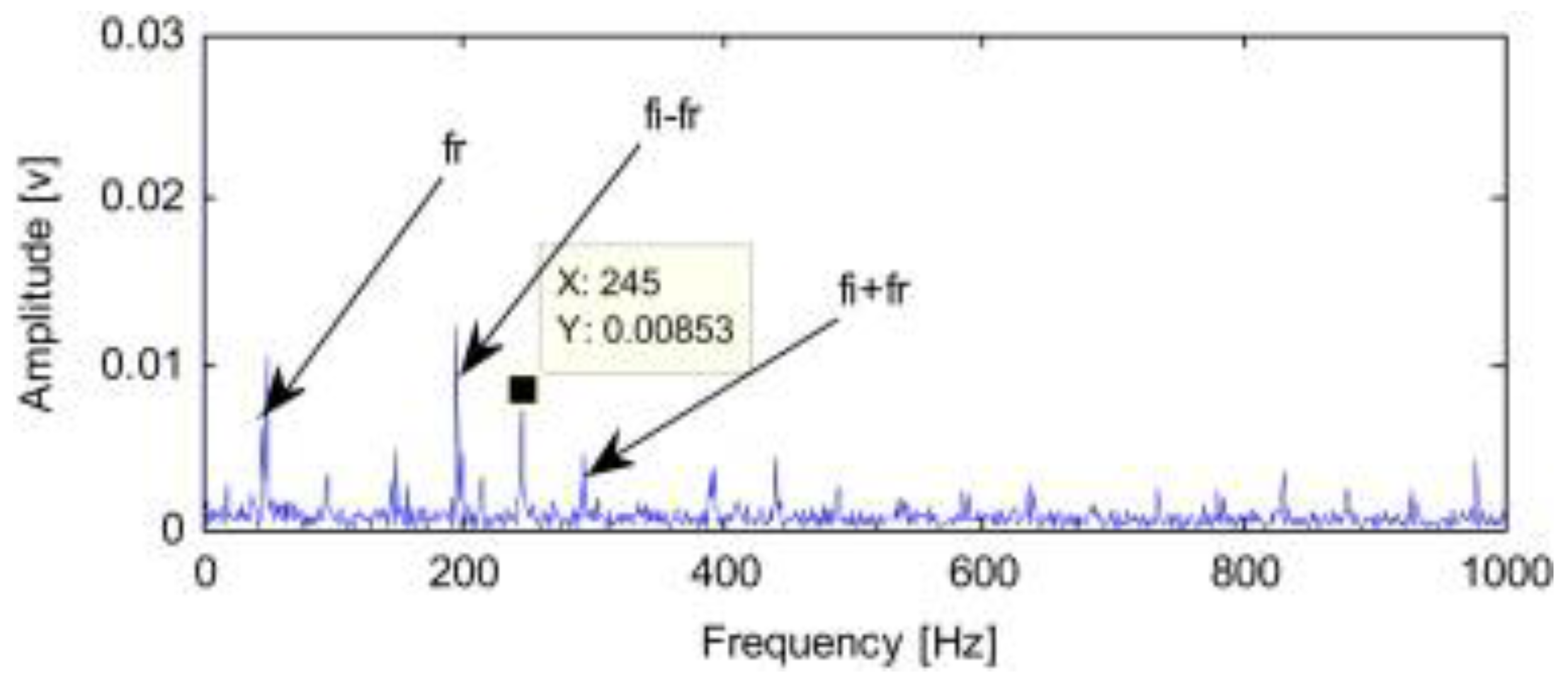
3.2. Illustration of RSSD Performance
3.3. Effects of RSSD Parameters
3.3.1. Effects of Q-Factors
3.3.2. Effects of Weight Coefficients
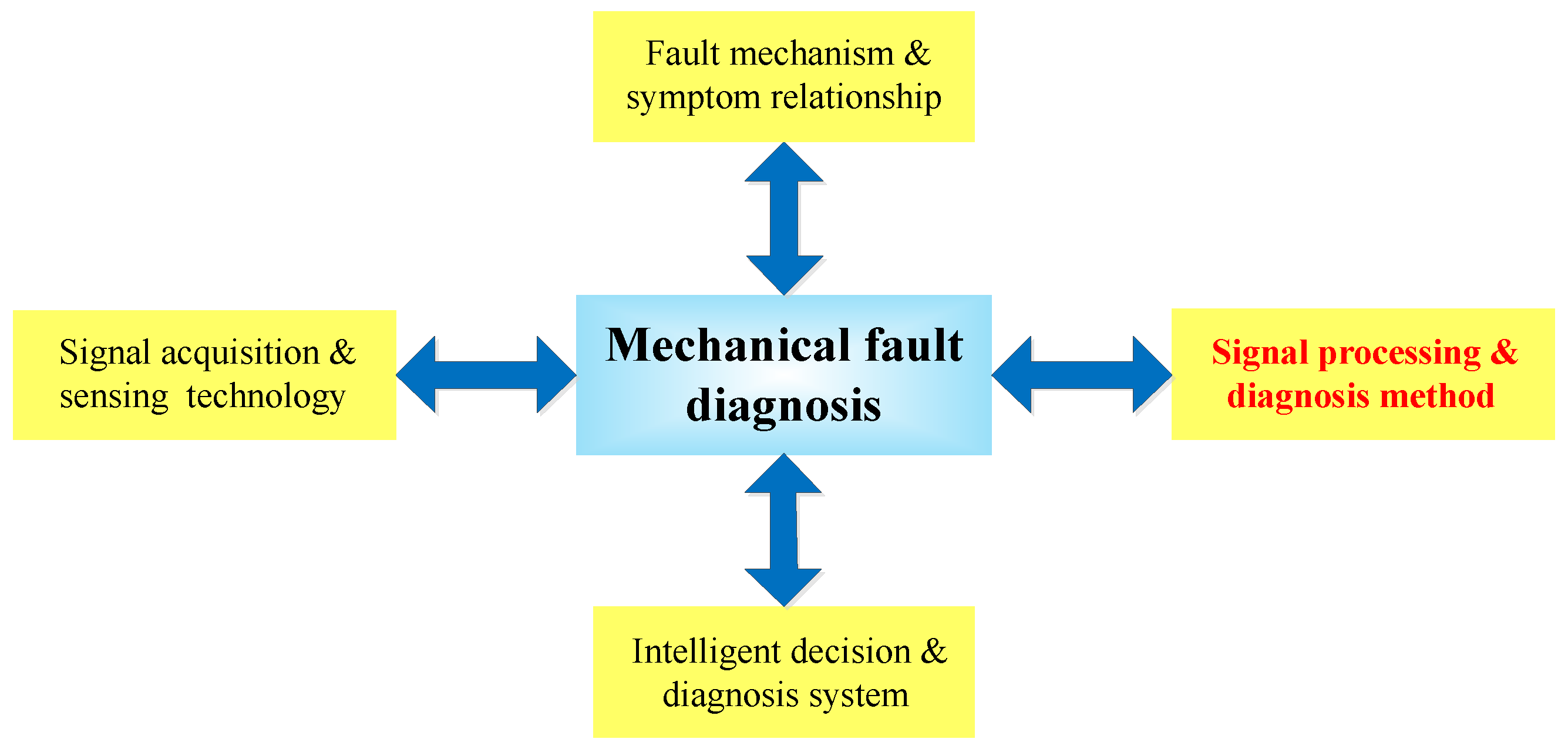
4. Applications of RSSD in Mechanical Fault Diagnosis
4.1. Original RSSD in Mechanical Fault Diagnosis
- (1)
- Construction of wavelet bases;
- (2)
- Optimized selection of numerous decomposition parameters;
- (3)
- Reconstruction of subband signals;
- (4)
- Sparse decomposition of multiple resonances.
4.2. Parameter Optimized RSSD in Mechanical Fault Diagnosis
4.3. Subband Optimized RSSD in Mechanical Fault Diagnosis
4.4. Integrated Optimized RSSD in Mechanical Fault Diagnosis
4.5. RSSD Combined with Other Methods in Mechanical Fault Diagnosis
5. Summary and Discussion
- (1)
- At present, the applications of RSSD mainly focus on crucial industrial components like bearings, gearboxes, and rotors. Through RSSD, a mechanical fault signal is decomposed into the high-resonance component, low-resonance component, and residual, after which fault information can be extracted from these resonance components. In general, RSSD is considered as a powerful and excellent tool for the feature detection of mechanical faults.
- (2)
- It must be stated that mechanical fault impact information will unavoidably scatter in high-resonance components, low-resonance components, and even residual components, due to the inherent coherence. This phenomenon can be thought as a kind of energy leakage. Different scholars are inclined to mine mechanical fault impact information from either high- or low-resonance components. Thankfully, they all have gained satisfactory diagnosis results. In fact, since these two perspective-based mechanical fault-diagnosis methods are both feasible, it is difficult to say that one approach will always outperform the others. Therefore, it is highly advisable to pay closer attention to the high- and low-resonance components simultaneously, as well as to the residual component. Moreover, it is the energy leakage that facilitates our seeking an optimized RSSD to preserve and extract mechanical fault-related information as richly as possible, which will be of great significance for early mechanical fault identification.
- (3)
- To date, one feasible solution to reduce energy leakage and preserve the richest fault features is to optimize RSSD decomposition parameters, mainly including Q-factors and weight coefficients. With a view to these parameters’ significant effects on decomposition results, an artificially selected parameter pair may be not capable of discovering sufficient fault features. Even worse, ill-selected decomposition parameters might yield misleading diagnosis results. To avoid these problems and pursue satisfactory diagnosis, many techniques such as genetic algorithm, kurtosis index, and iterative algorithms, are successively introduced to adaptively acquire optimal Q-factors, weight coefficients, redundancy factors, and decomposition levels. Compared to original RSSD, parameter optimized RSSD can generate resonance components with richer fault impulsive information and less energy leakage, which will make great contributions to diagnostic decision-making.
- (4)
- On the other hand, taking inevitable noise interference into consideration, fault information in resonance components obtained by parameter optimized RSSD may still be masked. As a result, many researchers have applied themselves to the energy distribution and reconstruction of subband signals, for the purpose of suppressing noise. Guided by a common concept, these studies have introduced specific indexes that can reveal fault information richness, and some de-noising techniques, including main subband, NCD, OGS, etc. The subbands with the richest information have been chosen to reconstruct mechanical fault vibration signals. It has been found that reconstructed signals with optimized subbands show outstanding performance in clearly detecting mechanical fault features, because broadband noise is obviously weakened. Moreover, an advanced RSSD, combining both parameter and subband optimization, will certainly perform better in diagnosing incipient mechanical faults than unilateral optimized RSSD, let alone original RSSD.
- (5)
- In early stages of identifying mechanical fault types assisted with RSSD, researchers employed RSSD alone, or optimized it with decomposition parameters and/or subband reconstruction. Recently, many studies attempt to develop superior fault diagnosis approaches by combining standard RSSD with additional techniques, which are attracting more and more attention. For instance, after pre-processing by EEMD, the IMF with the biggest kurtosis value is analyzed for fault feature extraction using RSSD; CS theory is utilized to obtain the sparsest representation of resonance components from compressed samples, which breaks through the limitation of signal length. Successful applications prove that these specific RSSD-based methods can outperform standard RSSD in many applications and provide constructive guidance for diagnosing mechanical faults.
6. Outstanding Issues and Solutions
6.1. Construction of Wavelet Bases
- Establish the dynamic models of mechanical systems and study vibration excitation mechanisms of various mechanical fault types; seek quantitative parameters that can characterize the morphology of fault vibration waveforms so as to reveal the mapping relationships between fault-induced vibration signal waveforms and mechanical fault types;
- On this basis, explore new construction means and construct targeted wavelet bases according to specific mechanical fault types, to make wavelet morphological characteristics match better with practical fault signals.
6.2. Parameter Optimization and Subband Reconstruction
- Thoroughly study parameters’ influences on decomposition results, mainly including the influences of Q-factors and weight coefficients, then set up reasonable indexes to quantitatively evaluate their influence levels;
- Based on quantitative influence levels, study parameters’ coupling effects on RSSD results; establish a multi-parameter fusion optimization problem and take full advantage of multiple optimization ideas to realize the highly efficient optimization of decomposition parameters;
- Research the intrinsic links between fault signal features and subband energy distribution of resulting high- and low-resonance components; then put forward new methods for subband reconstruction to guide the core feature extraction of mechanical fault vibration signals.
6.3. Sparse Decomposition of Multiple Resonances
- Investigate methods that can reduce inherent mutual coherence between resonance components, to promote the effective separation of each resonance component. As is known, mechanical fault-induced periodic signals usually correlate to natural frequency bands of systems, and the energy of resulting resonance components will merely concentrate on some specific subband groups. Considering that different signal components may lead to different frequency bands, a potential means is to utilize the specific subbands corresponding to respective frequency bands for signal decomposition with several resonances, rather than all J-level subbands. In this way, mutual coherence can be effectively dealt with. Additionally, as shown in Figure 4 and Figure 7, there is significant overlap of several adjacent subband responses: a latent scheme guides us to filter out some middle subbands whose frequency range can be filled up with their neighboring subbands. The vacant frequency ranges belonging to the filtered subbands can be prepared for another resonance component’s subbands. In this way, mutual incoherence between each resonance component can be feasibly enhanced. Notably, determining which subbands to filter relies heavily on the calculation of subband fc and BW with Equations (8) and (9), which needs a certain stock of a priori knowledge.
- Establish the optimization problem consisting of multiple resonances and develop a fast algorithm to seek its minimization;
- For potential mechanical fault types and resonances, seek characteristic variables or vectors that can describe mechanical fault vibration waveforms with several similar resonances. This direction offers an opportunity to further distinguish and separate resulting resonance components in view of signal structures.
7. Concluding Remarks
Acknowledgments
Conflicts of Interest
References
- Feng, Z.; Zuo, M.J. Fault diagnosis of planetary gearboxes via torsional vibration signal analysis. Mech. Syst. Signal Process. 2013, 36, 401–421. [Google Scholar] [CrossRef]
- Lei, Y.G.; Lin, J.; He, Z.J.; Zuo, M.J. A review on empirical mode decomposition in fault diagnosis of rotating machinery. Syst. Signal Process. 2013, 35, 108–126. [Google Scholar] [CrossRef]
- Yang, D.S.; Kou, Y.Z.; Tian, H.N. Actuality and development of malfunction diagnosis technology about gear case. Mech. Eng. Autom. 2014, 2, 223–224. [Google Scholar]
- Wang, G.B.; He, Z.J.; Chen, X.F.; Lai, Y.N. Basic research on machinery fault diagnosis—What is the prescription. J. Mech. Eng. 2013, 49, 63–72. [Google Scholar] [CrossRef]
- Márquez, F.P.G.; Tobias, A.M.; Pérez, J.M.P.; Papaelias, M. Condition monitoring of wind turbines: Techniques and methods. Renew. Energy 2012, 46, 169–178. [Google Scholar] [CrossRef]
- Chen, B.Q.; Zhang, Z.S.; Zi, Y.Y.; He, Z.J.; Sun, C. Detecting of transient vibration signatures using an improved fast spatial–spectral ensemble kurtosis kurtogram and its applications to mechanical signature analysis of short duration data from rotating machinery. Mech. Syst. Signal Process. 2013, 40, 1–37. [Google Scholar] [CrossRef]
- Klein, R.; Ingman, D.; Braun, S. Non-stationary signals: Phase-energy approach—Theory and simulations. Mech. Syst. Signal Process. 2001, 15, 1061–1089. [Google Scholar] [CrossRef]
- Zhu, Z.K.; Yan, R.; Luo, L.; Feng, Z.H.; Kong, F.R. Detection of signal transients based on wavelet and statistics for machine fault diagnosis. Mech. Syst. Signal Process. 2009, 23, 1076–1097. [Google Scholar] [CrossRef]
- Wang, W.Y. Early detection of gear tooth cracking using the resonance demodulation technique. Mech. Syst. Signal Process. 2001, 15, 887–903. [Google Scholar] [CrossRef]
- Nikolaou, N.G.; Antoniadis, I.A. Application of morphological operators as envelope extractors for impulsive-type periodic signals. Mech. Syst. Signal Process. 2003, 17, 1147–1162. [Google Scholar] [CrossRef]
- Selesnick, I.W. Resonance-based signal decomposition: A new sparsity-enabled signal analysis method. Signal Process. 2011, 91, 2793–2809. [Google Scholar] [CrossRef]
- Bobin, J.; Starck, J.L.; Fadili, J.M.; Moudden, Y.; Donoho, D.L. Morphological component analysis: An adaptive thresholding strategy. IEEE Trans. Image Process. 2007, 16, 2675–2681. [Google Scholar] [CrossRef] [PubMed]
- Tan, C.T.; Guo, B.; Selesnick, I. Resonance-based decomposition for the manipulation of acoustic cues in speech: An assessment of perceived quality. IEEE Workshop Appl. Signal Process. Audio Acoust. 2011, 333–336. [Google Scholar] [CrossRef]
- Si, T.N.N.; Ng, W.H. Bi-orthogonal rational discrete wavelet transform with multiple regularity orders and application experiments. Signal Process. 2013, 93, 3014–3026. [Google Scholar]
- Chaibi, S.; Lajnef, T.; Kachour, A.; Samet, M. Separation of transient and oscillatory cereberal activities using over-complete rational dilation wavelt transforms. Int. Multi-Conf. Syst. Signals Devices 2011, 1–7. [Google Scholar] [CrossRef]
- Sahbi, C.; Tarek, L.; Zied, S.; Mounir, S.; Abdennaceur, K. A reliable approach to distinguish between transient with and without HFOs using TQWT and MCA. J. Neurosci. Methods 2014, 232, 36–46. [Google Scholar]
- Reddy, G.R.S.; Rao, R. Extraction of fundamental component in power quality application using tunable-Q wavelet transform. Int. J. Signal Process. Image Process. Pattern Recognit. 2016, 9, 355–380. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, Z.M.; Li, T.Y. Low frequency oscillation modal parameter identification using resonance-based sparse signal decomposition and SSI method. Trans. China Electrotech. Soc. 2016, 31, 136–144. [Google Scholar]
- Zhao, Y.; Li, Z.M.; Nie, Y.H. A time-frequency analysis method for low frequency oscillation signals using resonance-based sparse signal decomposition and a frequency slice wavelet transform. Energies 2016, 9, 151. [Google Scholar] [CrossRef]
- Baradarani, A.; Maev, R.G.; Severin, F. Resonance based analysis of acoustic waves for 3D deep-layer fingerprint reconstruction. In Proceedings of the 2013 IEEE International Ultrasonics Symposium (IUS), Prague, Czech Republic, 21–25 July 2013; pp. 713–716. [Google Scholar] [CrossRef]
- Riahi, M.A.; Goudarzi, A. TQWT and WDGA: Innovative methods for ground roll attenuation. J. Geophys. Eng. 2013, 10, 554–579. [Google Scholar]
- Si, T.N.N.; Al-Ashwal, W.A. Sea clutter mitigation using resonance-based signal decomposition. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2257–2261. [Google Scholar]
- Woolford, S.; Burnett, I.S. Multiview 3d profilometry using resonance-based decomposition and three-phase shift profilometry. Int. Conf. Exp. Mech. 2014 2015. [Google Scholar] [CrossRef]
- Bayram, I.; Selesnick, I.W. Overcomplete discrete wavelet transforms with rational dilation factors. IEEE Trans. Signal Process. 2009, 57, 131–145. [Google Scholar] [CrossRef]
- Bayram, I.; Selesnick, I.W. Frequency-domain design of overcomplete rational-dilation wavelet transforms. IEEE Trans. Signal Process. 2009, 57, 2957–2972. [Google Scholar] [CrossRef]
- Selesnick, I.W. Wavelet transform with tunable Q-factor. IEEE Trans. Signal Process. 2011, 59, 3560–3575. [Google Scholar] [CrossRef]
- Selesnick, I.W. Sparse signal representations using the tunable Q-factor wavelet transform. Proc. SPIE Int. Soc. Opt. Eng. 2011, 8138, 815–822. [Google Scholar]
- Afonso, M.V.; Bioucas-Dias, J.M.; Figueiredo, M.A. Fast image recovery using variable splitting and constrained optimization. IEEE Trans. Image Process. 2010, 19, 2345. [Google Scholar] [CrossRef] [PubMed]
- Afonso, M.V.; Bioucas-Dias, J.M.; Figueiredo, M.A.T. An augmented lagrangian approach to the constrained optimization formulation of imaging inverse problems. IEEE Trans. Image Process. 2011, 20, 681–695. [Google Scholar] [CrossRef] [PubMed]
- Bendat, J.S.; Piersol, A.G. Random data: Analysis and measurement procedures. Meas. Sci. Technol. 2000, 1825–1826. [Google Scholar]
- Wang, S.B.; Huang, W.G.; Zhu, Z.K. Transient modeling and parameter identification based on wavelet and correlation filtering for rotating machine fault diagnosis. Mech. Syst. Signal Process. 2011, 25, 1299–1320. [Google Scholar] [CrossRef]
- Chen, X.M.; Yu, D.J.; Luo, J.S. Envelope demodulation method based on resonance-based sparse signal decomposition and its application in roller bearing fault diagnosis. J. Vib. Eng. 2012, 25, 628–636. [Google Scholar]
- Zhang, W.Y.; Yu, D.J.; Chen, X.M. Fault diagnosis of gears based on resonance-based sparse signal decomposition and envelope spectrum. China Mech. Eng. 2013, 24, 3349–3354. [Google Scholar]
- Xiang, W.W.; Cai, G.G.; Fan, W.; Huang, W.; Shang, L.; Zhu, Z. The research of the transient feature extraction by resonance-based method using double-TQWT. Lect. Notes Comput. Sci. 2014, 684–692. [Google Scholar] [CrossRef]
- Xiang, W.W.; Cai, G.G.; Fan, W.; Huang, W.G.; Li, S.; Zhu, Z.K. Transient feature extraction based on double-TQWT and its application in bearing fault diagnosis. J. Vib. Shock 2015, 34, 34–39. [Google Scholar]
- Huang, W.T.; Liu, Y.F.; Niu, P.L.; Wang, W.J. High resonance component of resonance-based sparse decomposition application in extraction of rolling bearing fault information. Adv. Mater. Res. 2013, 753–755, 2290–2296. [Google Scholar] [CrossRef]
- Huang, W.T.; Liu, Y.F.; Li, X.C. Resonance-based sparse decomposition application in extraction of rolling bearing weak fault information. Found. Intell. Syst. 2014, 823–831. [Google Scholar] [CrossRef]
- Cui, L.L.; Wu, N.; Mo, D.Y.; Wang, H.Q.; Chen, P. CQFB and PBP in diagnosis of local gear fault. Adv. Mech. Eng. 2014, 1–12. [Google Scholar] [CrossRef]
- Cui, L.L.; Mo, D.Y.; Wang, J. Composite Q-factor bases and applications to extraction of gear-box weak fault characteristics. J. Beijing Univ. Technol. 2014, 40, 1621–1626. [Google Scholar]
- Zhang, W.Y.; Yu, D.J.; Chen, X.M. Energy operator demodulating of signal’s resonance components for the compound fault diagnosis of gearbox. J. Vib. Eng. 2015, 28, 148–155. [Google Scholar]
- Chen, X.M.; Yu, D.J.; Luo, J.S. Early rub-impact diagnosis of rotors by using resonance-based sparse signal decomposition. China Mech. Eng. 2013, 24, 35–41. [Google Scholar]
- Chen, X.M.; Yu, D.J.; Li, R. Rub-impact diagnosis of rotors with resonance-based sparse signal decomposition and reassigned wavelet scalogram. J. Vib. Shock 2013, 32, 27–33. [Google Scholar]
- Wang, H.C.; Jin, C.; Dong, G.M.; Huo, B.Q.; Xu-Gang, H.U.; Miao, Z. Early rub-impact diagnosis of rotors based on tunable Q-factor wavelet transformation. J. Vib. Shock 2014, 33, 77–80. [Google Scholar]
- Chen, X.F.; Cai, G.G.; Cao, H.R.; Xin, W. Condition assessment for automatic tool changer based on sparsity-enabled signal decomposition method. Mechatronics 2015, 31, 50–59. [Google Scholar] [CrossRef]
- Mo, D.Y.; Cui, L.L.; Wang, J. Sparse signal decomposition method based on the dual Q-factor and its application to rolling bearing early fault diagnosis. J. Mech. Eng. 2013, 49, 37. [Google Scholar] [CrossRef]
- Cui, L.L.; Mo, D.Y.; Wang, H.Q.; Chen, P. Resonance-based nonlinear demodulation analysis method of rolling bearing fault. Adv. Mech. Eng. 2013, 5, 420694. [Google Scholar] [CrossRef]
- Huang, W.T.; Sun, H.J.; Liu, Y.F.; Wang, W.J. Feature extraction for rolling element bearing faults using resonance sparse signal decomposition. Exp. Tech. 2017, 41, 251–265. [Google Scholar] [CrossRef]
- Cai, G.G.; Chen, X.F.; He, Z.J. Sparsity-enabled signal decomposition using tunable Q-factor wavelet transform for fault feature extraction of gearbox. Mech. Syst. Signal Process. 2013, 41, 34–53. [Google Scholar] [CrossRef]
- Huang, W.T.; Fu, Q.; Dou, H.Y.; Dong, Z.Z. Resonance-based sparse signal decomposition based on genetic optimization and its application to composite fault diagnosis of rolling bearings. In Proceedings of the ASME 2015 International Mechanical Engineering Congress and Exposition, Houston, TX, USA, 13–19 November 2015. [Google Scholar]
- Huang, W.T.; Fu, Q.; Dou, H.Y. Resonance-based sparse signal decomposition based on the quality factors optimization and its application of composite fault diagnosis to planetary gearbox. J. Mech. Eng. 2016, 52, 44–51. [Google Scholar] [CrossRef]
- Li, X.; Yu, D.J.; Zhang, D.C. Fault diagnosis of rolling bearings based on the resonance-based sparse signal decomposition with optimal Q-factor. J. Vib. Eng. 2015, 28, 998–1005. [Google Scholar]
- Zhang, D.C.; Yu, D.J.; Zhang, W.Y. Energy operator demodulating of optimal resonance components for the compound faults diagnosis of gearboxes. Meas. Sci. Technol. 2015, 26, 115003. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Bo, Q.L.; Liu, H.B.; Lian, M.; Wang, F.B.; Zhang, J. Full-oscillatory components decomposition from noisy machining vibration signals by minimizing the Q-factor variation. Trans. Inst. Meas. Control 2016. [Google Scholar] [CrossRef]
- Shi, J. Morphology-Based Fault Feature Extraction and Resampling-Free Fault Identification Techniques for Rolling Element Bearing Condition Monitoring. Ph.D. Thesis, University of Ottawa, Ottawa, ON, Canada, 2015. [Google Scholar]
- Shi, J.; Liang, M. Intelligent bearing fault signature extraction via iterative oscillatory behavior based signal decomposition (IOBSD). Expert Syst. Appl. 2016, 45, 40–55. [Google Scholar] [CrossRef]
- Zhang, D.C.; Yu, D.J.; Li, X. Fault diagnosis of rolling bearing based on tunable-Q wavelet reconstruction. J. Aerosp. Power 2015, 30, 3051–3057. [Google Scholar]
- Luo, J.S.; Yu, D.J.; Liang, M. A kurtosis-guided adaptive demodulation technique for bearing fault detection based on tunable-Q wavelet transform. Meas. Sci. Technol. 2013, 24, 055009. [Google Scholar] [CrossRef]
- Tang, G.J.; Wang, X.L. Application of tunable Q-factor wavelet transform to feature extraction of weak fault for rolling bearing. Proc. CSEE 2016, 36, 746–754. [Google Scholar]
- Cai, T.T.; Silverman, B.W. Incorporating information on neighbouring coefficients into wavelet estimation. Sankhyā Indian J. Stat. Ser. B 2001, 63, 127–148. [Google Scholar]
- He, W.P.; Zi, Y.Y.; Chen, B.Q.; Shuai, W.; He, Z.J. Tunable Q-factor wavelet transform denoising with neighboring coefficients and its application to rotating machinery fault diagnosis. Sci. China Technol. Sci. 2013, 56, 1956–1965. [Google Scholar] [CrossRef]
- Chen, P.Y.; Selesnick, I.W. Overlapping Group Shrinkage/Thresholding and Denoising; Technical Report; Polytechnic Institute of New York University: New York, NY, USA, 2012. [Google Scholar]
- He, W.P.; Zi, Y.Y. Sparsity-assisted signal representation for rotating machinery fault diagnosis using the tunable Q-factor wavelet transform with overlapping group shrinkage. In Proceedings of the 2014 International Conference on Wavelet Analysis and Pattern Recognition (ICWAPR), Lanzhou, China, 13–16 July 2014; pp. 18–23. [Google Scholar] [CrossRef]
- He, W.P.; Zi, Y.Y.; Chen, B.Q.; Wu, F.; He, Z.J. Automatic fault feature extraction of mechanical anomaly on induction motor bearing using ensemble super-wavelet transform. Mech. Syst. Signal Process. 2014, 54, 457–480. [Google Scholar] [CrossRef]
- He, W.P.; Zi, Y.Y.; Wan, Z.G.; Chen, B.Q. Improved ensemble super-wavelet transform for vibration-based machinery fault diagnosis. J. Manuf. Sci. Eng. 2016, 138, 071012. [Google Scholar] [CrossRef]
- He, W.P.; Zi, Y.Y.; Chen, B.Q.; Yao, B.; Zhang, Z.S. Periodic sparsity oriented super-wavelet analysis with application to motor bearing fault detection of wind turbine. J. Mech. Eng. 2016, 52, 41. [Google Scholar] [CrossRef]
- Yu, F.J.; Zhou, F.X. Bearing early faults diagnosis based on tunable Q-factor wavelet transform and spectral kurtosis. J. Central South Univ. Sci. Technol. 2015, 11, 4122–4128. [Google Scholar]
- Sun, Y.S.; Yu, D.J.; Chen, X.M.; Li, R. Order domain analysis based on resonance-based sparse signal decomposition and its application to gear fault diagnosis. J. Vib. Shock 2013, 32, 88–94. [Google Scholar]
- Wang, H.C.; Chen, J.; Dong, G.M. Feature extraction of rolling bearing’s early weak fault based on EEMD and tunable Q-factor wavelet transform. Mech. Syst. Signal Process. 2014, 48, 103–119. [Google Scholar] [CrossRef]
- Mo, D.Y.; Cui, L.L.; Wang, J.; Gao, L.X. Application of parallel dual-Q-factors in extraction and blind separation of gearbox composite faults. Chin. J. Sci. Instrum. 2013, 34, 2013–2020. [Google Scholar]
- Luo, J.S.; Yu, D.J.; Liang, M. Enhancement of oil particle sensor capability via resonance-based signal decomposition and fractional calculus. Measurement 2015, 76, 240–254. [Google Scholar] [CrossRef]
- Wang, H.; Ke, Y.; Song, L.; Gang, T.; Peng, C. A sparsity-promoted decomposition for compressed fault diagnosis of roller bearings. Sensors 2016, 16, 1524. [Google Scholar] [CrossRef] [PubMed]
- Gan, M.; Wang, C.; Zhu, C.A. Fault feature enhancement for rotating machinery based on quality factor analysis and manifold learning. J. Intell. Manuf. 2015, 1–18. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, X.; Du, Z.; Yan, R. Kurtosis based weighted sparse model with convex optimization technique for bearing fault diagnosis. Mech. Syst. Signal Process. 2016, 80, 349–376. [Google Scholar] [CrossRef]
- Wang, C.; Gan, M.; Zhu, C.A. Intelligent fault diagnosis of rolling element bearings using sparse wavelet energy based on overcomplete DWT and basis pursuit. J. Intell. Manuf. 2015. [Google Scholar] [CrossRef]





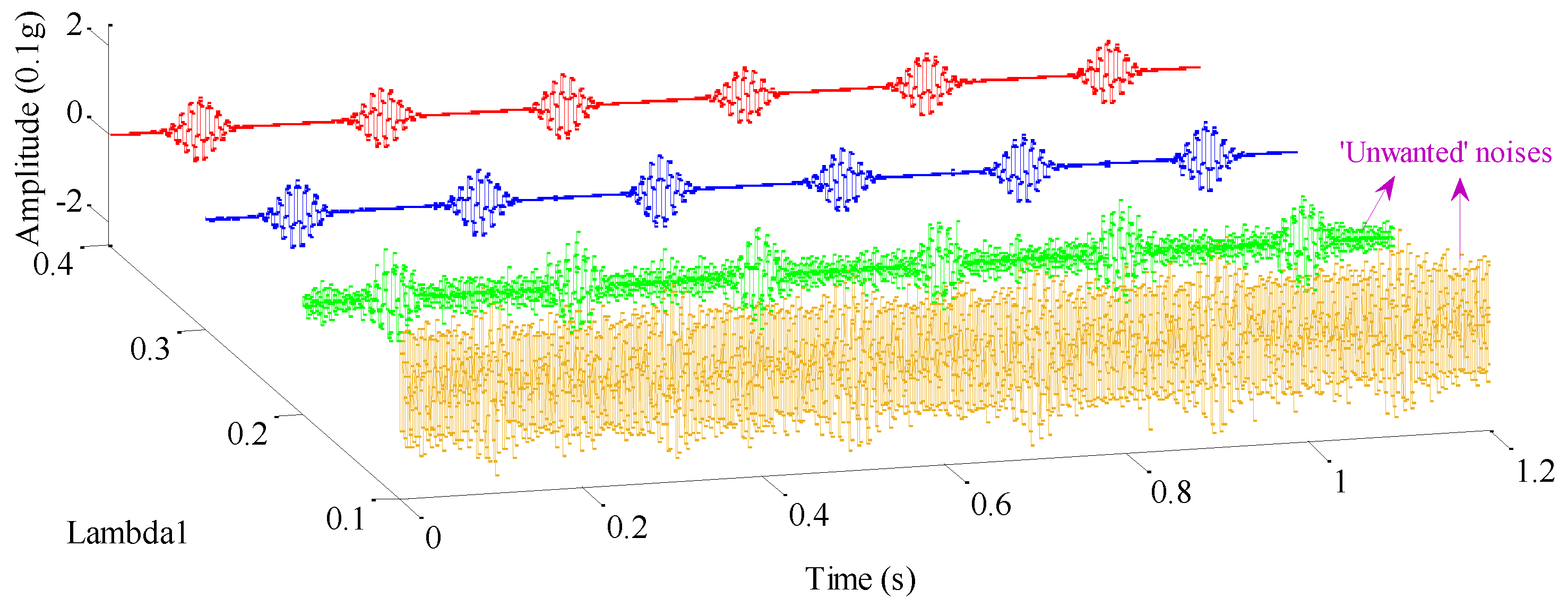
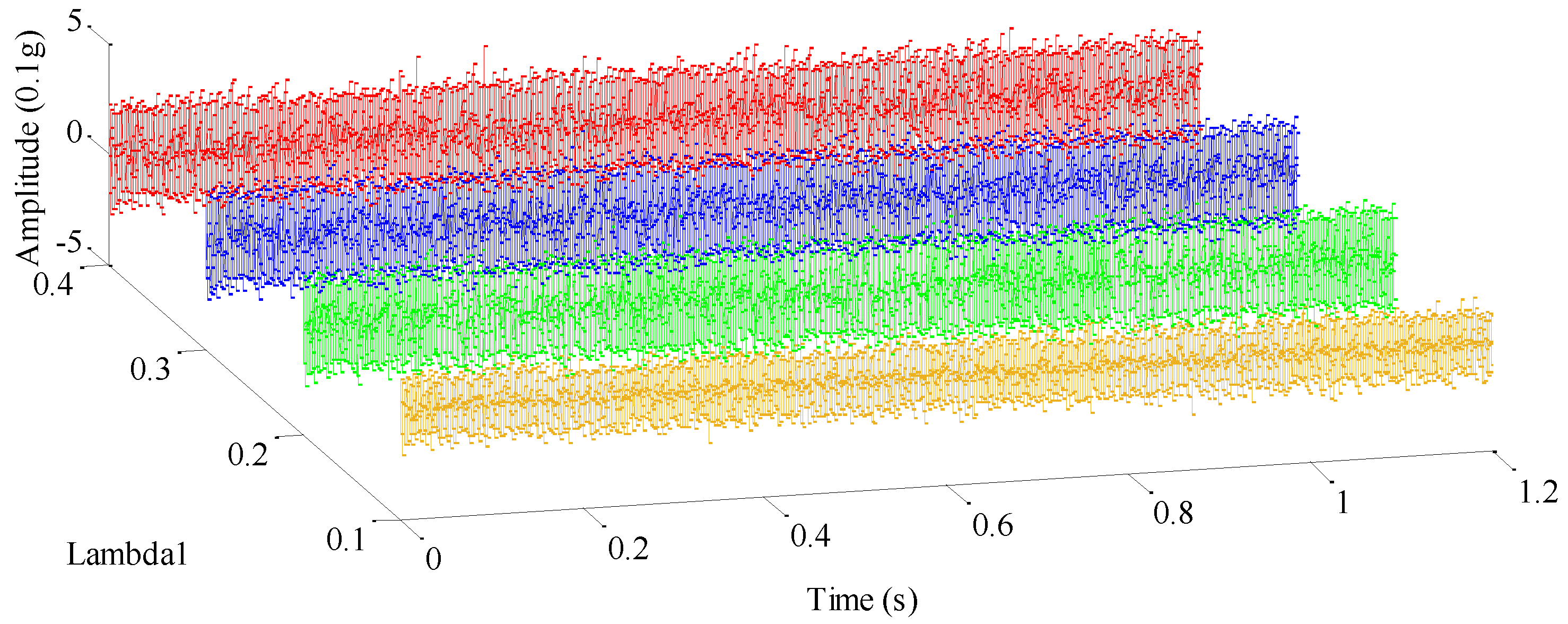
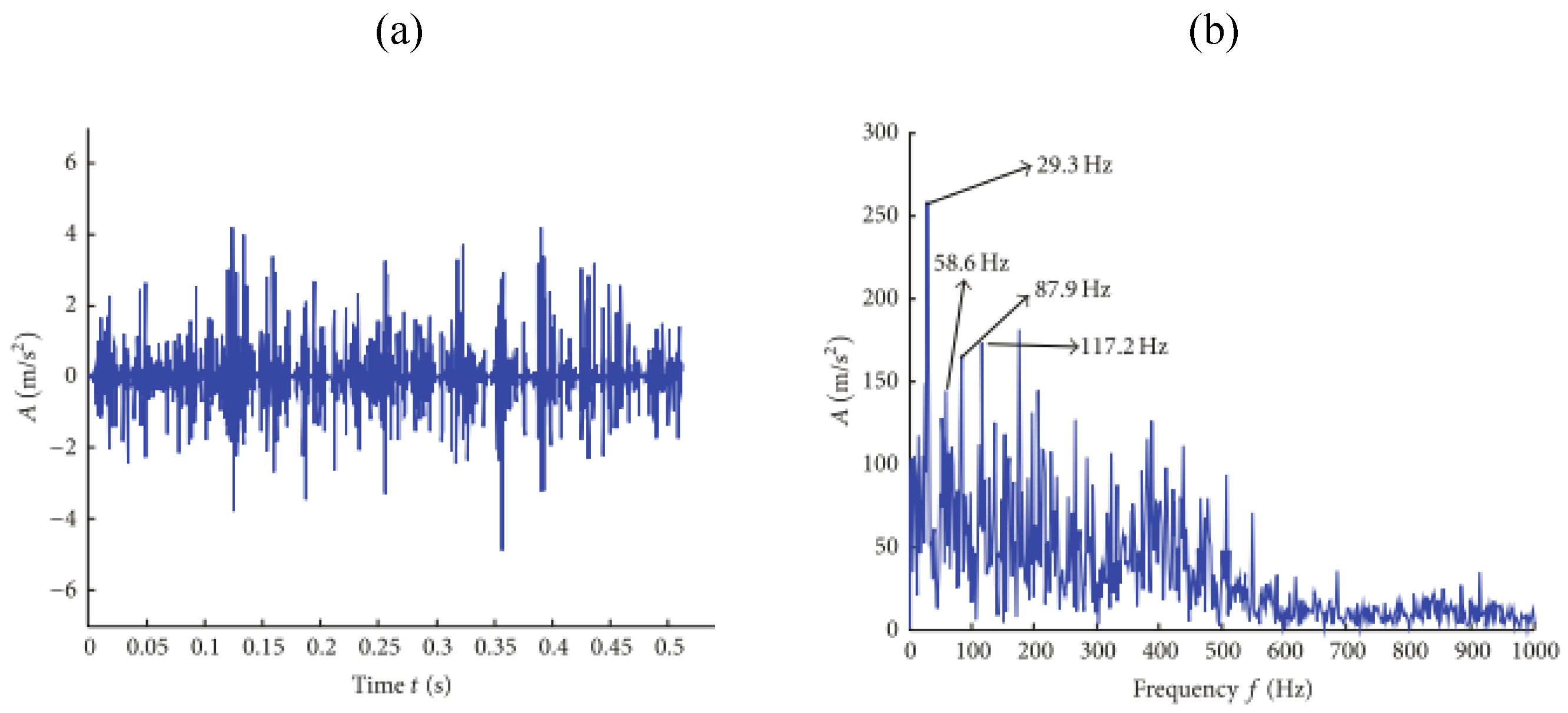
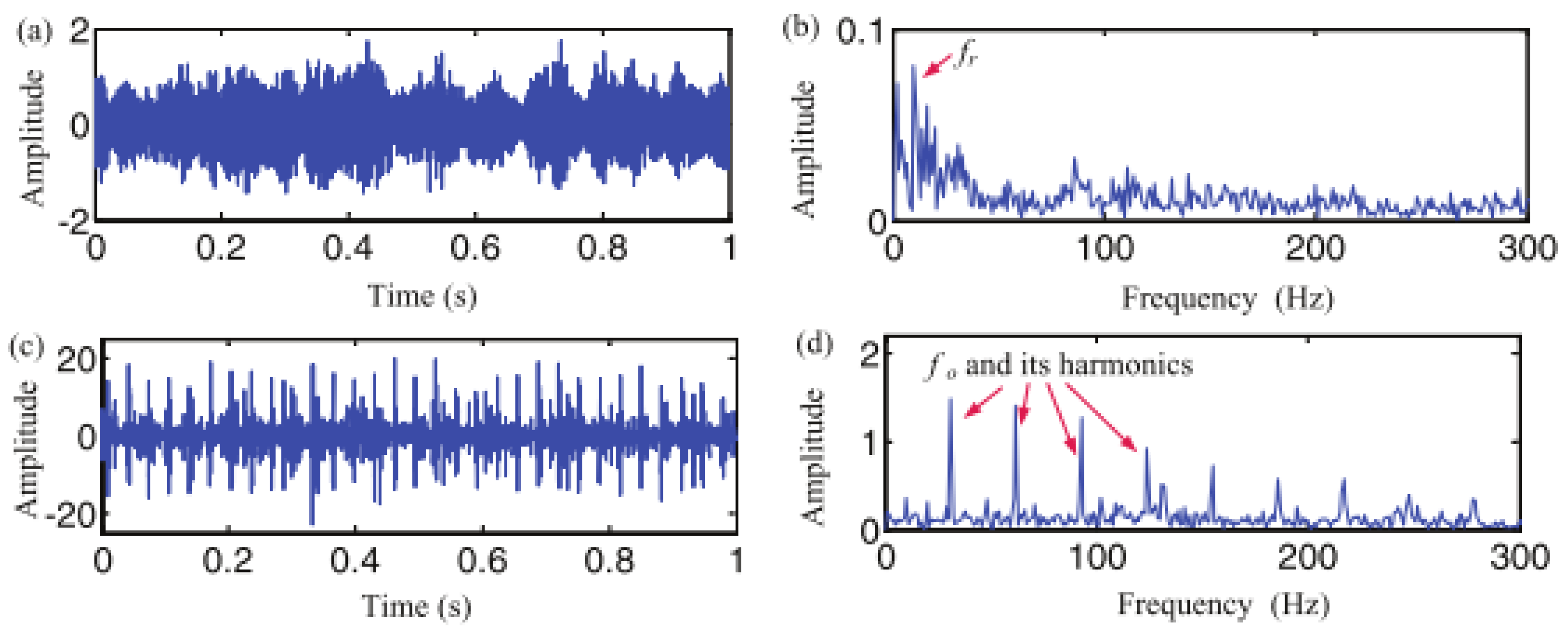




| Parameter | Symbol | Function Description |
|---|---|---|
| Quality factor | Q | Resonance degree |
| Redundancy factor | R | Overlapping rate between subband frequency responses |
| Decomposition level | J | Decomposition frequency range |
| Q1 | Q2 | Correlation Coefficient | Correlation Coefficient |
|---|---|---|---|
| (High) | (Low) | ||
| 2 | 1 | 0.3067 | 0.9710 |
| 3 | 1 | 0.3072 | 0.9656 |
| 4 | 1 | 0.3072 | 0.9703 |
| 5 | 1 | 0.3068 | 0.9710 |
| 6 | 1 | 0.3065 | 0.9721 |
| 7 | 1 | 0.3063 | 0.9730 |
| 8 | 1 | 0.3063 | 0.9743 |
| 9 | 1 | 0.3059 | 0.9754 |
| Correlation Coefficient | Correlation Coefficient | ||
|---|---|---|---|
| (High) | (Low) | ||
| 0.1 | 0.1 | 0.9182 | 0.8351 |
| 0.2 | 0.1 | 0.3856 | 0.9622 |
| 0.3 | 0.1 | 0.3072 | 0.9703 |
| 0.4 | 0.1 | 0.3057 | 0.9745 |
| 0.5 | 0.1 | 0.3053 | 0.9792 |
| 0.6 | 0.1 | 0.3048 | 0.9838 |
| 0.7 | 0.1 | 0.3041 | 0.9882 |
| 0.8 | 0.1 | 0.3032 | 0.9920 |
| Category | Objects | Supporting Techniques | References |
|---|---|---|---|
| Original RSSD | Bearing | None | [32,34,35,36,37] |
| Gearbox | None | [33,38,39,40] | |
| Rotor | None | [41,42,43] | |
| Others | None | [44] | |
| Parameter optimized RSSD | Bearing | Qualitative analysis | [45,46,47] |
| GA | [49,51] | ||
| Iteration | [54,55] | ||
| Gearbox | Evaluation index | [48] | |
| GA | [50,52] | ||
| Others | Iteration | [53] | |
| Subband optimized RSSD | Bearing | Main subband | [47] |
| Kurtosis | [56,57,58] | ||
| NCD | [60] | ||
| OGS | [62] | ||
| Gearbox | NCD | [60] | |
| Integrated optimized RSSD | Bearing | ESW | [63] |
| Improved ESW | [64] | ||
| PSOSW | [65] | ||
| Kurtosis, NCD | [66] | ||
| RSSD combined with others | Bearing | EEMD | [68] |
| FastICA | [69] | ||
| CS | [71] | ||
| Manifold learning | [72] | ||
| Kurtosis | [73] | ||
| PCA, SWE, Classifier | [74] | ||
| Gearbox | Chirplet path pursuit | [67] | |
| Oil | Fractional calculus | [70] |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, W.; Sun, H.; Wang, W. Resonance-Based Sparse Signal Decomposition and its Application in Mechanical Fault Diagnosis: A Review. Sensors 2017, 17, 1279. https://doi.org/10.3390/s17061279
Huang W, Sun H, Wang W. Resonance-Based Sparse Signal Decomposition and its Application in Mechanical Fault Diagnosis: A Review. Sensors. 2017; 17(6):1279. https://doi.org/10.3390/s17061279
Chicago/Turabian StyleHuang, Wentao, Hongjian Sun, and Weijie Wang. 2017. "Resonance-Based Sparse Signal Decomposition and its Application in Mechanical Fault Diagnosis: A Review" Sensors 17, no. 6: 1279. https://doi.org/10.3390/s17061279





