Measuring Tree Properties and Responses Using Low-Cost Accelerometers
Abstract
:1. Introduction
2. Materials and Methods
2.1. Theory
2.2. Sensor Description
2.3. Measurement Setup and Protocol
2.4. Data Processing
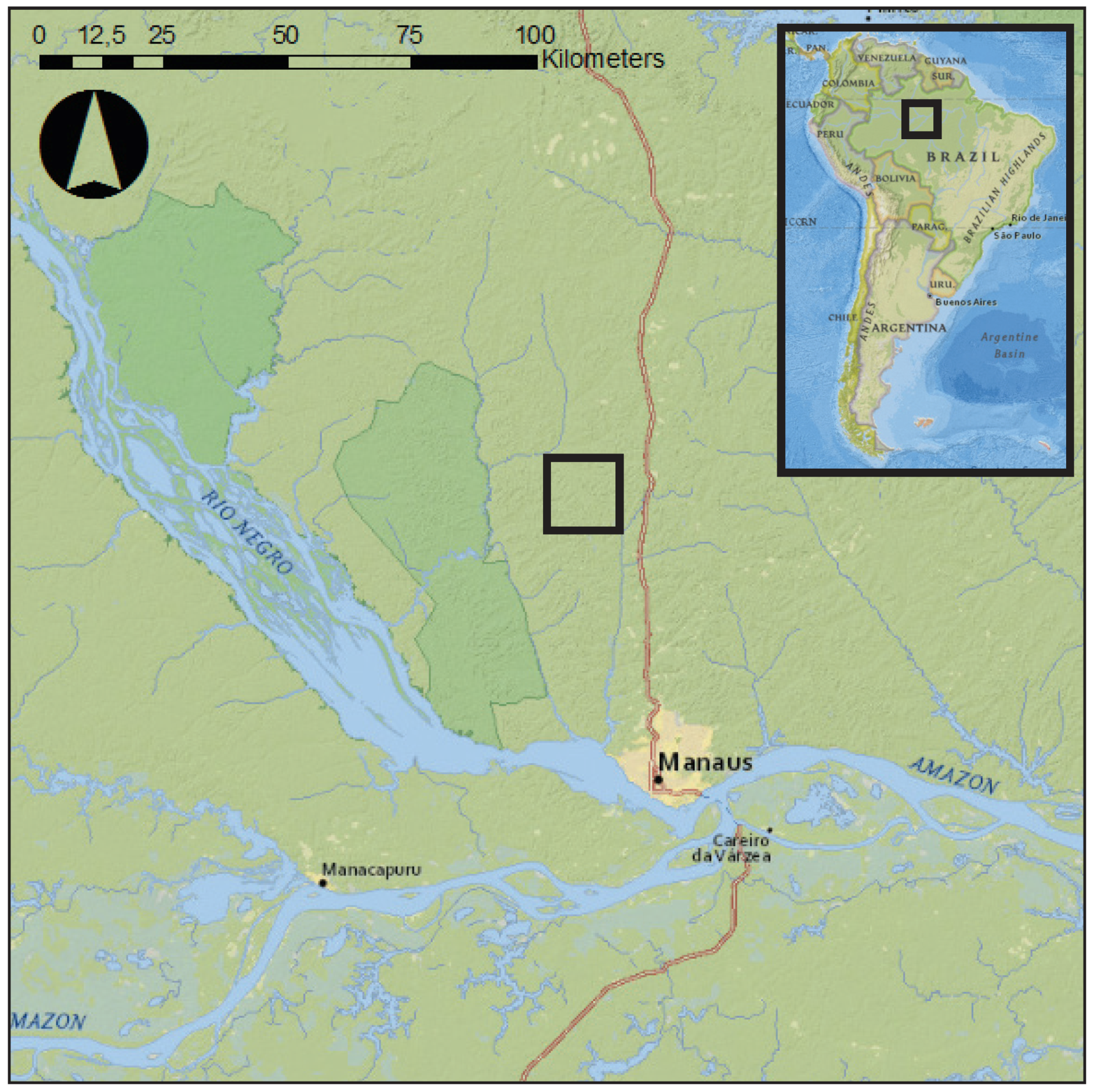
2.5. Case Study Field Site and Plant Material
3. Results and Discussion
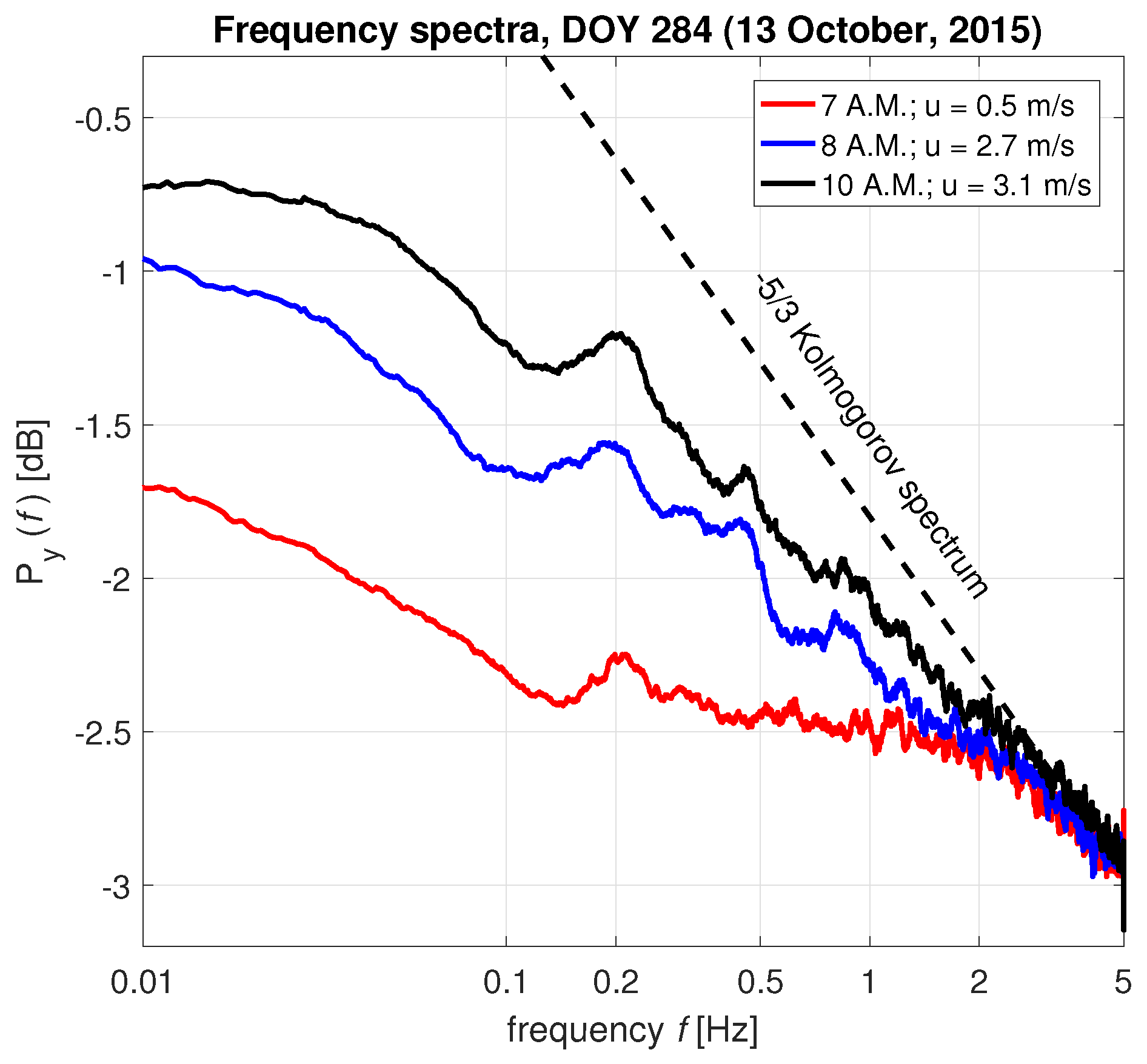
3.1. Interpretation of the Spectrum
3.2. Tree Mass
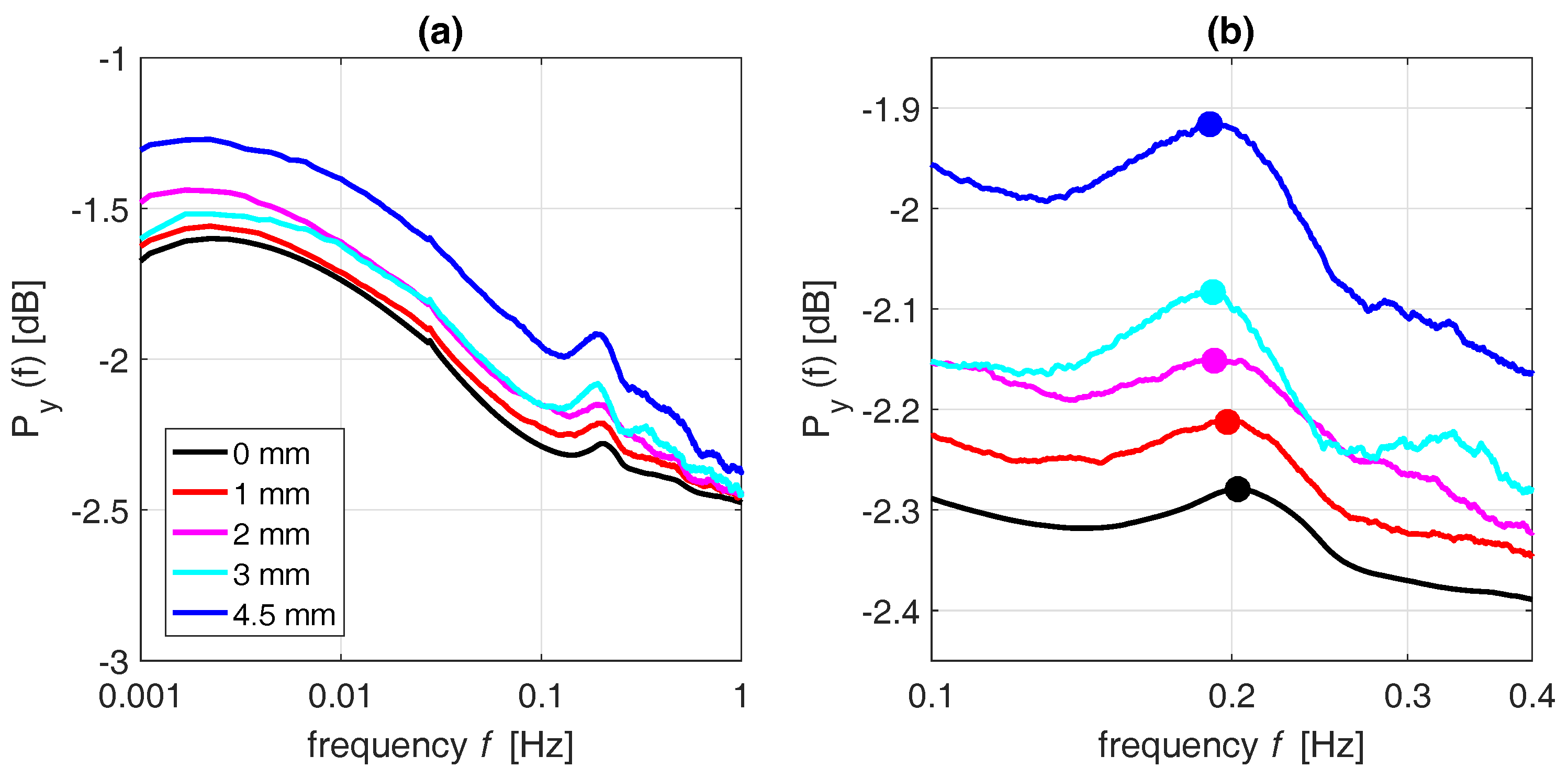
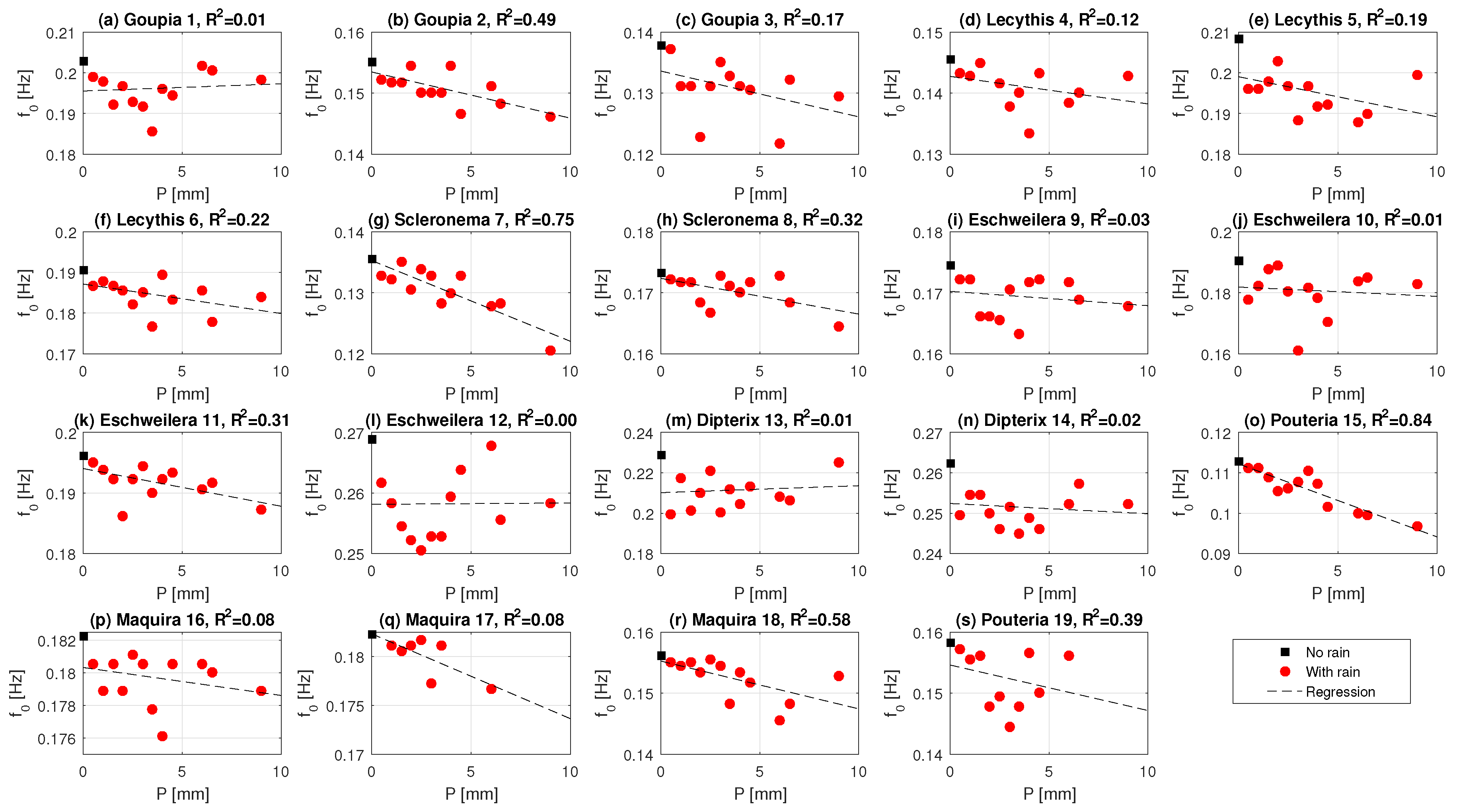
3.3. Effect of Precipitation
3.4. Energy Transfer from Wind to Tree Sway
3.5. Synthesis and Outlook
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Reichstein, M.; Bahn, M.; Ciais, P.; Frank, D.; Mahecha, M.D.; Seneviratne, S.I.; Zscheischler, J.; Beer, C.; Buchmann, N.; Frank, D.C.; et al. Climate extremes and the carbon cycle. Nature 2013, 500, 287–295. [Google Scholar] [CrossRef] [PubMed]
- Schlesinger, W.H.; Jasechko, S. Transpiration in the global water cycle. Agric. For. Meteorol. 2014, 189, 115–117. [Google Scholar] [CrossRef]
- Patton, E.G.; Sullivan, P.P.; Shaw, R.H.; Finnigan, J.J.; Weil, J.C. Atmospheric Stability Influences on Coupled Boundary Layer and Canopy Turbulence. J. Atmos. Sci. 2016, 73, 1621–1647. [Google Scholar] [CrossRef]
- Jasechko, S.; Sharp, Z.D.; Gibson, J.J.; Birks, S.J.; Yi, Y.; Fawcett, P.J. Terrestrial water fluxes dominated by transpiration. Nature 2013, 496, 347–350. [Google Scholar] [CrossRef] [PubMed]
- Gerrits, A.M.J. The Role of Interception in the Hydrological Cycle; TU Delft, Delft University of Technology: Delft, The Netherlands, 2010. [Google Scholar]
- Gerrits, A.; Savenije, H. Interception. In Treatise on Water Science; Wilderer, P., Ed.; Elsevier: Oxford, UK, 2011; pp. 89–101. [Google Scholar]
- Baldocchi, D.D.; Luxmoore, R.J.; Hatfield, J.L. Discerning the forest from the trees: An essay on scaling canopy stomatal conductance. Agric. For. Meteorol. 1991, 54, 197–226. [Google Scholar] [CrossRef]
- Hollinger, D.; Kelliher, F.; Byers, J.; Hunt, J.; McSeveny, T.; Weir, P. Carbon dioxide exchange between an undisturbed old-growth temperate forest and the atmosphere. Ecology 1994, 75, 134–150. [Google Scholar] [CrossRef]
- Sellers, P.; Dickinson, R.; Randall, D.; Betts, A.; Hall, F.; Berry, J.; Collatz, G.; Denning, A.; Mooney, H.; Nobre, C.; et al. Modeling the exchanges of energy, water, and carbon between continents and the atmosphere. Science 1997, 275, 502–509. [Google Scholar] [CrossRef] [PubMed]
- Baldocchi, D.D.; Amthor, J.S. Canopy photosynthesis: History. In Terrestrial Global Productivity; Academic Press: New York, NY, USA, 2001; pp. 9–31. [Google Scholar]
- Thuiller, W.; Lavergne, S.; Roquet, C.; Boulangeat, I.; Lafourcade, B.; Araujo, M.B. Consequences of climate change on the tree of life in Europe. Nature 2011, 470, 531–534. [Google Scholar] [CrossRef] [PubMed]
- Lindner, M.; Fitzgerald, J.B.; Zimmermann, N.E.; Reyer, C.; Delzon, S.; van der Maaten, E.; Schelhaas, M.J.; Lasch, P.; Eggers, J.; van der Maaten-Theunissen, M.; et al. Climate change and European forests: What do we know, what are the uncertainties, and what are the implications for forest management? J. Environ. Manag. 2014, 146, 69–83. [Google Scholar] [CrossRef] [PubMed]
- Lawrence, D.; Vandecar, K. Effects of tropical deforestation on climate and agriculture. Nat. Clim. Chang. 2015, 5, 27–36. [Google Scholar] [CrossRef]
- Stephenson, N.L.; Das, A.; Condit, R.; Russo, S.; Baker, P.; Beckman, N.; Coomes, D.; Lines, E.; Morris, W.; Rüger, N.; et al. Rate of tree carbon accumulation increases continuously with tree size. Nature 2014, 507, 90–93. [Google Scholar] [CrossRef] [PubMed]
- Steele-Dunne, S.C.; Friesen, J.; van de Giesen, N. Using Diurnal Variation in Backscatter to Detect Vegetation Water Stress. IEEE Trans. Geosci. Remote Sens. 2012, 50, 2618–2629. [Google Scholar] [CrossRef]
- Van Emmerik, T.; Steele-Dunne, S.C.; Judge, J.; van de Giesen, N. Impact of Diurnal Variation in Vegetation Water Content on Radar Backscatter From Maize During Water Stress. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3855–3869. [Google Scholar] [CrossRef]
- Van Emmerik, T.; Steele-Dunne, S.; Judge, J.; van de Giesen, N. Dielectric Response of Corn Leaves to Water Stress. IEEE Geosci. Remote Sens. Lett. 2017, 14, 8–12. [Google Scholar] [CrossRef]
- Huete, A.R.; Didan, K.; Shimabukuro, Y.E.; Ratana, P.; Saleska, S.R.; Hutyra, L.R.; Yang, W.; Nemani, R.R.; Myneni, R. Amazon rainforests green-up with sunlight in dry season. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Morton, D.C.; Nagol, J.; Carabajal, C.C.; Rosette, J.; Palace, M.; Cook, B.D.; Vermote, E.F.; Harding, D.J.; North, P.R. Amazon forests maintain consistent canopy structure and greenness during the dry season. Nature 2014, 506, 221–224. [Google Scholar] [CrossRef] [PubMed]
- Soudani, K.; François, C. Remote sensing: A green illusion. Nature 2014, 506, 165–166. [Google Scholar] [CrossRef] [PubMed]
- Helfter, C.; Shephard, J.D.; Martínez-Vilalta, J.; Mencuccini, M.; Hand, D.P. A noninvasive optical system for the measurement of xylem and phloem sap flow in woody plants of small stem size. Tree Physiol. 2007, 27, 169–179. [Google Scholar] [CrossRef] [PubMed]
- Drew, D.M.; Downes, G.M. The use of precision dendrometers in research on daily stem size and wood property variation: A review. Dendrochronologia 2009, 27, 159–172. [Google Scholar] [CrossRef]
- Gerrits, A.; Savenije, H.; Hoffmann, L.; Pfister, L. New technique to measure forest floor interception: An application in a beech forest in Luxembourg. Hydrol. Earth Syst. Sci. 2007, 11, 695–701. [Google Scholar] [CrossRef]
- Mayhead, G. Some drag coefficients for British forest trees derived from wind tunnel studies. Agric. Meteorol. 1973, 12, 123–130. [Google Scholar] [CrossRef]
- Koizumi, A.; Motoyama, J.I.; Sawata, K.; Sasaki, Y.; Hirai, T. Evaluation of drag coefficients of poplar-tree crowns by a field test method. J. Wood Sci. 2010, 56, 189–193. [Google Scholar] [CrossRef]
- Burgess, S.S.; Adams, M.A.; Turner, N.C.; Beverly, C.R.; Ong, C.K.; Khan, A.A.; Bleby, T.M. An improved heat pulse method to measure low and reverse rates of sap flow in woody plants. Tree Physiol. 2001, 21, 589–598. [Google Scholar] [CrossRef] [PubMed]
- Moore, J.R.; Maguire, D.A. Natural sway frequencies and damping ratios of trees: Concepts, review and synthesis of previous studies. Trees 2004, 18, 195–203. [Google Scholar] [CrossRef]
- Amtmann, R. Data acquisition system for wind induced tree vibration. In The Forest-Atmosphere Interaction; Springer: New York, NY, USA, 1985; pp. 149–159. [Google Scholar]
- Mayer, H. Wind-induced tree sways. Trees 1987, 1, 195–206. [Google Scholar] [CrossRef]
- Gardiner, B. The interactions of wind and tree movement in forest canopies. In Wind and Trees; Cambridge University Press: Cambridge, UK, 1995; pp. 41–59. [Google Scholar]
- Peltola, H. Swaying of trees in response to wind and thinning in a stand of Scots pine. Bound. Layer Meteorol. 1996, 77, 285–304. [Google Scholar] [CrossRef]
- Hassinen, A.; Lemettinen, M.; Peltola, H.; Kellomäki, S.; Gardiner, B. A prism-based system for monitoring the swaying of trees under wind loading. Agric. For. Meteorol. 1998, 90, 187–194. [Google Scholar] [CrossRef]
- Flesch, T.K.; Wilson, J.D. Wind and remnant tree sway in forest cutblocks. II. Relating measured tree sway to wind statistics. Agric. For. Meteorol. 1999, 93, 243–258. [Google Scholar] [CrossRef]
- Lohou, F.; Lopez, A.; Druilhet, A.; Brunet, Y.; Irvine, M.; Lamaud, E. The VENFOR Project: Response of a homogeneous forest canopy to wind stress through the analysis of accelerometer measurements. In Proceedings of the Wind Effects on Trees; University of Karlsruhe: Karlsruhe, Germany, 2003; pp. 109–116. [Google Scholar]
- Sellier, D.; Brunet, Y.; Fourcaud, T. A numerical model of tree aerodynamic response to a turbulent airflow. Forestry 2008, 81, 279–297. [Google Scholar] [CrossRef]
- Schindler, D.; Schönborn, J.; Fugmann, H.; Mayer, H. Responses of an individual deciduous broadleaved tree to wind excitation. Agric. For. Meteorol. 2013, 177, 69–82. [Google Scholar] [CrossRef]
- Selker, J.; Lane, J.; Rupp, D.; Hut, R.; Abou Najm, M.; Stewart, R.; van de Giesen, N.; Selker, F. The answer is blowing in the wind: Using wind induced resonance of trees to measure time varying canopy mass, including interception. In Proceedings of the AGU Fall Meeting Abstracts, San Francisco, CA, USA, 5–9 December 2011; Volume 1, p. 1155. [Google Scholar]
- Stewart, R.D.; Hut, R.; Rupp, D.E.; Gupta, H.; Selker, J.S. A resonating rainfall and evaporation recorder. Water Resour. Res. 2012, 48, W08601. [Google Scholar] [CrossRef]
- Llamas, R.; Niemeier, J.; Kruger, A.; Lintz, H.; Kleinknecht, G.; Miller, R. Diurnal cycles of tree mass obtained using accelerometers. In Proceedings of the AGU Fall Meeting Abstracts, San Francisco, CA, USA, 9–13 December 2013; Volume 1, p. 1575. [Google Scholar]
- Slayter, R. Plant-Water Relationships; Springer: Dordrecht, The Netherlands, 1967. [Google Scholar]
- Hsiao, T.C. Plant responses to water stress. Annu. Rev. Plant Physiol. 1973, 24, 519–570. [Google Scholar] [CrossRef]
- Van Emmerik, T.; Steele-Dunne, S.; Judge, J.; van de Giesen, N. A comparison between leaf dielectric properties of stressed and unstressed tomato plants. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 275–278. [Google Scholar]
- Friesen, J.; Van Beek, C.; Selker, J.; Savenije, H.; Van de Giesen, N. Tree rainfall interception measured by stem compression. Water Res. Res. 2008, 44. [Google Scholar] [CrossRef]
- Koizumi, A.; Shimizu, M.; Sasaki, Y.; Hirai, T. In situ drag coefficient measurements for rooftop trees. J. Wood Sci. 2016, 62, 363–369. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Proc. Math. Phys. Sci. 1991, 434, 9–13. [Google Scholar] [CrossRef]
- Chave, J.; Coomes, D.A.; Jansen, S.; Lewis, S.L.; Swenson, N.G.; Zanne, A.E. Towards a worldwide wood economics spectrum. Ecol. Lett. 2009, 12, 351–366. [Google Scholar] [CrossRef] [PubMed]
- Fauset, S.; Johnson, M.O.; Gloor, M.; Baker, T.R.; Monteagudo, A.; Brienen, R.J.; Feldpausch, T.R.; Lopez-Gonzalez, G.; Malhi, Y.; Ter Steege, H.; et al. Hyperdominance in Amazonian forest carbon cycling. Nat. Commun. 2015, 6, 6857. [Google Scholar] [CrossRef] [PubMed]
- Wagner, J. Beta Prototype Product Manual Acceleration Logger–Model AL100; Oregon Research Electronics: Lake Creek Drive, Tangent, OR, USA, 2015; Available online: http://www.orelectronics.net (accessed on 9 April 2015).
- Wagner, J. Application Note AL100: Optimizing Accelerometer Placement in Trees-Preliminary; Oregon Research Electronics: Lake Creek Drive, Tangent, OR, USA, 2015; Available online: http://www.orelectronics.net (accessed on 21 August 2015).
- Spatz, H.C.; Theckes, B. Oscillation damping in trees. Plant Sci. 2013, 207, 66–71. [Google Scholar] [CrossRef] [PubMed]
- Gentine, P.; Garelli, A.; Park, S.B.; Nie, J.; Torri, G.; Kuang, Z. Role of surface heat fluxes underneath cold pools. Geophys. Res. Lett. 2016, 43, 874–883. [Google Scholar] [CrossRef] [PubMed]
- Evans, R.; Ilic, J. Rapid prediction of wood stiffness from microfibril angle and density. For. Prod. J. 2001, 51, 53. [Google Scholar]
- Aumond, P.; Masson, V.; Lac, C.; Gauvreau, B.; Dupont, S.; Berengier, M. Including the drag effects of canopies: Real case large-eddy simulation studies. Bound.-Layer Meteorol. 2013, 146, 65–80. [Google Scholar] [CrossRef]
- Stull, R.B. An Introduction to Boundary Layer Meteorology; Springer Science & Business Media: New York, NY, USA, 2012; Volume 13. [Google Scholar]
- Whittaker, P.; Wilson, C.A.; Aberle, J. An improved Cauchy number approach for predicting the drag and reconfiguration of flexible vegetation. Adv. Water Resour. 2015, 83, 28–35. [Google Scholar] [CrossRef]
- Lopes, A.P.; Nelson, B.W.; Wu, J.; de Alencastro Graça, P.M.L.; Tavares, J.V.; Prohaska, N.; Martins, G.A.; Saleska, S.R. Leaf flush drives dry season green-up of the Central Amazon. Remote Sens. Environ. 2016, 182, 90–98. [Google Scholar] [CrossRef]
- Shaw, R.H.; Schumann, U. Large-eddy simulation of turbulent flow above and within a forest. Bound.-Layer Meteorol. 1992, 61, 47–64. [Google Scholar] [CrossRef]
- Shao, Y.; Liu, S.; Schween, J.H.; Crewell, S. Large-Eddy atmosphere–land-surface modelling over heterogeneous surfaces: Model development and comparison with measurements. Bound.-Layer Meteorol. 2013, 148, 333–356. [Google Scholar] [CrossRef]
- Schilperoort, B.; Coenders-Gerrits, M.; Luxemburg, W.; Cisneros Vaca, C.; Ucer, M. Verifying the distributed temperature sensing Bowen ratio method for measuring evaporation. In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 17–22 April 2016; Volume 18, p. 8486. [Google Scholar]
- Van Emmerik, T.; Coenders-Gerrits, A.; Wenninger, J. Partitioning of evaporation fluxes in summer and winter using stable isotope approach. In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 22–27 April 2012; Volume 14, p. 3779. [Google Scholar]



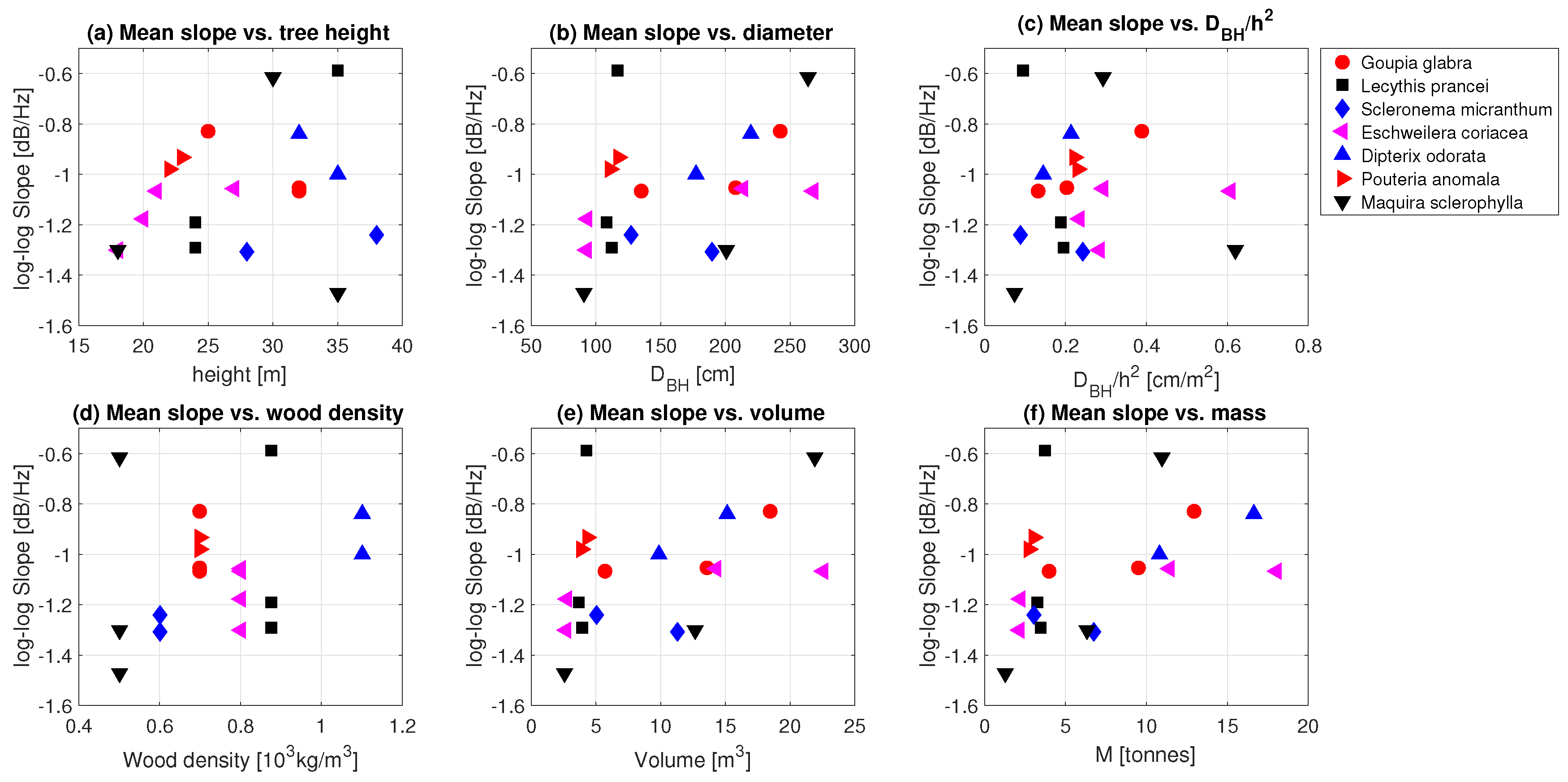


| Tree No. | Name | [10 kg/m] | Wood Density High–Low | Height [m] | [cm] |
|---|---|---|---|---|---|
| 1–3 | Goupia glabra (brevi-deciduous) | 0.7 | Low | 25–32 | 135.0–242.5 |
| 4–6 | Lecythis prancei (evergreen) | 0.875 | Intermediate | 24–35 | 108.4–116.5 |
| 7–8 | Scleronema micranthum (evergreen) | 0.6 | Low | 26–38 | 81.0–189.5 |
| 9–12 | Eschweilera coriacea (evergreen) | 0.8 | Intermediate | 18–27 | 92.4–268.0 |
| 13–14 | Dipterix odorata (evergreen) | 1.1 | High | 32–35 | 177.0–219.5 |
| 15–16 | Pouteria anomala (evergreen) | 0.7 | Low | 22–23 | 111.0–117.5 |
| 17–19 | Maquira sclerophylla (evergreen) | 0.5 | Low | 18–35 | 90.6–264.0 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Van Emmerik, T.; Steele-Dunne, S.; Hut, R.; Gentine, P.; Guerin, M.; Oliveira, R.S.; Wagner, J.; Selker, J.; Van de Giesen, N. Measuring Tree Properties and Responses Using Low-Cost Accelerometers. Sensors 2017, 17, 1098. https://doi.org/10.3390/s17051098
Van Emmerik T, Steele-Dunne S, Hut R, Gentine P, Guerin M, Oliveira RS, Wagner J, Selker J, Van de Giesen N. Measuring Tree Properties and Responses Using Low-Cost Accelerometers. Sensors. 2017; 17(5):1098. https://doi.org/10.3390/s17051098
Chicago/Turabian StyleVan Emmerik, Tim, Susan Steele-Dunne, Rolf Hut, Pierre Gentine, Marceau Guerin, Rafael S. Oliveira, Jim Wagner, John Selker, and Nick Van de Giesen. 2017. "Measuring Tree Properties and Responses Using Low-Cost Accelerometers" Sensors 17, no. 5: 1098. https://doi.org/10.3390/s17051098
APA StyleVan Emmerik, T., Steele-Dunne, S., Hut, R., Gentine, P., Guerin, M., Oliveira, R. S., Wagner, J., Selker, J., & Van de Giesen, N. (2017). Measuring Tree Properties and Responses Using Low-Cost Accelerometers. Sensors, 17(5), 1098. https://doi.org/10.3390/s17051098







