3.1. Time-Domain Reflectometry
Time domain reflectometry is a highly accurate and automatable method for the determination of the LWC of porous media and its electrical conductivity [
28]. LWC is inferred from the dielectric permittivity of the medium, whereas electrical conductivity is inferred from TDR signal attenuation. In a fairly simple approach, empirical and dielectric mixing models are used to relate a medium’s LWC, dielectric permittivity, and density. In some cases, the relationship between LWC and dielectric permittivity requires individual calibration when dealing with non-mineral (e.g., clay and organic matter, etc.) soil media or snow. Numerous TDR probe configurations provide users with site- and media- specific options. Hence, continuous developments in TDR technology and in other dielectric methods offer the promise for less expensive and more accurate tools for the electrical determination of LWC.
Time domain reflectometry is related to the measurement of the relative complex dielectric constant, which is a component of the capacitance [
24]. The capacitance is a constant of proportionality that relates the potential difference between conductors to the amount of equal, but opposite electric charges in each of them. Capacitance is quite dependent on the geometry of the two conductors and the relative complex dielectric constant [
46]. However, the relative complex dielectric constant (Equation (1)) is variable for most materials; it has a real and an imaginary part; both frequency dependent [
33]:
where
complex dielectric constant;
real dielectric constant;
dielectric loss;
conductivity;
angular frequency;
permittivity of free space; and
= (−1)
1/2.
Thus, the complex dielectric constant of a material can be determined from the propagation of a pulse along a transmission line. The velocity of a pulse (
) along a transmission line is given by:
where
, is the physical length of the transmission line (or length of the probe) and
is the time of propagation. Furthermore, distributed circuit analysis dictates that at high frequencies, and for non-magnetic materials [
27]:
The combination of both equations yields:
where
is the length of the line set by the user,
is the velocity of an electromagnetic wave in free space, and
is determined using the time domain reflectometer. Time domain reflectometry measures both the real and imaginary parts of the complex dielectric constant (as shown in Equation (1)). As such, the term “apparent dielectric constant”
is sometimes used. However, for low loss materials (i.e., snow),
and hence,
[
24,
25,
26,
46]. Therefore, in this paper the dielectric constant refers only to the real part.
In short, a TDR measurement unit consists of a pulse generator (generating a step pulse, which is being transformed to a lower frequency), a registration unit (an oscilloscope for commercially available TDR units) and one or several sets of rods (probes) mounted parallel in the studied medium. The dielectric constant (electrical permittivity) can be determined from the velocity of propagation of an electromagnetic wave through a medium. The generated pulse is reflected when it reaches the end of the rods. The travel time of the reflected pulse is a function of the dielectric constant of the surrounding medium. Because the difference in dielectric constant between water (K
w~80) and ice (K
I~3) is significant at the 1 MHz to 1 GHz range, the dielectric constant is primarily a function of the liquid water content of the snow [
26,
38,
39,
40]. Additionally, density variations in the snow have some influence in dielectric constant measurements due to the difference between the dielectric constants of air (K
A = 1) and ice (K
I~3) [
26]. This is particularly true for wet snow because it is a mixture of ice crystals, liquid water, and air.
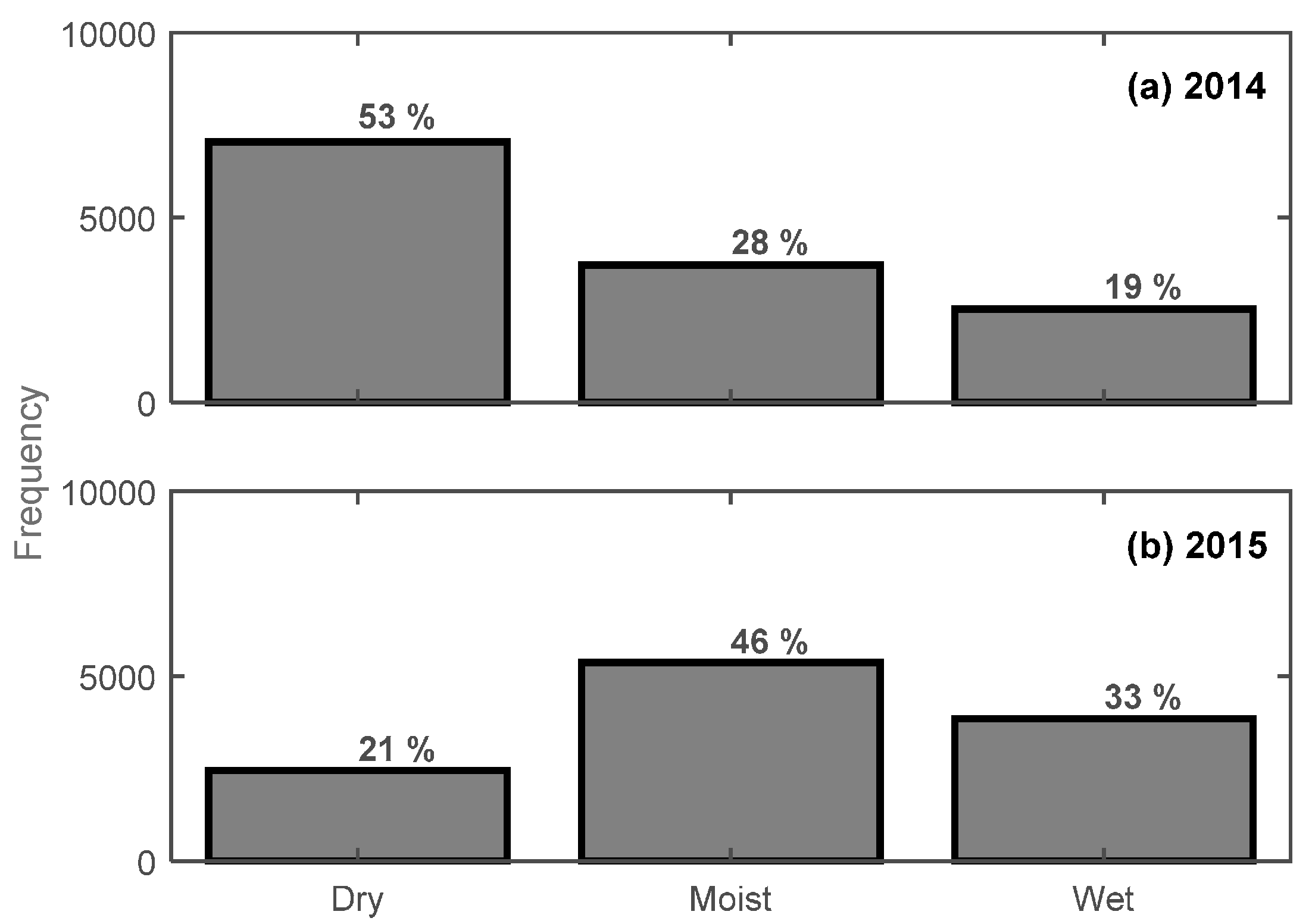
3.5. Liquid Water Content Simulations Using SNTHERM
SNTHERM is a freely available, Fortran-written, one-dimensional snowpack physical model that simulates snowpack properties and was first released on 1989. Since its origin, it has been enhanced multiple times to improve its algorithms [
48]. SNTHERM is energy and mass balance-driven. It has been used in several validation studies such as: snowpack spectral signature [
49], snow melting processes [
50], energy balances at regional scales, as well as discrete point scales, and for “under the canopy” snow [
51,
52]. A simplified version of the model is currently operational for snow mapping and forecasting in the United States [
53,
54,
55] and Bosnia [
56]. SNTHERM was developed using as foundation the mass and energy-balance snow model of Anderson [
57]. The vertical water movement is based on the work done by Colbeck [
58], in which the effective saturation of snow is a function of the current saturation level and the irreducible water saturation. Colbeck developed a flow model that accounts for multiple flow paths, transient ponding of water on ice layers, flow down distinct flow channels, and background flow simultaneously. He considered that the infiltration of liquid water through the ice layers is best described in a straightforward manner using his gravity flow theory [
59], but the movement of the water in the flow channels is somewhat more complicated. Colbeck explained that flow channels are generated when water entering a dry, cold snow develops “fingers” that propagate ahead of the background flow leaving areas of cold, dry snow behind, and that the liquid water saturation in snow is too low for fingers to develop spontaneously simply from a heavier fluid (water) displacing a lighter fluid (air). Therefore, he hypothesized that the fingers are caused by the many crusts and ice layers normally present in highly stratified snow covers. This situation occurs many times in most snow covers because wind and melt crusts often mark the horizon between snow from separate storms. After flow fingers are established by the first movement of water through a snow cover, these original flow channels become preferential paths for future waves of infiltrating water due to the grain growth and permeability increase associated with the presence of liquid water in snow. However, on the scale of days or weeks leading to seasonal snow melt-off, the heterogeneous nature of the flow field is an important feature of most seasonal covers. The problems of multiple flow paths are complicated by the temporary ponding of water on individual ice layers. Hence, the volume of ponded water per unit width is calculated for a horizontal ice layer undergoing a steady balance of inflow and discharge to regularly spaced drains. He then concluded that, if the ice layer is sloping, if water is seeping simultaneously through the ice layer, or if transient effects are important, the volume of ponded water has to be adjusted accordingly. Thus, water in the snowpack propagates at a rate dependent on the flux ahead and behind the flow going directly through the ice layers [
58]. However, the fluid flow model mentioned previously assumes horizontal homogeneity in the snow cover. In reality, seasonal snow covers that are undergoing freeze-thaw cycles, or that are subject to strong winds, develop crusts and ice layers, which complicate flow pattern. Thus, perforations arise in the crusts through which fingers of water flow at a much faster rate than through the crust itself [
58]. Field observations by Marsh and Woo [
60] of runoff rates from ripe snow in the Canadian Arctic showed that almost half the daily flow can be carried by fingers or flow channels that move ahead of the background front. They also developed a simulation model that incorporates the phenomenon of fingering [
61]. Later, Schneebeli [
62] showed that the location of fingers may not be stable in time and space. Additionally, more recent interpretations of preferential flow by Katsushima et al. [
63] and Hirashima et al. [
64] have demonstrated that flow fingers can develop even in isothermal conditions, and that ponding may allow to reach the necessary large concentrations of water. Within SNTHERM, snowpack layer densification is calculated based on three (3) main processes: destructive metamorphism or overburden compaction, constructive metamorphism or vapor movement and grain size change, and melt metamorphism or the gravitational water movement inside the snowpack [
57,
65,
66,
67]. The first two are merged into an overall compaction rate and the third metamorphism type is calculated based on the water balance. Destructive metamorphism is calculated as a function of snow viscosity [
65,
66]. Constructive metamorphism is a function of temperature and it is a process that has a faster rate when new snow density is greater than the density limit constant [
57]. As stated by the Special Report 91-16 of the United States Army Corps of Engineers [
48], and later on reported by [
68], the SNTHERM numerical solution is obtained using a variable grid of snow layers, each layer being governed by heat and mass balance equations. The model uses a control volume numerical procedure [
69] for spatial discretization that allows for the compaction of the snow. Lastly, a Crank-Nicholson central difference scheme is used to solve the partial differential equations in the time domain.
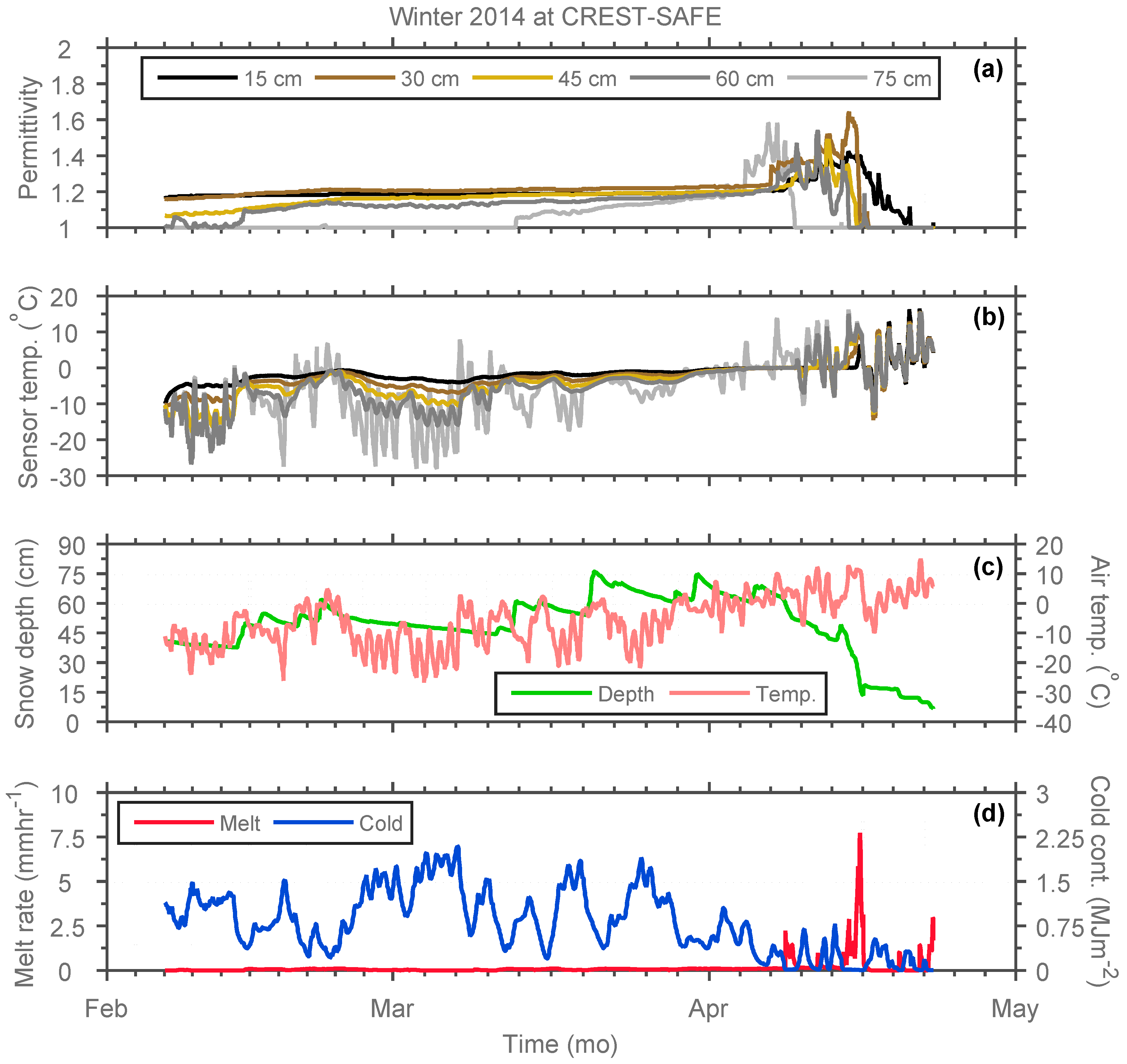
As mentioned in
Section 2, the CREST-SAFE experiment is a long-term field campaign where meteorological variables and snowpack properties are measured. The measured meteorological variables at the station are: air temperature, solar radiation, relative humidity, and wind speed and direction. The only meteorological parameter that is not measured at CREST-SAFE (that is needed for simulation purposes) is precipitation. Therefore, it was obtained from the National Weather Service (NWS) Station named KCAR [
70], located near (approximately 90 m away) the CREST-SAFE site at the Caribou Municipal Airport in Caribou, ME. The NWS uses the All Weather Precipitation Accumulation Gauge (AWPAG), instead of the traditional Heated Tipping Bucket (HTB) technology, in their Automated Surface Observing System (ASOS) stations to measure precipitation data. The AWPAG is essentially a weighing gauge where precipitation continuously accumulates within the collector, and as the weight increases, precipitation is recorded. The AWPAG has an 8-foot diameter outer shield to mitigate the wind effects on precipitation readings. Additionally, a transfer function provided by the World Meteorological Organization (WMO) is used to correct the precipitation measurements for undercatchment using daily average wind speed and maximum temperature observations performed by the ASOS station as well [
71]. SNTHERM needs two precipitation parameters as input: precipitation water equivalent and precipitation type (rain or snow). Both variables were given to the model as obtained from the NWS precipitation records—these provide both the liquid and solid precipitation snowfall data. The precipitation deposition scheme to obtain the new snow height as solid precipitation accumulates over the snow surface is performed by SNTHERM based on its built-in algorithm [
48]. Additional calibration parameters (i.e., irreducible water content for snow (0.017), density of new snow (73 kg/m
3), density limit for compaction of snow (96 kg/m
3), and the viscosity coefficient for overburden compaction (6.9 × 10
5 kg·s/m
2)) needed by SNTHERM to simulate the deposition scheme were established based on previous studies [
48,
57,
65,
66,
67,
72]. CREST-SAFE provides all of its meteorological data in an hourly time step via an automated routine [
73], whereas the NWS provides precipitation data in 15-min time steps. Naturally, the NWS precipitation data was aggregated to hourly time intervals. Hence, by weather-forcing SNTHERM with the meteorological dataset at CREST-SAFE, layered hourly simulated snowpack properties (i.e., LWC, depth, grain size, density, temperature, and SWE) for the station were obtained for the period of this study.
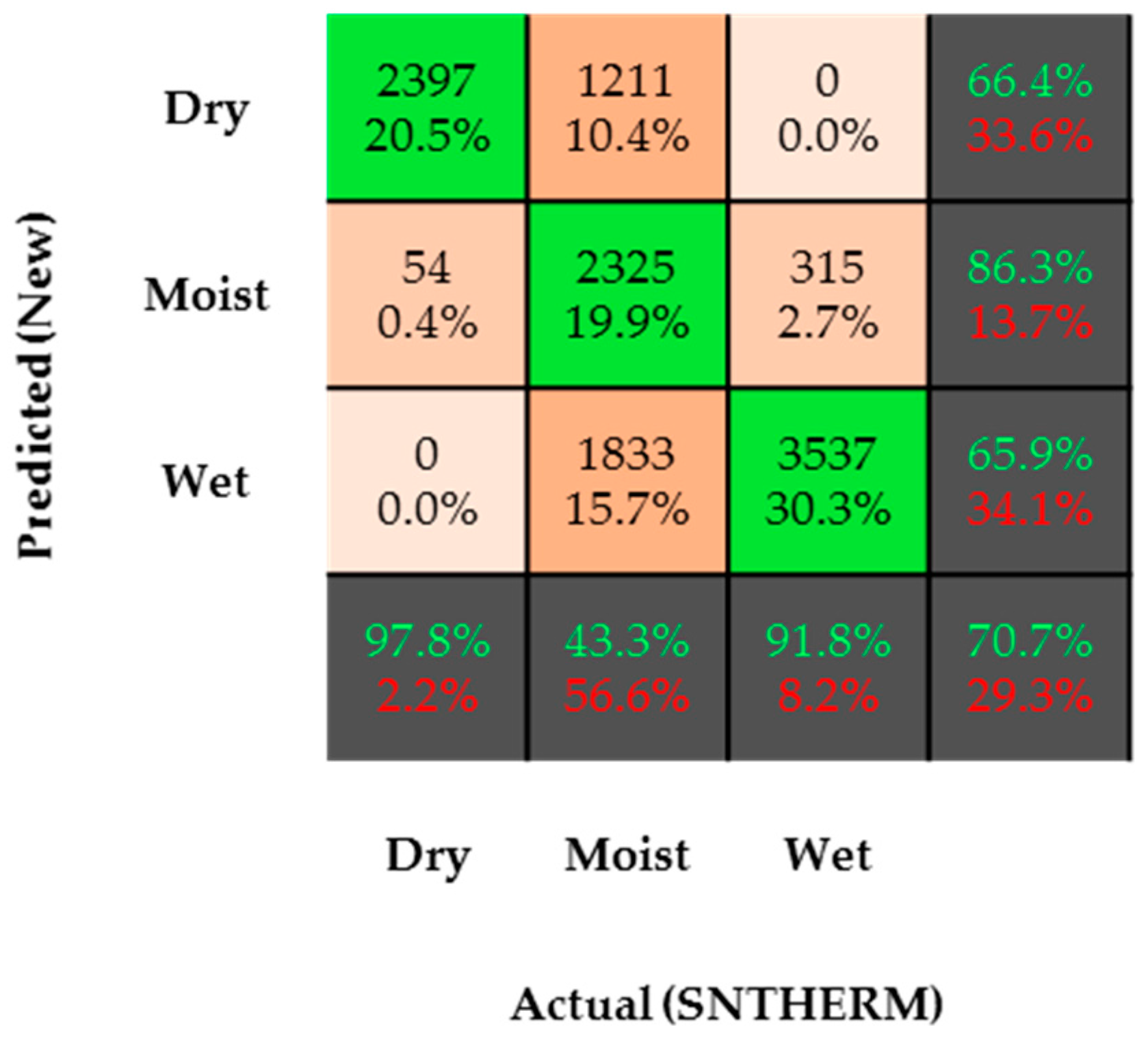
It should be noted that Corona et al. [
72] validated SNTHERM snowpack simulations (forced with CREST-SAFE in situ meteorological data) with three years (2010–2013) of CREST-SAFE in situ snowpack observations. More specifically, the SNTHERM evaluation was performed on properties such as: snow depth, SWE, density, temperature, and grain size, in addition to a layer-by-layer comparison of the snowpack properties. SNTHERM outputs showed high agreement with the observed data in properties like snow depth (R = 0.84), SWE (R = 0.77), density (R = 0.80), snow surface temperature (R = 0.98), and average snowpack temperature (R = 0.75). Conversely, the model was not very efficient when simulating properties like layer temperature (R = 0.54) and grain size (R = 0.60). Generally, SNTHERM appeared to simulate all snowpack properties closer to the snow surface better than those closer to the snow-ground interface. Additional studies by Lakhankar et al. [
73] and Koivusalo and Heikinheimo [
74] have also shown good agreement between various SNTHERM simulated snowpack properties and in situ observations. Lakhankar et al. demonstrated high agreement between bulk snow density (R = 0.97) and average grain size (R = 0.96) SNTHERM simulations and CREST-SAFE in situ observations. The differences in agreement between the studies by Corona et al. and Lakhankar et al. can be attributed to the fact that, in the former, the model vs. ground truth comparison was done at a layer-by-layer basis, whereas, for the latter, it was done with snowpack averages. Averaging snowpack properties will attenuate extreme (minimum and maximum) values in the dataset. Koivusalo and Heikinheimo compared SNTHERM simulations with in situ data from the Sodankylä Meteorological Observatory in Northern Finland. The results demonstrated high agreement between simulated and in situ snowpack properties such as: snow albedo, temperature, depth, SWE, and melt outflow. The proven good agreement between SNTHERM simulations and in situ snowpack properties, the CREST-SAFE-SNTHERM validation results by Corona et al., and the lack of in situ LWC measurements at the station led to the idea of using SNTHERM LWC simulations in this study.
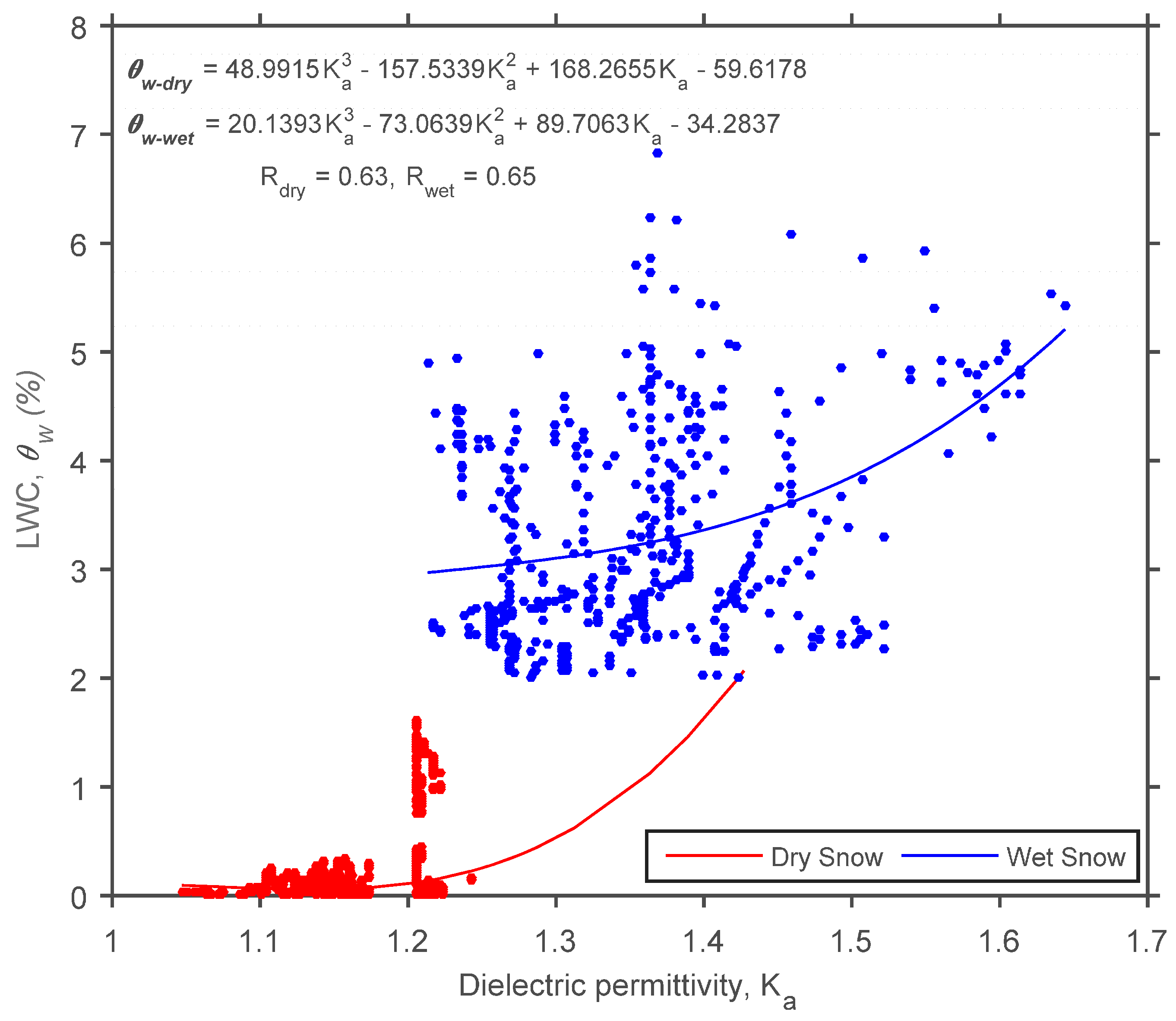
While, to our knowledge, SNTHERM LWC simulations have not been validated directly, we understand that the high agreement between SNTHERM and in situ data for other snowpack parameters (i.e., depth, SWE, and density) shown in previous validation efforts provides sufficient evidence indicating that the SNTHERM LWC simulations (forced with in situ meteorological parameters) are, in fact, accurate. Firstly, because snow density has been described by snow hydrologists as the ratio between SWE and snow depth (indicating an intrinsic relationship between all three snow parameters), and, more importantly, because—in a simplistic approach—SNTHERM LWC simulations at each node (layer)
are calculated using the ratio between nodal liquid water bulk density
and nodal bulk snowpack density
:
both of which are reliant on the SNTHERM calibration parameters (irreducible water content for snow, density of new snow, density limit for compaction of snow, and the viscosity coefficient for overburden compaction) that produced good validation agreement with the CREST-SAFE snow depth, SWE, and density observations, as stated previously. Each node containing a specific thickness; all amounting up to the total snowpack depth (n is the number of nodes/layers) and, consequently, LWC
at its pertinent time step (every hour, in this study):
Thus, accurate SNTHERM LWC simulations will be highly dependent on the already proven accurate snow depth, SWE, and density simulations. However, the mass contribution of liquid water in snow is small, albeit important for hydrology. Hence, good snow density reproduction may be (at least partially) insufficient to infer that LWC and, equally important, liquid water location within the snowpack are also well reproduced. Instead, these issues might generate uncertainties in SNTHERM LWC simulations. For this reason, possible sources of model uncertainty, as related to the results in
Section 4, will be discussed in
Section 5.
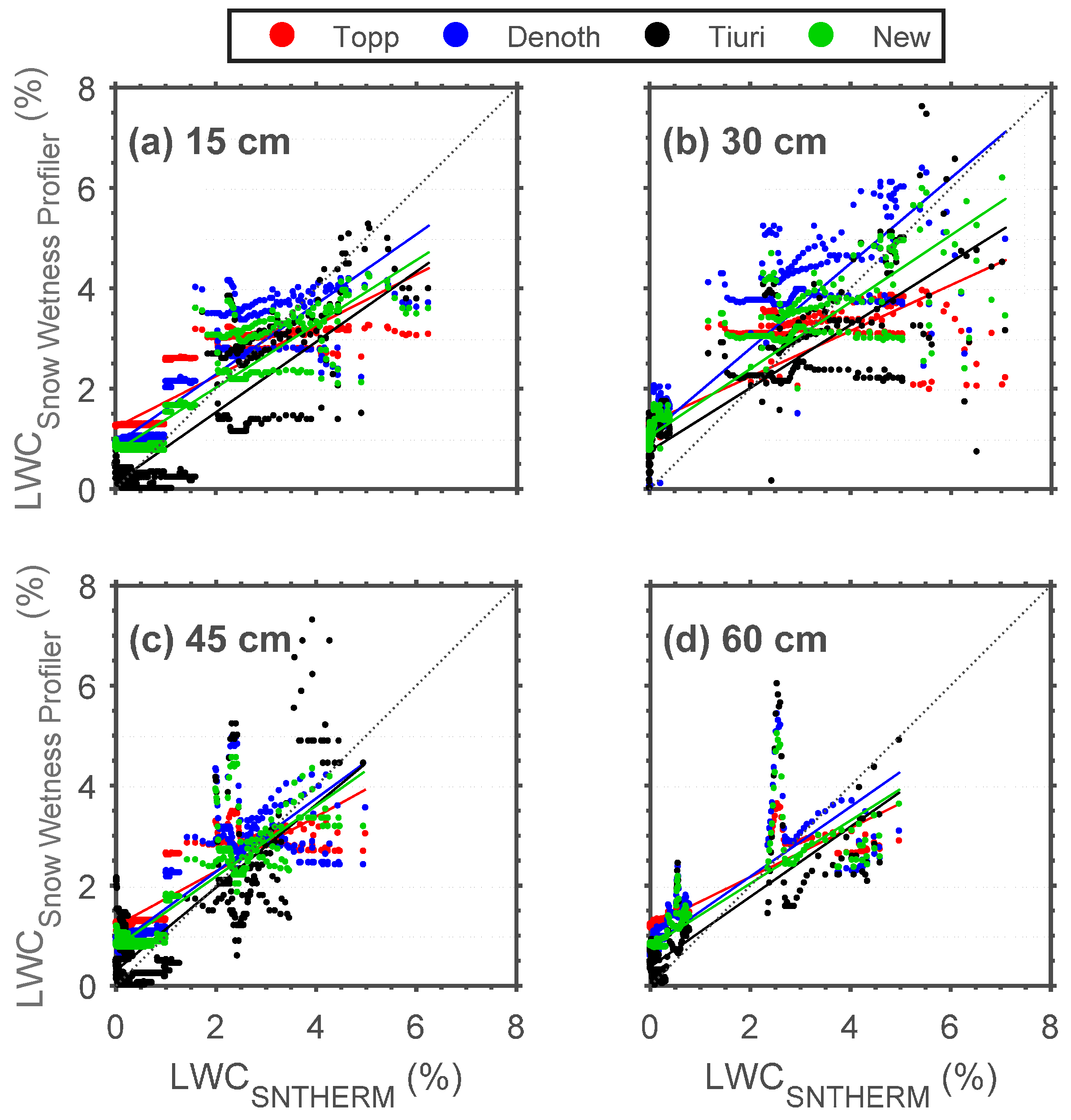
It should be mentioned actual SNTHERM node/layer (not bulk) snow LWC values were compared with LWC estimates at single layer depths. The process consisted of finding the cumulative (sum of node/layer thicknesses) snow depth that would lead to the specific SWP sensor height, then the SNTHERM-simulated LWC at that node was extracted and used for comparison with LWC estimates by the three empirical formulas. SNTHERM bulk snow density computations were only discussed because these are part of its density simulation procedure.
Note: The irreducible water content for snow is the minimum amount of water that a layer of snow can hold; controlling evaporation and sublimation in the snowpack. Density of new snow is the assumed density for snow precipitation. Density limit for compaction of snow is the upper limit on destructive metamorphism compaction. Lastly, the viscosity coefficient controls the compaction rate of the snowpack due to overburden.