A Novel Monopulse Technique for Adaptive Phased Array Radar
Abstract
:1. Introduction
2. Data Model
3. The Proposed Constrained Algorithm
3.1. Derivation of the Algorithm Used in a Linear Array
3.2. Extension to Planar Array Application
3.3. Summary and Computational Complexity of the Proposed Algorithm
- calculate the adaptive sum beam weights using (6). In this step, calculation of the sample matrix inversion (SMI) is the most expensive. Fortunately, we can use the recursive matrix inversion formula for the one rank updated sample covariance matrix [31] which can reduce the computational complexity to the level of where l is the dimension of the array manifold. The other matrix multiplication is also in the order of [32,33]. Therefore, the total computational complexity in this step is .
- Determine the parameter or the parameter pair as follows: in the linear array case, use (26) to determine , while in the planar array case, solve (35) for or directly make and close to zero to approximate the performance of the MVAM if seeking to reduce computational cost. In this step, determining the parameter according to (26) or directly choosing a small value close to zero does not require any computation. However, in the planar array case, optimization of the parameters requires recursive iteration to solve (35), thus it is not suggested for real-time applications.
- Use (16) for linear array applications or (31) for planar array applications to calculate the constrained difference beam weights. The sample matrix inversion is already calculated in the first step and the other matrix inversion in (16) and (31) is usually negligible because in practice. Therefore, the total computational complexity in this step is in the order of .
- Perform beamforming with the beam weights calculated in the previous steps and then calculate the monopulse ratio along with the angle estimates. This last step has the computational complexity of .
4. Performance Analysis of the Proposed Monopulse Estimator
4.1. Mean and Variance of the Proposed Estimator
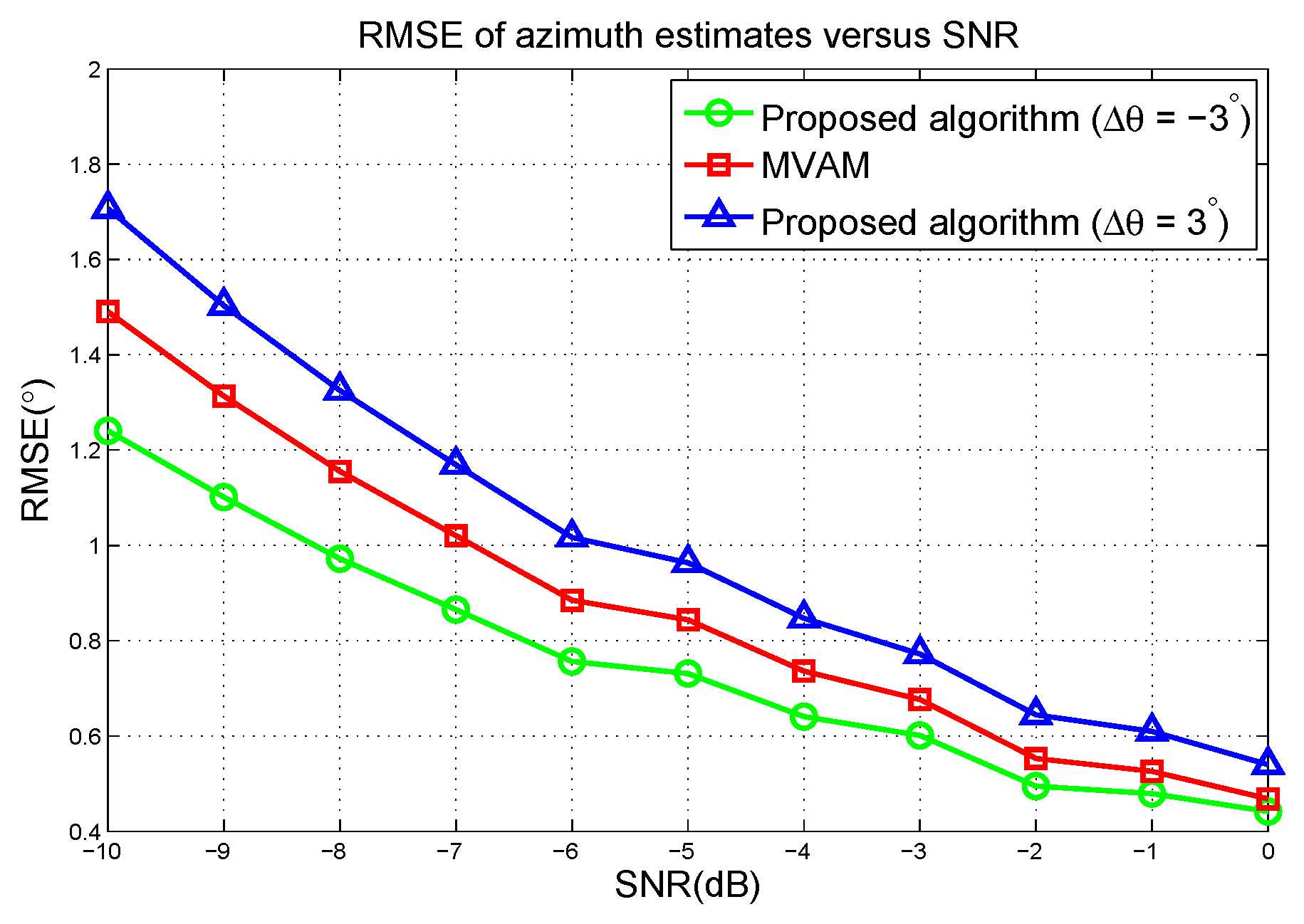
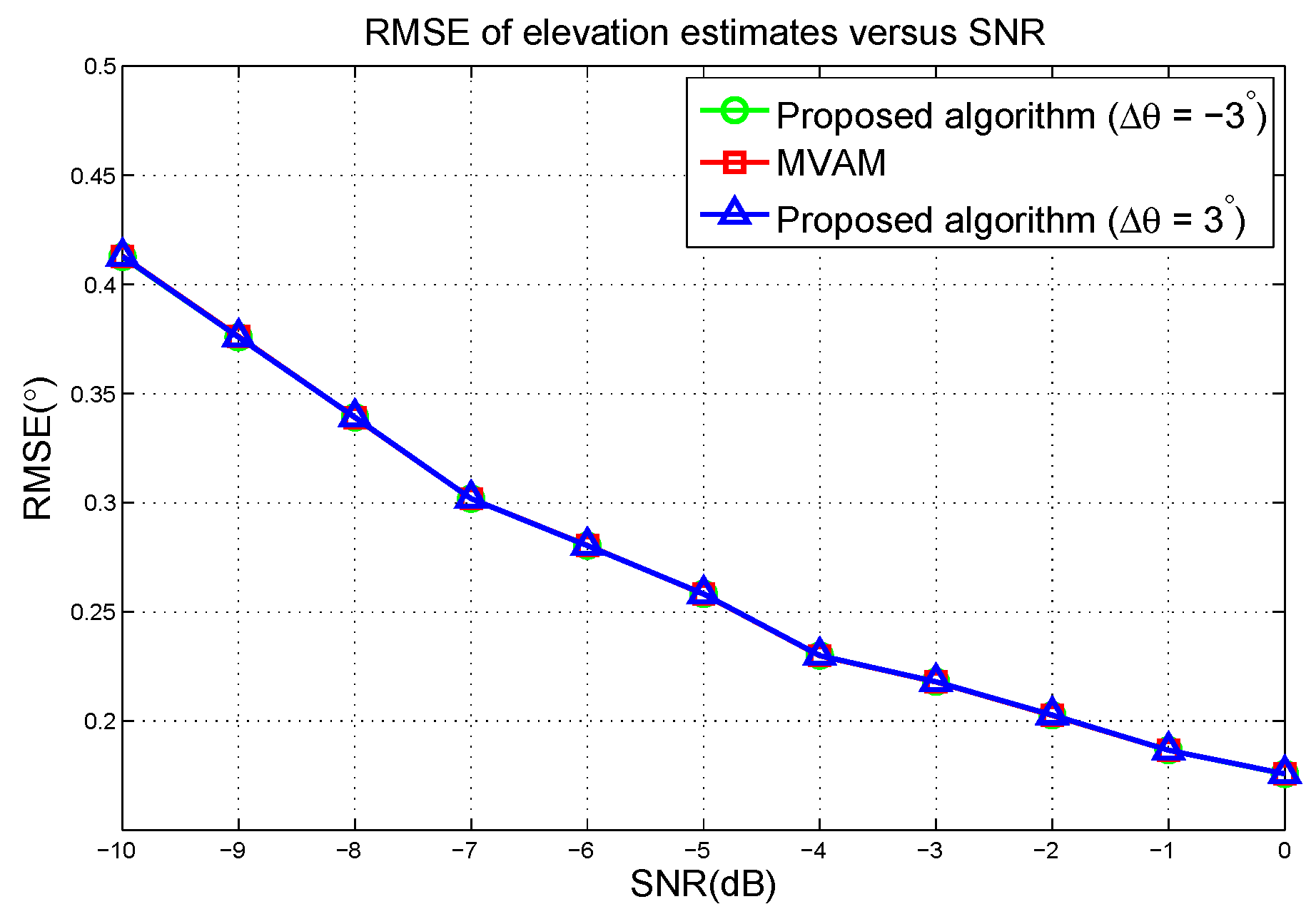
4.2. Comparison with MVAM
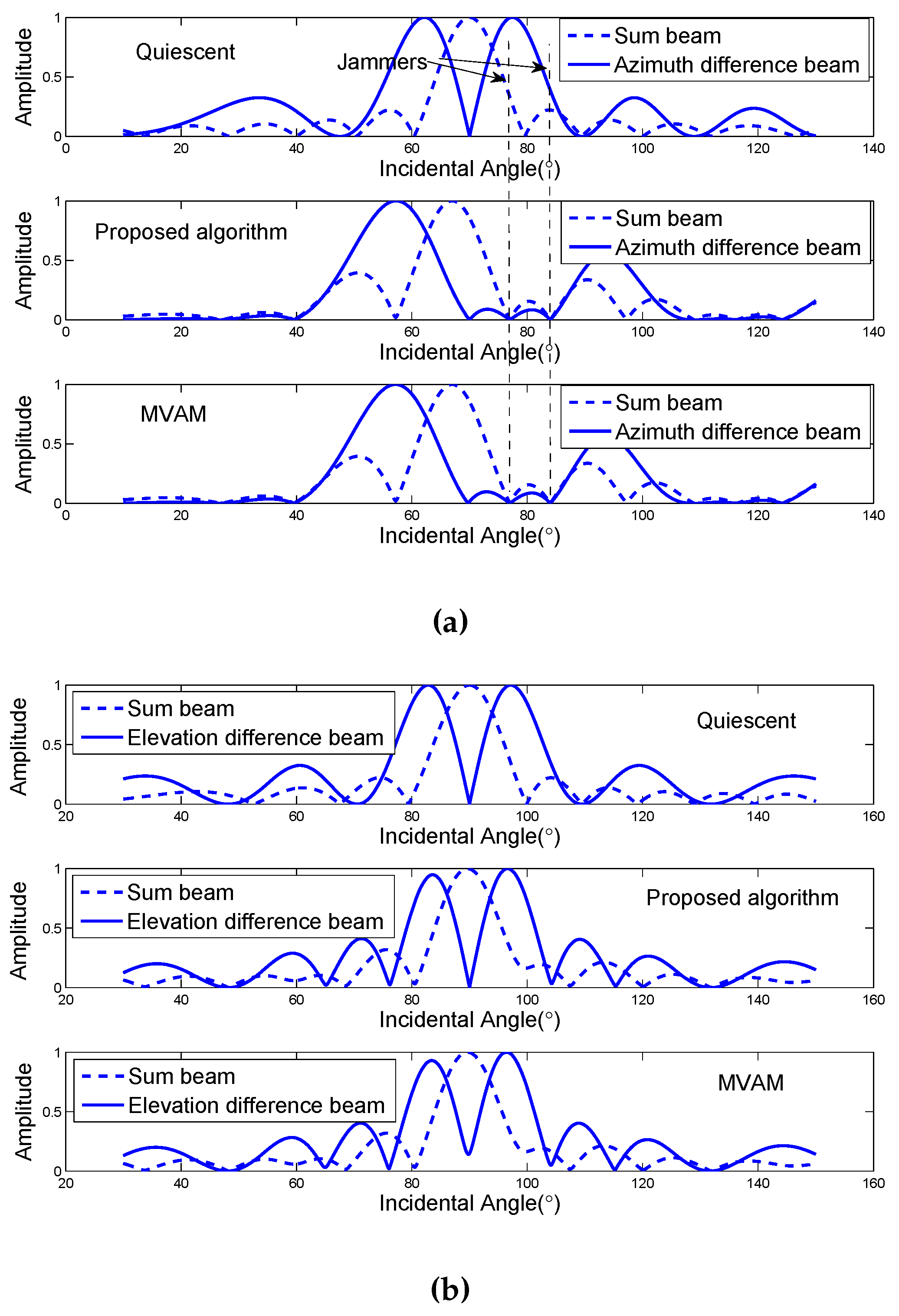
5. Numerical Examples and Applications
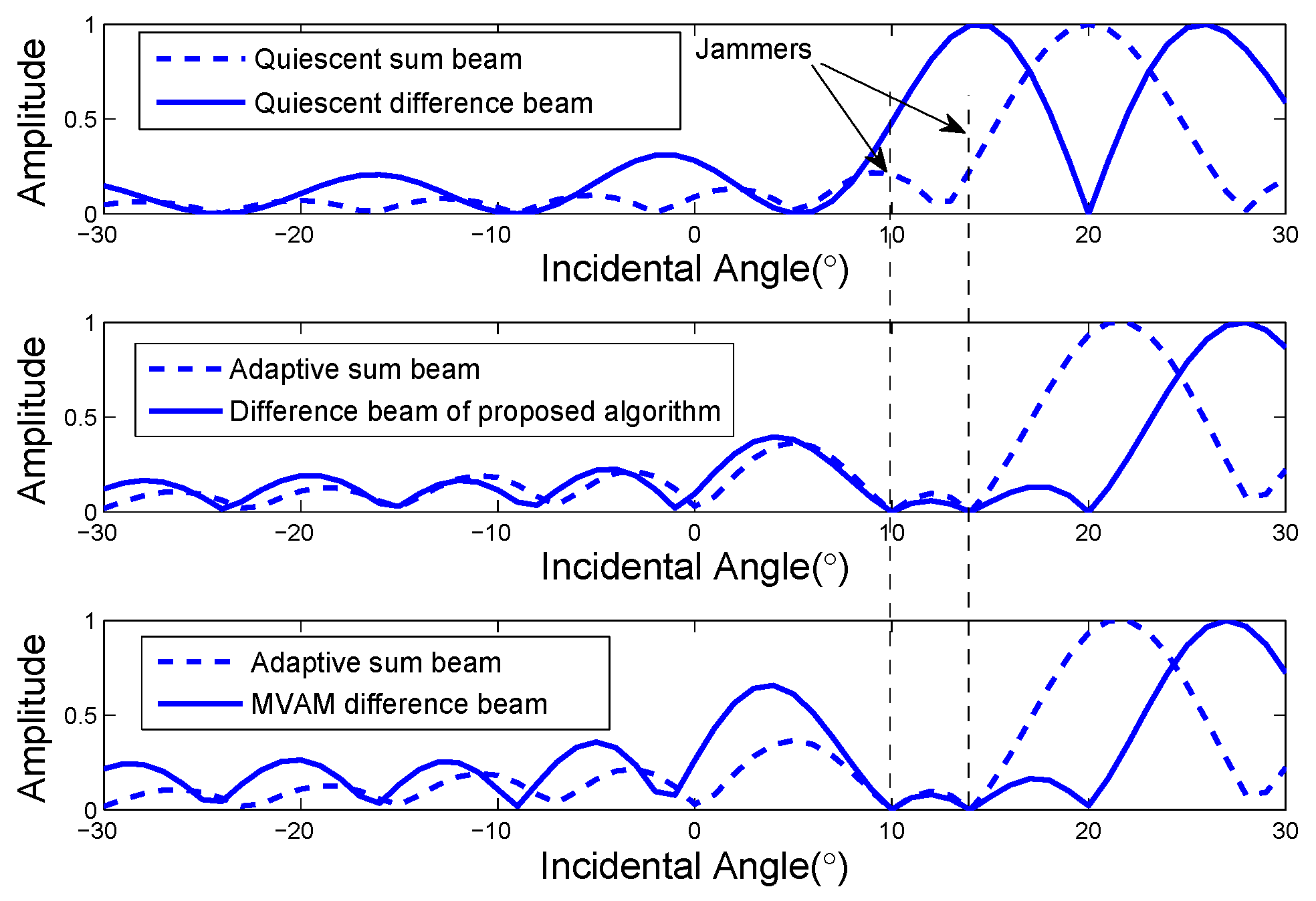
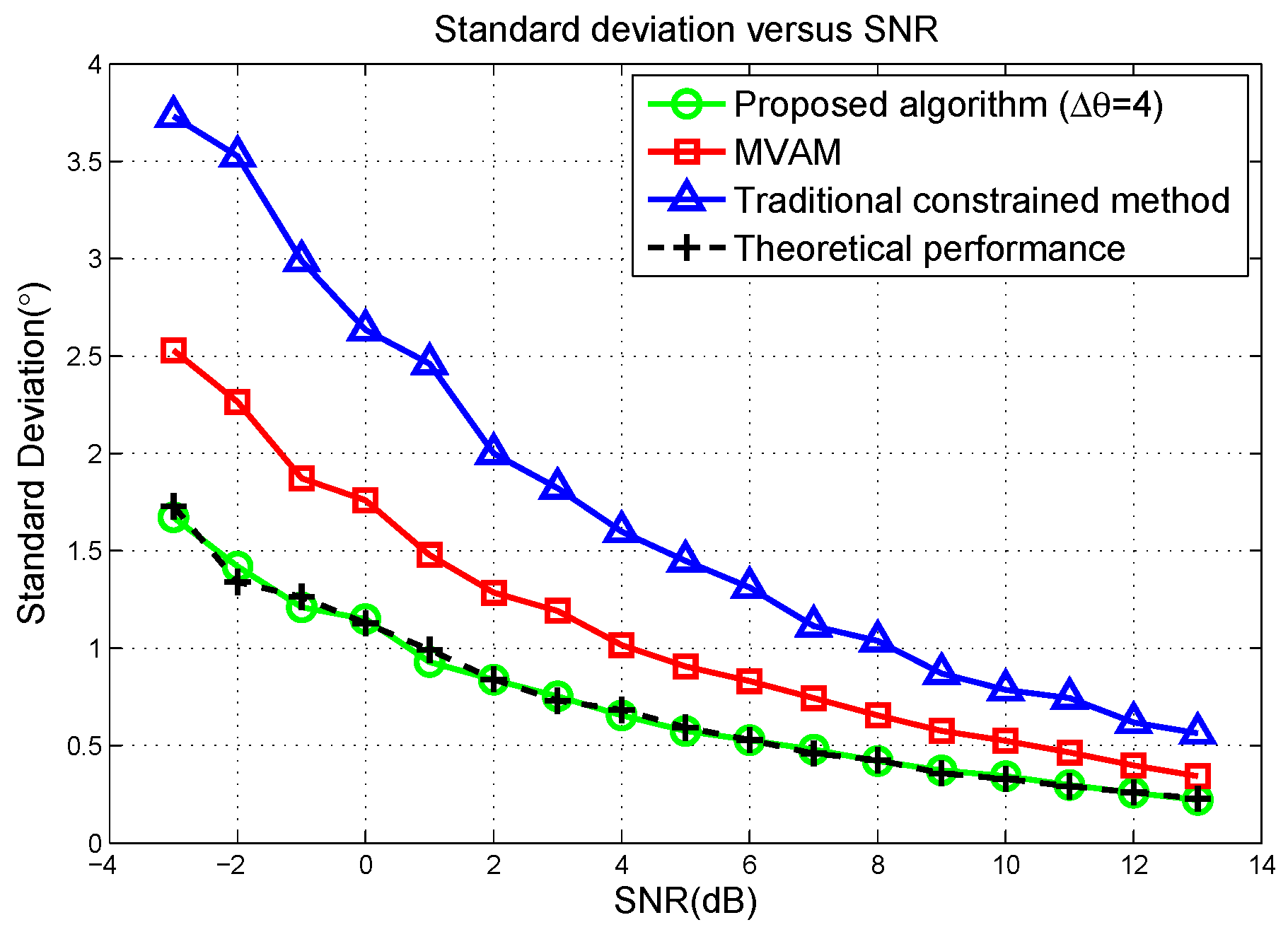
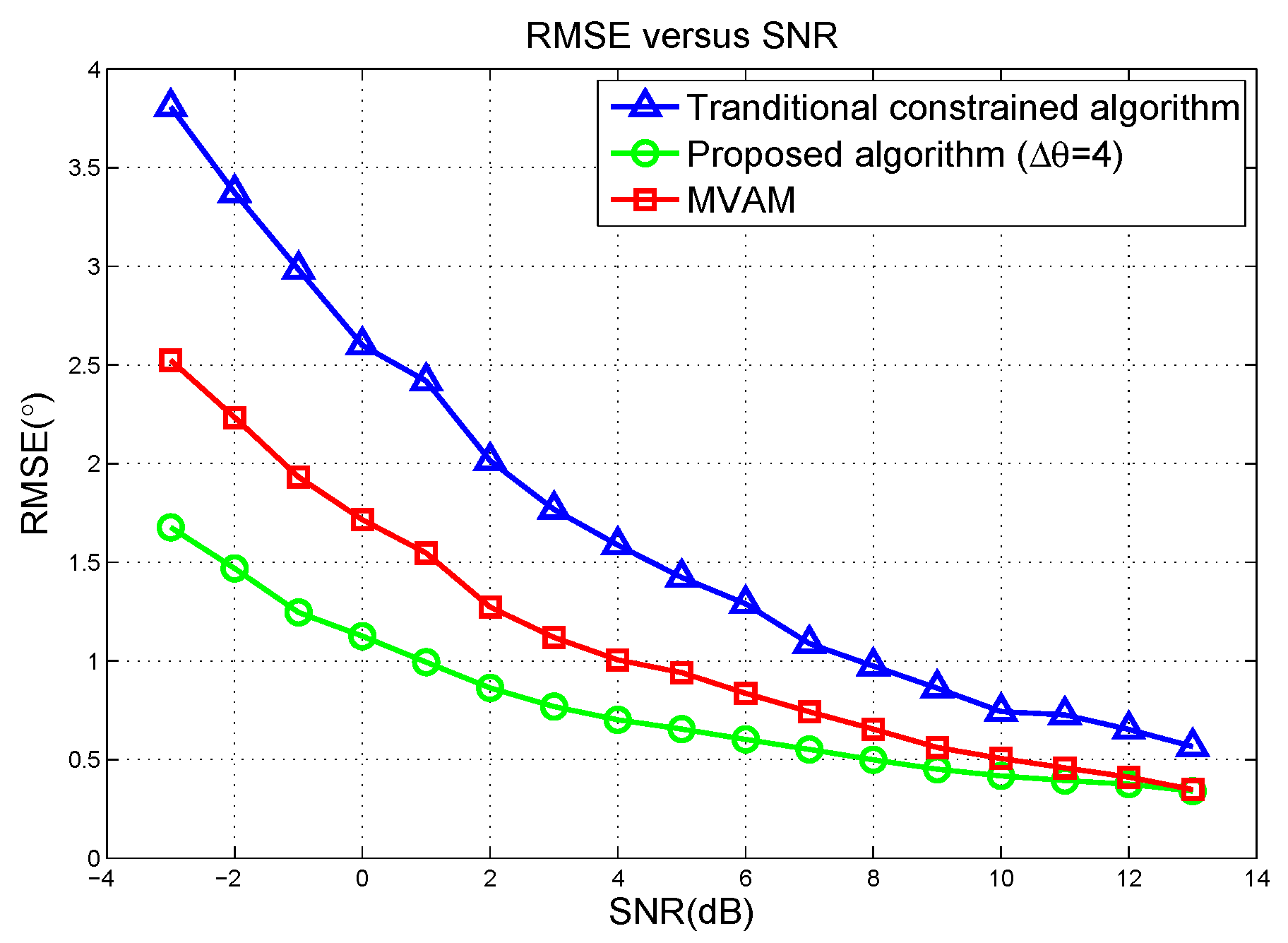
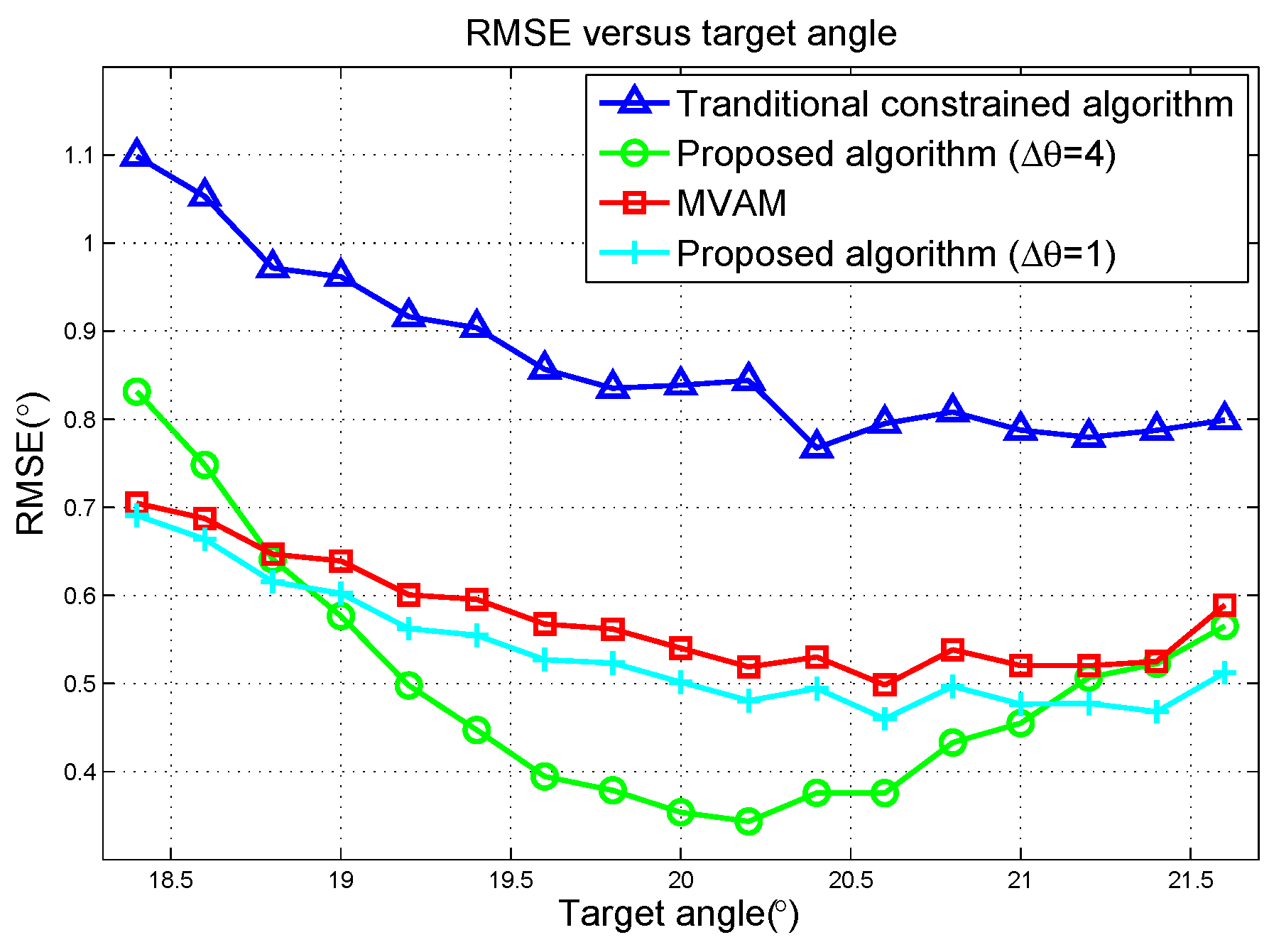
5.1. Simulation in Linear Array
5.2. Simulation in Planar Array
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Sherman, S.M. Monopulse Principles and Techniques; Artech House: Boston, MA, USA, 1984. [Google Scholar]
- Leonov, A.I.; Fomichev, K.I. Monopulse Radar; Artech House: Boston, MA, USA, 1984. [Google Scholar]
- Zhang, X.; Li, Y.; Yang, X.; Long, T.; Zheng, L. Sub-Array Weighting UN-MUSIC: A Unified Framework and Optimal Weighting Strategy. IEEE Signal Process. Lett. 2014, 21, 871–874. [Google Scholar]
- Stoica, P.; Nehorai, A. MUSIC, Maximum Likelihood and Cramer-Rao Bound. IEEE Trans. Acoust. Speech Signal Process. 1990, 38, 1783–1795. [Google Scholar] [CrossRef]
- Davis, R.C.; Brennan, L.E.; Reed, I.S. Angle Estimation with Adaptive Arrays in External Noise Fields. IEEE Trans. Aerosp. Electron. Syst. 1976, 12, 179–186. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, Q.; Hong, R.; Pan, P.; Deng, Z. A Novel Monopulse Angle Estimation for Wideband LFM Radars. Sensors 2016, 16, 817. [Google Scholar] [CrossRef] [PubMed]
- Nickel, U. Overview of Generalized Monopulse Estimation. IEEE Trans. Aerosp. Electron. Syst. 2006, 21, 27–56. [Google Scholar] [CrossRef]
- Lorenz, R.G.; Boyd, S.P. Robust Minimum Variance Beamforming. IEEE Trans. Signal Process. 2005, 53, 1684–1696. [Google Scholar] [CrossRef]
- Dudczyk, J.; Kawalec, A. Adaptive Forming of the Beam Pattern of Microstrip Antenna with the Use of an Artificial Neural Network. Int. J. Antennas Propag. 2012, 2012, 935073. [Google Scholar] [CrossRef]
- Theil, A. On Combining Adaptive Nullsteering with High-Resolution Angle Estimation under Main Lobe Interference Conditions. In Proceedings of the Record of the IEEE 1990 International Radar Conference, Arlington, VA, USA, 7–10 May 1990; pp. 295–297.
- Elnashar, A.; Elnoubi, S.M.; El-Mikati, H.A. Further Study on Robust Adaptive Beamforming with Optimum Diagonal Loading. IEEE Trans. Antennas Propag. 2006, 54, 3647–3658. [Google Scholar] [CrossRef]
- Vorobyov, S.A.; Gershman, A.B.; Luo, Z. Robust Adaptive Beamforming Using Worst-Case Performance Optimization: A Solution to the Signal Mismatch Problem. IEEE Trans. Signal Process. 2003, 51, 313–324. [Google Scholar] [CrossRef]
- Li, J.; Petre, S.; Wang, Z. On Robust Capon Beamforming and Diagonal Loading. IEEE Trans. Signal Process. 2003, 51, 1702–1715. [Google Scholar]
- Valeri, M.; Barbarossa, S.; Farina, A.; Timmoneri, L. Monopulse Estimation of Target DOA in External Noise Fields with Adaptive Arrays. In Proceedings of the IEEE International Symposium on Phased Array Systems and Technology, Boston, MA, USA, 15–18 October 1996; pp. 386–390.
- Nickel, U. Monopulse Estimation with Adaptive Arrays. IEE Proc. Radar Signal Process. 1993, 140, 303–308. [Google Scholar] [CrossRef]
- Nickel, U. Monopulse Estimation with Subarray-Adaptive Arrays and Arbitrary Sum and Difference Beams. IEE Proc. Radar Sonar Navig. 1996, 143, 232–238. [Google Scholar] [CrossRef]
- Nickel, U. Performance of Corrected Adaptive Monopulse Estimation. IEE Proc. Radar Sonar Navig. 1999, 146, 17–24. [Google Scholar] [CrossRef]
- Paine, A.S. Minimum Variance Monopulse Technique for an Adaptive Phased Array Radar. IEE Proc. Radar Sonar Navig. 1998, 145, 374–380. [Google Scholar] [CrossRef]
- Nickel, U. Performance Analysis of Space-Time Adaptive Monopulse. Signal Process. 2004, 84, 1561–1579. [Google Scholar] [CrossRef]
- Wu, R.; Su, Z.; Wang, L. Space-Time Adaptive Monopulse Processing for Airborne Radar in Non-homogeneous Environments. AEU Int. J. Electron. Commun. 2011, 65, 258–264. [Google Scholar] [CrossRef]
- Paine, A.S. Application of the Minimum Variance Monopulse Technique to Space-Time Adaptive Processing. In Proceedings of the IEEE International Conference on RADAR 2000, Alexandria, VA, USA, 7–12 May 2000; pp. 596–601.
- Ward, J. Maximum Likelihood Angle and Velocity Estimation with Space-Time Adaptive Processing Radar. In Proceedings of the Conference Record of the Thirtieth Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 3–6 November 1996; pp. 1265–1267.
- Ward, J. An Efficient Rooting Algorithm for Simultaneous Angle and Doppler Estimation with Space-Time Adaptive Processing for Radar. In Proceedings of the Conference Record of the Thirty-First Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 2–5 November 1997; pp. 1215–1218.
- Fante, R.L. Synthesis of Adaptive Monopulse patterns. IEEE Trans. Antennas Propag. 1999, 47, 773–774. [Google Scholar] [CrossRef]
- Seliktar, Y.; Holder, E.J.; Wiliams, D.B. An Adaptive Monopulse Processor for Angle Estimation in a Mainbeam Jamming and Coherent Interference Scenario. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Seattle, WA, USA, 12–15 May 1998; pp. 2037–2040.
- Seliktar, Y. Space-Time Adaptive Monopulse Processing. Ph.D. Thesis, Faculty of Electrical Engineering, Georgia Institute of Technology, Atlanta, GA, USA, 1998. [Google Scholar]
- Canuto, C.; Tabacco, A. Mathematical Analysis I; Springer: Milan, Italy, 2008. [Google Scholar]
- Gu, Y.; Goodman, N.A.; Hong, S.; Li, Y. Robust Adaptive Beamforming Based on Interference Covariance Matrix Sparse Reconstruction. Signal Process. 2014, 96, 375–381. [Google Scholar] [CrossRef]
- Gu, Y.; Leshem, A. Robust Adaptive Beamforming Based on Interference Covariance Matrix Reconstruction and Steering Vector Estimation. IEEE Trans. Signal Process. 2012, 60, 3881–3885. [Google Scholar]
- Brandwood, D.H. A Complex Gradient Operator and Its Application in Adaptive Array Theory. IEE Proc. F Commun. Radar Signal Process. 1983, 130, 11–16. [Google Scholar] [CrossRef]
- Zaharov, V.V.; Teixeira, M. SMI-MVDR Beamformer Implementations for Large Antenna Array and Small Sample Size. IEEE Trans. Circuits Syst. 2008, 55, 3317–3327. [Google Scholar] [CrossRef]
- Zhang, X.; Yu, F.X.; Guo, R.; Kumar, S.; Wang, S.; Chang, S. Fast Orthogonal Projection Based on Kronecker Product. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 Decemner 2015; pp. 2929–2937.
- Zhang, J.; Blum, R.S. Asymptotically Optimal Truncated Multivariate Gaussian Hypothesis Testing with Application to Consensus Algorithms. IEEE Trans. Signal Process. 2014, 62, 431–442. [Google Scholar] [CrossRef]
- Tullsson, B.E. Monopulse Tracking of Rayleigh Targets, a Simple Approach. IEEE Trans. Aerosp. Electron. Syst. 1991, 3, 520–531. [Google Scholar] [CrossRef]
- Nickel, U.R.O.; Chaumette, E.; Larzabal, P. Statistical Performance Prediction of Generalized Monopulse Estimation. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 381–404. [Google Scholar] [CrossRef]


| Method | Case 1 | Case 2 | Case 3 | Case 4 |
|---|---|---|---|---|
| Proposed algorithm | ||||
| MVAM |
| Method | Case 1 | Case 2 | Case 3 | Case 4 |
|---|---|---|---|---|
| Proposed algorithm | ||||
| MVAM |
| Method | Case 1 | Case 2 | Case 3 |
|---|---|---|---|
| Proposed algorithm | |||
| MVAM |
| Method | Case 1 | Case 2 | Case 3 |
|---|---|---|---|
| Proposed algorithm | |||
| MVAM |
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Li, Y.; Yang, X.; Zheng, L.; Long, T.; Baker, C.J. A Novel Monopulse Technique for Adaptive Phased Array Radar. Sensors 2017, 17, 116. https://doi.org/10.3390/s17010116
Zhang X, Li Y, Yang X, Zheng L, Long T, Baker CJ. A Novel Monopulse Technique for Adaptive Phased Array Radar. Sensors. 2017; 17(1):116. https://doi.org/10.3390/s17010116
Chicago/Turabian StyleZhang, Xinyu, Yang Li, Xiaopeng Yang, Le Zheng, Teng Long, and Christopher J. Baker. 2017. "A Novel Monopulse Technique for Adaptive Phased Array Radar" Sensors 17, no. 1: 116. https://doi.org/10.3390/s17010116





