A Review of Distributed Optical Fiber Sensors for Civil Engineering Applications
Abstract
:1. Introduction
1.1. Motivation for SHM
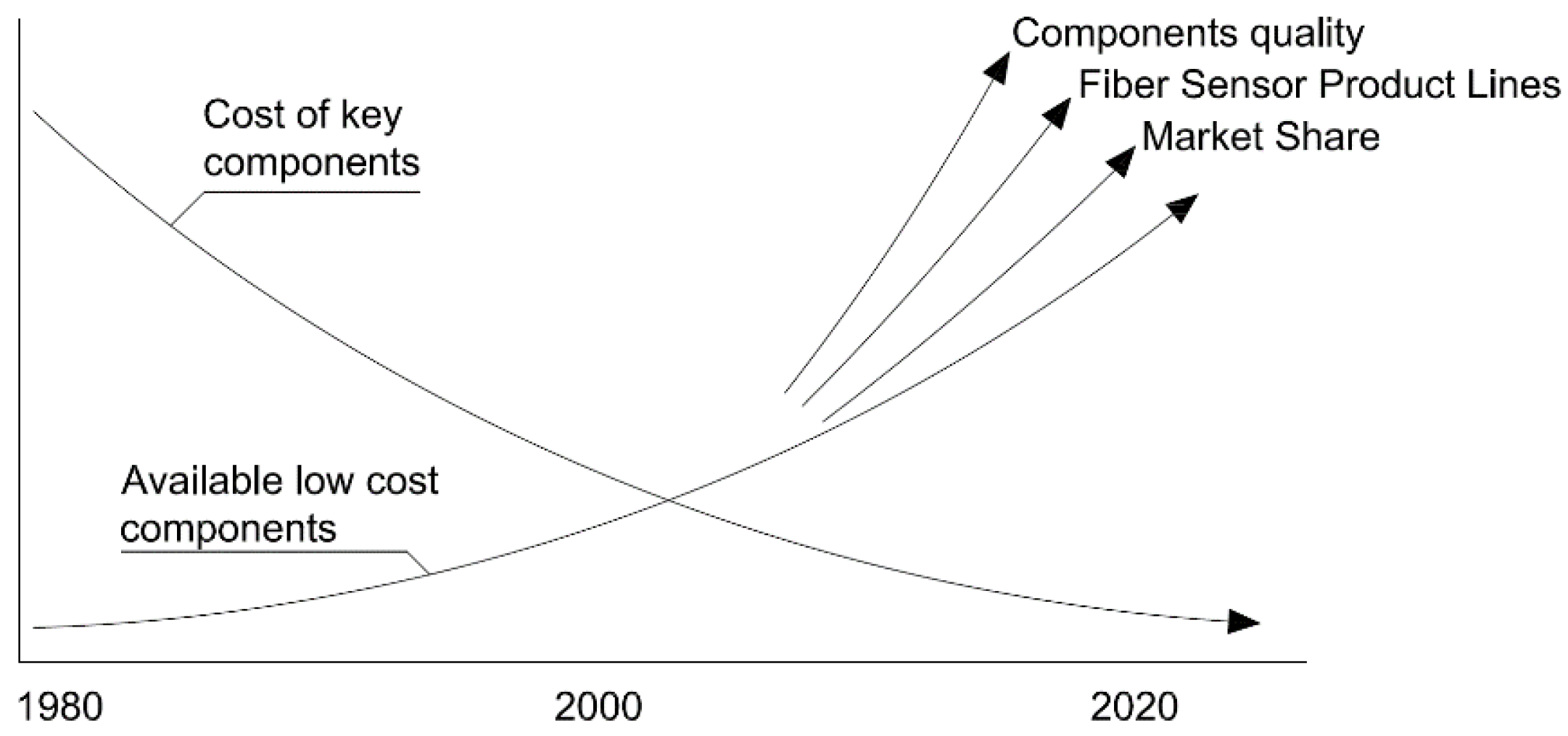
1.2. Optical Fiber Technology in SHM of Built Environment
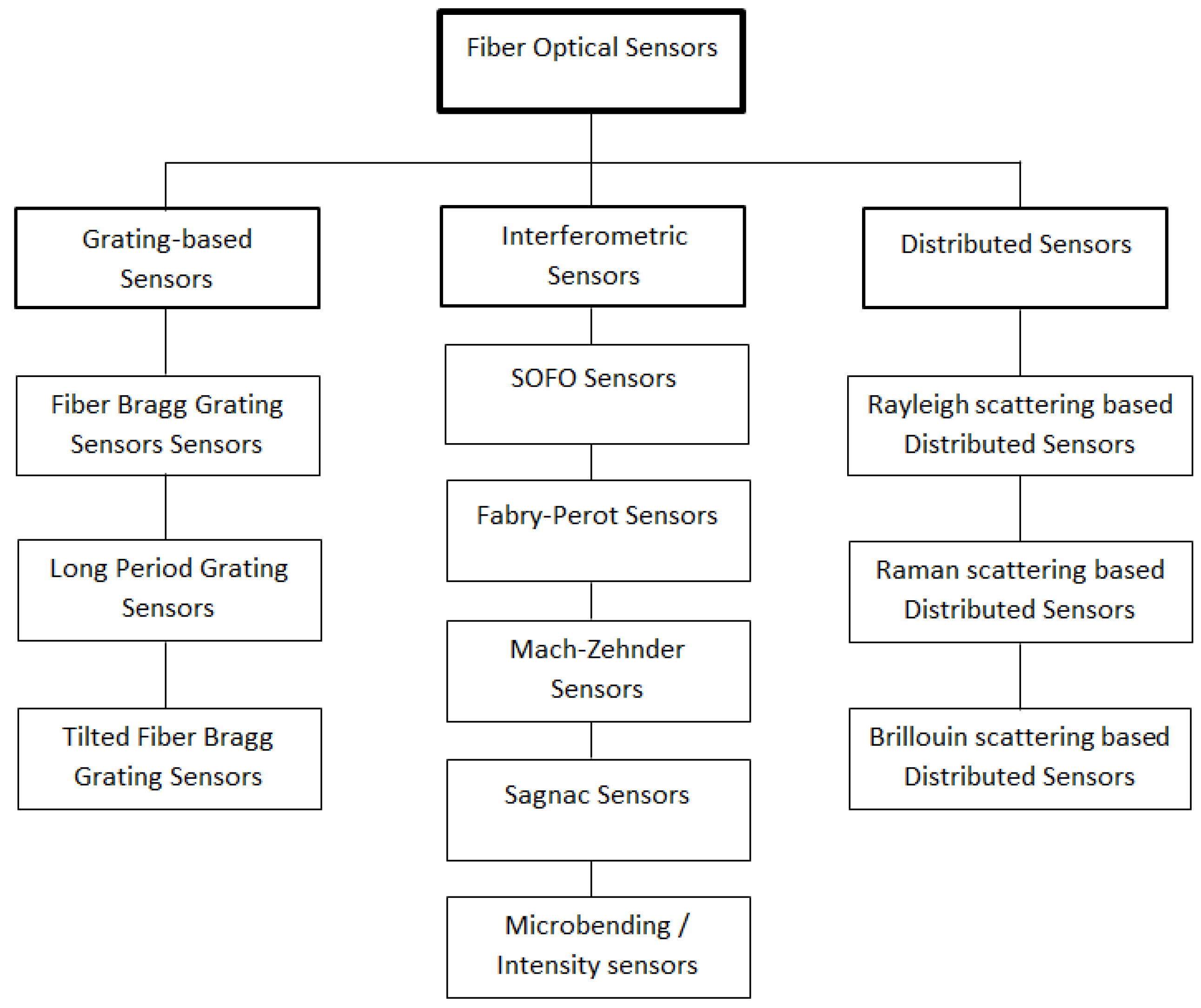
2. Fiber Optic Sensors
2.1. Introduction
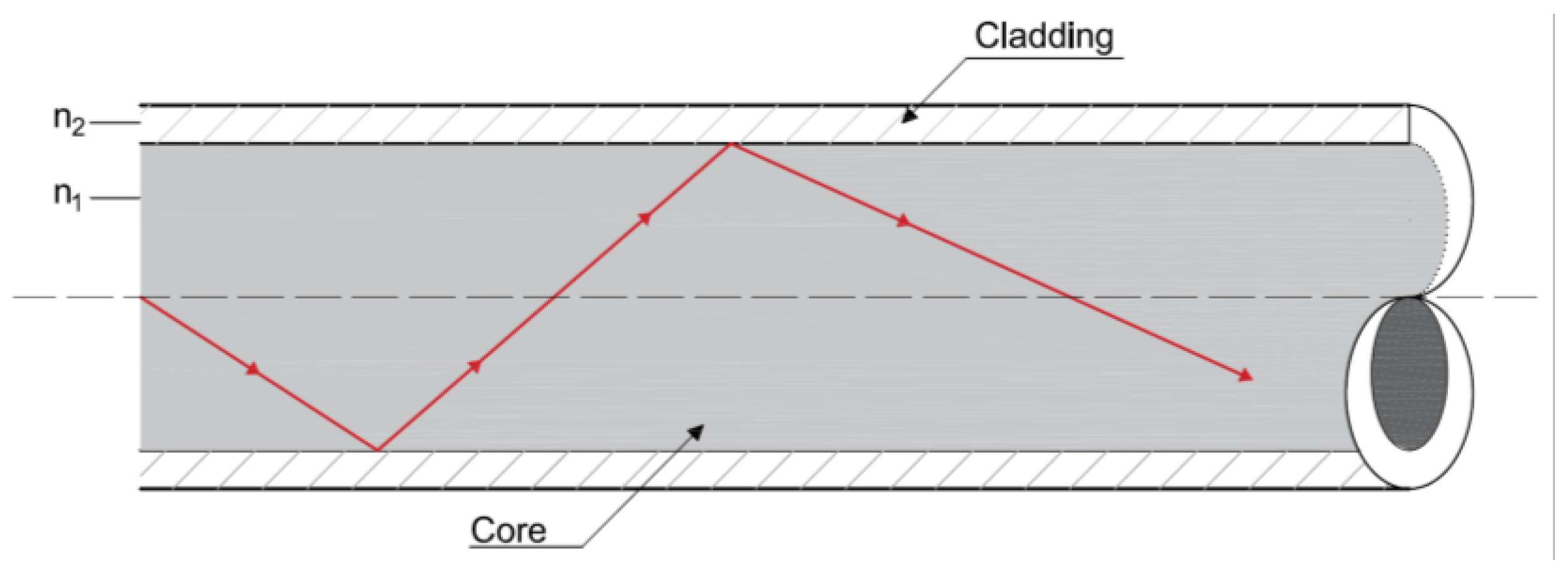
2.2. Basics of Fiber Optic Sensors
2.3. Distributed Fiber Optic Sensors
2.3.1. Scattering in Optical Fibers
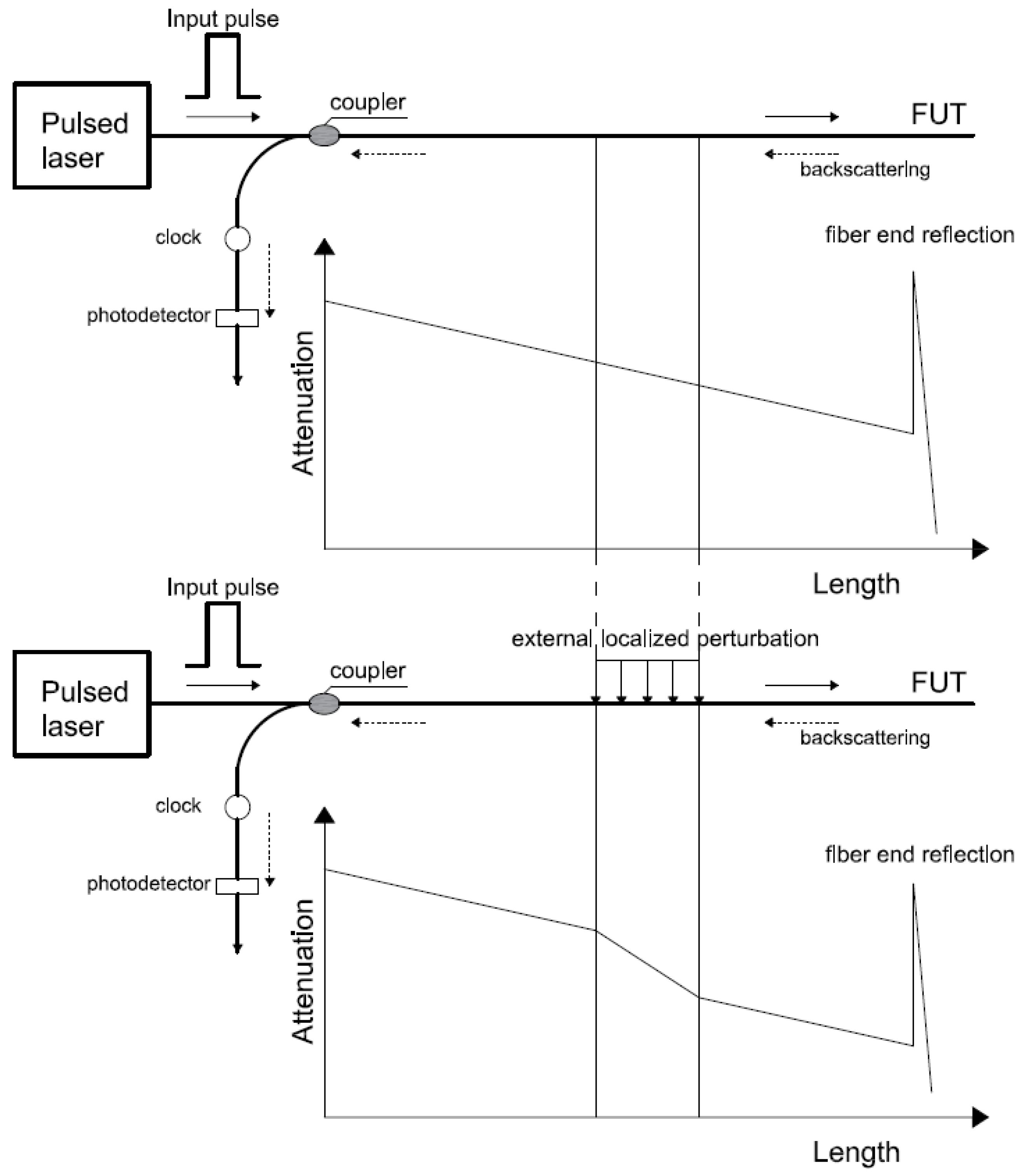
2.3.2. Time Domain Reflectometry—OTDR
BOTDR and BOTDA
2.3.3. Frequency Domain Reflectometry
3. Civil Engineering SHM Applications with DOFS
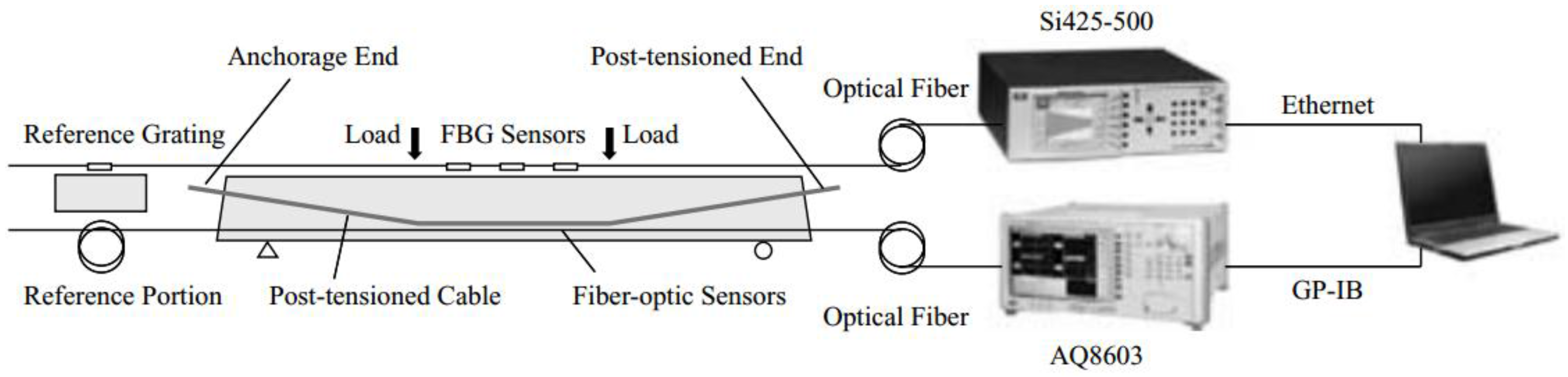
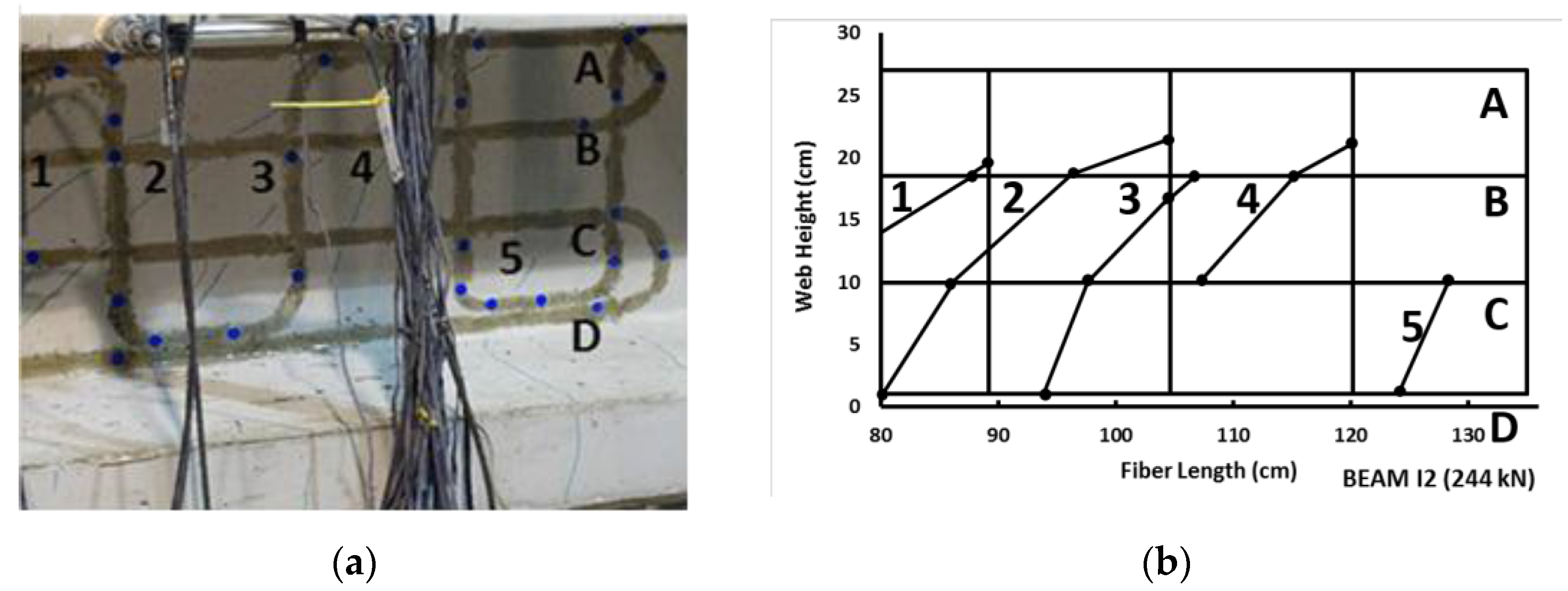
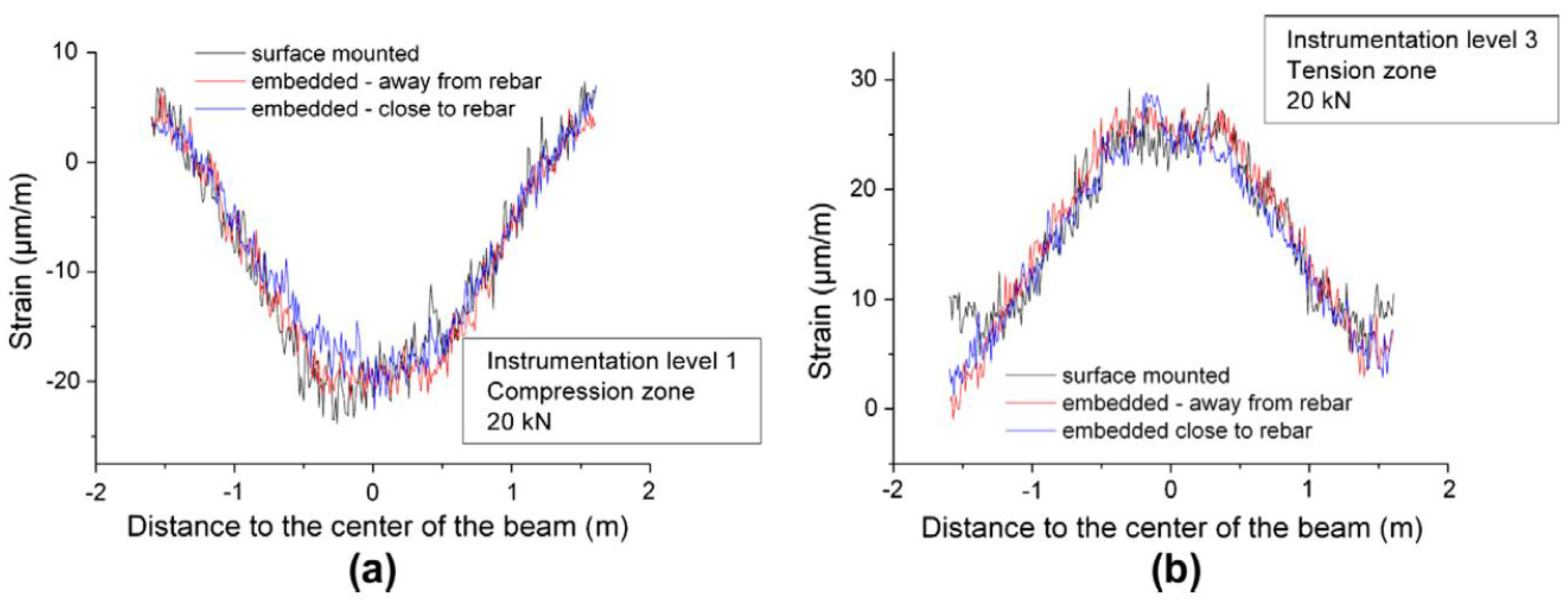
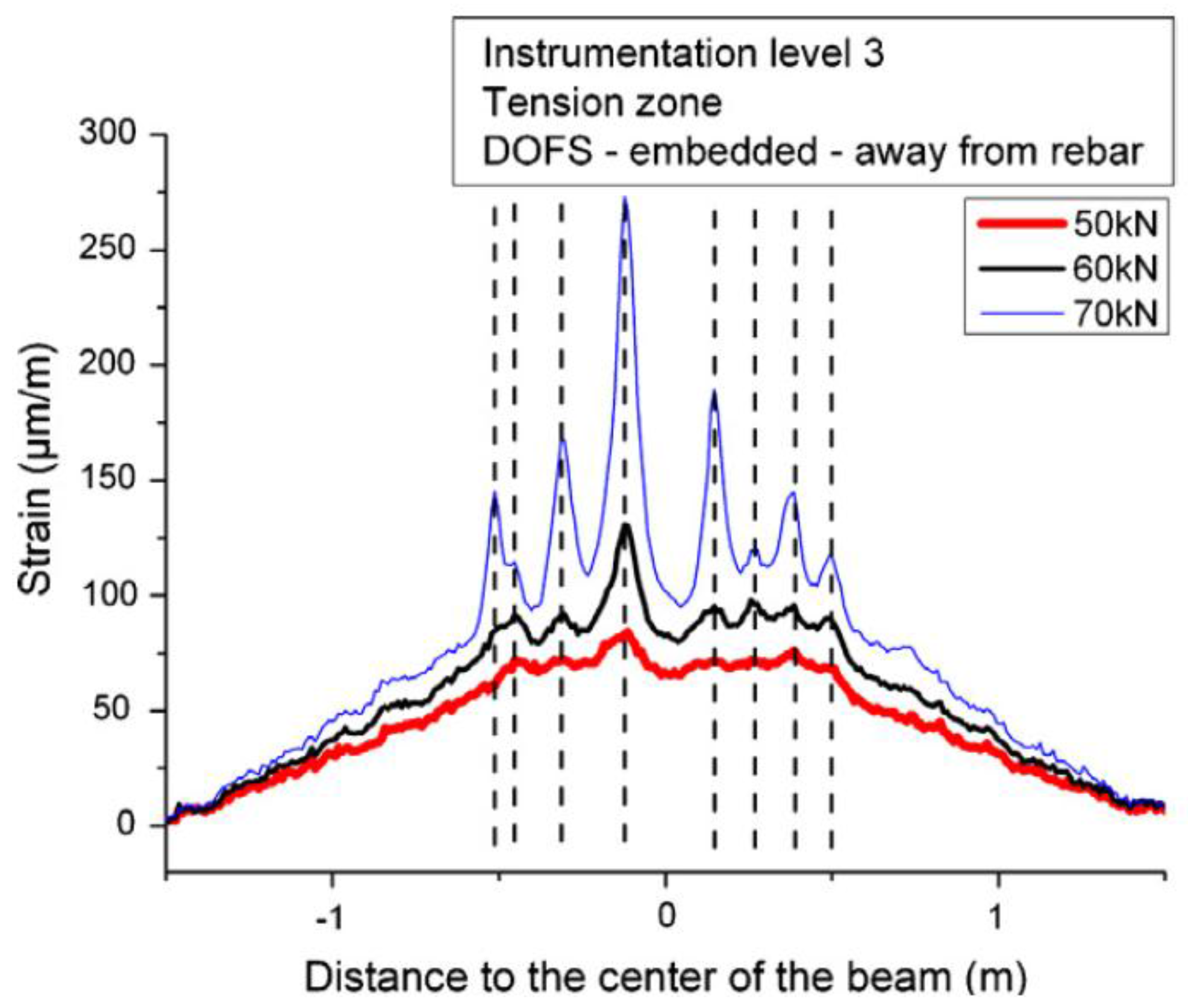
3.1. Laboratory Tests
3.2. Geotechnical Structures
3.3. Pipelines
3.4. Bridges
3.5. Dams
3.6. Examples in Other Fields
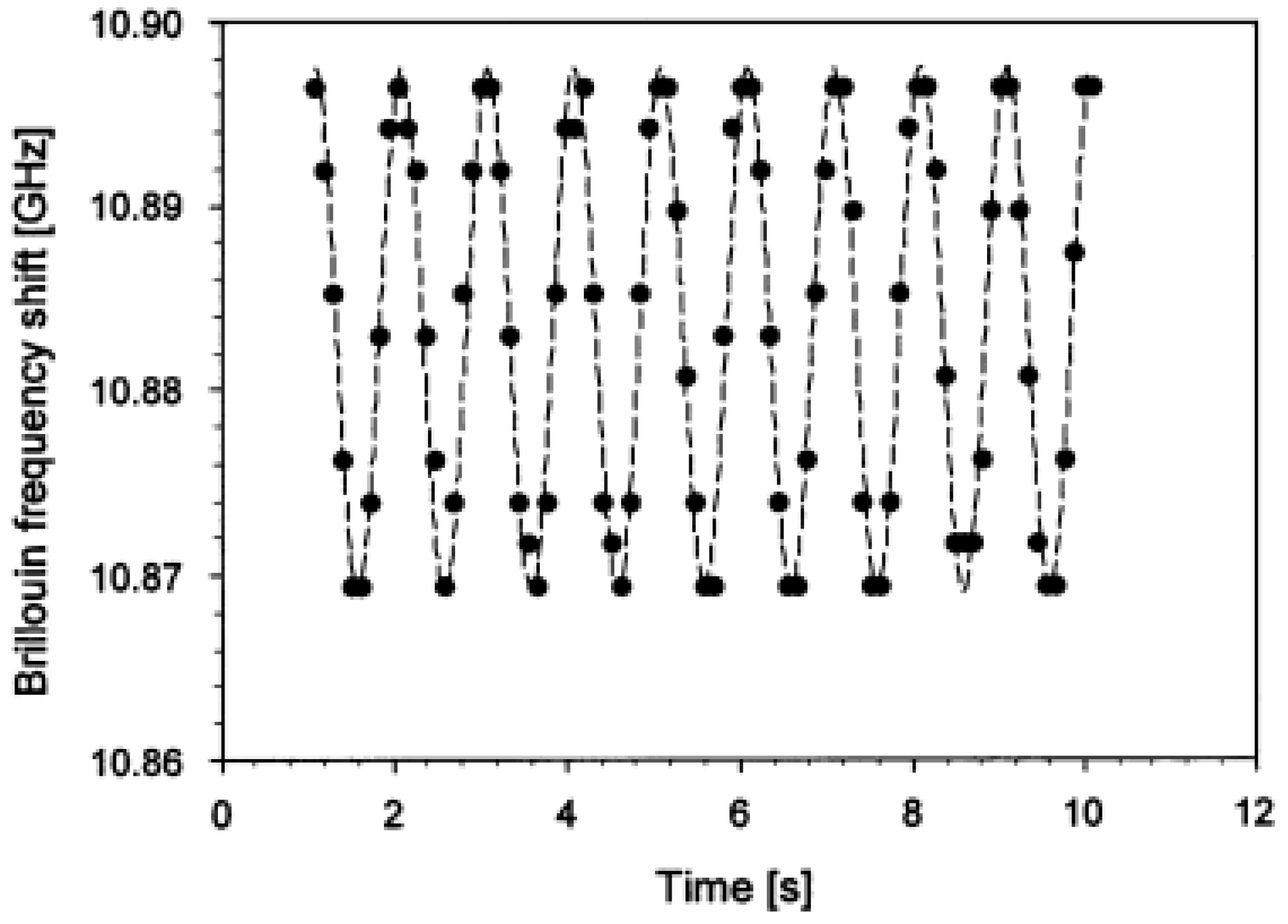
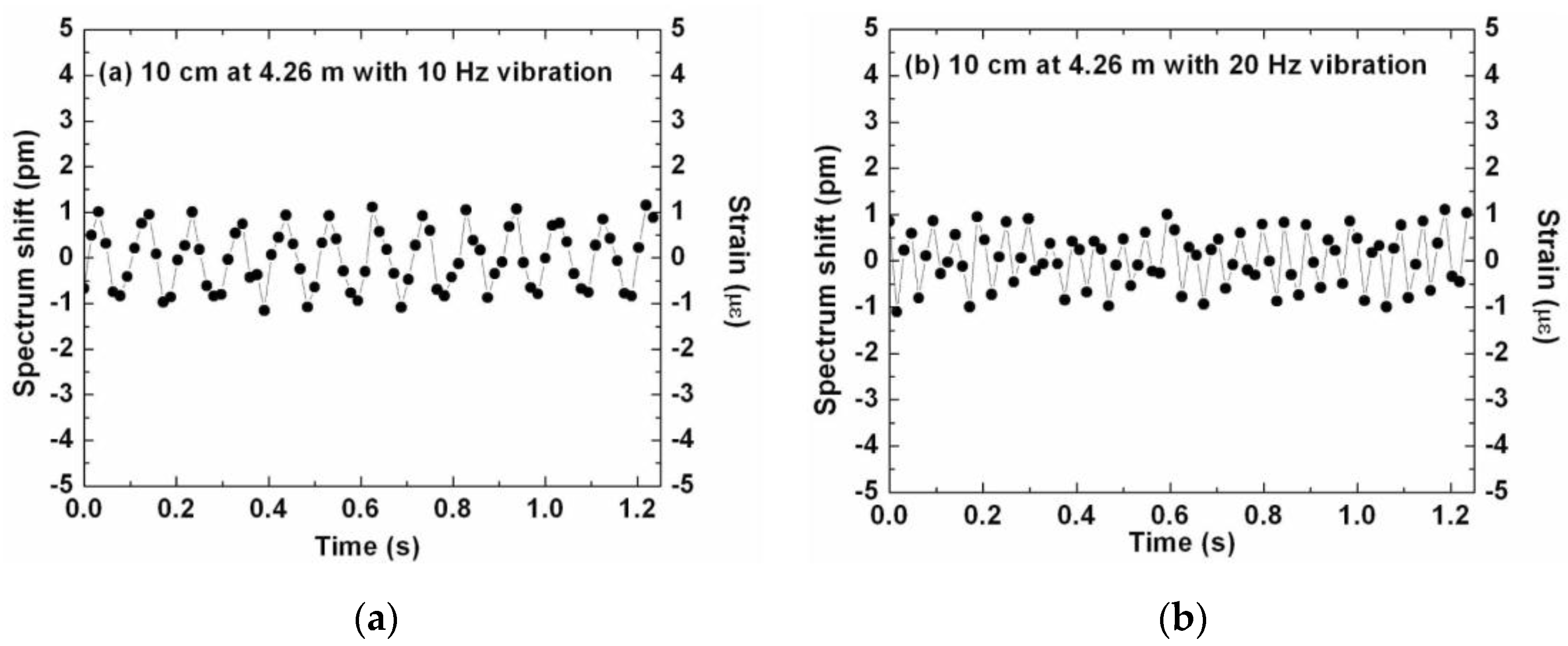
3.7. Dynamic Capabilities
4. Challenges When Using Distributed Optical Fibers
5. Conclusions
Acknowledgments
Conflicts of Interest
References
- ASCE. 2013 Report Card for America’s Infrastructure; American Society of Civil Engineers: Reston, VA, USA, 2013. [Google Scholar]
- López-Higuera, J.M.; Cobo, L.R.; Incera, A.Q.; Cobo, A. Fiber optic sensors in structural health monitoring. J. Lightwave Technol. 2011, 29, 587–608. [Google Scholar] [CrossRef]
- Farrar, C.R.; Worden, K. An introduction to structural health monitoring. Philos. Trans. A Math. Phys. Eng. Sci. 2007, 365, 303–315. [Google Scholar] [CrossRef] [PubMed]
- Kudva, J.N.; Marantidis, C.; Gentry, J.D.; Blazic, E. Smart structures concepts for aircraft structural health monitoring. In Proceedings of the 1993 North American Conference on Smart Structures and Materials, Albuquerque, NM, USA, 1–4 February 1993; pp. 964–971.
- Giurgiutiu, V.; Rogers, C.A. Recent advancements in the electromechanical (E/M) impedance method for structural health monitoring and NDE. In Proceedings of the 5th Annual International Symposium on Smart Structures and Materials, San Diego, CA, USA, 1–5 March 1998; pp. 536–547.
- Sohn, H.; Farrar, C.R.; Hemez, F.M.; Czarnecki, J.J. A Review of Structural Health Review of Structural Health Monitoring Literature 1996–2001; Los Alamos National Laboratory: Los Alamos, NM, USA, 2002. [Google Scholar]
- Lynch, J.P.; Loh, K.J. A summary review of wireless sensors and sensor networks for structural health monitoring. Shock Vib. Dig. 2006, 38, 91–130. [Google Scholar] [CrossRef]
- Glisic, B.; Inaudi, D.; Casanova, N. SHM process as perceived through 350 projects. In Proceedings of the SPIE Smart Structures and Materials + Nondestructive Evaluation and Health Monitoring, San Diego, CA, USA, 8 April 2010; pp. 48–76.
- Rice, J.A.; Mechitov, K.; Sim, S.-H.; Nagayama, T.; Jang, S.; Kim, R.; Spencer, B.F., Jr.; Agha, G.; Fujino, Y. Flexible smart sensor framework for autonomous structural health monitoring. Smart Struct. Syst. 2010, 6, 423–438. [Google Scholar] [CrossRef]
- Ye, X.W.; Su, Y.H.; Han, J.P. Structural health monitoring of civil infrastructure using optical fiber sensing technology: A comprehensive review. Sci. World J. 2014, 2014, 652329. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez, G.; Casas, J.R.; Villalba, S. SHM by DOFS in civil engineering: A review. Struct. Monit. Maint. 2015, 2, 357–382. [Google Scholar] [CrossRef]
- Glisic, B.; Hubbell, D.; Sigurdardottir, D.H.; Yao, Y. Damage detection and characterization using long-gauge and distributed fiber optic sensors. Opt. Eng. 2013, 52, 087101. [Google Scholar] [CrossRef]
- Bao, X.; Chen, L. Recent progress in distributed fiber optic sensors. Sensors 2012, 12, 8601–8639. [Google Scholar] [CrossRef] [PubMed]
- Glisic, B.; Inaudi, D. Development of method for in-service crack detection based on distributed fiber optic sensors. Struct. Health Monit. 2012, 11, 161–171. [Google Scholar] [CrossRef]
- Posenato, D.; Lanata, F.; Inaudi, D.; Smith, I.F.C. Model-free data interpretation for continuous monitoring of complex structures. Adv. Eng. Inf. 2008, 22, 135–144. [Google Scholar] [CrossRef]
- Udd, E. An overview of fiber-optic sensors. Rev. Sci. Instrum. 1995, 66, 4015. [Google Scholar] [CrossRef]
- Kersey, A.D. A review of recent developments in fiber optic sensor technology. Opt. Fiber Technol. 1996, 2, 291–317. [Google Scholar] [CrossRef]
- Grattan, K.T.V.; Sun, T. Fiber optic sensor technology: An overview. Sens. Actuators A Phys. 2000, 82, 40–61. [Google Scholar] [CrossRef]
- Lee, B. Review of the present status of optical fiber sensors. Opt. Fiber Technol. 2003, 9, 57–79. [Google Scholar] [CrossRef]
- Li, H.-N.; Li, D.-S.; Song, G.-B. Recent applications of fiber optic sensors to health monitoring in civil engineering. Eng. Struct. 2004, 26, 1647–1657. [Google Scholar] [CrossRef]
- Ferdinand, P. The evolution of optical fiber sensors technologies during the 35 last years and their applications in structure health monitoring. In Proceedings of the 7th European Workshop Structure Health Monitoring (EWSHM), Nantes, France, 8–11 July 2014.
- Leung, C.K.Y.; Wan, K.T.; Inaudi, D.; Bao, X.; Habel, W.; Zhou, Z.; Ou, J.; Ghandehari, M.; Wu, H.C.; Imai, M. Review: Optical fiber sensors for civil engineering applications. Mater. Struct. 2013, 48, 871–906. [Google Scholar] [CrossRef]
- Udd, E.; Spillman, W.B., Jr. Fiber Optic Sensors: An Introduction for Engineers and Scientists, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Giallorenzi, T.G.; Bucaro, J.A.; Dandridge, A.; Sigel, G.H.; Cole, J.H.; Rashleigh, S.C.; Priest, R.G. Optical fiber sensor technology. IEEE Trans. Microw. Theory Tech. 1982, 30, 472–511. [Google Scholar] [CrossRef]
- Francis, T.S.; Yin, S. Fiber Optic Sensors; Marcel Dekker Inc.: New York, NY, USA, 2002. [Google Scholar]
- Habel, W.R.; Krebber, K. Fiber-optic sensor applications in civil and geotechnical engineering. Photonic Sens. 2011, 1, 268–280. [Google Scholar] [CrossRef]
- Gupta, B.D. Fiber Optic Sensors: Principles and Applications; New India Publishing: New Delhi, India, 2006. [Google Scholar]
- Gholamzadeh, B.; Nabovati, H. Fiber optic sensors. Int. J. Electr. Comput. Energy Electron. Commun. Eng. 2008, 2, 1107–1117. [Google Scholar]
- Casas, J.R.; Cruz, P.J.S. Fiber optic sensors for bridge monitoring. J. Bridge Eng. 2003, 8, 362–373. [Google Scholar] [CrossRef]
- Guo, H.; Xiao, G.; Mrad, N.; Yao, J. Fiber optic sensors for structural health monitoring of air platforms. Sensors 2011, 11, 3687–3705. [Google Scholar] [CrossRef] [PubMed]
- Peairs, D.M.; Sterner, L.; Flanagan, K.; Kochergin, V. Fiber optic monitoring of structural composites using optical backscatter reflectometry. In Proceedings of the 41st International SAMPE Technical Conference, Wichita, KS, USA, 19–22 October 2009; pp. 19–22.
- Rodrigues, C.; Felix, C.; Figueiras, J. Fiber-optic-based displacement transducer to measure bridge deflections. Struct. Health Monit. 2010, 10, 147–156. [Google Scholar] [CrossRef]
- Barbosa, C.; Costa, N.; Ferreira, L.A.; Araújo, F.M.; Varum, H.; Costa, A.; Fernandes, C.; Rodrigues, H. Weldable fibre Bragg grating sensors for steel bridge monitoring. Meas. Sci. Technol. 2008, 19, 125305. [Google Scholar] [CrossRef]
- López-Higuera, J.M.; Misas, J.; Incera, A.Q.; Cuenca, J.E. Fiber optic civil structure monitoring system. Opt. Eng. 2005, 44, 1–10. [Google Scholar]
- Del Grosso, A.; Bergmeister, K.; Inaudi, D.; Santa, U. Monitoring of bridges and concrete structures with fibre optic sensors in Europe. IABSE Symp. Rep. 2001, 84, 15–22. [Google Scholar]
- Tennyson, R.C.; Mufti, A.A.; Rizkalla, S.; Tadros, G.; Benmokrane, B. Structural Health Monitoring of innovative bridges in Canada with fiber optic sensors. Smart Mater. Struct. 2001, 10, 560–573. [Google Scholar] [CrossRef]
- López-Higuera, J.M. Optical Sensors; Universidad de Cantabria: Cantabria, Spain, 1998. [Google Scholar]
- Boyd, R. Nonlinear Optics, 3rd ed.; Academic Press: Rochester, NY, USA, 2008. [Google Scholar]
- Cheng, J.-X.; Xie, X.S. Coherent Anti-Stokes Raman Scattering: Instrumentation, Theory, and Applications. J. Phys. Chem. B 2004, 108, 827–840. [Google Scholar] [CrossRef]
- Abalde-Cela, S.; Aldeanueva-Potel, P.; Mateo-Mateo, C.; Rodríguez-Lorenzo, L.; Alvarez-Puebla, R.A.; Liz-Marzán, L.M. Surface-enhanced Raman scattering biomedical applications of plasmonic colloidal particles. J. R. Soc. Interface 2010, 7, S435–S450. [Google Scholar] [CrossRef] [PubMed]
- Oakley, L.H.; Dinehart, S.A.; Svoboda, S.A.; Wustholz, K.L. Identification of organic materials in historical oil paintings using correlated extractionless surface-enhanced Raman scattering and fluorescence microscopy. Anal. Chem. 2011, 83, 3986–3989. [Google Scholar] [CrossRef] [PubMed]
- Henault, J.-M.; Moreau, G.; Blairon, S.; Salin, J.; Courivaud, J.-R.; Taillade, F.; Merliot, E.; Dubois, J.-P.; Bertrand, J.; Buschaert, S.; et al. Truly distributed optical fiber sensors for structural health monitoring: From the telecommunication optical fiber drawling tower to water leakage detection in dikes and concrete structure strain monitoring. Adv. Civ. Eng. 2010, 2010. [Google Scholar] [CrossRef]
- Kurashima, T.; Horiguchi, T.; Tateda, M. Distributed-temperature sensing using stimulated Brillouin scattering in optical silica fibers. Opt. Lett. 1990, 15, 1038–1040. [Google Scholar] [CrossRef] [PubMed]
- Bao, X.; Dhliwayo, J.; Heron, N.; Webb, D.J.; Jackson, D.A. Experimental and theoretical studies on a distributed temperature sensor based on Brillouin scattering. J. Lightwave Technol. 1995, 13, 1340–1348. [Google Scholar] [CrossRef]
- Zeng, X.; Bao, X.; Chhoa, C.Y.; Bremner, T.W.; Brown, A.W.; DeMerchant, M.D.; Ferrier, G.; Kalamkarov, A.L.; Georgiades, A.V. Strain measurement in a concrete beam by use of the Brillouin-scattering-based distributed fiber sensor with single-mode fibers embedded in glass fiber reinforced polymer rods and bonded to steel reinforcing bars. Appl. Opt. 2002, 41, 5105–5114. [Google Scholar] [CrossRef] [PubMed]
- Bastianini, F.; Matta, F.; Rizzo, A.; Galati, N.; Nanni, A. Overview of recent bridge monitoring applications using distributed Brillouin fiber optic sensors. J. Nondestruct. Test. 2007, 12, 269–276. [Google Scholar]
- Ravet, F.; Briffod, F.; Glisǐć, B.; Nikles, M.; Inaudi, D. Submillimeter crack detection with Brillouin-based fiber-optic sensors. IEEE Sens. J. 2009, 9, 1391–1396. [Google Scholar] [CrossRef]
- Motil, A.; Bergman, A.; Tur, M. State of the art of Brillouin fiber-optic distributed sensing. Opt. Laser Technol. 2015, 78, 1–23. [Google Scholar] [CrossRef]
- Shibata, N.; Waarts, R.G.; Braun, R.P. Brillouin-gain spectra for single-mode fibers having pure-silica, GeO2-doped, and P2O5-doped cores. Opt. Lett. 1987, 12, 269–271. [Google Scholar] [CrossRef] [PubMed]
- Tateda, M.; Horiguchi, T.; Kurashima, T.; Ishihara, K. First measurement of strain distribution along field-installed optical fibers using Brillouin spectroscopy. J. Lightwave Technol. 1990, 8, 1269–1272. [Google Scholar] [CrossRef]
- Shimizu, K.; Horiguchi, T.; Koyamada, Y.; Kurashima, T. Coherent self-heterodyne Brillouin OTDR for measurement of Brillouin frequency shift distribution in optical fibers. J. Lightwave Technol. 1994, 12, 730–736. [Google Scholar] [CrossRef]
- Galindez-Jamioy, C.A.; López-Higuera, J.M. Brillouin Distributed Fiber Sensors: An Overview and Applications. J. Sens. 2012, 2012. [Google Scholar] [CrossRef]
- Nikles, M.; Thevenaz, L.; Robert, P.A. Simple distributed temperature sensor based on Brillouin gain spectrum analysis. Proc. SPIE Int. Soc. Opt. Eng. 1994, 138–141. [Google Scholar]
- Uchida, S.; Levenberg, E.; Klar, A. On-specimen strain measurement with fiber optic distributed sensing. Measurement 2015, 60, 104–113. [Google Scholar] [CrossRef]
- Feng, X.; Zhou, J.; Sun, C.; Zhang, X.; Ansari, F. Theoretical and experimental investigations into crack detection with BOTDR-distributed fiber optic sensors. J. Eng. Mech. 2013, 139, 1797–1807. [Google Scholar] [CrossRef]
- Hotate, K.; Tanaka, M. Distributed fiber Brillouin strain sensing with 1 cm spatial resolution by correlation-based continuous wave technique. Proc. SPIE Int. Soc. Opt. Eng. 2000, 4185, 647–650. [Google Scholar] [CrossRef]
- Imai, M.; Nakano, R.; Kono, T.; Ichinomiya, T.; Miura, S.; Mure, M. Crack detection application for fiber reinforced concrete using BOCDA-based optical fiber strain sensor. J. Struct. Eng. 2010, 136, 1001–1008. [Google Scholar] [CrossRef]
- Belal, M.; Newson, T.P. A 5 cm spatial resolution temperature compensated distributed strain sensor evaluated using a temperature controlled strain rig. Opt. Lett. 2011, 36, 4728–4730. [Google Scholar] [CrossRef] [PubMed]
- Shen, S.; Wu, Z.; Yang, C.; Wan, C.; Tang, Y.; Wu, G. An improved conjugated beam method for deformation monitoring with a distributed sensitive fiber optic sensor. Struct. Health Monit. 2010, 9, 361–378. [Google Scholar] [CrossRef]
- Zadok, A.; Antman, Y.; Primerov, N.; Denisov, A.; Sancho, J.; Thevenaz, L. Random-access distributed fiber sensing. Laser Photonics Rev. 2012, 6, L1–L5. [Google Scholar] [CrossRef]
- Eickhoff, W.; Ulrich, R. Optical frequency domain reflectometry in single-mode fiber. Appl. Phys. Lett. 1981, 39, 693–695. [Google Scholar] [CrossRef]
- Nakayama, J.; Iizuka, K.; Nielsen, J. Optical fiber fault locator by the step frequency method. Appl. Opt. 1987, 26, 440–443. [Google Scholar] [CrossRef] [PubMed]
- Yu, F.T.S.; Zhang, J.; Yin, S.; Ruffin, P.B. A novel distributed fiber sensor based on the Fourier spectrometer technique. In Proceedings of the OSA Annual Meeting, Dallas, TX, USA, 2–7 October 1994; pp. 50–56.
- Juškaitis, R.; Mamedov, A.M.; Potapov, V.T.; Shatalin, S.V. Distributed interferometric fiber sensor system. Opt. Lett. 1992, 17, 1623–1625. [Google Scholar] [CrossRef] [PubMed]
- Rathod, R.; Pechstedt, R.D.; Jackson, D.A.; Webb, D.J. Distributed temperature-change sensor based on Rayleigh backscattering in an optical fiber. Opt. Lett. 1994, 19, 593–595. [Google Scholar] [CrossRef] [PubMed]
- Froggatt, M.; Moore, J. High-spatial-resolution distributed strain measurement in optical fiber with Rayleigh scatter. Appl. Opt. 1998, 37, 1735–1740. [Google Scholar] [CrossRef] [PubMed]
- Grave, J.H.L.; Haheim, M.L.; Echtermeyer, A.T. Measuring changing strain fields in composites with Distributed Fiber-Optic Sensing using the optical backscatter reflectometer. Compos. Part B Eng. 2015, 74, 138–146. [Google Scholar] [CrossRef]
- Soller, B.; Gifford, D.; Wolfe, M.; Froggatt, M. High resolution optical frequency domain reflectometry for characterization of components and assemblies. Opt. Express 2005, 13, 666–674. [Google Scholar] [CrossRef] [PubMed]
- Froggatt, M.; Soller, B.; Gifford, D.; Wolfe, M. Correlation and keying of Rayleigh scatter for loss and temperature sensing in parallel optical networks. In Proceedings of the Optical Fiber Communication Conference, Los Angeles, CA, USA, 23–27 February 2004.
- Froggatt, M.E.; Gifford, D.K.; Kreger, S.T.; Wolfe, M.S.; Soller, B.J. Distributed strain and temperature discrimination in unaltered polarization maintaining fiber. Opt. Fiber Sens. 2006. [Google Scholar] [CrossRef]
- Koshikiya, Y.; Fan, X.; Ito, F. Highly Sensitive Coherent Optical Frequency-domain Reflectometry Employing SSB-modulator with cm-level Spatial Resolution over 5 km. In Proceedings of the 33rd European Conference and Ehxibition of Optical Communication (ECOC), Berlin, Germany, 16–20 September 2007.
- Palmieri, L.; Schenato, L. Distributed optical fiber sensing based on Rayleigh scattering. Open Opt. J. 2013, 7, 104–127. [Google Scholar] [CrossRef]
- Tanner, M.G.; Dyer, S.D.; Baek, B.; Hadfield, R.H.; Woo Nam, S. High-resolution single-mode fiber-optic distributed Raman sensor for absolute temperature measurement using superconducting nanowire single-photon detectors. Appl. Phys. Lett. 2011, 99, 201110. [Google Scholar] [CrossRef]
- Park, J.; Bolognini, G.; Lee, D.; Kim, P.; Cho, P.; di Pasquale, F.; Park, N. Raman-based distributed temperature sensor with simplex coding and link optimization. IEEE Photonics Technol. Lett. 2006, 18, 1879–1881. [Google Scholar] [CrossRef]
- Dong, Y.; Zhang, H.; Chen, L.; Bao, X. 2 cm spatial-resolution and 2 km range Brillouin optical fiber sensor using a transient differential pulse pair. Appl. Opt. 2012, 51, 1229–1235. [Google Scholar] [CrossRef] [PubMed]
- Dong, Y.; Chen, L.; Bao, X. Extending the sensing range of Brillouin optical time-domain analysis combining frequency-division multiplexing and in-line EDFAs. J. Lightwave Technol. 2012, 30, 1161–1167. [Google Scholar] [CrossRef]
- Rao, Y.-J. Recent progress in applications of in-fibre Bragg grating sensors. Opt. Lasers Eng. 1999, 31, 297–324. [Google Scholar] [CrossRef]
- Zhou, Z.; Graver, T.W.; Hsu, L.; Ou, J. Techniques of advanced FBG sensors: Fabrication, demodulation, encapsulation, and their application in the structural health monitoring of bridges. Pac. Sci. Rev. 2003, 5, 116–121. [Google Scholar]
- Chan, T.H.T.; Yu, L.; Tam, H.-Y.; Ni, Y.-Q.; Liu, S.Y.; Chung, W.H.; Cheng, L.K. Fiber Bragg grating sensors for structural health monitoring of Tsing Ma bridge: Background and experimental observation. Eng. Struct. 2006, 28, 648–659. [Google Scholar] [CrossRef]
- Antunes, P.; Lima, H.; Varum, H.; André, P. Optical fiber sensors for static and dynamic health monitoring of civil engineering infrastructures: Abode wall case study. Measurement 2012, 45, 1695–1705. [Google Scholar] [CrossRef]
- Xu, G.Q.; Xiong, D.Y. Applications of fiber Bragg grating sensing technology in engineering. Chin. Opt. 2013, 6, 306–317. [Google Scholar]
- Miller, J.W.; Mendez, A. Fiber Bragg grating sensors: Market overview and new perspectives. In Fiber Bragg Grating Sensors: Recent Advancements, Industrial Applications and Market Exploitation; Bentham Science Publishers: Sharjah, United Arab Emirates, 2014; pp. 313–320. [Google Scholar]
- Hoult, N.A.; Ekim, O.; Regier, R. Damage/deterioration detection for steel structures using distributed fiber optic strain sensors. J. Eng. Mech. 2014, 140, 04014097. [Google Scholar] [CrossRef]
- Quiertant, M.; Baby, F.; Khadour, A.; Marchand, P.; Rivillon, P.; Billo, J.; Lapeyrere, R.; Toutlemonde, F.; Simon, A.; Cordier, J. Deformation monitoring of reinforcement bars with a distributed fiber optic sensor for the SHM of reinforced concrete structures. NDE 2012, 2012, 1–10. [Google Scholar]
- Deif, A.; Martín-Pérez, B.; Cousin, B.; Zhang, C.; Bao, X.; Li, W. Detection of cracks in a reinforced concrete beam using distributed Brillouin fibre sensors. Smart Mater. Struct. 2010, 19, 055014. [Google Scholar] [CrossRef]
- Glisic, B.; Yao, Y. Fiber optic method for health assessment of pipelines subjected to earthquake-induced ground movement. Struct. Health Monit. 2012, 11, 696–711. [Google Scholar] [CrossRef]
- Enckell, M.; Glisic, B.; Myrvoll, F.; Bergstrand, B. Evaluation of a large-scale bridge strain, temperature and crack monitoring with distributed fibre optic sensors. J. Civ. Struct. Health Monit. 2011, 1, 37–46. [Google Scholar] [CrossRef]
- Zhang, W.; Gao, J.; Shi, B.; Cui, H.; Zhu, H. Health monitoring of rehabilitated concrete bridges using distributed optical fiber sensing. Comput. Civ. Infrastruct. Eng. 2006, 21, 411–424. [Google Scholar] [CrossRef]
- Villalba, S.; Casas, J.R. Application of optical fiber distributed sensing to health monitoring of concrete structures. Mech. Syst. Signal Process. 2013, 39, 441–451. [Google Scholar] [CrossRef]
- Rodríguez, G.; Casas, J.R.; Villaba, S. Cracking assessment in concrete structures by distributed optical fiber. Smart Mater. Struct. 2015, 24, 035005. [Google Scholar] [CrossRef]
- Rodríguez, G.; Casas, J.R.; Villalba, S.; Barrias, A. Monitoring of shear cracking in partially prestressed concrete beams by distributed optical fiber sensors. In Proceedings of the 8th International Conference on Bridge Maintenance, Safety and Management, IABMAS 2016, São Paulo, Brazil, 26–30 June 2016.
- Henault, J.-M.; Quiertant, M.; Delepine-Lesoille, S.; Salin, J.; Moreau, G.; Taillade, F.; Benzarti, K. Quantitative strain measurement and crack detection in RC structures using a truly distributed fiber optic sensing system. Constr. Build. Mater. 2012, 37, 916–923. [Google Scholar] [CrossRef]
- Buchoud, E.; Henault, J.-M.; D’Urso, G.; Girard, A.; Blairon, S.; Mars, J.; Vrabie, V. Development of an automatic algorithm to analyze the cracks evolution in a reinforced concrete structure from strain measurements performed by an Optical Backscatter Reflectometer. In Proceedings of the 4th Workshop on Civil Structural Health Monitoring, Berlin, Germany, 23 November 2012.
- Gifford, D.K.; Froggatt, M.E.; Wolfe, M.S.; Kreger, S.T.; Soller, B.J. Millimeter resolution reflectometry over two kilometers. In Proceedings of the IEEE Avionics, Fiber-Optics and Photonics Technology Conference, Victoria, BC, USA, 2–5 October 2007.
- Gifford, D.K.; Kreger, S.T.; Sang, A.K.; Froggatt, M.E.; Duncan, R.G.; Wolfe, M.S.; Soller, B.J. Swept-wavelength interferometric interrogation of fiber Rayleigh scatter for distributed sensing applications. Proc. SPIE 2007, 6770. [Google Scholar] [CrossRef]
- Soller, B.J.; Gifford, D.K.; Wolfe, M.S.; Froggatt, M.E.; Yu, M.H.; Wysocki, P.F. Measurement of localized heating in fiber optic components with millimeter spatial resolution. In Proceedings of the 2006 Optical Fiber Communication Conference and the National Fiber Optic Engineers Conference, Anaheim, CA, USA, 5–10 March 2006.
- Sang, A.K.; Froggatt, M.E.; Gifford, D.K.; Kreger, S.T.; Dickerson, B.D. One centimeter spatial resolution temperature measurements in a nuclear reactor using Rayleigh scatter in optical fiber. IEEE Sens. J. 2008, 8, 1375–1380. [Google Scholar] [CrossRef]
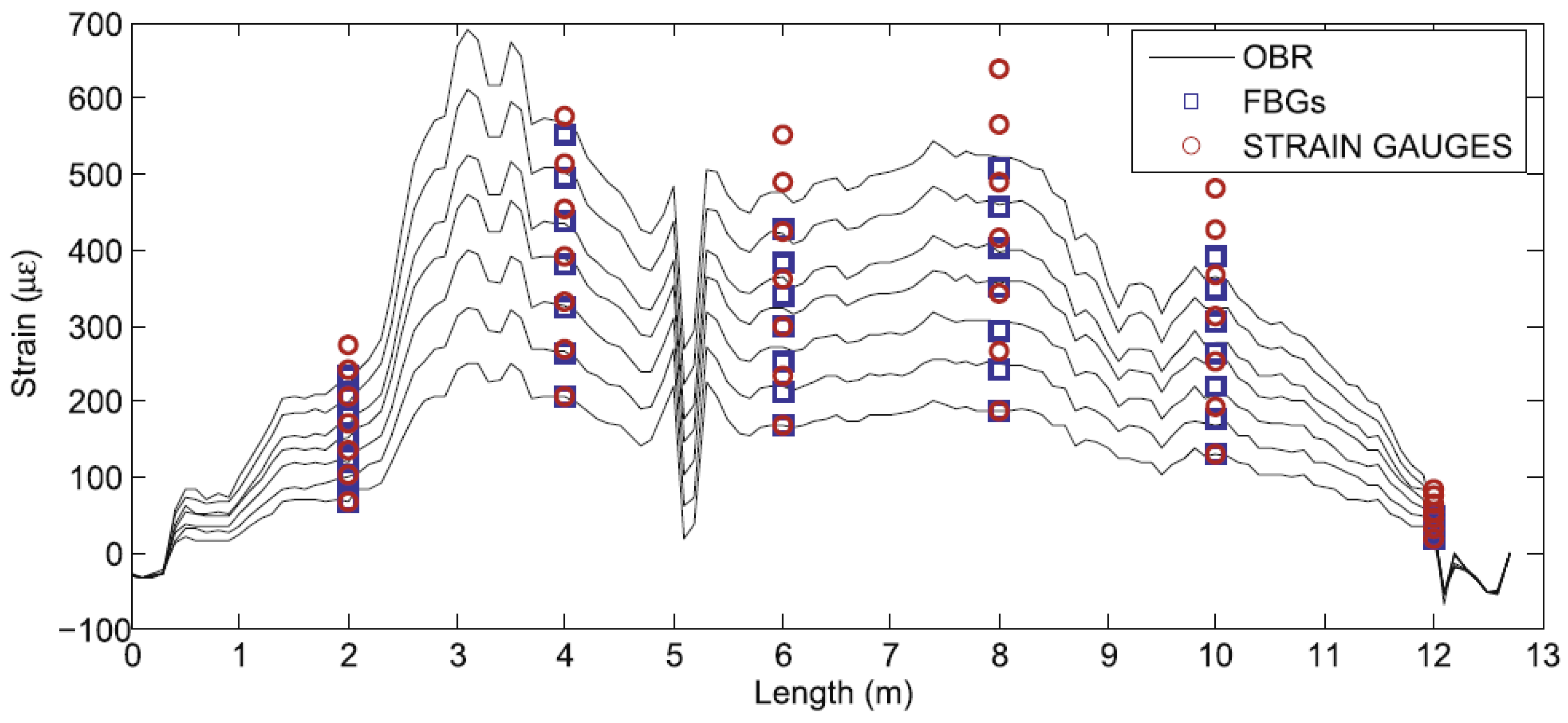
- Sierra-Pérez, J.; Torres-Arredondo, M.A.; Güemes, A. Damage and nonlinearities detection in wind turbine blades based on strain field pattern recognition. FBGs, OBR and strain gauges comparison. Compos. Struct. 2016, 135, 156–166. [Google Scholar] [CrossRef]
- Shi, B.; Sui, H.; Liu, J.; Zhang, D. The BOTDR-based distributed monitoring system for slope engineering. In Proceedings of the 10th IAEG International Congress, Nottingham, UK, 6–10 September 2006; pp. 1–5.
- Zhu, H.-H.; Shi, B.; Zhang, J.; Yan, J.-F.; Zhang, C.-C. Distributed fiber optic monitoring and stability analysis of a model slope under surcharge loading. J. Mt. Sci. 2014, 11, 979–989. [Google Scholar] [CrossRef]
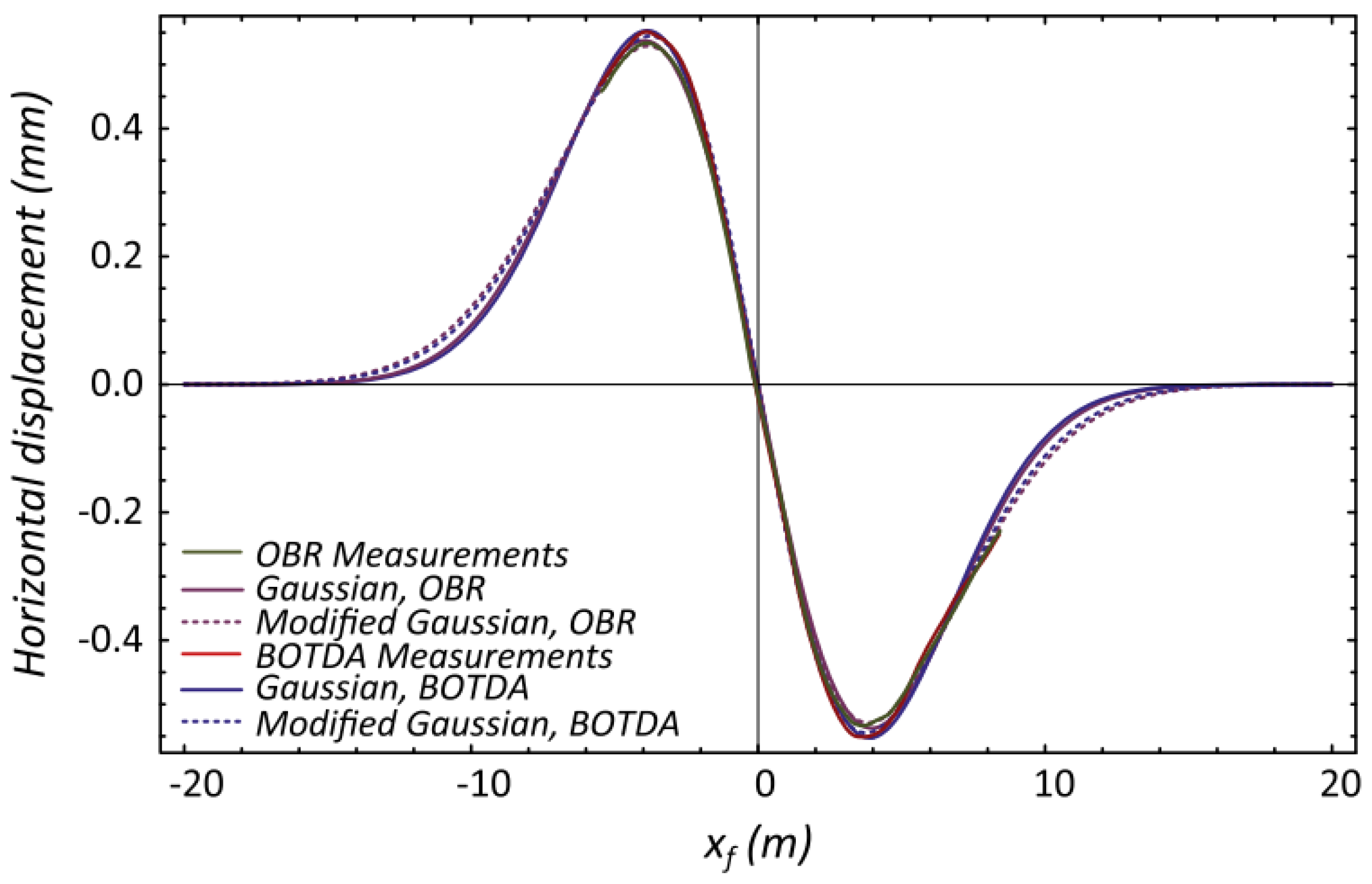
- Klar, A.; Dromy, I.; Linker, R. Monitoring tunneling induced ground displacements using distributed fiber-optic sensing. Tunn. Undergr. Space Technol. 2014, 40, 141–150. [Google Scholar] [CrossRef]
- Klar, A.; Linker, R. Feasibility study of automated detection of tunnel excavation by Brillouin optical time domain reflectometry. Tunn. Undergr. Space Technol. 2010, 25, 575–586. [Google Scholar] [CrossRef]
- Shi, B.; Xu, H.; Chen, B.; Zhang, D.; Ding, Y.; Cui, H.; Gao, J. A feasibility study on the application of fiber-optic distributed sensors for strain measurement in the Taiwan Strait Tunnel project. Mar. Georesour. Geotechnol. 2003, 21, 333–343. [Google Scholar] [CrossRef]
- Rajeev, P.; Kodikara, J.; Chiu, W.K.; Kuen, T. Distributed optical fibre sensors and their applications in pipeline monitoring. Key Eng. Mater. 2013, 558, 424–434. [Google Scholar] [CrossRef]
- Gue, C.Y.; Wilcock, M.; Alhaddad, M.M.; Elshafie, M.Z.E.B.; Soga, K.; Mair, R.J. The monitoring of an existing cast iron tunnel with distributed fibre optic sensing (DFOS). J. Civ. Struct. Health Monit. 2015, 5, 573–586. [Google Scholar] [CrossRef]
- Lanticq, V.; Bourgeois, E.; Magnien, P.; Dieleman, L.; Vinceslas, G.; Sang, A.; Delepine-Lesoille, S. Soil-embedded optical fiber sensing cable interrogated by Brillouin optical time-domain reflectometry (B-OTDR) and optical frequency-domain reflectometry (OFDR) for embedded cavity detection and sinkhole warning system. Meas. Sci. Technol. 2009, 20, 034018. [Google Scholar] [CrossRef]
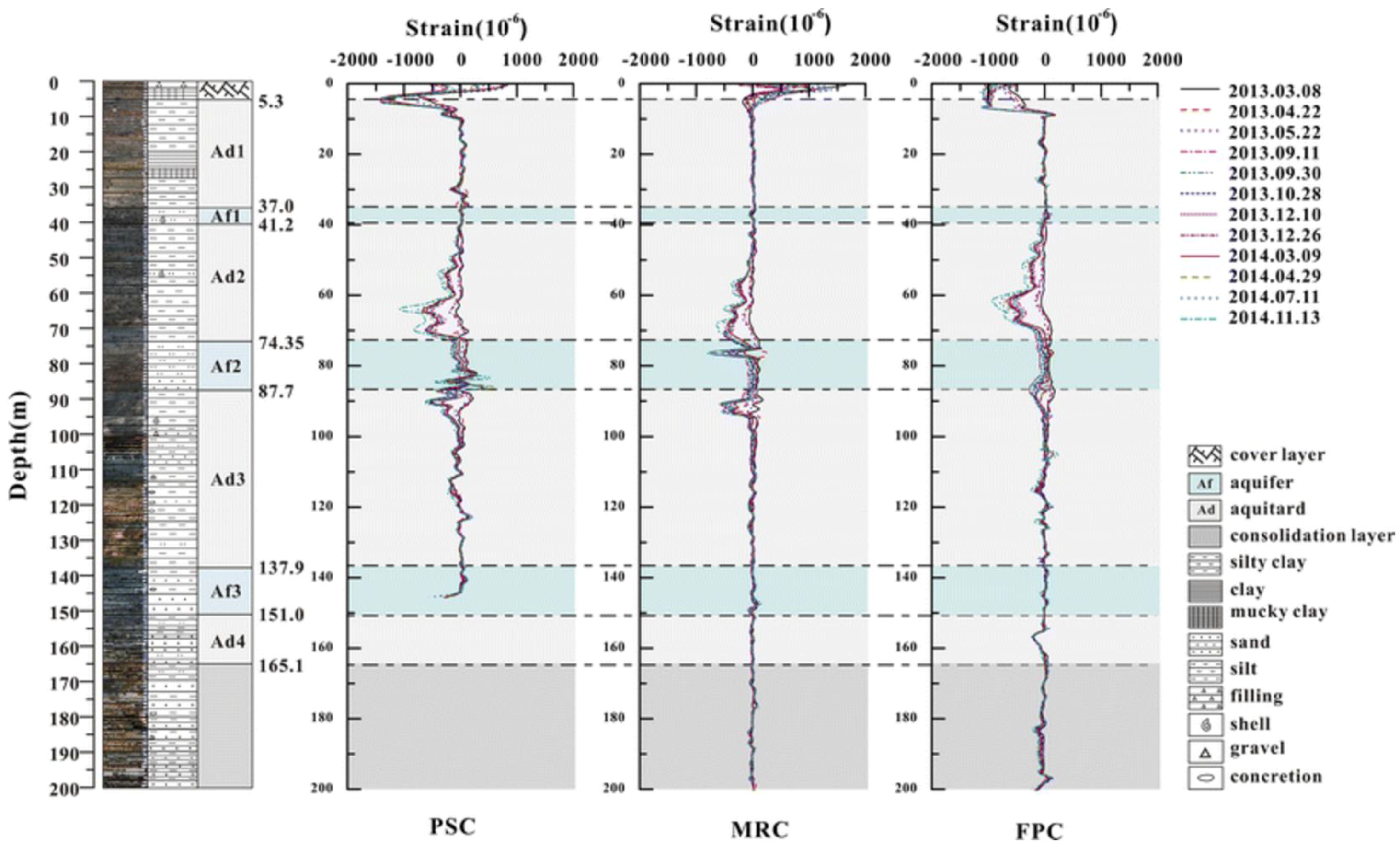
- Wu, J.; Jiang, H.; Su, J.; Shi, B.; Jiang, Y.; Gu, K. Application of distributed fiber optic sensing technique in land subsidence monitoring. J. Civ. Struct. Health Monit. 2015, 5, 587–597. [Google Scholar] [CrossRef]
- Cheng, G.; Shi, B.; Zhu, H.-H.; Zhang, C.-C.; Wu, J.-H. A field study on distributed fiber optic deformation monitoring of overlying strata during coal mining. J. Civ. Struct. Health Monit. 2015, 5, 553–562. [Google Scholar] [CrossRef]
- Glisic, B.; Oberste-ufer, K. Validation Testing of Fiber Optic Method for Buried Pipelines Health Assessment after Earthquake-Induced Ground Movement. In Proceedings of the 2011 NSF Engineering Research and Innovation Conference, Atlanta, GA, USA, 4–7 Jaunary 2011.
- Inaudi, D.; Glisic, B. Distributed fiber optic strain and temperature sensing for structural health monitoring. In Proceedings of the Third International Conference on Bridge Maintenance, Safety and Management, Porto, Portugal, 16–19 July 2006; pp. 963–964.
- Lim, K.; Wong, L.; Chiu, W.K.; Kodikara, J. Distributed fiber optic sensors for monitoring pressure and stiffness changes in out-of-round pipes. Struct. Control Health Monit. 2015, 23, 303–314. [Google Scholar] [CrossRef]
- Thévenaz, L.; Facchini, M.; Fellay, A.; Robert, P.; Inaudi, D.; Dardel, B. Monitoring of large structure using distributed Brillouin fibre sensing. In Proceedings of the 13th International Conference on Optical Fiber Sensors, Kyongju, Korea, 12–16 April 1999; pp. 5–8.
- Glisic, B.; Inaudi, D. Sensing tape for easy integration of optical fiber sensors in composite structures. In Proceedings of the 16th International Conference on Optical Fiber Sensors, Nara, Japan, 13–17 October 2003; Volume 1, pp. 291–298.
- Glišić, B.; Posenato, D.; Inaudi, D. Integrity monitoring of old steel bridge using fiber optic distributed sensors based on Brillouin scattering. In Proceedings of the 14th International Symposium on: Smart Structures and Materials & Nondestructive Evaluation and Health Monitoring, San Diego, CA, USA, 18–22 March 2007; Volume 6531. [CrossRef]
- Matta, F.; Bastianini, F.; Galati, N.; Casadei, P.; Nanni, A. Distributed strain measurement in steel bridge with fiber optic sensors: Validation through diagnostic load test. J. Perform. Constr. Facil. 2008, 22, 264–273. [Google Scholar] [CrossRef]
- Glisic, B.; Chen, J.; Hubbell, D. Streicker Bridge: A comparison between Bragg-grating long-gauge strain and temperature sensors and Brillouin scattering-based distributed strain and temperature sensors. In Proceedings of the SPIE Smart Structures and Materials + Nondestructive Evaluation and Health Monitoring, San Diego, CA, USA, 6–10 March 2011.
- Bastianini, F.; Rizzo, A.; Galati, N.; Deza, U.; Nanni, A. Discontinuous Brillouin strain monitoring of small concrete bridges: Comparison between near-to-surface and smart FRP fiber installation techniques. Proc. SPIE Int. Soc. Opt. Eng. 2005, 5765, 612–623. [Google Scholar]
- Bastianini, F.; Corradi, M.; Borri, A.; di Tommaso, A. Retrofit and monitoring of an historical building using “Smart” CFRP with embedded fibre optic Brillouin sensors. Constr. Build. Mater. 2005, 19, 525–535. [Google Scholar] [CrossRef]
- Villalba, V.; Casas, J.R.; Villalba, S. Application of OBR fiber optic technology in structural health monitoring of Can Fatjó Viaduct (Cerdanyola de Vallés-Spain). In Proceedings of the VI International Conference on Bridge Maintenance, Safety and Management, Lake Maggiore, Italy, 8–12 July 2012.
- Casas, J.; Villalba, S.; Villalba, V. Management and safety of existing concrete structures via optical fiber distributed sensing. In Maintenance and Safety of Aging Infrastructure: Structures and Infrastructures Book Series; CRC Press: Boca Raton, FL, USA, 2014; Volume 10, pp. 217–245. [Google Scholar]
- Zhao, X.; Lu, J.; Han, R.; Kong, X.; Wang, Y.; Li, L. Application of multiscale fiber optical sensing network based on Brillouin and fiber bragg grating sensing techniques on concrete structures. Int. J. Distrib. Sens. Netw. 2012, 2012. [Google Scholar] [CrossRef]
- Regier, R.; Hoult, N.A. Distributed strain behavior of a reinforced concrete bridge: Case study. J. Bridge Eng. 2014, 19. [Google Scholar] [CrossRef]
- Barrias, A.; Casas, J.R.; Villalba, S.; Rodriguez, G. Health Monitoring of real structures by distributed optical fiber. In Proceedings of the Fifth International Symposium on Life-Cycle Civil Engineering, IALCCE’16, Delft, The Netherlands, 16–19 October 2016.
- Inaudi, D.; Glisic, B. Application of distributed Fiber Optic Sensory for SHM. In Proceedings of the ISHMII-2, Shenzhen, China, 16–18 November 2005; pp. 163–169.
- Lan, C.; Zhou, Z.; Ou, J. Monitoring of structural prestress loss in RC beams by inner distributed Brillouin and fiber Bragg grating sensors on a single optical fiber. Struct. Control Health Monit. 2014, 21, 317–330. [Google Scholar] [CrossRef]
- Lally, E.M.; Reaves, M.; Horrell, E.; Klute, S.; Froggatt, M.E. Fiber optic shape sensing for monitoring of flexible structures. In Proceedings of the SPIE Smart Structures and Materials + Nondestructive Evaluation and Health Monitoring, San Diego, CA, USA, 26 April 2012; pp. 83452Y–83452Y-9.
- Froggatt, M.E.; Klein, J.W.; Gifford, D.K.; Kreger, S.T. Optical Position and/or Shape Sensing. U.S. Patent 8,773,650, 8 July 2014. [Google Scholar]
- Schulz, W.L.; Conte, J.P.; Udd, E. Long-gage fiber optic Bragg grating strain sensors to monitor civil structures. In Proceedings of the SPIE’s 8th Annual International Symposium on Smart Structures and Materials, Newport Beach, CA, USA, 30 July 2001; pp. 56–65.
- Sovran, I.; Motil, A.; Tur, M. Frequency-scanning BOTDA with ultimately fast acquisition speed. IEEE Photonics Technol. Lett. 2015, 27, 1426–1429. [Google Scholar] [CrossRef]
- Bernini, R.; Minardo, A.; Zeni, L. Dynamic strain measurement in optical fibers by stimulated Brillouin scattering. Opt. Lett. 2009, 34, 2613–2615. [Google Scholar] [CrossRef] [PubMed]
- Peled, Y.; Yaron, L.; Motil, A.; Tur, M. Distributed and dynamic monitoring of 4km/sec waves using a Brillouin fiber optic strain sensor. In Proceedings of the Fifth European Workshop on Optical Fibre Sensors, Krakow, Poland, 19–22 May 2013; p. 879434.
- Urricelqui, J.; Zornoza, A.; Sagues, M.; Loayssa, A. Dynamic BOTDA measurements based on Brillouin phase-shift and RF demodulation. Opt. Express 2012, 20, 26942–26949. [Google Scholar] [CrossRef] [PubMed]
- Dong, Y.; Ba, D.; Jiang, T.; Zhou, D.; Zhang, H.; Zhu, C.; Lu, Z.; Li, H.; Chen, L.; Bao, X. High-spatial-resolution fast BOTDA for dynamic strain measurement based on differential double-pulse and second-order sideband of modulation. IEEE Photonics J. 2013, 5, 2600407. [Google Scholar] [CrossRef]
- Peled, Y.; Motil, A.; Tur, M. Fast Brillouin optical time domain analysis for dynamic sensing. Opt. Express 2012, 20, 8584–8591. [Google Scholar] [CrossRef] [PubMed]
- Hotate, K.; Ong, S.S.L. Distributed dynamic strain measurement using a correlation-based Brillouin sensing system. IEEE Photonics Technol. Lett. 2003, 15, 272–274. [Google Scholar] [CrossRef]
- Song, K.-Y.; Hotate, K. Distributed fiber strain sensor with 1 kHz sampling rate based on Brillouin optical correlation domain analysis. Opt. East 2007, 2007, 67700J. [Google Scholar] [CrossRef]
- Song, K.Y.; Kishi, M.; He, Z.; Hotate, K. High-repetition-rate distributed Brillouin sensor based on optical correlation-domain analysis with differential frequency modulation. Opt. Lett. 2011, 36, 2062–2064. [Google Scholar] [CrossRef] [PubMed]
- Minardo, A.; Coscetta, A.; Pirozzi, S.; Bernini, R.; Zeni, L. Modal analysis of a cantilever beam by use of Brillouin based distributed dynamic strain measurements. Smart Mater. Struct. 2012, 21, 125022. [Google Scholar] [CrossRef]
- Bao, X.; Zhang, C.; Li, W.; Eisa, M.; El-Gamal, S.; Benmokrane, B. Monitoring the distributed impact wave on a concrete slab due to the traffic based on polarization dependence on stimulated Brillouin scattering. Smart Mater. Struct. 2008, 17, 015003. [Google Scholar] [CrossRef]
- Zhang, Z.; Bao, X. Distributed optical fiber vibration sensor based on spectrum analysis of Polarization-OTDR system. Opt. Express 2008, 16, 10240–10247. [Google Scholar] [CrossRef] [PubMed]
- Qin, Z.; Chen, L.; Bao, X. Wavelet denoising method for improving detection performance of distributed vibration sensor. IEEE Photonics Technol. Lett. 2012, 24, 542–544. [Google Scholar] [CrossRef]
- Zhou, D.-P.; Qin, Z.; Li, W.; Chen, L.; Bao, X. Distributed vibration sensing with time-resolved optical frequency-domain reflectometry. Opt. Express 2012, 20, 13138–13145. [Google Scholar] [CrossRef] [PubMed]






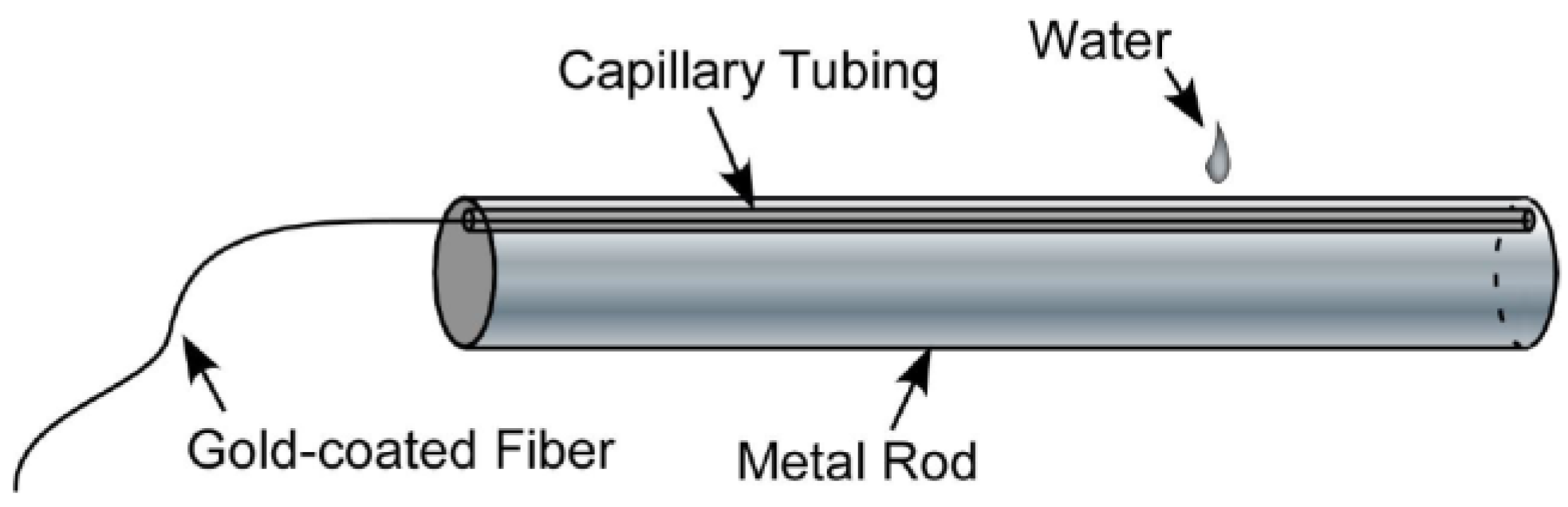





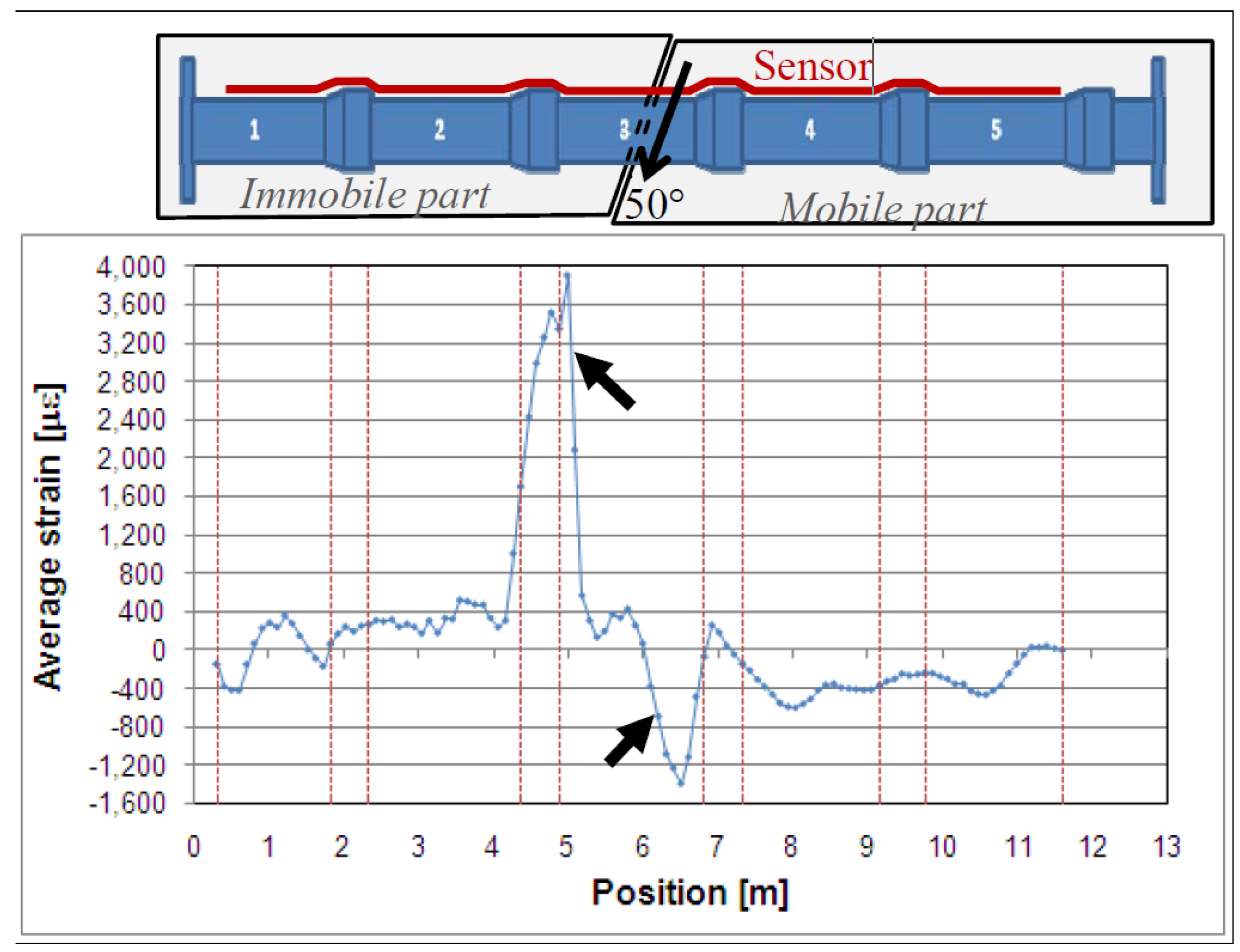


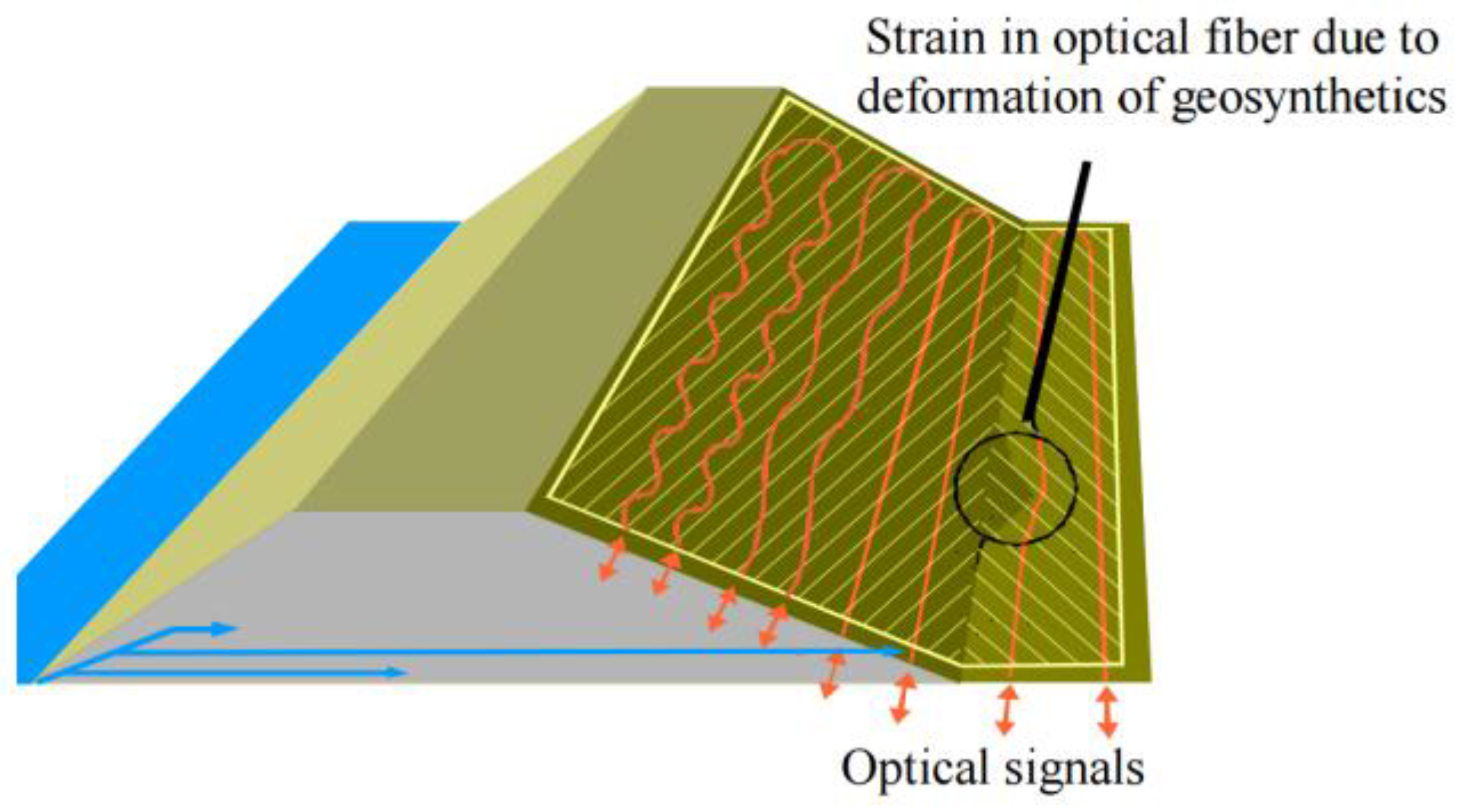

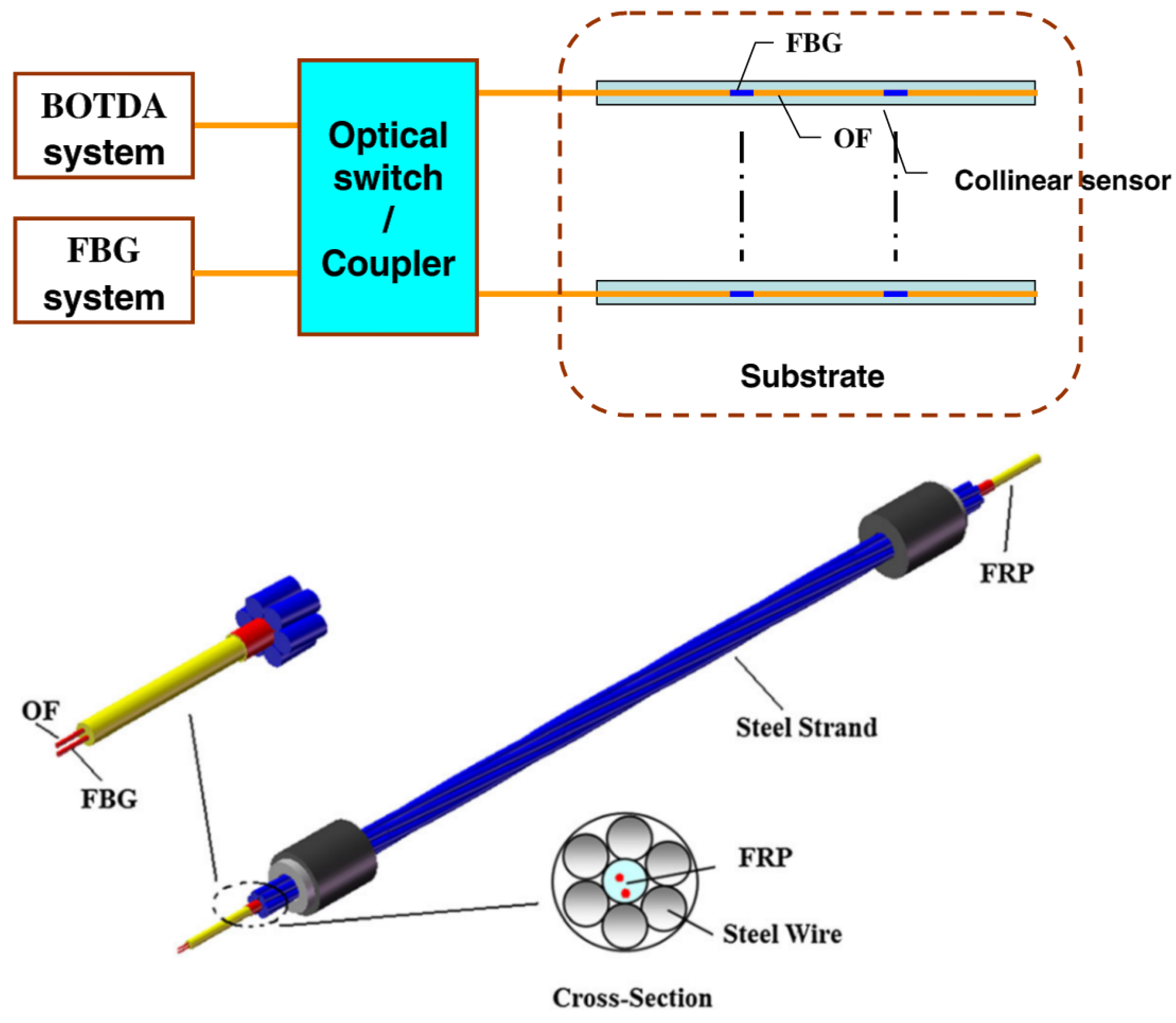
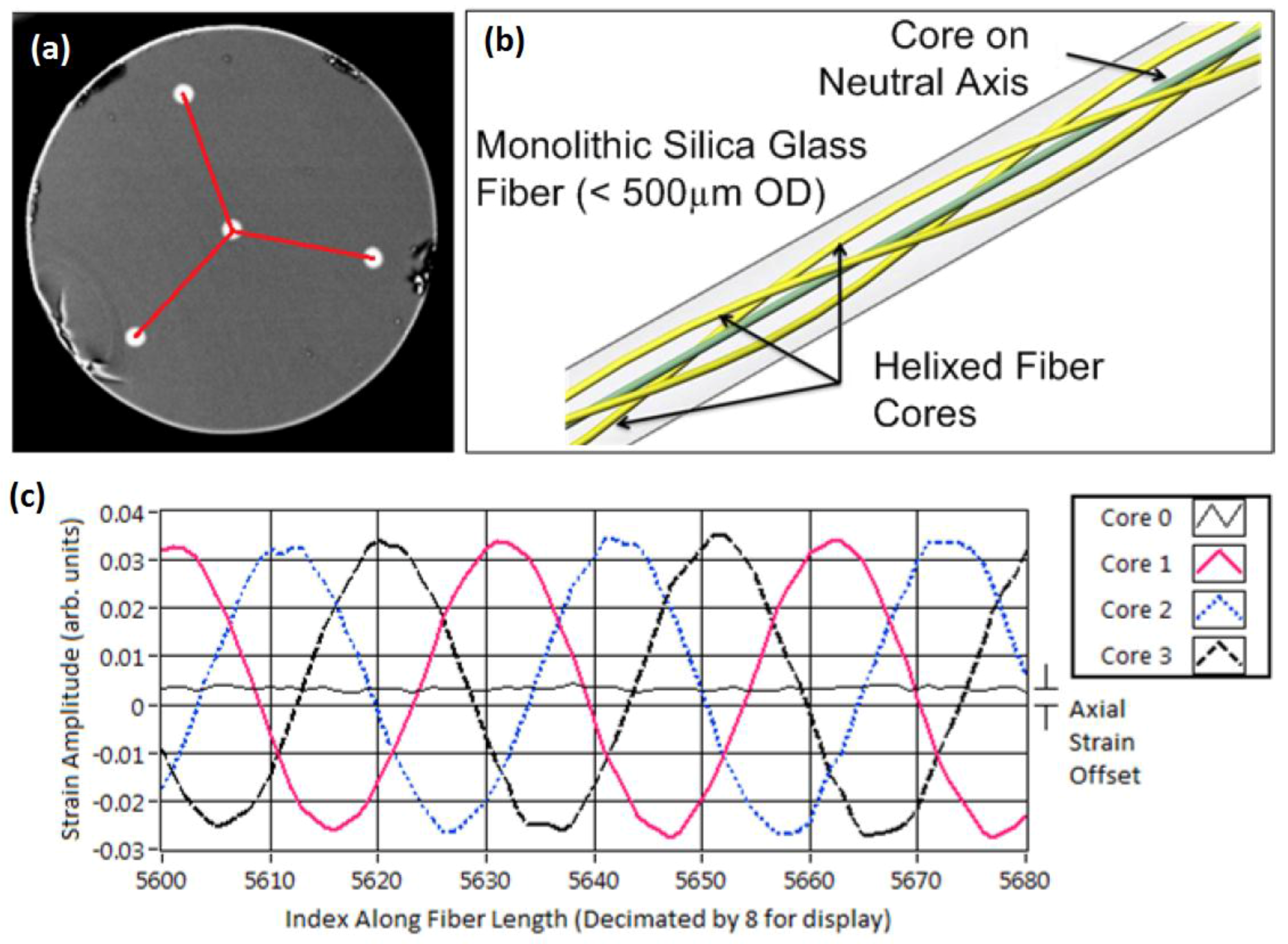

| Sensing Technology | Transducer Type | Sensing Range | Spatial Resolution | Main Measurands |
|---|---|---|---|---|
| Raman OTDR | Distributed | 1 km [73] | 1 cm [73] | Temperature |
| 37 km [74] | 17 m [74] | |||
| BOTDR | Distributed | 20–50 km | ≈1 m | Temperature and Strain |
| BOTDA | Distributed | 150–200 km [13] | 2 cm (2 km) [75] | Temperature and Strain |
| 2 m (150 km) [76] | ||||
| Rayleigh OFDR/OBR | Distributed | 50–70 m [11] | ≈1 mm [66] | Temperature and Strain |
| FBG | Quasi-distributed | ≈100 channels | 2 mm (Bragg length) [21] | Temperature, Strain and Displacement |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barrias, A.; Casas, J.R.; Villalba, S. A Review of Distributed Optical Fiber Sensors for Civil Engineering Applications. Sensors 2016, 16, 748. https://doi.org/10.3390/s16050748
Barrias A, Casas JR, Villalba S. A Review of Distributed Optical Fiber Sensors for Civil Engineering Applications. Sensors. 2016; 16(5):748. https://doi.org/10.3390/s16050748
Chicago/Turabian StyleBarrias, António, Joan R. Casas, and Sergi Villalba. 2016. "A Review of Distributed Optical Fiber Sensors for Civil Engineering Applications" Sensors 16, no. 5: 748. https://doi.org/10.3390/s16050748
APA StyleBarrias, A., Casas, J. R., & Villalba, S. (2016). A Review of Distributed Optical Fiber Sensors for Civil Engineering Applications. Sensors, 16(5), 748. https://doi.org/10.3390/s16050748







