Exponential Arithmetic Based Self-Healing Group Key Distribution Scheme with Backward Secrecy under the Resource-Constrained Wireless Networks
Abstract
:1. Introduction
- The new E-SGKD scheme solves the backward secrecy of E-SGKD schemes perfectly, i.e., the proposed scheme can satisfy the backward secrecy, and furthermore can resist the collusion attack. The construction method of this scheme can be applied to convert other P-SGKD schemes to secure E-SGKD schemes.
- The storage overhead of the new schemes is optimal, i.e., one element in .
- Thanks to the dual chains, the new E-SGKD scheme minimizes the communication cost, i.e., the number of the broadcast messages is reduced to the number of the sessions in which new group users join in.
- The new E-SGKD scheme is computationally secure, i.e., its security is based on the discrete logarithm problem.
2. Security Model
2.1. Network Model
2.2. General Description of SGKD
- SetUp: GM constructs personal secret for each legitimate group node, and sends it to by secure channel. can use personal secret to recover session keys from broadcast messages.
- Broadcast: GM creates message from according to the following conditions:
- -
- There exists a algorithm η, which for all , can recover with the knowledge of , that is: .
- -
- For any set of nodes , there exists no computational algorithm, which can recover with the knowledge of personal secrets of all nodes in R that is: is not feasible.
- SessionKeyRecovery: This algorithm is executed by user nodes. Each member recovers key from broadcast message with her personal secret that is: .
- SelfHealing: This algorithm is executed by user nodes to recover lost session keys. Given l, r, there exists an algorithm ζ, which can recover with the knowledge of by node , that is , where .
- GroupMemberAddition: When a node joins the group, GM sends his personal secret via a secure channel.
- GroupMemberRevocation: When is revoked from the group. The GM starts a new session and updates the session key, which can not be computed by .
2.3. Definition of Self-Healing Group Key Distribution
- (1)
- For a legitimate user , the session key can be computed by the j-th broadcast message , and ’s personal secret .
- (2)
- Either broadcast packet or personal secret alone can obtain any information about .
- (3)
- -revocation capability: For all , can compute if given the j-th broadcast message . However, the revoked user can not, where and , denote the users joining the group in session and revoked before and in session j.
- (4)
- Self-healing property: For any j (), a user, (), can recover the session key from broadcast messages .
3. The Basic E-SGKD Scheme
3.1. The Basic Construction
- SetUpSuppose denotes the users who join the group in the initial session. Each user has a unique identity i. GM randomly selects a t-degree polynomial as a secret masking polynomial. Then, the GM distributes the personal secret to each user via a secure channel, where using secret splitting algorithms in [37] has a better secrecy compared with distributing to directly.
- BroadcastSuppose denotes a set of users who are revoked before and in session j, where .
- -
- The GM constructs the j-th revocation polynomial aswhere denotes the identity of user
- -
- The GM selects a random value from , and computes andThen, the GM constructs the broadcast message asNote that if , . Let in denote the sequence of .
- SessionKeyRecovery
- -
- For a legitimate user , recovers the j-th session key by broadcast message as follows:
- *
- first uses his personal secret to compute .
- *
- computes .
- *
- evaluates .
- *
- Sincecomputes the session key as
- -
- Similarly, can recover the lost session keys by using , , () adopting the same method, i.e., self-healing property.
- -
- For a revoked user , . Thus, he can not obtain information about the session key .
- GroupMemberAdditionWhen a user, , joins the group in session j, the GM randomly selects a unique identity at random, and gets his personal secret from the GM via a secure communication channel. For security, GM starts a new session.
- GroupMemberRevocationWhen a user, , is revoked in session j, the GM then includes in and starts a new session.
3.2. The Security Problem
- computes .
- Since is not a revoked user in session j, i.e., , . Thus, computes .
- Notecomputes the j-th session’s session key as
3.3. The Countermeasure
4. The Novel E-SGKD Scheme
- SetupGM picks a t-degree polynomial at random and keeps it secret. The GM randomly selects a one-way hash function : . Then, the GM selects a session identifier at random. Note that the GM will randomly select a session identifier in session j. Each user obtains his personal secret } through a secure channel, where includes the group members who join the group in the initial session and, using secret splitting algorithms in [37], has a better secrecy compared with distributing to directly.
- BroadcastSuppose and , where consists of the users joining the group in session and is revoked before and in session j, and for each . Let denote the revoked users’ identities in . Note that if no users leave the group in session .
- -
- The GM randomly selects , , and a one-way hash function : . The GM uses as a seed and as a hash function to construct a hash chain as follows:Then, the GM constructs the j-th keys chain as follows:
- -
- The GM selects the random value for , where and . are different from each other and are never used for users’ identities. Then, the revocation polynomials are constructed as:where .Note that denotes the set of users joining the group in session and is revoked before and in session j. The number of users in is less than t, thus the degree of is less than t. However, the degree of is t. In the following computation, may expose some coefficients of . In order to keep the coefficients the polynomial secret, the set is randomly selected to pad the revocation polynomials to be t-degree, where for is different from each other and never used for users’ identities. Thus, the coefficients of the secret polynomial can be protected better.
- -
- The GM randomly selects a random value . Then, the GM computesand constructs the broadcast message asNote that if , . Let in be the sequence of .
- SessionKeyRecovery
- -
- For a legitimate user , uses the j-th broadcast message to compute the current session key and recover the lost session keys as:
- *
- computes , wherecomputes , and uses his personal secret to compute
- *
- computes and evaluates by decrypting . Then, obtains by using .
- *
- computes as
- *
- Finally, computes any by decrypting .
- -
- For a revoked user , . Thus, he can not obtain any information about .
- GroupMemberAdditionWhen a user, , joins the group in session j, GM randomly selects a unique identity v and a session identifier from , and distributes a personal key to him via a secure communication channel. For security, GM starts a new session.
- GroupMemberRevocationWhen a user, joins the group in session and is revoked in session j, GM includes in and starts a new session.
5. Security Analysis and Performance Comparison
5.1. Security Analysis
- (1)
- For a legitimate user , he can recover the session key by combining with his personal secret as described in the SessionKeyRecovery procedure.
- (2)
- On one hand, the session key has a relationship with the initial value of the j-th masking key chain, , and . However, because of the revocation polynomial, it is difficult to compute and only using the broadcast messages. Therefore, using the broadcast message alone can not obtain any information about . On the other hand, is chosen randomly and is independent of the personal secret so that using the personal secret alone can not obtain any information about .Thus, either the broadcast messages or the personal secrets alone can not obtain any information about .
- (3)
- We first consider a single user . For any revoked user , if , . Hence, he can not obtain any information about . Thus, for any revoked user, he alone can not obtain any information about . Furthermore, we consider the collusion of the users in . Because the personal secret of a user has a relationship with a session in which he joins the group, only the users joining the group in the same session can collude together. According to the Lagrange Interpolation method, only at least users coalesce to recover the corresponding . Since , the coalition of users in can not obtain . Therefore, can not obtain information about .
- (4)
- From the SessionKeyRecovery procedure, we learn that a legitimate user can recover the lost session keys from his joined session to the current session, which demonstrates that the new scheme has a self-healing property.
5.2. Performance Comparison
5.2.1. The Security Performance
5.2.2. The Storage Overhead
5.2.3. The Communication Overhead
- (1)
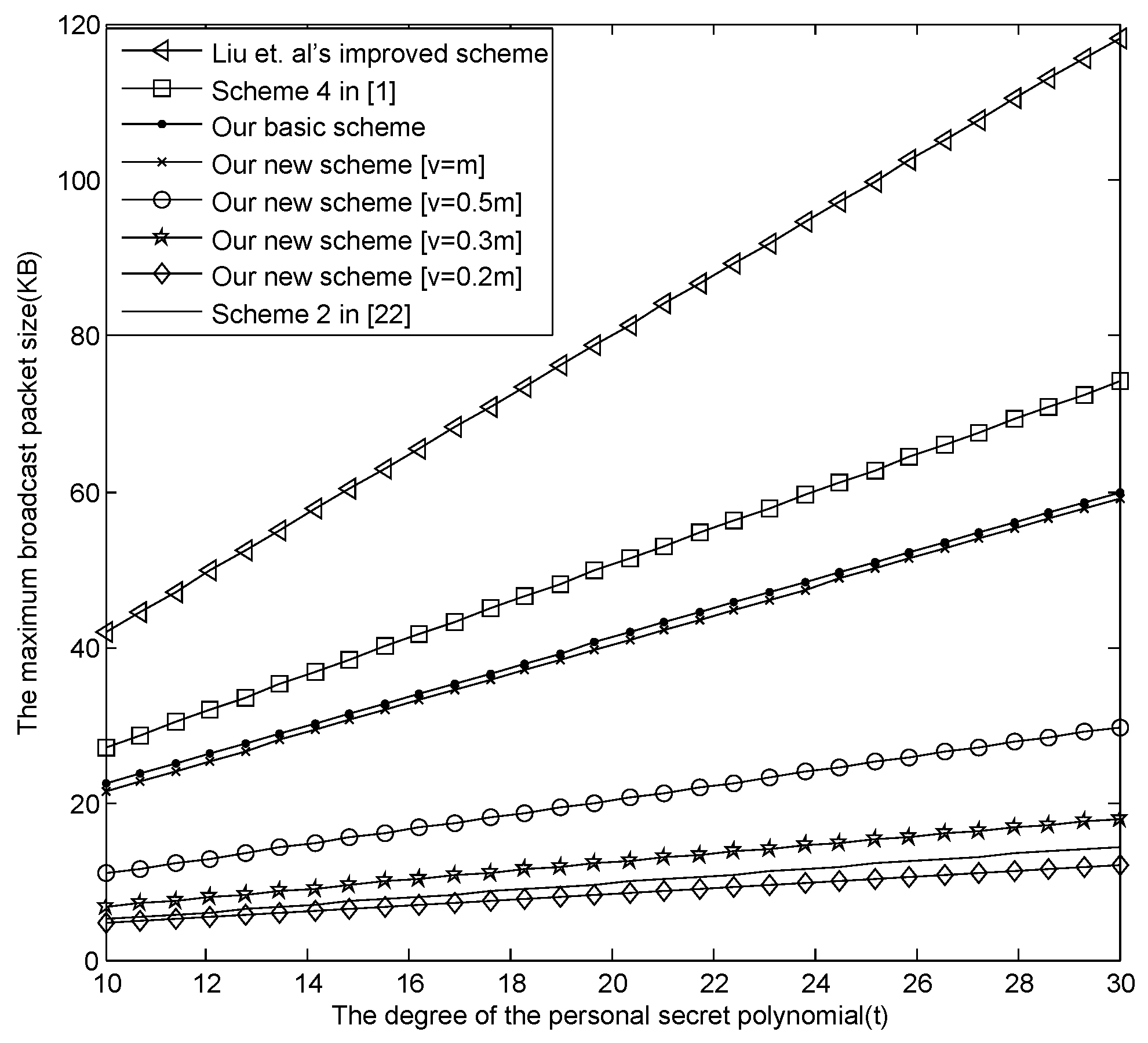
- The comparison among our basic E-SGKD scheme, our new E-SGKD scheme and Blundo et al.’s Scheme 4.Figure 1 describes the maximum size of the broadcast message changing with t, where , , and are discussed, respectively. From Figure 1, when , the maximum size of the broadcast message in our new E-SGKD scheme is nearly 12.25, 18.1094, 29.8281 and 59.125 KB with v = 6, 9, 15 and 30, while the maximum size of the broadcast message in Liu et al.’s improved scheme, Blundo et al.’s Scheme 4 and our basic E-SGKD scheme is nearly 118.1875, 74.0625 and 60 KB, respectively. Thus, our new E-SGKD scheme has the best performance, especially when the number of the joining sessions v is small since the size of the broadcast messages reduce with the value of v reduction. Note that when , the maximum size of the broadcast message in our new E-SGKD scheme is nearly 12.25 KB, which is even smaller than that (say 14.5313 KB) of Hong et al.’s Scheme 2 [22], which is the most efficient known P-SGKD scheme.
- (2)
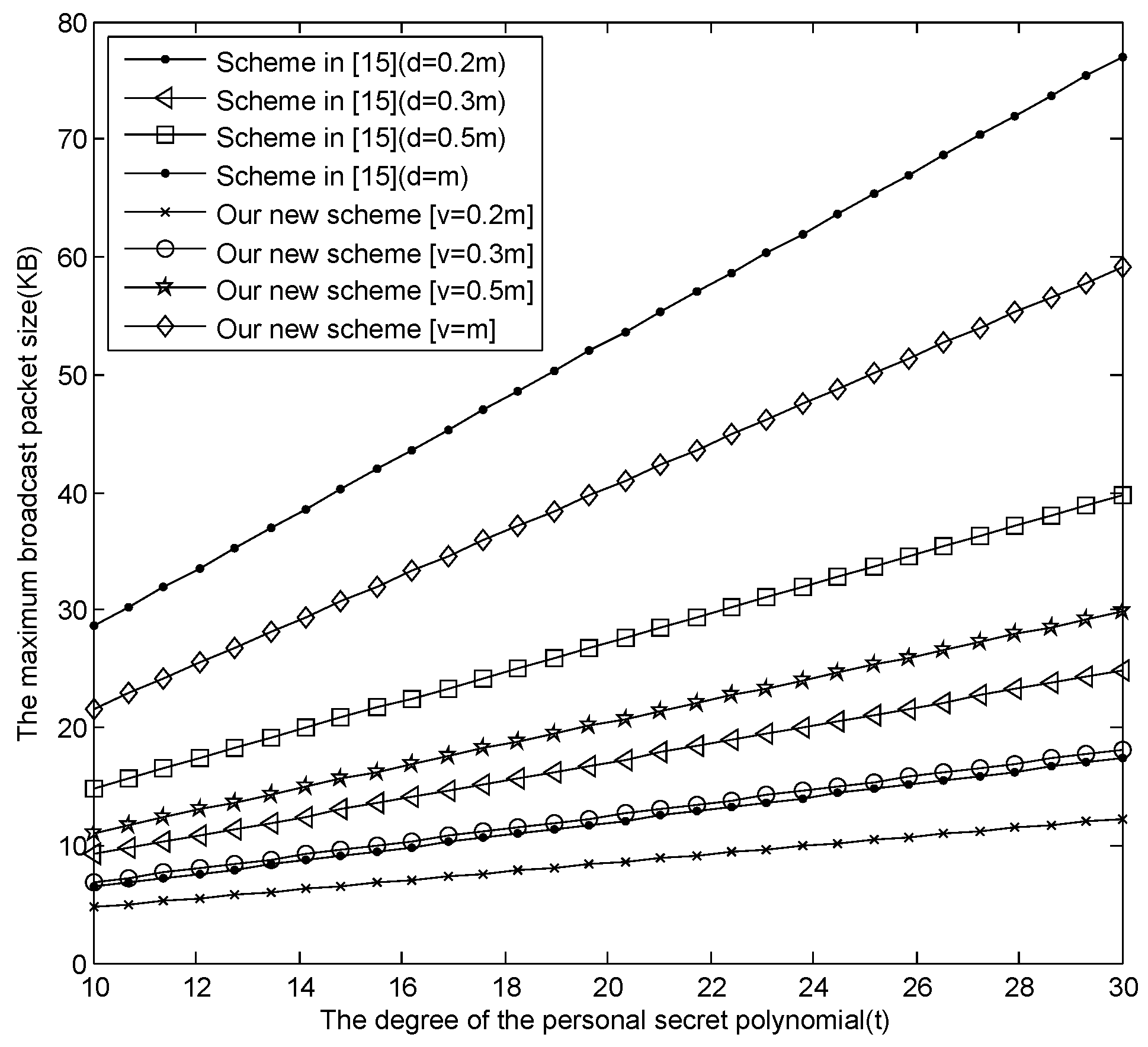
- The comparison between our new E-SGKD scheme and scheme [15]The communication overhead in scheme [15] is , which has a relationship with the size of the sliding windows. In general, we assume that the size of sliding windows (say d) is equal to the number of sessions (say v), in which there are users joining the group. Figure 2 describes the maximum size of the broadcast message changing with t, where , , and are discussed, respectively. From Figure 2, when , the maximum size of the broadcast message in our new E-SGKD scheme is nearly 12.25, 18.1094, 29.8281 and 59.125 KB with v = 6, 9, 15 and 30, while the maximum size of the broadcast message in scheme [15] is nearly 17.39, 24.84, 39.75 and 77.01 KB, respectively. Thus, our new E-SGKD scheme has lower communication overhead, when .
5.3. Practicality
- (1)
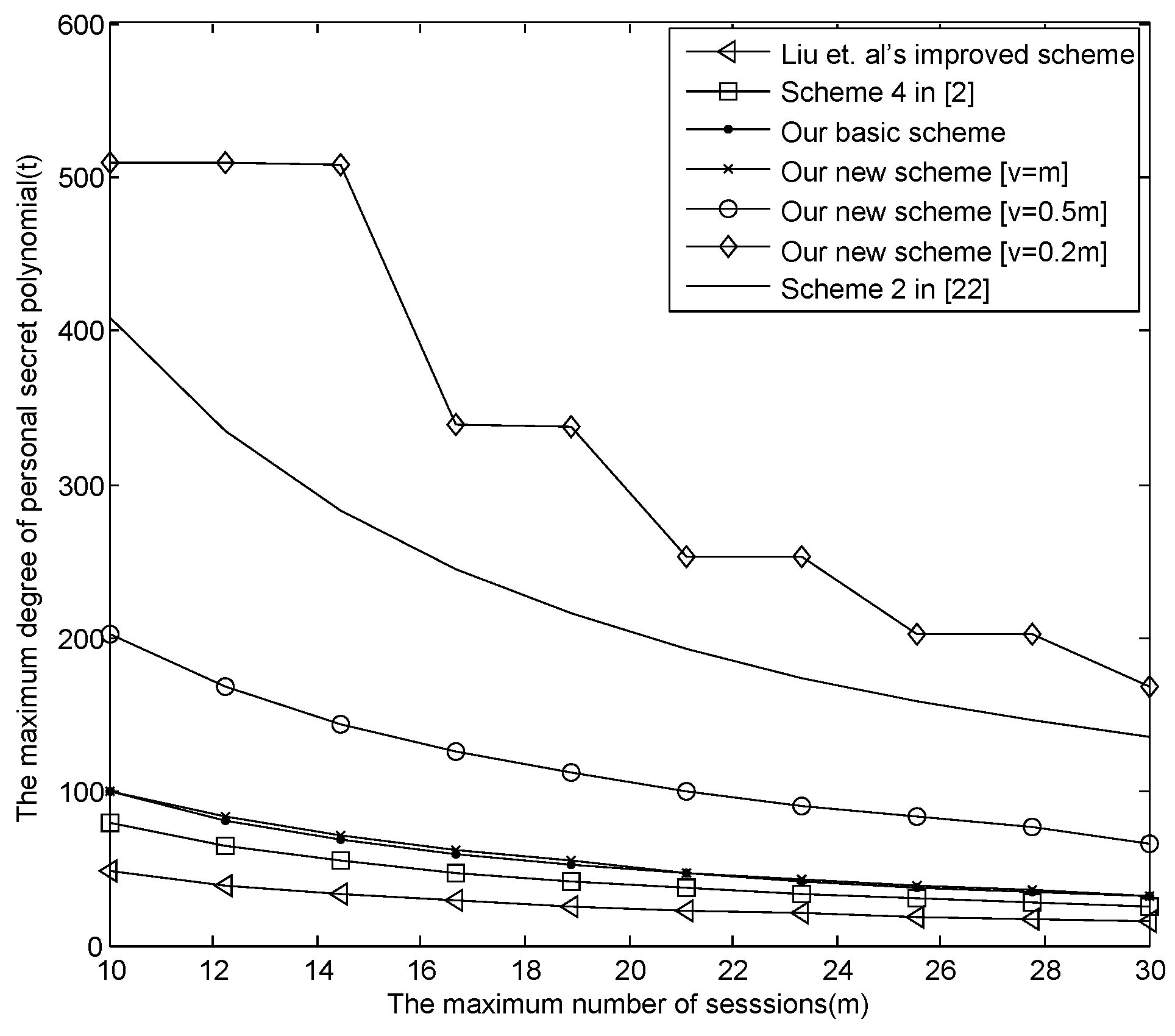
- The relationship between m and t.Figure 3 describes the relationship between m and t in the known E-SGKD schemes, our basic E-SGKD scheme and our new E-SGKD scheme, when the largest broadcast packet is constrained to 64 KB. From Figure 3, when , the largest degree of personal secret polynomial t in our basic E-SGKD scheme and our new E-SGKD scheme with are closed, i.e., 100 and 94, respectively, while t reaches 46 and 80 in “Liu et al.’s improved scheme" and Blundo et al.’s scheme [2]. When , the values of t in our basic E-SGKD scheme and our new E-SGKD scheme with are the same, i.e., 32, while the values of t in “Liu et al.’s improved scheme" and Blundo et al.’s Scheme [2] are 15 and 25, respectively.It is obvious that the range of m and t in our new scheme is larger than the range in other E-SGKD schemes when . For example, when and , where , the values of t in our new E-SGKD scheme are increased remarkably, say 202 and 509, respectively. Note that, when , the value of t even is larger than the value of t (say 410) in the most efficient known P-SGKD scheme, i.e, Hong et al.’s Scheme 2 [22]. Thus, our new E-SGKD scheme has the best performance.
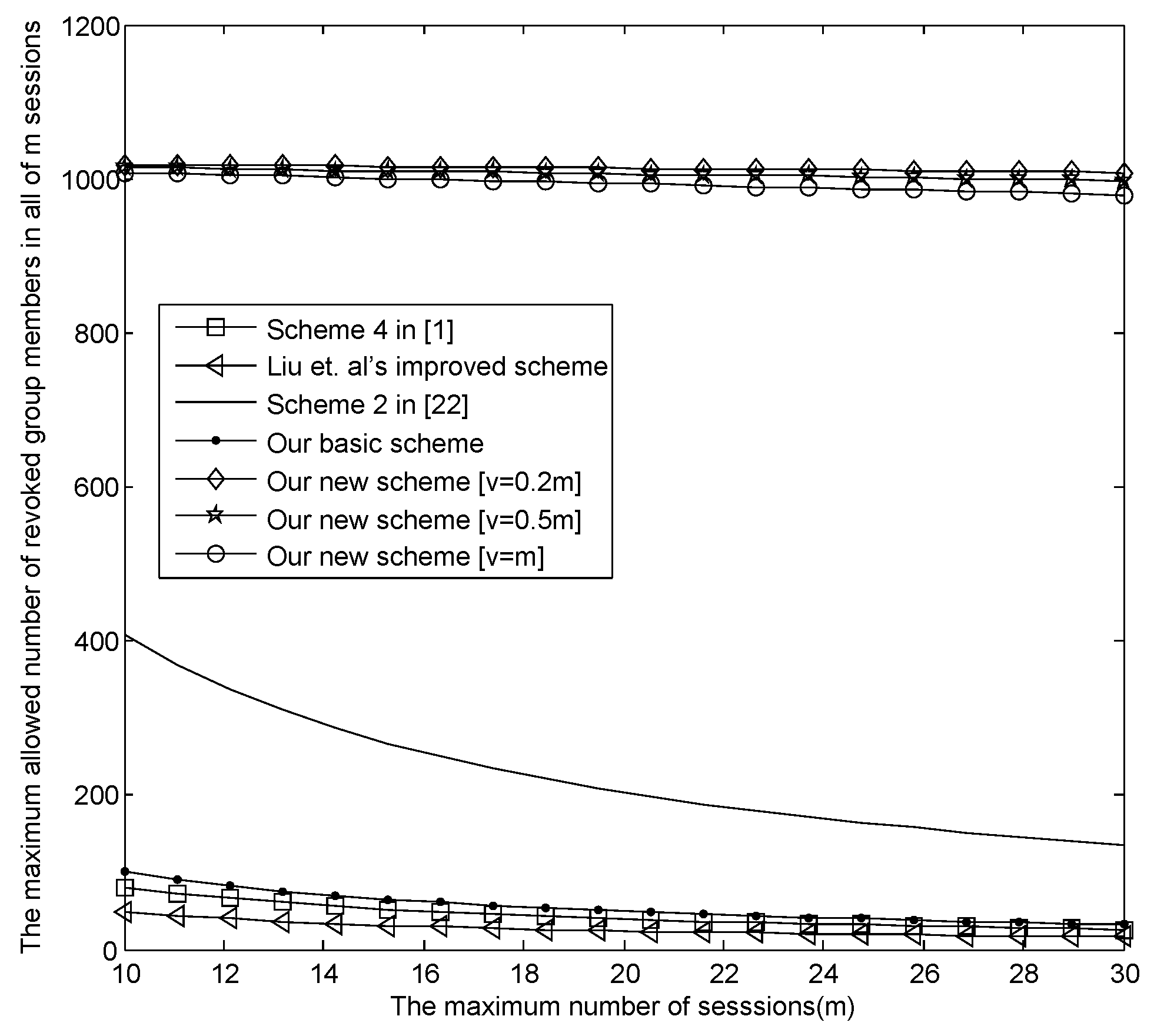
- The relationship between m and the maximum revoked users in all sessions .Figure 4 presents the relationship between m and the maximum revoked users in all sessions , where , , and , respectively. From Figure 4, when , in our new E-SGKD scheme is nearly 1000 with v = 6, 9, 15 and 30, while in Liu et al.’s improved scheme, Blundo et al.’s Scheme 4 and our basic E-SGKD scheme is nearly 15, 25 and 32, respectively. Additionally, we can find that in the most efficient P-SGKD scheme, i.e., Hong et al.’s Scheme 2 [22], is 135. Thus, our new E-SGKD scheme allows more revoked users than all other known E-SGKD schemes and P-SGKD schemes, i.e., the new scheme can resist more users’ collusion attacks.
6. Practicality in ZigBee Network
7. Application to Supervisory Control And Data Acquisition (SCADA) in Smart Grid
8. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Staddon, J.; Miner, S.; Franklin, M.; Balfanz, D.; Malkin, M.; Dean, D. Self-healing key distribution with revocation. In Proceedings of the 2002 IEEE Symposium on Security and Privacy, Berkeley, UK, 12–15 May 2002; pp. 241–257.
- Blundo, C.; D’Arco, P.; Santis, A.; Listo, M. Design of Self-Healing Key Distribution Schemes. Des. Codes Cryptogr. 2004, 32, 15–44. [Google Scholar] [CrossRef]
- Blundo, C.; D’Arco, P.; Santis, A. Definitions and bounds for self-healing key distribution schemes. In Proceedings of the Fuzzy Sets and Systems, 31st International Colloquium on Automata, Languages and Programming ICALP 04, Turku, Finland, 12–16 July 2004; pp. 234–245.
- Blundo, C.; D’Arco, P.; Santis, A. On Self-Healing Key Distribution Schemes. IEEE Trans. Inf. Theory 2006, 52, 5455–5467. [Google Scholar] [CrossRef]
- Dutta, R. Anti-collusive self-healing key distributions for wireless networks. Int. J. Wirel. Mob. Comput. 2014, 7, 362–377. [Google Scholar] [CrossRef]
- Chen, H.; Xie, L. Improved One-Way Hash Chain and Revocation Polynomial-Based Self-Healing Group Key Distribution Schemes in Resource-Constrained Wireless Networks. Sensors 2014, 14, 24358–24380. [Google Scholar] [CrossRef] [PubMed]
- Dutta, R.; Mukhopadhyay, S.; Collier, M. Computationally secure self-healing key distribution with revocation in wireless ad hoc networks. Ad Hoc Netw. 2010, 8, 597–613. [Google Scholar] [CrossRef]
- Dutta, R.; Mukhopadhyay, S.; Das, A.; Emmanuel, S. Generalized self-healing key distribution using vector space access structure. In Proceedings of the 7th International IFIP-TC6 Networking Conference on Ad Hoc and Sensor Networks, Singapore, 5–9 May 2008; pp. 612–623.
- Saez, G. On threshold self-healing key distribution schemes. Cryptogr. Coding 2005, 3796, 340–354. [Google Scholar]
- Tian, B.; Han, S.; Dillon, T.; Das, S. A self-healing key distribution scheme based on vector space secret sharing and one way hash chains. In Proceedings of the 2008 International Symposium on a World of Wireless, Mobile and Multimedia Networks, Newport Beach, CA, USA, 23–26 June 2008; pp. 1–6.
- Du, X.; Wang, Y.; Ge, J.; Wang, Y. An ID-based broadcast encryption scheme for key distribution. IEEE Trans. Broadcast. 2005, 51, 264–266. [Google Scholar] [CrossRef]
- Tian, B.; Han, S.; Dillon, T. A Self-Healing and Mutual-Healing Key Distribution Scheme Using Bilinear Pairings for Wireless Networks. In Proceedings of the IEEE/IFIP International Conference on Embedded and Ubiquitous Computing (EUC ’08), Shanghai, China, 17–20 December 2008; pp. 208–215.
- Han, S.; Tian, B.; Zhang, Y.; Hu, J. An effieient self-healing key distribution scheme with constant-size personal keys for wireless sensor networks. In Proceedings of the 2010 IEEE International Conference on Communications (ICC), Cape Town, South Africa, 23–27 May 2010; pp. 1–5.
- Rams, T.; Pacyna, P. Self-healing group key distribution with extended revocation capability. In Proceedings of the 2013 International Conference on Computing, Networking and Communications (ICNC), San Diego, CA, USA, 28–31 January 2013; pp. 347–353.
- Rams, T.; Pacyna, P. Long-Lived Self-Healing Group Key Distribution Scheme with Backward Secrecy. In Proceedings of the 2013 Conference on Networked Systems (NetSys), Stuttgart, Germany, 11–15 March 2013; pp. 59–65.
- Tian, B.; Han, S.; Hu, J. A mutual-healing key distribution scheme in wireless sensor networks. J. Netw. Comput. Appl. 2011, 34, 80–88. [Google Scholar] [CrossRef]
- Liu, Y.N.; Mao, L.; Harn, L. Group key distribution with full-healing property. In Proceedings of the 2014 23rd International Conference on Computer Communication and Networks (ICCCN), Shanghai, China, 4–7 August 2014; pp. 1–6.
- Liu, D.; Ning, P.; Sun, K. Efficient self-healing group key distribution with revocation capability. In Proceedings of the 10th ACM Conference on Computer and Communications Security, Washington, DC, USA, 27–30 October 2003; pp. 27–31.
- More, S.M.; Malkin, M.; Staddon, J. Sliding-window self-healing key distribution. In Proceedings of the 2003 ACM workshop on Survivable and Self-Regenerative Systems: In Association with 10th ACM Conference on Computer and Communications Security, Fairfax, VA, USA, 31 October 2003.
- Tian, B.; Han, S.; Parvin, S. Self-Healing Key Distribution Schemes for Wireless Networks. Comput. J. 2011, 54, 549–569. [Google Scholar] [CrossRef]
- Rams, T.; Pacyna, P. A Survey of Group Key Distribution Schemes With Self-Healing Property. IEEE Commun. Surv. Tutor. 2013, 15, 820–842. [Google Scholar] [CrossRef]
- Hong, D.; Kang, J. An efficient key distribution scheme with self-healing property. IEEE Commun. Lett. 2005, 9, 759–761. [Google Scholar] [CrossRef]
- Song, H.; Tian, B.; He, M. Efficient threshold self-healing key distribution with sponsorization for infrastructureless wireless networks. IEEE Trans. Wirel. Commun. 2009, 8, 1876–1887. [Google Scholar]
- Dutta, R.; Chang, E.; Mukhopadhyay, S. Constant storage self-healing key distribution with revocation in wireless sensor network. In Proceedings of the 2007 IEEE International Conference on Communications, Glasgow, UK, 24–28 June 2007; pp. 1323–1332.
- Dutta, R.; Mukhopadhyay, S. Designing scalable self-healing key distribution schemes with revocation capability. Parallel Distrib. Process. Appl. 2007, 4742, 419–430. [Google Scholar]
- Dutta, R.; Change, E.C.; Mukhopadhyay, S. Efficient self-healing key distribution with revocation for wireless sensor networks using one way key chains. Appl. Cryptogr. Netw. Secur. 2007, 4521, 385–400. [Google Scholar]
- Guo, H.; Zheng, Y.; Wang, B.; Li, Z. A Note on an Improved Self-Healing Group Key Distribution Scheme. Sensors 2015, 10, 25033–25038. [Google Scholar] [CrossRef] [PubMed]
- Zou, X.; Dai, Y.S. A robust and stateless self-healing group key management scheme. Commun. Technol. 2006, 1–4. [Google Scholar]
- Tian, B.; Han, S.; Dillon, T. An efficient self-healing key distribution scheme. In Proceedings of the 2010 IEEE International Conference on Communications (ICC), Cape Town, South Africa, 23–27 May 2010; pp. 1–5.
- Dutta, R.; Mukhopadhyay, S.; Emmanuel, S. Low bandwidth self-healing key distribution for broadcast encryption. In Proceedings of the 2008 Second Asia International Conference on Modelling & Simulation (AMS), Kuala Lumpur, Malaysia, 13–15 May 2008; pp. 867–872.
- Piao, Y.; Kim, J.; Tariq, U.; Hong, M. Polynomial-based key management for secure intra-group and inter-group communication. Comput. Math. Appl. 2013, 65, 1300–1309. [Google Scholar] [CrossRef]
- Xu, Q.; He, M. Improved constant storage self-healing key distribution with revocation in wireless sensor network. Inf. Secur. Appl. 2009, 5379, 41–55. [Google Scholar]
- Wang, Q.; Chen, H.; Xie, L.; Wang, K. Access-polynomial-based Self-healing Group Key Distribution Scheme for Resource-Constrained Wireless Networks. Secur. Commun. Netw. 2012, 5, 1363–1374. [Google Scholar] [CrossRef]
- Jiao, D.; Li, M.; Yu, Y. Self-Healing Key-Distribution Scheme with Collusion Attack Resistance Based on One-Way Key Chains and Secret Sharing in Wireless Sensor Networks. Int. J. Distrib. Sens. Netw. 2012, 2012, 283–294. [Google Scholar] [CrossRef]
- Sun, X.; Wu, X.; Huang, C. Modified access polynomial based self-healing key management schemes with broadcast authentication and enhanced collusion resistance in wireless sensor networks. Ad Hoc Netw. 2016, 37, 324–336. [Google Scholar] [CrossRef]
- Zheng, Y.; Guo, H. On the Security of a Self-Healing Group Key Distribution Scheme. Available online: http://eprint.iacr.org/2015/697.pdf (accessed on 25 April 2016).
- Ogiela, M.R.; Ogiela, U. Shadow Generation Protocol in Linguistic Threshold Schemes. Commun. Comput. Inf. Sci. 2009, 2009, 35–42. [Google Scholar]
- Gutierrez, J.A. Wireless Medium Access Control (MAC) and Physical Layer (PHY) Specifications for Low Rate Wireless Personal Area Networks (LR-WPANs). IEEE Standard for Information Technology 802.15.4. Institute of Electrical and Electronics: New York, NY, USA, 2003. [Google Scholar]
- ZigBee Document 0949r00ZB, ZigBee RF4CE Specification. Version 09. 17 March 2009. Available online: http://www.zigbee.org/zigbee-for-developers/network-specifications/zigbeerf4ce/ (accessed on 27 April 2016).
- Jiang, R.; Lu, R.; Luo, J. Efficient self-healing group key management with dynamic revocation and collusion resistance for SCADA in smart grid. Secur. Commun. Netw. 2015, 8, 1026–1039. [Google Scholar] [CrossRef]


| the i-th user node | |
| m | the maximum sessions |
| t | the maximum revoked users |
| v | the number of the sessions in which there are users joined the group |
| a finite field of order p, where p is a prime | |
| a multiplicative group of finite of order q | |
| g | a generater of |
| ’s personal secret | |
| symmetric encryption/decryption function | |
| the j-th key updating broadcast message | |
| one-way hash function | |
| the unique session identifier, chosen at random by GM for users who joined the group in session j, and for | |
| the initial value of j-th key chain chosen at random by GM for session j, , and for | |
| the -th key in the j-th key chain | |
| the set of users joining group in session and revoked before or in session j () | |
| the number of users in , and | |
| the set of users who are revoked before and in session j, and | |
| the number of users in | |
| the set of group members joining the group in session j and still legitimate in session j () | |
| the number of users in | |
| the set of legitimate group user in session j, and | |
| the number of users in |
| Scheme | Revocation Limit | Forward Secrecy | Backward Secrecy | Collusion Resistance | The Maximum Number of Collusion Attack Resistance |
|---|---|---|---|---|---|
| Construction 5 in [1] | t | Yes/t | No | No | 0 |
| Scheme 4 in [2] | t | Yes/t | No | No | 0 |
| Liu et al.’s improved scheme | t | Yes/t | No | No | 0 |
| Scheme in [14] | t | Yes/t | Yes/t | Yes | t |
| Scheme in [15] | t | Yes/t | Yes/t | Yes | t |
| Our basic scheme | t | Yes/t | No | No | 0 |
| Our new scheme | Yes/ | Yes/ | Yes |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, H.; Zheng, Y.; Zhang, X.; Li, Z. Exponential Arithmetic Based Self-Healing Group Key Distribution Scheme with Backward Secrecy under the Resource-Constrained Wireless Networks. Sensors 2016, 16, 609. https://doi.org/10.3390/s16050609
Guo H, Zheng Y, Zhang X, Li Z. Exponential Arithmetic Based Self-Healing Group Key Distribution Scheme with Backward Secrecy under the Resource-Constrained Wireless Networks. Sensors. 2016; 16(5):609. https://doi.org/10.3390/s16050609
Chicago/Turabian StyleGuo, Hua, Yandong Zheng, Xiyong Zhang, and Zhoujun Li. 2016. "Exponential Arithmetic Based Self-Healing Group Key Distribution Scheme with Backward Secrecy under the Resource-Constrained Wireless Networks" Sensors 16, no. 5: 609. https://doi.org/10.3390/s16050609





