Fast 2D DOA Estimation Algorithm by an Array Manifold Matching Method with Parallel Linear Arrays
Abstract
:1. Introduction
2. Signal Model and CRB
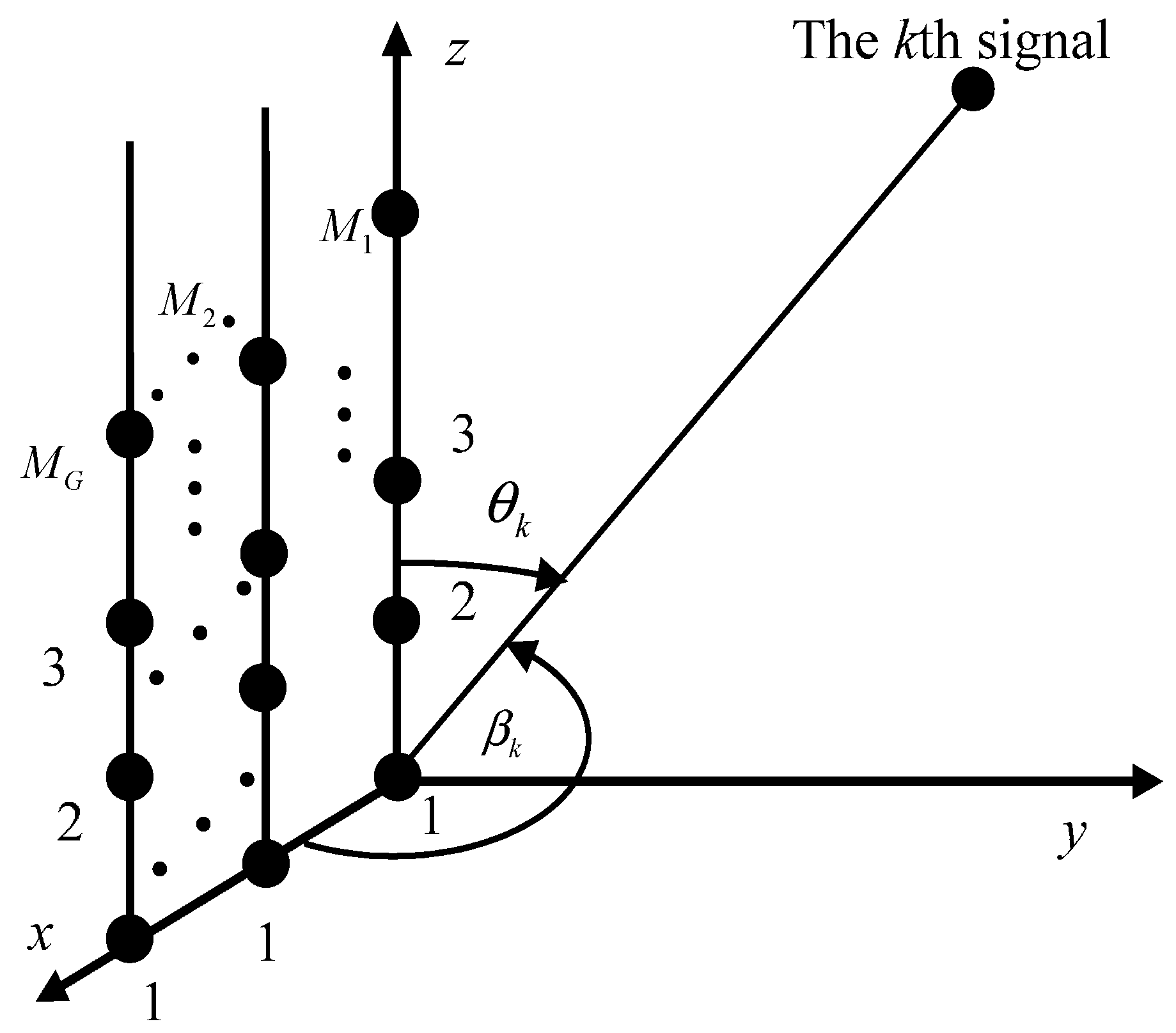
2.1. Signal Model of Parallel Array
2.2. CRB
3. Unilateral AMM Algorithm for Incoherent Signals
3.1. The Estimation of Elevation by PM Algorithm
3.2. Unilateral AMM Algorithm for the Estimation of Azimuth Angle
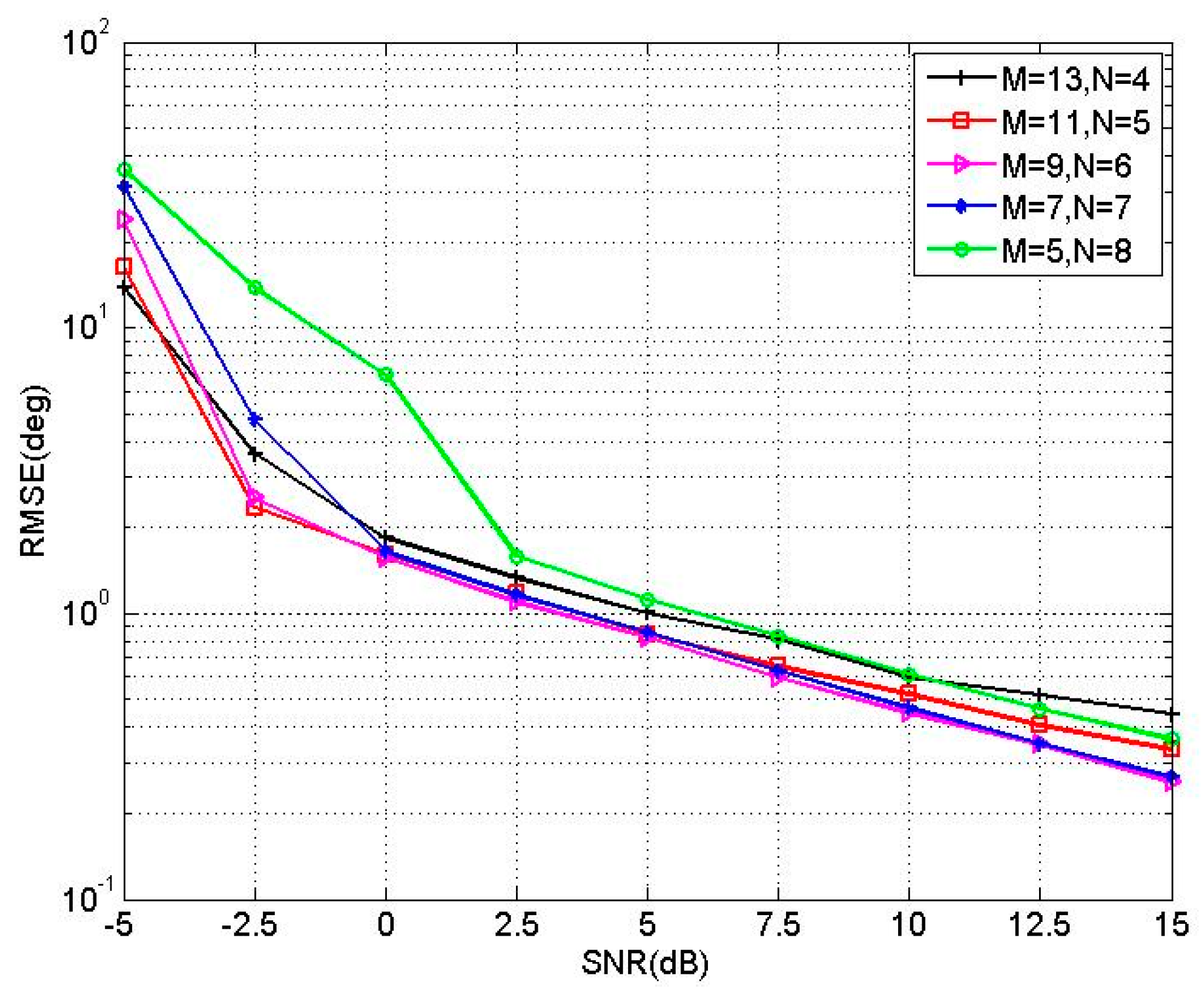
3.3. The Selection of M, N
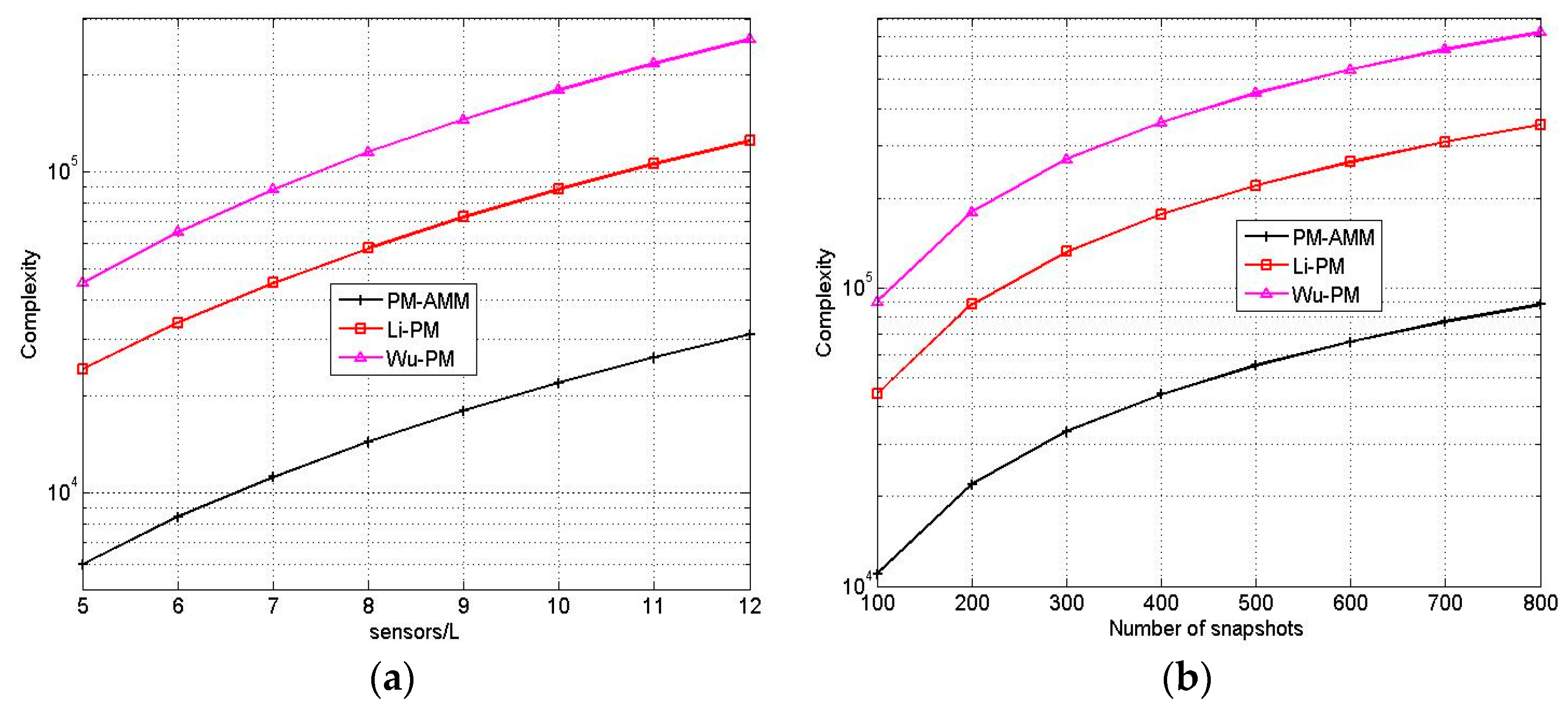
3.4. Complexity Analysis
4. Bilateral AMM Algorithm for Correlated Signals
4.1. The Estimation of Elevation by BCM-Based ESPRIT-Like Algorithm
4.2. Bilateral AMM Method for the Estimation of Azimuth Angle
4.3. Complexity Analysis
5. AMM Algorithm for L-Shaped Array
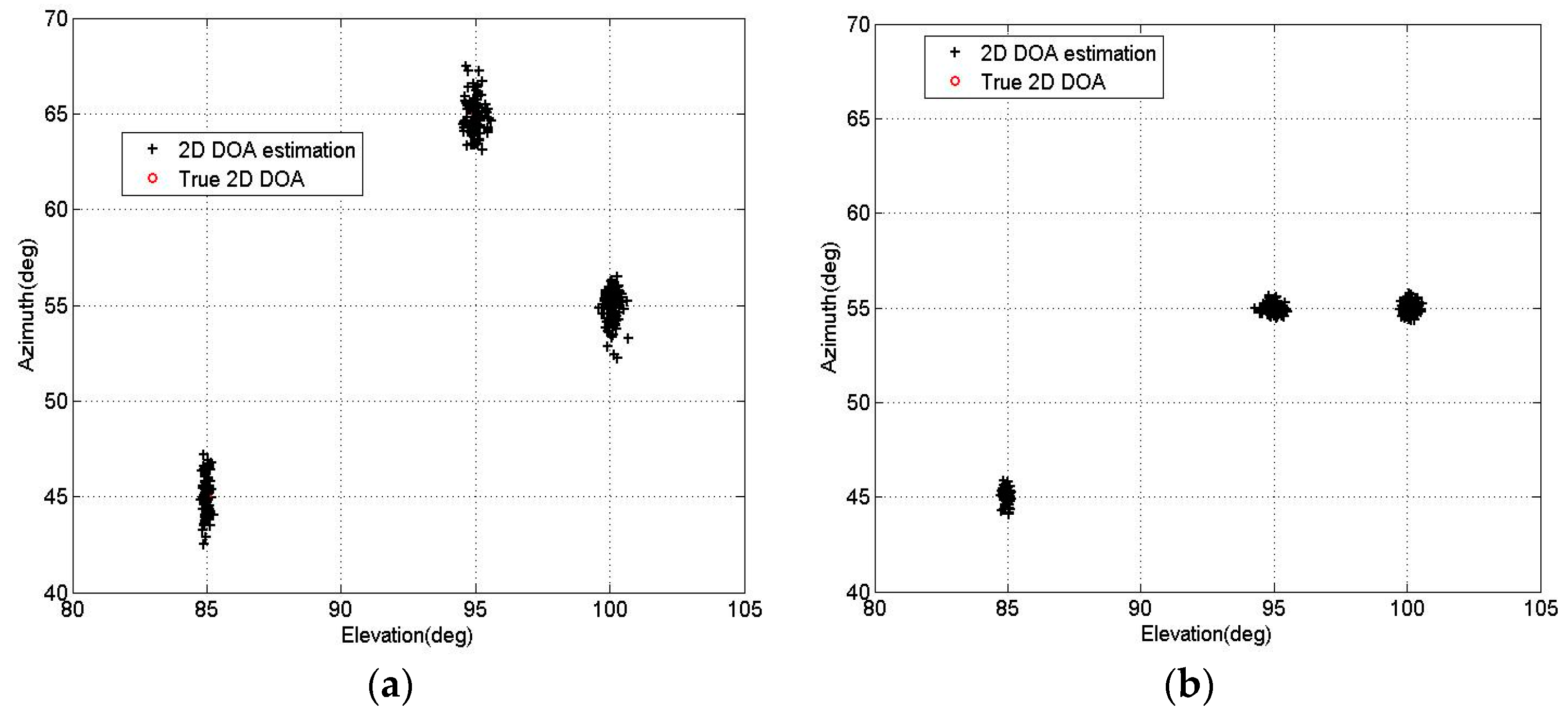
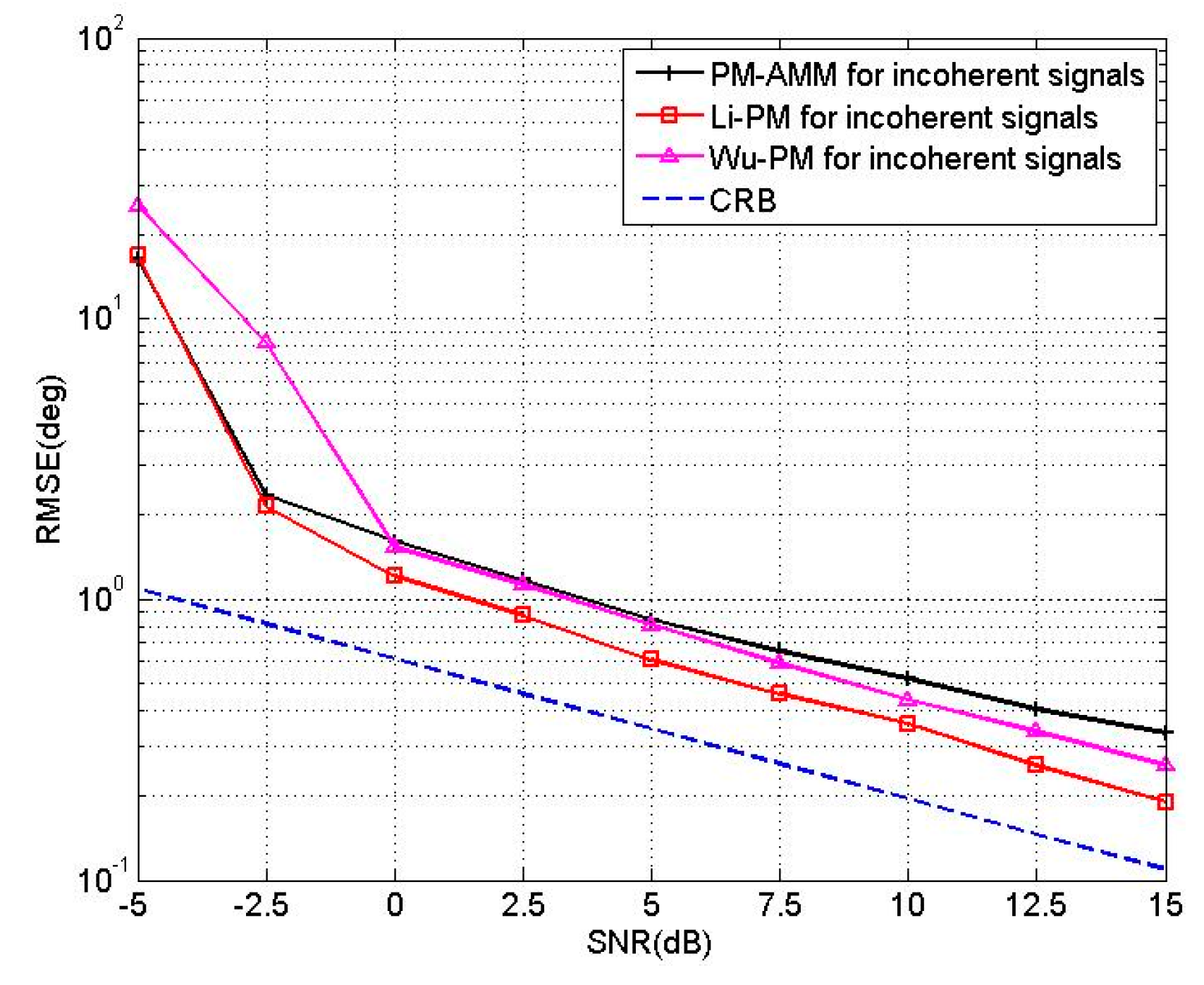
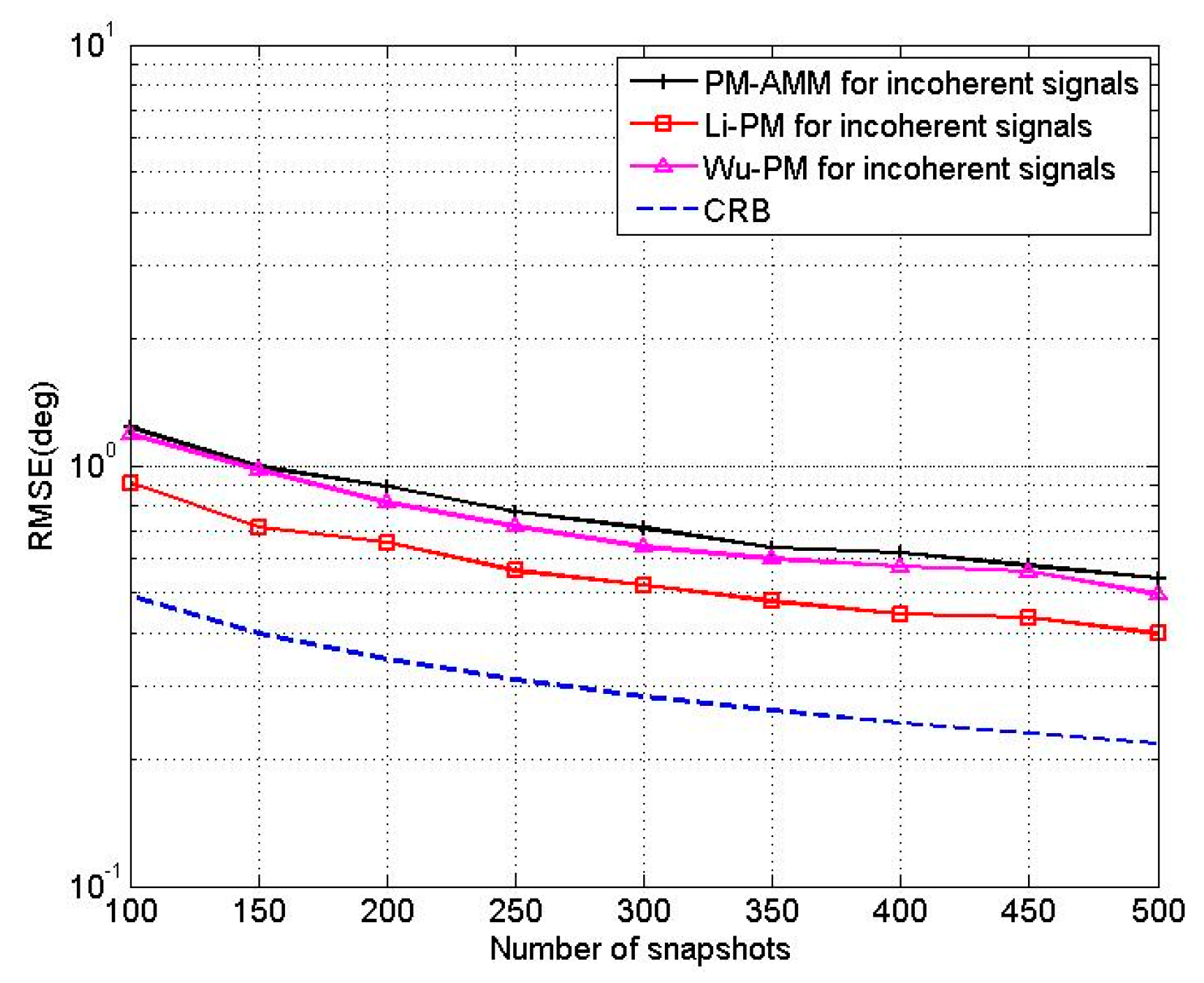
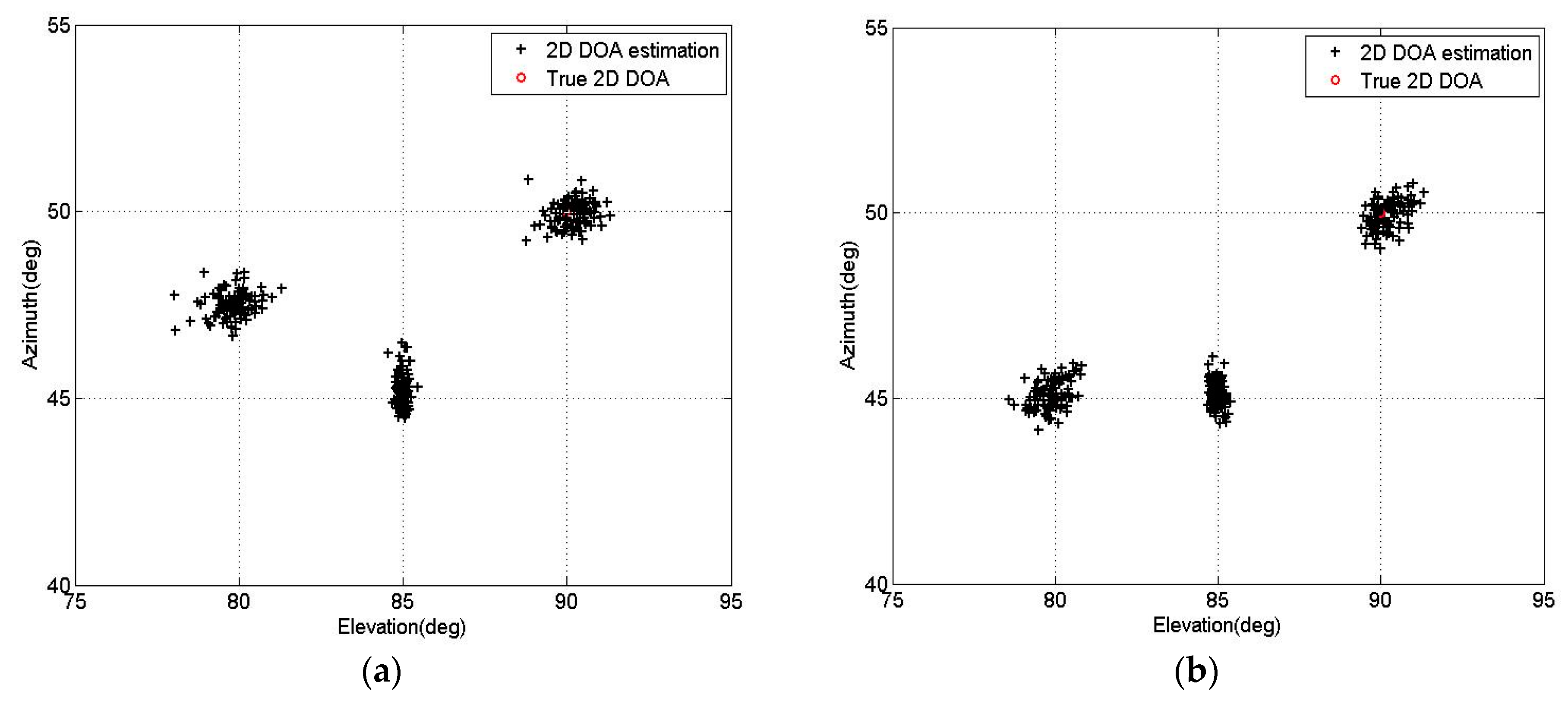
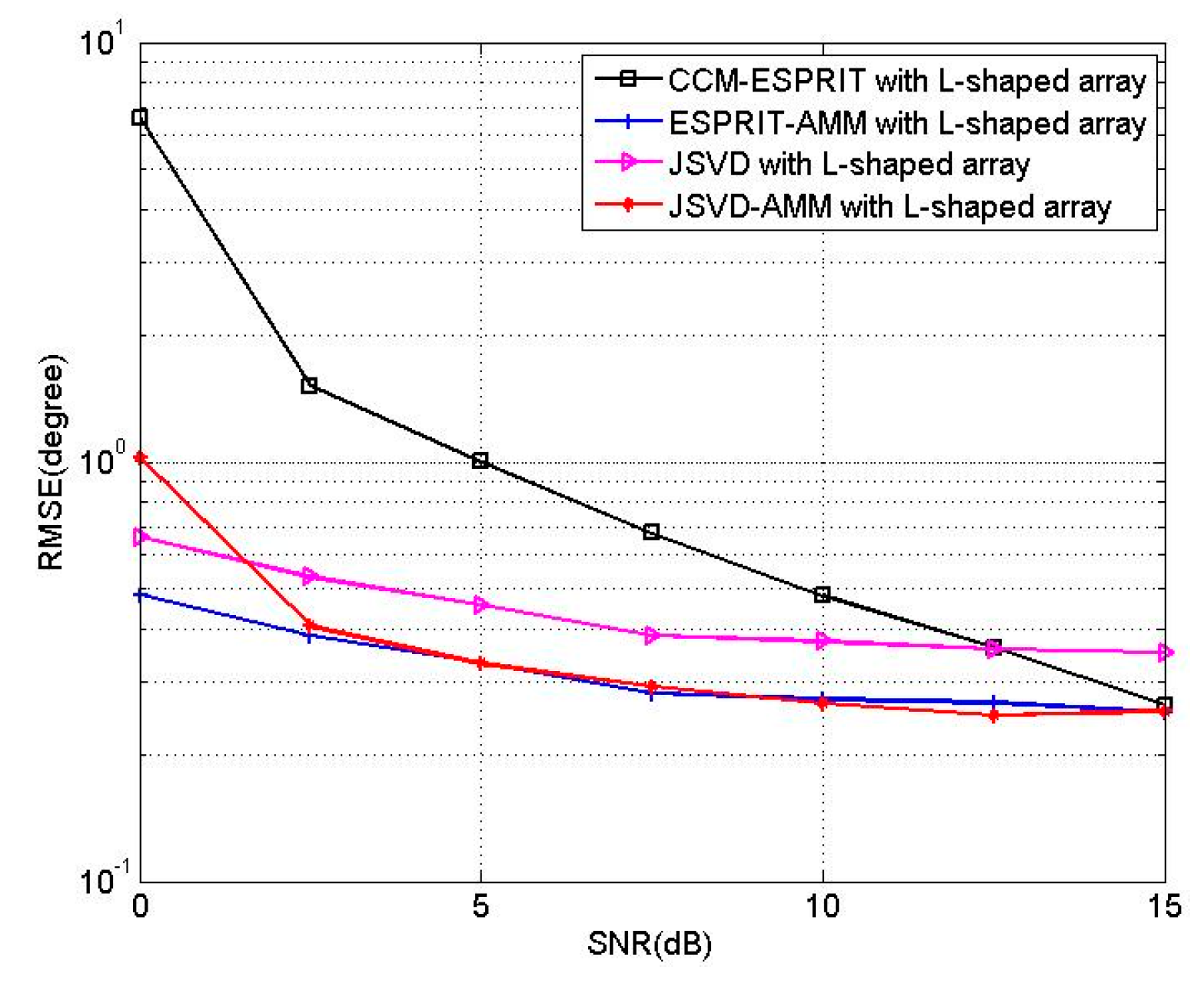
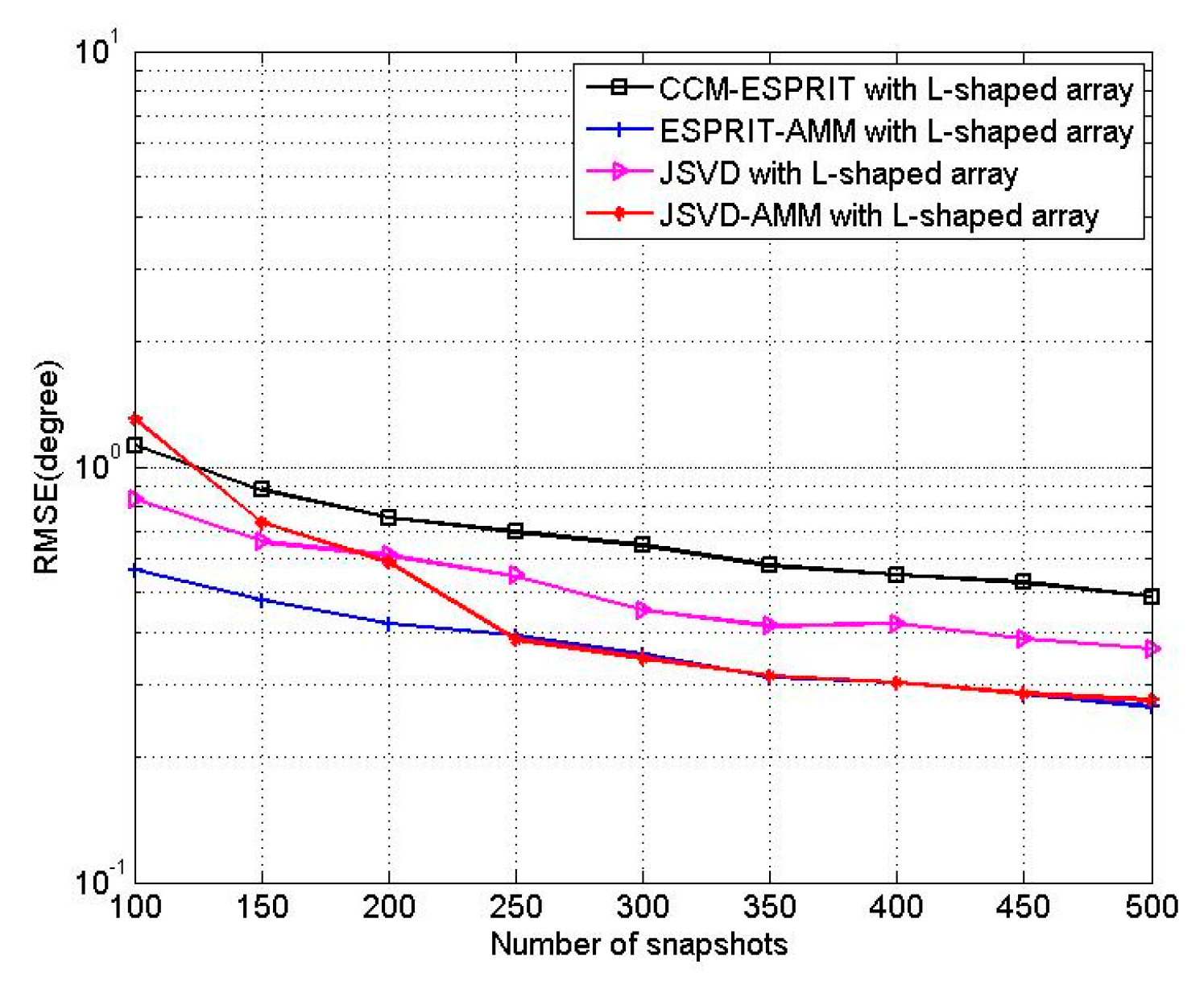
6. Simulation Results
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Notation
| [•]+ | Moore-Penrose generalized inverse |
| [•]T | transpose |
| [•]* | conjugate |
| [•]H | conjugate transpose |
| E[•] | statistical expectation |
| [M]i, | the ith row of matrix M |
| [M]:,i | the ith column of matrix M |
| [v]i | the ith element of vector v |
| IK | K × K identity matrix |
References
- Min, S.; Seo, D.; Lee, K.B.; Kwon, H.M.; Lee, Y.H. Direction-of-arrival tracking scheme for DS/CDMA systems: Direction lock loop. IEEE Trans. Wirel. Commun. 2004, 3, 191–202. [Google Scholar] [CrossRef]
- Li, J.; Zhang, X.F.; Chen, W.Y.; Hu, T. Reduced-dimensional ESPRIT for direction finding in monostatic MIMO radar with double parallel uniform linear arrays. Wirel. Pers. Commun. 2014, 77, 1–19. [Google Scholar] [CrossRef]
- Zhang, X.F.; Zhou, M.; Li, J.F. A PARALIND Decomposition-Based Coherent Two-Dimensional Direction of Arrival Estimation Algorithm for Acoustic Vector-Sensor Arrays. Sensors 2013, 13, 5302–5316. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, R.O. Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef]
- Inghelbrecht, V.; Verhaevert, J.; Hecke, T.V.; Rogier, H. The Influence of Random Element Displacement on DOA Estimates Obtained with (Khatri–Rao-) Root-MUSIC. Sensors 2014, 14, 21258–21280. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Roy, R.; Kailath, T. ESPRIT-estimation of signal parameters via rotational invariance techniques. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 984–995. [Google Scholar] [CrossRef]
- Marcos, S.; Marsal, A.; Benider, M. The propagator method for sources bearing estimation. Signal Process. 1995, 42, 121–138. [Google Scholar] [CrossRef]
- Nie, X.; Li, L.P. A computationally efficient subspace algorithm for 2-D DOA estimation with L-shaped array. IEEE Signal Process. Lett. 2014, 21, 971–974. [Google Scholar]
- Gu, J.F.; Wei, P. Joint SVD of two cross-correlation matrices to achieve automatic pairing in 2-D angle estimation problems. IEEE Antennas Wirel. Propag. Lett. 2007, 6, 553–556. [Google Scholar] [CrossRef]
- Wu, Y.T.; Liao, G.S.; So, H.C. A fast algorithm for 2-D direction-of-arrival estimation. Signal Process. 2003, 83, 1827–1831. [Google Scholar] [CrossRef]
- Tayem, N.; Kwon, H.M. L-shape 2-dimensional arrival angle estimation with propagator method. IEEE Trans. Antennas Propag. 2005, 53, 1622–1630. [Google Scholar] [CrossRef]
- Wang, G.M.; Xin, J.M.; Zheng, N.N.; Sano, A. Computationally efficient subspace-based method for two-dimensional direction estimation with L-shaped array. IEEE Trans. Signal Process. 2011, 59, 3197–3212. [Google Scholar] [CrossRef]
- Shu, T.; Liu, X.Z.; Lu, J.H. Comments on “L-shape 2-dimensional arrival angle estimation with propagator method”. IEEE Trans. Antennas Propag. 2008, 56, 1502–1503. [Google Scholar]
- He, J.; Liu, Z. Extended aperture 2-D direction finding with a two parallel-shaped-array using propagator method. IEEE Antennas Wirel. Propag. Lett. 2009, 8, 323–327. [Google Scholar]
- Li, J.F.; Zhang, X.F.; Chen, H. Improved two-dimensional DOA estimation algorithm for two-parallel uniform linear arrays using propagator method. Signal Process. 2012, 92, 3032–3038. [Google Scholar] [CrossRef]
- Xia, T.Q.; Zheng, Y.; Wan, Q.; Wang, X.G. Decoupled estimation of 2-D angles of arrival using two parallel uniform linear arrays. IEEE Trans. Antennas Propag. 2007, 55, 2627–2632. [Google Scholar] [CrossRef]
- Kikuchi, S.; Tsuji, H.; Sano, A. Pair-matching method for estimating 2-D angle with a cross-correlation matrix. IEEE Antennas Wirel. Propag. Lett. 2006, 5, 35–40. [Google Scholar] [CrossRef]
- Wei, Y.S.; Guo, X.J. Pair-matching method by signal covariance matrices for 2D-DOA estimation. IEEE Antennas Wirel. Propag. Lett. 2014, 13, 1199–1202. [Google Scholar]
- Yin, Q.Y.; Zou, L.H.; Robert, W.N. A high resolution approach to 2-D signal parameter estimation. J. China Inst. Commun. 1991, 12, 1–7. [Google Scholar]
- Pillai, S.U.; Kwon, B.H. Forward/backward spatial smoothing techniques for coherent signal identification. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 8–15. [Google Scholar] [CrossRef]
- Chen, Y.M. On spatial smoothing for two-dimensional direction-of-arrival estimation of coherent signals. IEEE Trans. Signal Process. 1997, 45, 1689–1696. [Google Scholar] [CrossRef]
- Chen, F.J.; Kwong, S.; Kok, C.W. ESPRIT-like two-dimensional DOA estimation for coherent signals. IEEE Trans. Aerosp. Electron. Syst. 2010, 46, 1477–1484. [Google Scholar] [CrossRef]
- Ren, S.W.; Ma, X.C.; Yan, S.F.; Hao, C.P. 2-D unitary ESPRIT-like direction-of-arrival (DOA) estimation for coherent signals with a uniform rectangular array. Sensors 2013, 13, 4272–4288. [Google Scholar] [CrossRef] [PubMed]
- Gu, J.F.; Wei, P.; Tai, H.M. 2-D direction-of-arrival estimation of coherent signals using cross-correlation matrix. Signal Process. 2008, 88, 75–85. [Google Scholar] [CrossRef]
- Chen, H.; Hou, C.P.; Wang, Q.; Huang, L.; Yan, W.Q. Cumulants-based Toeplitz matrices reconstruction method for 2-D coherent DOA estimation. IEEE Sens. J. 2014, 14, 2824–2832. [Google Scholar] [CrossRef]
- He, J.; Liu, Z. Two-dimensional direction finding of acoustic sources by a vector sensor array using the propagator method. Signal Process. 2008, 88, 2492–2499. [Google Scholar] [CrossRef]
- Stoica, P.; Nehorai, A. Performance study of conditional and unconditional direction-of-arrival estimation. IEEE Trans. Acoust. Speech Signal Process. 1990, 38, 1783–1795. [Google Scholar] [CrossRef]




© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, L.; Liu, S.; Li, D.; Jiang, Q.; Cao, H. Fast 2D DOA Estimation Algorithm by an Array Manifold Matching Method with Parallel Linear Arrays. Sensors 2016, 16, 274. https://doi.org/10.3390/s16030274
Yang L, Liu S, Li D, Jiang Q, Cao H. Fast 2D DOA Estimation Algorithm by an Array Manifold Matching Method with Parallel Linear Arrays. Sensors. 2016; 16(3):274. https://doi.org/10.3390/s16030274
Chicago/Turabian StyleYang, Lisheng, Sheng Liu, Dong Li, Qingping Jiang, and Hailin Cao. 2016. "Fast 2D DOA Estimation Algorithm by an Array Manifold Matching Method with Parallel Linear Arrays" Sensors 16, no. 3: 274. https://doi.org/10.3390/s16030274




