Three-Dimensional Continuous Displacement Measurement with Temporal Speckle Pattern Interferometry
Abstract
:1. Introduction
2. Theory
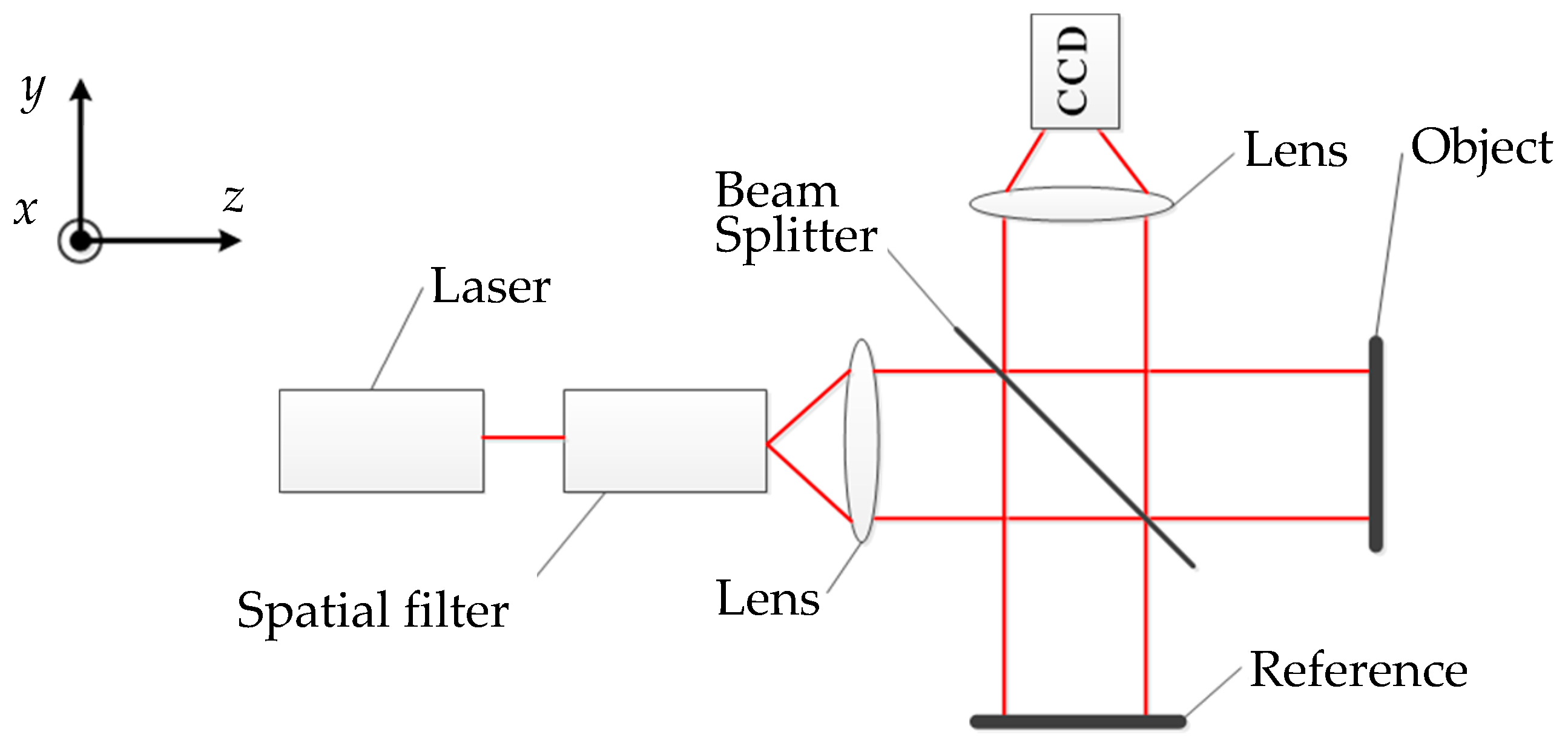
2.1. Principle of Out-of-Plane Measurement
2.2. Principle of In-Plane Measurement
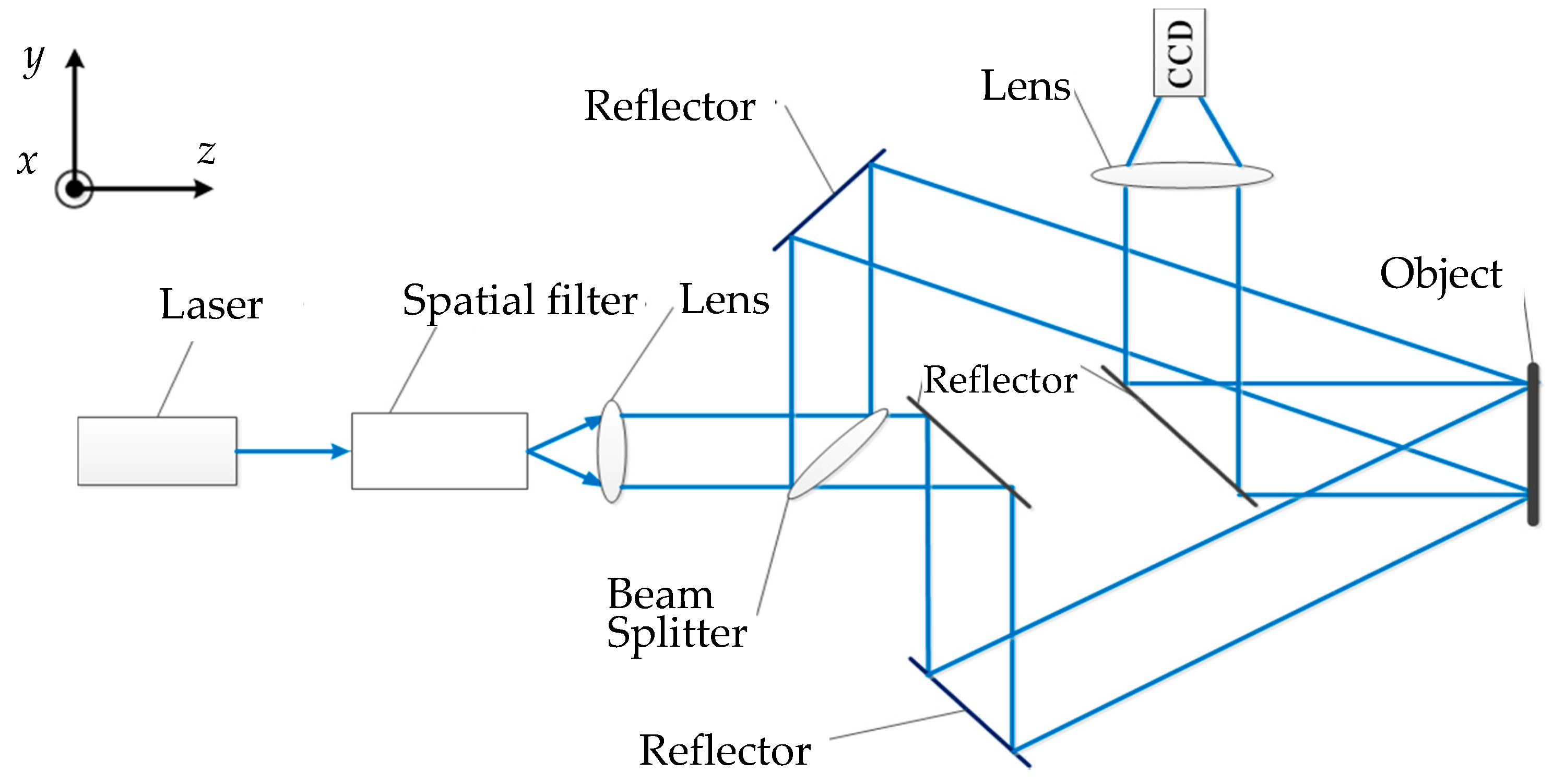
2.3. Principle of 3D Measurement
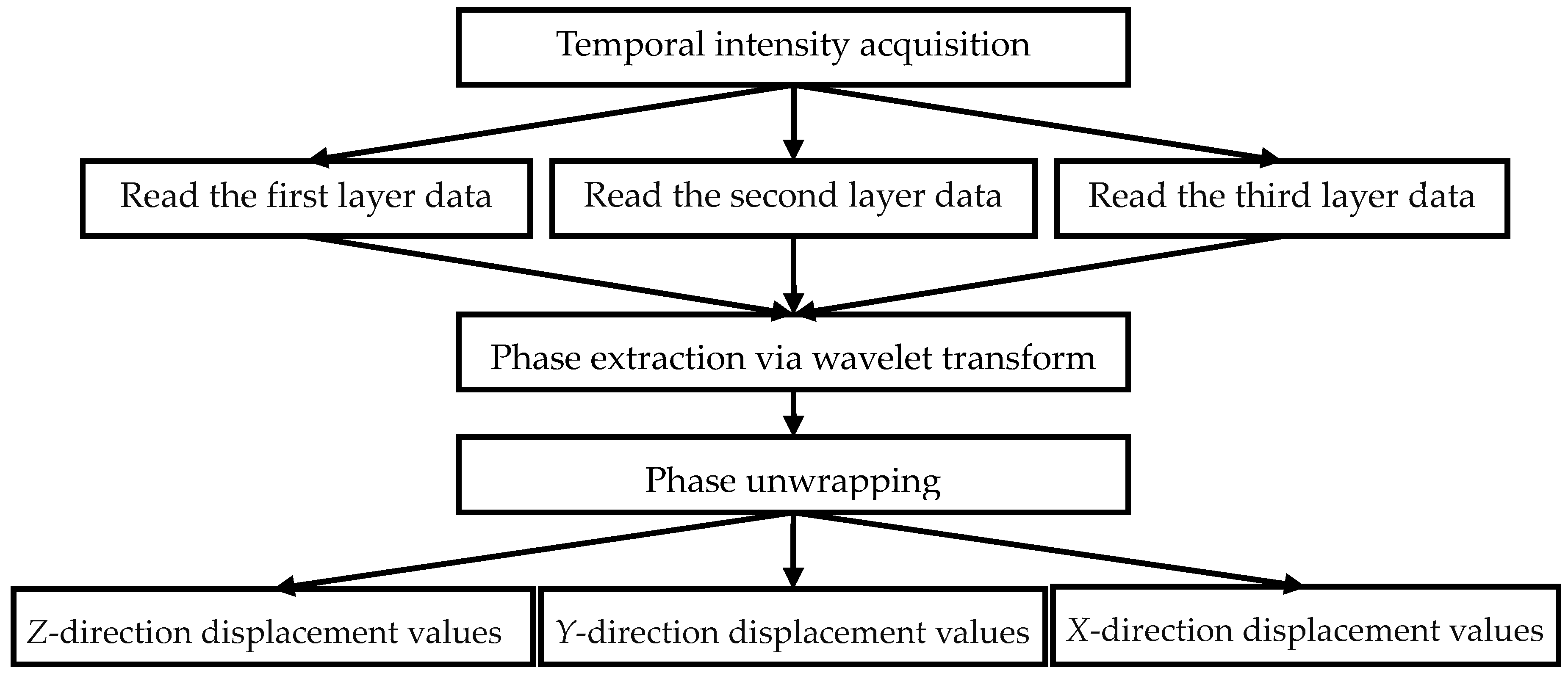
2.4. Principle of the Wavelet Transform Method and Signal Processing
3. Experiment and Results
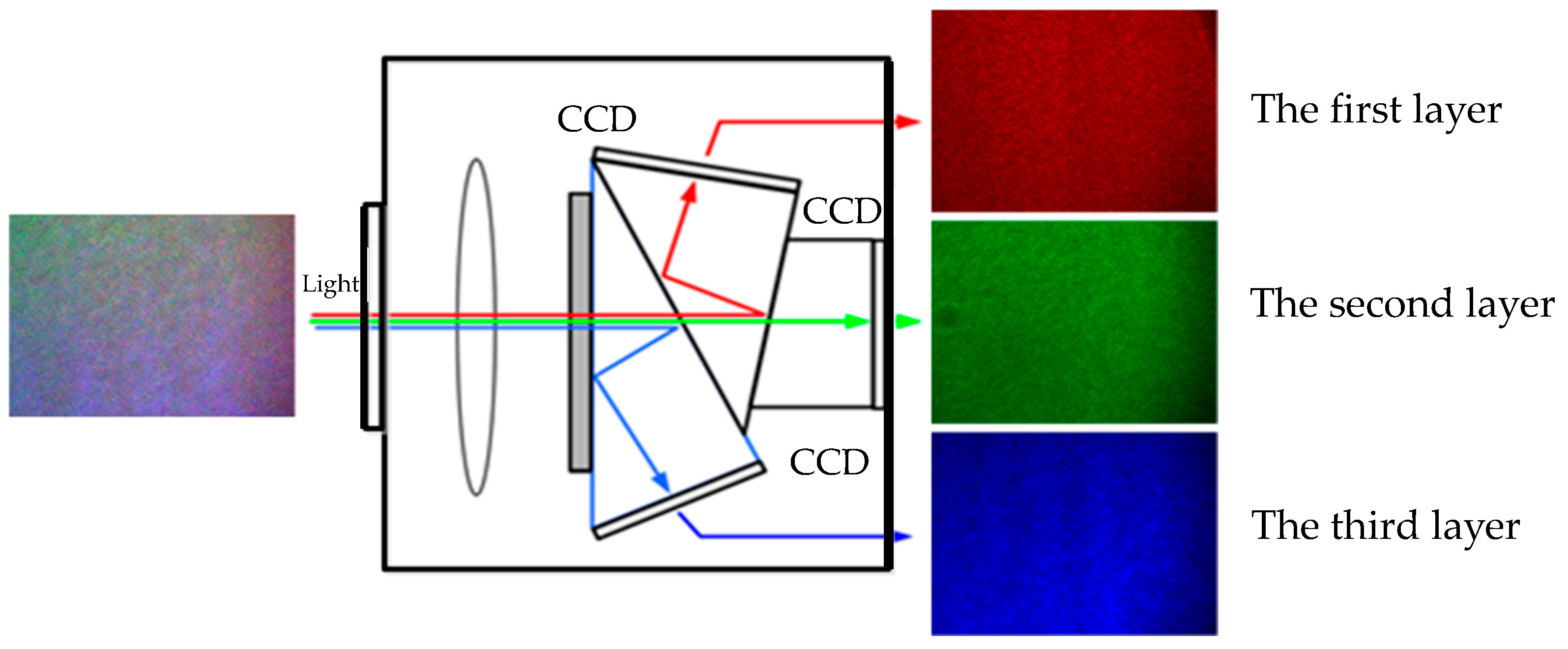
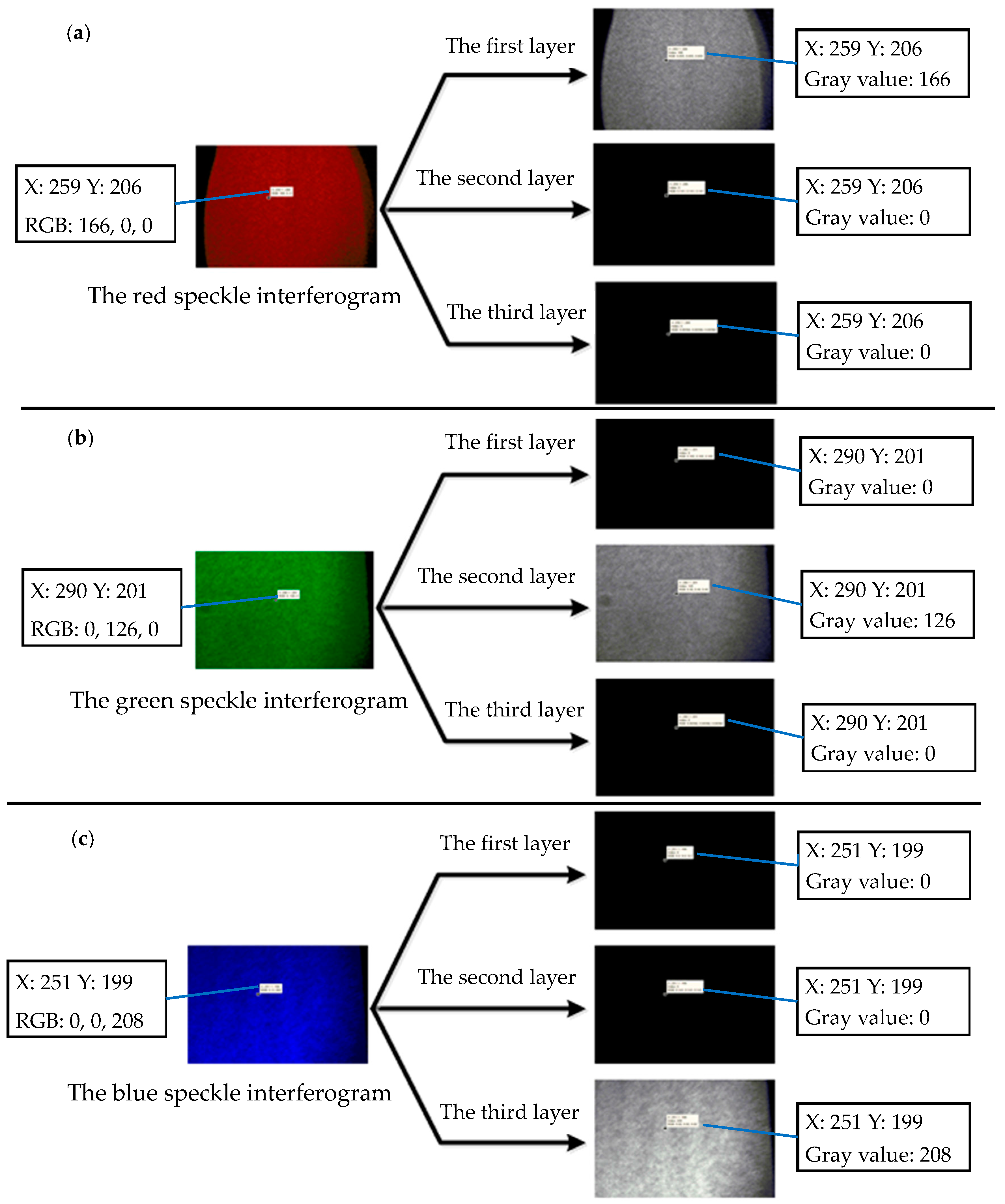
3.1. Verification Experiment of One Color CCD Camera Light Separation Capability
3.2. The Experiment of the 3D Displacement Measurement
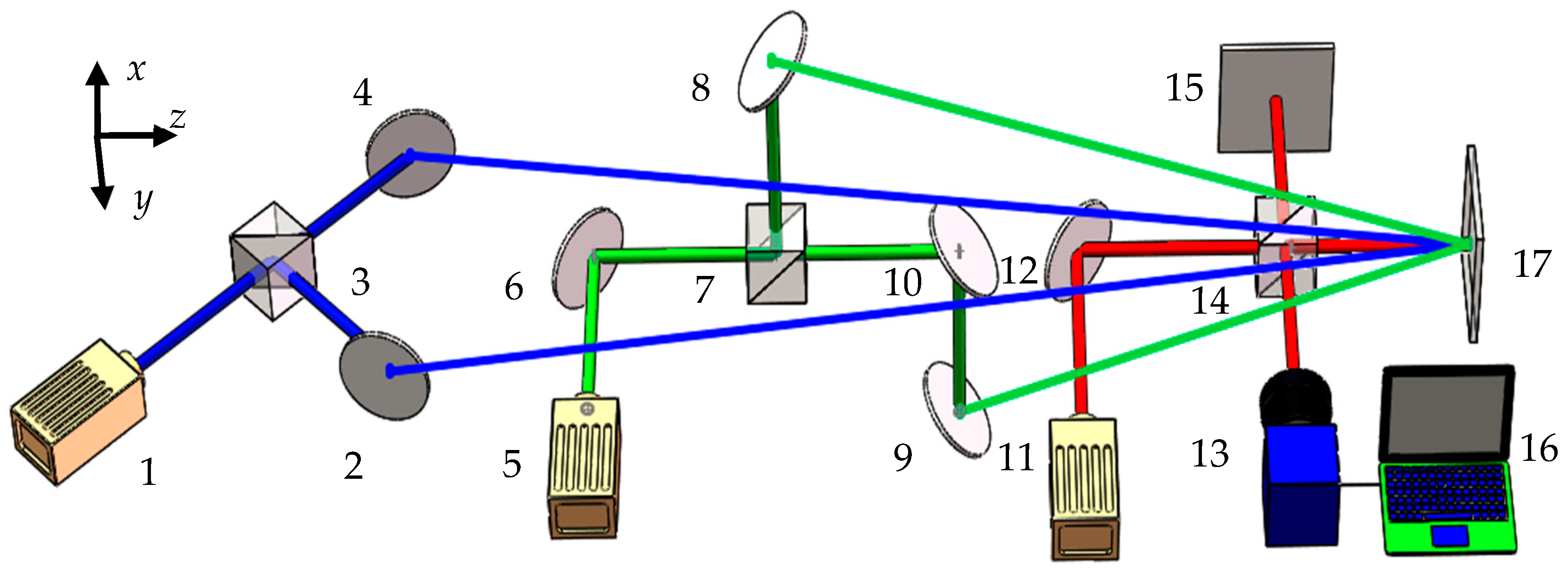
3.2.1. The Experiment
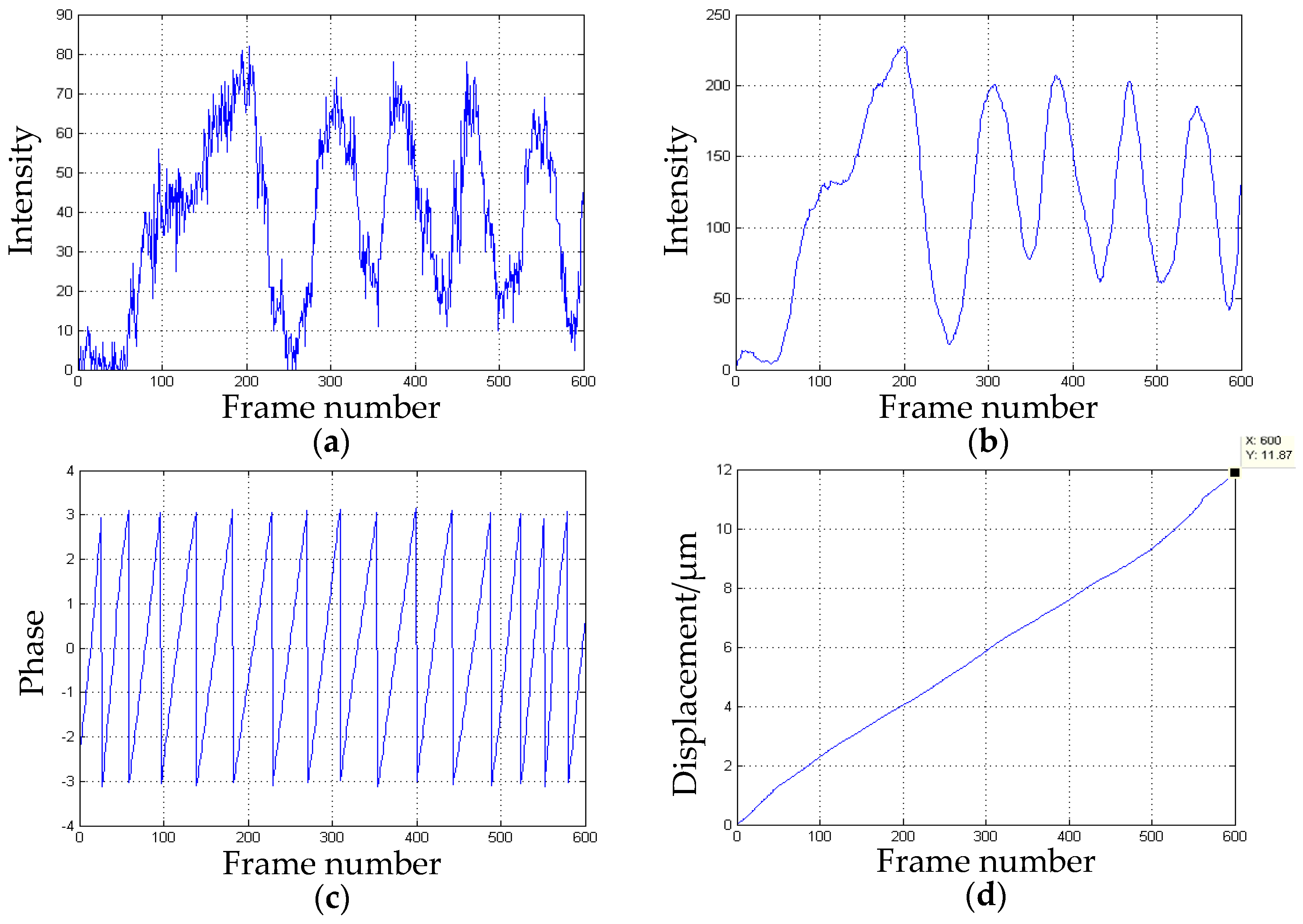
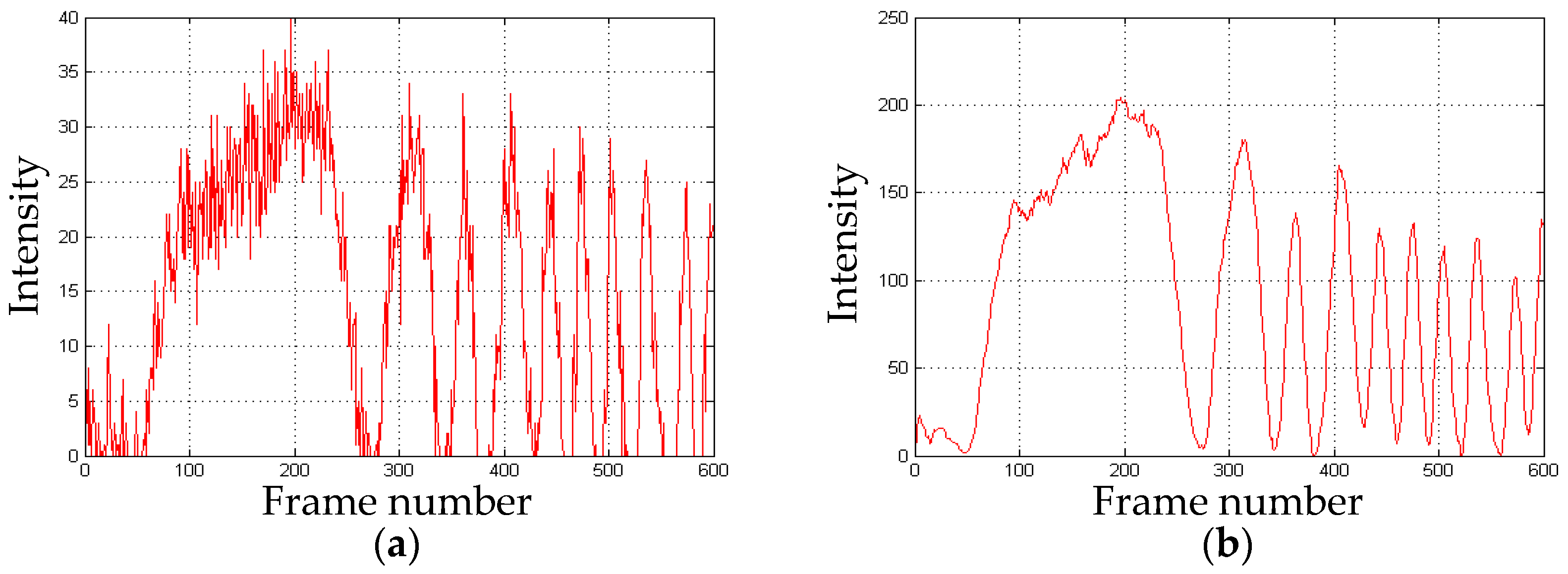
3.2.2. Multi-Detection Points Processing
4. Discussion
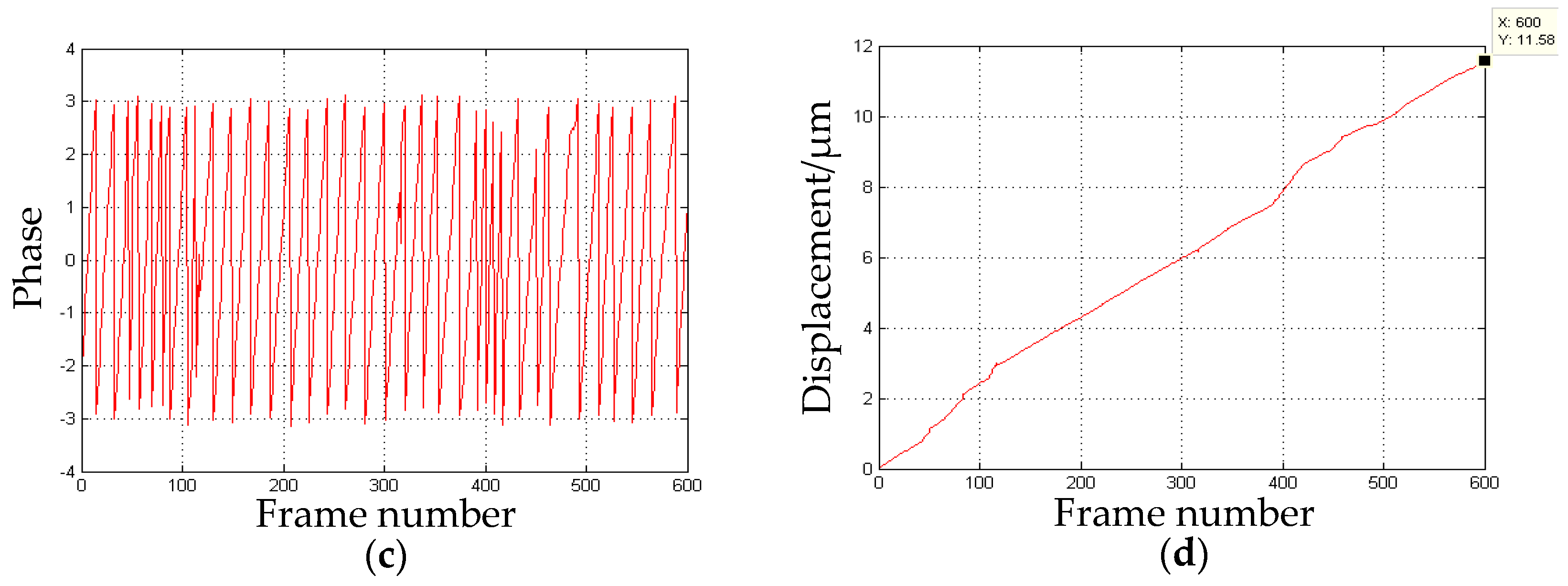
- The error of the displacement in the x-direction is the minimum in the three directions. As shown in Figure 11b, the peak to peak values and shapes of the waves after the first one are almost the same. Moreover, the intervals between the waves are also identical. These led to the most uniform change of the phase processed by the wavelet transform. Hence, a better phase unwrapping results are acquired.
- The accuracy of the displacement in the z-direction is more than 1%. Unlike the common-path layout in-plane measurement, the object and the reference is located in a different path, which is easier to be disturbed by the environment. To improve the accuracy, heterodyne speckle pattern interferometry (HSPI) is expected to be employed in future work.
- The experiment adopts several points of the metal plate to measure the accuracy of the system which are regarded as measurements of the full-field deformation and displacement. The whole object deformation and displacement will be obtained by processing each point of the object with the same algorithm.
- The wavelet transform is used to analyze the speckle interferograms. Compared with the Fourier transform, it can show more detail to obtain more accurate displacement information.
- The measurement resolution of the system is less than half a wavelength, which is limited by many factors, such as the stability of the laser source, sampling rate of the CCD camera used, the disturbance of the environment, etc. In our case, the main factor is the phase unwrapping algorithm, particularly the selection of the mother wavelet. The monitored distance of the system from the object can be from a few meters to 10 meters away in the laboratory, mainly depending on the coherence length of the laser source. In theory, as long as the speckle interferograms can be recorded, the measurement can be completed successfully. However, it is difficult to do this outdoors due to the rapid change of background light intensity, vibrations, and air disturbance, which are common problems in interfering instruments. On the other hand, the camera vibrations caused by ground motion affect the measuring accuracy as well.
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Yang, L.X.; Xie, X.; Zhu, L.Q.; Wu, S.J.; Wang, Y.H. Review of Electronic Speckle Pattern Interferometry (ESPI) for Three Dimensional Displacement Measurement. Chin. J. Mech. Eng. 2014, 27, 1–13. [Google Scholar] [CrossRef]
- Eric, B.F.; Lori, C.B.; Timothy, P.S.; Zamir, L.; Laurel, H.F.; Tommy, C.L.; Scott, R.G.; Aaron, C.K. Three-wavelength electronic speckle pattern interferometry with the Fourier-transform method for simultaneous measurement of microstructure-scale deformations in three dimensions. Appl. Opt. 2006, 45, 3218–3225. [Google Scholar]
- Tang, S.J.; Zhu, Q.; Chen, W.; Darwish, W.; Wu, B.; Hu, H.; Chen, M. Enhanced RGB-D Mapping Method for Detailed 3D Indoor and Outdoor Modeling. Sensors 2016, 16, 1589. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.H.; Xue, Q.; Wang, Z.; Gao, J.M. Analysis and Compensation for Lateral Chromatic Aberration in a Color Coding Structured Light 3D Measurement System. Sensors 2016, 16, 1426. [Google Scholar] [CrossRef] [PubMed]
- Feng, D.M.; Feng, M.Q. Vision-based multi-point displacement measurement for structural health monitoring. Struct. Control Health Monit. 2016, 23, 876–890. [Google Scholar] [CrossRef]
- Feng, M.Q.; Fukuda, Y.; Feng, D.M.; Mizuta, M. Nontarget vision sensor for remote measurement of bridge dynamic response. J. Bridge Eng. 2015, 20, 04015023. [Google Scholar] [CrossRef]
- Feng, D.M.; Feng, M.Q.; Ozer, E.; Fukuda, Y. A vision-based sensor for noncontact structural displacement measurement. Sensors 2015, 15, 16557–16575. [Google Scholar] [CrossRef] [PubMed]
- Philip, S.; Víctor, Á.; Francisco, D.; Eann, A.P. A simultaneous in- and out-of-plane displacement measurement method. Opt. Lett. 2011, 36, 10–12. [Google Scholar]
- Yano, Y.; Watanabe, Y.; Ishii, T.; Goka, S.; Sato, T.; Sekimoto, H. Real-Time Three-Dimensional Vibration Mode Visualization System Based on Laser Speckle Interference. In Proceedings of the 2010 IEEE International Frequency Control Symposium, Newport Beach, CA, USA, 1–4 June 2010.
- Tang, Z.Z.; Liang, J.; Xiao, Z.Z.; Guo, C. Large deformation measurement scheme for 3D digital image correlation method. Opt. Lasers Eng. 2012, 50, 122–130. [Google Scholar] [CrossRef]
- Gao, Y.H.; Sun, P. Three-Dimensional Phase Evaluation in ESPI by Using a Non-Cube Beam-Splitter. Exp. Mech. 2016, 56, 507–511. [Google Scholar] [CrossRef]
- Joenathan, C.; Franze, B.; Haible, P.; Tiziani, H.J. Speckle interferometry with temporal phase evaluation for measuring large-object deformation. Appl. Opt. 1998, 37, 2608–2614. [Google Scholar] [CrossRef] [PubMed]
- Adamczak, S.; Makiela, W.; Stepien, K. Investigating advantages and disadvantages of the analysis of a geometrical surface structure with the use of Fourier and wavelet transform. Metrol. Meas. Syst. 2010, 17, 233–244. [Google Scholar] [CrossRef]
- Hariharan, P. Optical Interferometry: The Post-Michelson Era. Aust. J. Phys. 1993, 46, 103–119. [Google Scholar]
- Yasuhiko, A. Development of in-plane and out-of-plane deformations simultaneous measurement method for the analysis of buckling. Opt. Eng. 2015, 54, 024102. [Google Scholar]
- Lionel, R.W. Review of fringe pattern phase recovery using the 1-D and 2-D continuous wavelet transforms. Opt. Lasers Eng. 2012, 50, 1015–1022. [Google Scholar]
- Liu, H.; Cartwright, A.N.; Basaran, C. Experimental verification of improvement of phase shifting moiré interferometry using wavelet-based image processing. Opt. Eng. 2004, 43, 1206–1214. [Google Scholar] [CrossRef]
- Zappa, E.; Busca, G. Comparison of eight unwrapping algorithms applied to Fourier-transform profilometry. Opt. Lasers Eng. 2008, 46, 106–116. [Google Scholar] [CrossRef]





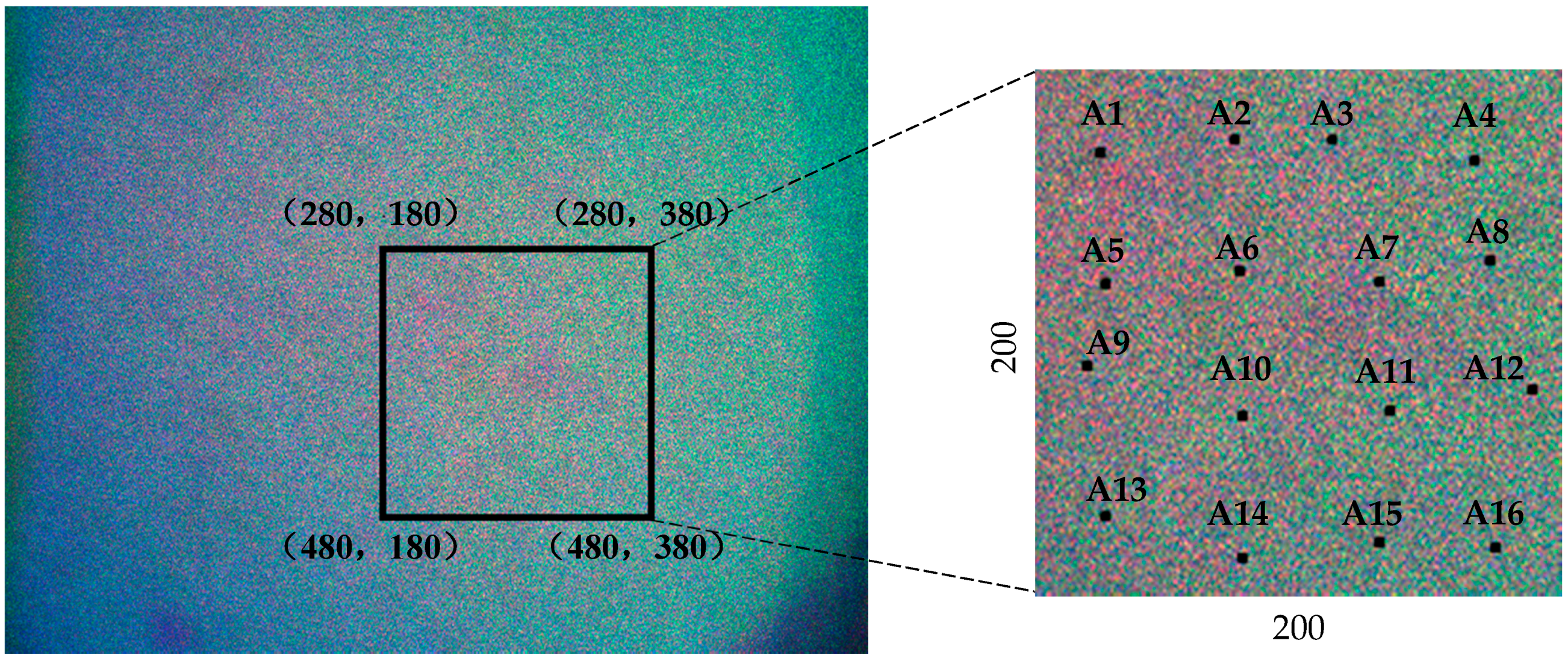
| x-Direction | y-Direction | z-Direction | |||||
|---|---|---|---|---|---|---|---|
| Name | Coordinate | Value/µm | Error/µm | Value/µm | Error/µm | Value/µm | Error/µm |
| A1 | (24, 30) | 11.99 | 0.09 | 13.23 | 0.27 | 11.99 | 0.19 |
| A2 | (74, 25) | 11.92 | 0.02 | 13.67 | 0.17 | 11.99 | 0.19 |
| A3 | (111, 26) | 12.00 | 0.10 | 13.26 | 0.24 | 11.88 | 0.08 |
| A4 | (166, 33) | 11.89 | 0.01 | 13.45 | 0.05 | 12.11 | 0.31 |
| A5 | (26, 80) | 11.78 | 0.12 | 13.21 | 0.29 | 11.68 | 0.12 |
| A6 | (76, 75) | 11.60 | 0.30 | 13.18 | 0.32 | 11.94 | 0.14 |
| A7 | (130, 78) | 11.86 | 0.04 | 13.26 | 0.24 | 11.89 | 0.11 |
| A8 | (172, 72) | 11.85 | 0.05 | 13.21 | 0.29 | 11.92 | 0.12 |
| A9 | (18, 111) | 11.94 | 0.04 | 13.93 | 0.43 | 11.89 | 0.09 |
| A10 | (78, 131) | 11.92 | 0.02 | 13.22 | 0.28 | 12.17 | 0.37 |
| A11 | (134, 128) | 11.98 | 0.08 | 13.25 | 0.25 | 11.97 | 0.17 |
| A12 | (188, 120) | 11.87 | 0.03 | 13.83 | 0.33 | 11.71 | 0.09 |
| A13 | (25, 169) | 12.02 | 0.12 | 13.85 | 0.35 | 11.88 | 0.08 |
| A14 | (77, 184) | 11.88 | 0.02 | 13.28 | 0.22 | 12.16 | 0.36 |
| A15 | (130, 179) | 12.10 | 0.20 | 13.23 | 0.27 | 11.58 | 0.22 |
| A16 | (174, 181) | 11.94 | 0.04 | 13.25 | 0.25 | 11.91 | 0.11 |
| Average | 11.91 | 0.01 | 13.39 | 0.11 | 11.92 | 0.12 | |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, J.; Gao, Z.; Wang, X.; Yang, S. Three-Dimensional Continuous Displacement Measurement with Temporal Speckle Pattern Interferometry. Sensors 2016, 16, 2020. https://doi.org/10.3390/s16122020
Qin J, Gao Z, Wang X, Yang S. Three-Dimensional Continuous Displacement Measurement with Temporal Speckle Pattern Interferometry. Sensors. 2016; 16(12):2020. https://doi.org/10.3390/s16122020
Chicago/Turabian StyleQin, Jie, Zhan Gao, Xu Wang, and Shanwei Yang. 2016. "Three-Dimensional Continuous Displacement Measurement with Temporal Speckle Pattern Interferometry" Sensors 16, no. 12: 2020. https://doi.org/10.3390/s16122020






