Optimization and Experimentation of Dual-Mass MEMS Gyroscope Quadrature Error Correction Methods
Abstract
:1. Introduction
2. Dual Mass MEMS Gyroscope Structure and Quadrature Error Model
2.1. Dual-Mass MEMS Gyroscope Structure
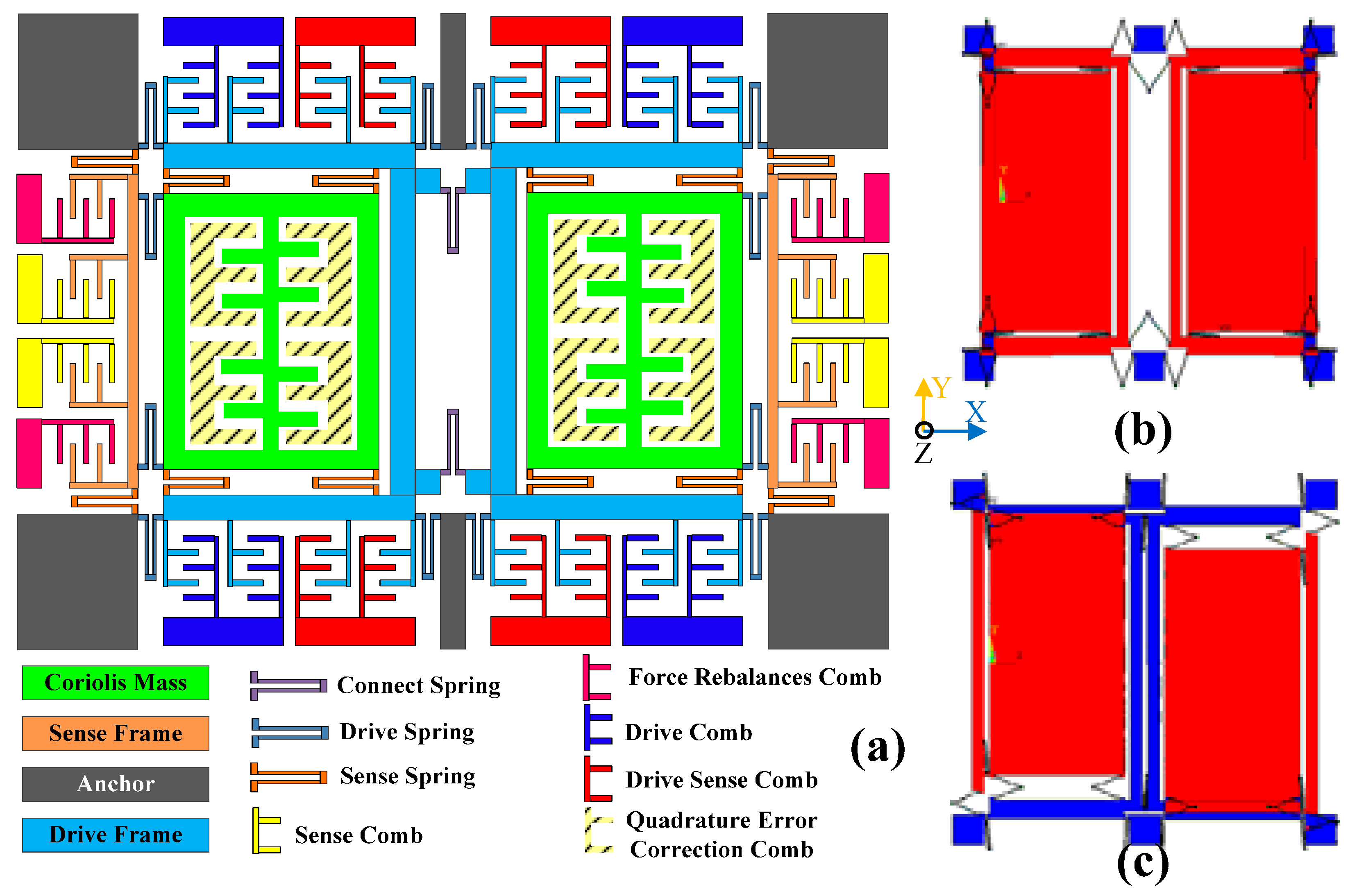
2.2. Quadrature Error Model
| Parameter | Value |
|---|---|
| ωd | 3488.9 × 2π rad/s |
| kx | 593.9 N/m |
| ky | 532.0 N/m |
| kyx, kxy | 0.1719 N/m |
| cyx | 1.29 × 10−7 N/m/s |
| Ax | 1.56 μm |
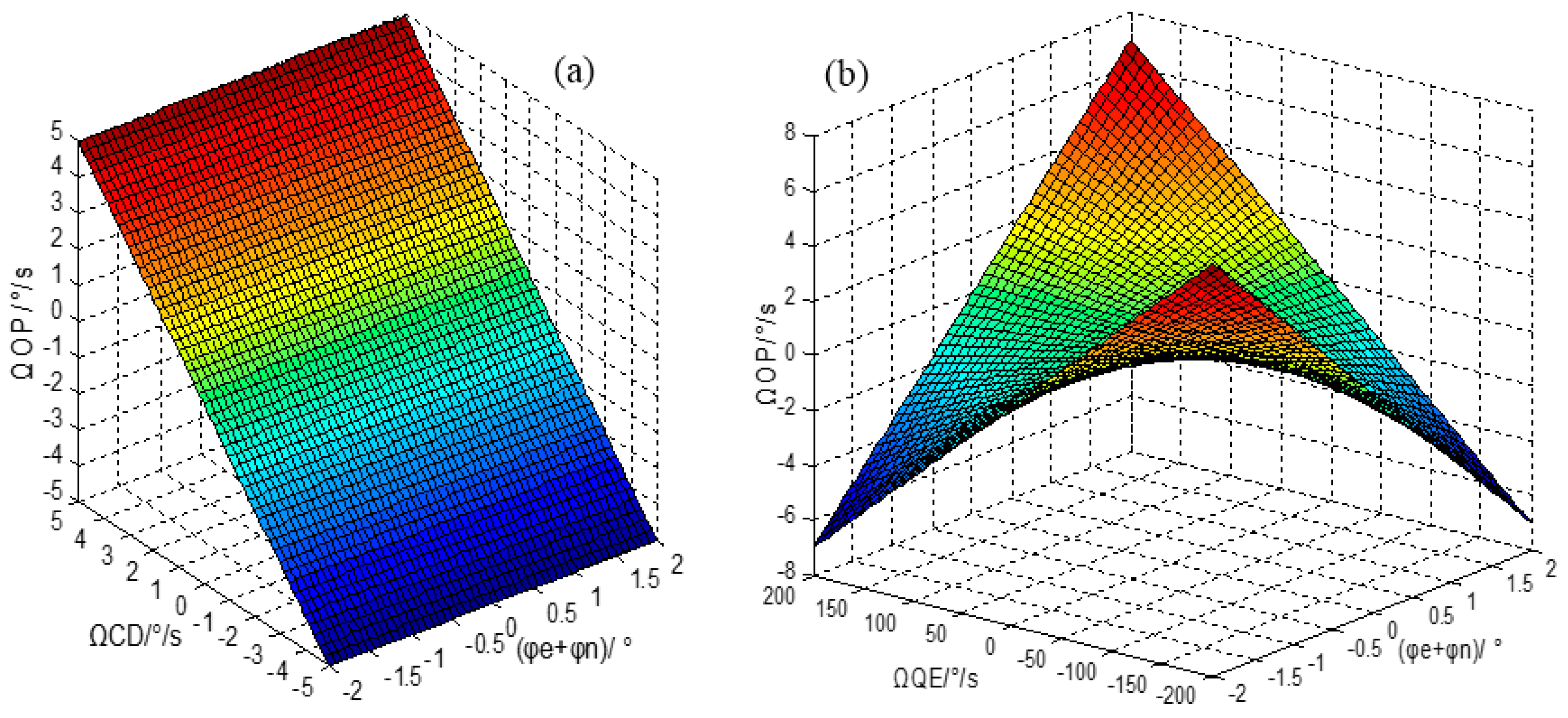
2.3. Dual-Mass Quadrature Error Model
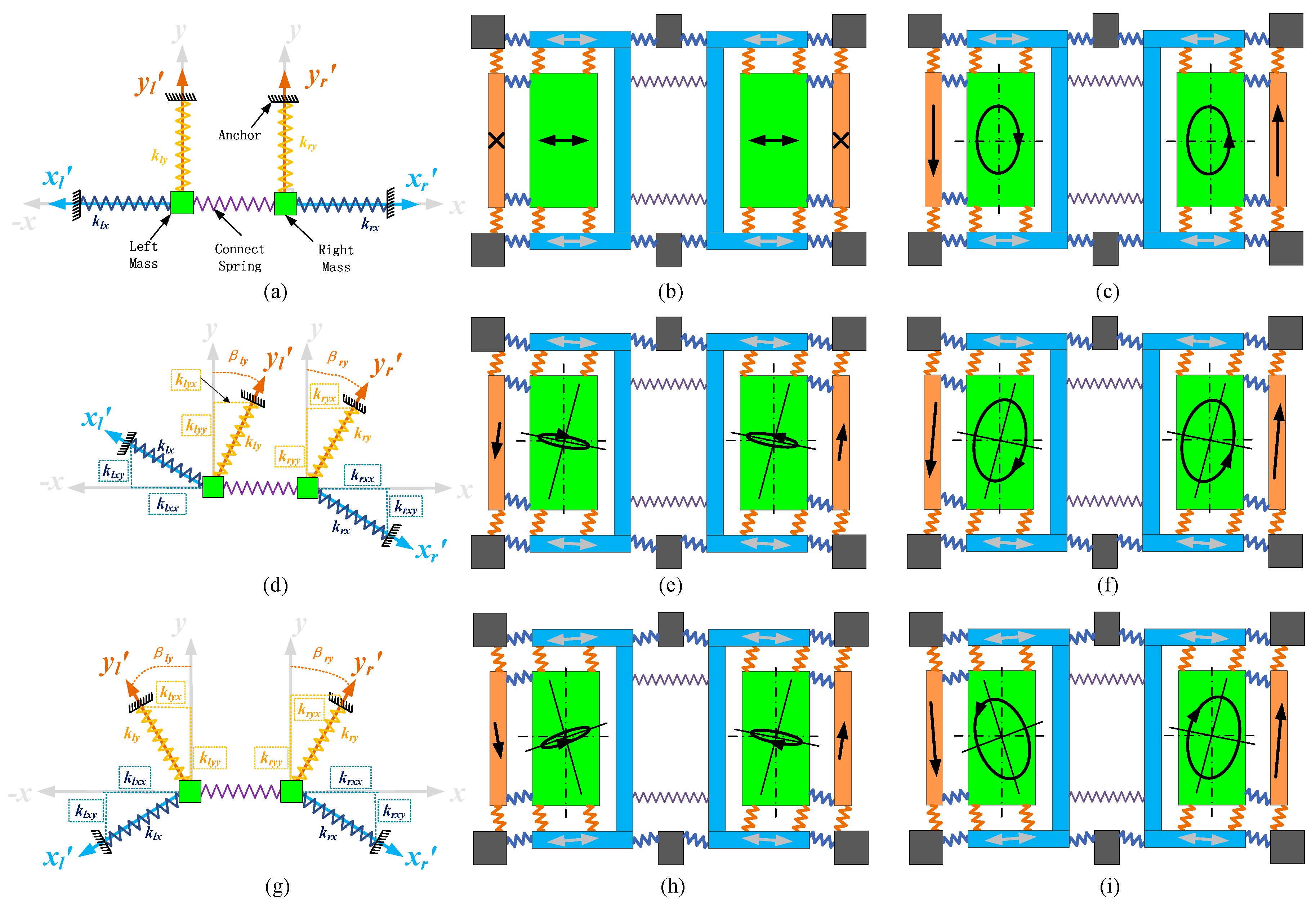
2.4. Dual-Mass Gyro Quadrature Error Correction Realization Methods
3. Dual-Mass Gyro Quadrature Error Correction Method
3.1. Quadrature Error Correction Methods and Gyro System
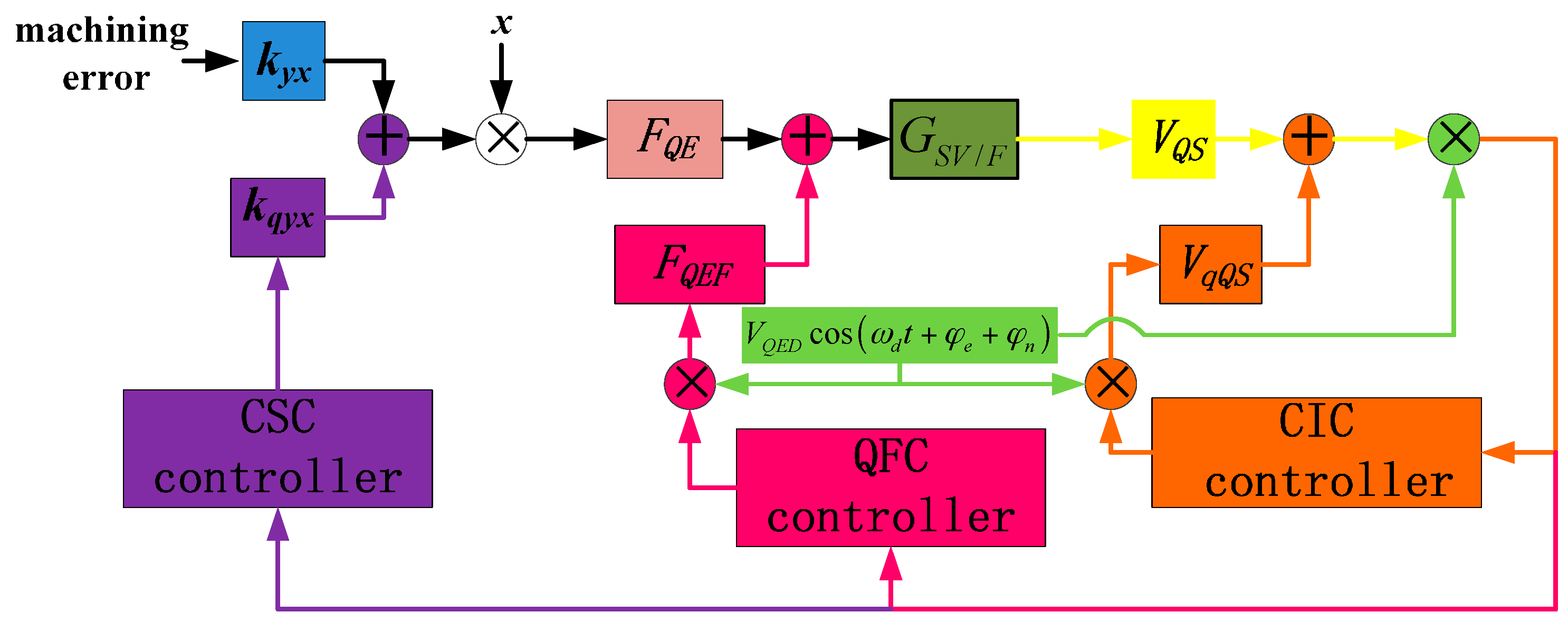
- The charge injecting correction (CIC) method focuses on the quadrature error signal VQS in the sense loop, and does not influence the movement of the gyro structure.
- The quadrature force correction (QFC) method takes quadrature error force FQE as the controlling object, and does not change the stiffness of the structure.
- The coupling stiffness correction (CSC) method aims at the quadrature error coupling stiffness directly, and in theory, this method eliminates quadrature error fundamentally.
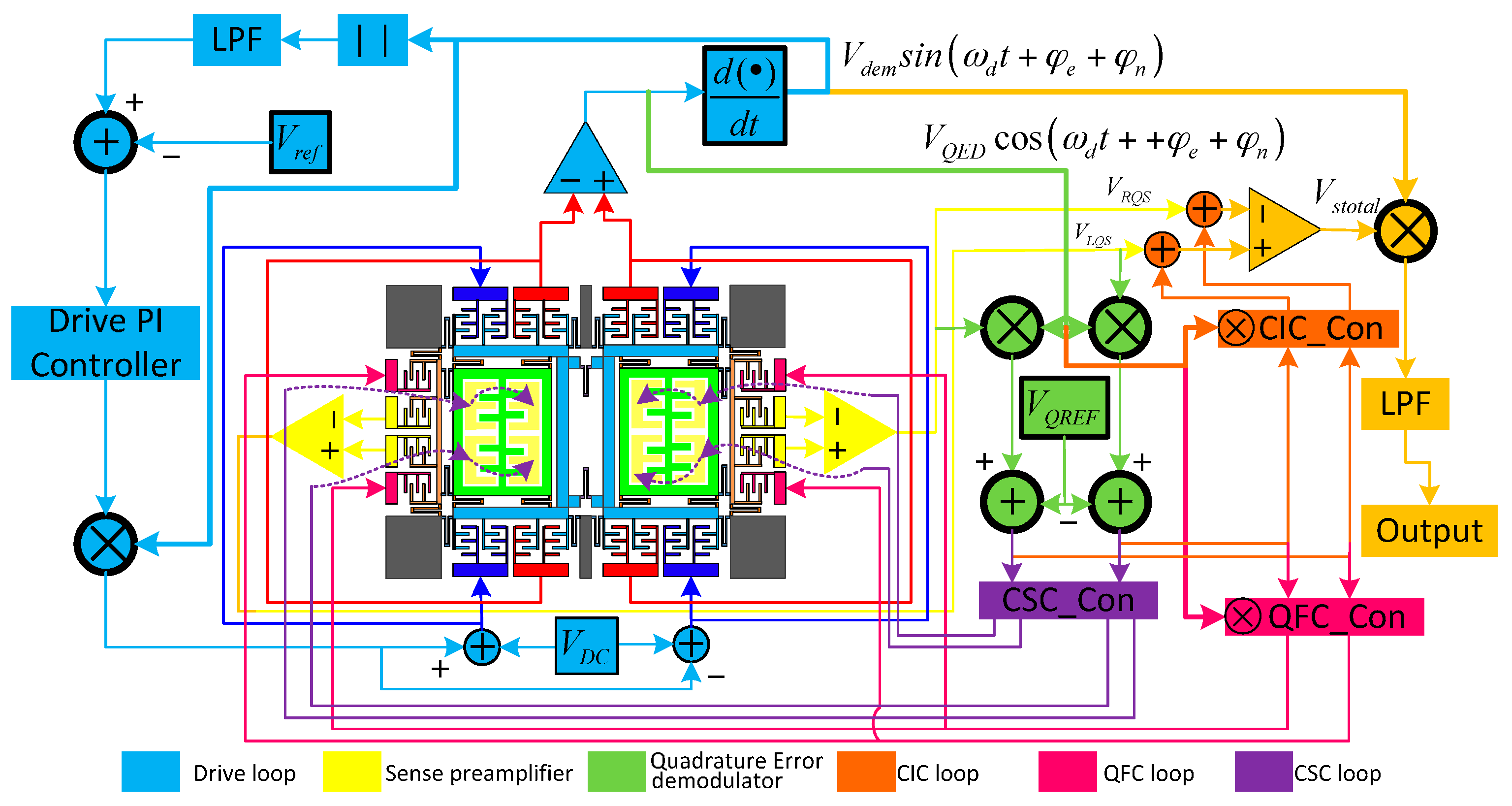
3.2. Charge Injecting Correction Method and System
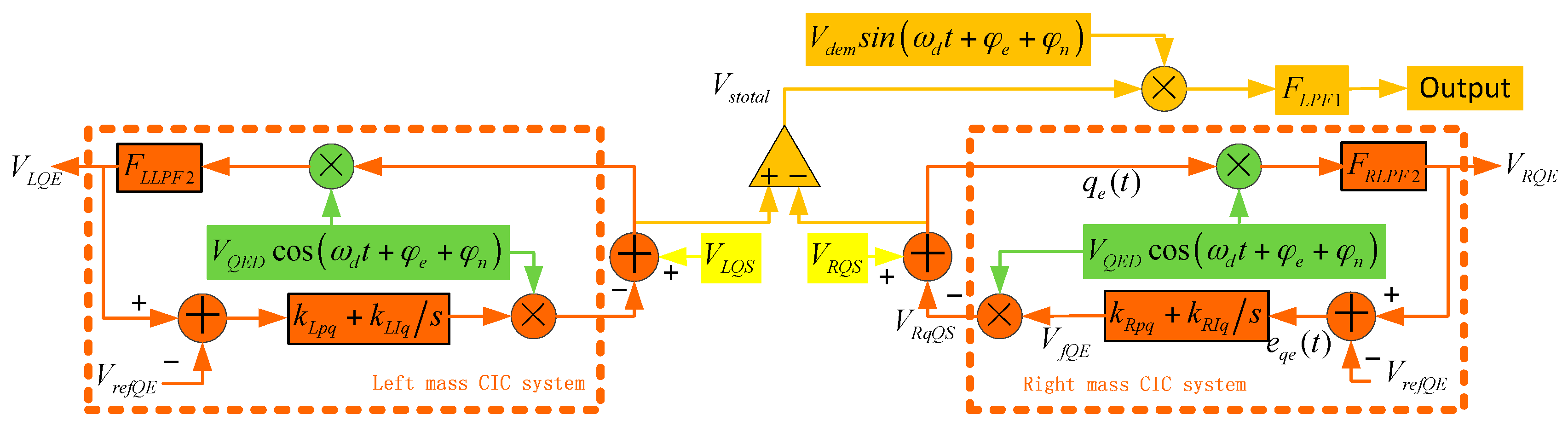
3.3. Quadrature Force Correction Method and System
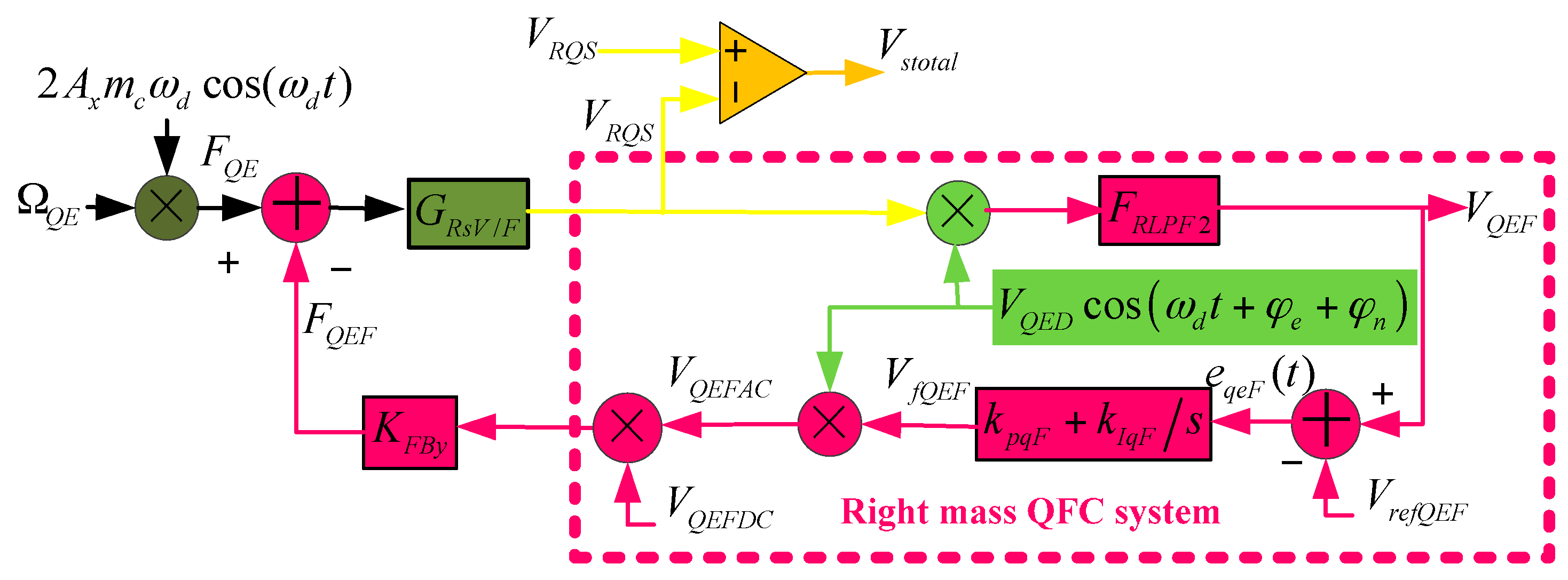
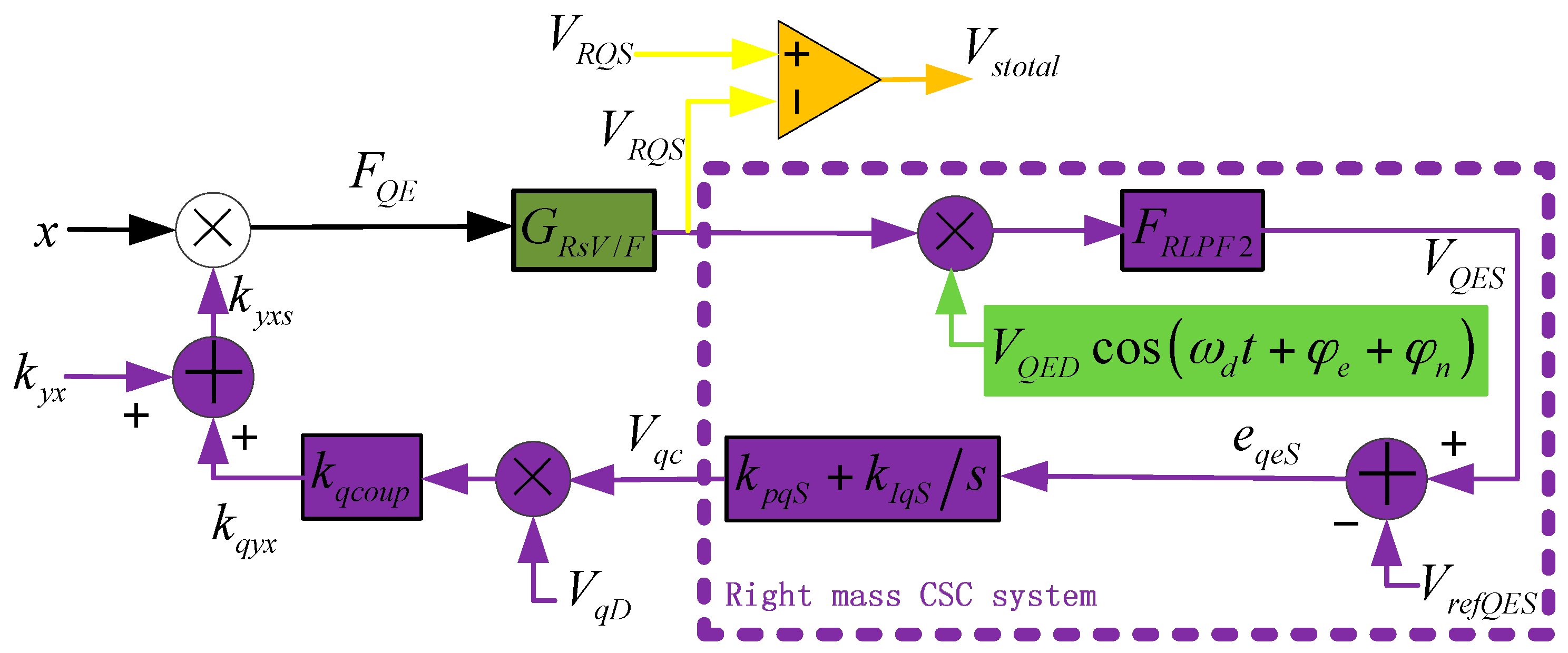
3.4. Coupling Stiffness Correction Method and System

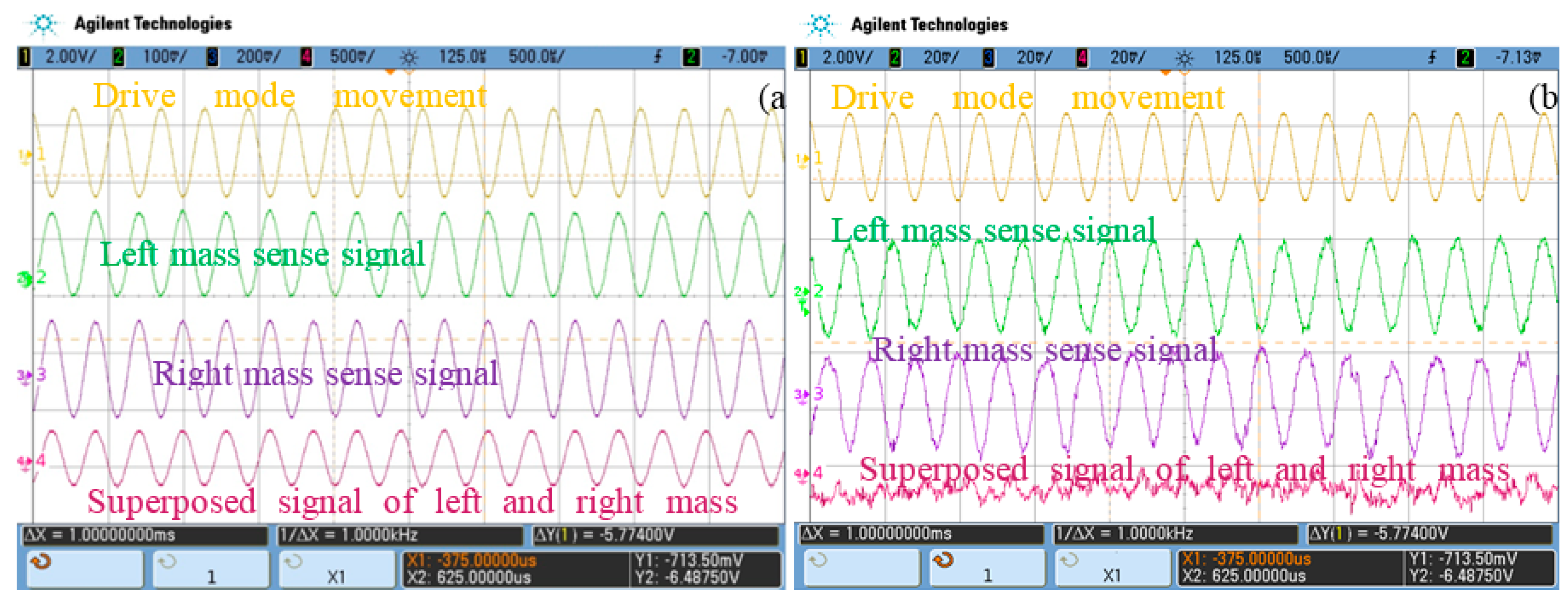
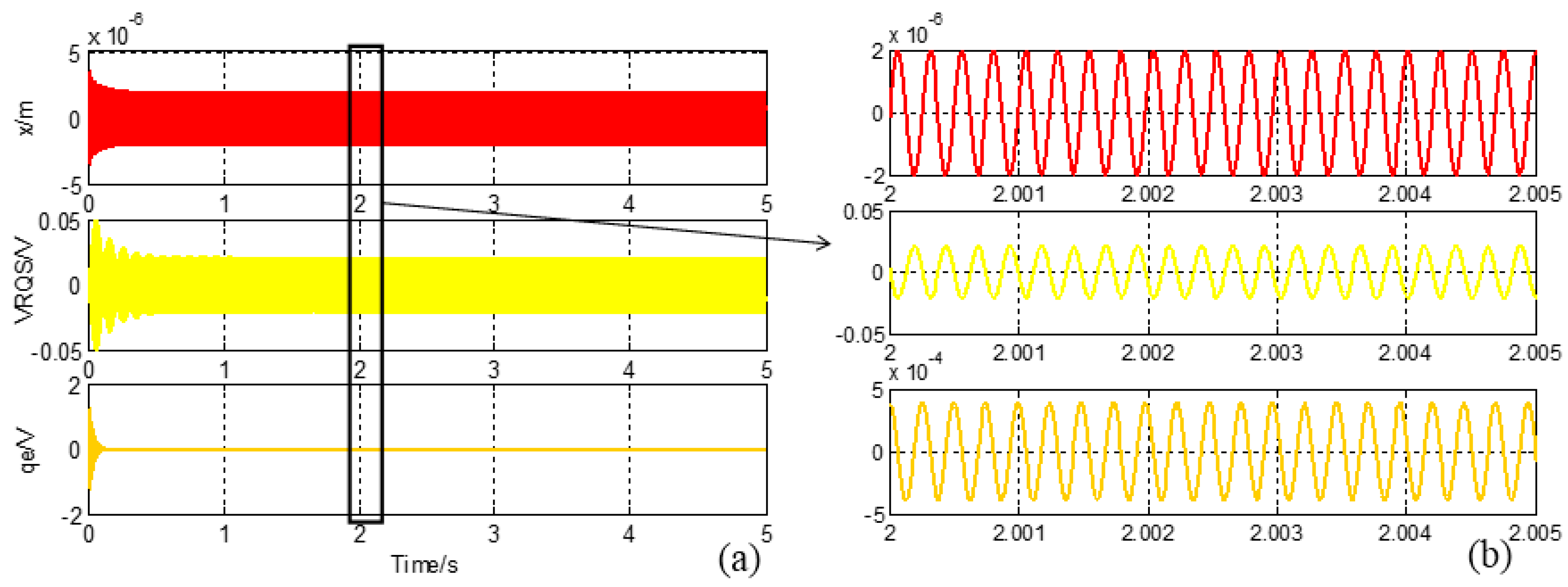
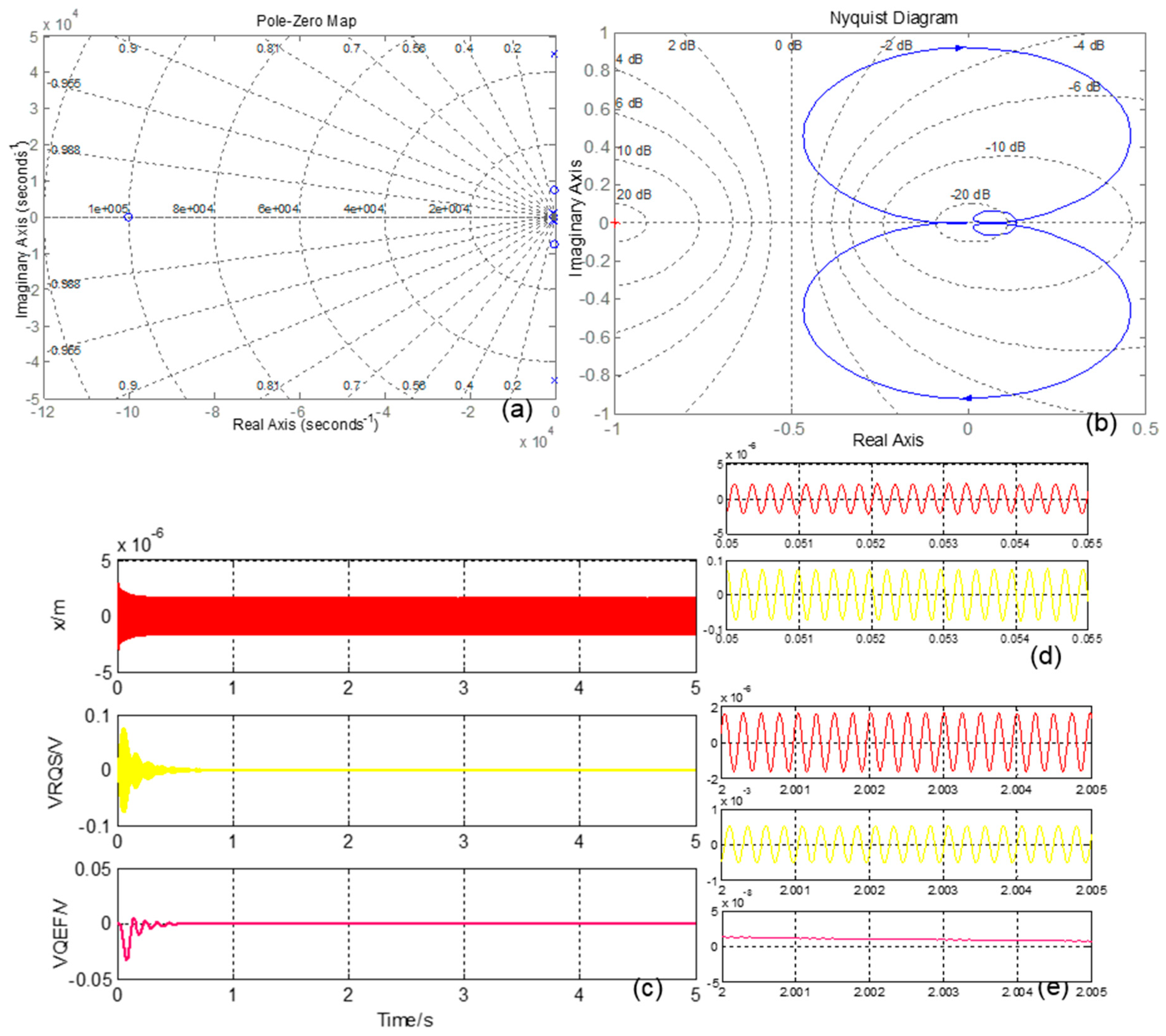
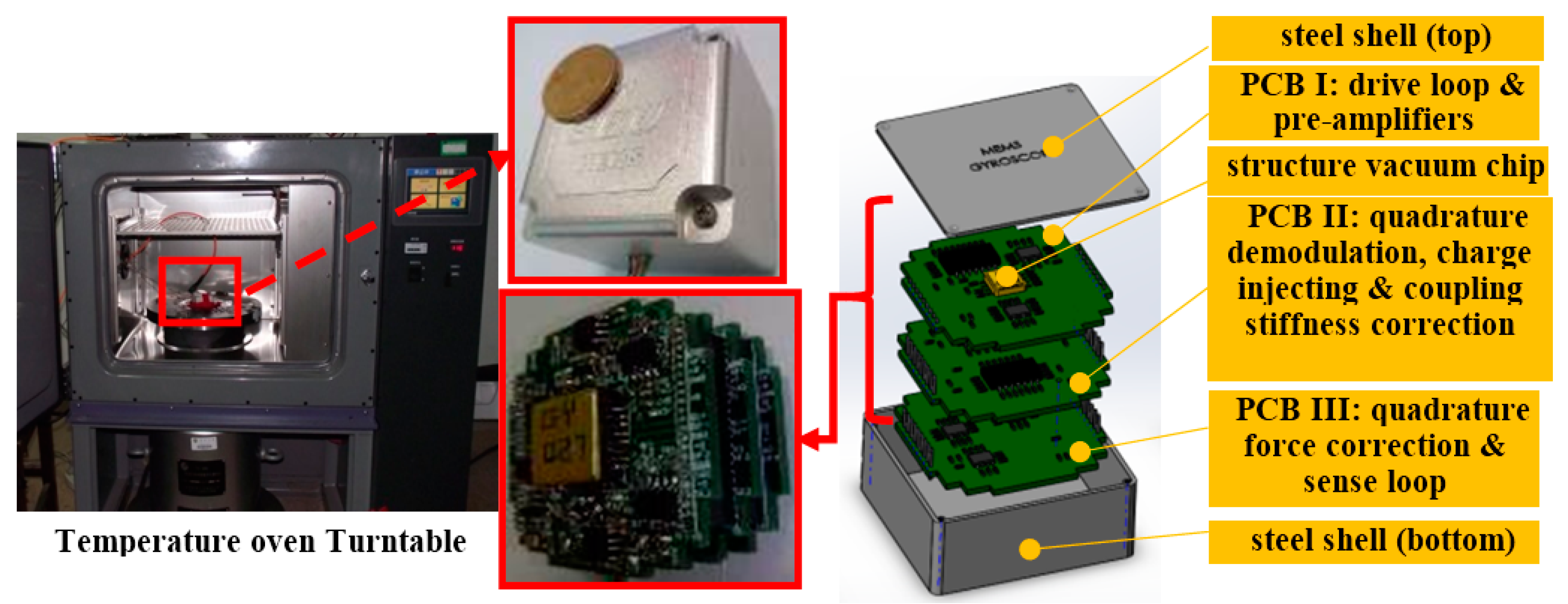
4. Experimental Section and Discussion
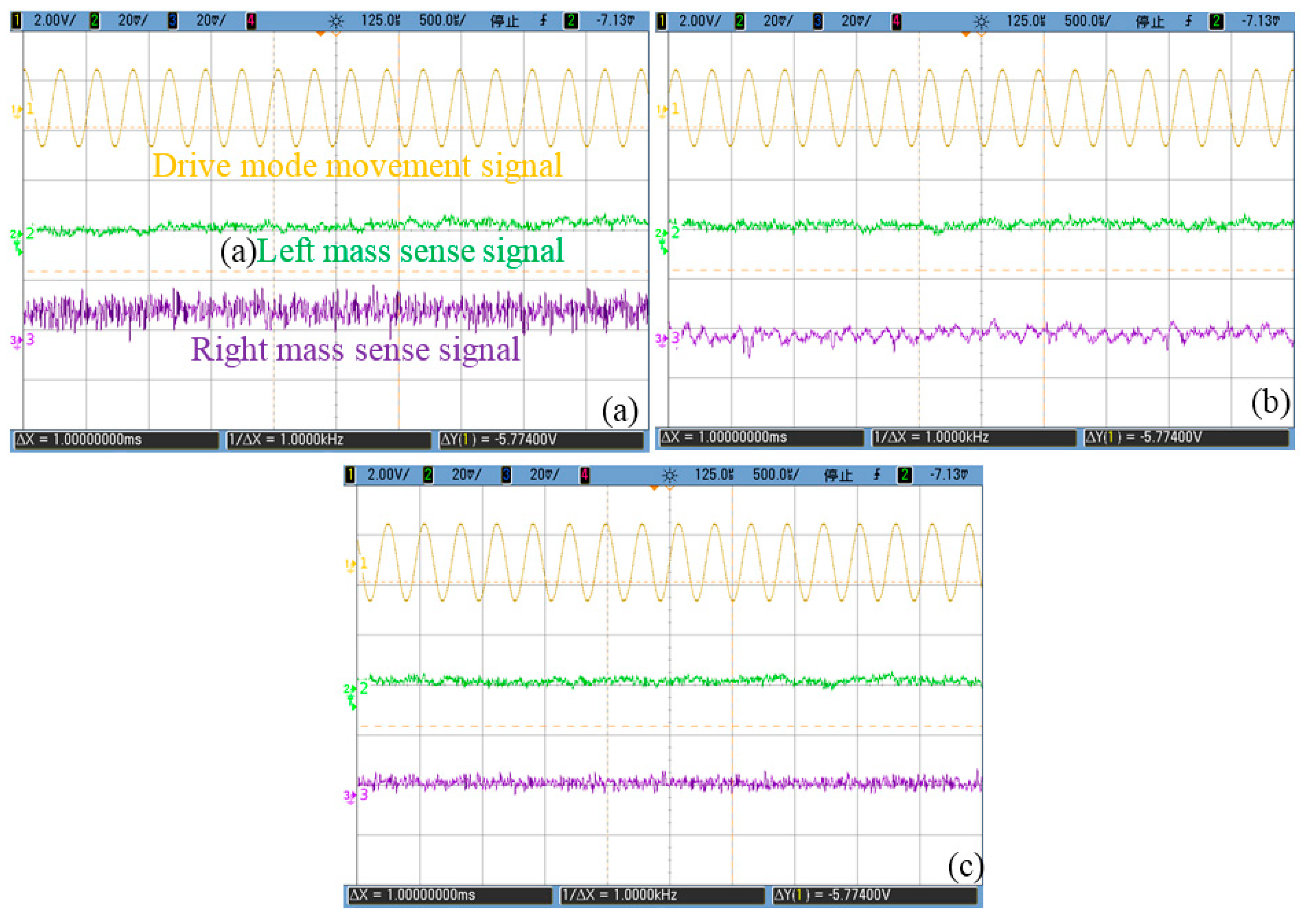
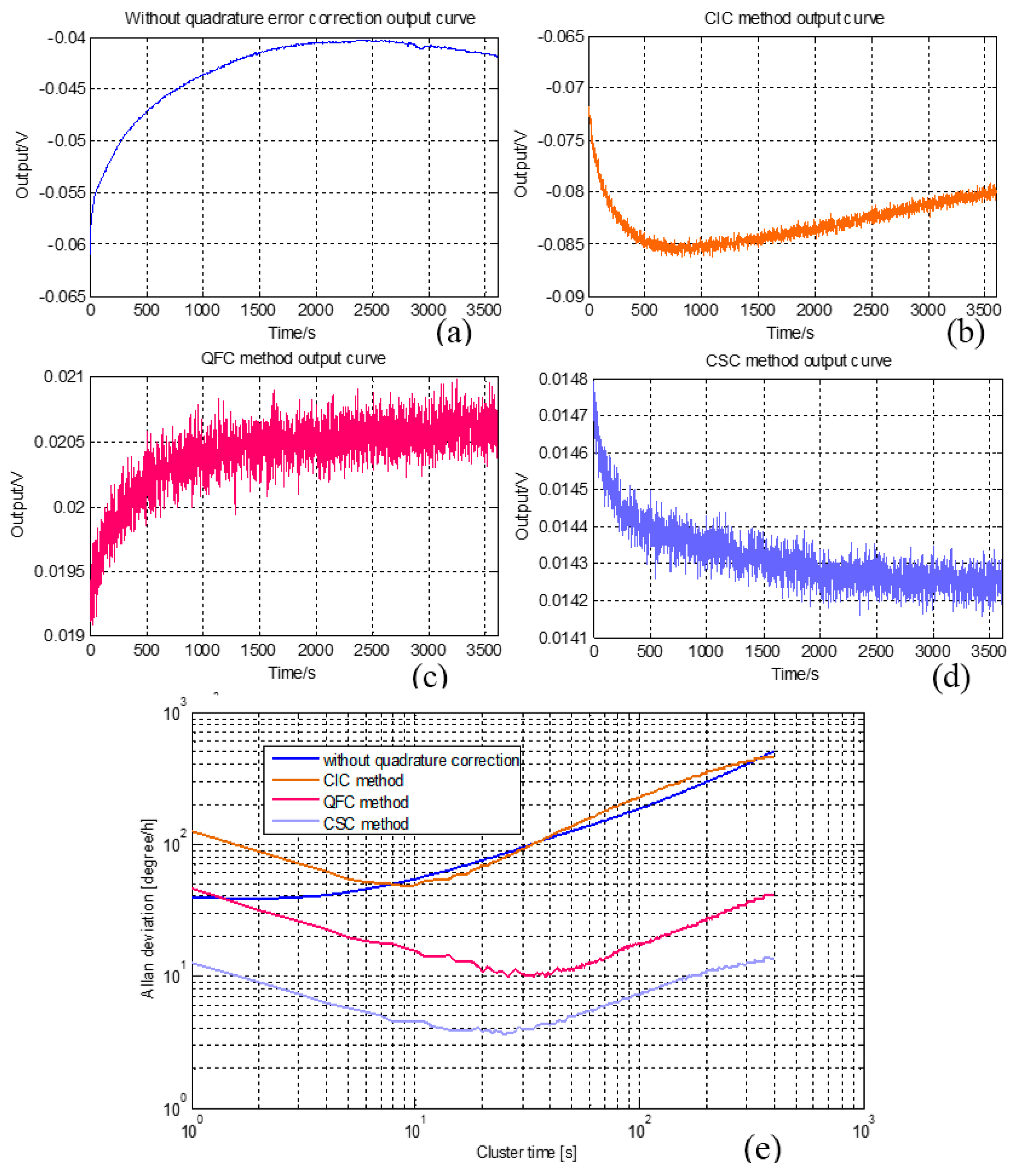
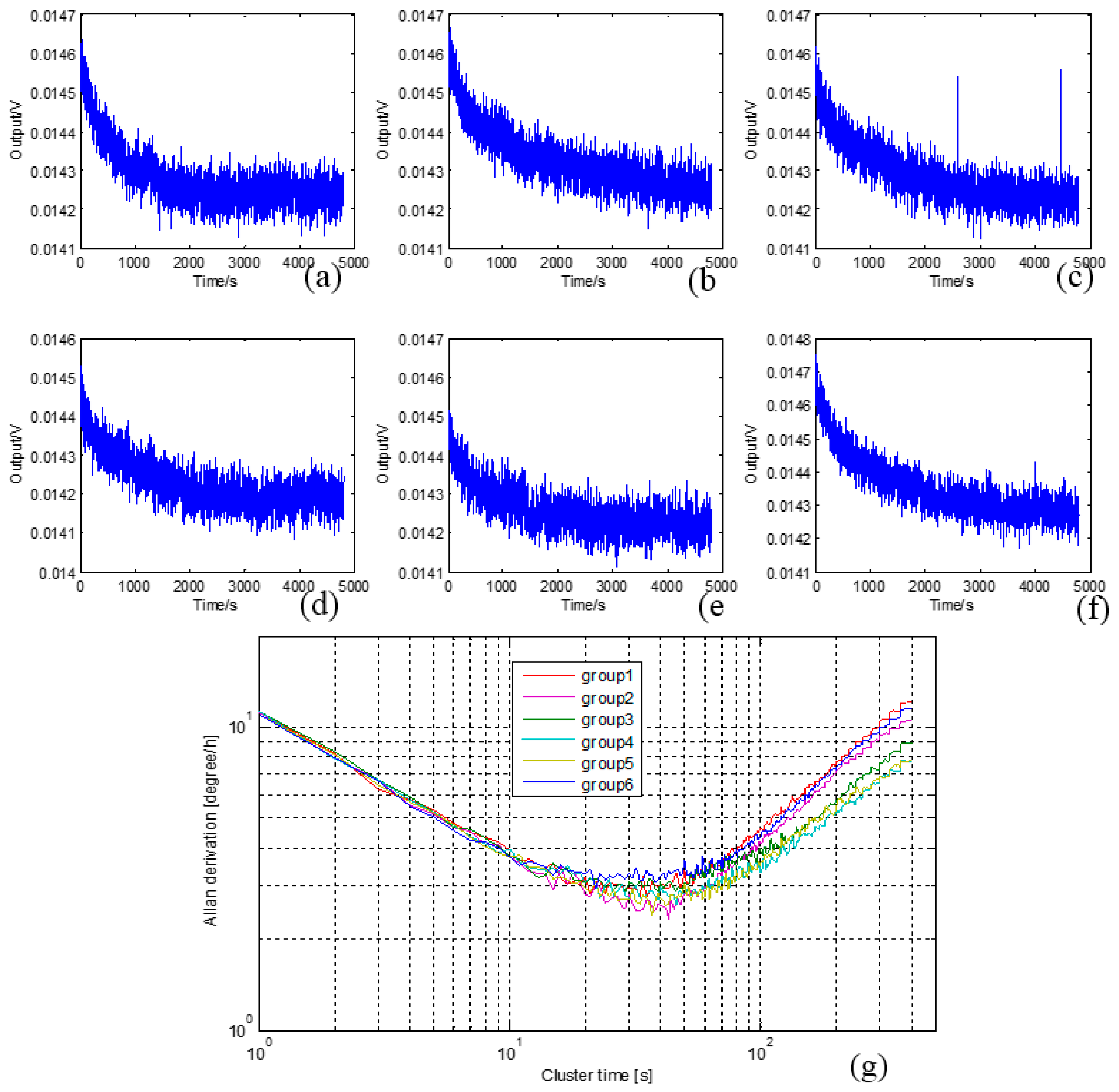
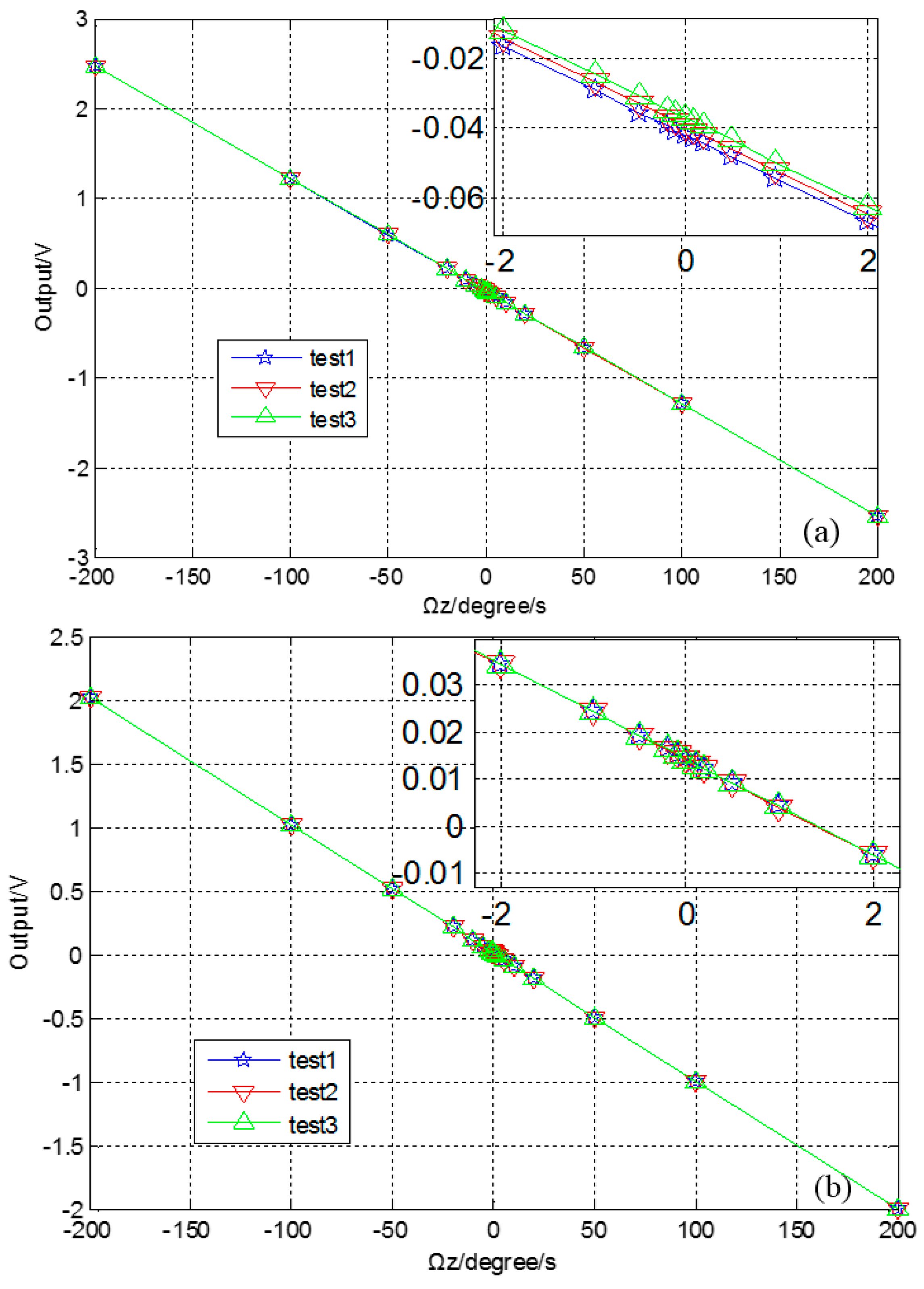
5. CSC System General Tests

| System | Parameter | Value | CSC Test Group | Parameter | Value |
| Without correction | Bias value | 4.16 °/s | |||
| Bias stability | 38 °/h | ||||
| ARW | 0.66 °/√h | 1 | Bias value | 1.747 °/s | |
| Scale factor nonlinearity | 925 ppm | Bias stability | 3.8 °/h | ||
| Scale factor repeatability | 818 ppm | 2 | Bias value | 1.752 °/s | |
| CIC method | Bias value | 7.92 °/s | Bias stability | 3.6 °/h | |
| Bias stability | 48 °/h | 3 | Bias value | 1.748 °/s | |
| ARW | 2.07 °/√h | Bias stability | 3.4 °/h | ||
| QFC method | Bias value | 2.26 °/s | 4 | Bias value | 1.741 °/s |
| Bias stability | 9.9 °/h | Bias stability | 3.1 °/h | ||
| ARW | 0.77 °/√h | 5 | Bias value | 1.744 °/s | |
| CSC method | Bias value | 1.749 °/s | Bias stability | 3.0 °/h | |
| Bias stability | 3.7 °/h | 6 | Bias value | 1.756 °/s | |
| ARW | 0.21 °/√h | Bias stability | 4.2 °/h | ||
| Scale factor nonlinearity | 660 ppm | ||||
| Scale factor repeatability | 403 ppm |
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zaman, M.; Sharma, A.; Hao, Z.; Ayazi, F. A mode-matched silicon-yaw tuning-fork gyroscope with subdegree-per-hour Allan deviation bias instability. J. Microelectromech. Syst. 2008, 6, 1526–1536. [Google Scholar] [CrossRef]
- Yang, C.; Li, H. Digital control system for the MEMS tuning fork gyroscope based on synchronous integral demodulator. IEEE Sens. J. 2015, 10, 5755–5764. [Google Scholar] [CrossRef]
- Antonello, R.; Oboe, R. Exploring the Potential of MEMS Gyroscopes: Successfully Using Sensors in Typical Industrial Motion Control Applications. IEEE Ind. Electron. Mag. 2012, 6, 14–24. [Google Scholar] [CrossRef]
- Xia, D.; Yu, C.; Kong, L. The development of micromachined gyroscope structure and circuitry technology. Sensors 2014, 14, 1394–1473. [Google Scholar] [CrossRef] [PubMed]
- Broquetas, A.; Comeron, A.; Gelonch, A.; Fuertes, J.; Castro, J.; Felip, D.; Lopez, M.; Pulido, J. Track detection in railway sidings based on MEMS gyroscope sensors. Sensors 2012, 12, 16228–16249. [Google Scholar] [CrossRef] [PubMed]
- Liewald, J.; Kuhlmann, B.; Balslink, T.; Trachtler, M.; Dienger, M.; Manoli, Y. 100 kHz MEMS vibratorygyroscope. J. Microelectromech. Syst. 2013, 5, 1115–1125. [Google Scholar] [CrossRef]
- Cao, H.; Li, H. Investigation of a vacuum packaged MEMS gyroscope architecture’s temperature robustness. Int. J. Appl. Electromagn. Mech. 2013, 4, 495–506. [Google Scholar]
- Tatar, E.; Alper, S.; Akin, T. Quadrature- error compensation and corresponding effects on the performance of fully decoupled MEMS gyroscopes. J. Microelectromech. Syst. 2012, 3, 656–667. [Google Scholar] [CrossRef]
- Chaumet, B.; Leverrier, B.; Rougeot, C.; Bouyat, S. A new silicon tuning fork gyroscope for aerospace applications. In Proceedings of the Symposium Gyro Technology 2009, Karlsruhe, Germany, 22–23 September 2009; pp. 1.1–1.13.
- Shkel, A. Precision navigation and timing enabled by micro technology: Are we there yet? In Proceedings of the SPIE Micro- and Nanotechnology Sensors, Systems, and Applications III, Orlando, FL, USA, 25 April 2013; pp. 1049–1053.
- Lutwak, R. Micro-technology for positioning, navigation, and timing towards PNT everywhere and always. In Proceedings of the 2014 International Symposium on Inertial Sensors and Systems (ISISS), Laguna Beach, CA, USA, 25–26 February 2014.
- Saukski, M.; Aaltonen, L.; Halonen, K. Zero-rate output and quadrature compensation in vibratory MEMS gyroscopes. IEEE Sens. J. 2007, 12, 1639–1652. [Google Scholar] [CrossRef]
- Tally, C.; Waters, R.; Swanson, P. Simulation of a MEMS Coriolis gyroscope with closed-loop control for arbitrary inertial force, angular rate, and quadrature inputs. In Proceedings of IEEE Sensors, Limerick, Ireland, 28–31 October 2011; pp. 1681–1684.
- Li, H.; Cao, H.; Ni, Y. Electrostatic stiffness correction for quadrature error in decoupled dual-mass MEMS gyroscope. J. Micro/Nanolith. MEMS MOEMS. 2014, 3. [Google Scholar] [CrossRef]
- Walther, A.; Blanc, C.L.; Delorme, N.; Deimerly, Y.; Anciant, R.; Willemin, J. Bias contributions in a MEMS tuning fork gyroscope. J. Microelectromech. Syst. 2013, 22, 303–308. [Google Scholar] [CrossRef]
- Cao, H.; Li, H.; Liu, J.; Shi, Y.; Tang, J.; Shen, C. An improved interface and noise analysis of a turning fork microgyroscope structure. Mech. Syst. Sign. Proc. 2016, 70–71, 1209–1220, in press. [Google Scholar] [CrossRef]
- Su, J.; Xiao, D.; Wu, X.; Hou, Z.; Chen, Z. Improvement of bias stability for a micromachined gyroscope based on dynamic electrical balancing of coupling stiffness. J. Micro/Nanolithogr. Mems Moems 2013, 3. [Google Scholar] [CrossRef]
- Ni, Y.; Li, H.; Huang, L. Design and application of quadrature compensation patterns in bulk silicon micro-gyroscopes. Sensors 2014, 14, 20419–20438. [Google Scholar] [CrossRef] [PubMed]
- Seeger, J.; Rastegar, A.; Tormey, T. Method and Apparatus for Electronic Cancellation of Quadrature Error. U.S. Patent 729,043,5B2, 6 November 2007. [Google Scholar]
- Maurer, M.; Northemann, T.; Manoli, Y. Quadrature compensation for gyroscopes in electro-mechanical bandpass ΣΔ-modulators beyond full-scale limits using pattern recognition. Procedia Eng. 2011, 25, 1589–1592. [Google Scholar] [CrossRef]
- Antonello, R.; Oboe, R.; Prandi, L.; Caminada, C.; Biganzoli, F. Open loop compensation of the quadrature error in MEMS vibrating gyroscopes. In Proceedings of the 35th Annual Conference of IEEE on Industrial Electronics (IECON '09), Porto, Portugal, 3–5 November 2009; pp. 4034–4039.
- Painter, C.; Shkel, A. Active structural error suppression in MEMS vibratory rate integrating gyroscopes. IEEE Sens. J. 2003, 5, 595–606. [Google Scholar] [CrossRef]
- Cao, H.; Li, H.; Sheng, X.; Wang, S.; Yang, B.; Huang, L. A novel temperature compensation method for a MEMS gyroscope oriented on a periphery circuit. Int. J. Adv. Robot. Syst. 2013, 10, 1–10. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, H.; Li, H.; Kou, Z.; Shi, Y.; Tang, J.; Ma, Z.; Shen, C.; Liu, J. Optimization and Experimentation of Dual-Mass MEMS Gyroscope Quadrature Error Correction Methods. Sensors 2016, 16, 71. https://doi.org/10.3390/s16010071
Cao H, Li H, Kou Z, Shi Y, Tang J, Ma Z, Shen C, Liu J. Optimization and Experimentation of Dual-Mass MEMS Gyroscope Quadrature Error Correction Methods. Sensors. 2016; 16(1):71. https://doi.org/10.3390/s16010071
Chicago/Turabian StyleCao, Huiliang, Hongsheng Li, Zhiwei Kou, Yunbo Shi, Jun Tang, Zongmin Ma, Chong Shen, and Jun Liu. 2016. "Optimization and Experimentation of Dual-Mass MEMS Gyroscope Quadrature Error Correction Methods" Sensors 16, no. 1: 71. https://doi.org/10.3390/s16010071






