In this section, the models of differential GNSS positioning using WL measurements are introduced. The case with regard to medium distances is focused on here.
2.1. Ambiguity Resolution Models
In medium and long baseline (>10 km) cases, residual atmospheric delays will affect the ambiguity resolution, therefore, the atmospheric errors have to be taken into account. There are two methods to deal with the residual atmospheric errors. The first one is to form combinations that can eliminate atmospheric errors or can reduce the impact of atmospheric errors to an extent that can be ignored, e.g., the Hatch-Melbourne-Wübbena (HMW) combination [
19,
30,
31]. The second one is to estimate the residual atmospheric delays as unknown parameters. Here, we focus on the method of forming combinations.
With triple-frequency or multi-frequency signals, more useful combinations can be formed [
26,
32,
33], such as EWL combinations. General triple-frequency phase combinations can be defined as [
26]:
where the combination coefficients
i,
j,
k are integers, and
f1,
f2,
f3, are three signal frequencies corresponding to B1, B3 and B2 of BDS or L1, L2 and L5 of GPS, respectively. The DD (double-differenced) phase measurements of three original DD observations in meters are Δφ
1, Δφ
2, Δφ
3, corresponding to,
f1,
f2 and
f3 According to [
26], the phase linear combinations can be classified as four categories: extra-wide-lane (EWL, λ ≥ 2.93 m), wide-lane (WL, 0.75 ≤ λ < 2.93 m), medium-lane (ML, 0.19 m ≤ λ < 0.75 m) and narrow-lane (NL, λ < 0.19 m) combinations.
Taking atmospheric errors into account, double-differenced phase and code combinations can be expressed as:
where
β is the ionospheric scale factor, the combination coefficients
l,
m,
n are integers,
ρ is the geometrical distance,
I is the ionospheric delay on the first frequency,
T is the tropospheric delay,
N is the ambiguity of phase combination,
λ is the wavelength of phase combination and
ε is the residual error.
Based on the former studies [
26,
33], several optimal and useful EWL combinations can be formed, for example, (0, 1, −1) and (1, −5, 4) of BDS. Considering the effects of the phase noise standard deviation and atmospheric errors, total noise level can be defined [
26], which is the ratio of the sum of errors and the wavelength. According to [
26], the total noise level of these EWL combinations is lower than 0.3 cycles in medium baselines case. Therefore, when implementing AR using these combinations, it is safe to ignore the atmospheric errors.
Theoretically, at least two independent EWL combinations can be formed using triple-frequency signals. The ambiguities of these two independent EWL combinations are determined first. A WL combination then can be derived by combining any of two independent EWL combinations. Therefore, we can fix the ambiguities of two EWL combinations firstly, and then form a WL signals from these two ambiguity-recovered EWL combinations for positioning. Theoretically, implementing wide-lane ambiguity resolution using this method is easier than that in dual-frequency case, because such EWL combinations cannot be found in dual-frequency case.
We will introduce the procedures of this method in detail in the following paragraphs. Two independent EWL combinations (EWL-I and EWL-II) have to be selected first, as listed in
Table 1. The characteristics of these selected combinations are also shown. As can be seen, the wavelength of the EWL combinations is up to several meters. Code combinations also have to be formed to constrain the phase combinations.
Table 2 shows the combinations we selected.
Table 1.
Characteristics of the selected phase combinations.
Table 1.
Characteristics of the selected phase combinations.
| Constellation | Combinations | Wavelength (m) | Ionospheric Scale Factor (m) | Noise Scale Factor (m) |
|---|
| BDS | EWL-I | (0, 1, −1) | 4.8842 | −1.5915 | 28.5287 |
| EWL-II | (1, −5, 4) | 6.3707 | 0.6521 | 172.6135 |
| GPS | EWL-I | (0, 1, −1) | 5.8610 | −1.7186 | 33.24 |
| EWL-II | (1, −6, 5) | 3.2561 | −0.0744 | 103.80 |
Table 2.
Characteristics of the selected code combinations.
Table 2.
Characteristics of the selected code combinations.
| Constellation | Combinations | Ionospheric Scale Factor (m) | Noise Scale Factor (m) |
|---|
| BDS | (0, 1, 1) | 1.5915 | 28.5287 |
| (1, 0, 0) | 1.0000 | 1.0 |
| GPS | (0, 1, 1) | 1.7186 | 33.24 |
| (1, 0, 0) | 1.0000 | 1.0 |
The first step is to resolve the ambiguity of the first EWL combination
. Both geometry-free and geometry based models can be used. The geometry-free model for EWL-I combination is as follows:
where
P indicates the code combinations.
λ indicates the wavelength
indicates the fixed ambiguities. The geometry-based model for EWL-I combination can be written as:
where
E is the identity matrix.
N indicates the ambiguities.
X indicates the baseline estimates, such as position.
A indicates the design matrix.
ε is the residual errors. As the ionospheric scale factor of Δ∇
P(0,11) is equal to that of Δ∇
φEWL-Ι, the ionspheric error can be completely eliminated. The tropospheric error is also eliminated. When using geometry-free model, rounding method is always used. When using geometry-based model, the Integer Least Squares (ILS) method is always used, which was investigated by many researchers [
34,
35,
36].
The second step is to resolve the ambiguity of the second EWL combination Δ∇
φEWL-∏ according to the following equation. Also, both geometry-free and geometry based models can be used. The geometry-free model is as follows:
The geometry-based model can be written as:
As the ionospheric factor of Δ∇P(0,11) is not equal to that of Δ∇φEWL-∏, the ionspheric error cannot be completely eliminated. However, the tropospheric error is eliminated.
Based on the above two independent resolved EWL ambiguities, the ambiguity of WL combination Δ∇
φ(1,0,–1) or Δ∇
φ(1,–1,0) can be computed according to the linear relationship, e.g.,
. Then, we can derive the WL observables which can be considered as precise pseudorange observables:
The success rate of WL AR is dependent on the success rate of the two EWL combinations. For dual-frequency signals, HMW combinations can be formed, which eliminate both geometric terms (including clock errors, tropospheric delay,
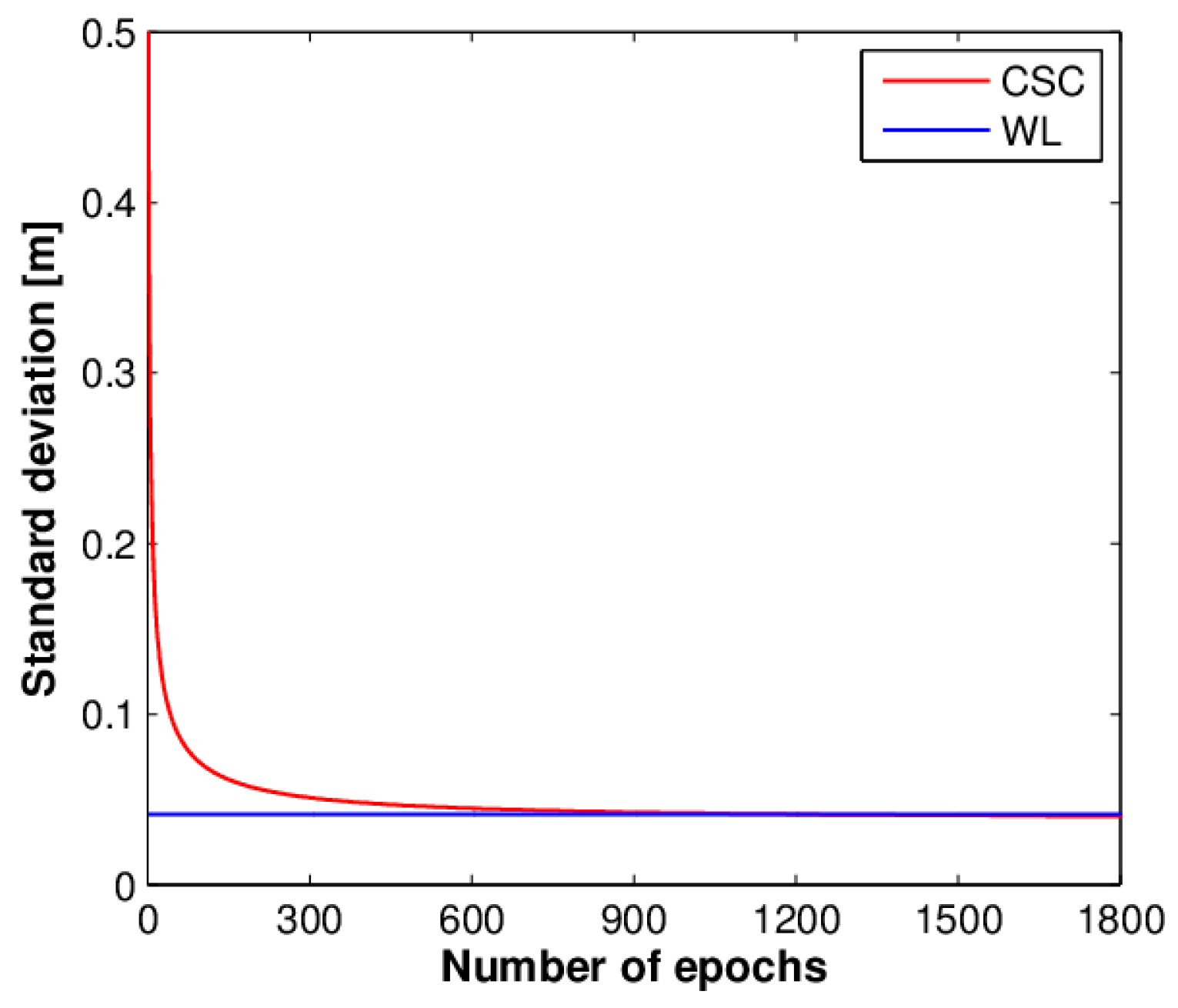
etc.) and ionospheric delays (first-order). In the double-difference case, only wide-lane ambiguities, multipath and measurement noise remain. Therefore, the ambiguities of WL measurement can be computed conveniently. Since the wavelength of the WL measurement is longer than 80 cm, we can fix its ambiguity much easier than that of original measurements [
17,
37].
The formula of DD HMW combination can be expressed as:
where
f1 and
f2 are the frequencies of the signals;
denotes the residual errors and observational noise of HMW combination, which is in units of wide-lane cycles.
is the wavelength of wide-lane measurements, which can be computed as follows:
where
c denotes the speed of light.
is the ambiguity of wide-lane measurements, which is defined as:
where
N1 and
N2 are the ambiguities of original measurements.
Using geometry-free model, WL ambiguities can be obtained:
where
indicates the averaged value of DD HMW combination. According to former studies [
17,
37], ten to thirty minutes are usually needed for averaging.