Mass Detection in Viscous Fluid Utilizing Vibrating Micro- and Nanomechanical Mass Sensors under Applied Axial Tensile Force
Abstract
:1. Introduction
2. Theory of Mass Determination in Fluid by the Axially Loaded Micro-/Nanomechanical-Based Mass Sensors
2.1. Statement of the Problem and the Basic Theory of the Mass Sensor
- (a)
- The beam length, L, exceeds its dominant cross-section scale WD, e.g., for a rectangular (circular) case L >> W (Dout), where W (Dout) is the resonator width (outer diameter);
- (b)
- The beam is made from isotropic linearly elastic solid material(s), and the shear deformations, rotary inertia, and internal friction effects are negligible;
- (c)
- The cross-section of the beam is uniform over its the entire length;
- (d)
- The beam vibrational amplitude is essentially smaller than any of its length scale;
- (e)
- Dissipative effects due to internal friction losses are negligibly small compared to those caused by the surrounding fluid (this assumption holds mainly just for the lower vibrational modes [11]);
- (f)
- Flexural resonant frequencies are distinct (it is always satisfied for the fundamental mode, whereas for the higher modes the coupling between flexural and torsional/longitudinal modes can be realized [12]);
- (g)
- Fluid surrounding beam is incompressible in nature;
- (h)
- The mass and size of the attached nanobead is essentially smaller than the mass of the beam itself, i.e., the attached mass does not change the beam mode shape and has negligibly small influence on the fluid-structure interaction.
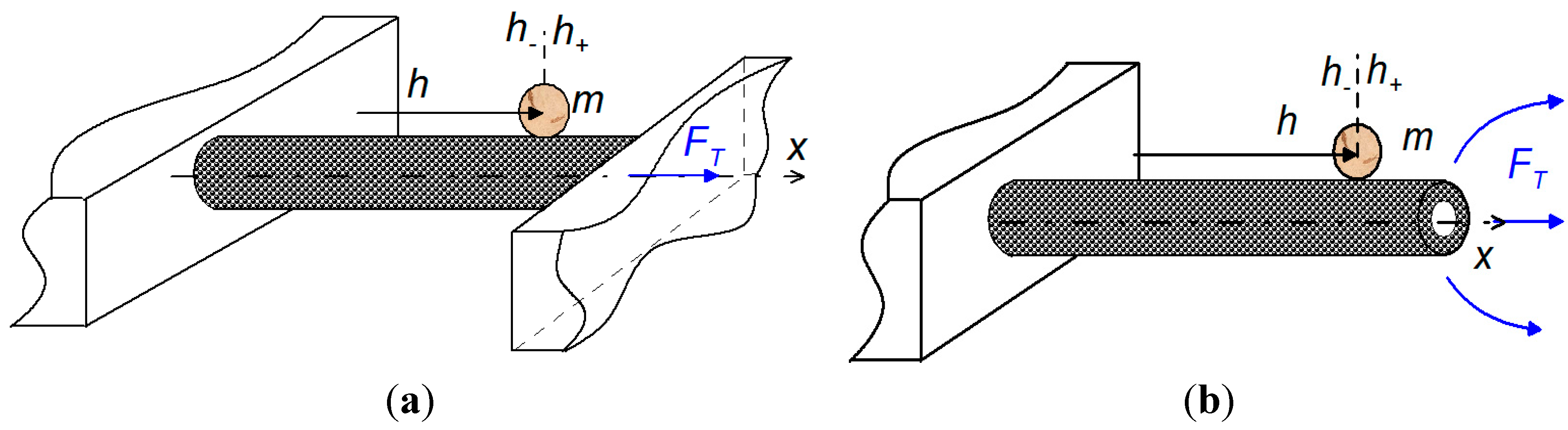
2.2. Procedure of the Single (Multiple) Mass Determination by Means of the Vibrating Suspended- and Cantilever-Based Mass Sensors under Intentionally Applied Axial Tensile Force
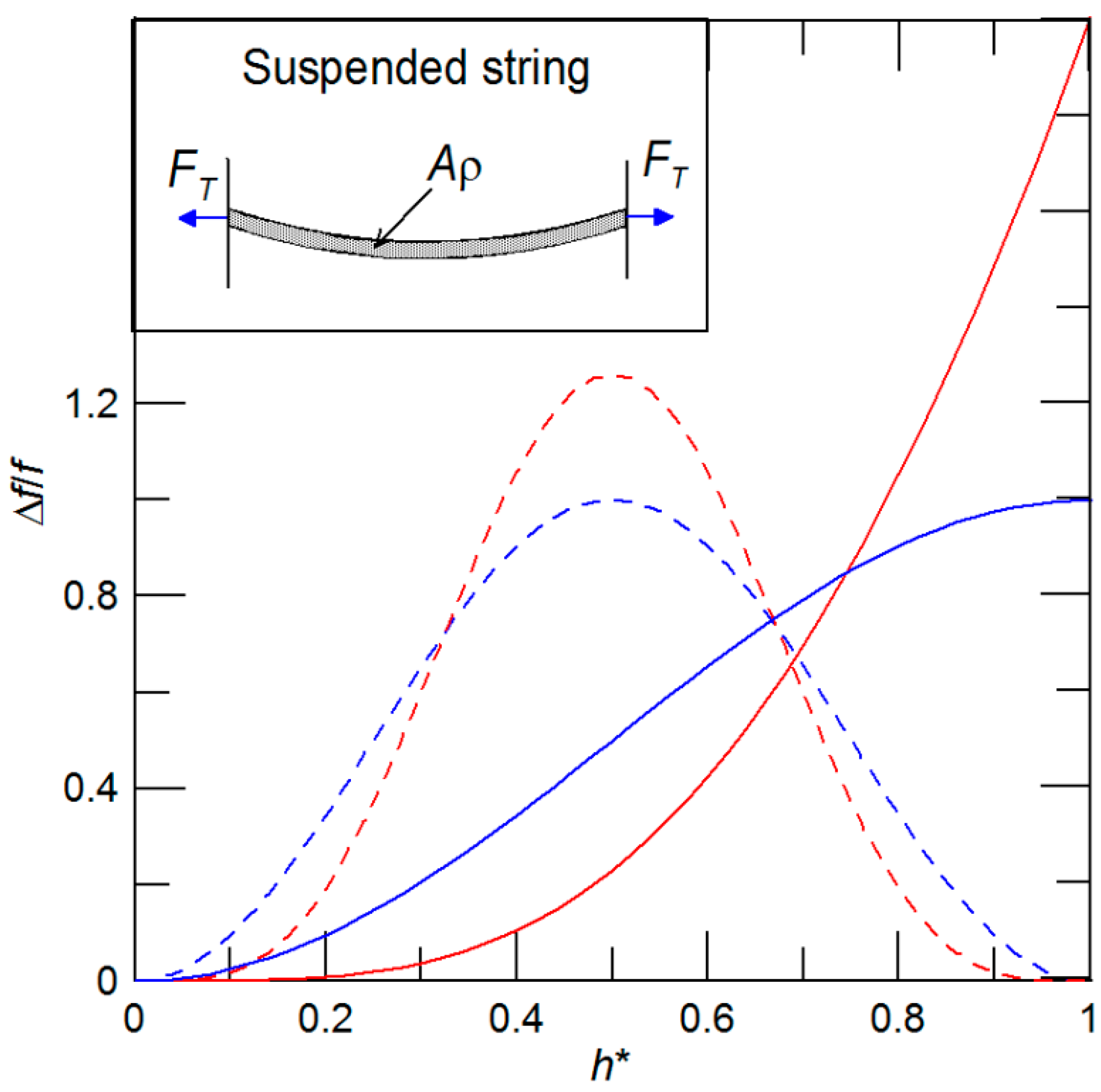
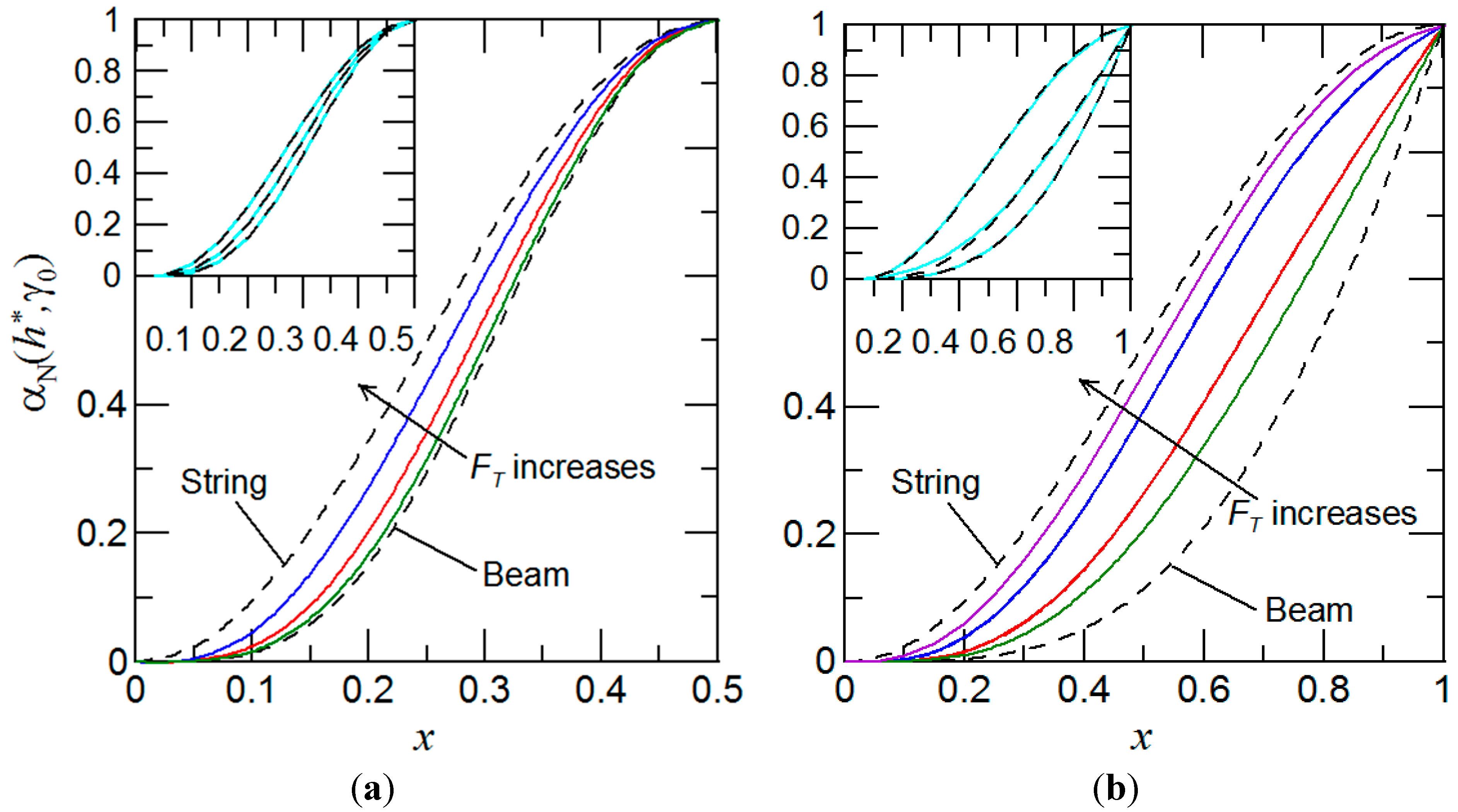
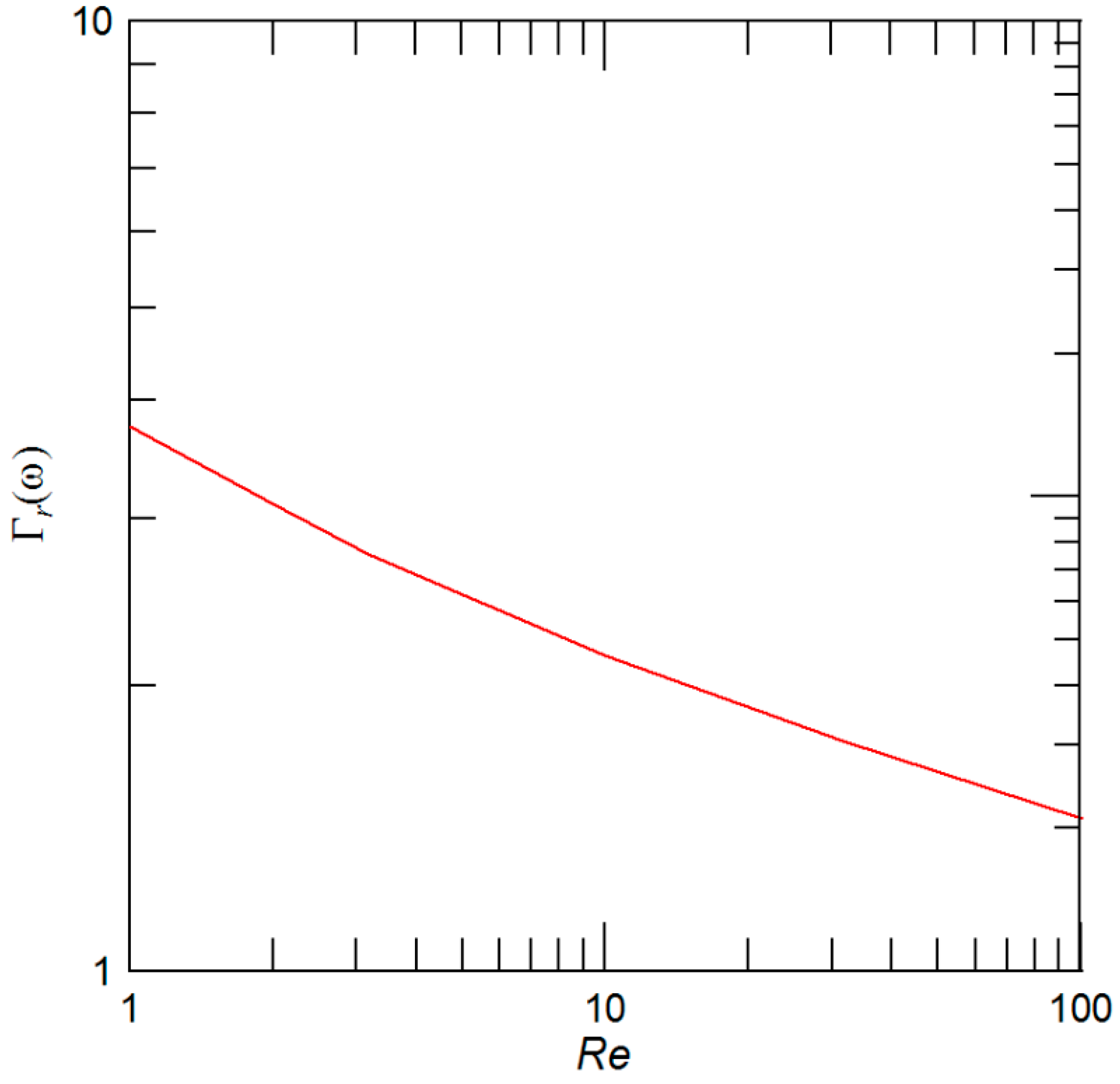
3. Results and Discussion
| Vacuum | Air | ||||
|---|---|---|---|---|---|
| (all cases) | T = 0.5 μm | T = 1 μm | T = 2 μm | T = 4 μm | |
| b = 0 | 6.84 | 6.68 | 6.76 | 6.80 | 6.82 |
| b = 2 | 10.54 | 10.30 | 10.42 | 10.48 | 10.51 |
| b = 5 | 15.96 | 15.61 | 15.78 | 15.87 | 15.91 |
| b = 8 | 20.01 | 19.59 | 19.80 | 19.91 | 19.96 |
| DI Water/24% GWS | ||||
|---|---|---|---|---|
| T = 0.5 μm | T = 1 μm | T = 2 μm | T = 4 μm | |
| b = 0 | 0.33/0.31 | 0.63/0.60 | 1.16/1.11 | 1.98/1.90 |
| b = 2 | 0.52/0.49 | 0.98/0.94 | 1.80/1.72 | 3.08/2.96 |
| b = 5 | 0.80/0.76 | 1.53/1.46 | 2.79/2.67 | 4.75/4.58 |
| b = 8 | 1.03/0.98 | 1.96/1.87 | 3.58/3.42 | 6.07/5.85 |
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
Appendix B
References
- Arlett, J.L.; Maloney, J.R.; Gudlewski, B.; Muluneh, M.; Roukes, M.L. Self-sensing micro- and nanocantilevers with attonewton-scale force resolution. Nano Lett. 2006, 6, 1000–1006. [Google Scholar] [CrossRef]
- O’Connell, A.D.; Hofheinz, M.; Ansmann, M.; Bialczak, R.C.; Lenander, M.; Lucero, E.; Neeley, M.; Sank, D.; Wang, H.; Weides, M.; et al. Quantum ground state and single-phonon control of a mechanical resonator. Nature 2010, 464, 697–703. [Google Scholar] [CrossRef] [PubMed]
- Rugar, D.; Budakian, R.; Mamin, H.J.; Chui, B.W. Single spin detection by magnetic resonance force microscopy. Nature 2004, 430, 329–332. [Google Scholar] [CrossRef] [PubMed]
- Stachiv, I.; Vokoun, D.; Jeng, Y.-R. Measurement of Young’s modulus and volumetric mass density/thickness of ultrathin films utilizing resonant based mass sensors. Appl. Phys. Lett. 2014, 104. [Google Scholar] [CrossRef]
- Jensen, K.; Kim, K.; Zettl, A. An atomic-resolution mass sensor. Nat. Nanotechnol. 2008, 3, 533–537. [Google Scholar] [CrossRef] [PubMed]
- Boisen, A.; Dohn, S.; Keller, S.S.; Smid, S.; Tenje, M. Cantilever-like micromechanical sensors. Rep. Prog. Phys. 2011, 74. [Google Scholar] [CrossRef]
- Hanay, M.S.; Kelber, S.; Naik, A.K.; Hentz, S.; Bullard, E.C.; Colinet, E.; Duraffourg, L.; Roukes, M.L. Single-protein nanomechanical mass spectrometry in real time. Nat. Nanotechnol. 2012, 7, 602–608. [Google Scholar] [CrossRef] [PubMed]
- Dohn, S.; Svendsen, W.; Boisen, A.; Hansen, O. Mass and position determination of attached particles on cantilever based mass sensors. Rev. Sci. Instrum. 2007, 78. [Google Scholar] [CrossRef] [PubMed]
- Dohn, S.; Schmid, S.; Amiot, F.; Boisen, A. Position and mass determination of multiple particles using cantilever based mass sensors. Appl. Phys. Lett. 2010, 97. [Google Scholar] [CrossRef] [Green Version]
- Stachiv, I.; Fedorchenko, A.I.; Chen, Y.-L. Mass detection by means of the vibrating nanomechanical resonators. Appl. Phys. Lett. 2012, 100. [Google Scholar] [CrossRef]
- Timoshenko, S.; Young, D.H.; Weaver, W. Vibration Problems in Engineering, 4th ed.; Wiley: New York, NY, USA, 1974. [Google Scholar]
- Raman, A.; Melcher, J.; Tung, R. Cantilever dynamics in atomic force microscopy. Nano Today 2008, 3, 20–27. [Google Scholar] [CrossRef]
- Verbridge, S.S.; Bellan, L.M.; Parpia, J.M.; Craighead, H.G. Optically driven resonance of nanoscale flexural oscillators in liquid. Nano Lett. 2006, 6, 2109–2114. [Google Scholar] [CrossRef] [PubMed]
- Sawano, S.; Arie, T.; Akita, S. Carbon nanotube resonator in liquid. Nano Lett. 2010, 10, 3395–3398. [Google Scholar] [CrossRef] [PubMed]
- Braun, T.; Barwich, V.; Ghatkesar, K.; Bredekamp, A.H.; Gerber, C.; Hegner, M.; Lang, H.P. Micromechanical mass sensors for biomolecular detection in a physiological environment. Phys. Rev. E 2005, 72. [Google Scholar] [CrossRef]
- Stachiv, I. On the nanoparticle or macromolecule mass detection in fluid utilizing vibrating micro-/nanoresonators including carbon nanotubes. Sens. Lett. 2013, 11, 613–616. [Google Scholar] [CrossRef]
- Stachiv, I. Impact of surface and residual stresses and electro-/magnetostatic axial loading on the suspended nanomechanical based mass sensors: A theoretical study. J. Appl. Phys. 2014, 115. [Google Scholar] [CrossRef]
- Wei, X.; Chen, Q.; Xu, S.; Peng, L.; Zuo, J. Beam to string transition of vibrating carbon nanotubes under axial tension. Adv. Funct. Mater. 2009, 19, 1753–1758. [Google Scholar] [CrossRef]
- Yoon, G.; Park, H.-J.; Na, S.; Eom, K. Mesoscopic model for mechanical characterization of biological protein materials. J. Comput. Chem. 2009, 30, 873–880. [Google Scholar] [CrossRef] [PubMed]
- Kwon, T.Y.; Eom, K.; Park, J.H.; Yoon, D.S.; Kim, T.S.; Lee, H.L. In situ real-time time monitoring of biomolecular interactions based on the resonating microcantilevers immersed in a viscous fluid. Appl. Phys. Lett. 2007, 90. [Google Scholar] [CrossRef]
- Wasisto, H.S.; Merzsch, S.; Stranz, A.; Waag, A.; Uhde, E.; Salthammer, T.; Peiner, E. Femtogram aerosol nanoparticle mass sensing utilising vertical silicon nanowire resonators. IET Micro. Nano Lett. 2013, 8, 554–558. [Google Scholar] [CrossRef]
- Wasisto, H.S.; Huang, K.; Merzsch, S.; Stranz, A.; Waag, A.; Peiner, E. Finite element modeling and experimental proof of NEMS-based silicon pillar resonators for nanoparticle mass sensing applications. Microsyst. Technol. 2014, 20, 571–584. [Google Scholar] [CrossRef]
- Chon, J.W.M.; Mulvaney, P.; Sader, J.E. Experimental validation of theoretical models for the frequency response of atomic force microscope cantilever beams immersed in fluids. J. Appl. Phys. 2000, 87. [Google Scholar] [CrossRef]
- Sader, J.E. Frequency response of cantilever beams immersed in viscous fluids with applications to the atomic force microscope. J. Appl. Phys. 1998, 84, 64–66. [Google Scholar] [CrossRef]
- Paul, M.R; Cross, M.C. Stochastic dynamics of nanoscale mechanical oscillators immersed in a viscous fluid. Phys. Rev. Lett. 2004, 92. [Google Scholar] [CrossRef]
- Basak, S.; Raman, A.; Garimella, S.V. Hydrodynamic loading of microcantilevers vibrating in viscous fluids. J. Appl. Phys. 2006, 99. [Google Scholar] [CrossRef]
- Brumley, D.R.; Willcox, M.; Sader, J.E. Oscillation of cylinders of rectangular cross section immersed in fluid. Phys. Fluids 2010, 22. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Fluid Mechanics; Pergamon Press: Oxford, UK, 1987. [Google Scholar]
- Rosenhead, L. Laminar Boundary Layers; Claredon Press: Oxford, UK, 1963. [Google Scholar]
- Stachiv, I.; Zapomel, J.; Chen, Y.-L. Simultaneous determination of the elastic modulus and density/thickness of ultrathin films utilizing micro-/nanoresonators under applied axial force. J. Appl. Phys. 2014, 115. [Google Scholar] [CrossRef]
- Fedorchenko, A.I.; Stachiv, I.; Wang, A.B; Wang, W.-C. Fundamental frequencies of mechanical systems with N-piecewise constant properties. J. Sound Vib. 2008, 317, 490–495. [Google Scholar] [CrossRef]
- Mohanty, P.; Harrington, D.A.; Roukes, M.L. Measurement of small forces in micron-sized resonators. Phys. B 2000, 284, 2143–2144. [Google Scholar] [CrossRef]
- Mamin, H.J.; Rugar, D. Sub-attonewton force detection at millikelvin temperatures. Appl. Phys. Lett. 2001, 79. [Google Scholar] [CrossRef]
- Bargatin, E.; Myers, B.; Arlett, J.; Gudlewski, B.; Roukes, M.L. Sensitive detection of nanomechanical motion using piezoresistive signal downmixing. Appl. Phys. Lett. 2005, 86. [Google Scholar] [CrossRef]
- Chiu, H.-W.; Hung, P.; Postma, H.W.C.; Bockrath, M. Atomic-scale mass sensing using carbon nanotube resonators. Nano Lett. 2008, 8, 4342–4346. [Google Scholar] [CrossRef] [PubMed]
- Purcell, S.T.; Vincent, P.; Journet, C.; Bihn, V.T. Tuning of nanotube mechanical resonances by electric field pulling. Phys. Rev. Lett. 2002, 89. [Google Scholar] [CrossRef]
- Kafumbe, S.M.M.; Burdess, J.S.; Harris, A.J. Frequency adjustment of microelectromechanical cantilevers using electrostatic pull down. J. Micromech. Microeng. 2005, 15, 1033–1036. [Google Scholar] [CrossRef]
- Salahun, E.; Queffelec, P.; Tanne, G.; Adenot, A.-L.; Acher, O. Correlation between magnetic properties of layered ferromagnetic/dielectric material and tunable microwave device applications. J. Appl. Phys. 2002, 91, 544–549. [Google Scholar] [CrossRef]
- Elmer, F.J.; Dreier, M. The eigen frequencies of a rectangular AFM cantilever in a medium. J. Appl. Phys. 1997, 81. [Google Scholar] [CrossRef]
- Lebedev, N.N.; Skalskaya, I.P.; Ufland, Y.S. Worked Problems in Applied Mathematics; Dover Publications: New York, NY, USA, 1979. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stachiv, I.; Fang, T.-H.; Jeng, Y.-R. Mass Detection in Viscous Fluid Utilizing Vibrating Micro- and Nanomechanical Mass Sensors under Applied Axial Tensile Force. Sensors 2015, 15, 19351-19368. https://doi.org/10.3390/s150819351
Stachiv I, Fang T-H, Jeng Y-R. Mass Detection in Viscous Fluid Utilizing Vibrating Micro- and Nanomechanical Mass Sensors under Applied Axial Tensile Force. Sensors. 2015; 15(8):19351-19368. https://doi.org/10.3390/s150819351
Chicago/Turabian StyleStachiv, Ivo, Te-Hua Fang, and Yeau-Ren Jeng. 2015. "Mass Detection in Viscous Fluid Utilizing Vibrating Micro- and Nanomechanical Mass Sensors under Applied Axial Tensile Force" Sensors 15, no. 8: 19351-19368. https://doi.org/10.3390/s150819351








