1. Introduction
For rotating aircraft, the attitude motion usually has three degrees-of-freedom (also called three channels) including pitch, yaw and rolling. According to the channel selection, the control systems of an aircraft can be divided into single-channel control systems and multi-channel control systems. For some aircraft, which rotate around their longitudinal axis at high rate, a single-channel control system is a good choice [
1,
2,
3], with many benefits such as less equipment, simple structure, light mass and a space saving layout. In the stable loop of a single-channel control system, the angular rate gyroscope is the key device. It is responsible for measuring the pitch and yaw of the rotating aircraft body, then it feeds the output signal back to the input end of the control system so that control system can adjust flight accuracy in time.
With the development of MEMS technology, MEMS gyroscopes are widely used in the areas of inertial navigation and guidance, since they many advantages including low cost, light mass, small volume and anti-shock properties,
etc. [
4,
5,
6]. Most MEMS gyroscopes are basically a vibratory gyroscope based on Coriolis force [
7,
8,
9,
10].
Common MEMS gyroscopes not only have sense structures, but also drive structures. In order to attain the maximum possible response gain and sensitivity, it is necessary to utilize resonance in both the drive and sense modes. This is mainly achieved by structure design or tuning the drive structure and sense structure resonant frequency to match [
11]. This paper will introduce a novel MEMS gyroscope, which has no drive structure, and only a sense structure [
12,
13]. It is mounted on a rotating aircraft, and can smartly determine the angular momentum by using the spin of the rotating aircraft, so it does not need a drive structure. Its proof-mass only has the detecting mode and its structure design is relatively simple, so its fabrication process is also not complex.
In addition, because of the high rate spin of rotating aircraft, a Magnus effect will exist. Generally, when we need to measure a transverse angular velocity input, two common MEMS gyroscopes will be orthogonally mounted on the rotating aircraft, and both the pitch channel and the yaw channel would produce coupling [
14]. In applications, it is found that the measured precision will be reduced and some form of compensation is usually necessary for common gyroscopes.
The non-driven MEMS gyroscope, which will be introduced in this paper, is installed on the rotating aircraft. When the aircraft is subjected to a transverse rotation, it can directly sense the transverse angular velocity input. In other words, it senses the resultant angular velocity of pitch and yaw. The amplitude of the output signal is proportional to the transverse angular velocity input. Then the output signal will be directly fed back to the input end of the control system, so the non-driven MEMS gyroscope does not need to compensate for the influence of the Magnus effect. What is more, it can automatically change the carrier frequency of the output signal with the change of spin frequency of the rotating aircraft, making it very suitable for damping in the stable loop of a single-channel control system for a rotating aircraft.
2. The Sensing Mechanism
The sensing element of the MEMS gyroscope is fabricated using a bulk micromechanical process on a single-crystalline silicon wafer.
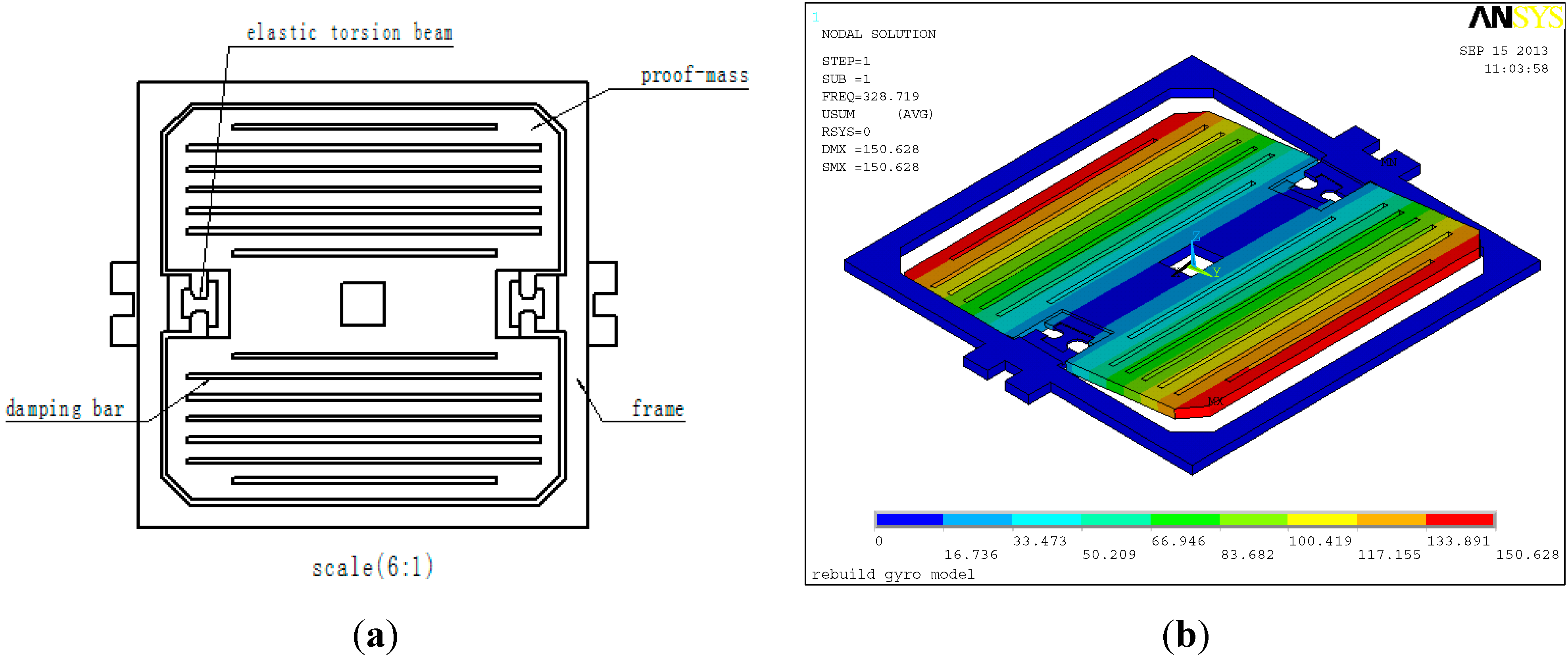
Figure 1 is the structural diagram and the vibrating mode of the sensing element.
Figure 1.
(a) The structural diagram; (b) the vibrating mode.
Figure 1.
(a) The structural diagram; (b) the vibrating mode.
Figure 1a shows that the sensing element is mainly composed of an outer frame and proof-mass. Two ends of the mass are elastic torsion beams. The proof-mass is suspended above the outer frame by a suspension system consisting of flexible beams. The outer frame is fixed on the substrate. The sensing element only has one degree-of-freedom, around which the proof-mass can produce vibrations. This DOF is the constrained center line formed by the elastic torsion beams, so the sensing element only has a sense structure, and no drive structure.
Figure 1b is the first order vibrational mode obtained by finite element analysis (FEA). In modal FEA analysis, according to the size of the sensing element and the material constants of single-crystal silicon, the type of sensing element is defined as SOLID45. Meanwhile, the analyst chooses SI units and sets
GP
a,
and
kg/m
3. The modal analysis result is shown in
Figure 1b. Max displacement is about
m, and the natural frequency is about 329 Hz.
In most of the reported MEMS vibratory rate gyroscopes, the proof-mass is driven into resonance in the drive direction by an external sinusoidal electrostatic or electromagnetic force. Ideally, it is desired to utilize resonance in both the drive and the sense modes. This is typically achieved by designing and if needed tuning the drive and sense resonant frequencies to match. Alternatively, the sense-mode is designed to be slightly shifted from the drive-mode to improve robustness and thermal stability, while intentionally sacrificing gain and sensitivity [
11]. The MEMS gyroscope introduced in this paper is a non-driven gyro. The proof-mass does not utilize any drive force such as an electrostatic or electromagnetic force to attain angular momentum. Here, the sensing element is packaged under a nitrogen environment, but is not vacuum packaged. As shown in
Figure 2, the use of a squeezed film to produce a damping moment is desired.
Figure 2.
The packaging schematic.
Figure 2.
The packaging schematic.
The packaging uses the parallel seam welding process, and impermeability is checked using the Bombing method. In this method, the tested device will be placed in a container, and then the container is filled with a certain pressure of helium. After 5–6 h, the tested device is taken out, and then placed in another container. The container is linked to a helium mass spectrometer leak detector. Finally, the impermeability of MEMS gyro can be measured by the leak detector.
In addition, because of the lack of a drive structure, the non-driven MEMS gyro does not need to tune the driving and sensing resonant frequencies to match to attain high gain and sensitivity, so its design is relatively simple, and the fabrication process is also not complex.
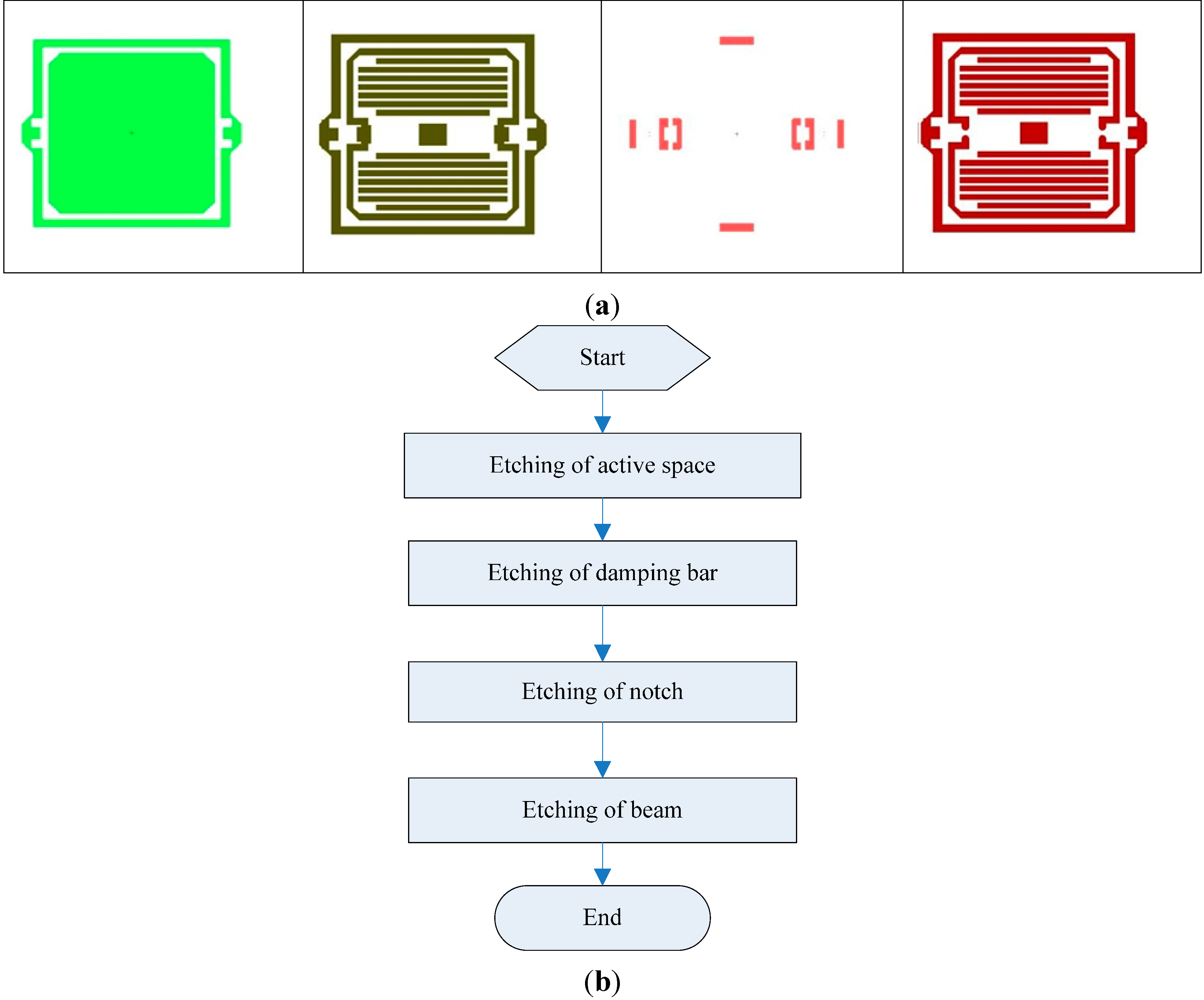
Twenty-five sensing elements can be fabricated on a single wafer, including oxidation, patterned by lithography, etching and so on.
Figure 3a shows four lithography photo-masks.
Figure 3b shows the fabrication flow of the sensing element. It includes four steps. In the first step, on a cleaned silicon wafer, oxidation will grow a 700 nm thick SiO
2 layer. Then through lithography and etching, the active space of sensing element will be obtained. In the second step the damping hole is etched, and then the thickness of the beam is reserved. In the third step the notch of the beam is etched. Finally, in the fourth step the buffer layer of the beam is etched, and beam structure will be formed. After the above four steps, the sensing element is finished.
This new MEMS gyroscope is installed on a rotating aircraft. The sensing element of the gyroscope will smartly utilize the spin of the rotating aircraft to drive the proof-mass and obtain angular momentum. When the aircraft is subject to a transverse rotation, the proof-mass will be acted on by a periodic Coriolis force and produce vibrations, so the MEMS gyroscope can sense an angular velocity input. The amplitude of the swing angle is proportional to the input angular velocity, while the frequency of the vibration corresponds to the spin frequency of the rotating aircraft. This vibration will be transformed into an alternating electrical signal via a capacitance detection circuit. The alternating electrical signal is called the output signal of the gyro. The specific working principle is shown in
Figure 4.
Figure 3.
(a) The step of photo-mask; (b) The fabrication flow of the sensing element.
Figure 3.
(a) The step of photo-mask; (b) The fabrication flow of the sensing element.
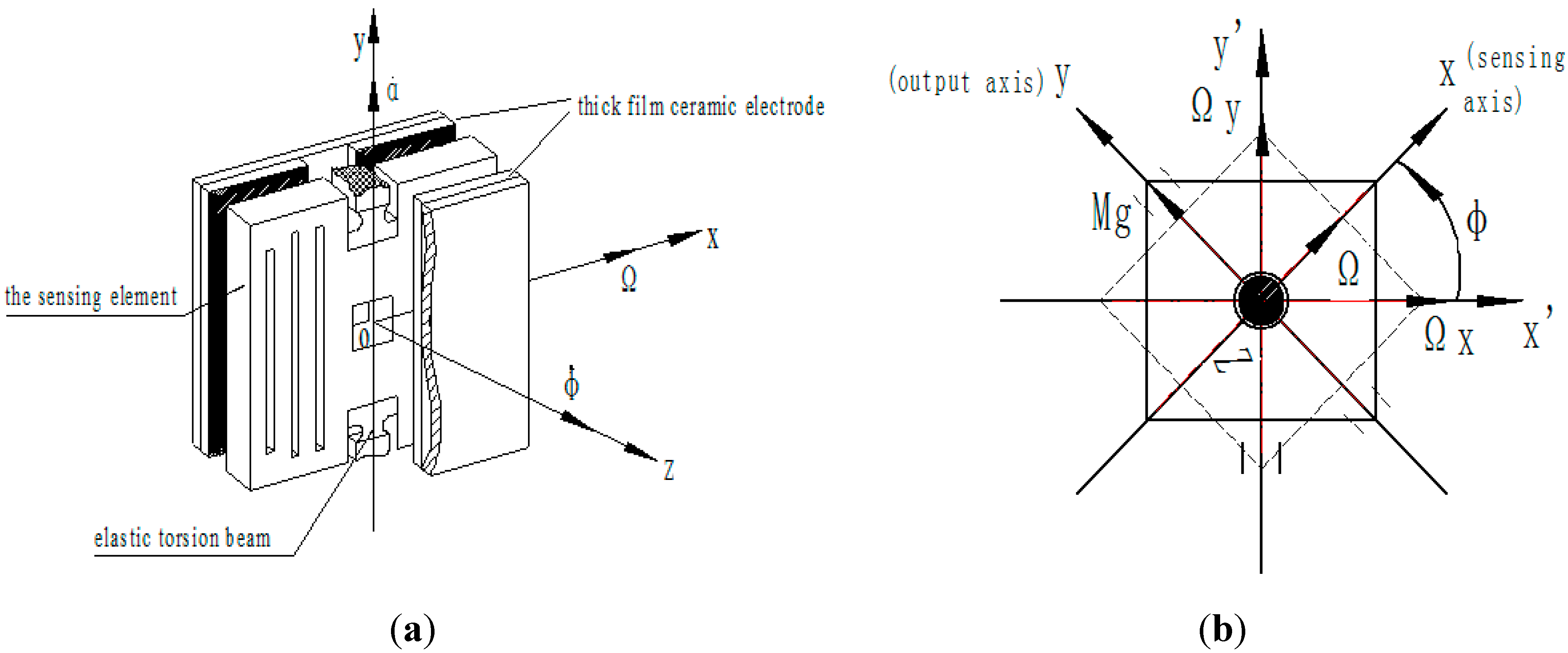
Figure 4.
(a) The structural diagram of the gyro; (b) The diagram of the working principle.
Figure 4.
(a) The structural diagram of the gyro; (b) The diagram of the working principle.
As shown in
Figure 4a, the coordinate system
is fixed on the sensing element of the MEMS gyroscope. The axis
is the output axis of the gyro (also called precession axis). The axis
is the input axis, while the
axis is called the drive axis. The axis
coincides with the longitudinal axis of the rotating aircraft’s body. As the body of the aircraft spins around the axis
with an angular velocity
, the sensing element will obtain the angular momentum. When the aircraft rotates around the axis
at an angular rate
, it will force the sensing element to produce a precession motion around the same axis
with the same angular rate
. Along the direction of the precession axis
, the precession torque will act on the sensing element.
With the spin of the aircraft, both
and
, which are on the quasi-body coordinate system
, will be projected onto the sensing axis
. Then the precession moment
will act on the output axis
, so the sensing element will produce a periodic vibration. An illustration of this movement can be found in
Figure 4b.
Besides, the precession torque can be balanced by the moments, which are respectively the inertia moment, damping moment and elastic moment. The sensing element has an angular acceleration to produce the inertia moment. Because of the angular velocity , a damping moment will exist between the sensing element and the thick film ceramic electrode. When the sensing element vibrates with angular velocity and has a swing angle of , the elastic torsion beams will produce an elastic torsion moment.
Thus, the sensing element has a degree-of-freedom on the direction of axis , and can rotate around the axis . The sensing element cannot rotate around the axis because the two ends of the sensing element are fixed on the outer frame by the elastic torsion beams. However, the angular velocity input on axis can be sensed, and the axis is also called the sensing axis. Although the MEMS gyroscope does not have a drive structure like common gyroscopes, it has the feature that it senses the input angular velocity using the spin of the rotating carrier. In other words, the input of the MEMS gyroscope is the angular velocity on the axis, and the output is the precession movement around the axis.
5. Experimental Validation
For the steady state solution of the angular vibration equation, after the sensing signal is detected by the signal processing circuit, the output voltage signal of the gyroscope can be obtained. Equation (31) is the output voltage signal of the gyroscope, where
is the transmission coefficient of the signal processing circuit:
The non-driven sensing element shares the angular rotation of the aircraft. When the gyroscope is subjected to an angular rotation, a sinusoidal Coriolis force is induced. The rotation-induced Coriolis force causes an energy transfer to the sense-mode proportional to the angular velocity input. In other words, the gyro’s sensing signal is an AM signal. Its envelope is proportional to the input angular velocity, and the carrier frequency corresponds to the spin frequency as shown in
Figure 7.
Figure 7.
The output voltage signal of the gyro.
Figure 7.
The output voltage signal of the gyro.
To validate that the above Equation (31) can correctly represent all sorts of attitude motions of the rotating aircraft, we will carry out an experimental validation under three common flight conditions of rotating aircraft.
The experimental platform is a precision three axis rate table. It has three axis systems, which are respectively called the rolling axis, pitching axis and yawing axis. As shown in
Figure 8, it uses a “U-U-T” structure. All three frameworks use mechanical bearings and form a shaft system. DC motors provide rotary torque. The optical encoder produces an angle signal, and the feedbacks of position and velocity are formed with this angle signal. Each framework is equipped with a conductive slip ring and dial.
The high precision rate table can simulate in the laboratory the attitude motion of a rotating aircraft. The inner framework is used to simulate the spin of the aircraft, and the middle framework and outer framework simulate the pitch and yaw, respectively. With the data acquisition card of the rate table, the output signal of the MEMS gyro can be obtained. Then these experimental data are compared with theoretical data to validate the correctness of the gyro signals. The main specifics of the rate table are listed in
Table 2 below.
Figure 8.
The experimental platform.
Figure 8.
The experimental platform.
Table 2.
The main specifics of the three axis rate table.
Table 2.
The main specifics of the three axis rate table.
| Angle | yaw | ±360° | Position control accuracy | yaw | ±0.001° |
| pitch | ±360° | pitch | ±0.001° |
| roll | ±360° | roll | ±0.3' |
| Dynamic accuracy | yaw | ±0.005° | Maximum angular acceleration | yaw | 3000°/s2 |
| pitch | ±0.005° | pitch | 4000°/s2 |
| Measured angle | roll | ±0.2° | roll | 4000°/s2 |
| Maximum angular velocity | yaw | ±500°/s | Rate accuracy | yaw or pitch | 0.001°/s~1°/s | 1 × 10−3 |
| pitch | ±500°/s | 1°/s~10°/s | 1 × 10−4 |
| roll | ±50 r/s | 10°/s | 2 × 10−5 |
| Minimum angular velocity | yaw | ±0.001°/s | roll | 1′/s~1°/s | 2 × 10−3 |
| pitch | ±0.001°/s | 1°/s~10°/s | 2 × 10−4 |
| roll | ±1'/s | 10°/s~2000°/s | 2 × 10−5 |
| >2000°/s | 2 × 10−6 |
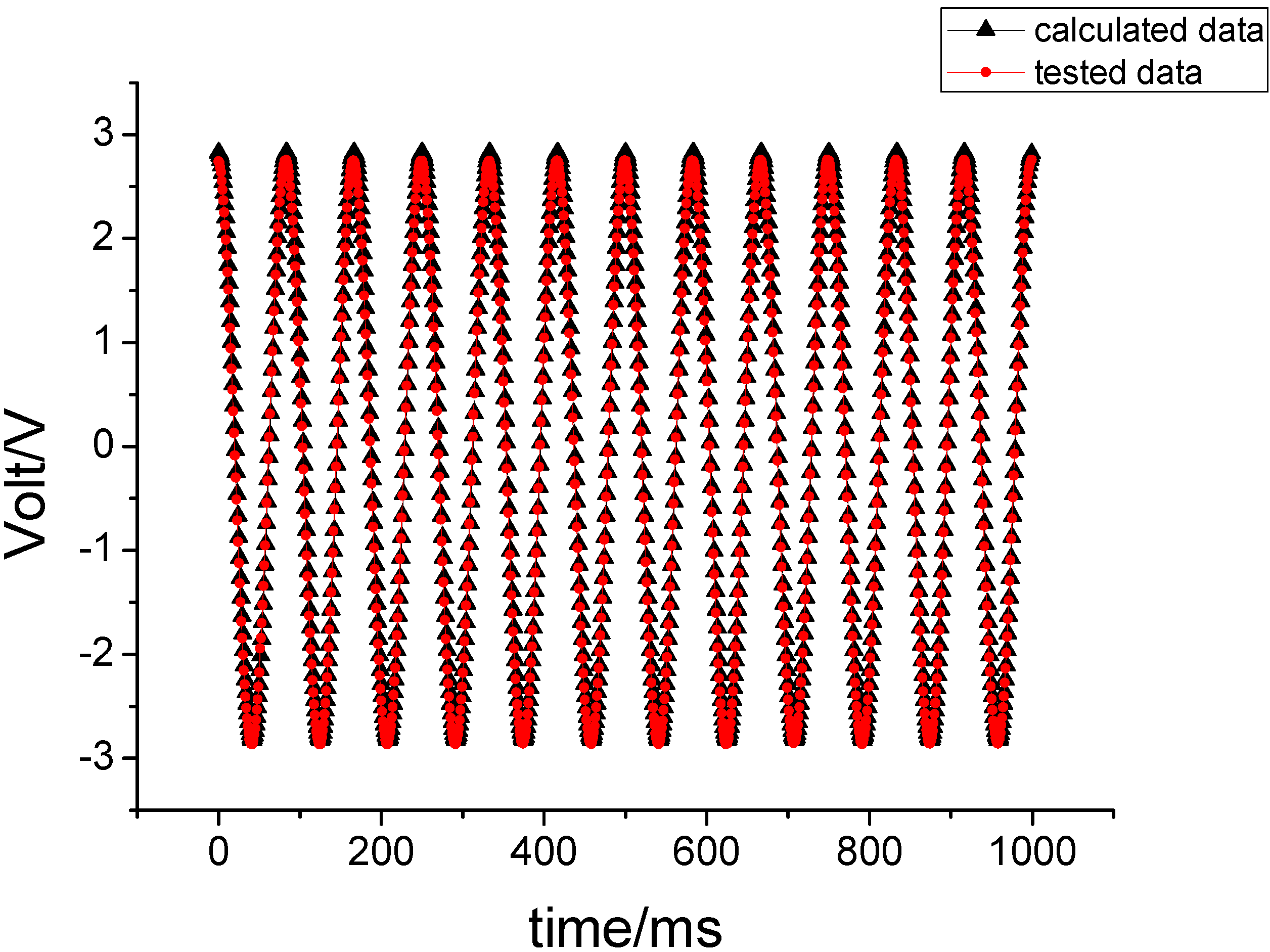
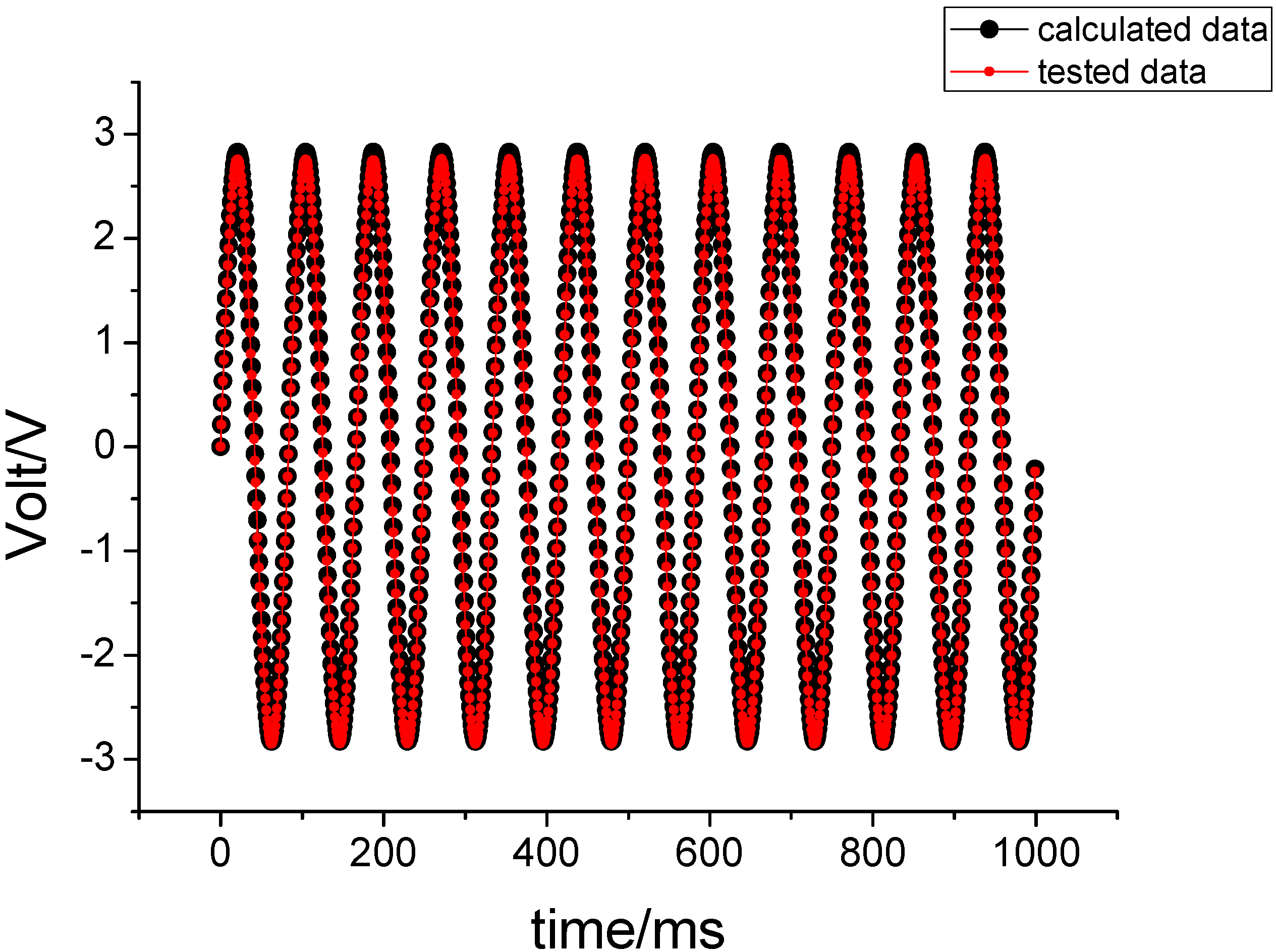
The MEMS gyroscope is mounted on the table board, and rolling axis is set to 12 Hz to simulate the spin frequency of a rotating aircraft.
5.3. Input Circular Vibration
When the flight carrier produces a circular vibration, in sensing plane, the angular vibrations would respectively be:
To derivate Equation (34) for time, the input angular velocities are:
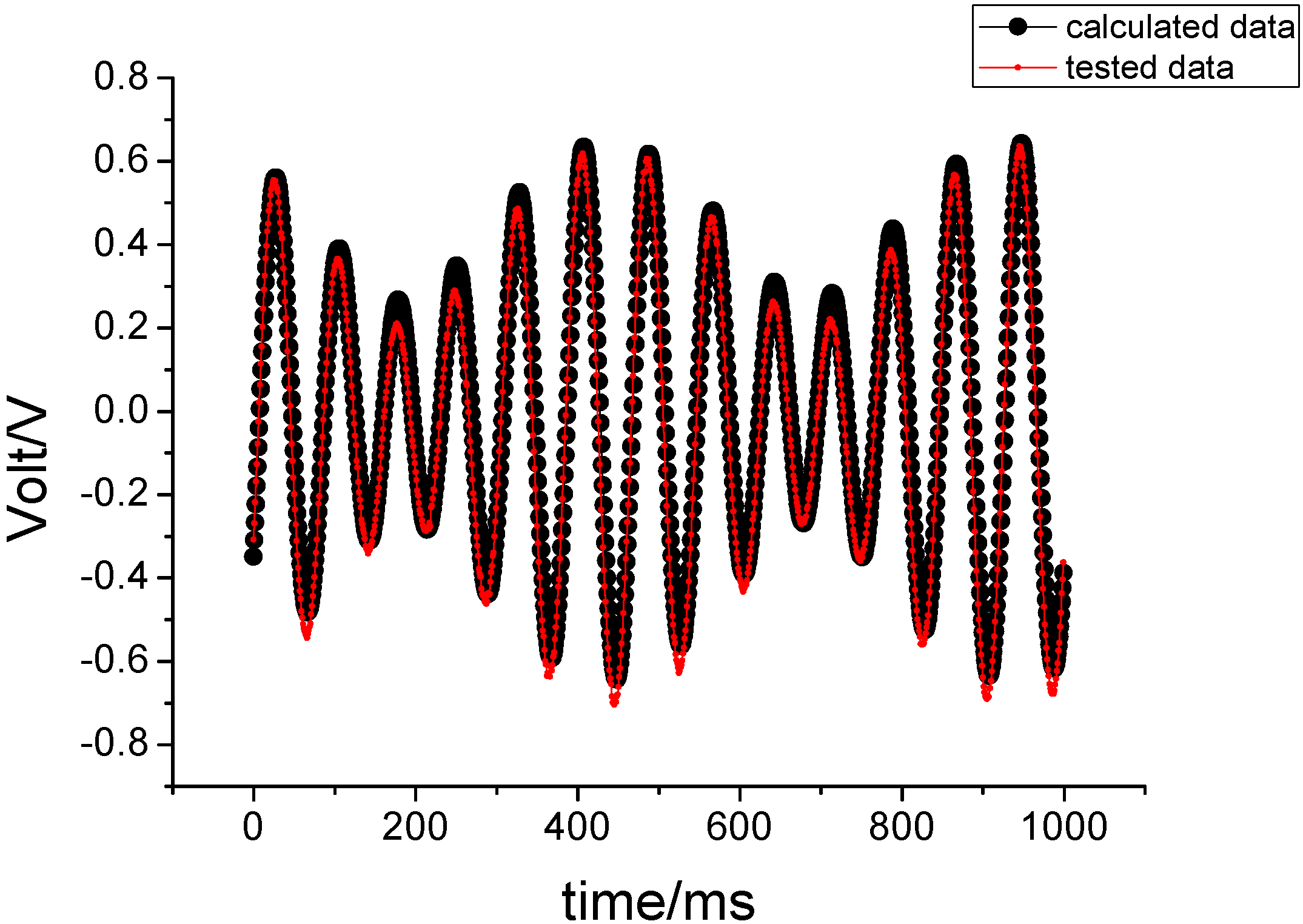
Thus, under circular vibration conditions, the output signal of the gyro is a resultant and complex amplitude modulation signal. When the phase difference is 135°, the corresponding output signal waveform is shown in
Figure 12.
Figure 12.
The output signal waveform of gyro under input circular vibration.
Figure 12.
The output signal waveform of gyro under input circular vibration.
In the test, in order to simulate the circular vibration, we enter an angular vibration of amplitude 5° and frequency 1 Hz on the pitching axis and yawing axis, respectively. The phase difference of the vibration is 135°.
Figure 13 compares the results of the sampling data and theoretical calculation data. Their comparison has a correlation coefficient of 0.9842, and they are also consistent in this case.
The simulation results in
Figure 13 demonstrate that the gyro can correctly sense the resultant angular velocity of pitch and yaw, even though the rotating aircraft is a very complex condition where it is simultaneously subjected to an angular vibration on the pitch axis or yaw axis. The envelope of the output signal is proportional to the value of the resultant angular velocity.
Figure 13.
The experimental results under input circular vibration.
Figure 13.
The experimental results under input circular vibration.
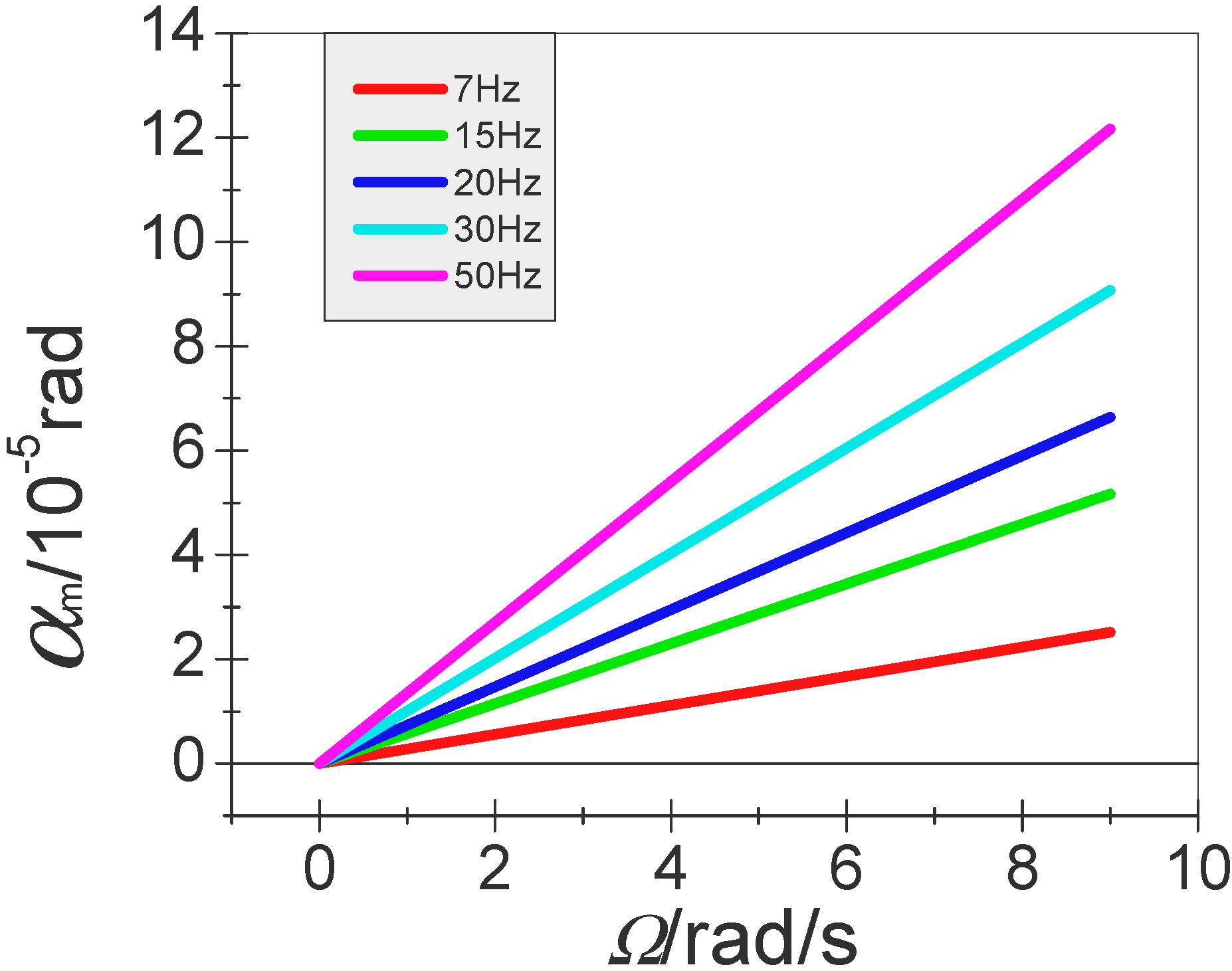
To summarize the above three cases, the design of the MEMS gyro is rational and the derived motion equation is also correct. In applications, the MEMS gyroscope is installed on a rotating aircraft. It uses the spin of the rotating aircraft as a driving force. When the carrier produces a transverse rotation, the MEMS gyroscope can sense the input angular velocity. Based on the Euler dynamics equation, the motion equation of the gyro has been derived. Its solution reveals that the vibration amplitude of the proof-mass is proportional to the input angular velocity, and the vibration frequency responds to the spin frequency of the aircraft, so the proposed MEMS gyroscope is very suitable for damping of a single-channel control system of a rotating aircraft.
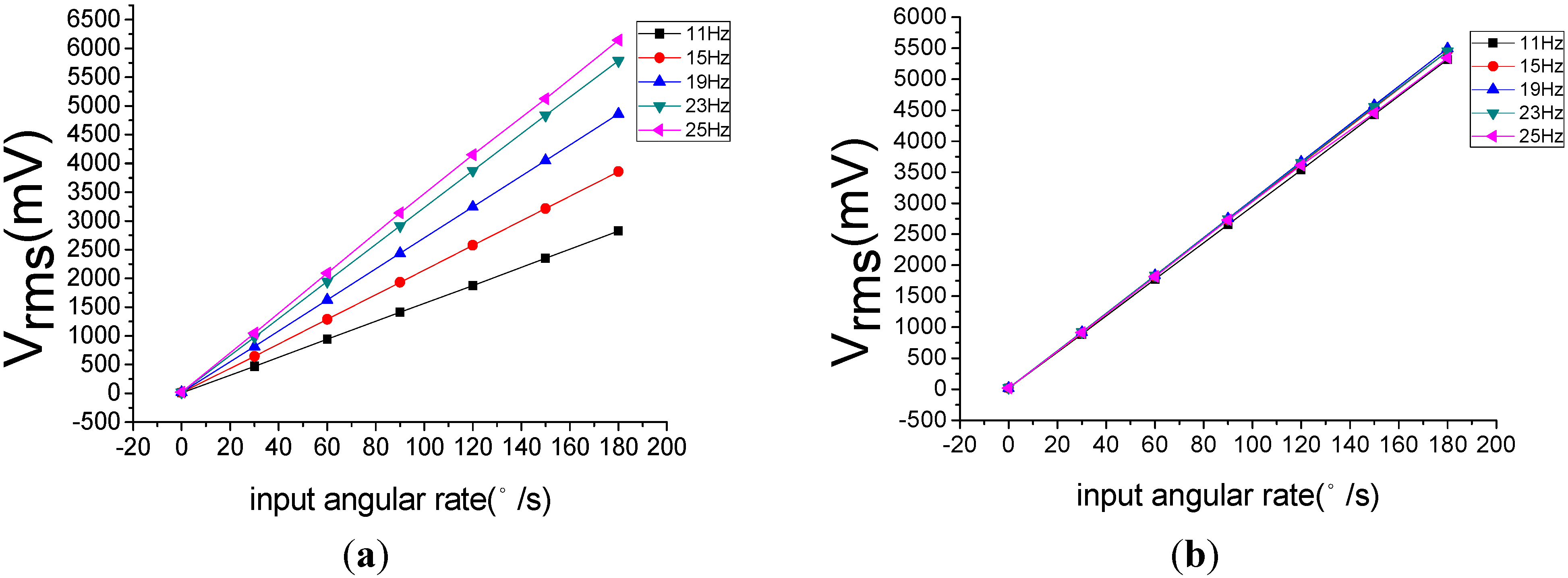
Using a rate table, experimental tests have been done for three cases of flight attitude. The results have shown that the design is rational and the obtained motion equations are actually correct. However, the sensitivity of gyroscope would be affected by the spin frequency of the rotating aircraft. With the increase of the spin frequency, the sensitivity increases. This change will cause instability of the scale factor of gyroscope. For a single channel control system, this change is acceptable. In a multi-channel control system application, in order to guarantee the measuring accuracy of the MEMS gyroscope, we need to compensate this influence.
Figure 14.
(a) The change before compensation; (b) the change after compensation.
Figure 14.
(a) The change before compensation; (b) the change after compensation.
Figure 14is a comparison of the scale factor before and after the compensation.
Figure 14a shows that the scale factor will change with the change of spin frequency, while the
Figure 14b demonstrates that the change of the scale factor has been effectively restrained.