High Frequency Variations of Earth Rotation Parameters from GPS and GLONASS Observations
Abstract
: The Earth's rotation undergoes changes with the influence of geophysical factors, such as Earth's surface fluid mass redistribution of the atmosphere, ocean and hydrology. However, variations of Earth Rotation Parameters (ERP) are still not well understood, particularly the short-period variations (e.g., diurnal and semi-diurnal variations) and their causes. In this paper, the hourly time series of Earth Rotation Parameters are estimated using Global Positioning System (GPS), Global Navigation Satellite System (GLONASS), and combining GPS and GLONASS data collected from nearly 80 sites from 1 November 2012 to 10 April 2014. These new observations with combining different satellite systems can help to decorrelate orbit biases and ERP, which improve estimation of ERP. The high frequency variations of ERP are analyzed using a de-trending method. The maximum of total diurnal and semidiurnal variations are within one milli-arcseconds (mas) in Polar Motion (PM) and 0.5 milli-seconds (ms) in UT1-UTC. The semidiurnal and diurnal variations are mainly related to the ocean tides. Furthermore, the impacts of satellite orbit and time interval used to determinate ERP on the amplitudes of tidal terms are analyzed. We obtain some small terms that are not described in the ocean tide model of the IERS Conventions 2010, which may be caused by the strategies and models we used or the signal noises as well as artifacts. In addition, there are also small differences on the amplitudes between our results and IERS convention. This might be a result of other geophysical excitations, such as the high-frequency variations in atmospheric angular momentum (AAM) and hydrological angular momentum (HAM), which needs more detailed analysis with more geophysical data in the future.1. Introduction
The Earth Rotation Parameters (ERPs) are changing due to geophysical excitation (such as redistribution of geophysical fluid mass) as well as lunisolar gravitational torque, including the motion of the rotation axis (Polar motion, PM) and its change rate (Length of Day, LOD). In addition, some larger crustal activities may also affect Earth's rotation. Hopkin [1] and Wu et al. [2] found that the Sumatra earthquake and Pleistocene deglaciation made the Earth's rotation rate change by several microseconds, respectively. The detailed theoretical mechanism accounting for the variations in Earth rotation was a hot issue over the past decades from decades to daily variations in Earth Rotation [3]. At present, several different approaches have been suggested for predicting and estimating high frequency variations. In previous research, variations in Earth Rotation from oceanic tides were predicted based on theoretical tidal [4] and hydrodynamical models [5]. The effects from geophysical excitation over long periods rather than days were studied at first. Then, shorter periods such as P1, K1 and O1 in the diurnal band and M2, S2 and N2 in semidiurnal band were considered [6–9]. In 1991, the stable Very Long Baseline Interferometry (VLBI) was first used to estimate variations and the effect of tides on Universal Time (UT) [10]. The coefficients of tidal amplitude for PM and UT then were estimated from VLBI data [11–17] and combined VLBI and GPS observations [18] as well as combined VLBI and ring laser observations [19]. Satellite Laser Ranging (SLR) data were also used to estimate the variations in ERPs [20]. At the same time, Ray et al. [21] and Chao et al. [22] predicted variations in ERP from a new tide model induced from TOPEX/Poseidon altimeter data. More recently, GPS data were applied to high frequency variations for ERP. The agreement between different techniques was at a level of 10–30 μas in PM and 1–3 ms in UT1 [23], followed by Steigenberger et al. [24]. Then, the effects of ocean and hydrology in PM and LOD also have been investigated from the observations of GRACE Satellites by Jin et al. [25–27], followed by Panafidina [28] and then the interactions between GPS orbits and ERP were investigated.
The International Earth Rotation and Reference System Service (IERS) estimates ERPs at a sub-millimeter precision. Using VLBI, SLR, Lunar Laser Ranging (LLR), GPS, and Doppler Orbitography by Radiopositioning Integrated on Satellite (DORIS). However, Most of the IERS ERP series, such as IERS C04 [29] and Bulletin A (rapid prediction ERP series) do not contain high frequency variations because they are smoothed by Vondrak filtering [30,31]. Recently, with improvement of GPS and GLONASS observation precision and networks, it provides a new opportunity to estimate high frequency variations of ERP. In this paper, ERP series with a time resolution of one hour are computed from GPS, GLONASS, and combined GPS and GLONASS observations. While combining both GPS and GLONASS will decrease the correlation between UT1 and orbit model since GPS and GLONASS has different orbital period. Then a de-trending method based on a smoothness priors approach is employed to obtain high frequency variations in ERP. Furthermore, these high frequency variations are analyzed with Fourier transform to investigate the components of tidal terms hidden in the variations. In addition, the impact of time interval used to estimate ERP, different strategies and models on tidal amplitudes are also discussed.
2. Data and Processing
2.1. GPS/GLONASS Observations
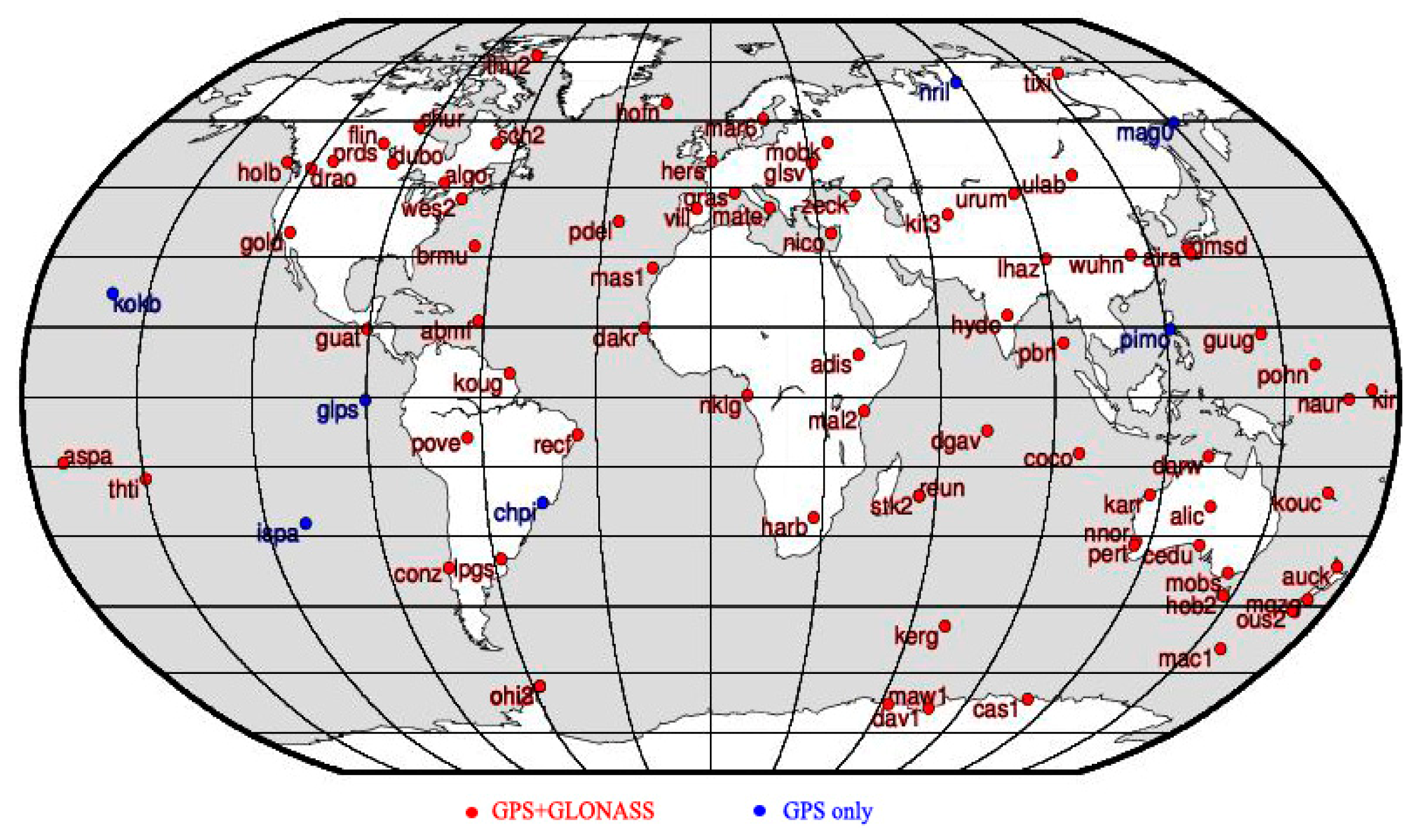
Up to now, about one hundred stations are available to track both GPS and GLONASS satellites simultaneously. The precision of ERP is related more to the distribution of the satellites than the number of stations [32] and does not improve much when the number of sites increases over 60 according to Wei et al. [33]. Here, about 80 sites from International GNSS Service (IGS) [34] are selected to estimate ERP.
First of all, these stations are core sites of International Terrestrial Reference Frame (ITRF) [35]. Second, the standard deviation of coordinates of the sites is less than 1 mm, while the standard deviation of velocity of the sites is less than 0.2 mm per year according to the publications of IGS. Finally all the stations satisfy a uniform distribution with stable and high quality observations. The distribution of these stations is shown in Figure 1 and observations of 526 days from these stations are collected since 11 January 2012.
2.2. Data Processing Models
The uninterrupted and continuous tracking stations established by IGS allow us to accumulate a large number of observations from GPS and GLONASS to estimate ERP from a few hours of data. This is a great advantage when compared to other technologies, such as SLR or VLBI, which does not have continuous observations. In this paper, ERPs are estimated for every hour with GPS and GLONASS observations, individually and by a combined GPS and GLONASS method. The theory and methods to determinate ERP were introduced in details in the references [32,36,37].
All GNSS data analysis was executed using Bernese 5.0 software [38] with double-difference observation. Apart from ERPs, the coordinates for sites, the troposphere zenith delays, initial phase ambiguities, and station clock errors were also taken into account when processing. The orbit was strongly constrained to the IGS precision ephemeris and some other models were used: The IERS2000 sub-daily PM model together with the IAU2000 Nutation model [39], the OT_CSRC ocean tide file [40] and the FES2004 Ocean loading correction [41]. Because troposphere delays differ from time to time, especially for some rapidly changing tropospheric conditions, if the tropospheric delay is not estimated at a sufficient temporal resolution, then parts of the delays will propagate into the ERP. At the same time, the sampling interval for the troposphere delays may have influences on diurnal and semidiurnal tidal periods. As a result, extreme care must be taken when sampling the troposphere delays. In this paper, site-specific troposphere delays were estimated every hour using the WET NIELL [42] mapping function. Additionally, the quasi-ionosphere-free (QIF) model [43] was deployed to deal with initial phase ambiguities.
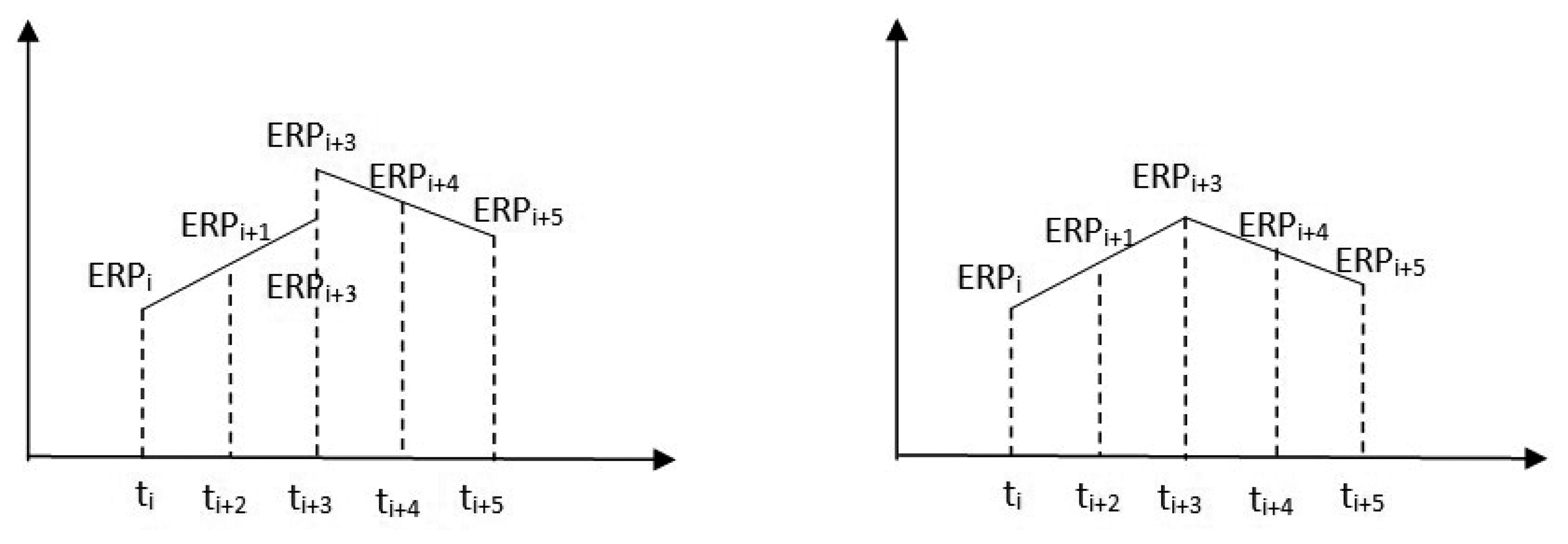
In the estimation of ERP, we divide a long interval (e.g., one day or 3 day arc) into several sub-interval of equal length (2 or 4 h). Then in any sub-interval [ti,ti+1], the ERP can be represented as following:
Figure 2 shows the principle of estimating ERPs and the constraint added to the interval borders. According to these conditions, we actually obtained an ERP solution every hour when the length of sub-interval is 2 h, but only 13 of them are independent. However, we will only obtain 12 sets of ERP with seven of them are independent when the length of sub-interval is 4 h, that is to say, the temporal resolution of ERP becomes two hour. By the way, because the sub-daily resolution of ERP will lead to singularity due to the correlations between daily retrograde motion of pole and the orientation of satellites orbital planes, as a consequence, the retrograde diurnal component in PM has to been blocked if ERPs are determined together with orbital elements. This can be completed by blocking it or removing it with a numerical filter. We refer readers to [3] for more information. In order to decrease the impacts of satellite orbit on diurnal terms of ERP, we also operate a computation of ERPs with long arc by combining the normal equations every three days.
3. Variations in ERP
3.1. ERP Results from GPS and GLONASS
According to the strategy described in Section 2.2, firstly, we estimate the daily ERP for one month and then compare them to IGS published values in order to assess the accuracy of our process strategy. The Root Mean Square (RMS) difference of PM and UT1-UTC is about 0.23 mas (0.31 mas) and 0.017 ms (0.027 ms) when compared our daily ERP from GPS (GLONASS) to the IGS values, respectively. These figures show a result with a good enough precision when considering that only about 80 sites are involved. Then ERPs are estimated with a frequency of 1 h for 526 days since 11 January 2012, but only the independent sets of ERPs are used here, that is to say the ERP are used every 2 h or 4 h. To give us a first indication of how larger is the high frequency variations, the ERP series are compared to IGS published values, too. This seems to be a strange comparison, because the ERP estimated with a sub-interval of 2 h from GPS, GLONASS and combined GPS + GLONASS contains many subdaily signals, however, the IGS published values do not contain the subdaily signal. Thus, to operate an appropriate and informative comparison, we firstly compute the daily average of the hourly ERPs for each day. Then the daily average series of ERPs are compared with the IGS values (at UTC 12:00:00). As we note, this comparison was operated only to give us a first indication of how larger is the high frequency variations. The statistic information of the differences between daily average results and IGS published values (at UTC 12:00:00) are shown in Table 1. It is clear that the precision of ERP from GPS is much higher than that from GLONASS. The result of ERP was improved distinctly by combined GPS and GLONASS. Furthermore, to our best knowledge, bringing in GLONASS observations can also reduce the impact of orbit model on ERPs. Because the period of GPS orbits is 12 h, which is identical to the semidiurnal tidal terms. Therefore, estimating ERP with GLONASS (period of GLONASS satellites is 11 h and 15 min) may help to reduce the correlation between orbit model and ERP which will be discussed at Section 3.3. The accuracy of PM in X and Y from combined GPS and GLONASS were improved by about 6%∼7% when compared to GPS only. Dach et al. [44] shows a similar improvement when estimate the positions. The accuracy of UT1-UTC is not as good as PM and combined result is slightly off. The most possible explanation for the accuracy of UT-UTC is that, as we mentioned before, we cannot estimate the UT1-UTC in an absolute sense. Thus, we introduce additional information (the first UT1-UTC offset (at UTC 00:00:00) of each long interval has been constrained to a prior value) so as to estimate the UT1-UTC. This method then leads to a little systematic error and a less improvement because only the UT1 rate is accessible to GPS/GLONASS, as a result, we actually need an offset value for each sub-interval if high precise UT1-UTC is expected.
3.2. High Frequency Variations in ERP Series
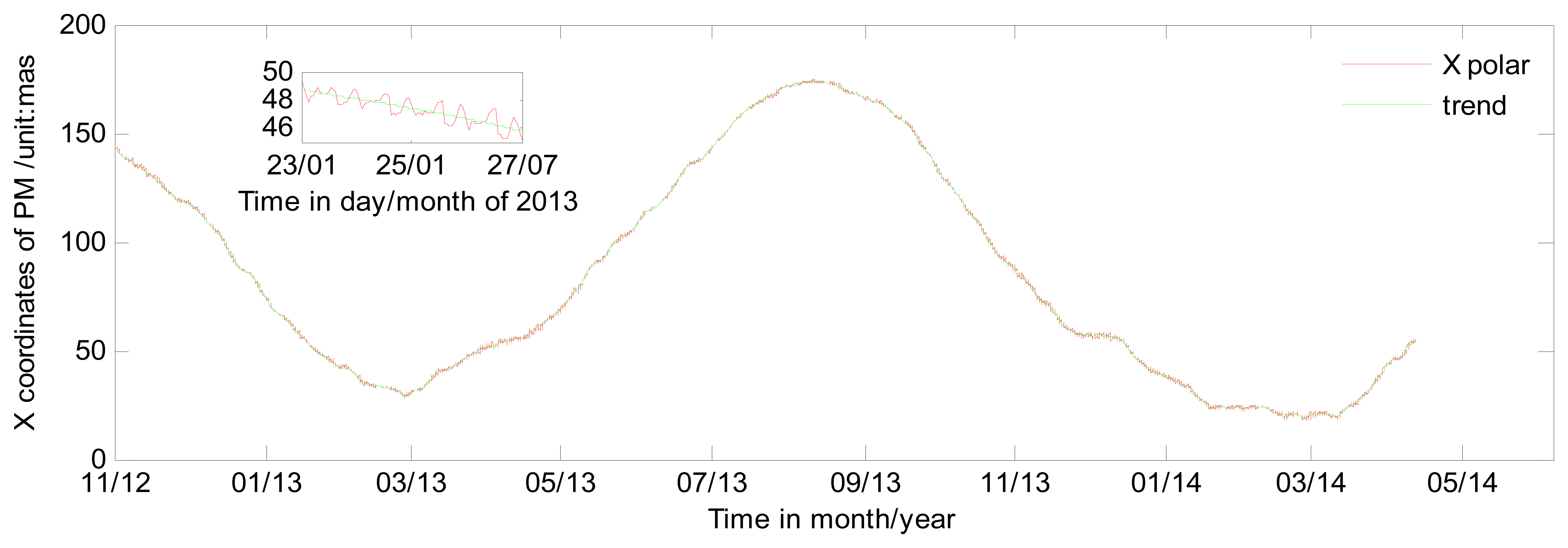
The ERP series directly estimated from GPS and GLONASS contains both low and high frequency variations. Apart from the subdaily variations, a long period term is also included in the ERP series we acquired. To obtain the subdaily variations in ERPs, the long period term is removed in the ERPs generated from GPS and GLONASS. This can be accomplished by subtracting a prior trend which is also an ERP series but without high frequency variations [23]. IERS C04 and Bulletin A published by IERS is the optional prior ERP series which do not contain high frequency variations after handling with Vondrak filtering. However, IERS C04 offers only one ERP per day. So, first of all, if IERS C04 is used as a prior ERP, we need to densify the C04 series to one ERP solution per hour through Lagrange interpolation because the time resolution of the ERP series we estimated is one hour. However, this Lagrange interpolation may add interpolation error. In this paper, we use a de-trending method based on a smoothness priors approach operating like a time-varying (Finite Impulse Response) FIR high pass filter [45]. Firstly, the entire ERP series can be considered to consist of two components:
Figure 3 shows the detail effects of the de-trending method. Upper left is the enlarged sub-figure of the ERP series from 23–27 January 2013. From Figure 3, we can see the de-trending method of smoothness priors approach performs very well in fitting the trends of ERP series, and the trends we acquire are very similar to IERS C04. Then the high frequency variations of ERP are generated by subtracting the trend from the original ERP series we estimate.
It is important to note that the series of high frequency variations of ERP contains both sub-daily variations and estimation error or other noises. The error from the empirical model we used and the detrending method may also alias into the high frequency variations. The high frequency variations in PM and UT1-UTC are shown in Figure 4 after removing the long period term. As seen in Figure 4, most of the high variations are within 1 mas in PM and 0.5 ms in UT1-UTC. Table 2 shows the detail statistics information of the high frequency variation series in PM and UT1-UTC. Furthermore, in order to analyze the impact of different sub-interval on the high frequency variations, ERP is also estimated with 4 h sub-interval observations. The statistic result of high frequency variations from four hour sub-interval are also given in Table 2.
As the results in Table 2 show, the combined GPS and GLONASS improves the precision of ERP when compared to GPS or GLONASS alone and the accuracy is improved again when ERPs are estimated using a long orbit arc of three days. In addition, the RMS of de-trend ERP is the minimum when ERP is generated from combined GPS and GLONASS with 3-day arc orbit by combining single day normal equations.
3.3. Analysis and Discussion
3.3.1. Spectrum Analysis of Subdaily ERP from Different Satellite Systems
To analyze the spectrum hidden in the series, the high frequency variations are converted to the frequency domain using a Fast Fourier Transform. Each high frequency variations series including X-pole, Y-pole and UT1-UTC can be expressed by a Fourier series independently as follows [17,24]:
To operate an appropriate comparison for these tidal terms, we firstly sum all the terms in the IERS tidal model and evaluate these whole tidal variations at the same epochs as our ERP series. The whole tidal variation series is regarded as a reference tidal variation series which then will be processed with the same method applied in our ERP series including the de-trending and FFT. Table 4 shows the amplitude of the prograde and retrograde PM at both diurnal and semidiurnal bands. In Table 4, we only list some main periodic terms, including both diurnal terms and semidiurnal terms. Furthermore, because the retrograde diurnal terms in PM are blocked in the IERS tidal model, these retrograde diurnal terms are not compared here. But for the semidiurnal terms, both prograde and retrograde are shown in the Table 4. As we can see, the largest difference for GPS and GLONASS occurs at 11.967 h (which corresponds to the semidiurnal term K2) and 24.058 h (which corresponds to the diurnal term P1) and 24.023 h (which corresponds to the diurnal term S1).
The differences of other terms whose period are not close to 12 h or 24 h are relatively small, but still exist. The most possible explanation is the different orbital period of GPS satellite (about 12 h) and the period of GLONASS (about 11 h 15 min). Although there is no algebraic relation between the orbital elements and tidal terms, the prograde tidal terms correspond to the translation of the orbital plane of each satellite. That is to say, the systematic changes of satellite in the orbit elements will lead to changes in the prograde tidal terms. For the GPS satellite, the period is about 12 h and the revolution is about 24 h in the inertial system, which is a systematic signal that propagates into those tidal terms with the same period. Furthermore, we can see that the terms of GNSS (combined GPS and GLONASS) at 24.058 h and 24.023 h is improved when compared to GPS only, because the difference between GPS and IERS is larger than that of GNSS. However, for those terms which are not so close to 12 h or 24 h (e.g., 26.859 h, 25.802 h), the combined result is dominated by GPS. In total, the standard deviation of the difference between GPS only and IERS 2010 is 18.33 μas. While the standard deviation of the difference between GNSS and IERS 2010 is 17.93 μas, which means the combined result is a little bit better than GPS only, overall. As a conclusion, the GPS satellite system has little impact on those tidal terms whose period is close to 24 h and 12 h. Thus, involving different satellite systems can reduce this impact in the theory, but our result is far to certify this adequately which need more investigation in the future.
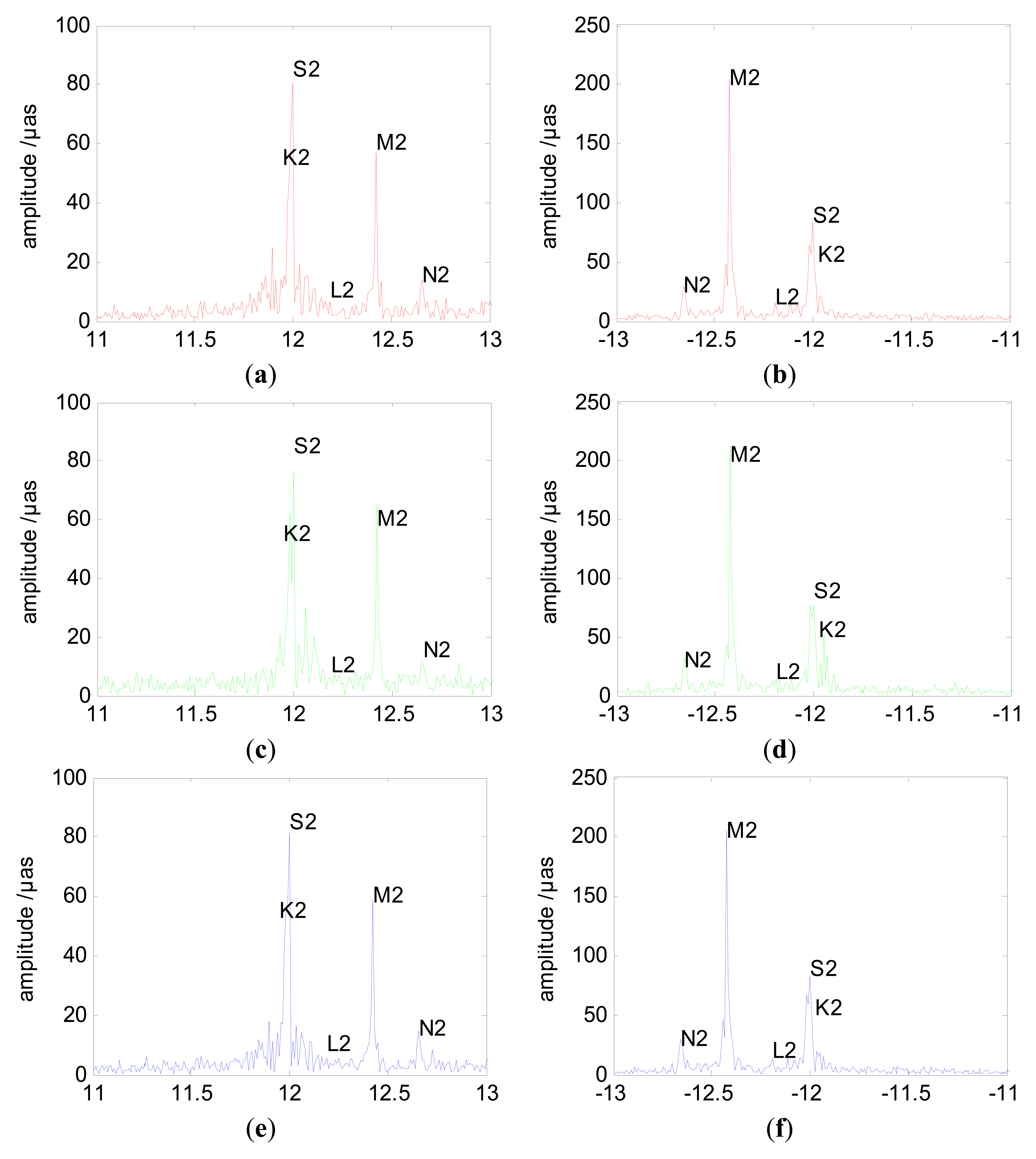
3.3.2. Spectrum Analysis of Subdaily ERP from Different Lengths of Sub-Intervals
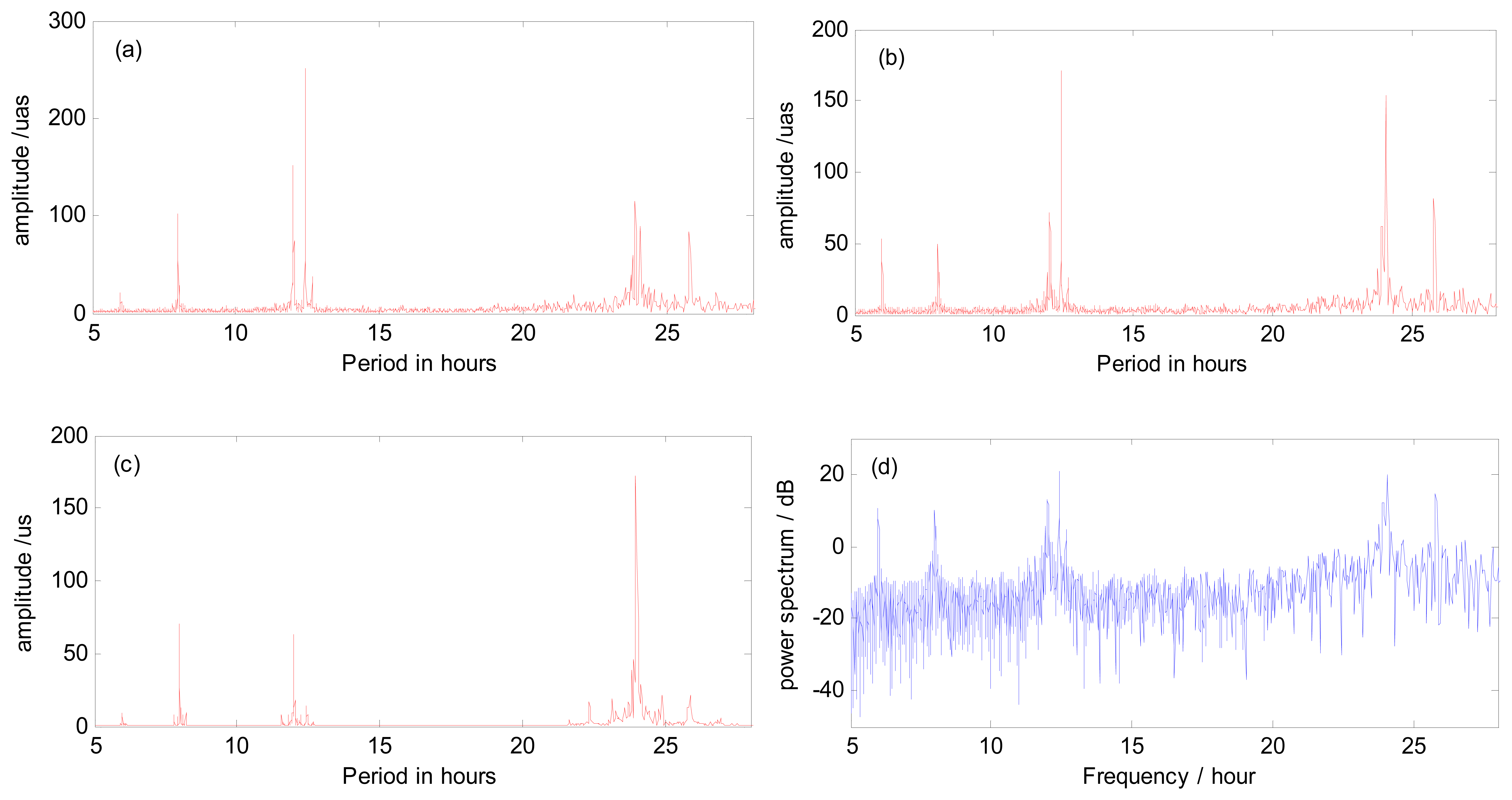
In this manuscript, we also estimated the ERP with 4 h sub-interval, namely ERP at a temporal resolution of 2 h. Figure 6a–c shows the amplitude spectrum analysis results of high frequency variations generated by combined GPS and GLONASS from 4 h sub-intervals with 3-day arc orbit. The amplitude spectrum analysis results almost show the same period terms in the X-pole and Y-pole. The amplitude spectral results of UT1-UTC show slightly different period terms than PM. Again, the amplitudes of these terms from UT1-UTC are extremely large when compared to IERS conventions. As we mentioned before, the reason is that the accuracy of UT1-UTC we estimated is not as good as PM due to the strategy we used. Other spurious signals may also be responsible for this. However, most of these periods are located around about 8 h, 12 h (semidiurnal variations) and 24 h (diurnal variations). Besides, we also get the detailed information about the amplitude of the noise as well as every period term. In addition, power spectrum analysis is also introduced to acquire a basic understanding of the energy distribution through all the period terms. As an example, the X-polar power spectrum analysis result is shown in Figure 6d. As the sub-figure shows, the power spectral peaks show almost the same result as the amplitude spectrum in that the main period terms are clustered together at one third day, semidiurnal and diurnal bands. As we may see, the power spectrum also shows a visible noise fluctuation. The most reasonable explanation is that when analyzing the power spectrum the whole series is regarded as a complete signal. If we divide the whole series into several pieces, the fluctuation can be smoothed.
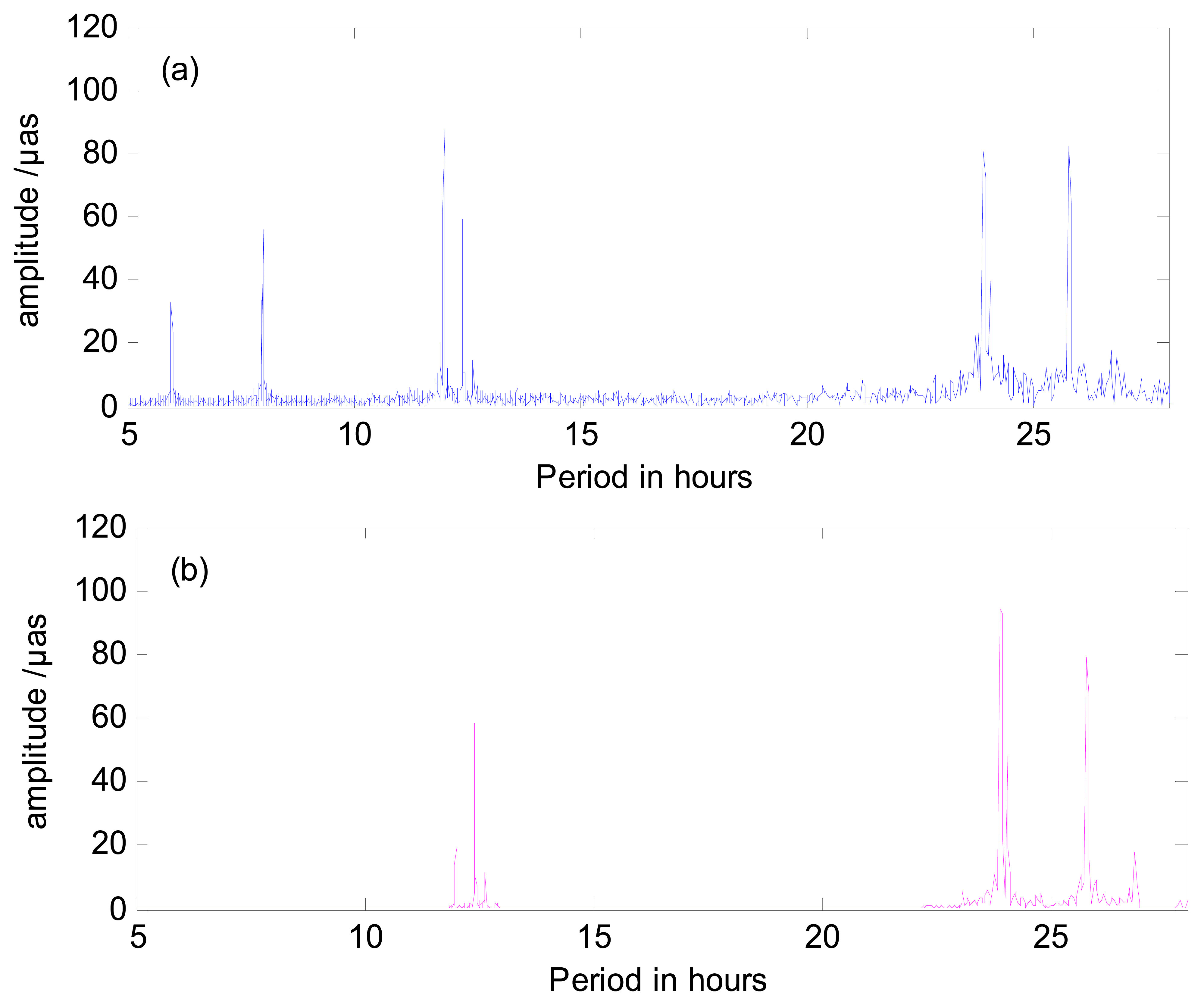
Furthermore, in order to analyze the impact of the length of sub-interval on the tidal amplitudes generated from the high frequency variations, the amplitudes of high frequency variations are estimated from both 2 h sub-interval and 4 h sub-interval. The amplitudes of prograde, retrograde PM and UT1-UTC generated from 2 h and 4 h sub-interval are compared. As we all know, the period terms (including diurnal and semidiurnal variations) generated from the high frequency variations are mainly the consequence of redistribution of geophysical fluid mass, especially the ocean tide. The tidal potential generated by moon and sun changes the ocean currents that cause the redistribution of earth fluid mass, which in return caused the variation in earth rotation. For instance, the period of 1.0024 days we obtain from the high frequency variations in ERP is one of the components of the ocean tides (which may correspond to P1 in IERS tide model). As a comparison, the prograde PM from IERS convention 2010 is shown in Figure 7 as well as our result. As Figure 7 shows, we obtain dozens of diurnal terms and semidiurnal terms. In addition, we also acquire several small terms, which are distributed around 1/3 d and 1/4 d. These short period terms are not included in the ocean tide model. Some of these short terms may be caused by the data processing method we use, but the most possible explanation is artifact. This has already been proved by analyzing the formal error spectra [23].
Table 5 shows the amplitudes of major period terms of PM and UT1-UTC obtained from high frequency variations. Most of these period terms listed below are included in ocean tide model in the IERS conventions 2010. In Table 5, we list 27 terms in total and the retrograde diurnal terms in PM are not shown here since they need to be blocked as we mentioned before.
Some of the period of these terms may be slightly different from the IERS Conventions. The most reasonable explanation is these period terms are not separated correctly due to the length of data we use. For example, the semidiurnal term of λ2 (0.5092406d) and L2 (0.5079842d) from the IERS might merge into one term at the period of 0.5079 d in our result. This should be improved if more than years of GNSS data were processed. For instance, to separate the largest 30 tidal terms completely given in IERS Convention, at least three or more years of GNSS data are needed. In the Table 5, the arrow (↑) (↓) means that the amplitude for the same tidal term computed from 2 h sub-interval is larger (smaller) than the amplitude computed from 4 h sub-interval. As the values listed in these tables show, 22 tidal amplitudes increase while 14 of them decrease in PM. It is also visible in UT1-UTC since 15 tidal amplitudes increase while 12 of them decrease. In conclusion, most of the amplitudes are increased when high frequency variations were generated from 2 h sub-interval GNSS observations. In another words, the amplitudes will be compressed or reduced when estimated ERP with a bit longer sub-interval. So in order to obtain the exactly amplitudes, it is better to determinate ERP at a higher frequency and shorter sub-interval as long as the precision is sufficient. However, the higher frequency is not necessarily better because it also relates to the accuracy of each parameter.
3.4. Influences of Different Models and Strategies
Apart from the time interval, there are various other factors that may impact on the estimation of ERP as well as the amplitudes of tidal terms. In this section, the influence of the prior information of ERP, ocean loading model, mapping function, and weighting function are discussed. Table 6 shows the impacts of different models or strategies on ERP. The factors we compared are (a) Bulletin A and C04 we use as prior information when estimating ERP; (b) ocean loading model (FES2004) and without ocean loading model; (c) weighting function (COSZ) and without weighting function (namely equally weighted); (d) mapping function of NIELL and HOPFIELD [47] when deal with the troposphere delays [48,49]. As Table 6 shows, the prior information of ERP has the minimal impact on ERP that can be ignored, while the impact of weighting function and ocean loading model demonstrate a visible impacts of different on ERP. The possible reason is that we set the cutoff angle at a low level (10°). When the elevation angle is small, the effect of multipath for some sites where there are many trees around (e.g., wuhn) becomes larger. Then the weighting function will have a visible impact on the estimation of parameters. So, as we suggested, weighting function and ocean loading model should be seriously considered when estimate ERP. As regarding to the mapping function, it also shows a very little influence.
The changes in ERP will leads to changes in the high frequency variations. Thus, the impact on amplitudes is also analyzed. Table 7 shows the impacts of difference processing options on tidal amplitudes. Here we only consider several major tides since the frequency resolution is not high enough to separate some ocean tides which are very close to each other. As we can see, Table 7 shows almost the same result as Table 6. Weighting function has shown a significant influence on the tidal amplitudes, while ocean load model also has a slight influence. As for prior information of ERP and mapping function, it shows a tiny difference. Other than these factors, the Reference Frame, sampling and orbit model may also have a slight impact on tidal amplitudes [23,28]. Here we did not cover all of them due to space reasons.
4. Conclusions
In this paper, the hourly ERPs time series are determined using GPS, GLONASS, and combining GPS and GLONASS data collected from 1 November 2012 to 10 April 2014. The observations come from nearly 80 IGS sites with a globally uniform distribution. We assess the precision of our ERP results by comparing them to the IGS solution. Our findings indicate that the accuracy of ERP can be improved by combining GPS and GLONASS. In addition, the correlation between the orbit model and ERP will also be reduced by combing these two different navigation systems. The high frequency variations in ERP are further studied using a de-trending method based on smoothness priors operating, like a time-varying FIR high pass filter. Our results show that most of the high frequency variations are within 1 mas for PM and within 0.5 ms for UT1-UTC. Furthermore, the spectrum of high frequency ERP variations is analyzed using a Fast Fourier Transform. As a result, we obtained several period terms for both PM and UT1-UTC around about 8 h, 12 h and 24 h bands. Most of these terms are components of ocean tides. By comparing the amplitudes generated from different time intervals, the result shows that the amplitude will be compressed or reduced when estimated ERP with a bit longer time interval. The amplitudes generated from different satellite systems have also been discussed. The results show that different orbits do have some effects on the tidal terms as we show with some figures as evidence, but our results are far from being able to certify this adequately and how this impact exactly happens need more investigation in the future. In addition, there are also some small terms that occurred in the high frequency variations of ERP. This may be caused by the models and strategies that we used in the data processing as well as artifacts. Some differences in the amplitudes from IERS may be caused by other geophysical excitations, such as the thermally driven atmospheric and high-frequency hydrological variations, which will be analyzed in the future with more geophysical data.
Acknowledgments
This research is supported by the National Keystone Basic Research Program (MOST 973) (No. 2012CB72000), National “863 Project” of China (No. 2008AA12Z308), National Natural Science Foundation of China (No. 41374012, 11173050 and 11373059), Main Direction Project of Chinese Academy of Sciences (Grant no. KJCX2-EW-T03) and Shanghai Science and Technology Commission Project (No. 12DZ2273300). We appreciate for the data from IGS and IERS as well as the advice from the reviewers.
Author Contributions
All authors contributed to the work presented in this paper. Erhu Wei and Shuanggen Jin were in charge of research and analysis. Lihua Wan designed the experiments and processed data, as well as wrote the draft. Erhu Wei and Shuanggen Jin revised the manuscript. Lihua Wan, Wenjie Liu, Yali Yang and Zhenghong Hu performed the experiments.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hopkin, M. Sumatran quake sped up Earth's rotation. Nature 2004, 30. [Google Scholar] [CrossRef]
- Wu, P.; Peltier, W.R. Pleistocene deglaciation and the Earth's rotation: A new analysis. Geophys. J. Int. 1984, 76, 753–791. [Google Scholar]
- Hefty, J.; Rothacher, M.; Springer, T.; Weber, R.; Beutler, G. Analysis of the first year of Earth rotation parameters with a sub-daily resolution gained at the CODE processing center of the IGS. J. Geod. 2000, 74, 479–487. [Google Scholar]
- Yoder, C.F.; Williams, J.G.; Parke, M.E. Tidal variations of Earth rotation. J. Geophys. Res. 1981, 86, 881–891. [Google Scholar]
- Baader, H.R.; Brosche, P.; Hövel, W. Ocean tides and periodic variations of the Earth's rotation. J. Geophys. Z. Geophys. 1983, 52, 140–142. [Google Scholar]
- Brosche, P.; Wünsch, J.; Seiler, U.; Sündermann, J. Periodic changes in Earth's rotation due to oceanic tides. Astron. Astrophys. 1989, 220, 318–320. [Google Scholar]
- Seiler, U. Periodic changes of the angular momentum budget due to the tides of the world ocean. J. Geophys. Res. 1991, 96, 10287–10300. [Google Scholar]
- Wünsch, J.; Seiler, U. Theoretical amplitudes and phases of the periodic polar motion terms caused by ocean tides. Astron. Astrophys. 1992, 266, 581–587. [Google Scholar]
- Gross, R.S. The effect of ocean tides on the Earth's rotation as predicted by the results of an ocean tide model. Geophys. Res. Lett. 1993, 20, 293–296. [Google Scholar]
- Brosche, P.; Wünsch, J.; Campbell, J.; Schuh, H. Ocean tide effects in universal time detected by VLBI. Astron. Astrophys. 1991, 245, 676–682. [Google Scholar]
- Sovers, O.J.; Jacobs, C.S.; Gross, R.S. Measuring rapid ocean tidal Earth orientation variations with very long baseline interferometry. J. Geophys. Res. 1993, 98, 19959–19971. [Google Scholar]
- Herring, T.A.; Dong, D.N. Measurement of diurnal and semidiurnal rotational variations and tidal parameters of Earth. J. Geophys. Res. 1994, 99, 18051–18071. [Google Scholar]
- Gipson, J.M. Very long baseline interferometry determination of neglected tidal terms in high-frequency Earth orientation variation. J. Geophys. Res. 1996, 101, 28051–28064. [Google Scholar]
- Haas, R.; Wünsch, J. Sub-diurnal earth rotation variations from the VLBI CONT02 campaign. J. Geodyn. 2006, 41, 94–99. [Google Scholar]
- Englich, S.; Heinkelmann, R.; Schuh, H. Re-assessment of ocean tidal terms in high-frequency earth rotation variations observed by VLBI. Proceedings of the IVS 2008 General Meeting, St. Petersburg, Russia, 2–6 March 2008; pp. 314–318.
- Artz, T.; Née Böckmann, S.T.; Nothnagel, A. Assessment of periodic sub-diurnal Earth rotation variations at tidal frequencies through transformation of VLBI normal equation systems. J. Geod. 2001, 8, 565–584. [Google Scholar]
- Artz, T.; Böckmann, S.; Nothnagel, A.; Steigenberger, P. Subdiurnal variations in the Earth's rotation from continuous very long baseline interferometry campaigns. J. Geophys. Res. 2010, 115. [Google Scholar] [CrossRef]
- Artz, T.; Bernhard, L.; Nothnagel, A.; Steigenberger, P.; Tesmer, S. Methodology for the combination of sub-daily Earth rotation from GPS and VLBI observations. J. Geod. 2012, 86, 221–239. [Google Scholar]
- Nilsson, T.; Böhm, J.; Schuh, H.; Schreiber, U.; Gebauer, A.; Klügel, T. Combining VLBI and ring laser observations for determination of high frequency Earth rotation variation. J. Geod. 2012, 62, 69–73. [Google Scholar]
- Watkins, M.M.; Eanes, R.J. Diurnal and semidiurnal variations in Earth orientation determined from LAGEOS laser ranging. J. Geophys. Res. 1994, 99, 18073–18079. [Google Scholar]
- Ray, R.D.; Steinberg, D.J.; Chao, B.F.; Cartwright, D.E. Diurnal and semidiurnal variations in the Earth's rotation rate induced by oceanic tides. Science 1994, 264, 830–832. [Google Scholar]
- Chao, B.F.; Ray, R.D.; Gipson, J.M.; Egbert, G.D.; Ma, C. Diurnal/semidiurnal polar motion excited by oceanic tidal angular momentum. J. Geophys. Res. 1996, 101, 20151–20163. [Google Scholar]
- Rothacher, M.; Beutler, G.; Weber, R.; Hefty, J. High-frequency variations in Earth rotation from Global Positioning System data. J. Geophys. Res. 2001, 106, 13711–13738. [Google Scholar]
- Steigenberger, P.; Rothacher, M.; Dietrich, R.; Fritsche, M.; Rülke, A.; Vey, S. Reprocessing of a global GPS network. J. Geophys. Res. 2006, 111. [Google Scholar] [CrossRef]
- Jin, S.G.; Chambers, D.P.; Tapley, B.D. Hydrological and oceanic effects on polar motion from GRACE and models. J. Geophys. Res. 2010, 115. [Google Scholar] [CrossRef]
- Jin, S.G.; Zhang, L.J.; Tapley, B.D. The understanding of length-of-day variations from satellite gravity and laser ranging measurements. Geophys. J. Int. 2011, 184, 651–660. [Google Scholar]
- Jin, S.G.; Hassan, A.A.; Feng, G.P. Assessment of terrestrial water contributions to polar motion from GRACE and hydrological models. J. Geod. 2012, 62, 40–48. [Google Scholar]
- Panafidina, N.; Seitz, M.; Hugentobler, U. Interaction between subdaily Earth rotation parameters and GPS orbits. Proceedings of the EGU General Assembly Conference, Vienna, Austria, 7–12 April 2013.
- Bizouard, C.; Gambis, D. The combined solution C04 for Earth orientation parameters consistent with international terrestrial reference frame 2005. In Geodetic Reference Frames; Springer: Heidelberg, Germany, 2009; pp. 265–270. [Google Scholar]
- Vondrak, J. A contribution to the problem of smoothing observational data. Bull. Astron. Inst. Czechoslov. 1969, 20, 349. [Google Scholar]
- Vondrák, J. Problem of smoothing observational data II. Bull. Astron. Inst. Czechoslov. 1977, 28, 84. [Google Scholar]
- Wang, Q.X.; Dang, Y.M.; Xu, T.H. The method of earth rotation parameter determination using GNSS observations and precision analysis. Proceedings of the China Satellite Navigation Conference (CSNC), Wuhan, China, 15–17 May 2013; pp. 247–256.
- Wei, E.H.; Li, G.W.; Chang, L.; Cao, Q. On the High-Frequency ERPs with GPS Observations. Geomat. Inf. Sci. Wuhan Univ. 2013, 38, 818–821. [Google Scholar]
- Dow, J.M.; Neilan, R.E.; Rizos, C. The international GNSS service in a changing landscape of global navigation satellite systems. J. Geod. 2009, 83, 191–198. [Google Scholar]
- Altamimi, Z.; Collilieux, X.; Métivier, L. ITRF2008: An improved solution of the international terrestrial reference frame. J. Geod. 2011, 85, 457–473. [Google Scholar]
- Xu, G.C. Applications of GPS Theory Algorithms. In GPS: Theory, Algorithms and Applications; Springer: Heidelberg, Germany, 2007; pp. 219–241. [Google Scholar]
- Wan, L.H.; Wei, E.H.; Jin, S.G. Earth rotation parameter estimation from GNSS and its impact on aircraft orbit determination. Proceedings of the China Satellite Navigation Conference (CSNC) 2014, Nanjing, China, 21–23 May 2014; pp. 105–114.
- Dach, R.; Hugentobler, U.; Fridez, P.; Meindl, M. Bernese GPS Software Version 5.0; Astronomical Institute, University of Bern: Bern, Switzerland, 2007. [Google Scholar]
- McCarthy, D.D.; Petit, G. IERS Technical Note No. 32, IERS Conventions; International Earth Rotation and Reference Systems Service: Frankfurt, Germany, 2003. [Google Scholar]
- McCarthy, D.D. IERS Technical Note No. 21, IERS Conventions; International Earth Rotation and Reference Systems Service: Frankfurt, Germany, 1996; pp. 1–95. [Google Scholar]
- Letellier, T.; Lyard, F.; Lefevre, F. The new global tidal solution: FES2004. Proceedings of the Ocean Surface Topography Science Team Meeting, St. Petersburg, FL, USA, 4–6 November 2004.
- Niell, A.E. Global mapping functions for the atmosphere delay at radio wavelengths. J. Geophys. Res. 1996, 101, 3227–3246. [Google Scholar]
- Mervart, L.; Schaer, S. Quasi-Ionosphere-Free (QIF) Ambiguity Resolution Strategy; Astronomical Institute, University of Berne: Berne, Switzerland, 1994. [Google Scholar]
- Dach, R.; Brockmann, E.; Schaer, S.; Beutler, G.; Meindl, M.; Prange, L.; Bock, H.; Jäggi, A.; Ostini, L. GNSS processing at CODE: Status report. J. Geod. 2009, 83, 353–365. [Google Scholar]
- Tarvainen, M.P.; Ranta-aho, P.O.; Karjalainen, P.A. An advanced detrending method with application to HRV analysis. IEEE Trans. Biomed. Eng. 2002, 49, 172–175. [Google Scholar]
- Petit, G.; Luzum, B. IERS Technical Note No. 36, IERS Conventions; International Earth Rotation and Reference Systems Service: Frankfurt, Germany, 2010. [Google Scholar]
- Hopfield, H.S. Two-quadratic tropospheric refractivity profile for correction satellite data. J. Geophys. Res. 1969, 74, 4487–4499. [Google Scholar]
- Jin, S.G.; Li, Z.C.; Cho, J.H. Integrated water vapor field and multi-scale variations over China from GPS measurements. J. Appl. Meteorol. Clim. 2008, 47, 3008–3015. [Google Scholar]
- Jin, S.G.; Luo, O.F.; Gleason, S. Characterization of diurnal cycles in ZTD from a decade of global GPS observations. J. Geod. 2009, 83, 537–545. [Google Scholar]

| PM in X/mas | PM in Y/mas | UT1-UTC/ms | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Max | Min | STD | Max | Min | STD | Max | Min | STD | |
| GPS only | 1.5465 | −1.7256 | 0.4079 | 1.6519 | −1.2389 | 0.4609 | 0.1071 | −0.4033 | 0.0842 |
| GLONASS only | 2.2049 | −1.8712 | 0.6763 | 2.4367 | −2.3954 | 0.6834 | 0.0953 | −0.5087 | 0.1021 |
| GPS/GLONASS | 1.5632 | −1.7111 | 0.3832 | 1.4584 | −1.1252 | 0.4301 | 0.1001 | −0.4140 | 0.0833 |
| PM in X/mas | PM in Y/mas | UT1-UTC/ms | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Max | Min | RMS | Max | Min | RMS | Max | Min | RMS | ||
| 2 h | GPS only | 1.5293 | −1.5849 | 0.4597 | 1.7599 | −1.7781 | 0.4112 | 0.6151 | −0.6398 | 0.2379 |
| GLONASS only | 2.2588 | −2.8308 | 0.5609 | 2.0416 | −2.1159 | 0.5404 | 0.6120 | −0.6541 | 0.2409 | |
| GPS/GLONASS | 1.5637 | −1.4488 | 0.4423 | 1.4535 | −1.4054 | 0.3891 | 0.5933 | −0.6253 | 0.2348 | |
| 3 days arc | 1.4471 | −1.7828 | 0.4477 | 1.5848 | −1.1956 | 0.3630 | 0.5893 | −0.5846 | 0.2329 | |
| 4 h | GPS only | 1.7325 | −1.763 | 0.4673 | 1.5932 | −1.5914 | 0.3857 | 0.6031 | −0.6091 | 0.2385 |
| GLONASS only | 2.2294 | −2.5976 | 0.5535 | 2.2496 | −1.7075 | 0.5026 | 0.6031 | −0.6685 | 0.2401 | |
| GPS/GLONASS | 1.4408 | −1.3897 | 0.4504 | 1.3427 | −1.2922 | 0.3680 | 0.5890 | −0.5966 | 0.2340 | |
| 3 days arc | 1.4012 | −1.4215 | 0.4374 | 1.3648 | −1.1626 | 0.3545 | 0.5788 | −0.5921 | 0.2331 | |
| Frequency of FFT/2π·d−1 | Period/h | X-pole/μas | Y-pole/μas | UT1-UTC/μs | |||
|---|---|---|---|---|---|---|---|
| Cos | Sin | Cos | Sin | Cos | Sin | ||
| Coefficient generated from GPS observations | |||||||
| 0.03723 | 26.859 | 1.467 | −15.679 | 14.017 | 1.073 | −3.50 | 1.69 |
| 0.03876 | 25.802 | 72.239 | 40.790 | −11.676 | 79.050 | 4.86 | −10.96 |
| 0.04156 | 24.058 | −15.409 | −100.467 | −137.990 | −40.446 | 73.33 | −18.50 |
| 0.04163 | 24.023 | −10.194 | −32.503 | 14.023 | 22.829 | 110.24 | 34.56 |
| 0.04181 | 23.918 | −21.341 | −118.263 | 34.166 | −60.994 | −38.18 | 30.43 |
| 0.04187 | 23.883 | 12.936 | 2.107 | −10.607 | −0.289 | 4.38 | 4.84 |
| 0.07898 | 12.662 | 26.751 | −28.465 | −23.818 | 1.166 | 2.75 | −1.08 |
| 0.08051 | 12.421 | −21.771 | 247.721 | 160.688 | −52.034 | −5.65 | 14.07 |
| 0.08331 | 12.003 | −115.643 | 98.433 | 52.203 | −39.150 | −69.59 | 17.48 |
| 0.08356 | 11.967 | −17.791 | −7.095 | 17.330 | 22.052 | −8.64 | −1.32 |
| Coefficient generated from GLONASS observations | |||||||
| 0.03723 | 26.859 | 0.376 | −10.878 | 8.841 | −15.765 | −3.66 | 1.58 |
| 0.03876 | 25.802 | 80.968 | 38.645 | −6.116 | 75.489 | 5.05 | −11.05 |
| 0.04156 | 24.058 | −48.380 | −89.783 | −168.672 | −20.558 | 70.73 | −13.14 |
| 0.04163 | 24.023 | 6.600 | 4.006 | −6.790 | 7.666 | 102.72 | 33.18 |
| 0.04181 | 23.918 | −61.392 | −105.817 | 28.908 | −26.770 | −37.08 | 26.60 |
| 0.04187 | 23.883 | −15.947 | 23.678 | −12.532 | 26.309 | 4.39 | 4.73 |
| 0.07898 | 12.662 | 26.652 | −27.803 | −29.961 | −4.131 | 2.66 | −1.28 |
| 0.08051 | 12.421 | −33.054 | 252.585 | 171.502 | −69.196 | −5.21 | 14.34 |
| 0.08331 | 12.003 | −121.566 | 57.062 | 67.587 | −30.709 | −46.14 | 11.70 |
| 0.08356 | 11.967 | −19.862 | −47.684 | 1.254 | 12.439 | −8.23 | −0.25 |
| Coefficient generated from combined GPS/GLONASS observations | |||||||
| 0.03723 | 26.859 | 1.300 | −14.456 | 11.975 | −0.178 | −3.46 | 1.61 |
| 0.03876 | 25.802 | 75.395 | 36.629 | −13.648 | 80.423 | 4.95 | −11.00 |
| 0.04156 | 24.058 | −24.198 | −100.922 | −150.297 | −40.290 | 72.34 | −16.68 |
| 0.04163 | 24.023 | −4.638 | −19.448 | 13.318 | 17.320 | 107.23 | 33.86 |
| 0.04181 | 23.918 | −31.986 | −113.014 | 28.017 | −50.420 | −38.00 | 28.82 |
| 0.04187 | 23.883 | 5.503 | 10.046 | −13.297 | 9.722 | 4.12 | 4.82 |
| 0.07898 | 12.662 | 27.813 | −26.343 | −27.294 | 1.034 | 2.65 | −1.20 |
| 0.08051 | 12.421 | −24.588 | 248.340 | 162.571 | −56.315 | −5.57 | 14.13 |
| 0.08331 | 12.003 | −126.292 | 84.260 | 50.162 | −32.255 | −59.07 | 14.64 |
| 0.08356 | 11.967 | −22.706 | −19.336 | 14.093 | 15.941 | −7.85 | −1.33 |
| Frequency of FFT/2π·d−1 | Period/h | Gps | Glonass | Gnss | Iers 2010 |
|---|---|---|---|---|---|
| Prograde | Prograde | Prograde | Prograde | ||
| Retrograde | Retrograde | Retrograde | Retrograde | ||
| 0.03723 | 26.859 | 14.902 | 12.507 | 13.228 | 17.975 |
| 0.03876 | 25.802 | 80.064 | 81.367 | 81.865 | 79.081 |
| 0.04156 | 24.058 | 33.644 | 52.383 | 40.610 | 48.038 |
| 0.04163 | 24.023 | 24.105 | 8.945 | 17.568 | 3.416 |
| 0.04181 | 23.918 | 86.622 | 80.504 | 81.671 | 94.152 |
| 0.04187 | 23.883 | 8.967 | 18.832 | 13.935 | 15.268 |
| 0.07898 | 12.662 | 14.150 | 11.312 | 14.5431 | 11.388 |
| 29.104 | 32.727 | 29.975 | 29.180 | ||
| 0.08051 | 12.421 | 57.057 | 65.249 | 58.952 | 58.288 |
| 204.765 | 212.812 | 206.067 | 206.179 | ||
| 0.08331 | 12.003 | 80.775 | 76.319 | 81.068 | 19.649 |
| 84.473 | 77.124 | 82.025 | 89.557 | ||
| 0.08356 | 11.967 | 12.397 | 24.749 | 17.053 | 4.382 |
| 20.568 | 28.280 | 19.501 | 20.549 | ||
| Frequency of FFT/2π·d−1 | Period/days | Amplitude from 4 h Sub-Interval | Amplitude from 2 h Sub-Interval | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Prograde PM/μas | Retrograde PM/μas | UT1-UTC μs | Prograde PM/μas | Retrograde PM/μas | UT1-UTC μs | |||||
| Diurnal terms in PM | ||||||||||
| 0.03723 | 1.1191 | 15.60 | 4.53 | 15.88 ↑ | 4.00 ↓ | |||||
| 0.03741 | 1.1136 | 16.47 | 2.25 | 18.79 ↑ | 2.30 ↑ | |||||
| 0.03876 | 1.0751 | 81.33 | 10.44 | 80.08 ↓ | 10.55 ↑ | |||||
| 0.04028 | 1.0343 | 14.61 | 7.85 | 13.49 ↓ | 7.52 ↓ | |||||
| 0.04053 | 1.0281 | 7.76 | 10.46 | 7.83 ↑ | 10.64 ↑ | |||||
| 0.04071 | 1.0235 | 5.52 | 2.78 | 3.44 ↓ | 3.30 ↑ | |||||
| 0.04144 | 1.0054 | 29.28 | 17.09 | 30.55 ↑ | 17.70 ↑ | |||||
| 0.04150 | 1.0039 | 18.27 | 24.23 | 17.68 ↓ | 23.56 ↓ | |||||
| 0.04156 | 1.0024 | 45.89 | 75.46 | 50.18 ↑ | 75.57 ↑ | |||||
| 0.04163 | 1.0010 | 24.98 | 115.94 | 26.41 ↑ | 115.59 ↓ | |||||
| 0.04169 | 0.9995 | 13.50 | 181.02 | 18.81 ↑ | 181.14 ↑ | |||||
| 0.04175 | 0.9981 | 73.76 | 35.97 | 73.85 ↑ | 36.20 ↑ | |||||
| 0.04181 | 0.9966 | 81.77 | 53.97 | 80.60 ↓ | 53.40 ↓ | |||||
| 0.04187 | 0.9951 | 18.55 | 6.53 | 20.36 ↑ | 6.87 ↑ | |||||
| 0.04205 | 0.9908 | 13.70 | 8.56 | 13.83 ↑ | 8.09 ↓ | |||||
| 0.04303 | 0.9683 | 4.69 | 6.61 | 5.69 ↑ | 6.18 ↓ | |||||
| 0.04474 | 0.9313 | 7.04 | 18.02 | 7.54 ↑ | 18.47 ↑ | |||||
| 0.04633 | 0.8994 | 2.73 | 1.70 | 3.22 ↑ | 1.15 ↓ | |||||
| Semidiurnal terms in PM | ||||||||||
| 0.07898 | 0.5276 | 13.93 | 28.41 | 3.17 | 13.73 ↓ | 29.61 ↑ | 3.09 ↓ | |||
| 0.08051 | 0.5176 | 60.15 | 204.04 | 15.87 | 60.67 ↑ | 203.24 ↓ | 15.95 ↑ | |||
| 0.08203 | 0.5079 | 6.79 | 10.06 | 3.89 | 7.42 ↑ | 9.70 ↓ | 3.64 ↓ | |||
| 0.08319 | 0.5009 | 18.88 | 72.00 | 15.33 | 21.27 ↑ | 71.42 ↓ | 15.27 ↓ | |||
| 0.08325 | 0.5005 | 10.63 | 52.81 | 10.59 | 10.77 ↑ | 51.56 ↓ | 10.88 ↑ | |||
| 0.08331 | 0.5001 | 77.81 | 89.58 | 61.38 | 83.89 ↑ | 88.47 ↓ | 61.77 ↑ | |||
| 0.08344 | 0.4994 | 43.52 | 24.42 | 26.38 | 46.13 ↑ | 21.57 ↓ | 26.50 ↑ | |||
| 0.08350 | 0.4990 | 41.44 | 3.21 | 8.51 | 41.12 ↓ | 3.54 ↑ | 8.18 ↓ | |||
| 0.08356 | 0.4987 | 16.48 | 21.79 | 8.13 | 16.41 ↓ | 24.04 ↑ | 8.43 ↑ | |||
| GNSS Models | Difference in X-Pole/mas | Difference in Y-Pole/mas | Difference in UT1-UTC/ms | |||
|---|---|---|---|---|---|---|
| Largest | RMS | Largest | RMS | Largest | RMS | |
| (a) | 0.240 | 0.062 | 0.030 | 0.096 | 0.052 | 0.018 |
| (b) | 0.470 | 0.173 | 0.830 | 0.280 | 0.040 | 0.016 |
| (c) | 1.360 | 0.655 | 2.120 | 0.842 | 0.367 | 0.114 |
| (d) | 0.230 | 0.070 | 1.090 | 0.201 | 0.020 | 0.007 |
| GNSS Models | Amplitudes in X-Pole/μas | Amplitudes in Y-Pole/μas | Amplitudes in UT1-UTC/μs | |||
|---|---|---|---|---|---|---|
| Largest Difference | RMS | Largest Difference | RMS | Largest Difference | RMS | |
| (a) | 3.17 | 1.73 | 7.41 | 4.02 | 0.45 | 0.27 |
| (b) | 9.14 | 4.56 | 7.81 | 5.94 | 0.92 | 0.55 |
| (c) | 19.93 | 10.21 | 59.63 | 33.28 | 13.83 | 8.77 |
| (d) | 4.33 | 2.07 | 13.22 | 6.02 | 0.76 | 0.43 |
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, E.; Jin, S.; Wan, L.; Liu, W.; Yang, Y.; Hu, Z. High Frequency Variations of Earth Rotation Parameters from GPS and GLONASS Observations. Sensors 2015, 15, 2944-2963. https://doi.org/10.3390/s150202944
Wei E, Jin S, Wan L, Liu W, Yang Y, Hu Z. High Frequency Variations of Earth Rotation Parameters from GPS and GLONASS Observations. Sensors. 2015; 15(2):2944-2963. https://doi.org/10.3390/s150202944
Chicago/Turabian StyleWei, Erhu, Shuanggen Jin, Lihua Wan, Wenjie Liu, Yali Yang, and Zhenghong Hu. 2015. "High Frequency Variations of Earth Rotation Parameters from GPS and GLONASS Observations" Sensors 15, no. 2: 2944-2963. https://doi.org/10.3390/s150202944






