A Multipoint Correction Method for Environmental Temperature Changes in Airborne Double-Antenna Microwave Radiometers
Abstract
: This manuscript describes a new type Ka-band airborne double-antenna microwave radiometer (ADAMR) designed for detecting atmospheric supercooled water content (SCWC). The source of the measurement error is investigated by analyzing the model of the system gain factor and the principle of the auto-gain compensative technique utilized in the radiometer. Then, a multipoint temperature correction method based on the two-point calibration method for this radiometer is proposed. The multipoint temperature correction method can eliminate the effect of changes in environmental temperature by establishing the relationship between the measurement error and the physical temperatures of the temperature-sensitive units. In order to demonstrate the feasibility of the correction method, the long-term outdoor temperature experiment is carried out. The multipoint temperature correction equations are obtained by using the least square regression method. The comparison results show that the measuring accuracy of the radiometer can be increased more effectively by using the multipoint temperature correction method.1. Introduction
Microwave radiometers have been widely used in many remote sensing applications in recent decades [1–3]. It is known that while total power radiometers have the simplest structure and measurement scheme, their sensitivity and stability are adversely affected by both noise and gain fluctuation [4]. Although some effective temperature compensation methods have been suggested recently for total power radiometers [5,6], it is still difficult to use them in practical applications. Historically, in order to eliminate the effect of the noise and gain variations, many switched-type radiometers have been developed [7–10], e.g., the Dicke radiometer, the null-balancing Dicke radiometer, the two-reference temperature radiometer, etc. However, all of these radiometers use negative feedback control and synchronous detection circuits, which add great complexity and cost to the systems. For this reason, the digital auto-gain compensation microwave radiometer (DGCMR) was proposed [11].
The DGCMR adopts fast analog-to-digital conversion and a software compensation technique, which can compensate the output value of the receiver according to the detected change of the system gain and greatly simplify the system structure. The remote sensing application experiments show that the DGCMR has high sensitivity and stability [12]. However, during the long-term outdoor experiments, we found that the output of the solid-state noise source fluctuates with the environmental temperature changes, which causes measurement errors owing to the digital auto-gain compensation technique. Luan and Zhao analyzed the characteristics of DGCMR and proposed a method of correcting the output value by using the physical temperature of the reference noise source [13]. In the correction procedure, the two-point calibration result can be corrected by the regression relationship between the correction brightness temperature value and the physical temperature of the noise reference source.
In this paper, firstly, a new type Ka-band (frequency is 31.65 GHz) airborne double-antenna microwave radiometer (ADAMR) is introduced. The ADAMR based on the digital auto-gain compensation technique is developed for detecting atmospheric supercooled water content. The detailed results of the sensitivity and stability experiments for this radiometer can be found in [14]. Secondly, we describe the principle of the digital auto-gain compensation technique and analyze the reason for the measurement errors caused by the compensation technique. Then, a multi-point temperature correction method for the two-point calibration equations is proposed. Finally, an outdoor temperature experiment is carried out for the ADAMR. The multi-point temperature correction equations are deduced by using the least square regression method and the experiment results demonstrate the efficiency of the correction method.
2. Radiometer Design and Temperature Correction Method
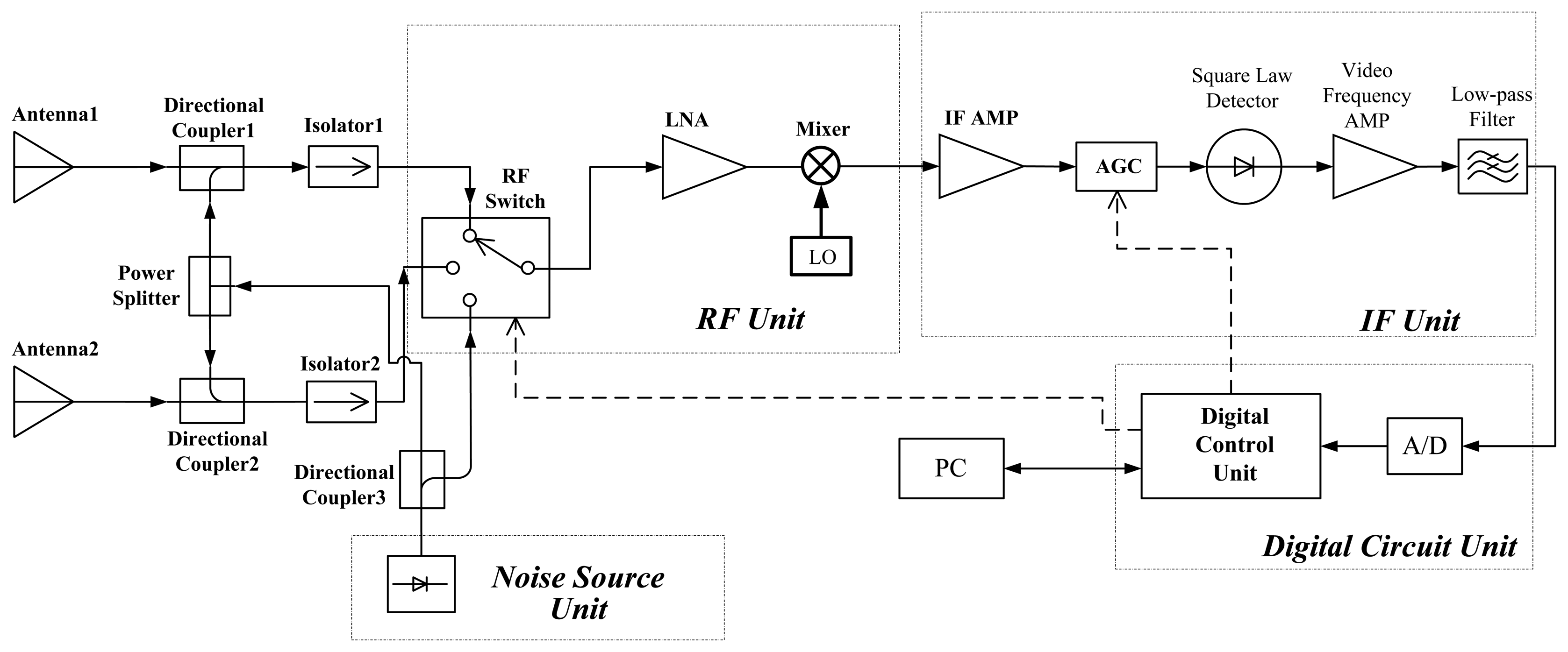
The ADAMR is designed for detecting the radiation brightness temperature from sky. It has been successfully used to retrieve the spatial distribution of SCWC using tomography due to the high sensitivity and the optimized double-antenna structure [15]. The block diagram of the radiometer is shown in Figure 1. The main technical specifications of the receiver and the antenna are listed in the following tables (Tables 1 and 2).
The heterodyne receiver uses a modularization structure, which consists of the radio frequency front end unit (RF unit), intermediate frequency amplifier unit (IF unit), noise source unit and digital circuit unit. In order to detect ultralow (<10 K) effective brightness temperature signals from the sky, the noise coupled technique is used [16]. The thermal noise signal of interest is received by the antennas and coupled into an extra noise signal generated from the solid-state noise source. Then, the noise signal is amplified and down-converted by the RF unit. In the IF unit, the IF amplifier and the auto gain controller (AGC) adjusts the amount of power transferred into the square law detector and the square-law detected voltage signal arrives at a low-pass filter through a differential amplifier, where the high frequency component is excluded. And then, the signal is digitized by a 12 bit A/D converter for auto-gain compensation and further processed in computer.
In order to obtain more observation information, we equip the radiometer receiver with two fixed antennas. The double-antenna elevation angles are 30° and 90°. This has proven to be the best combination of elevation angles according to the results of numerical simulations [17]. Figure 2 shows the main component units of the receiver and the double-antenna structure in the outdoor experiment.
The system gain factor of the radiometer can be expressed as following:
In order to eliminate the effects of the system gain fluctuation, we define a compensation coefficient , which can be expressed with Equations (2) and (4):
When α ≠ 1, considering the system gain is changed. Through digitizing the voltages and calculating the compensation coefficient by the digital circuit unit and computer, we can real-timely compensate the output voltage of system connecting the antenna by multiplying Equations (5) and (6):
Comparing Equations (3) and (7), we note that no matter how the system gain changes, the output voltage of the system connecting antenna always keeps constant . The observed brightness temperature TAi can be estimated by the two-point calibration equation:
Substituting Equation (8) into Equation (6), we can obtain the gain compensation coefficient:
Because the compensation coefficient is α ≠ 1, the system output voltage will be compensated incorrectly which causes the measuring error in observed brightness temperature. In order to correct this error, deriving from the physical temperature variation of the receiver, we define the measuring error as ΔTAi. The corrected antenna temperature can be expressed as . Considering that the fluctuation of the reference noise and receiver noise temperature mainly stem from the temperature drifts of the temperature sensitive components: noise diode in the noise source unit, RF LNA in the RF unit, and square-law detector in the IF unit, we can correct the two-point calibration equation by using the relationship between the measuring error ΔTAi and the physical temperatures of the temperature sensitive units above. The internal structure of the radiometer is shown in Figure 2, we can see that all the units of the radiometer are mounted on the same metal baseplate. Taking into account the interaction between the sensitive units, we express the measuring error ΔTAi with the multiplication of temperature functions related to each unit as:
3. Temperature Experiment Results
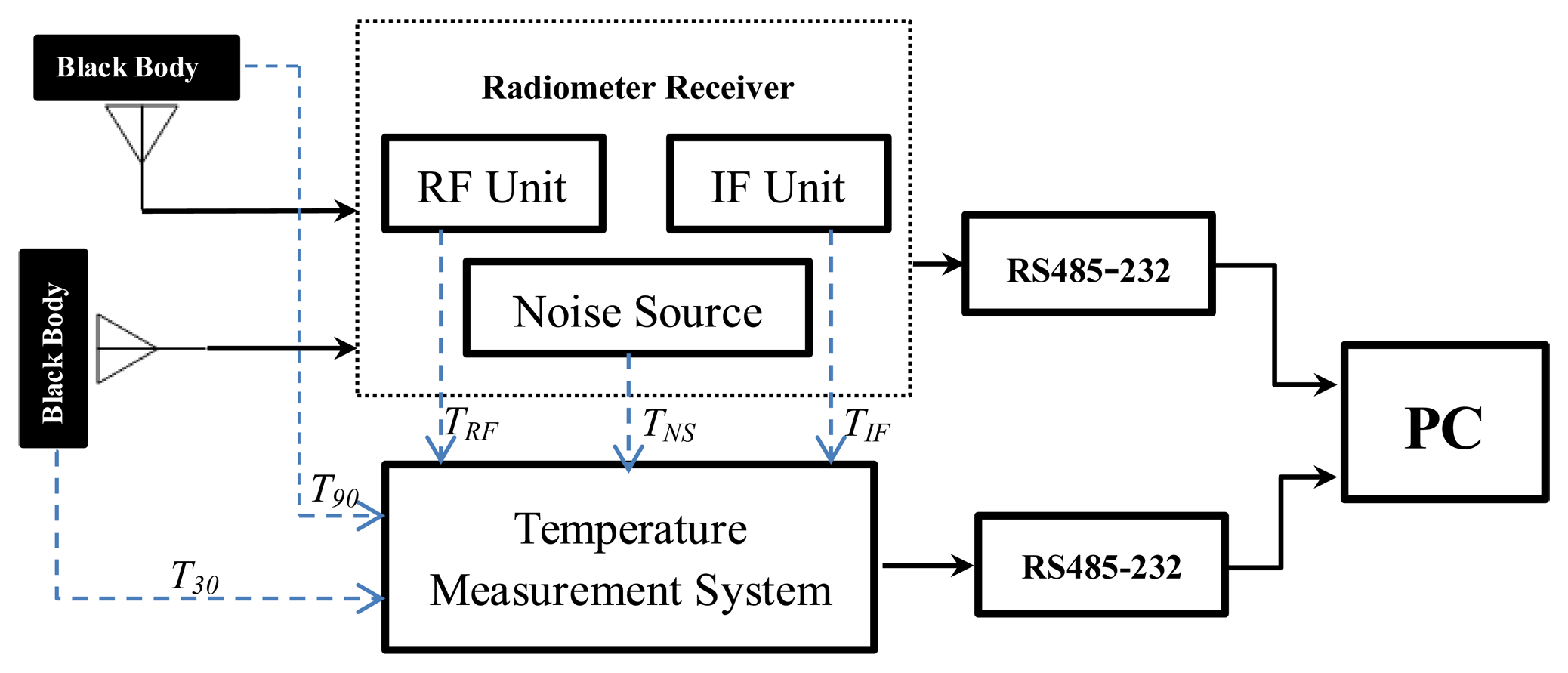
Before the experiment, we calibrated the radiometer system using two-point calibration method which combines the blackbody and the meteorological calibration. In the calibration curve, the high-temperature point is the black body temperature and the low-temperature point is the clear sky brightness temperature collected from a weather station. The calibration equations of the two antenna channels are Equations (13) and (17), respectively. From (UTC +8:00) 11:00 AM, September 22, 2013 to 08:45 AM September 26, 2013, the outdoor temperature experiment for ADAMR was carried out at the Northeast Institute of Geography and Agricultural Ecology, Chinese Academy of Sciences in Changchun City, Jilin Province (East longitude 125°24′, North latitude 43°59′).
The connection block diagram of this temperature experiment is shown in Figure 3. During the experiment, the two antenna apertures are covered by two pieces of microwave black body material, respectively, as the observed target. The temperature measurement system collects the temperatures of the observed target, the noise source, the RF, and the IF units by the temperature probes (DS18B20). Then the recorded temperature and the radiometer output voltage data are transferred real-timely to PC via a RS485-232 serial communication interface for further processing. Figure 4 shows the temperatures of the noise source, the RF, and the IF units recorded by the temperature measurement system. Due to the large size of the data, we take the accumulative average value per minute as the measurement value of this minute.
3.1. Results of 30° Antenna Channel
The temperature of the target ranges from 276 K to 311 K. The uncorrected two-point calibration equation is:
We obtain the relationship between the temperature of reference source TNS and the measurement error ΔTB30 by using the 2nd-order polynomial fit method:
The one-point temperature correction equation can be expressed as:
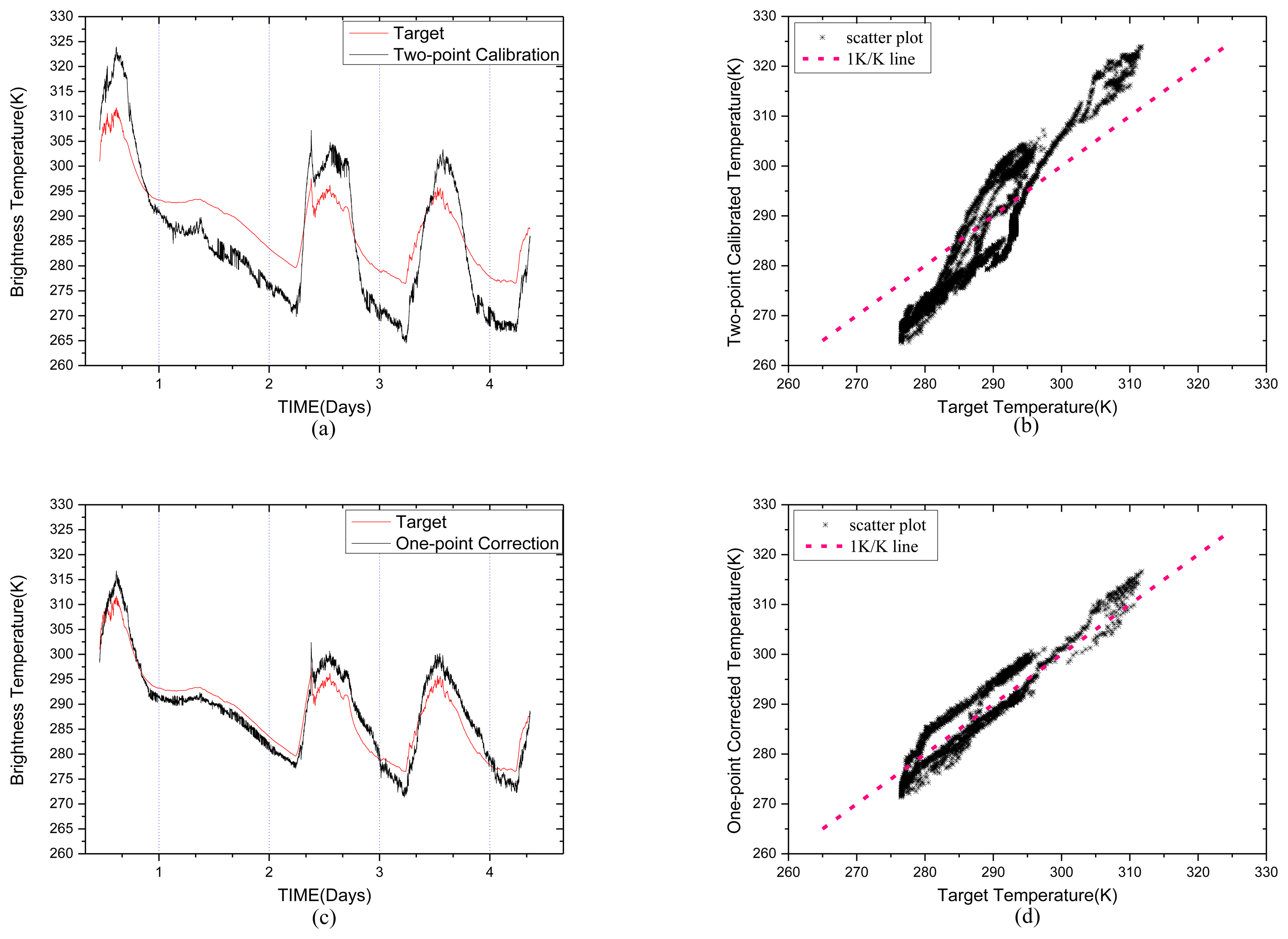
Figure 5c shows the one-point corrected temperature curve. We can see that the one-point correction method can compensate the effect caused by the variation of the environment temperature to a certain extent compared with the two-point calibration method. The RMSE of two-point calibration temperature is 7.3798 K, while the RMSE of the one-point corrected temperature is 3.0306 K. Figure 5b,d show the scatter points of the estimated temperature using the two methods above respectively. The correlation coefficients are 0.945 in Figure 5b and 0.952 in Figure 5d.
We use the temperatures of the units shown in Figure 4 and the measurement error to extract coefficients of the multi-point temperature correction equation by least squares method. The corrected calibration equation is:
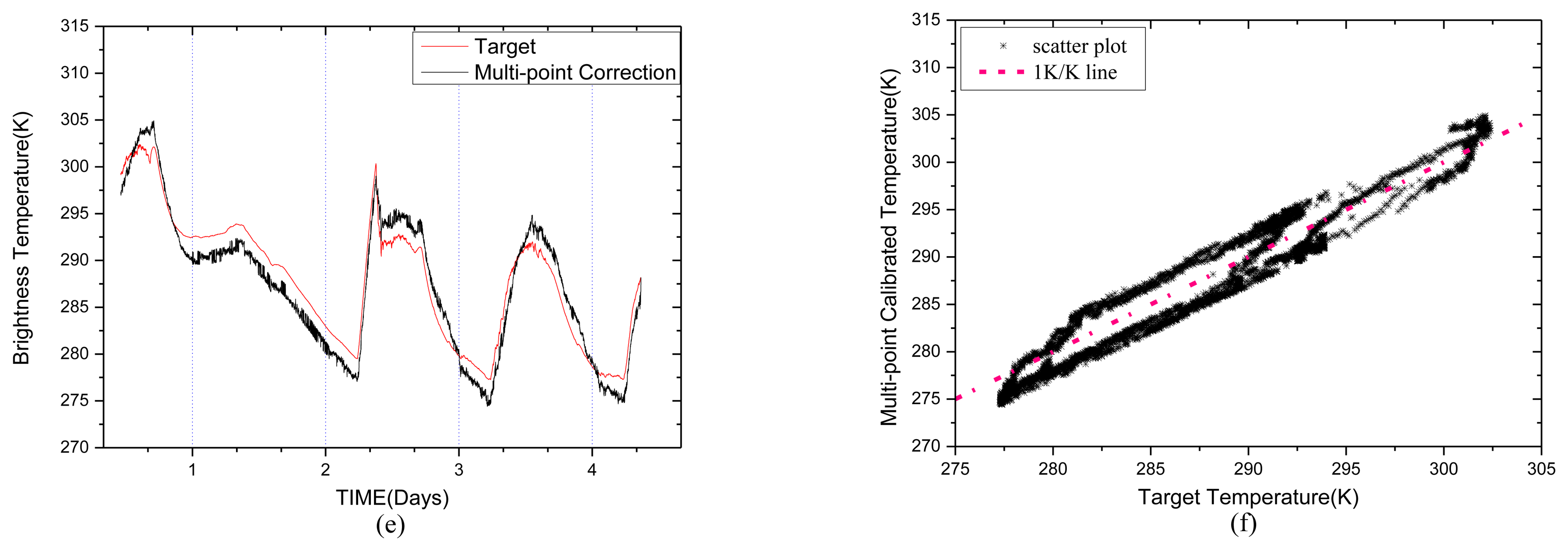
The results of the corrected calibration are shown in Figure 5e,f. The RMSE is 1.8426 K, and the correlation coefficient is 0.9764.
3.2. Results of 90° Antenna Channel
The black body target physical temperature and the brightness temperature estimated by the two-point calibration method are shown in Figure 6a. The temperature of the target ranges from 277 K to 302 K. The uncorrected two-point calibration equation is:
The relationship between the temperature of reference source TNS and the measurement error ΔTB90 is:
The one-point temperature correction equation can be expressed as:
Figure 6c shows the curve of one-point corrected temperature. The RMSE of two-point calibration temperature is 5.6248 K, while the RMSE of the one-point corrected temperature is 2.6740 K. Figure 6b,d show the scatter points of the estimated temperature using the two methods above respectively. The correlation coefficients are 0.918 in Figure 6b and 0.943 in Figure 6d.
We can extract coefficients of the multi-point temperature correction equation by least squares method using the temperatures of the units and the measurement error. The corrected calibration equation is:
The results of the corrected calibration are shown in Figure 6e,f. The RMSE is 2.0433 K, and the correlation coefficient is 0.965.
4. Conclusions
This paper introduces a new type Ka-band airborne double-antenna microwave radiometer for detecting atmospheric supercooled water content. Although the auto-gain compensative technique can eliminate the effect of the system gain fluctuation and greatly simplify the structure of the radiometer receiver, it also imports measurement errors when the radiometer operates in varying temperature environments. For this reason, we propose a new multi-point temperature correction method and carried out a long-term outdoor temperature experiment with the radiometer. The results demonstrate that the temperatures of the two antenna channels corrected by using this method have higher correlation with the target temperatures than the uncorrected two-point calibration and the one-point temperature correction methods. Since the brightness temperature is the key parameter for retrieving SCWC, it is important to obtain highly accurate flight observation brightness temperature data. This new multipoint correction method will be able to eliminate the effect of the dramatic changes caused by the aircraft cabin temperature on the airborne radiometer and improve SCWC retrieval accuracy effectively in further flight observation experiments.
Acknowledgments
This research is supported by the Main Direction Program of Knowledge Innovation of Chinese Academy of Sciences (KZCX2-YW-JS30).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wang, J.R.; Newton, R.W.; Rouse, J.W. Passive Microwave Remote Sensing of Soil Moisture: The Effect of Tilled Row Structure. IEEE Trans. Geosci. Rem. Sens. 1980, GE-18, 296–302. [Google Scholar]
- Karstens, U.; Simmer, C.; Ruprecht, E. Remote Sensing of Cloud Liquid Water. Meteorol. Atmos. Phys. 1994, 54, 157–171. [Google Scholar]
- Njoku, E.G.; Jackson, T.J.; Lakshmi, V.; Chan, T.K. Soil Moisture Retrieval from AMSR-E. IEEE Trans. Geosci. Rem. Sens. 2003, 41, 215–229. [Google Scholar]
- Ulaby, F.T.; Moore, R.K.; Fung, A.K. Radiometer system. In Microwave Remote Sensing (Active and Passive); Addison-Wesley: Reading, MA, USA, 1981; Volume 1, pp. 344–431. [Google Scholar]
- Thompson, D.A.; Rogers, R.L.; Davis, J.H. Temperature Compensation of Total Power Radiometer. IEEE Trans. Microw. Theory Tech. 2003, 51, 2073–2078. [Google Scholar]
- Chae, C.S.; Kwon, J.H.; Kim, Y.H. A Study of Compensation for Temporal and Spatial Physical Temperature Variation in Total Power Radiometers. IEEE Sens. J. 2012, 12, 2306–2312. [Google Scholar]
- Dicke, R.H. The Measurement of Thermal Radiation at Microwave Frequencies. Rev. Sci. Instrum. 1946, 17, 268–275. [Google Scholar]
- Machin, K.E.; Ryle, M.; Vonberg, D.D. The Design of an Equipment for Measuring Small Radio Frequency Noise Powers. Proc. IEE (Lond.) 1952, 99, 127–134. [Google Scholar]
- Goggins, W.B. A microwave feedback radiometer. IEEE Trans. Aerosp. Electron. Syst. 1967, AES-3, 83–90. [Google Scholar]
- Hach, J.P. A very Sensitive Airborne Microwave Radiometer Using Two Reference Temperatures. IEEE Trans. Microwave Theory 1968, 16, 629–636. [Google Scholar]
- Zhang, J.R.; Zhao, K. Digital Gain Compensative Microwave Radiometer. Patent CN96220486.2, 1996. [Google Scholar]
- Zheng, X.M.; Zhao, K.; Zhang, S.W. Results of Roil Moisture Inversion from Radiometer Biased by Periodic Change of Row Structure on Farmland. J. Remote Sens. 2012, 16, 1310–1330. [Google Scholar]
- Luan, H.; Zhao, K. Correction Technique of Environmental Temperature Change for Digital Auto Gain Compensative Microwave Radiometer. J. Infrared Millim. Waves 2008, 27, 143–146. [Google Scholar]
- Sun, J.; Zhao, K.; Jiang, T.; Gu, L.J. A new airborne Ka-band double-antenna microwave radiometer for cloud liquid water content measurement. Proceedings of SPIE International Symposium on Optical Engineering + Applications, San Diego, CA, USA, 25 August 2013.
- Zhou, J.; Lei, H.C.; Ji, L. Improvement of Liquid Water Content Retrieval Accuracy by Multilevel Detection in Cloud Tomography. J. Atmos. Ocean Technol. 2013, 30, 301–312. [Google Scholar]
- Sun, H.Y.; Zhao, K. Study of Noise Coupled Digital Auto-Gain Compensative Microwave Radiometer. J. Beijing. Univ Posts Telecommun 2007, 30, 100–104. [Google Scholar]
- Zhou, J.; Lei, H.C.; Chen, H.B.; Wang, Y.F.; Ji, L. Retrieval of Cloud Liquid Water Content Distribution At Vertical Section for Microwave Radiometer Using 2D Tomography. Chin. J. Atmos. Sci. 2010, 5, 1011–1025. [Google Scholar]




| Frequency (GHz) | Bandwidth on IF (MHz) | Noise Figure (dB) | Sensitivity (K) | Linearity | Integration Time (ms) | Range of Measurement Temperature (K) | Stability (K) |
|---|---|---|---|---|---|---|---|
| 31.65 | 400 | ≤5 | ≤0.2 | r ≥ 0.9995 | 300 | 10–350 | ≤1 |
| Antenna Type | Antenna Aperture (mm) | Antenna Gain (dB) | 3 dB Beam Width (deg) | Antenna Sidelobe Level (dB) | VSWR |
|---|---|---|---|---|---|
| Dielectric Lens | 250 | ≥32 | 4.2 | ≤ −32 | ≤1.3 |
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Sun, J.; Zhao, K.; Jiang, T. A Multipoint Correction Method for Environmental Temperature Changes in Airborne Double-Antenna Microwave Radiometers. Sensors 2014, 14, 7820-7830. https://doi.org/10.3390/s140507820
Sun J, Zhao K, Jiang T. A Multipoint Correction Method for Environmental Temperature Changes in Airborne Double-Antenna Microwave Radiometers. Sensors. 2014; 14(5):7820-7830. https://doi.org/10.3390/s140507820
Chicago/Turabian StyleSun, Jian, Kai Zhao, and Tao Jiang. 2014. "A Multipoint Correction Method for Environmental Temperature Changes in Airborne Double-Antenna Microwave Radiometers" Sensors 14, no. 5: 7820-7830. https://doi.org/10.3390/s140507820




