The Dual Carrier ABSK System Based on a FIR Bandpass Filter
Abstract
: The special impacting filter (SIF) with IIR structure has been used to demodulate ABSK signals. The key points of SIF, including the resonance circuit's high Q value and the “slope-phase discrimination” character of the filter sideband, are demonstrated in the paper. The FIR narrow-band bandpass filtering system, which can also provide the impact-filtering effect, is proposed. A dual carrier system of ABSK signals is designed with the proposed FIR filter as its receiver. The simulation results show that the FIR filter can work well. Moreover, compared to the traditional SIF, the proposed FIR filter can not only achieve higher spectral efficiency, but also give better demodulation performance.1. Introduction
With the rapid development of information technology, the traditional wireless communication systems which employ wasteful static spectrum allocation can no longer take full advantage of the spectrum. Meanwhile, the radio spectrum has become more and more complicated and fragmented. Therefore numerous efficient transmission techniques have been proposed to maximize utilization of the spectrum, which could also provide remarkable economic benefits [1–6].
The Asymmetry Binary Shift Keying (ABSK) modulation [7], proposed by Wu, is a typical kind of efficient transmission technique. There are two types of the modulation: the Extended Binary Phase Shift Keying (EBPSK) modulation and the EBPSK with Continuous Phase (CP-EBPSK) modulation. The modulation waveforms corresponding to code “0” and “1” have very tiny differences, which could be erased by a traditional finite impulse response (FIR) or infinite impulse response (IIR) filter. Therefore a special filter, called special impacting filter (SIF) [8], has been proposed for use as their receiver. The SIF with narrow bandwidth can produce high impact at the phase jumping point of the ABSK modulation waveform and greatly improve the output SNR, so threshold decision can be used next to the SIF to judge the code directly. Though the SIF receiver with IIR structure is easy to implement, the stabilization is not good. Because of the unstable performance of the SIF, we consider a FIR narrow-band bandpass filtering system instead.
2. The Mechanism of the SIF
Let H(s) be the system function, for the sake of notational simplicity, we denote:
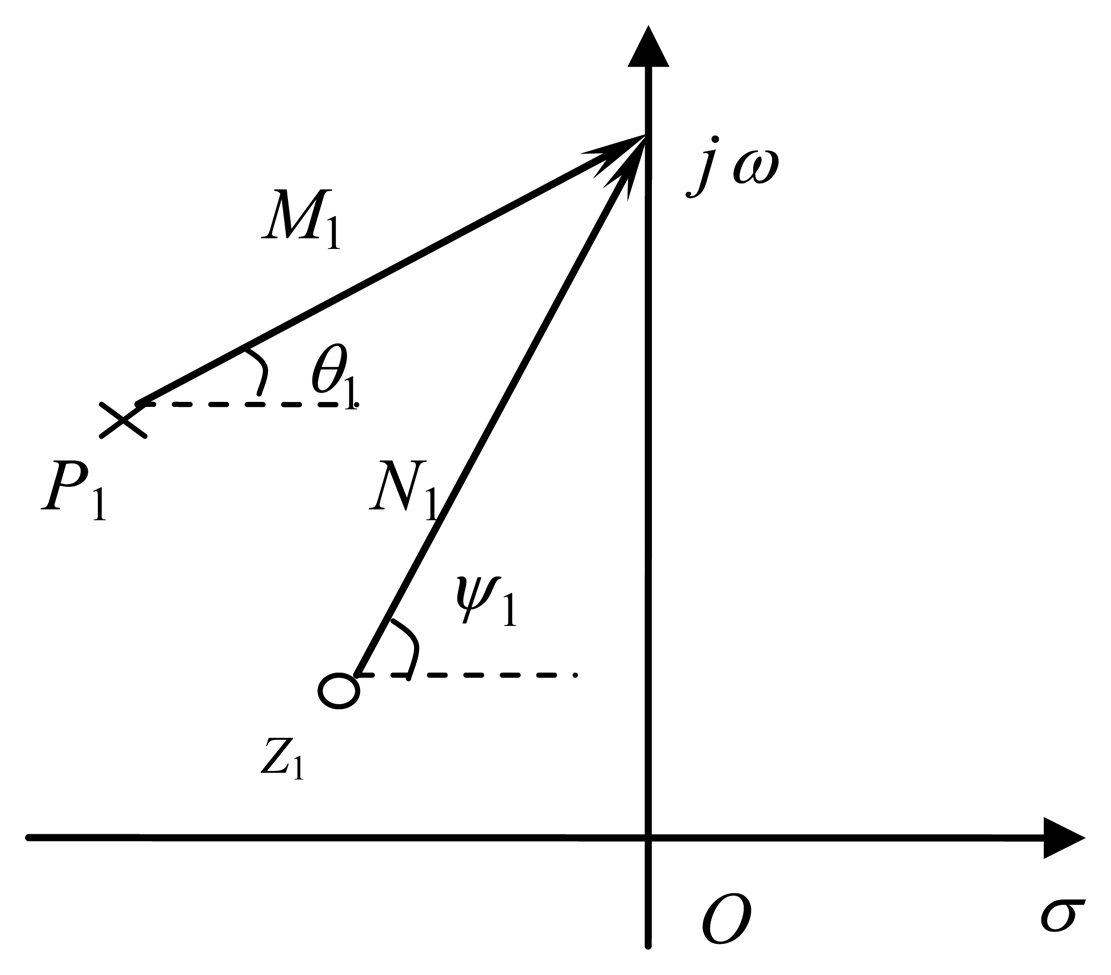
Note that the frequency response depends on the distribution of zeros and poles. The numerator and denominator mean the vectors from the zeros and poles to the point jω on the imaginary axis, respectively, as shown in Figure 1.
N1 and M1 are the modules of the vector respectively, ψ1 and θ1 are the angles of the vector respectively. Without loss of generality, the complex factors of zeros and poles are given by:
Equation (2) can be rewritten as:
is the system function's module;
φ(ω) = ej[(ψ1 + ψ2 +…+ ψm)−(θ1+θ2+…+θn)] is the phase.
With ω moving along the imaginary axis, the module and angle change as well, the relationship between module and phase could be explained by the following explanation. If the circuit has high Q value and the transfer function has a couple of poles and zeros adjacent to the imaginary axis respectively, that is:
The amplitude-frequency response reach a peak and the phase-frequency response decrease rapidly when the poles approaching the point ω = ωi; when the zeros approach the point ω = ωj, the result is just the opposite, as shown in Figure 2a,b, respectively.
So we conclude that the steeper transitional band of the amplitude-frequency curves, the steeper of the phase-frequency curves [9]. If the frequency fd is located in the biggest slope of the phase-frequency curve, the tiny change of phase will bring big change of the frequency. The big range frequency shift mapping in the amplitude-frequency curves would show the amplitude changes fiercely, we call it “slope-phase discrimination”.
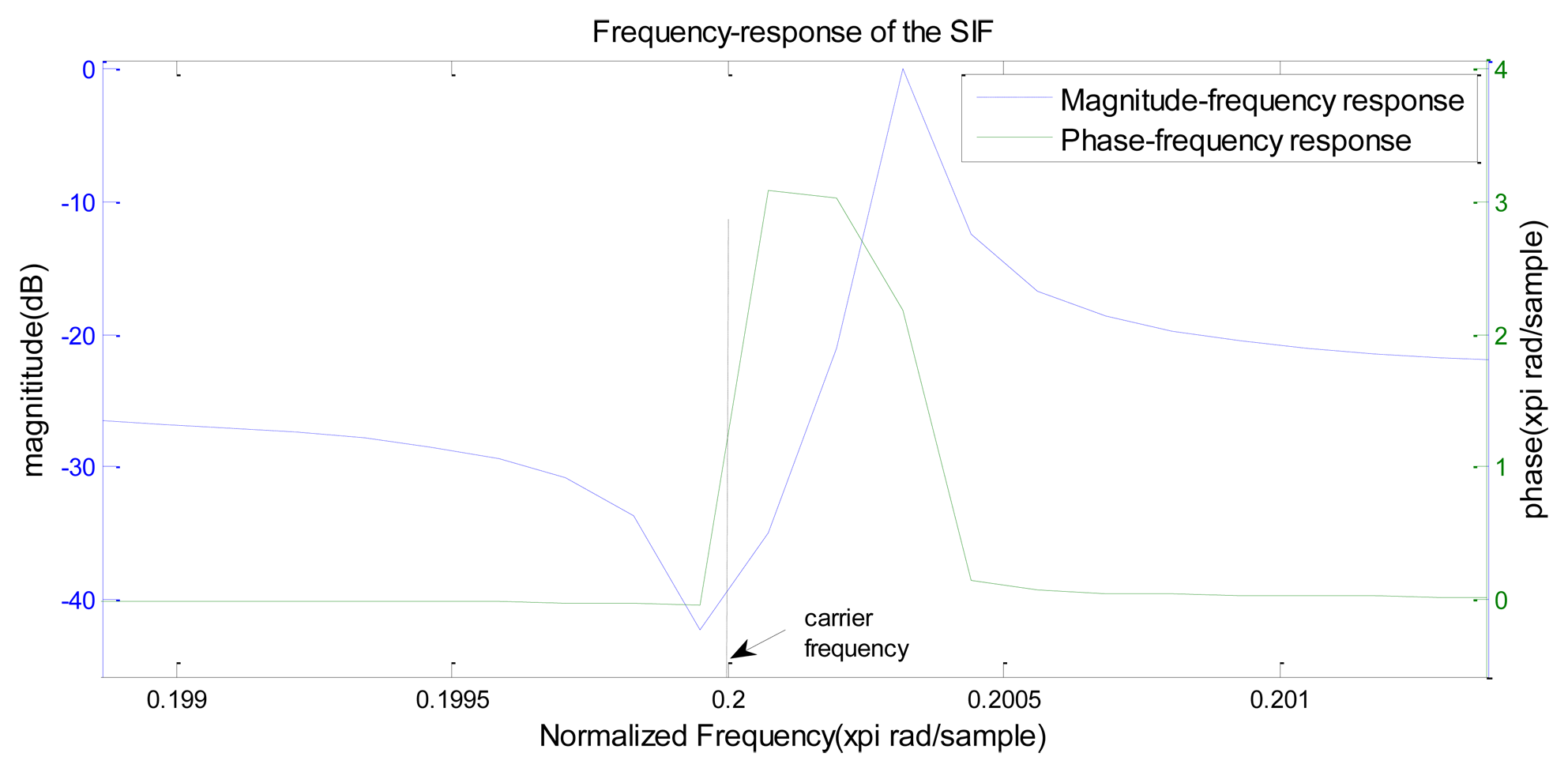
At present the SIR which has one or more conjugate zeros and multi-poles is adopted to be used as ABSK signal receiver. The zeros are located on the unit circle; the poles are close to the imaginary axis, so the IIR impacting filter has very high Q value and steep resonance peak, as well as high frequency selectivity. The ideal phase-frequency curve of the impacting filter has its steepest slope near the carrier frequency, so as to achieve differential effects on the ABSK signal phase. The tiny change of the carrier's phase can bring about obvious amplitude changes. For an ABSK signal, if the codes “0” and “1” have the same amplitude, the ABSK signal is a PM signal. When the frequency of the carrier is located between the zeros and poles, i.e., the steepest part of the filter's phase-frequency curve, the ABSK signal can achieve the magnitude impact after filtering. Figure 3 shows the magnification of one segment of the SIF's frequency response, where it can be seen that the SIF meets the requirements of “slope-phase discrimination”.
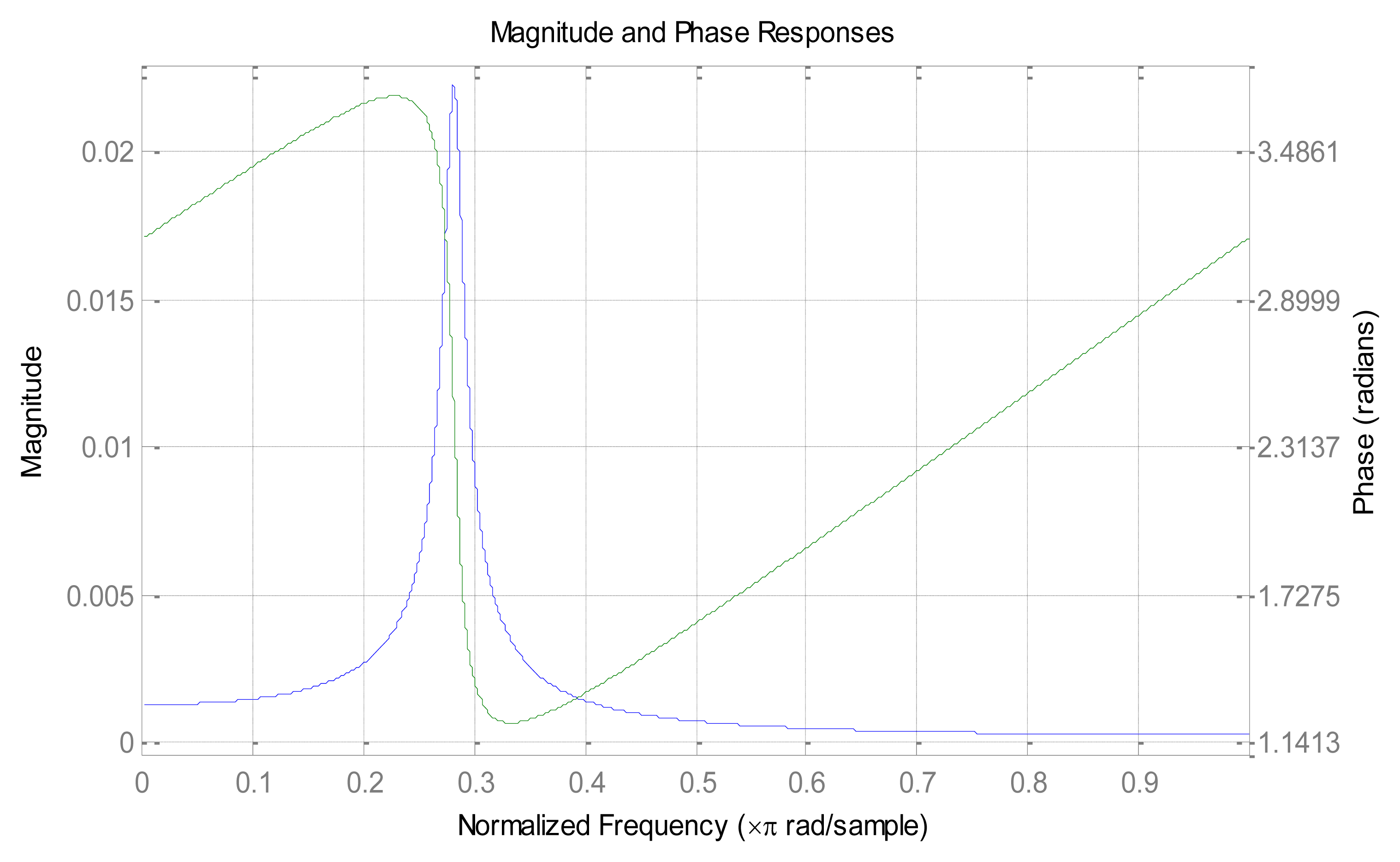
Based on the above description, there are two key points for the impacting effect: the “slope-phase discrimination” character and the high Q value of resonance circuit. We know that the bandwidth of transmission signal is inversely proportional to the Q value, and thus a larger Q value can lead to narrower transmission bands and better circuit selectivity. Because the FIR narrow-band filter has natural steep transmission bands, we can infer that the ABSK signal's carrier frequency can be placed on the steepest slope of the transmission bands to obtain the “slope-phase discrimination” effect. The frequency response of the FIR narrow-band filter satisfies the condition of “slope-phase discrimination”, as shown in Figure 4.
Figure 5 shows the impacting effect of the FIR narrow-band filter. It can be seen that the code “1” can be impacted after filtering, whether the carrier frequency is located in the left or right transmission bands of the FIR filter.
3. FIR Narrow-Band Bandpass Filtering System
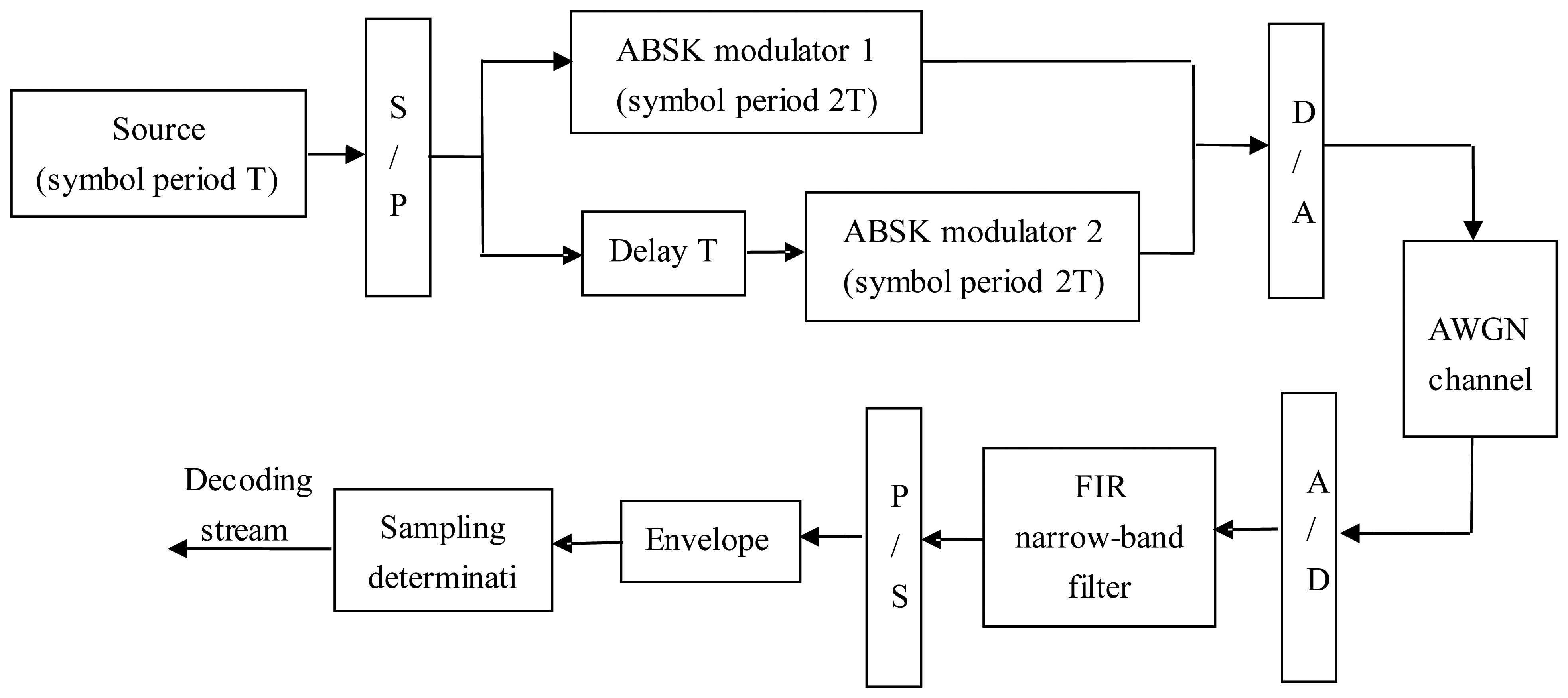
In order to increase the transmission rate and restrain the inter-symbol and multipath interference, the practical communication system usually use the multi-carrier parallel transmission, such as OFDM, which decomposes the data flow to several sub-data flows, and thus the sub-data flows have much lower transmission rates. A multi-carrier ABSK communication system has been proposed in [10], where the receive filter bank contains at least two SIFs, and each sub-channel has one SIF cascading with at least one notch filter. The dual carrier ABSK communication system used in this paper has two subcarriers. The traditional demodulation of ABSK multi-carrier system is complex; each sub-channel has its own demodulation process, which includes SIF, carrier synchronization, sampling synchronization, bit synchronization, envelope detection, and sample decision respectively. Furthermore, the performance of the complex receiver with IIR structure is unstable. However, the impacting effect of FIR narrow-band filter shown in Figure 5 can be considered to replace the IIR SIF banks, and the dual-carrier ABSK communication system based on the FIR narrow-band filter is proposed as follows:
- (1)
At the transmission end, the respective data bits of the data sequence (denoted T as the symbol period, 2R bps data rate) was alternately modulated on the carrier frequency fc1 and fc2, respectively (denoted 2T as the new symbol period, R bps data rate). Set one sub carrier time-delay T to avoid the both carrier's “1” occurs simultaneously, i.e., make the two “1” to be frequency separation and time-division, in order to ensure the sparsity of the demodulated time signal;
- (2)
At the receiving end, the FIR narrow-band filter is used as receiver, as shown in Figure 4. The two carrier frequencies fc1 and fc2 were placed on the left and right transition bands of the steepest slope. Because of the “slope-phase discrimination” character of FIR sideband, symbol “1” can be impacted, and then the envelope detector outputs a 2R bps rate pulse, and realizes code rate doubled in one passband finally. Figure 6 shows the block diagram of the dual-carrier ABSK communication system with digital narrowband filter as its receiver.
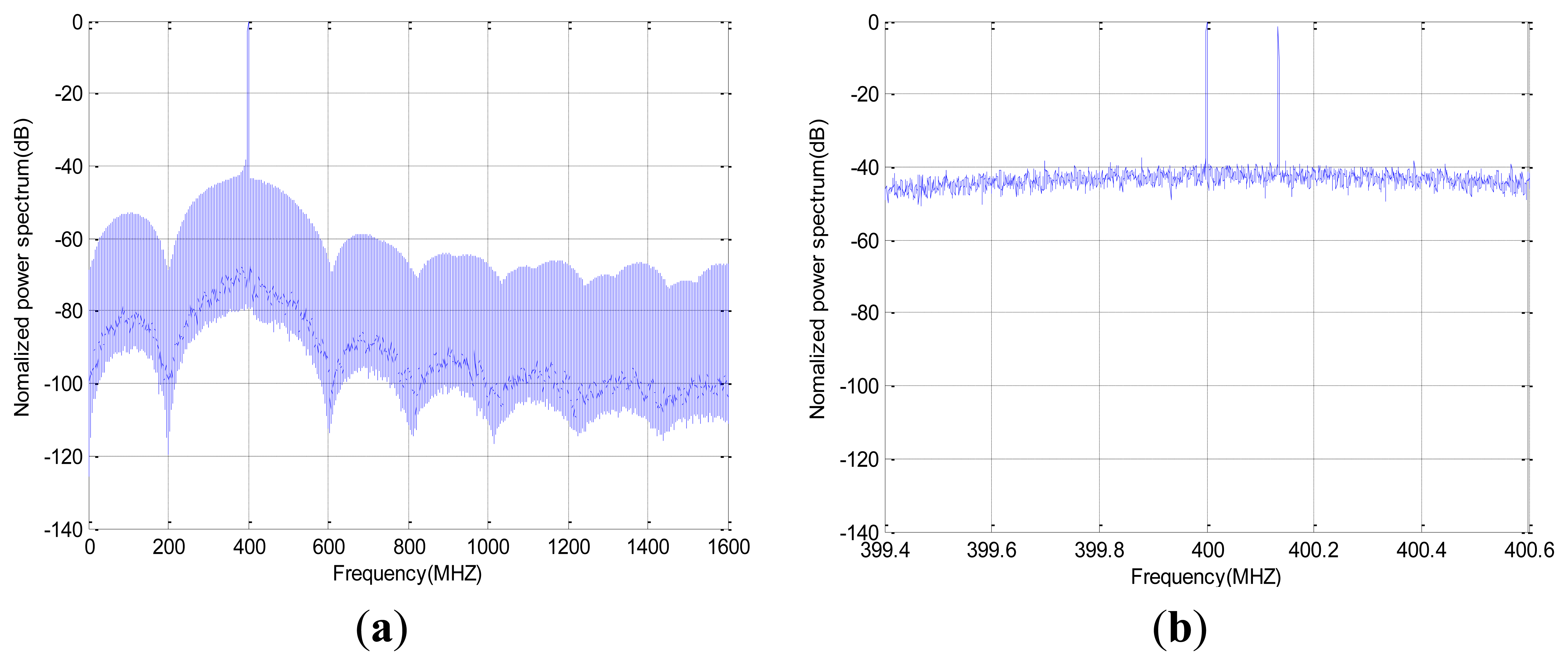
The dual-carrier ABSK signal's frequency spectrum is shown in Figure 7. It can be seen that the dual-carrier system has efficient usage of spectrum.
4. Simulation and Numerical Results
In our work, the EBPSK modulated signal is chosen as the transmit signal (set A = B = 1, θ = π) [11–16], which can be described as follows:
Let us consider the following specifications of the system:
Bit rate R = 1 M bps (symbol period T = 10−6 s);
Carrier frequency fc = 400 MHz;
The bit-rate of each sub-channel EBPSK signal is 0.5M bps, the parameters of the two modulated EBPSK signal are given by: fc1 = 400 MHz, K1:N1 = 2:400; fc2i = fc1 + Δfci, I = 1,2,3,4; Δfc1 = 0.002HMz, Δfc2 = 0.004 MHz, Δfc3 = 0.006 MHz, Δfc4 = 0.01Hz, the duty K2i:N2i changed with fc2i.
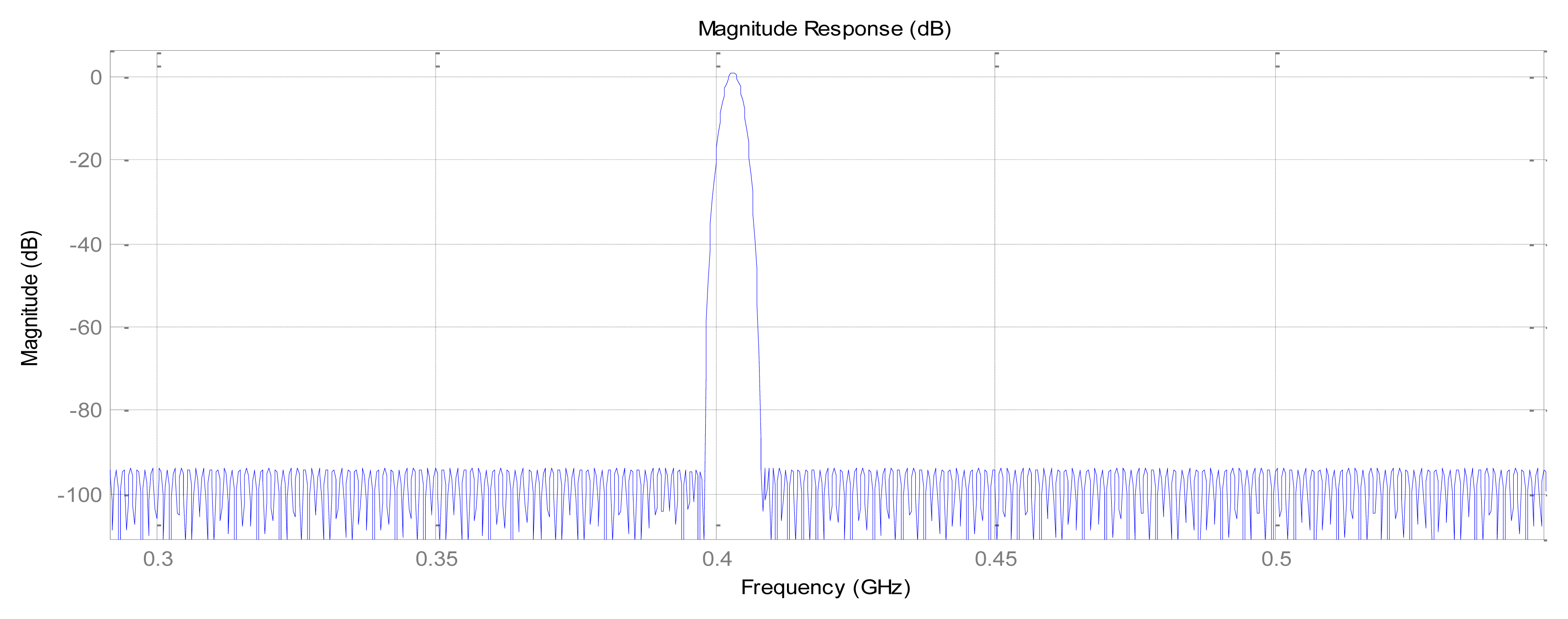
“Slope-phase discrimination” is mainly manifested in the dramatic changes of magnitude brought by the phase changes, so the construction of extremely steep narrow transition bands of the FIR filter is very necessary. The realization of the construction is through comprehensive selection of the pass-band frequency fpass, stop-band frequency fstop and pass stop-band attenuation coefficient apass and astop. Here, we present one design example of FIR narrow-band filter to demonstrate the effectiveness of the proposed principle. Set fc1 = 400 MHz, fc24 = 400.01 MHz, according to the above principles, Kaiser Window is chosen to realize the FIR filter, set fs = 1.2 GHz, transition bandwidth 0.005 MHz, pass stop-band fluctuations 0.01. Specific parameters: fstop1 = 399.999 MHz, fpass1 = 400.004 MHz, fpass2 = 400.006 MHz, fstop2 = 400.011 MHz, apass= −1 dB, astop1 = astop2 = −100 dB; the frequency response of the FIR narrow-band filter is shown in Figure 8, where it can be seen the steep slope of about 90° fluctuates near the transition bands.
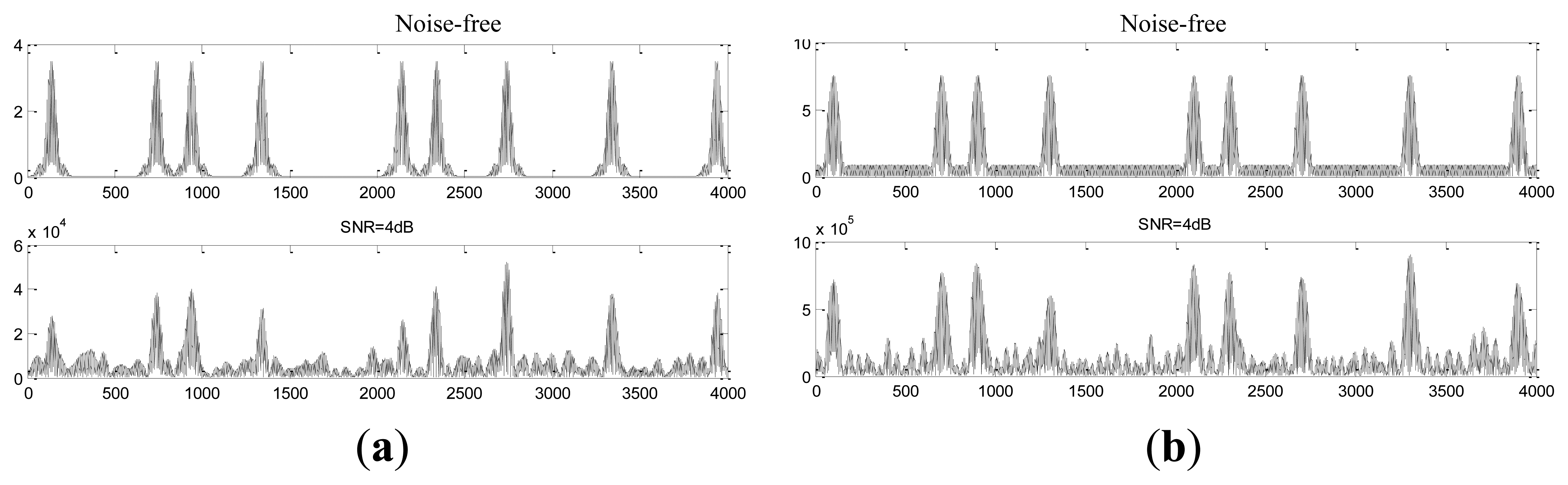
Let the two independent signals and their superposition signals pass the designed FIR narrow-bandpass filter, and the filtering results are shown in Figure 9. It can be seen the designed FIR narrow-bandpass filter could impact not only the single-carrier signal, but also the dual-carrier signals.
5. Performance
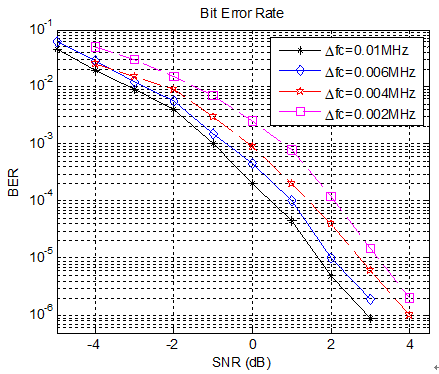
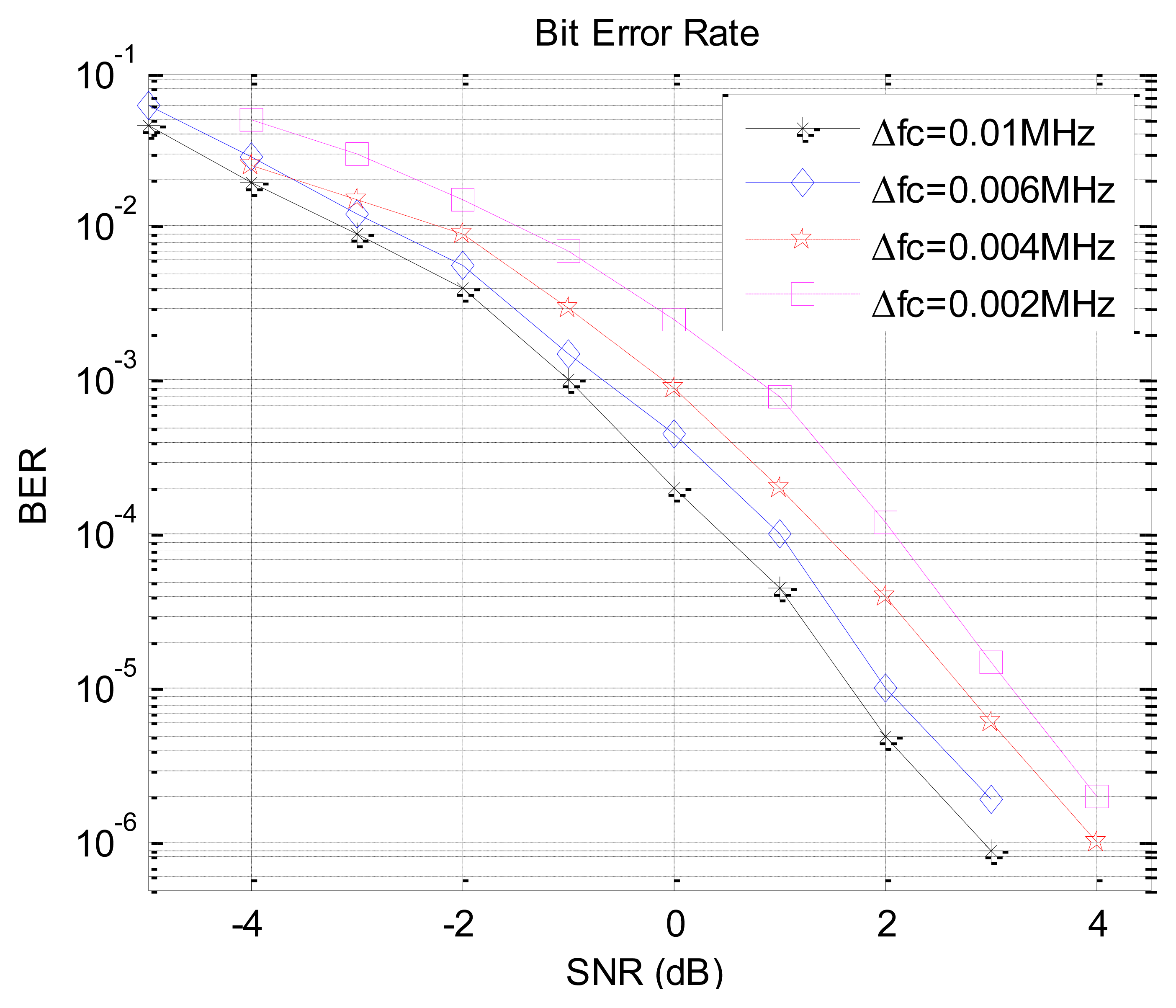
Without channel coding and bandpass shaping in the additive white Gaussian noise (AWGN) channel, the ADC sampling frequency of receiver is 1.2 GHz, and the proposed FIR narrow-band filter is used to filter the received signal. The BER performance of the EBPSK dual-carrier system is shown in Figure 10.
As shown in Figure 10, with the interval of fc1 and fc2i increasing, the mutual interference between two EBPSK signals becomes much lower and the system demodulation performance becomes much better. While the frequency interval is 0.01 MHz, the SNR (signal to noise ratio) sensitivity is 1.7 dB at the BER of 10−5. Even for the other three smaller carrier frequency spacing, the required SNR is no more than 4 dB.
6. System Performance Comparison with IIR SIF
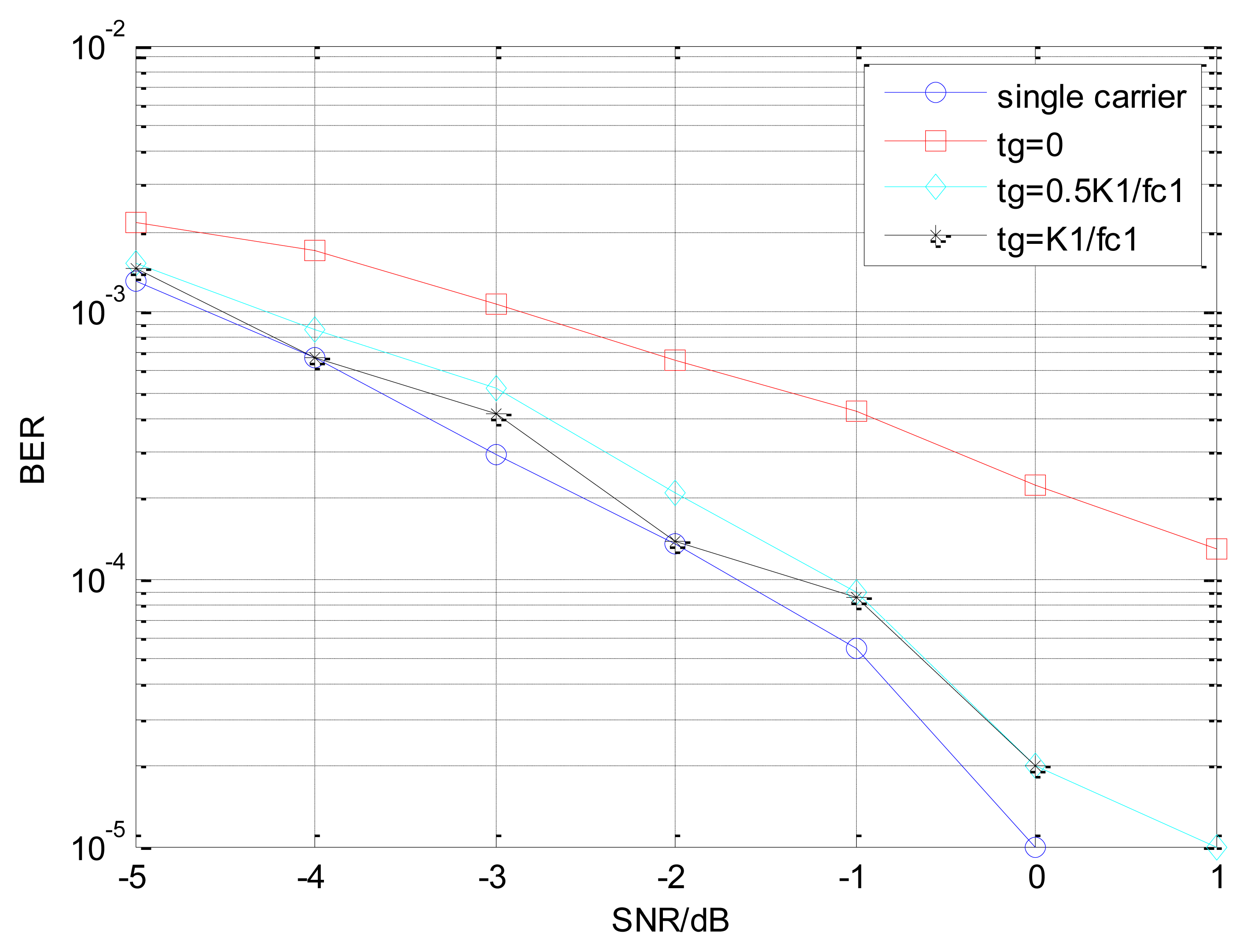
Figure 11 shows the BER performance of the dual-carrier system which adopts the time division method to demodulate the two channels, with the IIR SIF as its receiver. The carrier cycle of sub-carrier is same to the first carrier's, but the second channel has a transition delay tg. The system demodulates the two channels of signal respectively, which suppresses the one channel to demodulate another. The frequency interval between the dual-carrier is 0.1 MHz, and the tg of the second channel gets 0, 0.5 K1/fc1, K1/fc1 respectively. As shown in Figure 11, the BER performance becomes better when the time delay is increased. The BER performance of FIR narrow-bandpass filter system is almost the same as the IIR digital filter system, while tg = 0, but the structure of the former is much simpler.
7. Conclusions
Simulation results show that the proposed FIR narrowband filter used in the receiver can not only achieve high spectral efficiency, but also give excellent demodulation performance, compared to the previous IIR digital filter bank. The proposed filter also has the following advantages:
- (1)
Enhanced system stability: the receiver structure has been greatly simplified [17,18];
- (2)
Compared to the SIF, the proposed filter can quickly transit to the steady state with short transient waveform tail, so the FIR filter can reduce the inter-symbol interference and achieve higher bit rate;
- (3)
No feedback loop could discard the starting oscillation, which greatly enhance the transmission of small data packet communications efficiency;
We will next design a multi-rate narrowband FIR filter to achieve the performance of an elliptic IIR filter. To further improve the spectral efficiency, we consider using the comb filter at the receiver end to achieve greater capacity for intensive multi-carrier communication.
Acknowledgments
The authors would like to thank the support of the National Natural Science Foundation of China (NSFC), under the Grant 61271204 and 61302096. The work is supported by the National Key Technology R&D Program under the grant 2012BAH15B02.
Author Contributions
Zhimin Chen and Lenan Wu conceived and designed the study. Zhimin Chen and Jiwu Wang performed the experiments and wrote the paper. Zhimin Chen reviewed and edited the manuscript. All authors read and approved the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Walker, H.R. VPSK and VMSK Modulation Transmit Digital Audio and Video at 15 Bits/sec/Hz. IEEE Trans. Broadcast Eng 1997, 43, 96–103. [Google Scholar]
- Walker, H.R. Digital Modulation Device in a System and Method of Using the Same U.S. Patent 6,445,737, 3 September 2002.
- Bobier, J.A. Missing Cycle Based Carrier Modulation. U.S. Patent 6,968,014, 22 November 2005. [Google Scholar]
- Zheng, G.; Feng, J.; Jia, M. Very Minimum Chirp Keying as a Novel Ultra Narrow Band Communication Scheme. Proceedings of the 6th International Conference on Information, Communications & Signal Processing, Singapore, 10–13 December 2007.
- Zheng, G.X.; Yang, W.Y. The Orthogonal Very Minimum Chirp Keying (OVMCK) Modulations with Very High Bandwidth Efficiency. Proceedings of IEEE Antennas and Propagation Society International Symposium, San Diego, CA, USA, 5–11, July 2008; pp. 3182–3185.
- Li, B.; Zhou, Z.; Zou, W. RPPK modulation with high data rates. Sci. China Inf. Sci 2010, 53, 344–354. [Google Scholar]
- Wu, L.; Feng, M.; Qi, C.; He, F. Recent patents on ultra narrow band modulations. Recent Pat. Signal Process 2011, 1, 36–47. [Google Scholar]
- Feng, M.; Gao, P.; Wu, L. Analysis and simulation of special filtering based on ultra narrow band modulated signal. J. Southeast Univ. Nat. Sci. Ed 2010, 40, 227–230. [Google Scholar]
- Oppenheim, A.V. Signals and Systems, 2nd ed.; Xi'an Jiaotong University Press CO., LTD.: Shanxi, China, 1999; pp. 302–370. [Google Scholar]
- Chen, Z.; Wu, L.; Chen, X. The impacting filter bank design for MCP-EBPSK multicarrier demodulation. J. Signal Process 2012, 28, 1063–1068. [Google Scholar]
- Feng, M.; Wu, L.; Gao, P. From special analogous crystal filters to digital impacting filters. Digit. Signal Process 2012, 22, 690–696. [Google Scholar]
- Chen, X.; Wu, L. Nonlinear detection for a high rate extended binary phase shift keying system. Sensors 2013, 13, 4327–4347. [Google Scholar]
- He, F.; Wu, L. Analysis of Power Spectrum of Continuous Phase Waveforms for Binary Modulation Communications. Proceedings of the International Conference on Ultra Modern Telecommunications & Workshops, St. Petersburg, Russia, 12–14 October 2009.
- Man, F.; Wu, L. High efficiency transmission scheme based on improved CP-EBPSK modulation. Proceedings of the 8th International Conference on Computing Technology and Information Management, Seoul, Korea, 24–26 April 2012.
- Jin, Y.; Wu, L.; Feng, M.; Deng, L. An MCP-EBPSK modem with random-polar. J. Electron. Inf. Technol 2012, 34, 1647–1652. [Google Scholar]
- Jin, Y.; Wu, L.; Feng, M.; Deng, L. An M-ary and continuous phase modem with random-polar. Chin. J. Radio Sci 2012, 27, 931–936. [Google Scholar]
- Jin, Y.; Wu, L.; Chen, Y.; Yu, J. Design of digital impacting filter in CP-EBPSK with random-polar communication system. J. Electron 2012, 29, 28–333. [Google Scholar]
- Wang, H.; Wang, H.; Mao, Z.; Wang, Y. An Ultra Narrow Bandwidth Demodulation Algorithm Based on Time-Frequency Distribution. Telecommun. Eng 2010, 50, 43–46. [Google Scholar]


© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Chen, Z.; Wu, L.; Wang, J. The Dual Carrier ABSK System Based on a FIR Bandpass Filter. Sensors 2014, 14, 5644-5653. https://doi.org/10.3390/s140305644
Chen Z, Wu L, Wang J. The Dual Carrier ABSK System Based on a FIR Bandpass Filter. Sensors. 2014; 14(3):5644-5653. https://doi.org/10.3390/s140305644
Chicago/Turabian StyleChen, Zhimin, Lenan Wu, and Jiwu Wang. 2014. "The Dual Carrier ABSK System Based on a FIR Bandpass Filter" Sensors 14, no. 3: 5644-5653. https://doi.org/10.3390/s140305644
APA StyleChen, Z., Wu, L., & Wang, J. (2014). The Dual Carrier ABSK System Based on a FIR Bandpass Filter. Sensors, 14(3), 5644-5653. https://doi.org/10.3390/s140305644