Analytical Calculation of Sensing Parameters on Carbon Nanotube Based Gas Sensors
Abstract
: Carbon Nanotubes (CNTs) are generally nano-scale tubes comprising a network of carbon atoms in a cylindrical setting that compared with silicon counterparts present outstanding characteristics such as high mechanical strength, high sensing capability and large surface-to-volume ratio. These characteristics, in addition to the fact that CNTs experience changes in their electrical conductance when exposed to different gases, make them appropriate candidates for use in sensing/measuring applications such as gas detection devices. In this research, a model for a Field Effect Transistor (FET)-based structure has been developed as a platform for a gas detection sensor in which the CNT conductance change resulting from the chemical reaction between NH3 and CNT has been employed to model the sensing mechanism with proposed sensing parameters. The research implements the same FET-based structure as in the work of Peng et al. on nanotube-based NH3 gas detection. With respect to this conductance change, the I–V characteristic of the CNT is investigated. Finally, a comparative study shows satisfactory agreement between the proposed model and the experimental data from the mentioned research.1. Introduction
To date, numerous gases have been found to be harmful to organic life. These materials are difficult to observe and sense due mainly to their gaseous nature. Therefore, a sensor or detection system is an essential component in environments where these gases are in the ambient air and human presence is unavoidable e.g., chemical material production settings, etc. [1–4]. The term nanomaterial refers to structures with at least one dimension between 1 and 100 nm. When these materials are appropriately engineered, they present a variety of outstanding and adjustable chemical and physical properties [5–7]. The range of applications where nanomaterials are used is rapidly growing as it is possible to control and manipulate their structures and this has led to the creation of unique and novel research fields in the nanotechnology area. Enhanced characteristics and functions as well as the creation of new materials are among the major outcomes of research into the subject matter [8,9]. In addition, these materials have been given extensive attention in developing industries and technologies due to their exceptional physical properties such as electrical and thermal conductivity, high physical strength and high surface-to-volume ratios which in turn allow for their application in biological, medical and chemical settings [3,10–12]. From an industrial perspective, the practical use of these nanomaterials has resulted in remarkable improvements in mechanical, electrical, optical and magnetic properties and has revolutionized the fields in which these properties can be applied [13].
Carbon nanotubes (CNTs), also known by some researchers as “buckytubes” [14] are among the most interesting classes of nanomaterials as they possess outstanding characteristics including high strength, large electrical and thermal conductivity as well as rigidity and high surface to volume ratios [15,16].
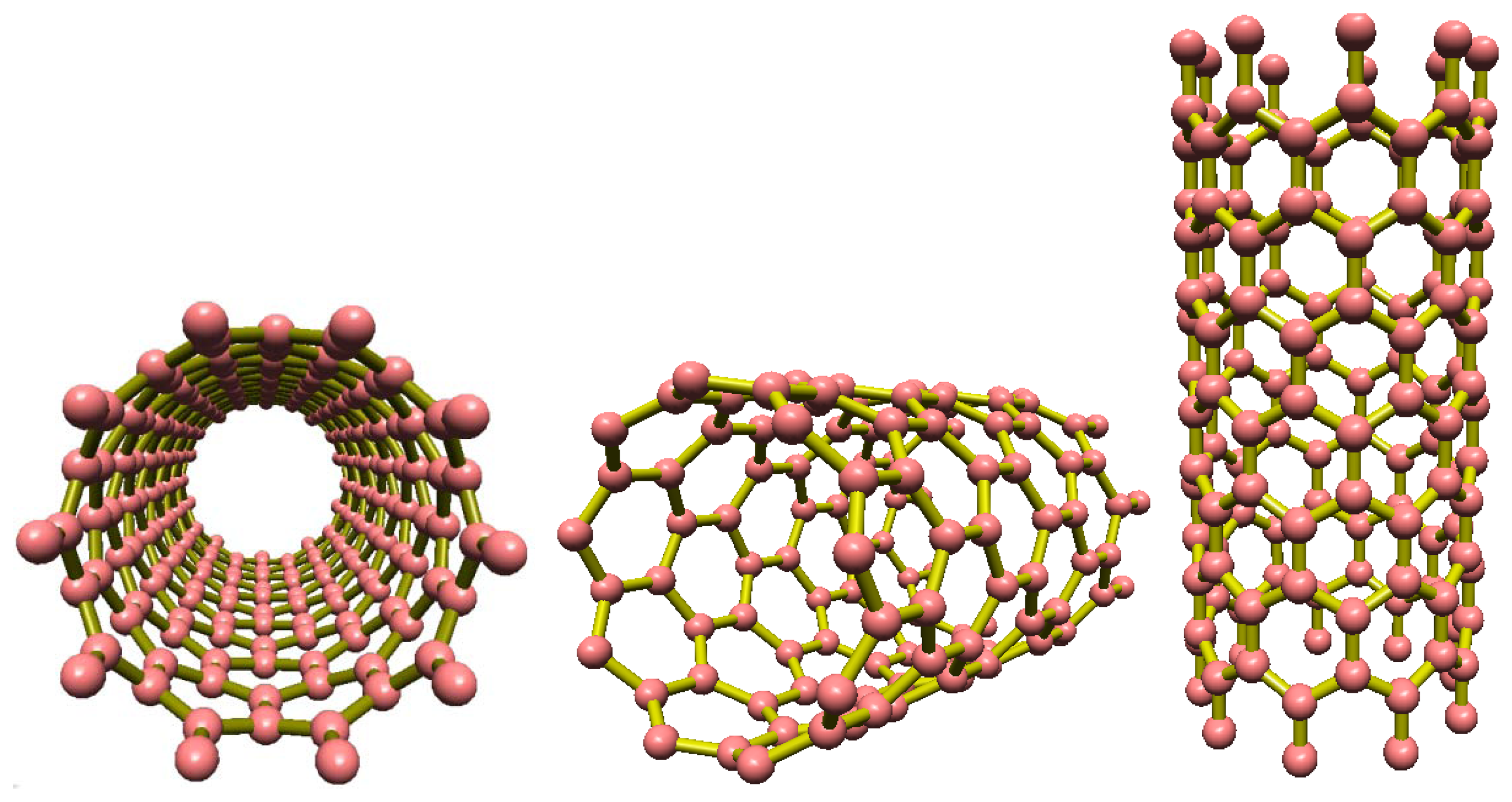
As shown in Figure 1, a single-walled carbon nanotube (SWCNT) is a single layer of carbon atoms formed into a cylindrical network of connected atoms resulting in a tube with a diameter measured in nanometers and a length measured on a micrometer scale [17–19]. The aforementioned properties along with additional features such as small size and high electrical sensitivity make CNTs ideal candidates for use as nanosensors. Experimental and theoretical studies reveal that these nanometer sized CNTs exhibit unique electrical characteristics making them metallic or semiconducting based on their radial dimensions and chiralities [20,21]. More specifically, SWCNTs have the proven ability to sense different small molecules such as NO2, NH3, HCl, Cl2, etc. One suitable configuration for the use of carbon nanotubes in measuring devices is one in which the CNT is placed as an electrical wire between two electrodes. By applying a specific gate bias voltage, CNT conductance is used as the measured variable. Mechanical deformations [22] and/or chemical doping can significantly affect conductance as the CNT electrical properties are heavily dependent upon the atomic structure. Such variations in electrical properties can be easily detected by measuring the electric current. This makes CNTs valuable minute sensors able to detect changes in their environment as they have already been employed in highly sensitive electronic molecule detections [23,24]. In this article, a basic model of how CNTs can be used in gas detection applications has been proposed and the results from the suggested mathematical model are compared with those obtained from the experimental works of other researchers implementing a similar framework. The applicability of the proposed model is validated by the satisfactory agreement of our findings with the experimental data [25].
1.1. Carbon Nanotube FETs
It is a well-known fact that the characteristics of carbon nanotubes are strongly dependent on their physical properties such as diameter and chirality [26]. For instance, carbon nanotubes can be either single-walled or multi-walled with varying inherent bandgaps. Based on the chirality of their structure, single-walled nanotubes can be either metallic conductors or semiconductors. Semiconducting SWCNTs can be used in the fabrication of FET devices able to operate at room temperature and in ambient conditions [27].
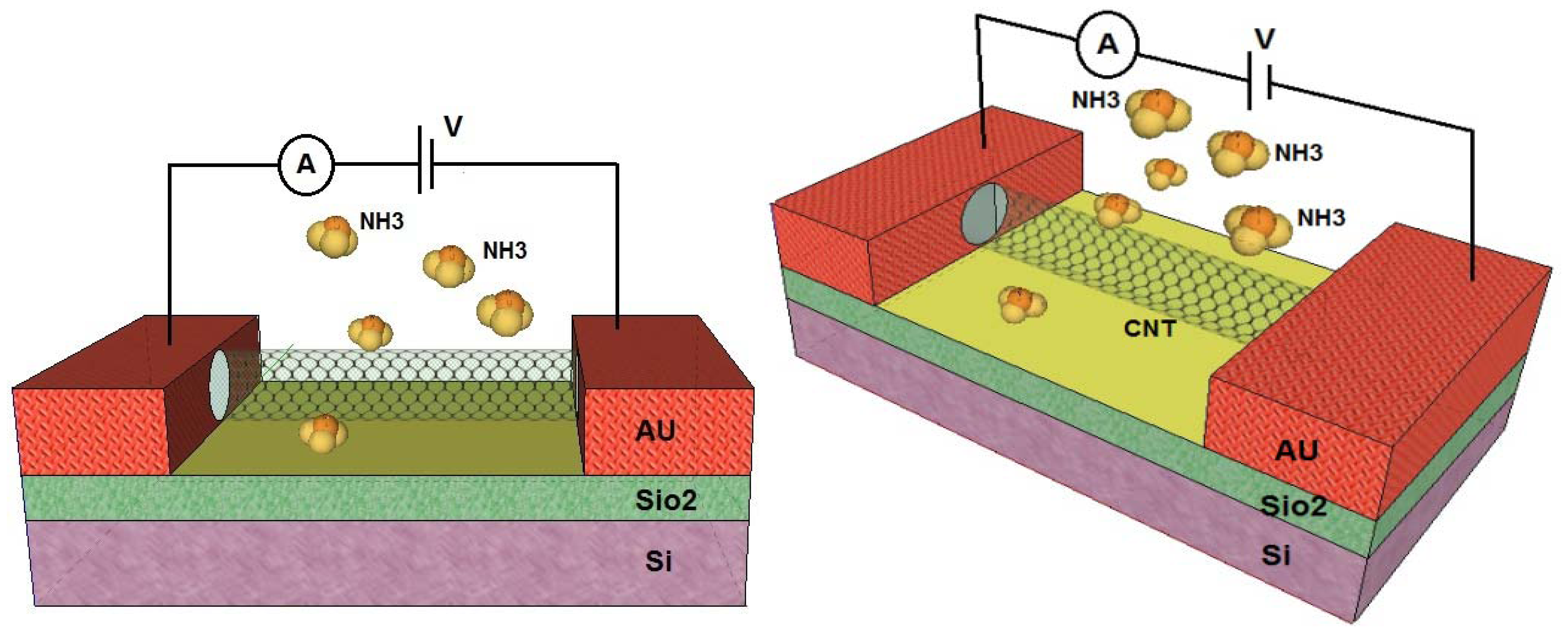
Semiconducting SWCNTs have been shown to exhibit significant changes in conductance in response to different gases. As can be seen in Figure 2, the structure of the proposed gas sensor using CNTs as the conducting channel looks quite similar to conventional metal-oxide semiconductor field effect transistors (MOSFETs) which comprise a source metal, a drain metal, a silicon back gate and the gate insulator [18,19,28]. A CNT channel connects the source and drain electrodes, and the gate is separated from the channel by a dielectric barrier layer. In most studies, SiO2 acts as a dielectric layer while silicon is employed as the back gate [29]. When gas molecules are in contact with the CNT surface, carrier concentration will change due to the variability of the current in the drain and the source which is a measurable parameter [30,31].
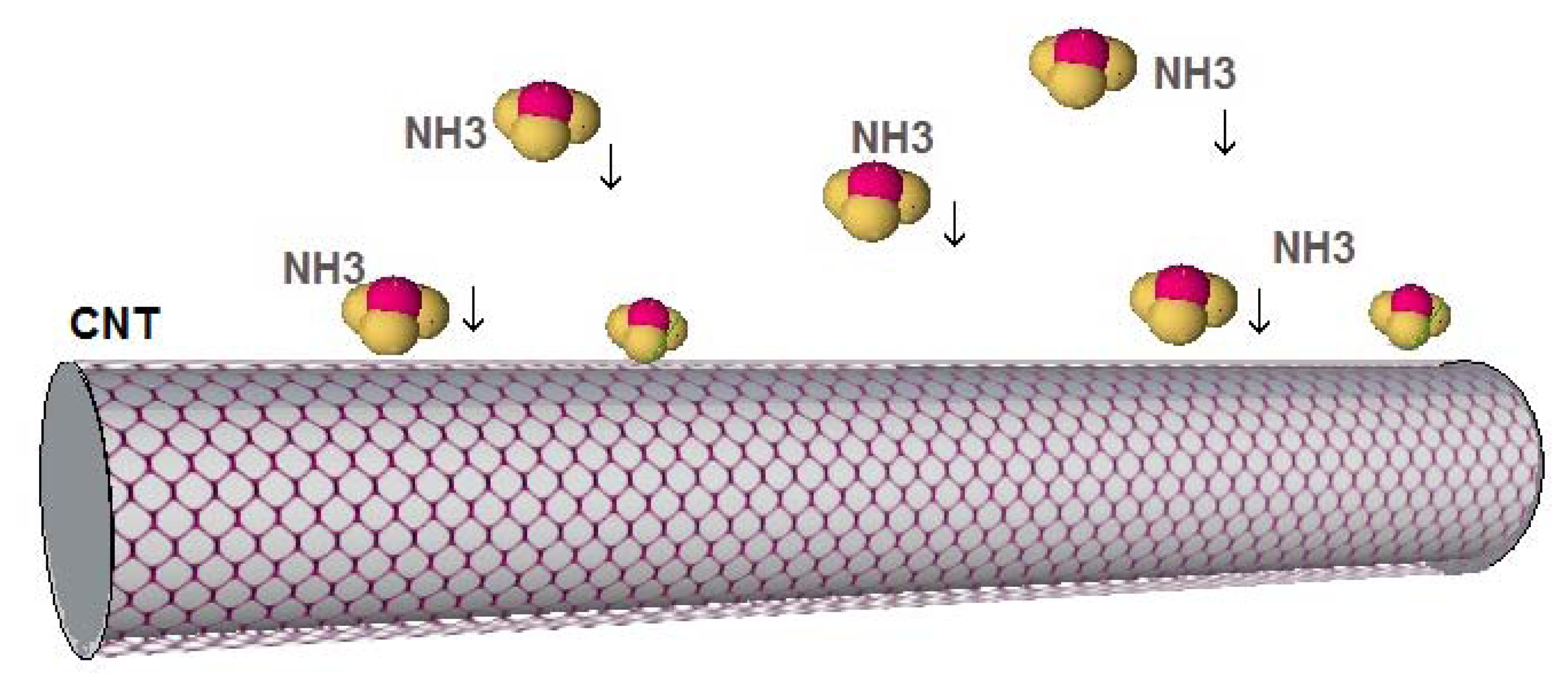
The best gas sensor can be defined as one which is able to detect even one chemical or gas molecule or atom [32,33]. Numerous theoretical studies that have been recently carried out on gas molecular adsorption on the CNT have reported that NO2, H2O, NH3, CO, and NO molecules are physically adsorbed on the pristine CNT. NH3 and CO molecules act as donors, while H2O and NO2 serve as acceptors [34].
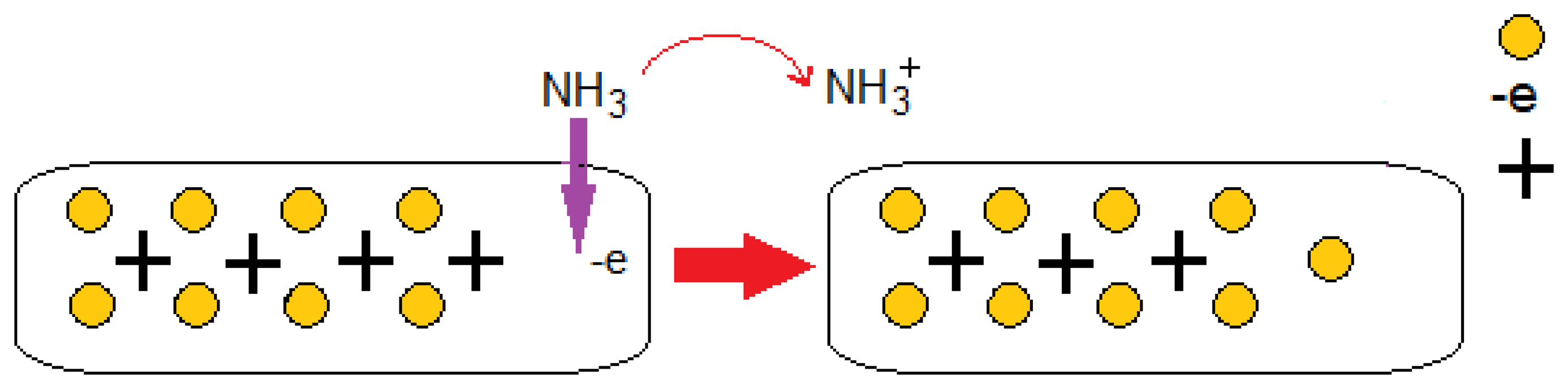
Gases such as CO2, CO, NO, NO2, and O2, can withdraw electrons, while NH3 functions as an electron-donating molecule as shown in Figure 3 [35]. The CO2 and O2 adsorption generates a p-type semiconductor while the adsorption of NH3 results in n-type behavior. Figure 4 illustrates a schematic of CNTs when electron donor NH3 gas molecules are in the atmosphere around the sensor. These strong adsorption effects stem from the inherent properties of gas molecules and the bonding characteristics between these molecules and the CNT. Since it is always important to obtain n-type and/or p-type semiconducting CNT for incorporation in nanoscale electronic devices (e.g., p-n junction and n-type and p-type nanoscale field-effect transistors), the consequent p- or n-type semiconducting behavior can be experimentally detected by applying gate voltage, which can be useful from the application perspective [36].
2. Proposed Model
Considering the energy dispersion relation, we begin by modeling a single layer graphene band structure. Deriving it using the Taylor series expansion near the Fermi points, we attempt to model the CNT band structure [27]:
Since the number of actual modes (E) at a given energy is significantly influenced by the sub-band location, one can use the parabolic approximation of the band diagram when the related energy includes the bottom of the conduction band. In other word, mode density M(E) increases with energy [37]. Taking into account the spin degeneracy, the number of conduction channels can be defined as:
Changing the integral boundaries as below, Equation (5) can be rewritten as [37]:
The conductance characteristic demonstrates the performance of the NH3 gas sensor based on a CNT nanostructure. It has been revealed that when the CNT gas sensor is exposed to NH3, the conductance changes [44]. We have proposed a model based on the reported experimental data and the relationship between conductance, gas concentration and temperature as follows [45]:
When the sensor is exposed to the gases at different temperatures, we can define three conductance parameters, namely Gwog, GwgT and GwgF. The first parameter, Gwog, is the conductance without gas; GwgT is assumed to represent changes in conductivity depending on T parameter and the last one, GwgF, is based on different gas concentration values with constant temperature. It is shown that when CNT gas sensor is exposed to NH3, the conductance ratio changes with respect to temperature and various concentrations [35]. As Eg results in varying channel conductance, the parameters that have a strong influence on gas sensor conductance are gas concentration and its temperature. As it has been demonstrated that Eg depends on temperature and gas concentration, we can write:
Finally, Equations (9) and (10) are employed to obtain the gas sensor conductance model as:
Moreover, the relationship between current and conductance can be derived from Fermi-Dirac integral form of general conductance model of SWCNT as:
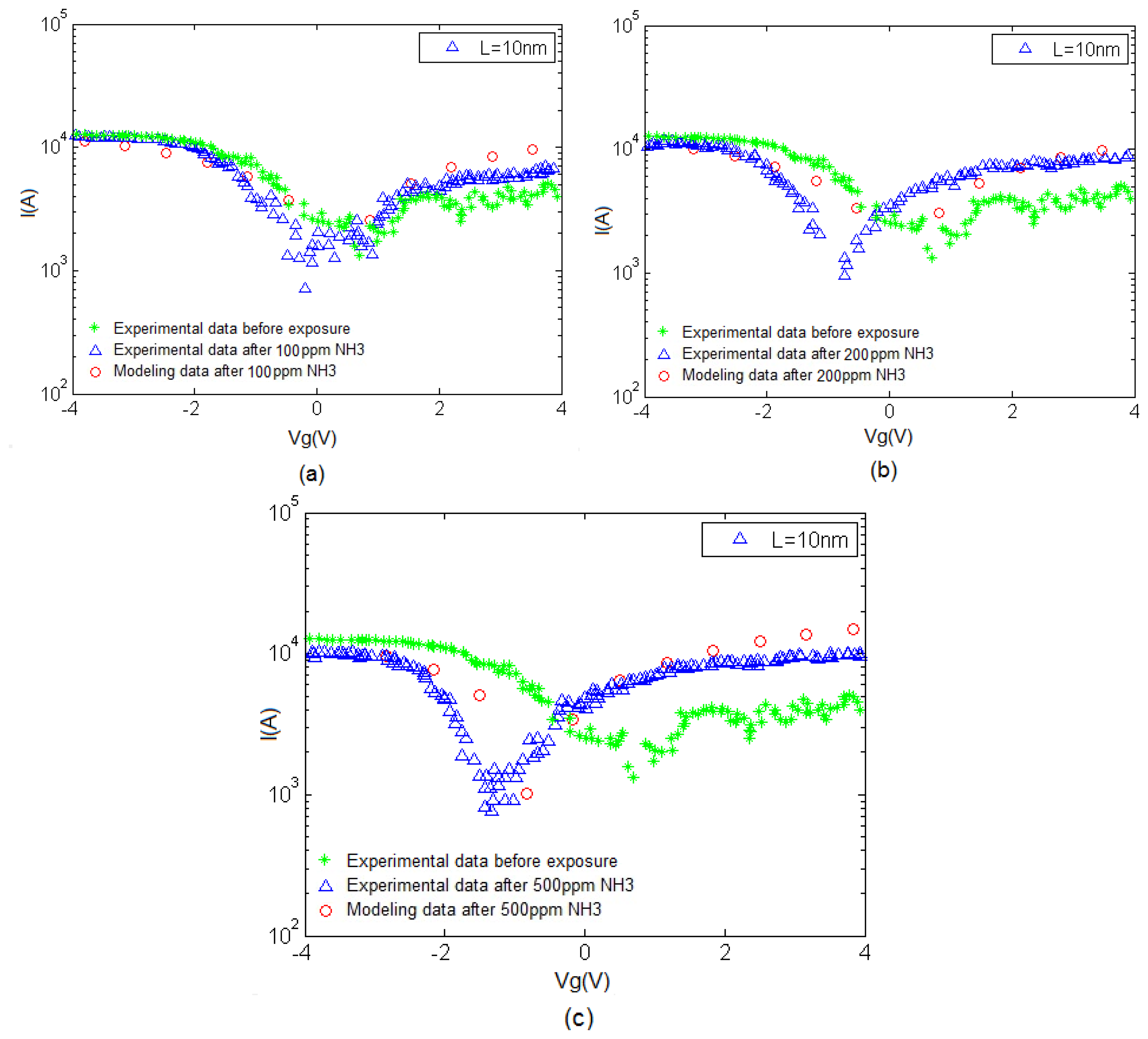
As shown in Figure 4, gas sensor performance based on CNT nanostructure is assessed by the current-voltage characteristic before gas exposure and after exposure to NH3. There is a favorable agreement between the proposed gas sensor model based on CNT and experimental results extracted from [25].
Charge transfer is involved within the sensing mechanism of CNT-based gas sensors. This phenomenon is likely to occur during the interaction between gas molecules and the CNT surface. CNT conductivity is modified during this interaction. Thus, electrons move from NH3 molecules to CNTs. Figure 5 illustrate the I–V characteristics of the CNT gas sensor corresponding to temperatures of 25, 50, 100, and 150 °C, respectively. As can be seen, with the increase in temperature, the CNT I–V characteristics have increased.
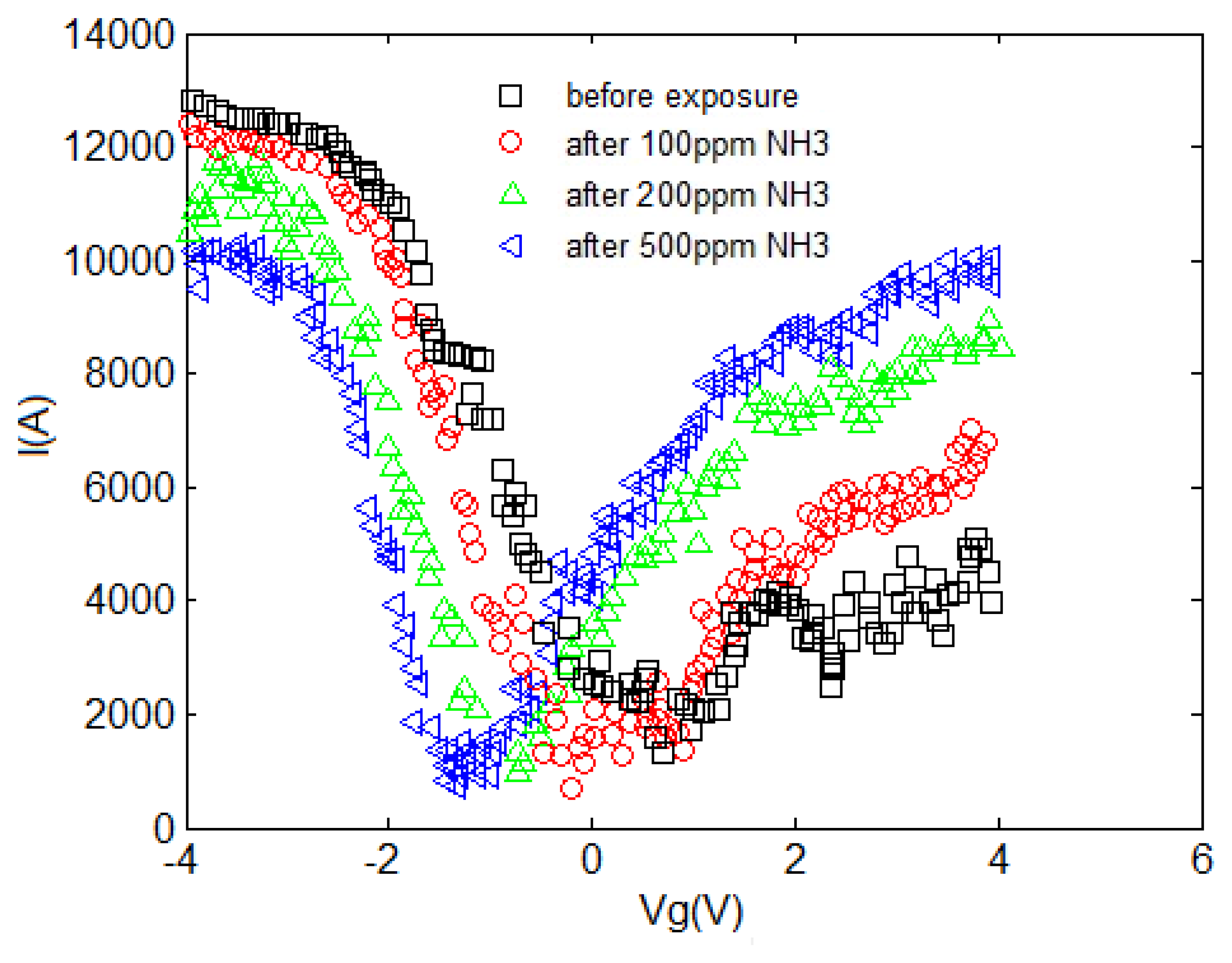
In Figure 6, the I–V characteristics before and after exposure to NH3 at 200 °C and different gas concentration values are indicated. It is evident that increasing the temperature and gas concentration causes the conductivity to increase as well. A benchmark of the proposed model coupled with an experimental counterpart is illustrated which shows that at higher temperatures, conductivity escalates dramatically when the concentration is raised.
The I–V characteristic of the proposed model compared with experimental results is depicted in Figure 7. An increase in current can be associated with the charge transfer between NH3 and CNT when the NH3 molecules operate as the donor. This phenomenon is also known as chemical doping by gas molecules. The sensitivity can be observed in this figure, indicating the response of CNT-based gas sensor under 100, 200 and 500 ppm NH3 gas. A clear illustration approving the satisfactory agreement between the proposed model and extracted data is provided. In the suggested model, different temperature and concentration values are demonstrated in the form of δ and λ parameters, respectively to reach an agreement with reported data as shown in Table 1.
According to the analytical model,δ is suggested as the temperature control parameter and it is obtained by iteration method. Based on the extracted data, the analytical model in our study shows that the rate of change in conductivity depending on temperature gives better results by:
Parameters a and b are extracted as a = 0.012 and b = 0.046. Also, λ is defined as a gas concentration control parameter calculated by iterative method which shows that the rate of change in conductivity depends on gas concentration given by:
Finally, our proposed model for the I–V characteristic of CNT FET-based gas sensor can be obtained by substituting the sensing parameters δ and λ from Equations (15) and (16) into Equation (14) which can be written as:
3. Conclusions
Outstanding properties such as high sensitivity as well as remarkable carrier transport features make CNTs promising candidates for use in nanosensors. It has been verified that CNTs experience a measureable change in conductance levels when exposed to NH3. Conductance also escalates as the gas concentration and temperature are increased. This interesting characteristic makes CNTs ideally suited for employment in gas detection systems. The proposed model incorporates two control parameters, namely the temperature control (δ) and gas concentration control (λ). In addition, a comparative analysis between a FET-based model for a CNT sensor structure and a similar experimental work by [25] has been done to confirm the validity and viability of the proposed model. To minimize error, coefficients δ and λ are calculated by iteration method. I–V characteristics of the gas sensor are considered for the comparative study under exposure to different gas concentrations and temperatures which shows favorable agreement between the presented model and experimental data.
Acknowledgments
The authors would like to thank Ministry of Higher Education (MOHE), Malaysia (grant Vot. No. 4F382) and the Universiti Teknologi Malaysia (grants Vot. No. 03H86 and Vot. No. 04H40) for the financial support received during the investigation.
Author Contributions: E.A., Z.B. and M.T.A. did the analytical modeling and derivation of mathematical equations. M.H.A. and M.A.B.S. did the data analysis and comparative study. A.E., R.Y., S.M.Z.I. and H.K. prepared the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lin, Z.-D.; Hsiao, C.-H.; Young, S.-J.; Huang, C.-S.; Chang, S.-J.; Wang, S.-B. Carbon nanotubes with adsorbed Au for sensing gas. IEEE Sens. J. 2013, 13, 2423–2427. [Google Scholar]
- Karimi, F.A.; Hediyeh; Ahmadi, M.T.; Rahmani, M.; Akbari, E.; Kiani, M.J.; Khalid, M. Analytical modeling of graphene-based DNA sensor. Sci. Adv. Mater. 2012, 4, 1142–1147. [Google Scholar]
- Akbari, E.; Ahmadi, M.T.; Kiani, M.J.; Feizabadi, H.K.; Rahmani, M.; Khalid, M. Monolayer graphene based CO2 gas sensor analytical model. J. Comput. Theor. Nanosci. 2013, 10, 1301–1304. [Google Scholar]
- Kiga, N.; Takei, Y.; Inaba, A.; Takahashi, H.; Matsumoto, K.; Shimoyama, I. Cnt-fet gas sensor using a functionalized ionic liquid as gate. Proceedings of the 2012 IEEE 25th International Conference on Micro Electro Mechanical Systems, Paris, France, 29 January–2 February 2012.
- Avouris, P.; Appenzeller, J.; Martel, R.; Wind, S.J. Carbon nanotube electronics. Proc. IEEE 2003, 91, 1772–1784. [Google Scholar]
- Amiri, I.S.; Ahsan, R.; Shahidinejad, A.; Ali, J.; Yupapin, P.P. Characterisation of bifurcation and chaos in silicon microring resonator. IET Commun. 2012, 6, 2671–2675. [Google Scholar]
- Akbari, E.; Ahmadi, M.T.; Yusof, R.; Ghadiry, M.H.; Saeidmanesh, M. Gas concentration effect on channel capacitance in graphene based sensors. J. Comput. Theor. Nanosci. 2013, 10, 2449–2452. [Google Scholar]
- Pregl, S.; Weber, W.M.; Nozaki, D.; Kunstmann, J.; Baraban, L.; Opitz, J.; Mikolajick, T.; Cuniberti, G. Parallel arrays of Schottky barrier nanowire field effect transistors: Nanoscopic effects for macroscopic current output. Nano Res. 2013, 6, 381–388. [Google Scholar]
- Kiani, M.J.; Ahmadi, M.T.; Akbari, E.; Rahmani, M.; Karimi, F.A.H.; Khairi, F. Analytical modeling of bilayer graphene based biosensor. J. Biosens. Bioelectron. 2013, 4, 131. [Google Scholar]
- Ahmad, S. Carbon nanostructures fullerenes and carbon nanotubes. IETE Tech. Rev. 1999, 16, 297–310. [Google Scholar]
- Kang, X.; Wang, J.; Wu, H.; Aksay, I.A.; Liu, J.; Lin, Y. Glucose oxidase–graphene–chitosan modified electrode for direct electrochemistry and glucose sensing. Biosens. Bioelectron. 2009, 25, 901–905. [Google Scholar]
- Li, W.-Y.; Xu, L.-N.; Chen, J. Co3O4 nanomaterials in lithium‐ion batteries and gas sensors. Adv. Funct. Mater. 2005, 15, 851–857. [Google Scholar]
- Keshavarzi, A.; Raychowdhury, A.; Kurtin, J.; Roy, K.; De, V. Carbon nanotube field-effect transistors for high-performance digital circuits - Transient analysis, parasitics, and scalability. IEEE Trans. Electron Devices 2006, 53, 2718–2726. [Google Scholar]
- Ouyang, Y.; Yoon, Y.; Fodor, J.K.; Guo, J. Comparison of performance limits for carbon nanoribbon and carbon nanotube transistors. Appl. Phys. Lett. 2006, 89, 203107. [Google Scholar]
- Das, S.; Lahiri, I.; Kang, C.; Choi, W. Engineering carbon nanomaterials for future applications: Energy and bio-sensor. Proceedings of the Micro- and Nanotechnology Sensors, Systems, and Applications Iii, Orlando, FL, USA, 25 April 2011.
- Baughman, R.H.; Zakhidov, A.A.; de Heer, W.A. Carbon nanotubes—The route toward applications. Science 2002, 297, 787–792. [Google Scholar]
- Panzer, M.; Zhang, G.; Mann, D.; Hu, X.; Pop, E.; Dai, H.; Goodson, K.E. Thermal properties of metal-coated vertically-aligned single wall nanotube films. Proceedings of the 2006 10th Intersociety Conference on Thermal and Thermomechanical Phenomena in Electronics Systems, San Diego, CA, USA, 30 May 2006–2June 2006; Volumes 1 and 2, pp. 1306–1313.
- Tans, S.J.; Verschueren, A.R.; Dekker, C. Room-temperature transistor based on a single carbon nanotube. Nature 1998, 393, 49–52. [Google Scholar]
- Martel, R.; Schmidt, T.; Shea, H.R.; Hertel, T.; Avouris, Ph. Single- and multi-wall carbon nanotube field-effect transistors. Appl. Phys. Lett. 1998, 73, 2447–2449. [Google Scholar]
- Panzer, M.A.; Zhang, G.; Mann, D.; Hu, X.; Pop, E.; Dai, H.; Goodson, K.E. Thermal properties of metal-coated vertically aligned single-wall nanotube arrays. J. Heat Transf.-Trans. Asme. 2006, 130, 1306–1313. [Google Scholar]
- Saito, R.; Dresselhaus, G.; Dresselhaus, M.S. Physical Properties of Carbon Nanotubes; World Scientific: Hackensack, NJ, USA, 1998; Volume 4. [Google Scholar]
- Suehiro, J.; Zhou, G.; Imakiire, H.; Ding, W.; Hara, M. Controlled fabrication of carbon nanotube NO2 gas sensor using dielectrophoretic impedance measurement. Sens. Actuators B-Chem. 2005, 108, 398–403. [Google Scholar]
- Chen, R.J.; Bangsaruntip, S.; Drouvalakis, K.A.; Kam, N.W.S.; Shim, M.; Li, Y.; Kim, W.; Utz, P.Z.; Utz, H. Noncovalent functionalization of carbon nanotubes for highly specific electronic biosensors. Proc. Natl. Acad. Sci. USA 2003, 100, 4984–4989. [Google Scholar]
- Star, A.; Han, T.-R.; Gabriel, J.-C.P.; Bradley, K.; Grüner, G. Interaction of aromatic compounds with carbon nanotubes: Correlation to the Hammett parameter of the substituent and measured carbon nanotube FET response. Nano Lett. 2003, 3, 1421–1423. [Google Scholar]
- Peng, N.; Zhang, Q.; Chow, C.L.; Tan, O.K.; Marzari, N. Sensing mechanisms for carbon nanotube based NH3 gas detection. Nano Lett. 2009, 9, 1626–1630. [Google Scholar]
- Pesetski, A.A.; Baumgardner, J.E.; Folk, E.; Przybysz, J.X.; Adam, J.D.; Zhang, H. Carbon nanotube field-effect transistor operation at microwave frequencies. Appl. Phys. Lett. 2006. [Google Scholar]
- Wang, D.; Yu, Z.; McKernan, S.; Burke, P.J. Ultrahigh frequency carbon nanotube transistor based on a single nanotube. IEEE Trans. Nanotechnol. 2007, 6, 400–403. [Google Scholar]
- Heller, I.; Janssens, A.M.; Männik, J.; Minot, E.D.; Lemay, S.G.; Dekker, C. Identifying the mechanism of biosensing with carbon nanotube transistors. Nano Lett. 2008, 8, 591–595. [Google Scholar]
- Uchida, K.; Saitoh, M.; Kobayashi, S. Carrier transport and stress engineering in advanced nanoscale transistors from (100) and (110) transistors to carbon nanotube FETs and beyond. Proceedings of the IEEE International Electron Devices Meeting 2008, Technical Digest, San Francisco, CA, USA, 15–17 December 2008; pp. 569–572.
- Ding, L.; Wang, S.; Zhang, Z.; Zeng, Q.; Wang, Z.; Pei, T.; Yang, L.; Liang, X.; Shen, J.; Chen, Q.; et al. Y-contacted high-performance n-Type single-walled carbon nanotube field-effect transistors: Scaling and comparison with Sc-contacted devices. Nano Lett. 2009, 9, 4209–4214. [Google Scholar]
- Postma, H.W.C.; Teepen, T.; Yao, Z.; Grifoni, M.; Dekker, C. Carbon nanotube single-electron transistors at room temperature. Science 2001, 293, 76–79. [Google Scholar]
- Ding, W.D.; Hayashi, R.; Suehiro, J.; Zhou, G.; Imasaka, K.; Hara, M. Calibration methods of carbon nanotube gas sensor for partial discharge detection in SF6. IEEE Trans. Dielectr. Electr. Insul. 2006, 13, 353–361. [Google Scholar]
- Kiani, M.J.; Ahmadi, M.T.; Akbari, E.; Karimi, H.; Che Harun, F.K. Graphene nanoribbon based gas sensor. Key Eng. Mater. 2013, 553, 7–11. [Google Scholar]
- Cho, T.S.; Cambridge, M.A.; Lee, K.-J.; Kong, J.; Chandrakasan, A.P. The design of a low power carbon nanotube chemical sensor system. Proceedings of the 2008 45th ACM/IEEE Design Automation Conference, Anaheim, CA, USA, 8–13 June 2008; 2008; Volumes 1 and 2, pp. 84–89. [Google Scholar]
- Santangelo, S.; Faggio, G.; Messina, G.; Fazio, E.; Neri, F.; Neri, G. On the hydrogen sensing mechanism of Pt/TiO2/CNTs based devices. Sens. Actuators B-Chem. 2013, 178, 473–484. [Google Scholar]
- McEuen, P.L.; Fuhrer, M.S.; Park, H. Single-walled carbon nanotube electronics. Nanotechnol. IEEE Trans. 2002, 1, 78–85. [Google Scholar]
- Ahmadi, M.T.; Johari, Z.; Amin, N.A.; Mousavi, S.M.; Ismail, R. Carbon nanotube conductance model in parabolic band structure. Proceedings of the 2010 IEEE International Conference on Semiconductor Electronics (ICSE), Melaka, Malaysia, 28–30 June 2010; 2010. [Google Scholar]
- Ahmadi, M.T.; Johari, Z.; Amin, N.A.; Fallahpour, A.H.; Ismail, R. Graphene nanoribbon conductance model in parabolic band structure. J. Nanomater 2010, 2010. [Google Scholar] [CrossRef]
- Datta, S. Electronic Transport in Mesoscopic Systems 2002; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Peres, N.; Neto, A.H.C.; Guinea, F. Conductance quantization in mesoscopic graphene. Phys. Rev. B. 2006, 73, 195411. [Google Scholar]
- Dingle, R.B.; Dingle, R. Asymptotic Expansions: Their Derivation and Interpretation 1973; Academic Press: London, UK, 1973. [Google Scholar]
- Zaharah, J.; Ahmadi, M.T.; Chek, D.C.Y.; Amin, N.A.; Ismail, R. Modelling of graphene nanoribbon fermi energy. J. Nanomater 2010, 2010. [Google Scholar] [CrossRef]
- Gunlycke, D.; Areshkin, D.; White, C. Semiconducting graphene nanostrips with edge disorder. Appl. Phys. Lett. 2007, 90, 142104:1–142104:3. [Google Scholar]
- Yoon, H.J.; Jun, D.H.; Yang, J.H.; Zhou, Z.; Yang, S.S.; Cheng, M.M.-C. Carbon dioxide gas sensor using a graphene sheet. Sens. Actuators B-Chem. 2011, 157, 310–313. [Google Scholar]
- Xia, J.L.; Chen, F.; Li, J.; Tao, N. Measurement of the quantum capacitance of graphene. Nat. Nanotechnol. 2009, 4, 505–509. [Google Scholar]
- Kim, R.; Lundstrom, M. Notes on Fermi-Dirac Integrals, 2nd ed.; Purdue University: West Lafayette, IN, USA, 2008. [Google Scholar]

| T (°C) | F (ppm) | δ | λ |
|---|---|---|---|
| 25 | 50 | −4 | 0.0 |
| 0 | 3 | ||
| 50 | 50 | −2 | 0.0 |
| 0 | 3 | ||
| 10 | 50 | −1 | 0.0 |
| 0 | 0 | 3 | |
| 15 | 50 | −0.8 | 0.0 |
| 0 | 0 | 3 | |
| 20 | 10 | −0.5 | 0.0 |
| 0 | 0 | 1 | |
| 20 | 20 | −0.5 | 0.0 |
| 0 | 0 | 2 | |
| 20 | 50 | −0.5 | 0.0 |
| 0 | 0 | 3 |
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Akbari, E.; Buntat, Z.; Ahmad, M.H.; Enzevaee, A.; Yousof, R.; Iqbal, S.M.Z.; Ahmadi, M.T.; Sidik, M.A.B.; Karimi, H. Analytical Calculation of Sensing Parameters on Carbon Nanotube Based Gas Sensors. Sensors 2014, 14, 5502-5515. https://doi.org/10.3390/s140305502
Akbari E, Buntat Z, Ahmad MH, Enzevaee A, Yousof R, Iqbal SMZ, Ahmadi MT, Sidik MAB, Karimi H. Analytical Calculation of Sensing Parameters on Carbon Nanotube Based Gas Sensors. Sensors. 2014; 14(3):5502-5515. https://doi.org/10.3390/s140305502
Chicago/Turabian StyleAkbari, Elnaz, Zolkafle Buntat, Mohd Hafizi Ahmad, Aria Enzevaee, Rubiyah Yousof, Syed Muhammad Zafar Iqbal, Mohammad Taghi. Ahmadi, Muhammad Abu Bakar Sidik, and Hediyeh Karimi. 2014. "Analytical Calculation of Sensing Parameters on Carbon Nanotube Based Gas Sensors" Sensors 14, no. 3: 5502-5515. https://doi.org/10.3390/s140305502
APA StyleAkbari, E., Buntat, Z., Ahmad, M. H., Enzevaee, A., Yousof, R., Iqbal, S. M. Z., Ahmadi, M. T., Sidik, M. A. B., & Karimi, H. (2014). Analytical Calculation of Sensing Parameters on Carbon Nanotube Based Gas Sensors. Sensors, 14(3), 5502-5515. https://doi.org/10.3390/s140305502





