Contour-Based Corner Detection and Classification by Using Mean Projection Transform
Abstract
: Image corner detection is a fundamental task in computer vision. Many applications require reliable detectors to accurately detect corner points, commonly achieved by using image contour information. The curvature definition is sensitive to local variation and edge aliasing, and available smoothing methods are not sufficient to address these problems properly. Hence, we propose Mean Projection Transform (MPT) as a corner classifier and parabolic fit approximation to form a robust detector. The first step is to extract corner candidates using MPT based on the integral properties of the local contours in both the horizontal and vertical directions. Then, an approximation of the parabolic fit is calculated to localize the candidate corner points. The proposed method presents fewer false-positive (FP) and false-negative (FN) points compared with recent standard corner detection techniques, especially in comparison with curvature scale space (CSS) methods. Moreover, a new evaluation metric, called accuracy of repeatability (AR), is introduced. AR combines repeatability and the localization error (Le) for finding the probability of correct detection in the target image. The output results exhibit better repeatability, localization, and AR for the detected points compared with the criteria in original and transformed images.1. Introduction
Feature detection is a fundamental issue in image processing and computer vision that is directly related to interest points. Corner points are considered important features for feature extraction [1]. Corner detection is a low-level image processing technique that is widely used in different computer vision applications [2], such as camera calibration [3], target tracking [4], transformed image identification (TII) [5], image registration [6], 3D polyhedral building modelling from aerial imagery [7], multi-scale feature extraction from LIDAR data [8], 2D and 3D building extraction [9,10], and automotive applications [11]. However, different approaches require a different perspective for the corner definition. Historically, the terms of the corner point refer to the terms of both the interest point and the region of interest [12]. Generally, the corner detection in an image is the point on the contour at which two straight edges meet at a particular angle or the location at which the direction of the contour changes significantly [2].
Numerous corner detection methods have been introduced over the last several decades. These methods can be divided into three main categories: intensity-based detectors [13–17], model-based detectors [18,19], and contour-based detectors [1,4,20–25]. Each category has its own competencies for different types of areas and images. Recently, the third category has received more attention in terms of robustness and efficient computational cost. Model-based detectors extract the corner points by matching a predefined corner model to the image and calculating the similarity for detecting corner points. Their algorithms limit the detection to specific tasks, such as finding chessboard corners [3]. For general and flexible corner detection, defining a general corner model is difficult and does not cover all types of corners for different image types with different scene properties. Intensity-based detectors attract more attention than model-based detectors [1]. Intensity-based detectors use the grey-level information of the image to detect the corner points by applying the first- or second-order derivative on the images. The second-order derivatives of intensity-based methods are noise sensitive and are rarely used in the literature [1]. In 1977, Moravec [14] introduced the idea of finding the corner points as ‘points of interest’ that have high-intensity variations in the vertical and horizontal directions. Harris and Stephen [15] proposed the most famous corner detector method, known as the Harris (Plessey) method, to improve upon Moravec's idea. The Harris method is based on approximates of the auto-correlation of the gradient in different directions. The Harris method is the most well-known method in the literature, but it cannot detect high-order corners [1]. A high-order corner is a point at which three or more contour regions meet [1]. The Harris method uses the Gaussian filter to reduce the FP corners in noisy images and increases the localization accuracy of the detector. Noble [26] proved that the Harris corner detector is only robust in ‘L’-type corners. Based on these weaknesses, Shi and Tomasi [13] improved the Harris detector with a minor correction and calculated the minimum eigenvalues. Smith and Brady [16] introduced the Smallest Uni-value Segment with an Assimilating Nucleus (SUSAN), which used a gradient convolution of a circle mask called the USAN area to detect the corner points on a grey-level image. Yang et al. [27] improved the SUSAN method using a self-adoptive threshold and a rotating coordinate system, but the method was not sufficient for high accuracy of localization. Several improvements have been proposed for the Harris and SUSAN methods [28–36]. Grey-scale methods are sensitive to noise and are not as accurate for detecting the exact corner point location.
Robustness to noise is an important issue for contour-based detectors [37], and researchers have proposed several algorithms over the last decade to address this problem. Contour-based detectors consist of three main steps: edge detection, contour extraction, and decision making on the contour [1]. The basic idea of contour-based methods was proposed by Rosenfeld and Johnston [23] in 1973 to calculate the angle of the curves on digital imagery. Subsequently, Kitchen and Rosenfeld [38] introduced their corner detector based on the change in direction of the gradient (first- and second-order derivatives) on the contour. This method is considered the first cornerness measure of the edge map in the literature. Coeurjolly et al. [39] extended the Worring and Smeulders [40] corner classification to a discrete method based on an estimation of the discrete osculating circle. Nguyen and Debled-Rennesson [41] extended the estimator proposed in [39] using blurred segments. Malgouyres et al. [42] introduced a discrete binomial convolution for a convergent estimator to reduce the noise effect. Kerautret and Lachaud [43] subsequently introduced a discrete curvature estimation-based method to calculate the curvature radius passing from the corner points.
Over the last two decades, curvature scale space (CSS) methods have been widely used as corner detectors in the literature due to their high performance. CSS-based detectors exhibit some weaknesses, which are considered in this paper. They generally use second-order derivatives, which can cause an increase in the FP rate because of contour variation. Additionally, they require a Gaussian scale selection to smooth the curve area, which is application based and a difficult task. The basic idea was introduced by Rattarangsi and Chin [44] in 1992, and the basic CSS-based methods were proposed by Mokhtarian and Suomela [20] in 1998 and modified by Han and Poston [21] in 2001. CSS-based detectors use several planar curves that are smoothed using multi-scale Gaussian functions to calculate the local curvatures. Thresholding is used to remove the FP corner points from the candidate corners. CSS-based detectors are sensitive to noise on the contour, and the curvature estimation uses high-order derivatives to reduce the localization accuracy and high false rate [37]. A large-scale Gaussian function reduces noise but affects the corner localization, whereas a small-scale Gaussian function is sensitive to noise. To address these problems, Awrangjeb and Lu [37] proposed chord-to-point distance accumulation (CPDA) using the adoptive threshold method based on Han and Poston's idea [21]. The CPDA method uses a discrete curvature estimation that is more robust to the local variation. These authors used three chords of different lengths to estimate three normalized discrete curvature values at each point of the smoothed curve. They then multiplied the normalized values to achieve the curvature product. The candidate corners were selected from the maximum of the absolute curvature products. Because intensity variation information is not effective for extracting the corner candidate [1], a universal corner model (UCM) was proposed in [1] using the anisotropic directional derivative (ANDD) filter to improve the CPDA method to reduce the effect of the intensity variation of the contour and improve the localization accuracy. The proposed kernel in the ANDD filter is a Gaussian-based kernel based on sampling the continuous anisotropic functions with ρ as the anisotropic factor and σ as the scale parameter. Because the ANDD method is based on an anisotropic Gaussian kernel for smoothing, it changes the contour to the curve, and it is difficult to select an appropriate Gaussian scale [45]. Thus, ANDD is insufficient for detecting corners with both a high detection rate and repeatability with an acceptable Le. Elias and Laganiere [25] proposed a method named JUDOCA, which defined the junctions as a meeting point of two or more ridges in the gradient domain. The region of a circle mask to measure the cornerness is used after edge detection and Gaussian filtering to detect the corners. An edge extraction process in CSS-based detectors is a sensitive operation that may cause the original corner point in the contour to be missed and the diagonal lines to be aliased on the edge. Anti-aliasing filters cannot affect the edge map. These problems affect the FP rate and localization accuracy of the detectors. Some studies combine corner detection categories to achieve better performance. Escalera and Armingol [3] used a hybrid corner detection to extract corners on a chessboard using the Hough transform for the contour and then established the chessboard corner models, but this method is limited to a specific task.
In this paper, a new projection transform, called mean projection transform (MPT), is proposed to extract the corner candidates and address the aliasing problem. Next, a parabolic fit approximation is used to determine the corner points in the extracted candidates. This method reduces problems related to the existing CSS-based algorithms. The proposed method is compared to the detectors presented in [1,25,37] because these detectors claim to provide better detection performance compared to the other available methods.
This paper is organized as follows: Section 2 discusses the MPT method for selecting corner candidates. Section 3 presents the parabolic fit approximation to confirm corner points from the MPT candidates and localize them. Section 4 discusses the evaluation results and proposes a new corner detection evaluation method called AR, which addresses the limitations of the current evaluation metrics for FP and FN points; the proposed corner detector is then assessed using Le, repeatability, and AR.
2. Mean Projection Transform
A new projection transform based on the mean of integral values in both the horizontal and vertical directions is proposed. Contour-based detectors use contour information to extract the corner candidates and corner points. Based on CSS problems regarding contour aliasing and variation, the MPT method is proposed to extract the corner candidates. MPT representation guarantees that the detector only selects candidates that have high curvature, and it addresses the aforementioned problems.
2.1. Global Mean Projection Transform
MPT is a transform that consists of the integrals over straight lines in a digital image. If f(X) = f(x, y) is a function of the image signal (L) in ℝ2, then MPT is a transform of L, where the mean of the integrals in vertical and horizontal directions is calculated using Equation (1):
The arc-length t on the line (L) can be written as Equation (2):
This equation can also be written as:
The MPT that considers the multi-directional integral can be formulated as Equation (5):
MPT calculates the mean of the integrals in an input image in both the vertical and horizontal directions of line L. The parameters of MPT can detect the available angular contours from a straight contour on the edge map of the objects in an image. The MPT of the sample image is shown in Figure 1. The image contains at least a corner where the MPT representation of the image includes more than a segment or peak.
MPT calculates the integral of f(x, y) for each line and the mean of the vertical and horizontal integrals in all directions θ є [0,2π). The output of MPT has more than a peak for each significant change in the contour direction. The coordinate of a corner point may not be extracted using the MPT function, but the corner candidates can be extracted to address the aliasing problem of CSS-based detectors and reduce the FP rate significantly.
2.2. Projection of the Corner
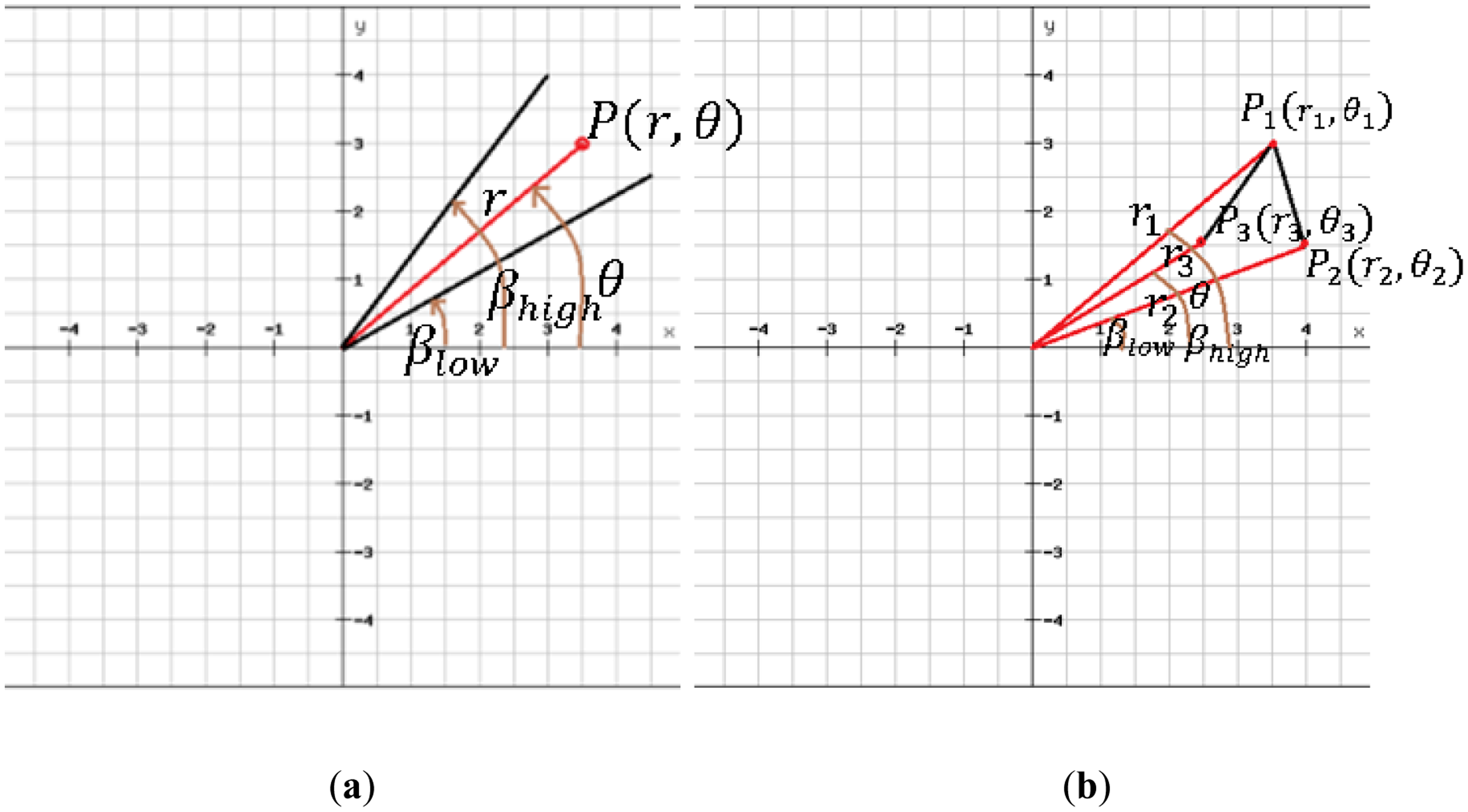
A projection of universal corner model (PUCM) describes all corner types. The basic corner model (BCM) of a curve is the area in which the horizontal and vertical integrals are significantly different than the non-corner model (NCM). In the polar coordinate system, the BCM and NCM can be defined by Equation (6) [1]:
The MPT representation of the BCM is presented in Equation (8):
Equation (8) has two zero values for θ = β ± π and two extremes for θ = β and θ = β + π. The results for different directions are the projection of the object for both the vertical and horizontal views simultaneously. Some corner models and non-corner models are manually extracted from the contour of the object, and their MPT representations are shown in Figure 3.
As shown in Figure 4b, the PUCM of the corner models has at least two separated peaks in the MPT representation because the integral values in the horizontal and vertical directions are calculated. In contrast, the straight line has only one peak in the MPT model, as Figure 4a demonstrates. The input image is swept by a moving window to select all candidates using MPT. The default moving window is 9 × 9, but the size of the moving window is an initial parameter that can be adjusted based on the image size. In large-scale images, the moving window size should be large enough to detect corners properly.
3. Corner Point Detection: Approximation of the Parabolic Fit
Curvature extraction and angle estimation are the key features of the contour-based corner detection methods. CSS detectors extract the curve, analyze the curvature properties of the contour map, and then detect the corner points. Γ is considered the curvature at a point, as presented in Equation (9) [44]:
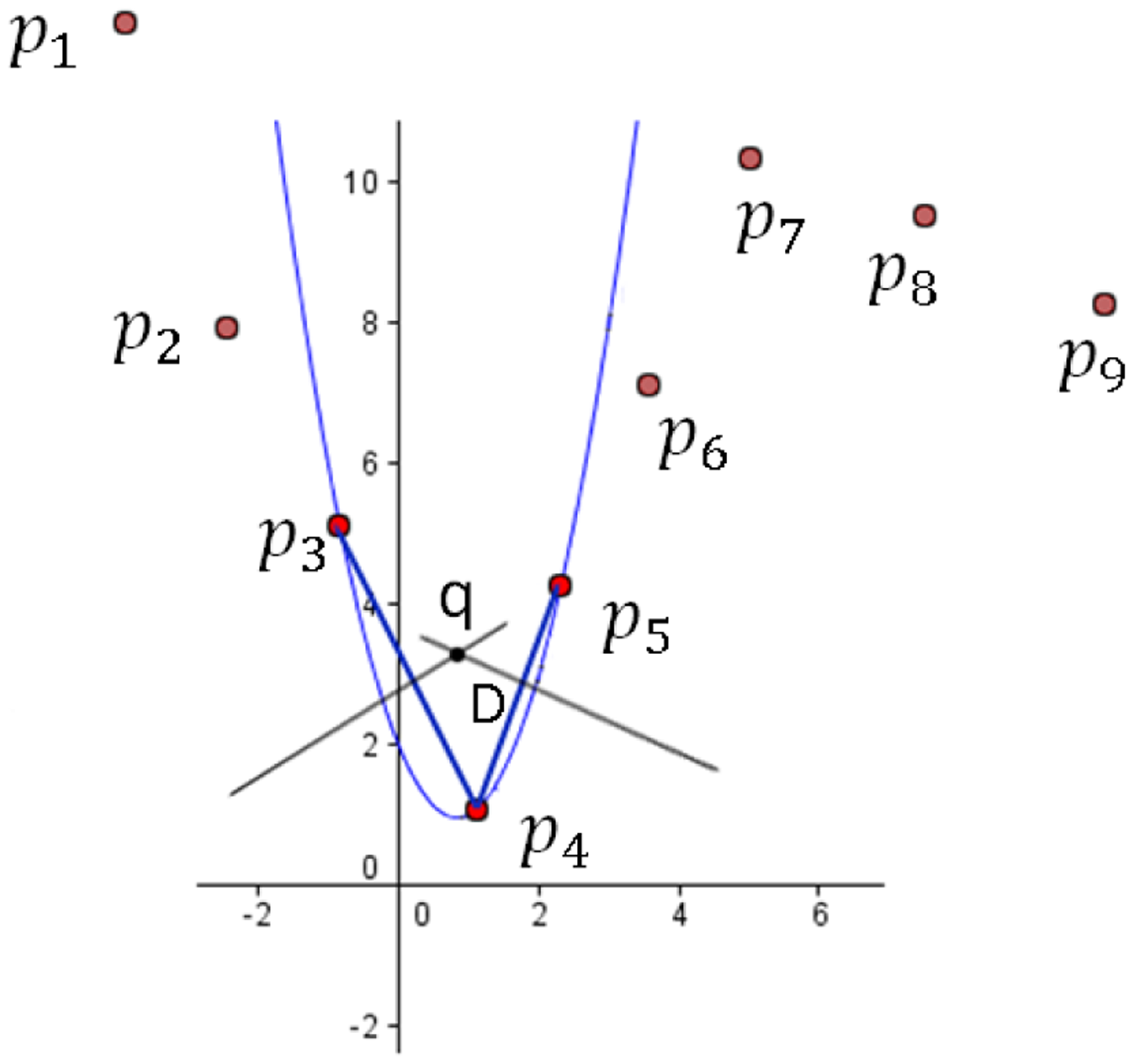
Orthogonal lines meet at the center point of the parabola ρ, which are defined as D. If ρi denotes ρ (pi, ε), then pipj is a segment δh(pipj) ≤ ε if pipj intersect at di+1,…,dj−1, and the parabola radius passing the points is:
Generally, the approximation of the parabolic fit is robust to the local variation [46]. Therefore, it can estimate the curvature without the curve-smoothing process. Compared to other CSS-based estimators, the proposed method is not sensitive to the aliasing of the edge map; thus, it detects the corner points with higher performance.
4. Experimental Results and Evaluation Metrics
To evaluate the proposed method, a dataset called “image database and corner detection” [47] and some standard images that are commonly used in the corner detection assessments are applied. The compared criteria are CPDA [37], ANDD [1], and JUDOCA [25], which claim to have the most accuracy among the current standard methods. The repeatability, Le, and AR are employed as the performance comparison metrics. All dataset images are transformed with different types of attacks for use as test inputs. Eighteen different rotated images have angle θ in [−90°, +90°] at 10° apart, excluding 0°. The combined transformations, including rotation and scale transform with different rotations θ in [−20, +20] at 10° apart and scale factors sx, sy in [0.9,1.3], are used for assessment. Figure 6 presents some sample results of the different methods in a normal image situation. Some FP corners are detected due to an aliasing issue on contours, especially in the ANDD method, as shown in Figure 6c.
In addition to the simple images, the proposed method indicates good performance in complex shapes. Figure 7 shows two commonly used grayscale images, a 512 × 512 Lab and 1,600 × 1,163 checkerboard used in the experiment as samples. Accurate chessboard corner detection is quite useful for camera calibrations, as used in [3].
4.1. Receiver Operating Characteristic (ROC)
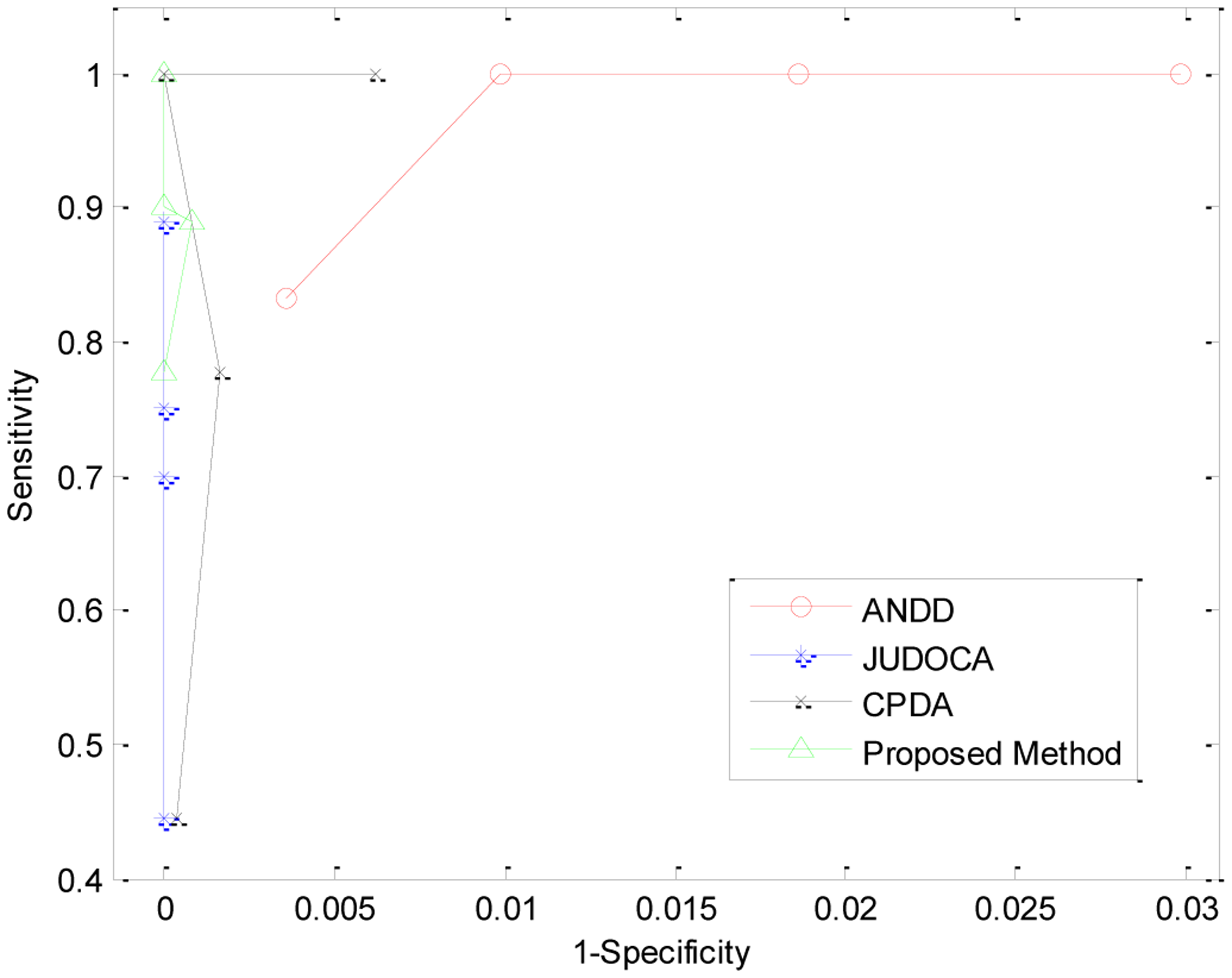
In detection theory, the receiver operating characteristic, or ROC, is a graphical plot that illustrates the performance of the system based on detection rates to provide a more appropriate comparison [48]. In this section, we used the ROC to compare the performance of different methods based on FP and true-positive (TP) rates to calculate sensitivity and specificity. Specificity relates to the detector's ability to identify negative results. Sensitivity is the ability of a detector to identify positive results. Higher sensitivity shows few FNs, and low specificity shows many FPs. Figure 8 illustrates the ROC plot of four detectors.
When comparing the performance of the detectors considering the ROC plot, a detector is better when its plot points are located on the top-left side of the plot area, which shows higher sensitivity and specificity. To determine the FNs and FPs, human judges generate the ground truth [49].
Among the detectors, CPDA attains comparable detection performance with the proposed method. The proposed method concentrates in the top-left of the graph, which indicates higher TPs and few FPs, indicating higher performance. JUDOCA provides the lowest FPs in comparison with the others, whereas ANDD shows many FPs and fewer FNs.
4.2. Localization Error
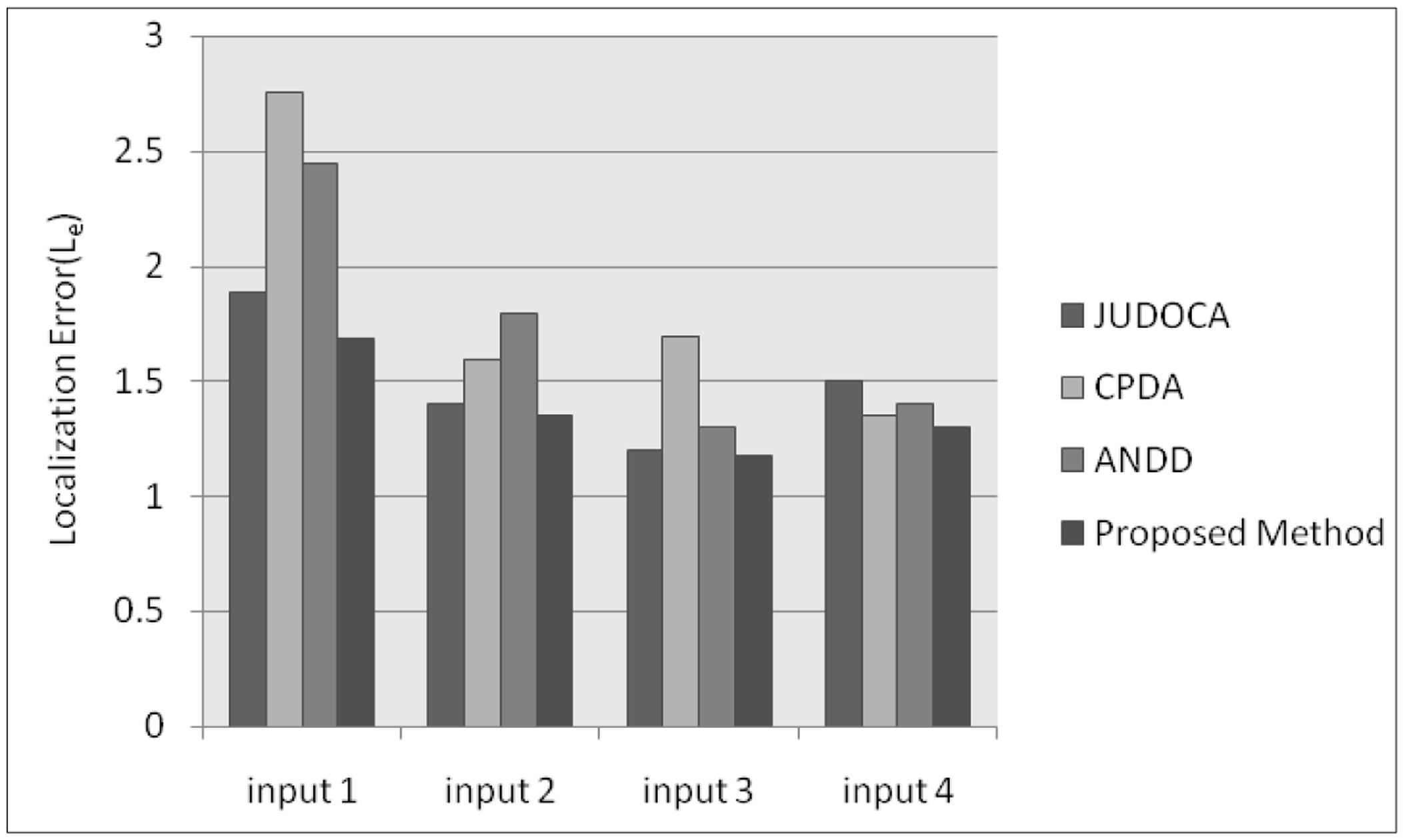
The Le is a common evaluation method for a corner detector [50]. Le can measure the robustness and accuracy of the detected corners and can be defined by:
4.3. Average Repeatability
Average repeatability (Ravg) is another evaluation method in the literature related to the corner and interest point detectors [1,51]. This method is more reliable than Le to show the robustness of the detector because it automatically calculates the average number of detected corners in the original and transformed images. This method is easier to implement, can be completely automatic without human operations and is more secure in terms of human mistakes. Average repeatability measures the robustness of the detector for different transformations and can be defined by:
To compare the proposed method with other methods, the same dataset with the same conditions is used to evaluate the results. The proposed method outperforms the other methods in different conditions. For the combined rotation and scale transform, after the proposed method, the best results are achieved by CPDA [37]. The worst average repeatability for all of the methods is for the combined rotation and scale transforms. The proposed method indicates higher average repeatability results for different effects compared to the other methods. This average repeatability is achieved because the powerful MPT method for candidate selection is applied to detect the initial candidates from the original image. Therefore, the aliasing problem, which causes several FP detections, is addressed, and the approximation of the parabolic fit method supports the localization performance by finding the point coordinates of the corners.
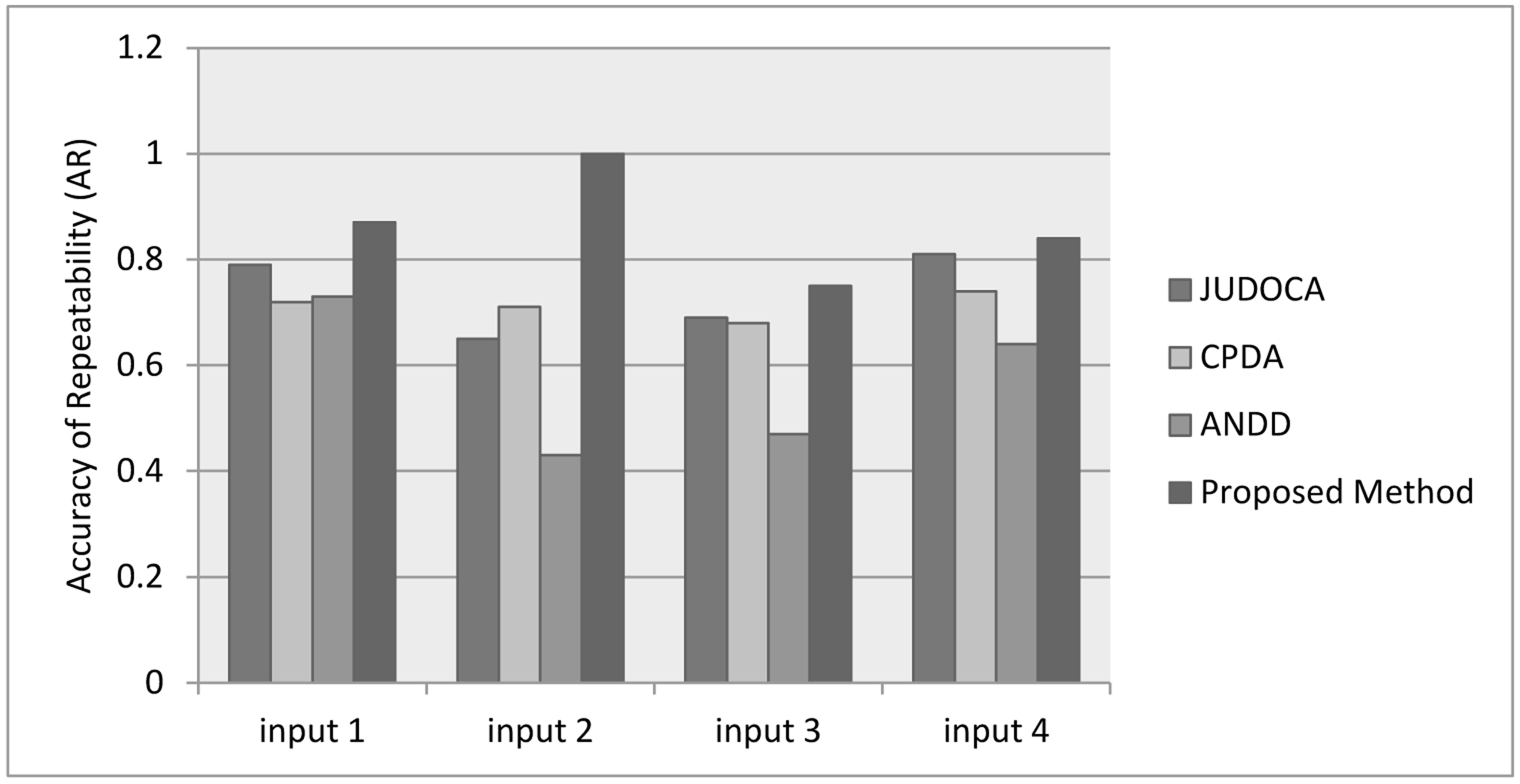
4.4. Accuracy of Repeatability
When comparing the effect of the transformation on the results, the repeatability and localization parameters are not sufficient because they do not directly consider FPs and FNs. FPs and FNs are quite important in corner detection methods and should directly affect the evolution result. Moreover, average repeatability does not consider the ground truth information, which means that it does not determine whether the detected points in the original image are localized correctly. Therefore, a new comparison method based on both the Le and the repeatability is proposed. The new comparison method, known as AR, is sensitive to FNs and FPs and thus significantly affects the FNs and FPs given in the results. Therefore, AR is a good measurement technique for corner detection methods.
In the proposed comparison method, each corner point is analyzed to provide a probability of Pi, and the mean of probability for all points generates the AR, as defined in:
In the first step, δxy = min(D) = dxy is obtained. Then, column y and row x corresponding to dxy are eliminated. Therefore, matrix D is M−1 × M′−1. This process continues until all elements in matrix D are eliminated. In each step, δxy = min(D) = dxy is the closest distance between the ground truth Gx and the result point Ry. For each point, the probability is calculated using the maximum size of the ground truth or result image, as defined in Equation (17). The maximum distance in an image is its diagonal, which is the maximum error in localization. Thus, dividing by the maximum error gives a normalized Pij between 0 and 1 that can be assumed as the correctness probability of the TP location:
5. Conclusions and Future Work
This paper introduced a new corner detection method based on contour information. Candidate selection using a new image transformation called MPT was the basic approach of this paper. MPT calculates the mean of the integral of the image contour in both the horizontal and vertical directions. After selecting the corner candidates by MPT, an efficient curvature estimation based on parabolic approximation was used to confirm and localize the corner points in the candidates. The results were evaluated by Le repeatability, and AR, which indicate the robustness and accuracy of the proposed method. AR was proposed as an evaluation metric that highlights FP and FN more than other metrics in the assessment results. The proposed method outperforms the other standard methods in terms of Le, repeatability, and AR. Future work may research the projection of the corners in different aspects and may result in better corner candidate selection and a higher repeatability and AR. An efficient corner detection algorithm can be used in different computer vision applications, such as point matching, mobile robot vision, and image registration.
Acknowledgments
The authors would like to thank the Center for Artificial Intelligence Technology (CAIT), Faculty of Information Science and Technology, National University of Malaysia (UKM) and the anonymous reviewers for their constructive comments. This research was, partially funded by the ERGS/1/2012/STG07/UKM/02/9 grant from the UKM.
Author Contributions
All authors contributed extensively to the work presented in this paper. Seyed Mostafa Mousavi Kahaki conceived the basic idea of the paper. Md Jan Nordin supervised the project. Amir Hossein Ashtari designed and performed AR evaluation metric. Seyed Mostafa Mousavi Kahaki conducted the experiment and wrote the main paper, and then Md Jan Nordin and Amir Hossein Ashtari wrote the supplementary information. The critical revision was done by Seyed Mostafa Mousavi Kahaki and Amir Hossein Ashtari.
Conflicts of Interes
The authors declare no conflict of interest.
References
- Shui, P.-L.; Zhang, W.-C. Corner detection and classification using anisotropic directional derivative representations. IEEE Trans. Image Process. 2013, 22, 3204–3218. [Google Scholar]
- Awrangjeb, M.; Lu, G.; Fraser, C.S. Performance comparisons of contour-based corner detectors. IEEE Trans. Image Process. 2012, 21, 4167–4179. [Google Scholar]
- Escalera, A.D.; Armingol, J.M. Automatic chessboard detection for intrinsic and extrinsic camera parameter calibration. Sensors 2010, 10, 2027–2044. [Google Scholar]
- Forlenza, L.; Carton, P.; Accardo, D.; Fasano, G.; Moccia, A. Real time corner detection for miniaturized electro-optical sensors onboard small unmanned aerial systems. Sensors 2012, 12, 863–877. [Google Scholar]
- Awrangjeb, M. Contour-Based Corner Detection and Robust Geometric Point Matching Techniques. Ph.D. Thesis, Monash University, Melbourne, Australia, 2008. [Google Scholar]
- Zitova, B.; Flusser, J. Image registration methods: A survey. Image Vis. Comput. 2003, 21, 977–1000. [Google Scholar]
- Hammoudi, K.; Dornaika, F. A featureless approach to 3D polyhedral building modeling from aerial images. Sensors 2011, 11, 228–259. [Google Scholar]
- Li, Y.; Olson, E. A general purpose feature extractor for light detection and ranging data. Sensors 2010, 10, 10356–10375. [Google Scholar]
- Awrangjeb, M.; Zhang, C.; Fraser, C.S. Building detection in complex scenes thorough effective separation of buildings from trees. ASPRS J. Photogramm. Eng. Remote Sens. 2012, 78, 729–745. [Google Scholar]
- Awrangjeb, M.; Zhang, C.; Fraser, C.S. Automatic extraction of building roofs using LIDAR data and multispectral imagery. ISPRS J. Photogramm. Remote Sens. 2013, 83, 1–18. [Google Scholar]
- Llorca, D.F.; Sánchez, S.; Ocaña, M.; Sotelo, M.A. Vision-based traffic data collection sensor for automotive applications. Sensors 2010, 10, 860–875. [Google Scholar]
- Rosten, E.; Porter, R.; Drummond, T. Faster and better: A machine learning approach to corner detection. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 105–119. [Google Scholar]
- Shi, J.; Tomasi, C. Good Features to Track. Proceedings of the 1994 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 21–23 June 1994; pp. 593–600.
- Moravec, H.P. Towards Automatic Visual Obstacle Avoidance. Proceedings of the 5th International Joint Conference on Artificial Intelligence, Cambridge, MA, USA, 22 August 1977; p. p. 584.
- Harris, C.; Stephens, M. A combined corner and edge detector. Proc. Alvey Vis. Conf. 1988, 1988, 23:21–23:26. [Google Scholar]
- Smith, S.M.; Brady, J.M. SUSAN-A new approach to low level image processing. Int. J. Comput. Vis. 1997, 23, 45–78. [Google Scholar]
- Gao, X.; Sattar, F.; Quddus, A.; Venkateswarlu, R. Multiscale Contour corner detection based on local natural scale and wavelet transform. Image Vis. Comput. 2007, 25, 890–898. [Google Scholar]
- Olague, G.; Hernández, B. A new accurate and flexible model based multi-corner detector for measurement and recognition. Pattern Recogn. Lett. 2005, 26, 27–41. [Google Scholar]
- Sinzinger, E.D. A model-based approach to junction detection using radial energy. Pattern Recogn. 2008, 41, 494–505. [Google Scholar]
- Mokhtarian, F.; Suomela, R. Robust image corner detection through curvature scale space. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 1376–1381. [Google Scholar]
- Han, J.H.; Poston, T. Chord-to-Point distance accumulation and planar curvature: A new approach to discrete curvature. Pattern Recogn. Lett. 2001, 22, 1133–1144. [Google Scholar]
- Awrangjeb, M.; Lu, G. An improved curvature scale-space corner detector and a robust corner matching approach for transformed image identification. IEEE Trans. Image Process. 2008, 17, 2425–2441. [Google Scholar]
- Rosenfeld, A.; Johnston, E. Angle detection on digital curves. IEEE Trans. Comput. 1973, C-22, 875–878. [Google Scholar]
- Freeman, H.; Davis, L.S. A corner-finding algorithm for chain-coded curves. IEEE Trans. Comput. 1977, C-26, 297–303. [Google Scholar]
- Elias, R.; Laganiere, R. JUDOCA: Junction detection operator based on circumferential anchors. IEEE Trans. Image Process. 2012, 21, 2109–2118. [Google Scholar]
- Noble, J.A. Finding corners. Proced. Alvey Vis. Conf. 1987, 1987, 37:31–37:38. [Google Scholar]
- Yang, Z.; Han, X.; Guo, F. A Novel Corner Detection Based on Improved SUSAN Model. In Measuring Technology and Mechatronics Automation Iv. Pts 1 and 2; Hou, Z.X., Ed.; Trans. Tech. Publications: Durnten-Zurich, Switzerland, 2012; Volume 128, pp. 469–472. [Google Scholar]
- Kovacs, A.; Sziranyi, T. Harris function based active contour external force for image segmentation. Pattern Recogn. Lett. 2012, 33, 1180–1187. [Google Scholar]
- LI, Y.; Li, J. Harris corner detection algorithm based on improved contourlet transform. Procedia Eng. 2011, 15, 2239–2243. [Google Scholar]
- Liu, Y.; Chen, H.; Guo, Y.; Sun, W.; Zhang, Y. The Research of Remote Sensing Image Matching Based on the Improved Harris Corner Detection Algorithm. In Advanced Materials and Information Technology Processing. Pts 1–3; Xiong, J.Q., Ed.; Trans. Tech. Publications: Durnten-Zurich, Switzerland, 2011; Volume 271–273, pp. 201–204. [Google Scholar]
- Liu, Y.; Hou, M.; Rao, X.; Zhang, Y. A Steady Corner Detection of Gray Level Images Based on Improved Harris Algorithm. Proceedings of the IEEE International Conference on Networking, Sensing and Control (ICNSC), Sanya, China, 6–8 April 2008; pp. 708–713.
- Zhang, X.; Ji, X.H. An Improved Harris Corner Detection Algorithm for Noised Images. In Materials Science and Information Technology. Pts 1–8; Zhang, C.S., Ed.; Trans Tech Publications Ltd: Stafa-Zurich, The Switzerland, 2012; Volume 433, pp. 6151–6156. [Google Scholar]
- Duan, X.; Zheng, G.; Chao, H. An Adaptive Real-Time Descreening Method Based on SVM and Improved SUSAN Filter. Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, Dallas, TX, USA, 14–19 March 2010; pp. 1462–1465.
- Gao, C.; Zhu, H.; Guo, Y. Analysis and improvement of SUSAN algorithm. Signal Process. 2012, 92, 2552–2559. [Google Scholar]
- He, W.; Deng, X. A Modified SUSAN Corner Detection Algorithm Based on Adaptive Gradient Threshold for Remote Sensing Image. Proceedings of the 2010 International Conference on Optoelectronics and Image Processing, Haiko, China, 11–12 November 2010; pp. 40–43.
- Zhao, J.; Ma, H.; Men, G. A New Corner Detection Algorithm with Susan Fast Hierarchical Method. Proceedings of the 2009 International Asia Symposium on Intelligent Interaction and Affective Computing, Wuhan, China, 8–9 December 2009; pp. 112–115.
- Awrangjeb, M.; Lu, G. Robust image corner detection based on the chord-to-point distance accumulation technique. IEEE Trans. Multimed. 2008, 10, 1059–1072. [Google Scholar]
- Kitchen, L.; Rosenfeld, A. Gray-level corner detection. Pattern Recogn. Lett. 1982, 1, 95–102. [Google Scholar]
- Coeurjolly, D.; Miguet, S.; Tougne, L. Discrete Curvature Based on Osculating Circle Estimation. In Visual Form; Arcelli, C., Cordella, L., Baja, G., Eds.; Springer Berlin: Heidelberg, Germany, 2001; Volumne 2059, pp. 303–312. [Google Scholar]
- Worring, M.; Smeulders, A.W.M. Digital curvature estimation. CVGIP Image Underst 1993, 58, 366–382. [Google Scholar]
- Nguyen, T.; Debled-Rennesson, I. Curvature Estimation in Noisy Curves. In Computer Analysis of Images and Patterns; Kropatsch, W., Kampel, M., Hanbury, A., Eds.; Springer Berlin: Heidelberg, Germany, 2007; Volume 4673, pp. 474–481. [Google Scholar]
- Malgouyres, R.; Brunet, F.; Fourey, S. Binomial Convolutions and Derivatives Estimation from Noisy Discretizations. In Discrete Geometry for Computer Imagery; Coeurjolly, D., Sivignon, I., Tougne, L., Dupont, F., Eds.; Springer Berlin: Heidelberg, Germany, 2008; Volume 4992, pp. 370–379. [Google Scholar]
- Kerautret, B.; Lachaud, J.-O. Robust Estimation of Curvature along Digital Contours with Global Optimization. In Discrete Geometry for Computer Imagery; Coeurjolly, D., Sivignon, I., Tougne, L., Dupont, F., Eds.; Springer Berlin: Heidelberg, Germany, 2008; Volume 4992, pp. 334–345. [Google Scholar]
- Rattarangsi, A.; Chin, R.T. Scale-based detection of corners of planar curves. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 430–449. [Google Scholar]
- Awrangjeb, M. Efficient and Effective Transformed Image Identification. Proceedings of the 2008 IEEE 10th Workshop Multimedia Signal Processing, Cairns, Australia, 8–10 October 2008; pp. 563–568.
- Yang, Z.; Seo, Y.-H.; Kim, T.-W. Adaptive triangular-mesh reconstruction by mean-curvature-based refinement from point clouds using a moving parabolic approximation. Comput. Aided Design 2010, 42, 2–17. [Google Scholar]
- Awrangjeb, M. Image Database and Corner Detection. 2007. Available online: http://users.monash.edu.au/∼mawrangj/Corner_detection_dataset.zip (accessed on 18 February 2014). [Google Scholar]
- Bowyer, K.; Kranenburg, C.; Dougherty, S. Edge detector evaluation using empirical ROC curves. Comput. Vis. Image Underst. 2001, 84, 77–103. [Google Scholar]
- Mokhtarian, F.; Mohanna, F. Performance evaluation of corner detectors using consistency and accuracy measures. Comput. Vis. Image Underst. 2006, 102, 81–94. [Google Scholar]
- Zhang, X.H.; Wang, H.X.; Smith, A.W.B.; Ling, X.; Lovell, B.C.; Yang, D. Corner detection based on gradient correlation matrices of planar curves. Pattern Recogn. 2010, 43, 1207–1223. [Google Scholar]
- Schmid, C.; Mohr, R.; Bauckhage, C. Evaluation of interest point detectors. Int. J. Comput. Vis. 2000, 37, 151–172. [Google Scholar]






© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Kahaki, S.M.M.; Nordin, M.J.; Ashtari, A.H. Contour-Based Corner Detection and Classification by Using Mean Projection Transform. Sensors 2014, 14, 4126-4143. https://doi.org/10.3390/s140304126
Kahaki SMM, Nordin MJ, Ashtari AH. Contour-Based Corner Detection and Classification by Using Mean Projection Transform. Sensors. 2014; 14(3):4126-4143. https://doi.org/10.3390/s140304126
Chicago/Turabian StyleKahaki, Seyed Mostafa Mousavi, Md Jan Nordin, and Amir Hossein Ashtari. 2014. "Contour-Based Corner Detection and Classification by Using Mean Projection Transform" Sensors 14, no. 3: 4126-4143. https://doi.org/10.3390/s140304126




