Characterization of the Bell-Shaped Vibratory Angular Rate Gyro
Abstract
: The bell-shaped vibratory angular rate gyro (abbreviated as BVG) is a novel shell vibratory gyroscope, which is inspired by the Chinese traditional bell. It sensitizes angular velocity through the standing wave precession effect. The bell-shaped resonator is a core component of the BVG and looks like the millimeter-grade Chinese traditional bell, such as QianLong Bell and Yongle Bell. It is made of Ni43CrTi, which is a constant modulus alloy. The exciting element, control element and detection element are uniformly distributed and attached to the resonator, respectively. This work presents the design, analysis and experimentation on the BVG. It is most important to analyze the vibratory character of the bell-shaped resonator. The strain equation, internal force and the resonator's equilibrium differential equation are derived in the orthogonal curvilinear coordinate system. When the input angular velocity is existent on the sensitive axis, an analysis of the vibratory character is performed using the theory of thin shells. On this basis, the mode shape function and the simplified second order normal vibration mode dynamical equation are obtained. The coriolis coupling relationship about the primary mode and secondary mode is established. The methods of the signal processing and control loop are presented. Analyzing the impact resistance property of the bell-shaped resonator, which is compared with other shell resonators using the Finite Element Method, demonstrates that BVG has the advantage of a better impact resistance property. A reasonable means of installation and a prototypal gyro are designed. The gyroscopic effect of the BVG is characterized through experiments. Experimental results show that the BVG has not only the advantages of low cost, low power, long work life, high sensitivity, and so on, but, also, of a simple structure and a better impact resistance property for low and medium angular velocity measurements.1. Introduction
The bell-shaped vibratory angular rate gyro (abbreviated as BVG) is a novel shell vibratory gyroscope, which is inspired by the Chinese traditional bell. It senses angular velocity through the standing wave precession effect. The Bell-shaped resonator is a core component of the BVG and looks like the millimeter-level Chinese traditional bell, such as QianLong Bell and Yongle Bell. BVG has not only the advantages of low cost, low power, long work life, high sensitivity, and so on, but also a simple structure and good anti-impact performance for low and medium velocity angular measurements [1–4].
The classic vibratory shell solid wave gyro includes: a hemispherical resonator gyro, a cylinder gyro, a ring vibratory gyro, a disc plant vibratory gyro, and so on [5,6]. Those are high accuracy mechanical gyros, which have a high quality factor (Q factor). At present, the HRGis the highest accuracy of coriolis vibratory gyros and has many mature products. It is widely used for aircraft navigation, strategic accuracy systems, oil borehole exploration, planetary exploration, etc. [7,8]. HRG has attracted many researchers, such as Lynch and Shatalov, about modeling the theory, processing the signal, analyzing the error, etc. [9–11]. The future development direction of HRG will be achieved through micromechanics [12]. The cylinder vibratory gyro is designed by Innalabs, Waston, BAE, and is widely used for some low and medium precision occasions, such as oil borehole exploration and vehicle navigation [13,14]. There are many researchers researching this. For example, Loveday analyzed the error of the cylinder vibratory gyro and presented an analysis method about the imperfect cylinder resonator [15]; Kristiansen researched the nonlinear model of the cylinder resonator and presented a control method and observations [16]; Wu Xuezhong analyzed the character of resonator vibration, temperature and error and presented a method of error compensation [17,18]. A ring vibratory gyro is widely used in MEMSand has many types. However, the accuracy is lower and lower than HRG [19–22]. The hemispherical resonator of HRG is made of quartz, which does not bear high impact. Besides, HRG used electrostatic excitation and capacitance detection, which are complex and expensive. The cylinder vibratory gyro is made of metal and uses the piezoelectric element to excite and detect. However, the impact resistance property, accuracy and vibration stability are restricted by the structure of the cylinder. Pointing to this condition, Innalabs uses the quartz to fabricate the resonator. In this way, the cylinder vibratory gyro improves accuracy and stability. However, the impact resistance property and cost are influenced by the material [23]. In conclusion, a high impact resistance, low cost, high performance gyro is in great need for the current market.
The proposed bell-shaped vibratory angular rate gyro is inspired by the traditional Chinese bell. Changing the resonator structure of the traditional vibratory gyro improves accuracy and impact resistance. There are many characteristics of the traditional Chinese bell, which includes beautiful sound, vibration stability, a steady mode shape, good impact resistance, etc. Therefore, the project group decided to use the bell structure to make the vibratory gyro, which is named the bell-shaped vibratory angular rate gyro; the resonator is bell-shaped. It is made by a constant modulus alloy, using piezoelectricity to excite and detect. This improves the impact resistance property and maintains the advantages of low cost and high performance. It is desired that the bell structure improves the performance of the gyro. For the novel structure of the gyro, the project group published an article, which describes the design procedure and preliminary experimentation and does not deeply analyze the theory of the BVG. Besides, the angle of the standing wave precession is detected through a capacitance sensor [24]. In the 1970s, Lynch and other researchers proposed a bell gyro. It is the same as a hemispherical resonator gyro, different from the BVG [25–27]. Since then, there has been no other resource published.
There are many problems using a bell structure to make a gyro. It is difficult to analyze the bell-shaped resonator, because the vibratory character is very complex and the middle surface is not described using the single linear function. To summarize, the revolution vibratory shell finds a method to solve the vibratory problem of a bell-shaped resonator. For the HRG, VA Matveev and other researchers used the theory of a thin shell to analyze the character of a hemispherical resonator. He presents the equilibrium differential equation and derives the governing equation [1]. This method is an important method for HRG, currently. Shatalov, Kristiansen and others used the Hamilton principle to analyze the character of the HRG and presented a simplified equation [10,16]. Leissa and others used the Ritz-Rayleigh analysis method to research the character of many types of revolution shell in the vibration control field. However, it only analyzes the natural frequency based on assuming the mode shape [28,29]. For the bell-shaped resonator, it chooses the thin shell theory to solve the problem. Others methods have many hypotheses that are not appropriate for a bell-shaped resonator [1,30]. The structure of a bell-shaped resonator chooses the parabolical structure. It is convenient to analyze and model. Based on the structure, this paper analyses the vibratory character of a bell-shaped resonator and designs the prototypal gyro.
In this article, we explore bell-shaped resonator structure and present the design, analysis and experimentation of the BVG. The important work is as follows: to design the structure of a bell-shaped resonator and present the principle of the work, shown in Section 2. In Section 3, a theoretical analysis of the proposed resonator is performed using the theory of thin shells. The strain equation, internal force and resonator's equilibrium differential equation are derived in the orthogonal curvilinear coordinate system. On this basis, the mode shape function and the simplified second order normal vibration mode dynamical equation are obtained. In Section 4, the coriolis coupling relationship about the primary mode and secondary mode is established. The method of the signal processing of the BVG and the control loop of the prototype are presented. In Section 5, to analyze the impact resistance property of the bell-shaped resonator, which is compared with other shell resonators using the Finite Element Method, demonstrates that the BVG has the advantage of better impact resistance. In Section 6, a reasonable method of installation and a prototypal gyro are designed. The gyroscopic effect of the BVG is characterized through experimentation. Experiment results show that the BVG has not only the advantages of low cost, low power, long work life, high sensitivity, and so on, but also a simple structure and better impact resistance for low and medium angular velocity measurements. Finally, some important conclusions are drawn.
2. Design Concept
2.1. The Structure of the Gyroscope
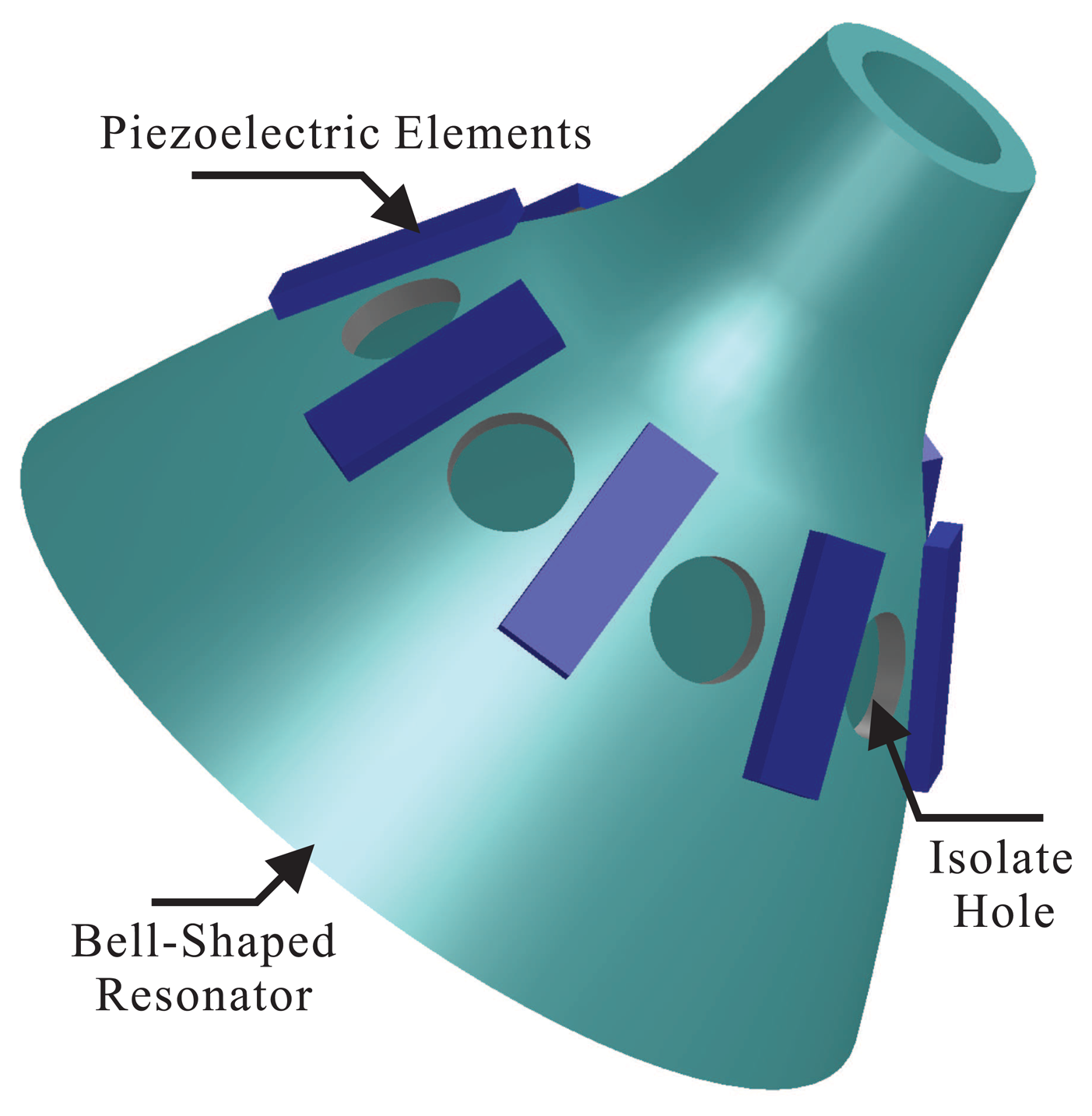
The core component of the BVG is a bell-shaped resonator, which influences the performance of the gyro directly. The key of the BVG is the structure of the bell-shaped resonator. The bell-shaped resonator is inspired by the traditional Chinese bell, as shown in Figure 1. As far as we known, there are many characteristics of traditional Chinese bells that includes beautiful sound, vibration stability, steady mode shape, high impact resistance etc. The technology of multiple surface fusions is very important. However, it has not been explained clearly until now [31]. It is convenient to describe a bell-shaped resonator using the revolution parabolic structure, which maintains the vibratory character of the traditional bell, as shown in Figure 2.
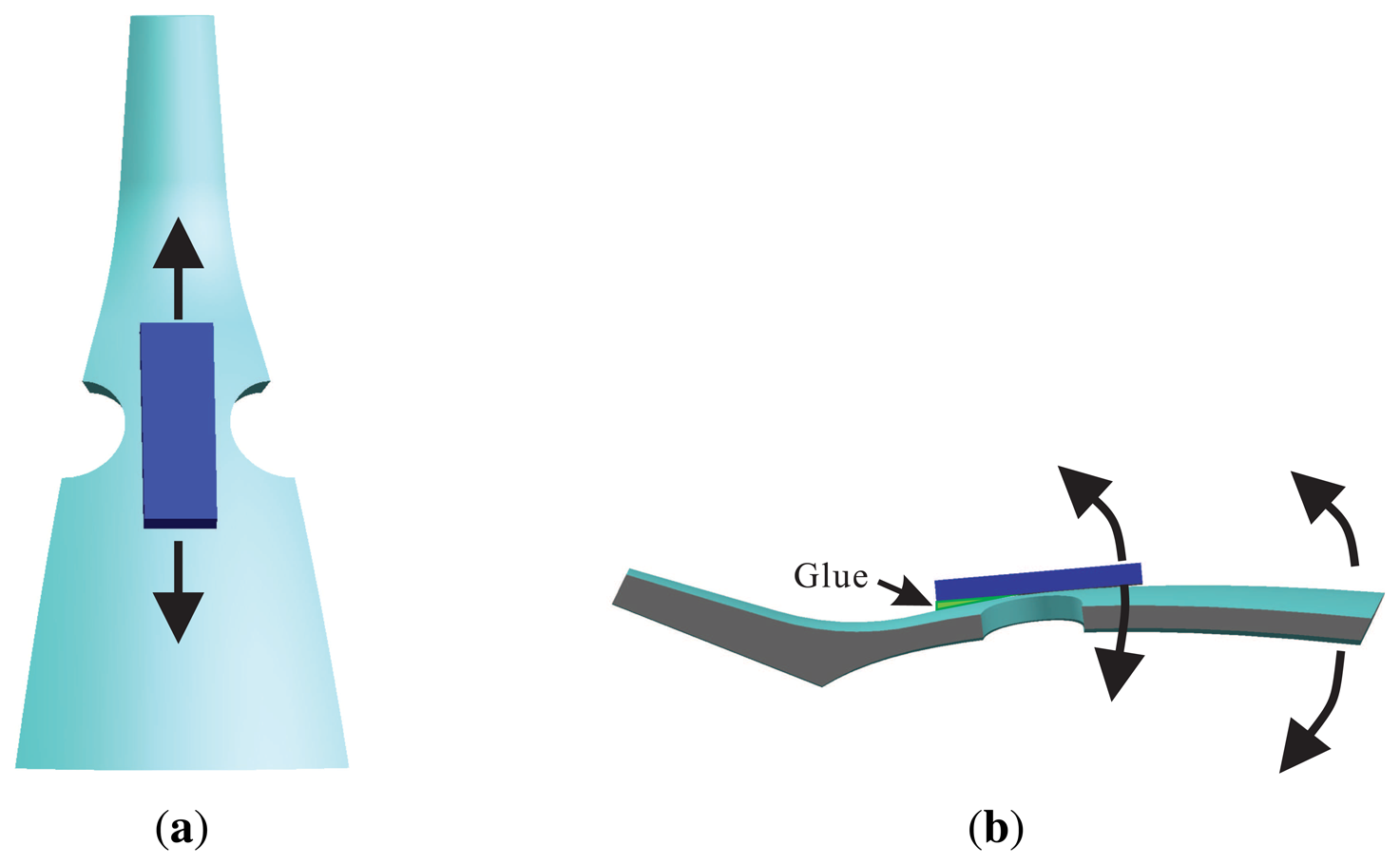
The bell-shaped resonator looks like the traditional bell, which is designed by a parabolic structure intuitively. In order to reduce the cost and design procedure, the structure of the top, middle and bottom merge into a parabola, and this is achieved to integrate the design. This merge does not change the vibratory character of the structure. The position of the excitation electrode and the detection electrode is very important for the BVG. For the actual bell, to excite bell vibration, one uses a stick to hit the wall of the bell. The vibration effect is very significant. However, the bell-shaped resonator selects the position on the wall of bell. In order to ensure the power consumption and cost of the gyro, it controls the mode shape and detects the precession of the standing wave based on piezoelectricity. The piezoelectric elements are attached to the wall of the bell-shaped resonator to excite the primary mode and detect the second mode. Using the isolated hole reduces the disturbance between neighboring electrodes, as shown in Figure 3.
2.2. Working Principle
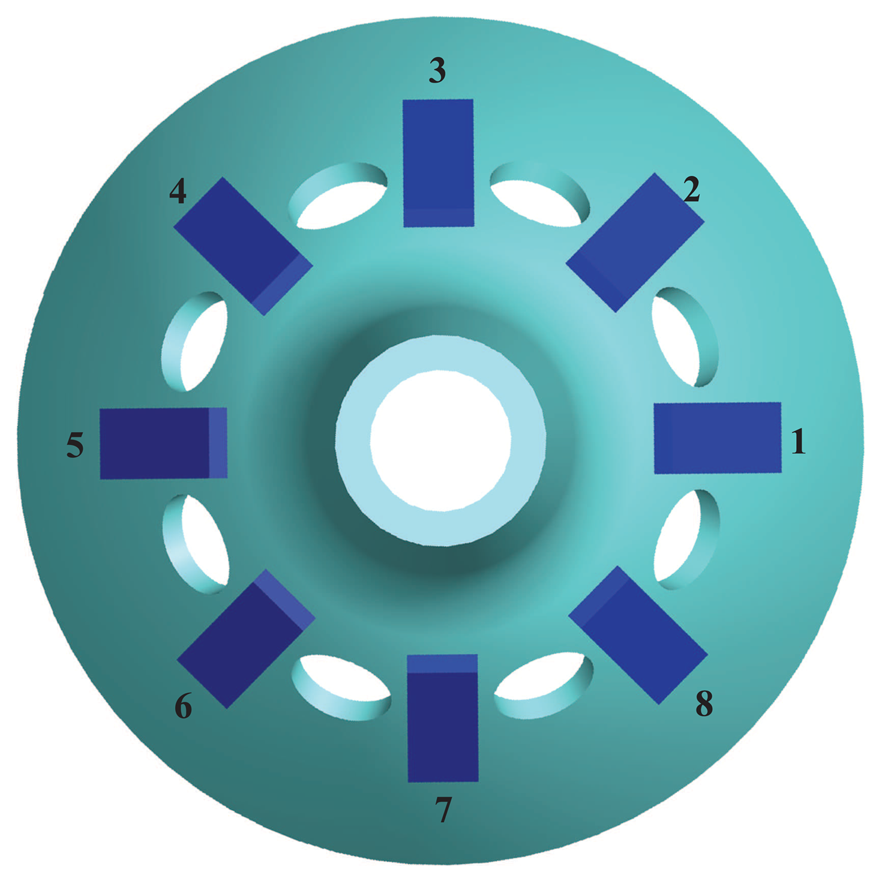
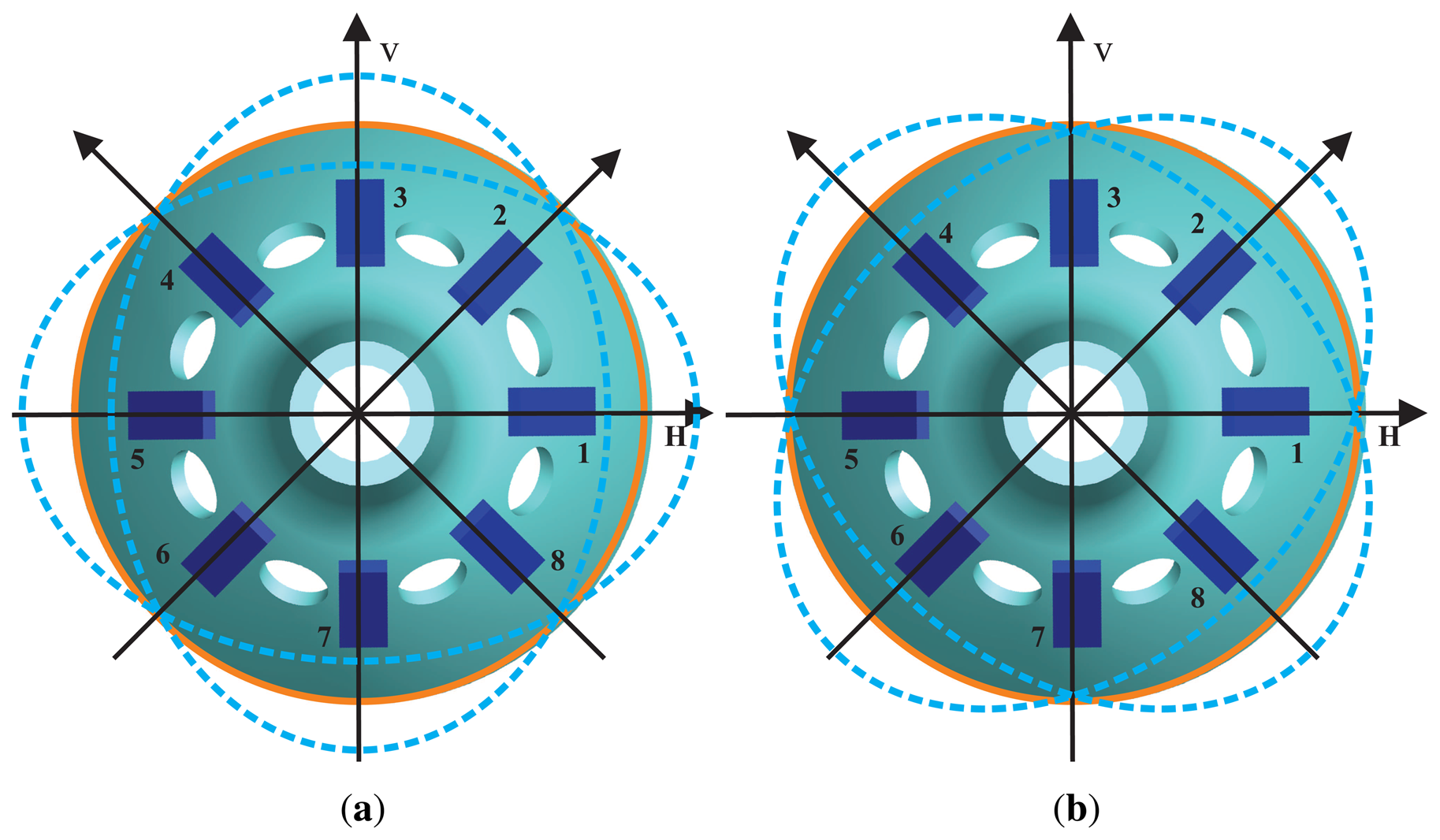
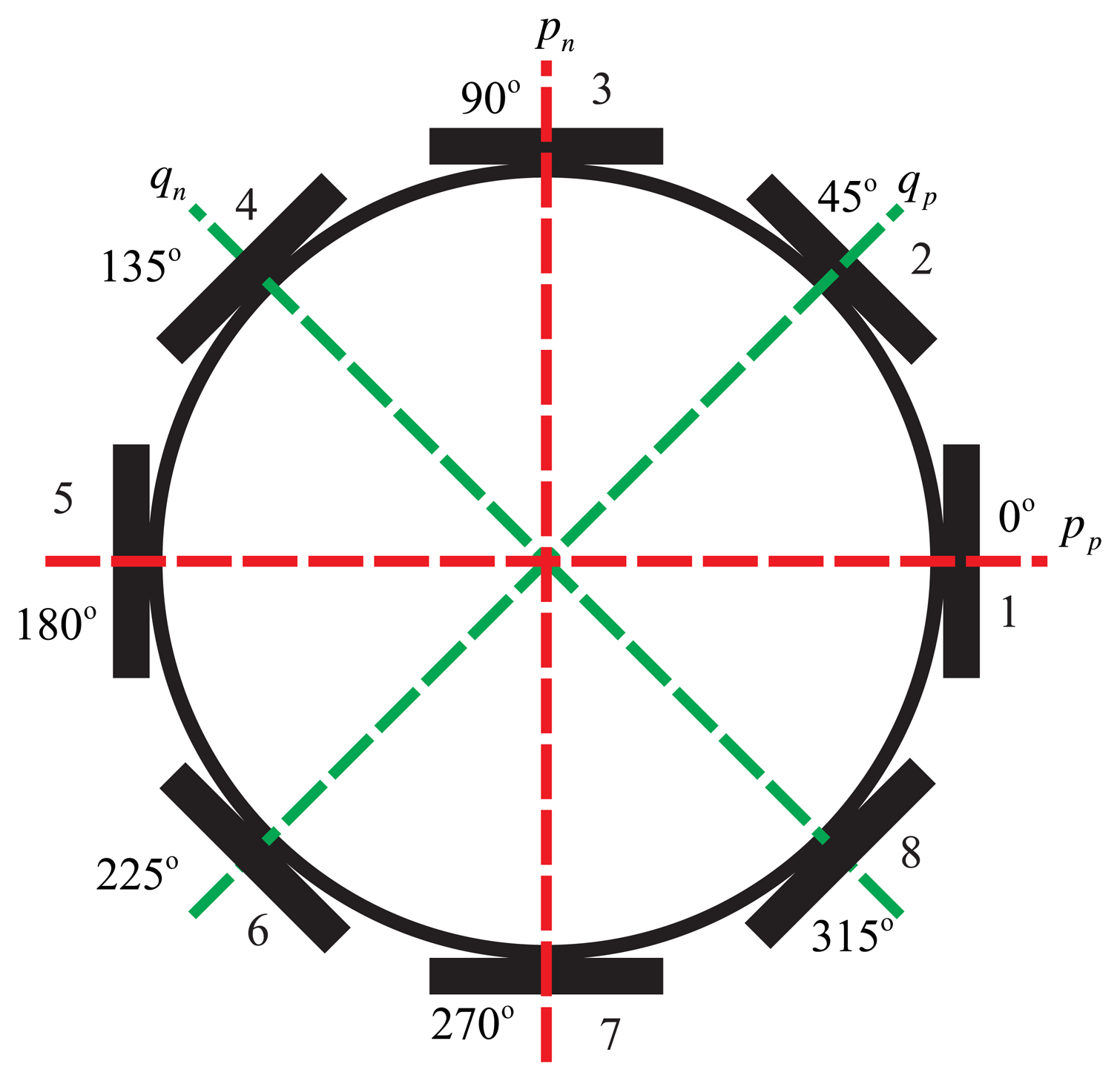
The BVG sensitizes angular velocity through the standing wave precession effect. The eight piezoelectric elements are attached to the wall of the bell-shaped resonator uniformly, as shown in Figure 4. Based on the inverse piezoelectric effect, excitation electrodes excite the bell-shaped resonator, and the resonator produces a work mode, which is named the primary mode or the excite mode, shown in Figure 5a. For the vibration shell, the same work frequency has two types of modes, which are different, 45°. The other mode is named the second mode or sensitive mode, shown in Figure 5b. The coriolis couples them. The amplitude of the second mode is proportional to the input angular velocity and produces the standing wave precession. In Figure 6, when the angular velocity is applied to the axis of symmetry counterclockwise, the sanding wave angle changes. The precession angle is –ϑ and proportional to the frame rotation angular velocity.
During practical application, the stress wave propagates on the resonator, causing the standing wave, and the piezoelectric elements sensitize the stress wave and solve the angular velocity. In order to reduce the influence of piezoelectric elements when the resonator is rotated and to improve the excitation efficiency, the elements should be set near the constrained boundary. Such an excitation type is like the principle of leverage, using a small amount of force to achieve a large deformation to improve the excitation efficiency.
The piezoelectric elements chose the PZT5A, which was polarized in the thickness direction. The first and fifth elements contract and expand while applying an alternating current signal (in Figure 7a). When the top of the elements are bounded, the contraction and expansion force will transfer to the bend force (in Figure 7b) and excite the shell vibration. The piezoelectric elements and resonator are attached together by conductive adhesives. Controlling the painting procedure makes a rigid connection between them. The one pole of elements connected to the resonator is the GND, the others are the signal of the input or output. The piezoelectric element senses the vibratory signal based on the piezoelectric effect. Using the third and seventh element feedback signals and the first and fifth excitation elements, standing wave steady control is achieved. The control loop includes an amplitude control loop and a frequency control loop. With particular emphasis, the work mode of the BVG is the force-rebalance mode [15,18]. The second and sixth elements sensitized angle of precession is used as the controller input to drive the fourth and eight elements to restrain the precession of standing wave. The amplitude of restrain variable is proportional to the angular velocity and is used as the output signal of the BVG after calibration.
3. Modeling and Simulation
For the shell vibratory gyro, the analysis of the resonator vibratory character is very important and focuses on the mode shape function, precession factor and natural frequency. The BVG is a novel structure in the vibratory gyro field and has a unique vibratory character. The analysis of internal force distribution and the equilibrium differential equation are presented using the theory of thin shells. It derives the simplified second normal vibration mode dynamic equation based on the parameters of the gyro.
3.1. Coordinate System
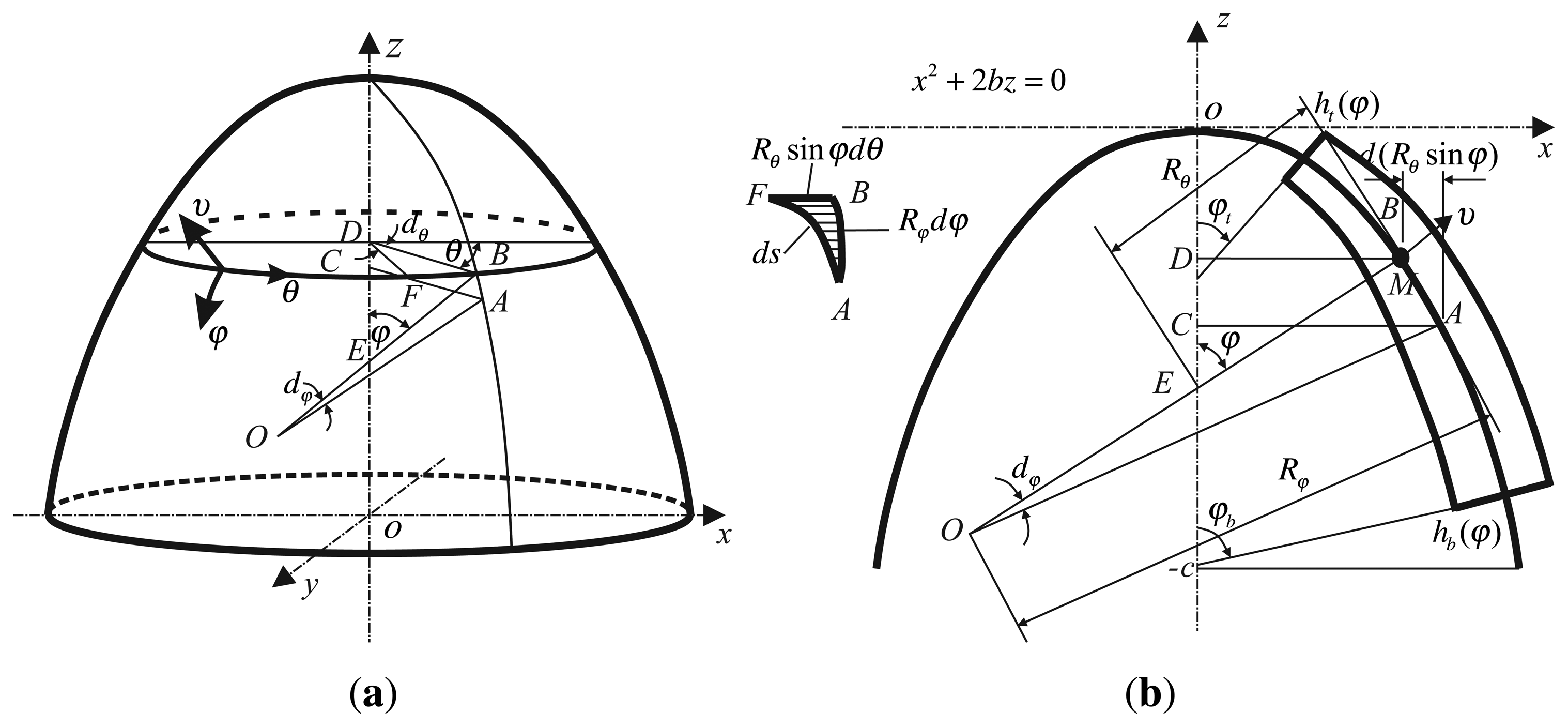
The bell-shaped resonator is a parabolical structure and described in the orthogonal curvilinear coordinate system (φ, θ, v), shown in Figure 8[32,33]. In the Cartesian coordinate system, oxyz, the axis of symmetry is axis z. The cross-section is shown in Figure 8b. The origin is used as the peak of the parabola, described in coordinates as:
In Figure 8, the principal curvature is the direction of the meridian and circumference, respectively. The three axis are (φ, θ, v), where φ is the angle between the normal vector of the tangent and the axis of symmetry on the bell-shaped resonator; θ is the circumference angle; v is the thickness of the resonator. The variable basic relationship is as follows in Appendix A.
In the orthogonal curvilinear coordinate system, it is not only convenient to describe the point motion, but also to express the thickness of the resonator. The vibratory character of the bell-shaped resonator is presented in this coordinate.
3.2. Shell Equations of the Resonator
Based on the theory of thin shells and the Kirchhoff-Lyav hypothesis, the bell-shaped resonator's character as presented includes the relationship of internal force, the equilibrium differential equation and the dynamic equation [1,34,35].
3.2.1. Strain Equation
For the isotropic three-dimensional elastic shell element, the middle surface geometric equation of the bell-shaped resonator is obtained in the orthogonal curvilinear coordinate system, (φ, θ, v). It can be expressed as:
Substituting Equation (2) into Equation (3), the linear strain is as follows:
3.2.2. Internal Force
Based on the transformation relation in the orthogonal curvilinear coordinate system and the expression of internal force in the theory of thin shells, the internal force of the bell-shaped resonator is presented. Using the relations between the mechanical force and stress, one can derive the mechanical membrane forces and bending moments for the bell-shaped resonator [32–34]:
3.2.3. Equilibrium Differential Equation
According the the D'Alembert principle, if the sum of force and inertial force and the torque are all equal to zero, which is applied to the isolated unit, then the unit is in a state of equilibrium. The bell-shaped resonator is fit for this principle. As far as we know, the middle surface of the bell-shaped resonator cannot stretch. The three components of tangential displacement in the shell bending equation are equal to zero. It can be expressed as [1]:
The normal force and shearing force are equal to zero:
Therefore, we can derive the equilibrium differential equation (for specific derivation, see Appendix B):
The angular velocity, Ω, is along the axis of symmetry in the inertial space; the expression is:
According to the Coriolis Theorem, the absolute velocity of point P motion relative to inertial space can be expressed as:
The absolute acceleration is as follows:
The load of rotation is the load of the middle surface on the bell-shaped resonator and derived in:
Substituting Equation (15) into Equation (21) derives the equilibrium differential equation:
3.3. The Second Order Normal Vibration Mode Dynamical Equation
To solve the Equation (15), the displacement vector of an arbitrary point in the bell-shaped resonator is developed according to the second order normal vibration mode, which is not stretched:
According to Equations (13) and (14), the relationship is:
Equation (24) describes the boundary condition of the bell-shaped resonator. The solution of this equation is named the mode shape function or Rayleigh functions [33]:
Substituting Equation (23) into Equation (22), the differential equation is about p (t) and q (t). Calculating using Maple finds that the equation is too complex to solve using the traditional method. For the HRG, the equation is easier than the BVG, which is solved through the Bubnov-Galerkin method [36-38]. The equation of BVG is too complex to simplify (for specific derivation, see Appendix C).
For Equation (22), the equilibrium differential equation and dynamic equation are presented, which include control force and torque. It means that the governing equation of the control loop is achieved about the bell-shaped resonator. For the Coriolis Vibratory Gyro, the simplified second order normal mode of the resonator is the second order orthogonal spring system. It can be expressed as [1,10,39,40]:
The precession factor is:
The typical analytical method does not solve this complex problem, but it clearly describes the vibratory procedure, the force and equilibrium relation. In practice, the Finite Element Method is widely used for the bell-shaped resonator to analyze the natural frequency, mode shape and work mode.
3.4. Mode Shape of Resonator
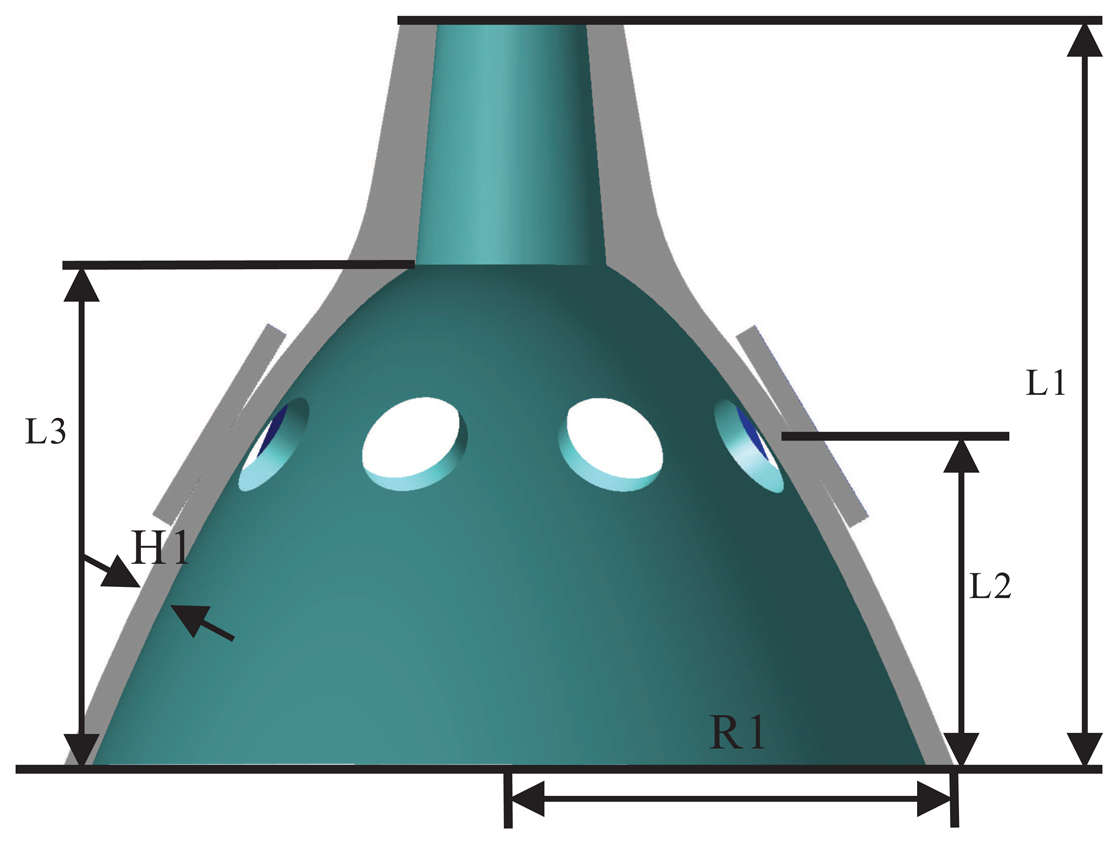
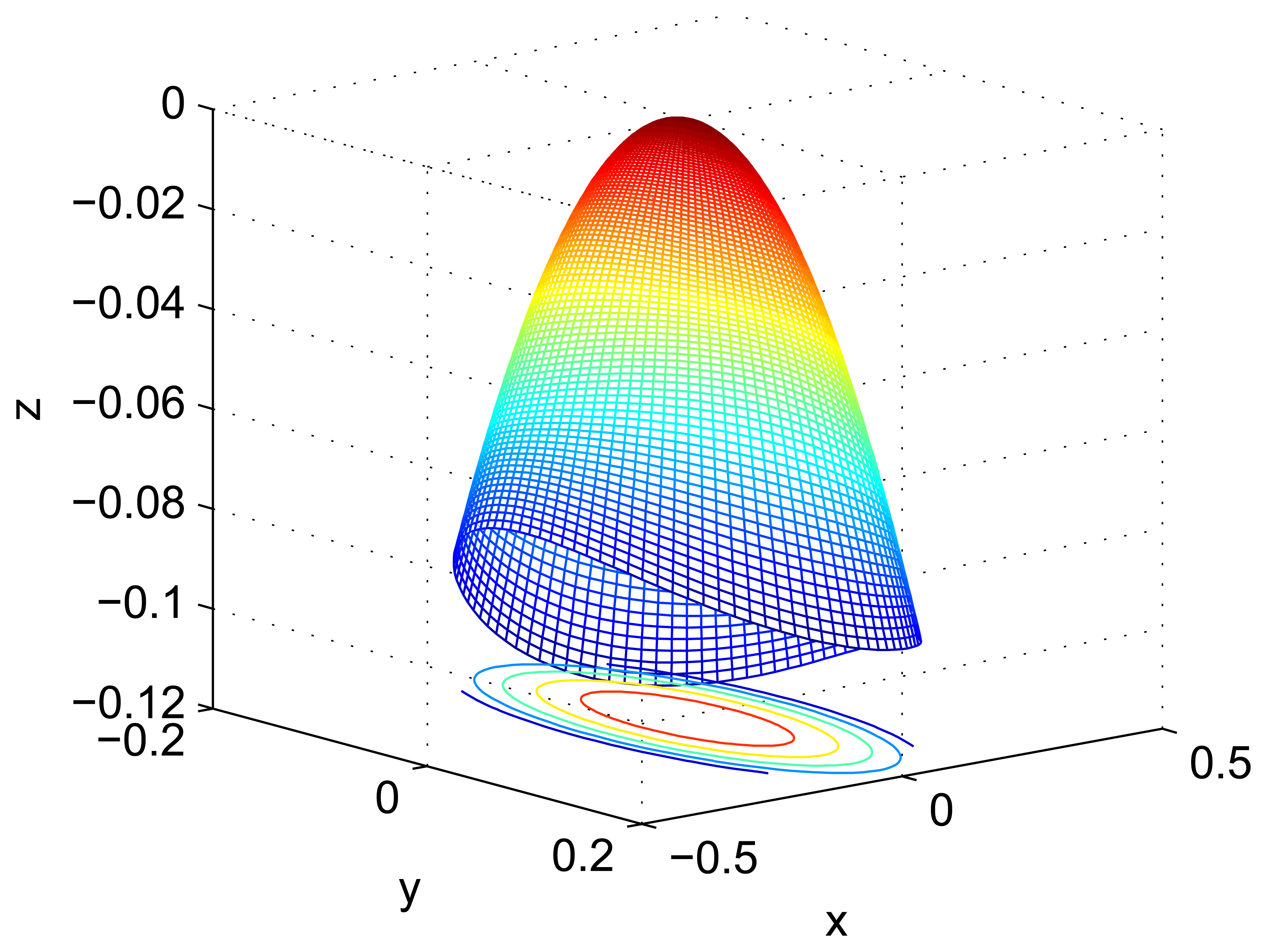
Analysis of the vibratory character is based on the theory of thin shells. It is very necessary to know the overall mode shape of the bell-shaped resonator. The modal simulation is presented using FEM. The main structure parameters of the resonator are as follows: L1 = 21 mm, R1 = 11 mm, H1 = 0.7 mm, L2 = 9 mm, L3 = 15 mm; as shown in Figure 9. The material parameters and simulation condition is followed in Table 1. The modal analyzed results show the work mode shape in Figure 10, and the natural frequency is: 5, 909.3 Hz. The mode shape is a four antinode shape.
Using the mode shape function of Section 3.3, the simulation result is shown in Figure 11 in Matlab. This demonstrates that the Equation (25) is similar as the result of FEM. However, the amplitude of the mode shape is different between them. The reason is about the error of simulation and amplitude coefficient.
4. Governing Equation and Signal Process
The mode shape control about the standing wave on the circumference is very important for the BVG. Equation (27) describes the second order normal mode of the resonator that is a traditional second order spring system. This type of equation is a simplified Foucault Pendulum function. The form of the standing wave is the foundation of the governing equation and signal process of the BVG. The transversal surface of the standing wave of the bell-shaped resonator is shown in Figure 12.
The transversal surface of the standing wave is the vibratory ring. On the ring, there are two rigid axes, p and q. p is the axis of the primary mode, and q is the axis of the second mode [41,42]. Coriolis force couples the motion between two axes, p and q. In Figure 12, the pn is the control axis of p (first and fifth element); pp is the sensitive axis of p (third and seventh element); qn is the control axis of q (second and sixth element); qp is the sensitive axis of q (fourth and eighth element). The relationship of p and q is described in Equation (27). In the literature [15,16,36,39], researchers present the general vibratory equation for the coriolis vibratory gyro:
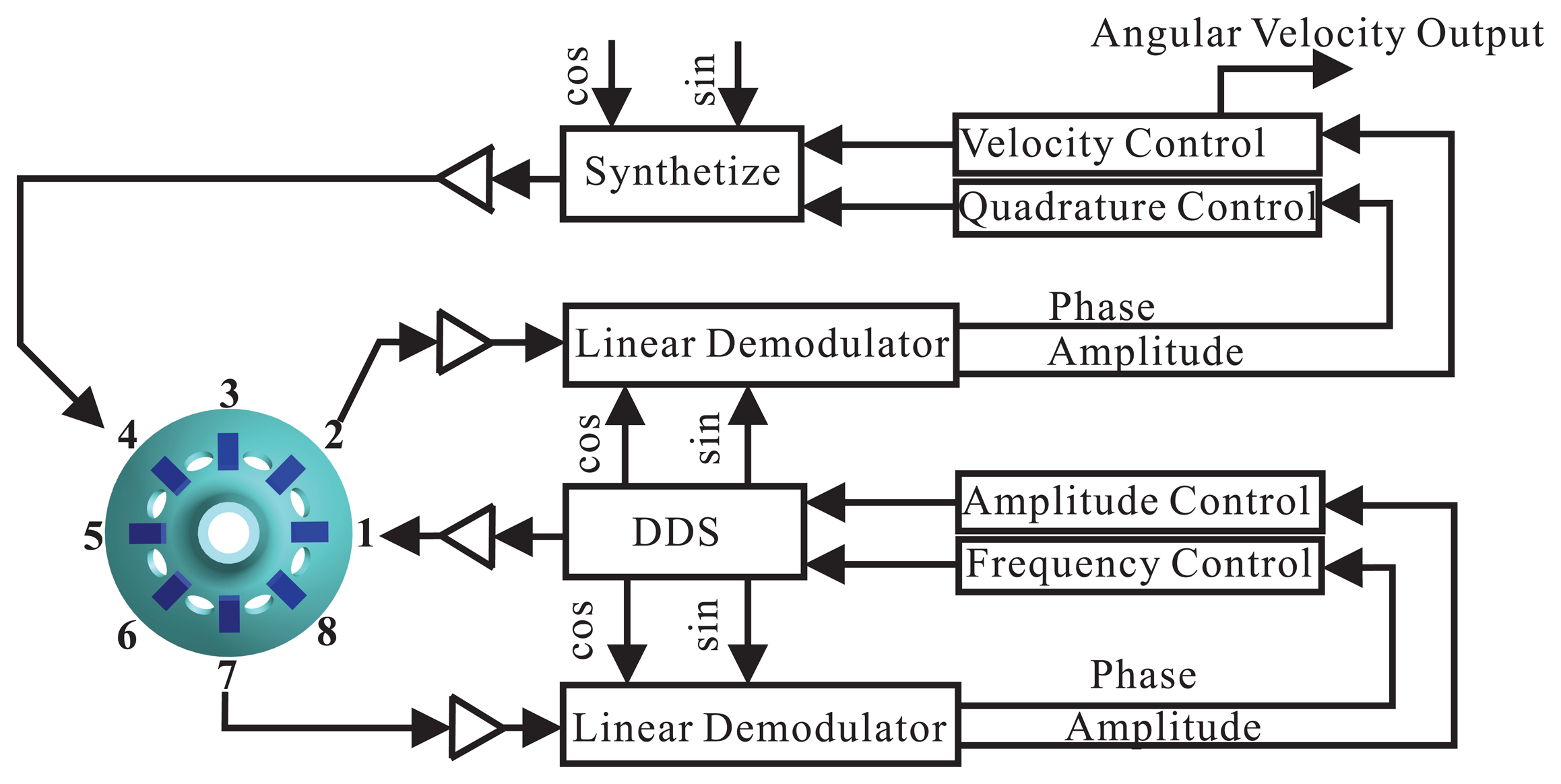
The diagram of the BVG signal process method is shown in Figure 13. The control loops include an amplitude control loop, a frequency control loop, a quadrature control loop and a rate control loop [13–15,18]. The authors had written an article about this in the The 32nd Chinese Control Conference [40]. It will be published in July 2013.
5. Analysis of Impact Dynamic
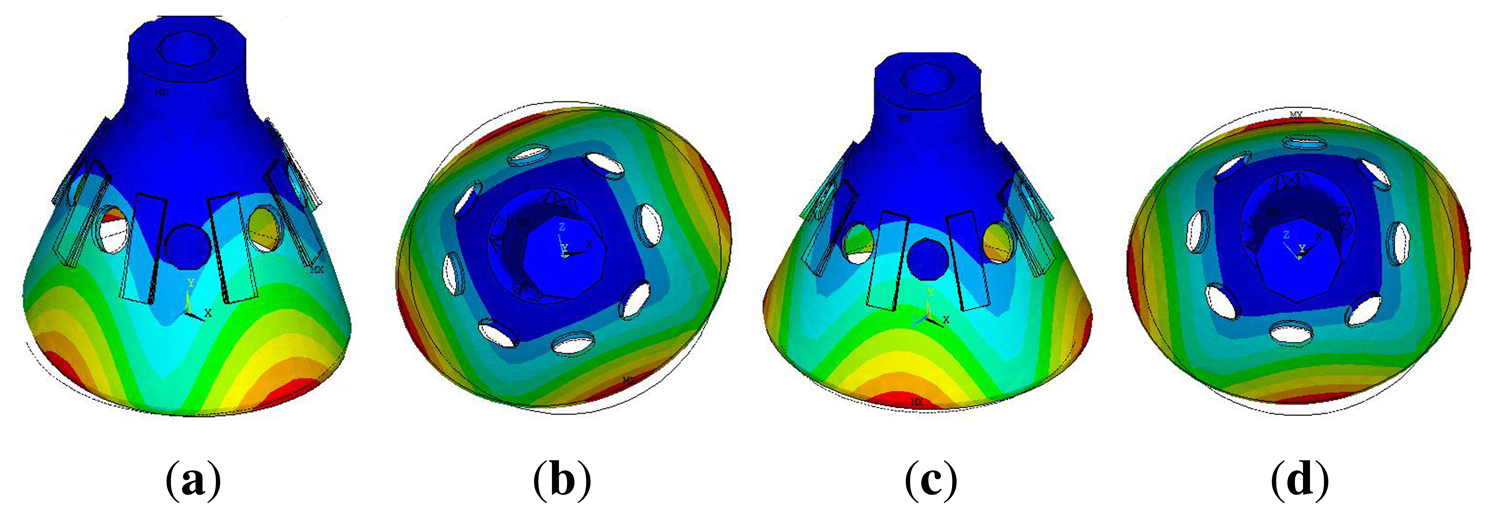
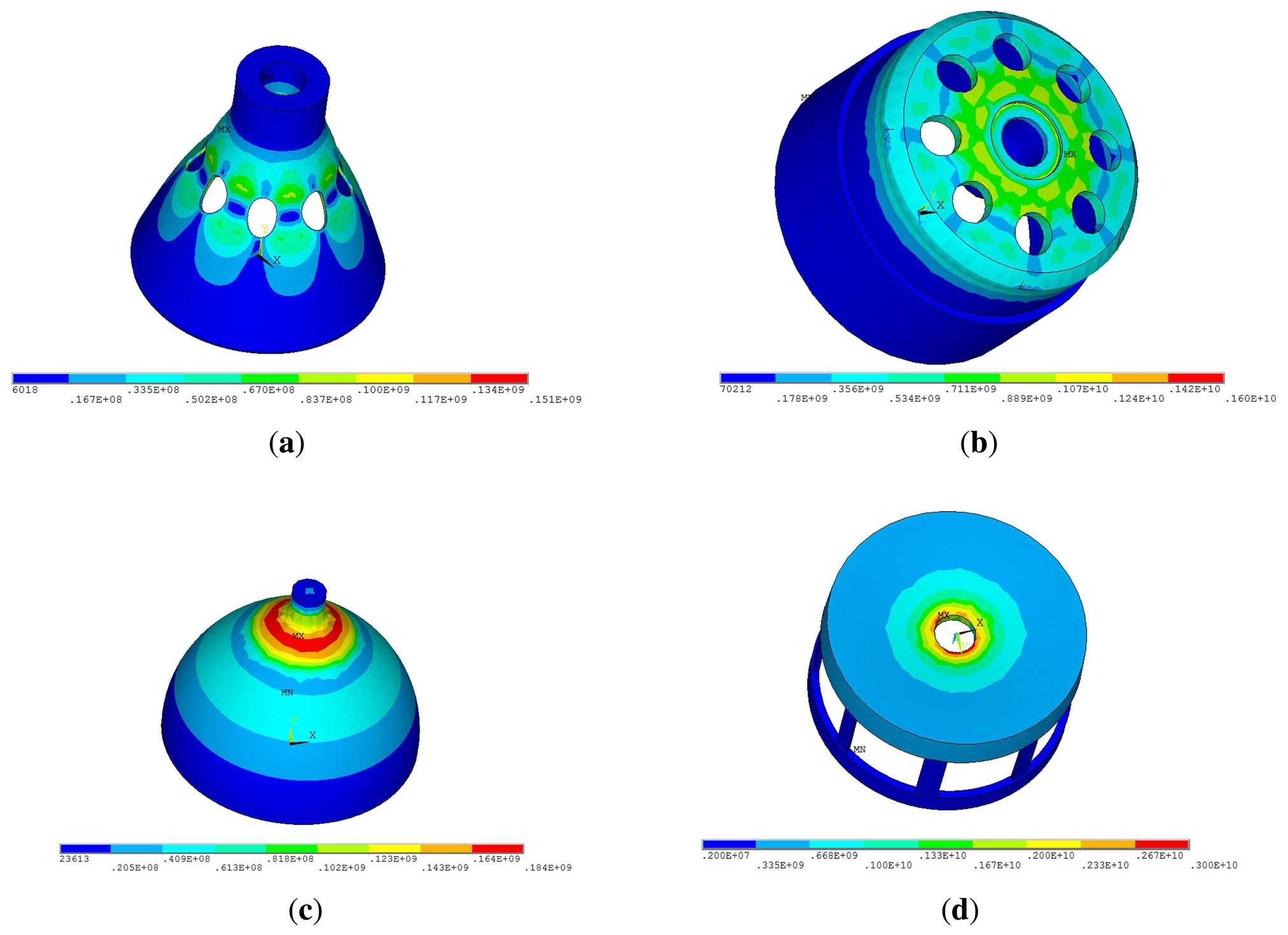
The bell-shaped vibratory angular rate gyro's greatest strength is its remarkable impact resistance property. Using FEM to compare the hemispherical resonator gyro [1], the cylinder vibratory gyro [17] and the novel ring vibratory gyro [18] in the 20,000 × g gravitational field, the stress cloud charts are shown in Figure 14. All the gyro have the same height (21 mm), the same edge width (22 mm) and the same thickness (0.7 mm) using Ni43CrTi. The simulation condition is the same same as the paper [24].
The maximum stress of HRG is 181 MPa; the cylinder vibratory gyro is 1,600 MPa; the novel ring vibratory gyro is 3,000 MPa; the BVG is 151 MPa. The result shows that the bell-shaped resonator has the best impact resistance property. Based on the mechanics of materials, the tensile strength of Ni43CrTi is 500 MPa. Therefore, the bell-shaped resonator does not get damaged in 20,000 × g. During the impact process, the resonator produces a small deformation. It is quickly restored after the impact. The control loop also can restrain the influence of the small deformation, too.
6. Fabrication and Experiments
6.1. Fabrication
The main structure of the BVG includes the bell-shaped resonator, a fixed axis and a foundation. These connect together through mechanical technology, as shown in Figure 15. The procedure is as follows:
Step1: The piezoelectric element with the wire attached on the wall of the bell-shaped resonator;
Step2: The fixed axis fastens the bell-shaped resonator to the foundation;
Step3: The wire connects to the insulated joint on the foundation.
Finally, the 9 wires connected to the signal process system include 8 wires of piezoelectric elements and GND. The wires connect to the circuit board through the insulated joint, which is installed on the foundation. The prototypal bell-shaped resonator is shown in Figure 16.
6.2. Experiment
The experiment of the bell-shaped resonator includes: natural frequency test, mode shape test, coriolis test and gyroscopic effect test. The natural frequency and mode shape have been tested in [24]. In this paper, it focuses on the other test.
6.2.1. Coriolis Test
The sine alternating current signal (Vpp = 10V) is applied to the first and fifth element. In order to readout the signal clearly, the output signal of the piezoelectric element is processed by the operator amplitude and summed by the piezoelectric element with the same axis. In the test, the Lissajous pattern is a good method to analyze the coriolis effect about the two axes, p and q. The oscilloscope that was chosen is the Tektronix TDS 3032B. Channel 1 connects to the pp axis, used as x. Channel 2 connects the qp axis, used as y. When Ω = 0, the picture is as shown in Figure 17a. When Ω ≠ 0, the picture is as shown in Figure 17b.
During the test, the bell-shaped resonator is in an uncontrolled situation. The frequency split of the tested bell-shaped resonator is 0.5 Hz. In the static state, the two axes exit the vibratory coupling. This described Lissajous pattern is not the line. When the angular velocity is applied to the sensitive axis, the couple effect is very obvious and the standing wave produces precession. The bell-shaped resonator is already sensitive to the coriolis effect.
6.2.2. Gyroscopic Effect Test
The prototypal BVG includes power, a signal sample board and a signal processing board, as shown in Figure 18.
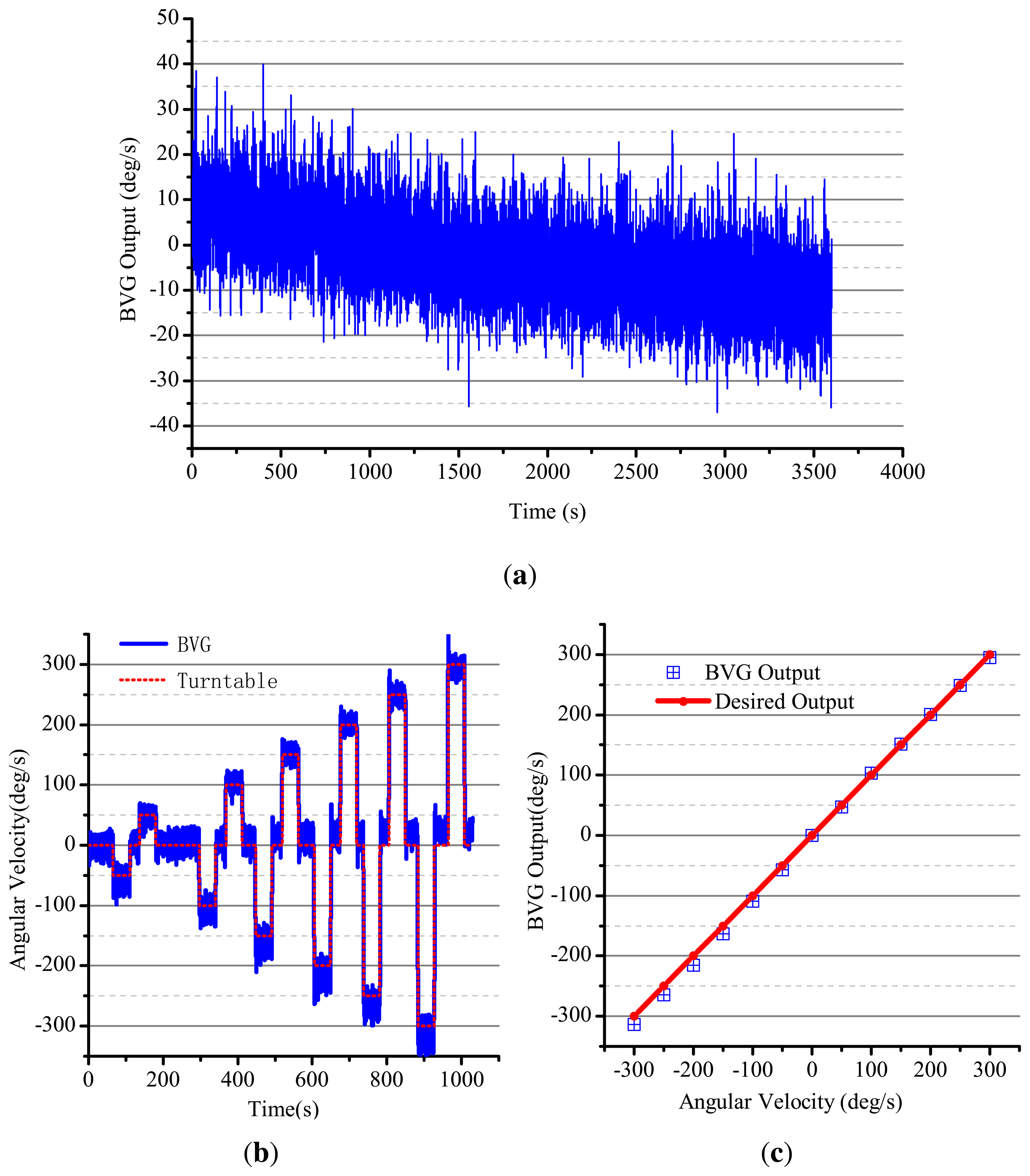
The BVG is fixed on the high-precision angular velocity turntable to test the gyroscopic effect. The results are shown in Figure 19. According to the original output of the BVG, only thick calibration of the BVG is convenient for analysis. The range of the BVG is about ±300°/s. The zero drift curve is shown in Figure 19a. The noise of the gyro is very large, and the signal to noise ratio (SNR) is low. The dynamic experiment curve is shown in Figure 19b,c. Using the 50 Hz FIRfilter, the zero drift instability is 22.5°/h and linearity is 1.24%. This index can be controlled by the filter. The index is poorer than the other shell vibratory gyro [13,14,18]. The reason for the poor performance is as follow:
The manufacturing technology has imperfections. Specifically, the piezoelectric element is difficult to stick on the resonator with a curved surface of variable curvature.
There is no temperature compensation for the bell-shaped resonator. The long work time leads to a change of the frequency and influences the drift. The bell-shaped resonators vibratory characteristics change as the temperature changes.
Structure processing error and control loop error exist. Improving the method of restraining the frequency split and designing the control loop is needed.
The parameters of the governing equation of the bell-shaped resonator are not exact.
In the future, important work is needed: improving the manufacturing technology and the control loop design, designing a temperature compensation method, etc. The performance of a prototypal BVG is not satisfactory, but the method of design and analysis is demonstrated perfect.
7. Conclusions
Based on the orthogonal curvilinear coordinate system, the equilibrium differential equation using the theory of thin shells is presented, and the motion of the point on the bell-shaped resonator is described. The vibratory character of the resonator is analyzed with the input angular velocity. On this basis, the mode shape function and the simplified second order normal vibration mode dynamical equation are obtained. The Coriolis coupling relationship about the primary mode and the secondary mode is established. The method of signal processing of the BVG and the control loop of the prototype is presented. To analyze the impact resistance property of the bell-shaped resonator, which is compared with the other shell resonator using the Finite Element Method, demonstrates that the BVG has the advantage of better impact resistance property. A reasonable means of installation and the prototypal gyro are designed. The gyroscopic effect of the BVG is characterized through experimentation. The experimental results shows that the zero drift instability is 22.5°/h and linearity is 1.24%. The index is poorer than other shell vibratory gyros. The main reason is: the manufacturing technology has imperfections; there is not any temperature compensation; structure processing error and control loop error exist; the parameters of the governing equation of the bell-shaped resonator are not exact. In the future, important work includes improvement of the performance of the BVG. In conclusion, the BVG has not only the advantages of low cost, low power, long work life, high sensitivity, and so on, but also a simple structure and better impact resistance for low and medium angular velocity measurements.
Acknowledgments
This work is supported by the National Nature Science Foundation of China (Grant No.61031001, 61261160497).
A. Variable Basic Relationship
The variable basic relationship is as follows:
Differential of arc length:
Differential of volume:
Curvature:
Radius of curvature:
Lame constants:
Domain of definition:
where φt is the angle between the normal vector of the tangent and the axis of symmetry on the bell-shaped resonator top edge; φb is the bottom edge; h (φ) is the thickness of the resonator, which is about φ.
B. Equilibrium Equation
According to the theory of thin shells, the basic equilibrium is as follows in Equation (37):
For the orthogonal curvilinear coordinate system:
Using the hypothesis condition in the paper, the equilibrium differential equation is derived.
C. Solution of Equilibrium Equation
The solution of Equation (22) is derived by the Bubnov-Galerkin method [1,34,38,39,43]. Substituting Equations 10–12 into Equation (15), as follows in Equation (39):
The Nφ, Nθ, Nv are the left form of Equation (39);, the motion equation, L, of the bell-shaped resonator circumferential direction is as follows in Equation (41):
Substituting the variables into Equation (41), it is derived by the Bubnov-Galerkin method, as follows:
For the orthogonal curvilinear coordinate system:
Simplifying, Equation (43) is as follows in Equation (44):
The dynamic equation of the bell-shaped resonator is derived through the integral operation. However, the equation is too complex to solve. Using the difference method solves this equation, maybe. This work is ongoing.
Conflict of Interest
The authors declare no conflict of interest.
References
- Matveev, V.; Basarab, M. Solid State Wave Gyro; National Defense Industry Press: Beijing, China, 2009. [Google Scholar]
- Hopkin, I.D.; Fell, C.P.; Townsend, K.; Mason, T.R. Vibrating Structure Gyroscope. U.S. Patent 5932804 1999. [Google Scholar]
- Singh, A. Piezoelectric gyro sensor technology. Def. Sci. J. 2007, 57, 95–103. [Google Scholar]
- Burdess, J.; Harris, A.; Cruickshank, J.; Wood, D.; Cooper, G. A review of vibratory gyroscopes. Eng. Sci. Educ. J. 1994, 3, 249–254. [Google Scholar]
- Shkel, A.M. Type I and Type II Micromachined Vibratory Gyroscopes. Proceedings of 2006 IEEE/ION PLANS—Position, Location, And Navigation Symposium, San Diego, CA, USA, 25–27 April 2006; pp. 24–27.
- Yang, J. A review of analyses related to vibrations of rotating piezoelectric bodies and gyroscopes. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2005, 52, 698–706. [Google Scholar]
- Rozelle, D.M. The Hemispherical Resonator Gyro: From Wineglass to the Planets. Proceedings of 19th AAS/AIAA Space Flight Mechanics Meeting, Savannah, GA, USA, 8–12 February 2009; pp. 1157–1178.
- Matthews, A.; Rybak, F. Comparison of hemispherical resonator gyro and optical gyros. IEEE Aerosp. Electron. Syst. Mag. 1992, 7, 40–46. [Google Scholar]
- Lynch, D.D.; Savava, R.R.; Campanile, J.J. Hemispherical Resonator Gyro Control. U.S. Patent 7318347 2008. [Google Scholar]
- Shatalov, M.Y.; Joubert, S.V.; Coetzee, C.E. The influence of mass imperfections on the evolution of standing waves in slowly rotating spherical bodies. J. Sound Vib. 2011, 330, 127–135. [Google Scholar]
- Wang, X.; Wu, W.; Fang, Z.; Luo, B.; Li, Y.; Jiang, Q. Temperature drift compensation for hemispherical resonator gyro based on natural frequency. Sensors 2012, 12, 6434–6446. [Google Scholar]
- Stewart, R.E. Micro Hemispheric Resonator Gyro. U.S. Patent 8109145 2012. [Google Scholar]
- Chikovani, V.; Okon, I.; Barabashov, A.; Tewksbury, P. A Set of High Accuracy Low Cost Metallic Resonator CVG. Proceedings of 2008 IEEE/ION PLNS—Position, Location and Navigation Symposium, Monterey, CA, USA, 5–8 May 2008; pp. 238–243.
- Watson, W.S. Vibratory Gyro Skewed Pick-off Driver Geometry. Proceedings of 2010 IEEE/ION PLNS—Position, Location and Navigation Symposium, Indian Wells, CA, USA, 4–6 May 2010; pp. 171–179.
- Loveday, P.W. Analysis and Compensation of Imperfection Effects in Piezoelectric Vibratory Gyroscopes. Ph.D. Thesis, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 1999. [Google Scholar]
- Kristiansen, D. Modeling of Cylinder Gyroscopes and Observer Design for Nonlinear Oscillations. Ph.D. Thesis, Department of Engineering Cybernetics Norwegian University of Science and Technology, Trondheim, Norwegian, 2000. [Google Scholar]
- Xi, X.; Wu, Y.; Wu, X.; Tao, Y.; Wu, X. Modeling and analysis of the stress effects for trimmed cupped resonator under varying temperature. Sens. Actuators A Phys. 2013, 185, 429–440. [Google Scholar]
- Tao, Y.; Wu, X.; Xiao, D.; Wu, Y.; Cui, H.; Xi, X.; Zhu, B. Design, analysis and experiment of a novel ring vibratory gyroscope. Sens. Actuators A Phys. 2011, 168, 286–299. [Google Scholar]
- Gallacher, B. Principles of a Micro-Rate Integrating Ring Gyroscope. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 658–672. [Google Scholar]
- Ayazi, F.; Najafi, K. A HARPSS polysilicon vibrating ring gyroscope. Microelectromech. Syst. J. 2001, 10, 169–179. [Google Scholar]
- Yoon, S.W.; Lee, S.; Najafi, K. Vibration sensitivity analysis of MEMS vibratory ring gyroscopes. Sens. Actuators A Phys. 2011, 171, 163–177. [Google Scholar]
- Asokanthan, S.F.; Cho, J. Dynamic stability of ring-based angular rate sensors. J. Sound Vib. 2006, 295, 571–583. [Google Scholar]
- Chikovani, V.; Yatsenko, Y.A.; Barabashov, A.; Marusyk, P.; Umakhanov, E.; Taturin, V. Improved accuracy metallic resonator CVG. IEEE Aerosp. Electron. Syst. Mag. 2009, 24, 40–43. [Google Scholar]
- Su, Z.; Fu, M.; Li, Q.; Liu, N.; Liu, H. Research on bell-shaped vibratory angular rate gyros character of resonator. Sensors 2013, 13, 4724–4741. [Google Scholar]
- Loper, E.J., Jr.; Lynch, D.D. Sonic Vibrating Bell Gyro. U.S. Patent 4157041 1979. [Google Scholar]
- Lynch, D.D. Bell Gyro Improved Means for Operating. U.S. Patent 3656354 1972. [Google Scholar]
- Denis, R.E. Bell Gyro Method of Making Same. U.S. Patent 3680391 1972. [Google Scholar]
- Kang, J.H.; Leissa, A. Three-dimensional field equations of motion, and energy functionals for thick shells of revolution with arbitrary curvature and variable thickness. J. Appl. Mech. 2001, 68, 953–954. [Google Scholar]
- Leissa, A.W.; Kang, J.H. Three-dimensional vibration analysis of paraboloidal shells. JSME Int. J. Ser. C 2002, 45, 2–7. [Google Scholar]
- Qatu, M.S.; Sullivan, R.W.; Wang, W. Recent research advances on the dynamic analysis of composite shells: 2000–2009. Compos. Struct. 2010, 93, 14–31. [Google Scholar]
- Ansari, J. Finite Element Vibration Analysis and Modal Testing of Bells. Proceedings of the 2006 IJME-INTERTECH Conference, Union, NJ, USA, 19–21 October 2006.
- Tzou, H.; Ding, J. Optimal control of precision paraboloidal shell structronic systems. J. Sound Vib. 2004, 276, 273–291. [Google Scholar]
- Hao, Y.H. Research on an Active Control of Precision Smart Flexible Paraboloidal Shell Systems. Ph.D. Thesis, Harbin Institued of Technology, Heilongjiang, China, 2009. [Google Scholar]
- Lun, X.Z. Elasticity; Higher Education Press: Beijing, China, 2009. [Google Scholar]
- Leissa, A.W. Vibration of Shells; Scientific and Technical Information Office, National Aeronautics and Space Administration: Washington, DC, USA, 1973. [Google Scholar]
- Lynch, D. Vibratory Gyro Analysis by the Method of Averaging. Proceedings of 2nd Saint Petersburg Conf. on Gyroscopic Technology and Navigation, Saint Petersburg, Russia, 24–25 May 1995; pp. 26–34.
- Qi, J.; Chen, X.; Ren, S.; Wang, C. Dynamic Error Mechanism Analysis of HRG. Proceedings of 2008 IEEE 2nd International Symposium on Systems and Control in Aerospace and Astronautics, Shenzhen, China, 10–12 December 2008; pp. 1–6.
- Zhao, H.B.; Ren, S.Q.; Li, W. Establishment of dynamics equation of HRG resonator and calculation of natural frequency. Harbin Gongye Daxue Xuebao (in Chinese) 2010, 42, 1702–1706. [Google Scholar]
- Lynch, D. Coriolis Vibratory Gyros; Symposium Gyro Technology: Stuttgart, Germany, 1998. [Google Scholar]
- Liu, N.; Su, Z.; Liu, H. Research on Control Loop for Solid Vibratory Gyroscope. Proceedings of The 32nd Chinese Control Conference, Xi'an, China, 26–28 July 2013.
- Yoon, S.W.; Lee, S.; Najafi, K. Vibration sensitivity analysis of MEMS vibratory ring gyroscopes. Sens. Actuators A 2011, 171, 163–177. [Google Scholar]
- Eley, R.; Fox, C.; McWilliam, S. Coriolis coupling effects on the vibration of rotating rings. J. Sound Vib. 2000, 238, 459–480. [Google Scholar]
- Wang, X.; Fang, Z.; Wu, W.Q.; Lou, B.; Li, Y. Procession analysis of HRG resonator based on two dimensional mass vibrations. J. Chin. Inert. Technol. 2011, 19, 121–126. [Google Scholar]






| Name of the Parameters (Unit) | Value |
|---|---|
| Material | Ni43CrTi (3J53) |
| Density (kg/m3) | 8,170 |
| Poisson's ratio | 0.3 |
| Young modulus (GPa) | 196.76 |
| Yield strength (MPa) | 500 |
| Simulation method | Transient dynamic |
| Mesh generation method | Free |
| Release ratio | 1E – 4 |
| Piezoelectric element | PZT-5A |
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Liu, N.; Su, Z.; Li, Q.; Fu, M.; Liu, H.; Fan, J. Characterization of the Bell-Shaped Vibratory Angular Rate Gyro. Sensors 2013, 13, 10123-10150. https://doi.org/10.3390/s130810123
Liu N, Su Z, Li Q, Fu M, Liu H, Fan J. Characterization of the Bell-Shaped Vibratory Angular Rate Gyro. Sensors. 2013; 13(8):10123-10150. https://doi.org/10.3390/s130810123
Chicago/Turabian StyleLiu, Ning, Zhong Su, Qing Li, Mengyin Fu, Hong Liu, and Junfang Fan. 2013. "Characterization of the Bell-Shaped Vibratory Angular Rate Gyro" Sensors 13, no. 8: 10123-10150. https://doi.org/10.3390/s130810123




