Advanced Respiratory Motion Compensation for Coronary MR Angiography
Abstract
: Despite technical advances, respiratory motion remains a major impediment in a substantial amount of patients undergoing coronary magnetic resonance angiography (CMRA). Traditionally, respiratory motion compensation has been performed with a one-dimensional respiratory navigator positioned on the right hemi-diaphragm, using a motion model to estimate and correct for the bulk respiratory motion of the heart. Recent technical advancements has allowed for direct respiratory motion estimation of the heart, with improved motion compensation performance. Some of these new methods, particularly using image-based navigators or respiratory binning, allow for more advanced motion correction which enables CMRA data acquisition throughout most or all of the respiratory cycle, thereby significantly reducing scan time. This review describes the three components typically involved in most motion compensation strategies for CMRA, including respiratory motion estimation, gating and correction, and how these processes can be utilized to perform advanced respiratory motion compensation.1. Introduction
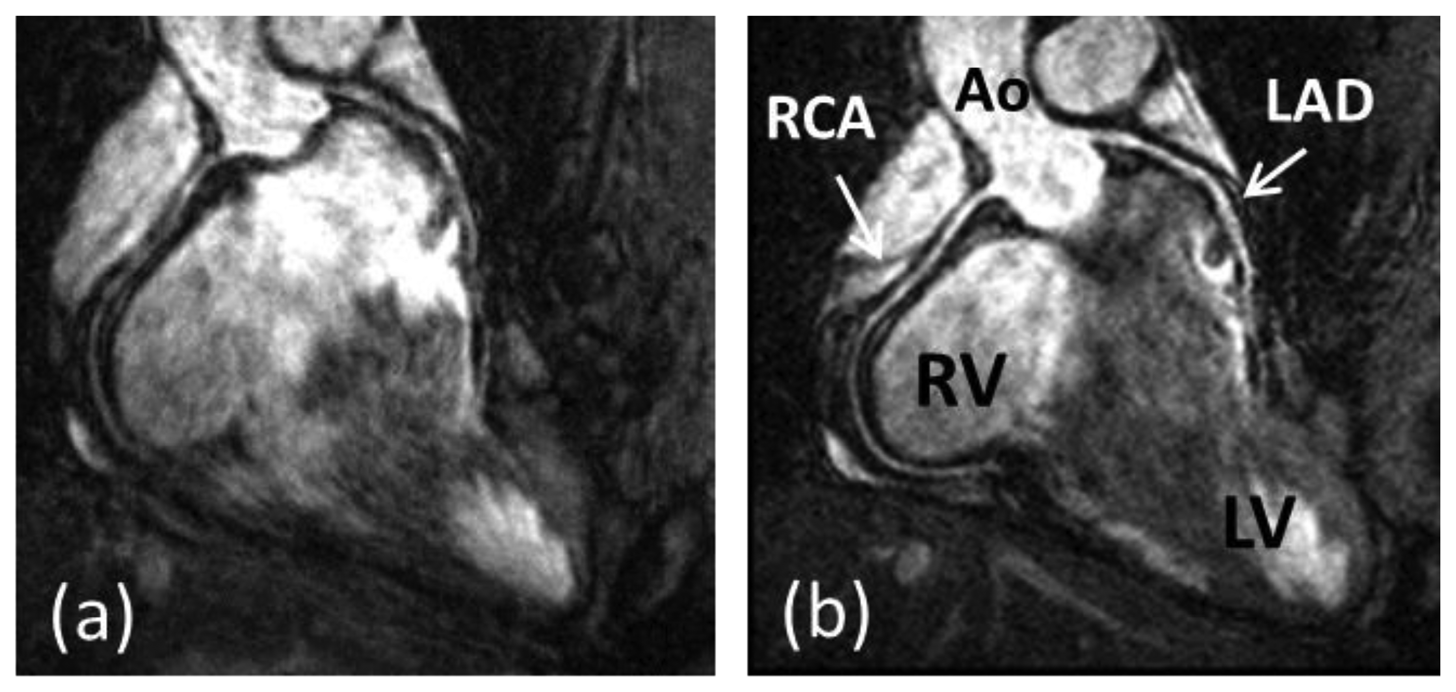
Coronary artery disease (CAD) is the leading cause of death in the Western world and developing countries [1]. The gold standard imaging modality for detection of CAD is X-ray angiography, which is invasive, exposes patients to potentially harmful radiation and requires iodinated contrast agents. Multi-Detector Computed Tomography (MDCT) has been shown to be a reliable technique for non-invasive detection of coronary artery stenosis [2]. However, MDCT, like X-ray, utilizes ionizing radiation. Furthermore, the diagnostic accuracy of MDCT is reduced in patients with heavily calcified plaques. In recent decades coronary magnetic resonance angiography (CMRA) has emerged as a non-invasive alternative for the diagnosis of CAD without exposing patients to potentially harmful radiation or nephrotoxic contrast agents. But despite advancements in CMRA hardware and software techniques, artifacts due to residual coronary artery motion remain an impediment to diagnostic CMRA in a small but significant amount of patients. Several studies have investigated respiration induced coronary motion along the foot–head (FH), left–right (LR), and anterior–posterior (AP) directions throughout the respiratory cycle [3–6]. Although the principal motion component is predominately in the FH direction and is often one order of magnitude larger than the CMRA spatial resolution, the displacement magnitude in the LR or AP direction has high subject specific variability and can contribute to motion artifacts in CMRA. Furthermore, rotation and non-rigid motion such as affine or even non-linear deformation may occur between the end-expiratory and end-inspiratory respiratory phase [7–10]. As a result, CMRA is particularly susceptible to respiratory motion artifacts due to the relatively slow data acquisition speed of MRI and the high spatial resolution required to visualize the coronary artery lumen. The main coronary arteries, which consist of the right coronary artery (RCA) and the left main (LM) artery which branches into the left anterior descending (LAD) artery and left circumflex (LCX) artery, have a diameter of approximately 3 mm in the proximal coronary segments which reduces to 1 mm in more distal segments. A respiratory motion corrupted CMRA dataset is shown in Figure 1(a), along with the same dataset after respiratory motion correction in Figure 1(b), reformatted to visualize the RCA and LAD.
For diagnostic purposes it is desirable to detect obstructive coronary stenosis of at least 50% reduction of the coronary lumen. Thus, CMRA spatial resolution is typically on the order of 0.7 to 1.3 mm. This extends the CMRA scan time beyond what can be comfortably acquired within a breath-hold. In comparison, due to superior acquisition speed, X-ray angiography and MDCT allows for data acquisition with sub-millimeter resolution within a single breath-hold, which effectively minimizes the problem or respiratory motion. Although respiratory motion compensation in the early days of CMRA involved breath-holding [12], image acquisition typically only employed two-dimensional (2D) encoding and therefore provided limited coverage of the coronary arteries [13–15]. As the coronary arteries are long and tortuous, three-dimensional (3D) coverage is important to visualize one or more coronary arteries in a single scan. Developments in MRI acceleration techniques including partial Fourier [16] and parallel imaging [17,18] have enabled 3D CMRA data acquisitions within a single breath-hold [19–21]. Further acceleration may be achieved with compressed sensing [22–24] although its efficacy in conjunction with breath-hold CMRA has yet to be established. Notwithstanding these technical developments, the relatively long breath-hold durations of approximately 20–25 s may be difficult to achieve in patients with CAD which is why free-breathing motion compensated CMRA approaches are typically favoured.
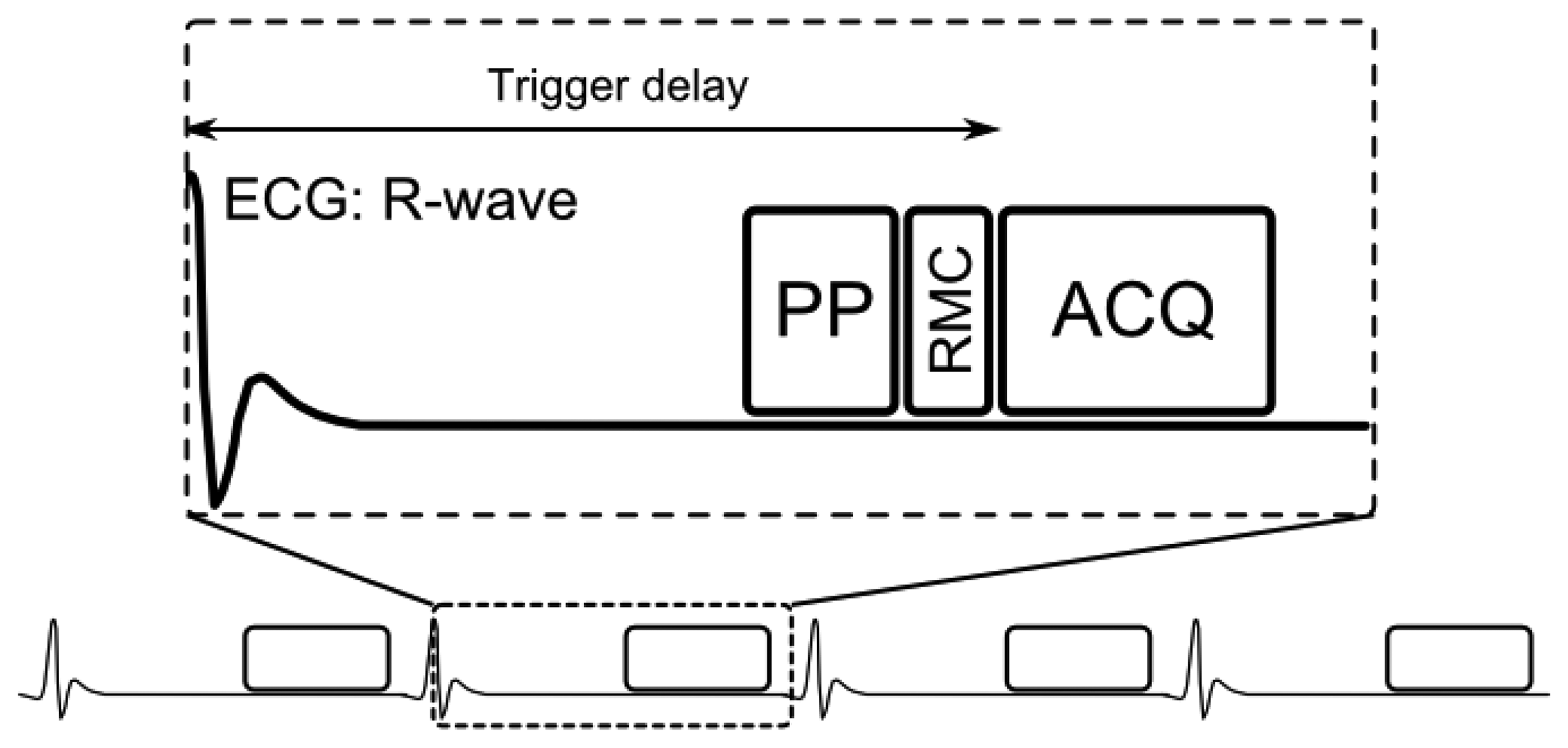
A generic CMRA sequence is shown in Figure 2, where the segmented k-space data acquisition is synchronized with the ECG to minimize cardiac motion related artifacts [25]. Various magnetization preparation pulses such as T2prep [26] and fat suppression [27] are used to improve visualization of the coronary lumen, and respiratory motion compensation is employed to suppress respiratory motion artifacts. There are essentially three separate processes for respiratory motion compensation which can be used separately or in concert in CMRA to reduce respiratory motion artifacts: (i) motion estimation, (ii) gating and (iii) correction. The focus of this review is to describe these motion compensation processes. However, it is worth noting that there are alternative methods to minimize motion artifacts in MRI, for example by signal averaging or using motion insensitive k-space trajectories such as radial [28,29] or spiral [30] sampling.
2. Respiratory Motion Estimation
Most respiratory compensation strategies rely on some sort of motion estimation information as input to the gating or correction algorithms. There are a number of ways in which motion estimation can be achieved, from external monitoring devices to MRI based techniques, so called respiratory navigators.
2.1. External Devices
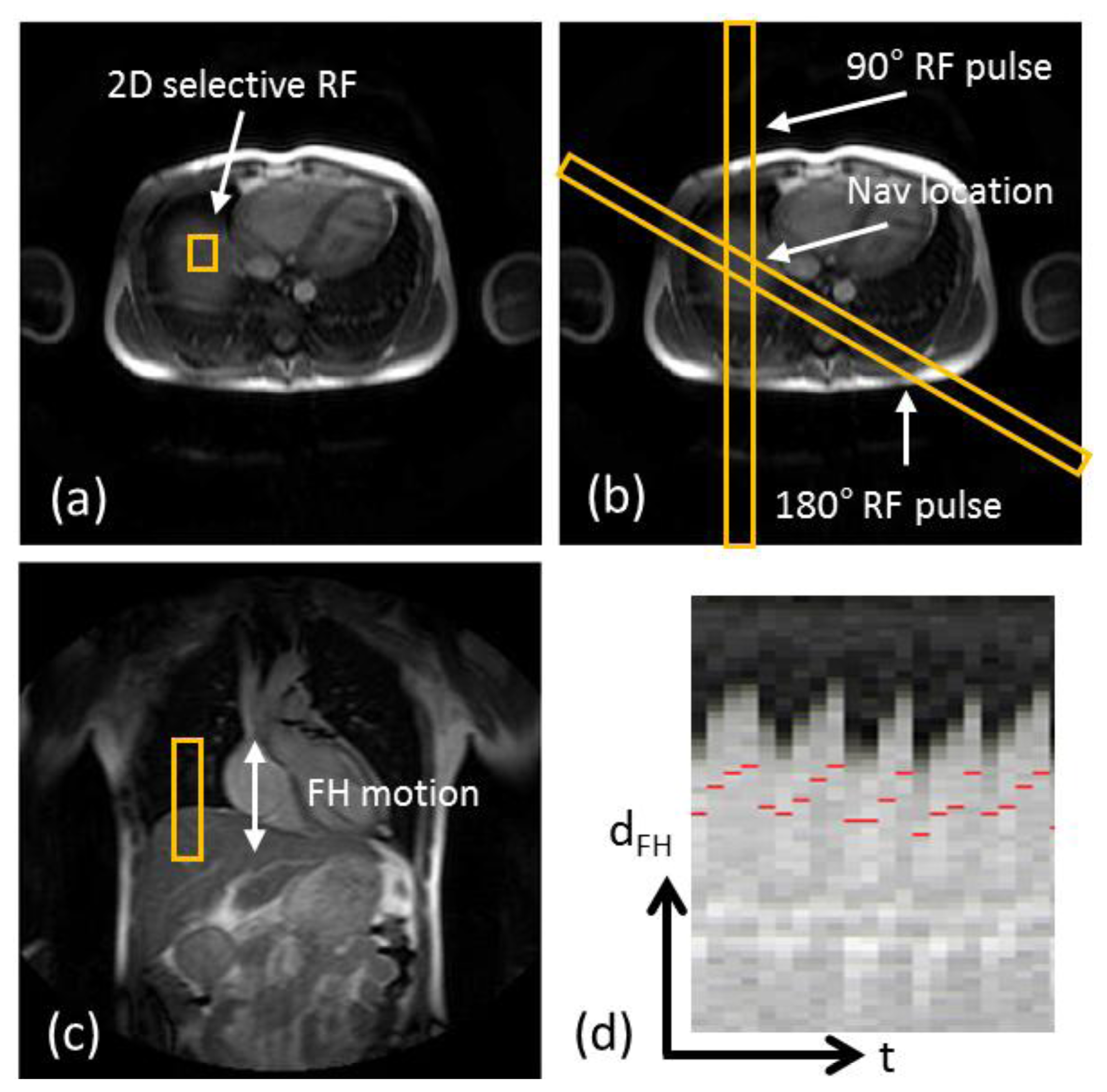
The most commonly used external respiratory monitoring device in cardiovascular MRI is the respiratory bellows [31,32], which measures pressure differences between the abdomen and a tightly wrapped belt to establish whether the respiratory cycle is in inspiration or expiration. Other techniques to perform respiratory motion estimation with external devices include measuring the electric impedance between ECG leads [33] or the more recently developed ultra wideband electromagnetic sensor [34]. The advantage of utilizing external devices for respiratory motion estimation is that the motion information may be obtained with a very high temporal resolution due to the low dimensionality of the measurements. Therefore, external devices can be useful in conjunction with simple respiratory gating such as the accept/reject algorithm which will be described in the following section. An additional advantage of external devices is that they are independent of the MRI acquisition and can be acquired in parallel with the CMRA, which is particularly important for steady-state MRI sequences. Nevertheless, for high-resolution imaging such as CMRA, external devices alone may be insufficient to adequately compensate for the respiratory motion. This is because they typically only provide relative information about respiration, which can be used to determine the respiratory phase (inspiration or expiration) but not any absolute motion information, such as displacement, rotation, etc. Therefore, its usefulness for the purpose of respiratory motion correction is very limited.
3. Respiratory Gating Strategies
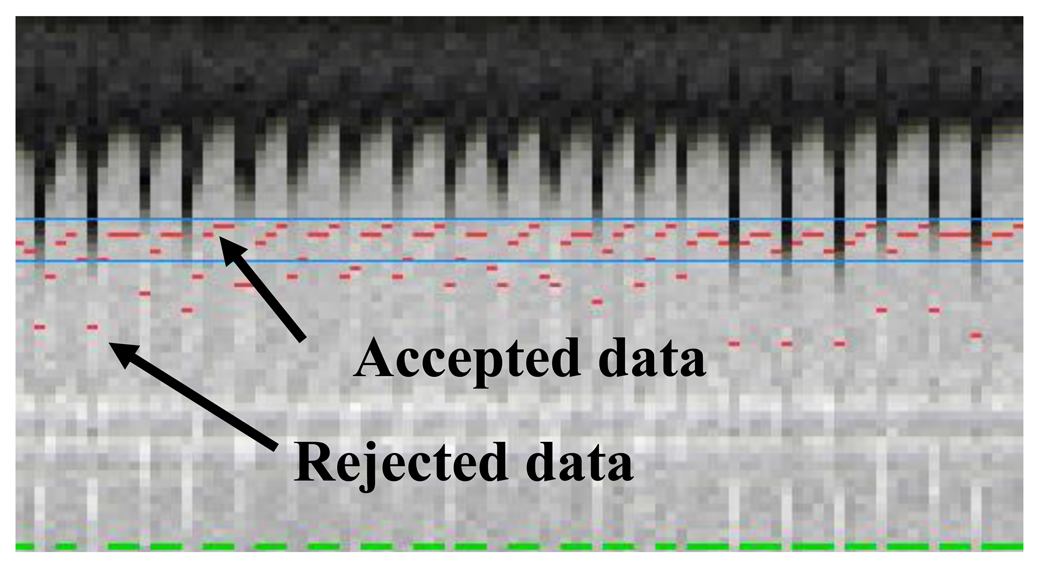
The most commonly used approach for respiratory gating is to limit image acquisition to the most quiescent respiratory phase, which usually is end expiration, and reject data acquired outside of the “respiratory gating window”. Figure 5 shows a time series of diaphragmatic 1D navigator signals during a scan, including the respiratory gating window (blue lines) within which acquired image data is accepted. This method, called the accept-reject algorithm (ARA) [70,71], is an effective and relatively simple to implement method for reducing the respiratory motion; however, the drawback is that the scan time is inversely proportional to the size of the gating window leading to an even further extended scan time for small gating windows. The magnitude of the diaphragmatic motion is normally around 15–30 mm, however a navigator gating window of 5 mm diaphragmatic motion is often used which leads to a navigator efficiency (the number of accepted navigator positions divided by the total number of navigator acquisitions) of approximately 25%–50%, occasionally resulting in a quadrupled scan time (or more) in the event of irregular breathing or respiratory drift. An alternative to using a fixed respiratory gating window with variable and unpredictable navigator efficiency is to predefine the navigator efficiency, which leads to a variable gating window size but predictable scan time [72].
A retrospective gating method was described by Li et al. [73]. The approach involves oversampling data with a certain factor, typically five, during free breathing. For each data point, out of the five acquired samples, the one with the least amount of respiratory motion is used for reconstruction. However, the total scan time becomes greatly increased, proportional to the oversampling factor, and the technique is sensitive to respiratory drift where possibly all five data acquisitions for a certain k-space point could be acquired with a large displacement relative to other data points. More efficient gating strategies have been proposed, typically involving some sort of ordering scheme whereby k-space data acquired in the central area of k-space is gated to a quiescent phase of the respiratory cycle, and vice-versa the outer k-space lines are acquired in a phase with more respiratory motion. As the central lines contain most of the image energy, motion during their acquisition is more likely to cause motion artifacts. Respiratory ordered phase encoding (ROPE) [74], centrally ordered phase encoding (COPE) [75] and hybrid ordered phase encoding (HOPE) [76] are three such methods which were implemented for 2D cardiac imaging. ROPE was extended to 3D and used for CMRA and shows improvements compared to the ARA [77].
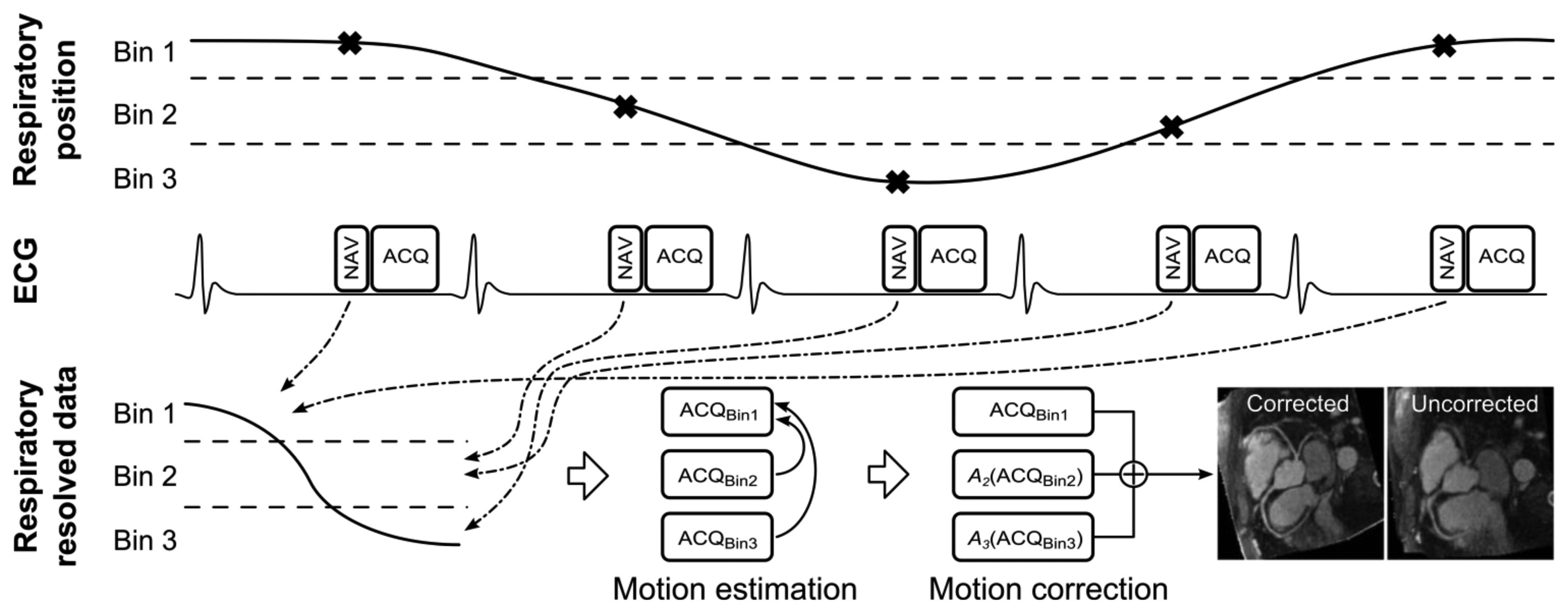
The diminishing variance algorithm (DVA) is a gating technique which does not utilize a predefined gating window, but instead terminates when the acquired navigator variance reaches a certain thresh-hold [78]. First, a complete dataset is acquired allowing navigator positions throughout the whole respiratory cycle. In the following acquisitions the data which has been acquired with the largest navigator values (furthest away from end-expiration) is re-acquired, thus reducing the total variance of the navigator acquisition. This is repeated until the navigator variance reaches a predefined threshold or exceeds a time limit. Phase encoding with automatic window selection (PAWS) [79] is a gating approach which divides the respiratory cycle in to several bins and each bin is assigned a starting point in k-space. The scan is terminated when data from three adjacent bins are fully acquired. Recently, this approach has been extended to 3D radial phase encoding imaging which allows for a smoother motion distribution between bins [80]. The performance of retrospective gating, ARA, DVA and PAWS were compared in a study by Nguyen et al. [81] which found PAWS to be the most effective and efficient for free breathing CMRA.
4. Respiratory Motion Correction Strategies
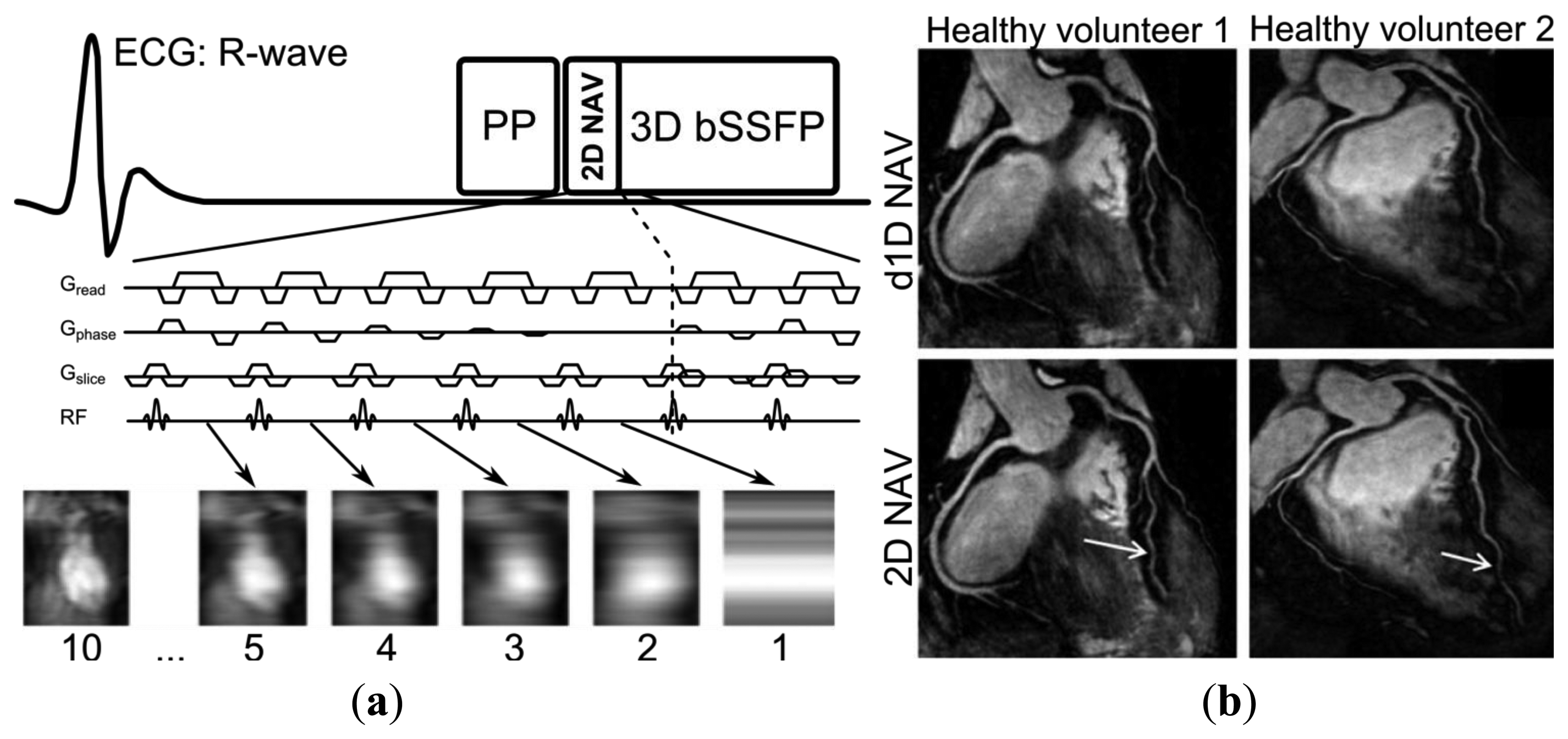
Respiratory motion correction can be either prospective or retrospective, where prospective correction involves estimating the motion before every acquired k-space segment, using previously described motion estimation techniques, and correcting for it by updating the gradient, excitation and acquisition parameters accordingly. Retrospective correction involves correcting for the motion after the scan is completed, which relaxes the real-time constraints for motion estimation, but prohibits adjustment of slice position due to through-plane motion. It is worth mentioning that prospective motion correction is limited to affine corrections, a set of linear transformations including translation, rotation, scaling and shearing which can be applied for prospective motion correction by adapting the linear gradient waveforms [82], whereas retrospective motion correction can be used for correction with more degrees-of-freedom, such as non-linear correction [69]. Although respiratory motion estimation typically precedes motion correction, this is not a strict requirement. A method has been developed whereby the respiratory motion is iteratively corrected without prior motion estimation by maximizing an edge sharpness metric in image space [83].
4.1. Translational Correction
Translational correction, in conjunction with ARA gating, is the most commonly used respiratory motion compensation approach, as respiratory motion can be well approximated by translational motion in the end-expiratory phase. The translational motion Δax, along encoding direction x, creates a phase shift θx inversely proportional to the image field-of-view, FOVx, and can be calculated as:
For prospective translational correction of in-plane motion, the spatial encoding gradients can be appropriately adjusted, and if translational correction is performed in the through-plane direction (slice encoding) then the phase of the RF pulse and A/D sampler will be modulated as well, resulting in a corresponding change in position of the excited imaging plane. For obliquely aligned, small slab CMRA such as targeted scans, through-plane respiratory motion may be substantial which requires prospective correction [84]. Whole-heart CMRA [85] with an axial orientation experiences the dominant respiratory motion component (FH motion) along the slice encoding direction which may introduce significant through-plane motion unless prospective correction is used. Nevertheless, the absolute respiratory induced displacement of the heart is typically on the order of magnitude smaller than the 3D FOV of whole-heart CMRA, particularly for coronal or sagittal orientations, which mitigates the effects of through plane motion and enables the use of retrospective translational correction. Typically, retrospective translational motion is performed in k-space, where the phase shift θx can be applied to the raw data sample kj at k-space index j acquired along encoding direction x as:
4.2. Higher Order Correction
While translational correction is adequate in the majority of cases if the CMRA scan is gated to the most quiescent respiratory phase, rotation and non-rigid motion correction such as affine correction has to be considered if no respiratory gating is employed [7], which is desirable to minimize scan time. Affine models describe a combination of linear transformations including rotation, shear and scale, as well as translation. A 3D affine transformation A transforms the point r = [x, y, z, 1]T to r′ = [x′, y′, z′, 1]T according to:
A drawback of higher order motion correction is that the data post-processing becomes increasingly computationally expensive and time-consuming as respiratory motion estimation and correction is performed with more degrees of freedom. Excessive post-processing durations may impede the clinical utility of advanced motion correction strategies, although in many cases the post-processing can be expedited by the use of parallel computing [87].
5. Conclusions
The problem of respiratory motion has plagued the field of free-breathing CMRA for many years and yet it remains a largely unsolved challenge. In the last decade the predominant research trend has been moving away from diaphragmatic navigators with motion models of varying complexity and towards direct motion compensation of the respiratory induced heart motion. This includes self-navigation and image based-navigation techniques, the former offering improved ease-of-use while the latter provides motion correction with more degrees-of-freedom. Furthermore, improved motion estimation accuracy allows for advanced motion correction algorithms incorporating affine and non-linear correction, obviating the need for respiratory gating. Despite the potential of some of these advanced methods to compensate for almost all of the respiratory motion, it is unlikely that they will receive widespread clinical use unless they can be seamlessly integrated into the clinical workflow, and without adding complexity to the cardiovascular MRI examination. The main aim of motion compensation in CMRA should not only be to make the scans faster and more robust towards respiratory motion, but also make the scans easier to perform so as to reduce operator dependence and requirement for specialized training. So far, advanced compensation approaches have only been used in small research studies involving healthy volunteers whereas most patient studies have been limited to simple diaphragmatic motion compensation techniques. Further work is required to assess the clinical merits of these emerging approaches. To this end, a focus on integrating the new methods into clinical practice is needed, including maximizing ease of use and minimizing post-processing times.
Conflict of Interest
The authors declare no conflict of interest.
References
- Go, A.S.; Mozaffarian, D.; Roger, V.L.; Benjamin, E.J.; Berry, J.D.; Borden, W.B.; Bravata, D.M.; Dai, S.; Ford, E.S.; Fox, C.S.; et al. Heart disease and stroke statistics—2013 update: A report from the american heart association. Circulation 2013, 127, e6–e245. [Google Scholar]
- Dewey, M. Coronary CT versus MR angiography: Pro CT—The role of CT angiography. Radiology 2011, 258, 329–339. [Google Scholar]
- Wang, Y.; Riederer, S.J.; Ehman, R.L. Respiratory motion of the heart-kinematics and the implications for the spatial-resolution in coronary imaging. Magn. Reson. Med. 1995, 33, 713–719. [Google Scholar]
- Keegan, J.; Gatehouse, P.; Yang, G.Z.; Firmin, D. Coronary artery motion with the respiratory cycle during breath-holding and free-breathing: Implications for slice-followed coronary artery imaging. Magn. Reson. Med. 2002, 47, 476–481. [Google Scholar]
- Danias, P.G.; Stuber, M.; Botnar, R.M.; Kissinger, K.V.; Edelman, R.R.; Manning, W.J. Relationship between motion of coronary arteries and diaphragm during free breathing: Lessons from real-time MR imaging. Am. J. Roentgenol. 1999, 172, 1061–1065. [Google Scholar]
- Jahnke, C.; Nehrke, K.; Paetsch, I.; Schnackenburg, B.; Gebker, R.; Fleck, E.; Nagel, E. Improved bulk myocardial motion suppression for navigator-gated coronary magnetic resonance imaging. J. Magn. Reson. Imaging 2007, 26, 780–786. [Google Scholar]
- Shechter, G.; Ozturk, C.; Resar, J.R.; McVeigh, E.R. Respiratory motion of the heart from free breathing coronary angiograms. IEEE Trans. Med. Imaging 2004, 23, 1046–1056. [Google Scholar]
- McLeish, K.; Hill, D.L.G.; Atkinson, D.; Blackall, J.M.; Razavi, R. A study of the motion and deformation of the heart due to respiration. IEEE Trans. Med. Imaging 2002, 21, 1142–1150. [Google Scholar]
- Manke, D.; Nehrke, K.; Bornert, P.; Rosch, P.; Dossel, O. Respiratory motion in coronary magnetic resonance angiography: A comparison of different motion models. J. Magn. Reson. Imaging 2002, 15, 661–671. [Google Scholar]
- Fischer, R.W.; Botnar, R.M.; Nehrke, K.; Boesiger, P.; Manning, W.J.; Peters, D.C. Analysis of residual coronary artery motion for breath hold and navigator approaches using real-time coronary MRI. Magn. Reson. Med. 2006, 55, 612–618. [Google Scholar]
- Henningsson, M.; Prieto, C.; Chiribiri, A.; Vaillant, G.; Razavi, R.; Botnar, R.M. Whole-heart coronary MRA with 3D affine motion correction using 3D image-based navigation. Magn. Reson. Med. 2013. [Google Scholar] [CrossRef]
- Atkinson, D.J.; Edelman, R.R. Cineangiography of the heart in a single breath hold with a segmented turboFLASH sequence. Radiology 1991, 178, 357–360. [Google Scholar]
- Edelman, R.R.; Manning, W.J.; Burstein, D.; Paulin, S. Coronary arteries: Breath-hold MR angiography. Radiology 1991, 181, 641–643. [Google Scholar]
- Meyer, C.H.; Hu, B.S.; Nishimura, D.G.; Macovski, A. Fast spiral coronary artery imaging. Magn. Reson. Med. 1992, 28, 202–213. [Google Scholar]
- Manning, W.J.; Li, W.; Edelman, R.R. A preliminary report comparing magnetic resonance coronary angiography with conventional angiography. N. Engl. J. Med. 1993, 328, 828–832. [Google Scholar]
- McGibney, G.; Smith, M.R.; Nichols, S.T.; Crawley, A. Quantitative evaluation of several partial Fourier reconstruction algorithms used in MRI. Magn. Reson. Med. 1993, 30, 51–59. [Google Scholar]
- Pruessmann, K.P.; Weiger, M.; Scheidegger, M.B.; Boesiger, P. SENSE: Sensitivity encoding for fast MRI. Magn. Reson. Med. 1999, 42, 952–962. [Google Scholar]
- Griswold, M.A.; Jakob, P.M.; Heidemann, R.M.; Nittka, M.; Jellus, V.; Wang, J.; Kiefer, B.; Haase, A. Generalized autocalibrating partially parallel acquisitions (GRAPPA). Magn. Reson. Med. 2002, 47, 1202–1210. [Google Scholar]
- Wielopolski, P.A.; van Geuns, R.J.; de Feyter, P.J.; Oudkerk, M. Breath-hold coronary MR angiography with volume-targeted imaging. Radiology 1998, 209, 209–219. [Google Scholar]
- Li, D.; Carr, J.C.; Shea, S.M.; Zheng, J.; Deshpande, V.S.; Wielopolski, P.A.; Finn, J.P. Coronary arteries: Magnetization-prepared contrast-enhanced three-dimensional volume-targeted breath-hold MR angiography. Radiology 2001, 219, 270–277. [Google Scholar]
- Niendorf, T.; Hardy, C.J.; Giaquinto, R.O.; Gross, P.; Cline, H.E.; Zhu, Y.; Kenwood, G.; Cohen, S.; Grant, A.K.; Joshi, S.; Rofsky, N.M.; Sodickson, D.K. Toward single breath-hold whole-heart coverage coronary MRA using highly accelerated parallel imaging with a 32-channel MR system. Magn. Reson. Med. 2006, 56, 167–176. [Google Scholar]
- Lustig, M.; Donoho, D.; Pauly, J.M. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn. Reson. Med. 2007, 58, 1182–1195. [Google Scholar]
- Akcakaya, M.; Nam, S.; Hu, P.; Moghari, M.H.; Ngo, L.H.; Tarokh, V.; Manning, W.J.; Nezafat, R. Compressed sensing with wavelet domain dependencies for coronary MRI: A retrospective study. IEEE Trans. Med. Imaging 2011, 30, 1090–1099. [Google Scholar]
- Akcakaya, M.; Basha, T.A.; Chan, R.H.; Manning, W.J.; Nezafat, R. Accelerated isotropic sub-millimeter whole-heart coronary MRI: Compressed sensing versus parallel imaging. Magn. Reson. Med. 2013. [Google Scholar] [CrossRef]
- Felblinger, J.; Lehmann, C.; Boesch, C. Electrocardiogram acquisition during MR examinations for patient monitoring and sequence triggering. Magn. Reson. Med. 1994, 32, 523–529. [Google Scholar]
- Botnar, R.M.; Stuber, M.; Danias, P.G.; Kissinger, K.V.; Manning, W.J. Improved coronary artery definition with T2-weighted, free-breathing, three-dimensional coronary MRA. Circulation 1999, 99, 3139–3148. [Google Scholar]
- Bornert, P.; Stuber, M.; Botnar, R.M.; Kissinger, K.V.; Manning, W.J. Comparison of fat suppression strategies in 3D spiral coronary magnetic resonance angiography. J. Magn. Reson. Imaging 2002, 15, 462–466. [Google Scholar]
- Spuentrup, E.; Katoh, M.; Stuber, M.; Botnar, R.; Schaeffter, T.; Buecker, A.; Gunther, R.W. Coronary MR imaging using free-breathing 3D steady-state free precession with radial k-space sampling. RoFo 2003, 175, 1330–1334. [Google Scholar]
- Stehning, C.; Bornert, P.; Nehrke, K.; Eggers, H.; Dossel, O. Fast isotropic volumetric coronary MR angiography using free-breathing 3D radial balanced FFE acquisition. Magn. Reson. Med. 2004, 52, 197–203. [Google Scholar]
- Bornert, P.; Stuber, M.; Botnar, R.M.; Kissinger, K.V.; Koken, P.; Spuentrup, E.; Manning, W.J. Direct comparison of 3D spiral vs. Cartesian gradient-echo coronary magnetic resonance angiography. Magn. Reson. Med. 2001, 46, 789–794. [Google Scholar]
- Ehman, R.L.; McNamara, M.T.; Pallack, M.; Hricak, H.; Higgins, C.B. Magnetic resonance imaging with respiratory gating: Techniques and advantages. Am. J. Roentgenol. 1984, 143, 1175–1182. [Google Scholar]
- Santelli, C.; Nezafat, R.; Goddu, B.; Manning, W.J.; Smink, J.; Kozerke, S.; Peters, D.C. Respiratory bellows revisited for motion compensation: Preliminary experience for cardiovascular MR. Magn. Reson. Med. 2011, 65, 1097–1102. [Google Scholar]
- Felblinger, J.; Boesch, C. Amplitude demodulation of the electrocardiogram signal (ECG) for respiration monitoring and compensation during MR examinations. Magn. Reson. Med. 1997, 38, 129–136. [Google Scholar]
- Thiel, F.; Kosch, O.; Seifert, F. Ultra-wideband sensors for improved magnetic resonance imaging, cardiovascular monitoring and tumour diagnostics. Sensors 2010, 10, 10778–10802. [Google Scholar]
- Ehman, R.L.; Felmlee, J.P. Adaptive technique for high-definition MR imaging of moving structures. Radiology 1989, 173, 255–263. [Google Scholar]
- McConnell, M.V.; Khasgiwala, V.C.; Savord, B.J.; Chen, M.H.; Chuang, M.L.; Edelman, R.R.; Manning, W.J. Comparison of respiratory suppression methods and navigator locations for MR coronary angiography. Am. J. Roentgenol. 1997, 168, 1369–1375. [Google Scholar]
- Danias, P.G.; McConnell, M.V.; Khasgiwala, V.C.; Chuang, M.L.; Edelman, R.R.; Manning, W.J. Prospective navigator correction of image position for coronary MR angiography. Radiology 1997, 203, 733–736. [Google Scholar]
- Nehrke, K.; Bornert, P.; Groen, J.; Smink, J.; Bock, J.C. On the performance and accuracy of 2D navigator pulses. Magn. Reson. Imaging 1999, 17, 1173–1181. [Google Scholar]
- Firmin, D.; Keegan, J. Navigator echoes in cardiac magnetic resonance. J. Cardiov. Magn. Reson. 2001, 3, 183–193. [Google Scholar]
- Stuber, M.; Botnar, R.M.; Danias, P.G.; Kissinger, K.V.; Manning, W.J. Submillimeter three-dimensional coronary MR angiography with real-time navigator correction: Comparison of navigator locations. Radiology 1999, 212, 579–587. [Google Scholar]
- Nehrke, K.; Bornert, P.; Manke, D.; Bock, J.C. Free-breathing cardiac MR imaging: Study of implications of respiratory motion—Initial results. Radiology 2001, 220, 810–815. [Google Scholar]
- Taylor, A.M.; Keegan, J.; Jhooti, P.; Firmin, D.N.; Pennell, D.J. Calculation of a subject-specific adaptive motion-correction factor for improved real-time navigator echo-gated magnetic resonance coronary angiography. Magn. Reson. Med. 1999, 1, 131–138. [Google Scholar]
- Scott, A.D.; Keegan, J.; Firmin, D.N. Motion in cardiovascular MR imaging. Radiology 2009, 250, 331–351. [Google Scholar]
- Moghari, M.H.; Hu, P.; Kissinger, K.V.; Goddu, B.; Goepfert, L.; Ngo, L.; Manning, W.J.; Nezafat, R. Subject-specific estimation of respiratory navigator tracking factor for free-breathing cardiovascular MR. Magn. Reson. Med. 2012, 67, 1665–1672. [Google Scholar]
- Kim, W.Y.; Danias, P.G.; Stuber, M.; Flamm, S.D.; Plein, S.; Nagel, E.; Langerak, S.E.; Weber, O.M.; Pedersen, E.M.; Schmidt, M.; Botnar, R.M.; Manning, W.J. Coronary magnetic resonance angiography for the detection of coronary stenoses. N. Engl. J. Med. 2001, 345, 1863–1869. [Google Scholar]
- Nagata, M.; Kato, S.; Kitagawa, K.; Ishida, N.; Nakajima, H.; Nakamori, S.; Ishida, M.; Miyahara, M.; Ito, M.; Sakuma, H. Diagnostic accuracy of 1.5-T unenhanced whole-heart coronary MR angiography performed with 32-channel cardiac coils: Initial single-center experience. Radiology 2011, 259, 384–392. [Google Scholar]
- Yang, Q.; Li, K.; Liu, X.; Du, X.; Bi, X.; Huang, F.; Jerecic, R.; Liu, Z.; An, J.; Xu, D.; Zheng, H.; Fan, Z.; Li, D. 3.0T whole-heart coronary magnetic resonance angiography performed with 32-channel cardiac coils: A single-center experience. Circ. Cardiovasc. Imaging 2012, 5, 573–579. [Google Scholar]
- Hamdan, A.; Asbach, P.; Wellnhofer, E.; Klein, C.; Gebker, R.; Kelle, S.; Kilian, H.; Huppertz, A.; Fleck, E. A prospective study for comparison of MR and CT imaging for detection of coronary artery stenosis. JACC Cardiovasc. Imaging 2011, 4, 50–61. [Google Scholar]
- Pouleur, A.C.; de Waroux, J.B.P.; Kefer, J.; Pasquet, A.; Vanoverschelde, J.L.; Gerber, B.L. Direct comparison of whole-heart navigator-gated magnetic resonance coronary angiography and 40- and 64-slice multidetector row computed tomography to detect the coronary artery stenosis in patients scheduled for conventional coronary angiography. Circ. Cardiovasc. Imaging 2008, 1, 114–121. [Google Scholar]
- Nehrke, K.; Bornert, P. Prospective correction of affine motion for arbitrary MR sequences on a clinical scanner. Magn. Reson. Med. 2005, 54, 1130–1138. [Google Scholar]
- Manke, D.; Nehrke, K.; Bornert, P. Novel prospective respiratory motion correction approach for free-breathing coronary MR angiography using a patient-adapted affine motion model. Magn. Reson. Med. 2003, 50, 122–131. [Google Scholar]
- Larson, A.C.; White, R.D.; Laub, G.; McVeigh, E.R.; Li, D.; Simonetti, O.P. Self-gated cardiac cine MRI. Magn. Reson. Med. 2004, 51, 93–102. [Google Scholar]
- Stehning, C.; Bornert, P.; Nehrke, K.; Eggers, H.; Stuber, M. Free-breathing whole-heart coronary MRA with 3D radial SSFP and self-navigated image reconstruction. Magn. Reson. Med. 2005, 54, 476–480. [Google Scholar]
- Piccini, D.; Littmann, A.; Nielles-Vallespin, S.; Zenge, M.O. Respiratory self-navigation for whole-heart bright-blood coronary MRI: Methods for robust isolation and automatic segmentation of the blood pool. Magn. Reson. Med. 2012, 68, 571–579. [Google Scholar]
- Nguyen, T.D.; Spincemaille, P.; Prince, M.R.; Wang, Y. Cardiac fat navigator-gated steady-state free precession 3D magnetic resonance angiography of coronary arteries. Magn. Reson. Med. 2006, 56, 210–215. [Google Scholar]
- Lai, P.; Bi, X.; Jerecic, R.; Li, D. A respiratory self-gating technique with 3D-translation compensation for free-breathing whole-heart coronary MRA. Magn. Reson. Med. 2009, 62, 731–738. [Google Scholar]
- Henningsson, M.; Smink, J.; Razavi, R.; Botnar, R.M. Prospective respiratory motion correction for coronary MR angiography using a 2D image navigator. Magn. Reson. Med. 2013, 69, 486–694. [Google Scholar]
- Kawaji, K.; Spincemaille, P.; Nguyen, T.D.; Thimmappa, N.; Cooper, M.A.; Prince, M.R.; Wang, Y. Direct coronary motion extraction from a 2D fat image navigator for prospectively gated coronary MR angiography. Magn. Reson. Med. 2013. [Google Scholar] [CrossRef]
- Wu, H.H.; Gurney, P.T.; Hu, B.S.; Nishimura, D.G.; McConnell, M.V. Free-breathing multiphase whole-heart coronary MR angiography using image-based navigators and three-dimensional cones imaging. Magn. Reson. Med. 2012. [Google Scholar] [CrossRef]
- Scott, A.D.; Keegan, J.; Firmin, D.N. Beat-to-beat respiratory motion correction with near 100% efficiency: A quantitative assessment using high-resolution coronary artery imaging. Magn. Reson. Imaging 2011, 29, 568–578. [Google Scholar]
- Keegan, J.; Gatehouse, P.D.; Yang, G.Z.; Firmin, D.N. Non-model-based correction of respiratory motion using beat-to-beat 3D spiral fat-selective imaging. J. Magn. Reson. Imaging 2007, 26, 624–629. [Google Scholar]
- Hansen, M.S.; Atkinson, D.; Sorensen, T.S. Cartesian sense and k-t sense reconstruction using commodity graphics hardware. Magn. Reson. Med. 2008, 59, 463–438. [Google Scholar]
- Fluck, O.; Vetter, C.; Wein, W.; Kamen, A.; Preim, B.; Westermann, R. A survey of medical image registration on graphics hardware. Comput. Method. Program. Biomed. 2011, 104, e45–e57. [Google Scholar]
- Spuentrup, E.; Manning, W.J.; Botnar, R.M.; Kissinger, K.V.; Stuber, M. Impact of navigator timing on free-breathing submillimeter 3D coronary magnetic resonance angiography. Magn. Reson. Med. 2002, 47, 196–201. [Google Scholar]
- Henningsson, M.; Koken, P.; Stehning, C.; Razavi, R.; Prieto, C.; Botnar, R.M. Whole-heart coronary MR angiography with 2D self-navigated image reconstruction. Magn. Reson. Med. 2012, 67, 437–445. [Google Scholar]
- Deshpande, V.S.; Chung, Y.C.; Zhang, Q.; Shea, S.M.; Li, D. Reduction of transient signal oscillations in true-FISP using a linear flip angle series magnetization preparation. Magn. Reson. Med. 2003, 49, 151–157. [Google Scholar]
- Bhat, H.; Ge, L.; Nielles-Vallespin, S.; Zuehlsdorff, S.; Li, D. 3D radial sampling and 3D affine transform-based respiratory motion correction technique for free-breathing whole-heart coronary MRA with 100% imaging efficiency. Magn. Reson. Med. 2011, 65, 1269–1277. [Google Scholar]
- Pang, J.; Bhat, H.; Sharif, B.; Fan, Z.; Thomson, L.E.; Labounty, T.; Friedman, J.D.; Min, J.; Berman, D.S.; Li, D. Whole-heart coronary MRA with 100% respiratory gating efficiency: Self-navigated three-dimensional retrospective image-based motion correction (TRIM). Magn. Reson. Med. 2013. [Google Scholar] [CrossRef]
- Schmidt, J.F.; Buehrer, M.; Boesiger, P.; Kozerke, S. Nonrigid retrospective respiratory motion correction in whole-heart coronary MRA. Magn. Reson. Med. 2011, 66, 1541–1549. [Google Scholar]
- Sachs, T.S.; Meyer, C.H.; Hu, B.S.; Kohli, J.; Nishimura, D.G.; Macovski, A. Real-time motion detection in spiral MRI using navigators. Magn. Reson. Med. 1994, 32, 639–645. [Google Scholar]
- Oshinski, J.N.; Hofland, L.; Mukundan, S., Jr.; Dixon, W.T.; Parks, W.J.; Pettigrew, R.I. Two-dimensional coronary MR angiography without breath holding. Radiology 1996, 201, 737–743. [Google Scholar]
- Moghari, M.H.; Chan, R.H.; Hong, S.N.; Shaw, J.L.; Goepfert, L.A.; Kissinger, K.V.; Goddu, B.; Josephson, M.E.; Manning, W.J.; Nezafat, R. Free-breathing cardiac MR with a fixed navigator efficiency using adaptive gating window size. Magn. Reson. Med. 2012, 68, 1866–1875. [Google Scholar]
- Li, D.; Kaushikkar, S.; Haacke, E.M.; Woodard, P.K.; Dhawale, P.J.; Kroeker, R.M.; Laub, G.; Kuginuki, Y.; Gutierrez, F.R. Coronary arteries: Three-dimensional MR imaging with retrospective respiratory gating. Radiology 1996, 201, 857–863. [Google Scholar]
- Bailes, D.R.; Gilderdale, D.J.; Bydder, G.M.; Collins, A.G.; Firmin, D.N. Respiratory ordered phase encoding (ROPE): A method for reducing respiratory motion artefacts in MR imaging. J. Comput. Assist. Tomogr. 1985, 9, 835–838. [Google Scholar]
- Haacke, E.M.; Patrick, J.L. Reducing motion artifacts in two-dimensional Fourier transform imaging. Magn. Reson. Imaging 1986, 4, 359–376. [Google Scholar]
- Jhooti, P.; Wiesmann, F.; Taylor, A.M.; Gatehouse, P.D.; Yang, G.Z.; Keegan, J.; Pennell, D.J.; Firmin, D.N. Hybrid ordered phase encoding (HOPE): An improved approach for respiratory artifact reduction. J. Magn. Reson. Imaging 1998, 8, 968–980. [Google Scholar]
- Jhooti, P.; Keegan, J.; Gatehouse, P.D.; Collins, S.; Rowe, A.; Taylor, A.M.; Firmin, D.N. 3D coronary artery imaging with phase reordering for improved scan efficiency. Magn. Reson. Med. 1999, 41, 555–562. [Google Scholar]
- Sachs, T.S.; Meyer, C.H.; Irarrazabal, P.; Hu, B.S.; Nishimura, D.G.; Macovski, A. The diminishing variance algorithm for real-time reduction of motion artifacts in MRI. Magn. Reson. Med. 1995, 34, 412–422. [Google Scholar]
- Jhooti, P.; Gatehouse, P.D.; Keegan, J.; Bunce, N.H.; Taylor, A.M.; Firmin, D.N. Phase ordering with automatic window selection (PAWS): A novel motion-resistant technique for 3D coronary imaging. Magn. Reson. Med. 2000, 43, 470–480. [Google Scholar]
- Kolbitsch, C.; Prieto, C.; Smink, J.; Schaeffter, T. Highly efficient whole-heart imaging using radial phase encoding-phase ordering with automatic window selection. Magn. Reson. Med. 2011, 66, 1008–1018. [Google Scholar]
- Nguyen, T.D.; Spincemaille, P.; Cham, M.D.; Weinsaft, J.W.; Prince, M.R.; Wang, Y. Free-breathing 3-dimensional steady-state free precession coronary magnetic resonance angiography: Comparison of four navigator gating techniques. Magn. Reson. Imaging 2009, 27, 807–814. [Google Scholar]
- Maclaren, J.; Herbst, M.; Speck, O.; Zaitsev, M. Prospective motion correction in brain imaging: A review. Magn. Reson. Med. 2013, 69, 621–636. [Google Scholar]
- Moghari, M.H.; Roujol, S.; Chan, R.H.; Hong, S.N.; Bello, N.; Henningsson, M.; Ngo, L.H.; Goddu, B.; Goepfert, L.; Kissinger, K.V.; Manning, W.J.; Nezafat, R. Free-breathing 3D cardiac MRI using iterative image-based respiratory motion correction. Magn. Reson. Med. 2012. [Google Scholar] [CrossRef]
- Stuber, M.; Botnar, R.M.; Danias, P.G.; Sodickson, D.K.; Kissinger, K.V.; van Cauteren, M.; de Becker, J.; Manning, W.J. Double-oblique free-breathing high resolution three-dimensional coronary magnetic resonance angiography. J. Am. Coll. Cardiol. 1999, 34, 524–531. [Google Scholar]
- Weber, O.M.; Martin, A.J.; Higgins, C.B. Whole-heart steady-state free precession coronary artery magnetic resonance angiography. Magn. Reson. Med. 2003, 50, 1223–1228. [Google Scholar]
- Batchelor, P.G.; Atkinson, D.; Irarrazaval, P.; Hill, D.L.; Hajnal, J.; Larkman, D. Matrix description of general motion correction applied to multishot images. Magn. Reson. Med. 2005, 54, 1273–1280. [Google Scholar]
- Shams, R.; Sadeghi, P.; Kennedy, R.; Hartley, R. Parallel computation of mutual information on the GPU with application to real-time registration of 3D medical images. Comput. Method. Program. Biomed. 2010, 99, 133–146. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Henningsson, M.; Botnar, R.M. Advanced Respiratory Motion Compensation for Coronary MR Angiography. Sensors 2013, 13, 6882-6899. https://doi.org/10.3390/s130606882
Henningsson M, Botnar RM. Advanced Respiratory Motion Compensation for Coronary MR Angiography. Sensors. 2013; 13(6):6882-6899. https://doi.org/10.3390/s130606882
Chicago/Turabian StyleHenningsson, Markus, and Rene M. Botnar. 2013. "Advanced Respiratory Motion Compensation for Coronary MR Angiography" Sensors 13, no. 6: 6882-6899. https://doi.org/10.3390/s130606882



