Fast Nearly ML Estimation of Doppler Frequency in GNSS Signal Acquisition Process
Abstract
: It is known that signal acquisition in Global Navigation Satellite System (GNSS) field provides a rough maximum-likelihood (ML) estimate based on a peak search in a two-dimensional grid. In this paper, the theoretical mathematical expression of the cross-ambiguity function (CAF) is exploited to analyze the grid and improve the accuracy of the frequency estimate. Based on the simple equation derived from this mathematical expression of the CAF, a family of novel algorithms is proposed to refine the Doppler frequency estimate with respect to that provided by a conventional acquisition method. In an ideal scenario where there is no noise and other nuisances, the frequency estimation error can be theoretically reduced to zero. On the other hand, in the presence of noise, the new algorithm almost reaches the Cramer-Rao Lower Bound (CRLB) which is derived as benchmark. For comparison, a least-square (LS) method is proposed. It is shown that the proposed solution achieves the same performance of LS, but requires a dramatically reduced computational burden. An averaging method is proposed to mitigate the influence of noise, especially when signal-to-noise ratio (SNR) is low. Finally, the influence of the grid resolution in the search space is analyzed in both time and frequency domains.1. Introduction
The main purpose of the acquisition and tracking systems of a Global Navigation Satellite System (GNSS) receiver is to provide an estimate of the Doppler frequency ƒd, the code delay τ, and the phase of the carrier, ϕ, of the signal transmitted by each visible satellite. The task of the acquisition system is to detect the visible satellites and to provide, for each detected satellite, a coarse estimate of ƒd and τ. This parameter vector is then passed to the tracking systems, whose task is to refine this estimate. The refinement of Doppler frequency estimate is generally performed by a classic phase lock loop (PLL), which requires an initial estimate much more accurate than the one provided by the acquisition system. Therefore it is necessary to improve the accuracy of the estimate to an acceptable level before starting the operations of the phase tracking loop. A system typically adopted by a GNSS receiver to reach this goal is a frequency lock loop (FLL), which is generally integrated within a PLL. The first refinement is done by a robust FLL operating at wideband, then the loop bandwidth is gradually reduced and finally the system switches to a PLL scheme [1,2]. Other methods [3,4] refine the frequency estimate by exploiting the phase difference between two successive periods of data. An interpolation method is introduced in Reference [5] to estimate the true value of the Doppler frequency, but it is based on an empirical approximation.
In most of the previous methods, usually the estimates of ƒd and τ are picked in a search plane only considering the peak cell without any usage of the other cells. In the fields of communications, audio, medical, instrumentation, and others [6], the problem of estimating the frequency of a tone contaminated with noise is tackled for example by Quinn [7,8], MacLeod [9,10], and Jacobsen [6,11], by exploiting the idea of refining the final frequency estimate using the peak sample and two neighbors of the discrete Fourier components. At the same time there are other methods, studied in Reference [12,13], which utilize the phase information. These methods cannot be directly applied to the acquisition of a GNSS signal, because of the very low signal-to-noise ratio and the different signal model, but they can inspire us to do some innovation in GNSS frequency estimation.
In this paper, the peak and neighbor points of the cross-ambiguity function (CAF) in the frequency domain are used to derive a simple formula that greatly improves the accuracy of the frequency estimate provided by the acquisition system. The CAF was initially derived in Reference [14] using statistical principles, then Reference [15] presented a new approach of the CAF derivation. Furthermore in this paper the approximation in CAF main lobe is analyzed in details, based on this approximation, and a new family of methods for refining the estimate of the Doppler frequency is proposed, which exploits the cells close to the peak in the search plane. Compared with the traditional methods, these methods significantly improve the accuracy without increasing the computation complexity or using additional received data.
A preliminary version of this work was presented in Reference [16]. With respect to that previous work, here we extend and complete all the mathematical derivations, extend the performance analysis with appropriate comparisons, derive and discuss the Cramer-Rao lower bound (CRLB) for the frequency estimator showing that the proposed approach is close to the CRLB (quasi-ML approach), and include the theoretical analysis of other non-AWGN nuisances.
This paper is organized as follows. In Section 2 the signal model is presented and the approximate mathematical expression of the CAF in the main lobe is obtained. In Section 3 a new family of algorithms is derived and proved to work perfectly in the absence of noise. In Section 4 the performance of the proposed algorithms is investigated in the presence of additive noise; both the CRLB and a least-square (LS) solution are derived as benchmark, and the comparison shows that the new algorithms can approach very closely the CRLB. Besides that, a simple averaging approach based on non-coherent sums is proposed to improve the accuracy of the algorithms in low SNR conditions. Furthermore, in Section 5, the effects of other nuisances, uncorrelated with the additive noise, are analyzed, and some countermeasures are proposed. Finally, in Section 6 the conclusion is drawn.
2. Fundamentals of the New Algorithms
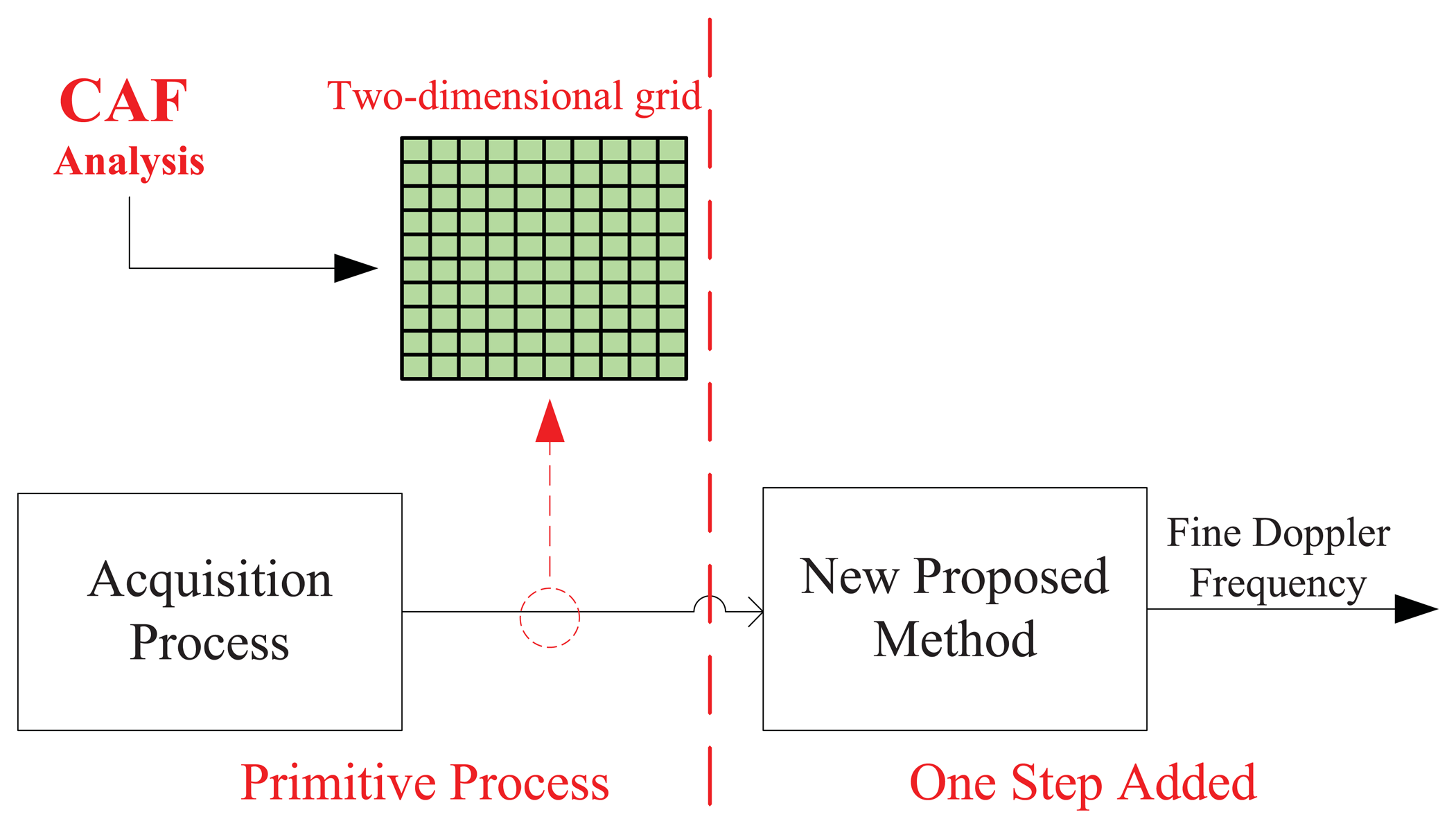
The basic scheme of the acquisition method proposed in this paper is illustrated in Figure 1. The left part of the figure indicates the traditional GNSS acquisition process from which a two-dimensional search grid (marked in green color) is generally obtained, while the right side shows the presence of a new additional block able to refine the Doppler frequency estimate in a simple way. The innovation proposed in this paper refers to the algorithms used by this additional block to refine the frequency estimate.
2.1. Acquisition Process
The acquisition system for GNSS application is based on the maximum-likelihood estimation theory, which can be briefly described as follows [17].
The incoming sampled signal can be denoted as a vector
The ML estimate of the parameter vector a can be found by maximizing the likelihood function, which depends on the probability density function (PDF), that is
If the energy of the test signal r̅(n) (that is the term in Equation (3)) does not depend on a̅, then it is possible to show [17] that the corresponding ML estimate âML of a is
In GNSS field, without considering the influence of noise, the received signal, after down-conversion and sampling, can be written as [1]
From Equation (7), we can learn that in principle, the satellite signal actually contains four unknown parameters: code delay (τ), Doppler frequency (fd), carrier phase (φ) and data bit. However in the acquisition process, only two of them are estimated, which are τ and fd.
With respect to the parameter data bit, in the implementation, a non-coherent acquisition scheme is used to solve the problem, so here we assume that there is no data-transition in the accumulation period.
Considering the parameter carrier phase, its influence can be removed by involving two components in the acquisition process that are in-phase component (I) and 90° phase-shifted quad-phase (Q) component [19]. Therefore, the test signal r̅(n) can be written as
Equation (9) is known as cross-ambiguity function (CAF). Based on Equations (4) and (5), the ML estimate of [τ, fd] can be obtained [17], as
There are mainly three acquisition schemes [19]: serial search acquisition, parallel frequency space search acquisition and parallel code phase search acquisition. No matter what kind of scheme is used, a two-dimensional search grid (Figure 4) is always obtained, and the resulting estimated vector is selected as the location of the peak cell, and, at the same time, the other cells in the search grid are abandoned. However, because of the large frequency searching step fsp, the frequency estimate error is located in the range , so the initial Doppler frequency estimate is usually not accurate enough to pass to the tracking loop directly.
In order to refine the Doppler frequency estimate, a system typically used is the Frequency Lock Loop (FLL) mentioned in Reference [1,2]. An FLL needs additional data and a special structure, which is generally embedded inside the tracking loops. Another typical technique [3,4], which exploits the phase relation of consecutive data (p.150 in Reference [3]), also needs additional data, and, at the same time, encompasses an ambiguity problem in the phase measurement that has to be solved. Actually this technique is essentially similar to an FLL with a particular discriminator.
In this paper, we develop new methods to refine the Doppler frequency estimate, based only on the search grid already evaluated by the acquisition; that is, we do not have to compute new correlations, but we only use the neighbor cells of the CAF peak, already available in the search grid.
2.2. Analytical Expression of the CAF
The CAF [15] is used in radar, sonar and other similar systems to estimate the time delay and the Doppler shift of an incoming signal. An accurate estimation of these signal parameters generally requires the evaluation of several CAF samples, at the cost of an increased computational complexity. In this paper we propose a family of methods that exploits the knowledge of an approximate expression of the analytical formula of the CAF, given in Reference [15], to reach a trade-off between accuracy and complexity.
Following the approach presented in Reference [15], the CAF associated to the generic i-th satellite code, locally generated for each trial value of code delay τ̅ and Doppler frequency f̅d, can be written as
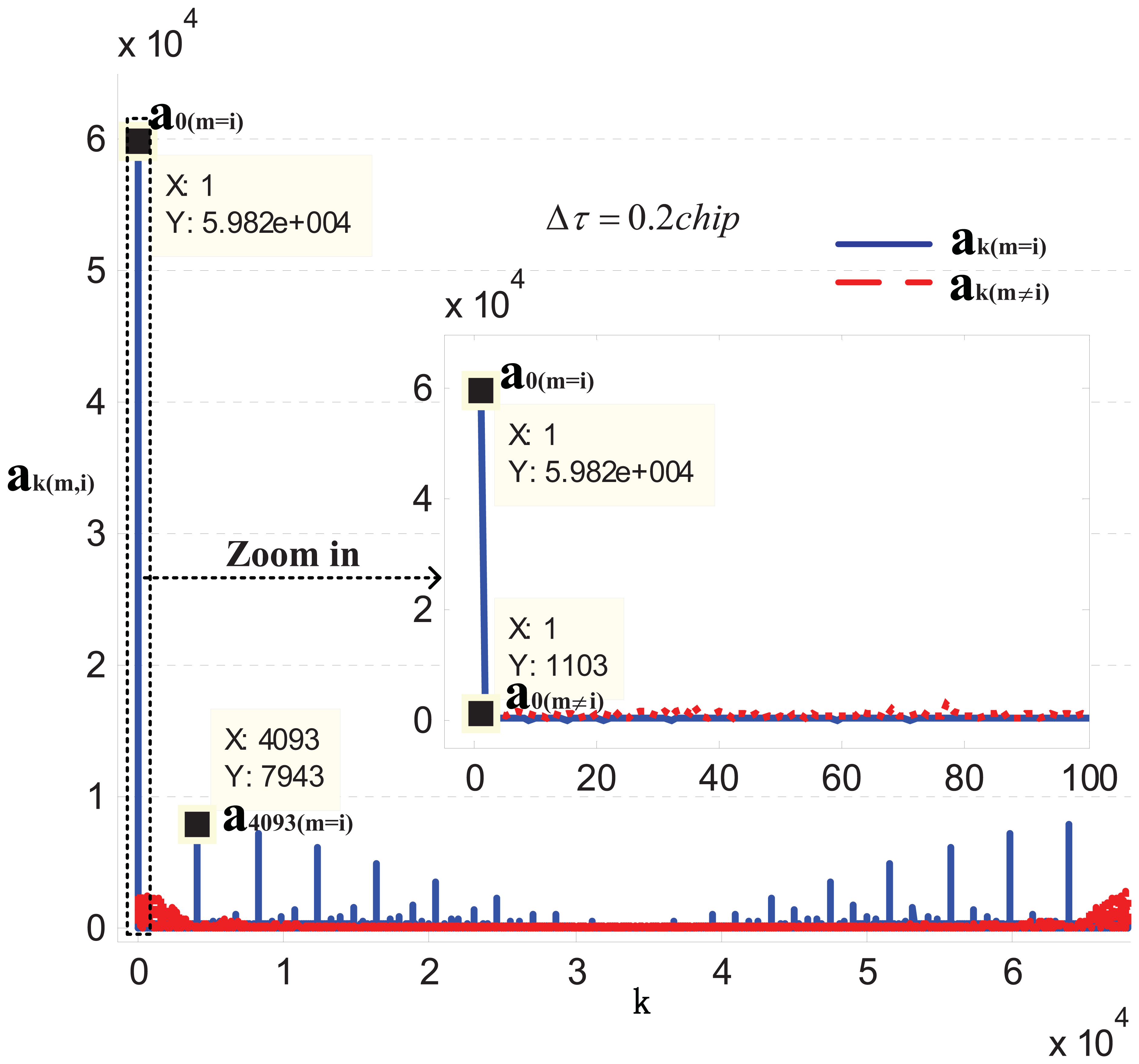
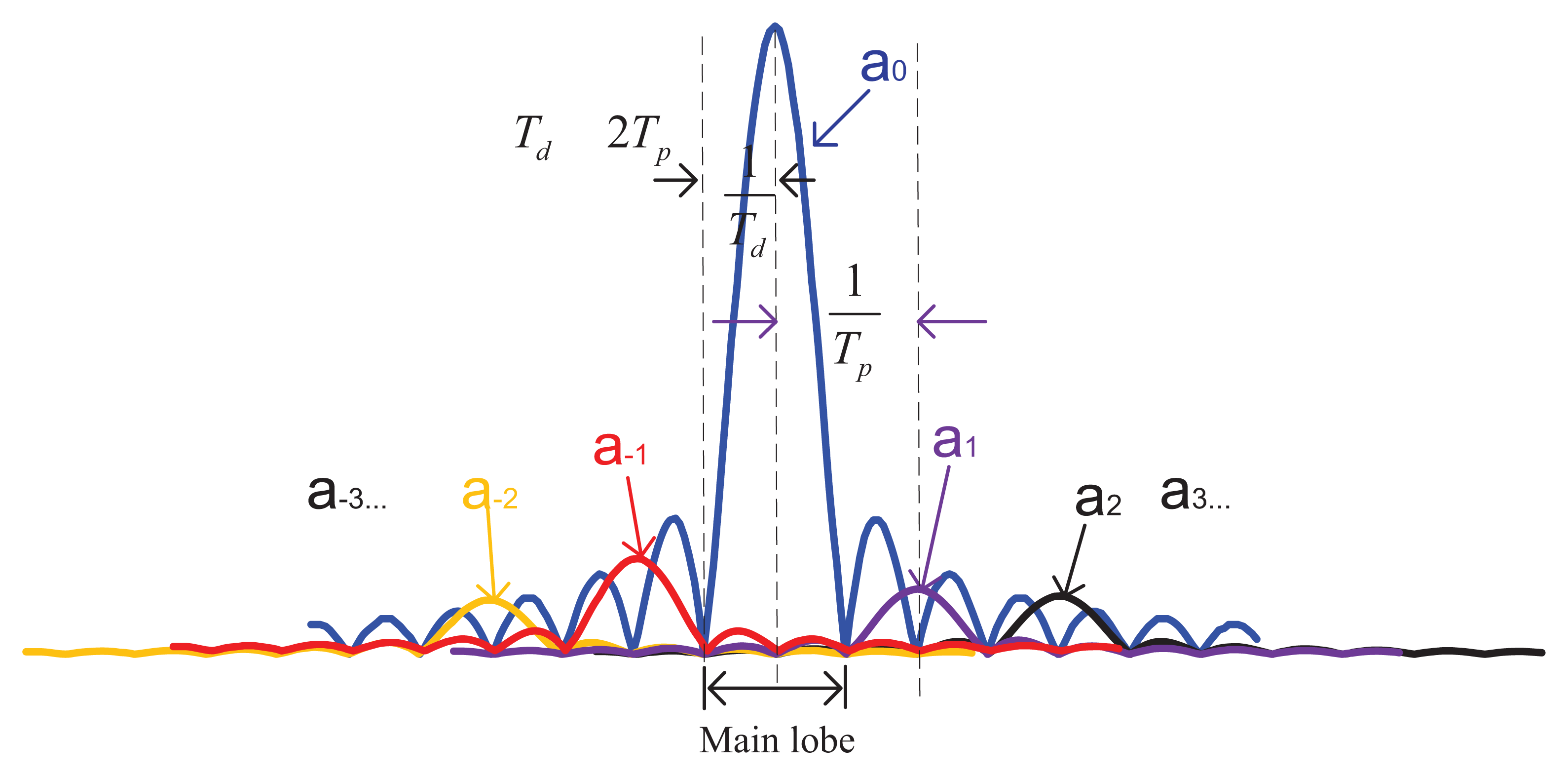
In Figure 2 the distribution of ak(m,i) is shown in the case τm −r̅ = 0.2 Tch, where Tch is the chip duration. Thanks to the property of Pseudo Random Noise (PRN) code, as expected, a0(m=i) predominates over the other ak(m,i). To better understand the nature of the summation in Equation (12), let us refer to Figure 3 where for simplicity, we represent the quantity
The validity of this approximation can be improved in two ways:
By enlarging the integration time Td. In fact as Td increases, the adjacent components will “move” away relatively In other words, as Td increases the width of the lobe decreases, while the distance between two sinc functions stays constant, as it depends on the code period.
By decreasing the values of the adjacent coefficients (a−2a−1a1a2 …). This can be obtained by improving the accuracy of code delay estimate, so as to work close to the maximum of R(Δτ).
Based on the CAF expression in Equation (19), new algorithms for a better estimation of the Doppler frequency are discussed hereafter, both in ideal (i.e., noiseless, Section 3) and realistic (Section 4) scenarios.
3. Doppler Frequency Evaluation in the Absence of Noise
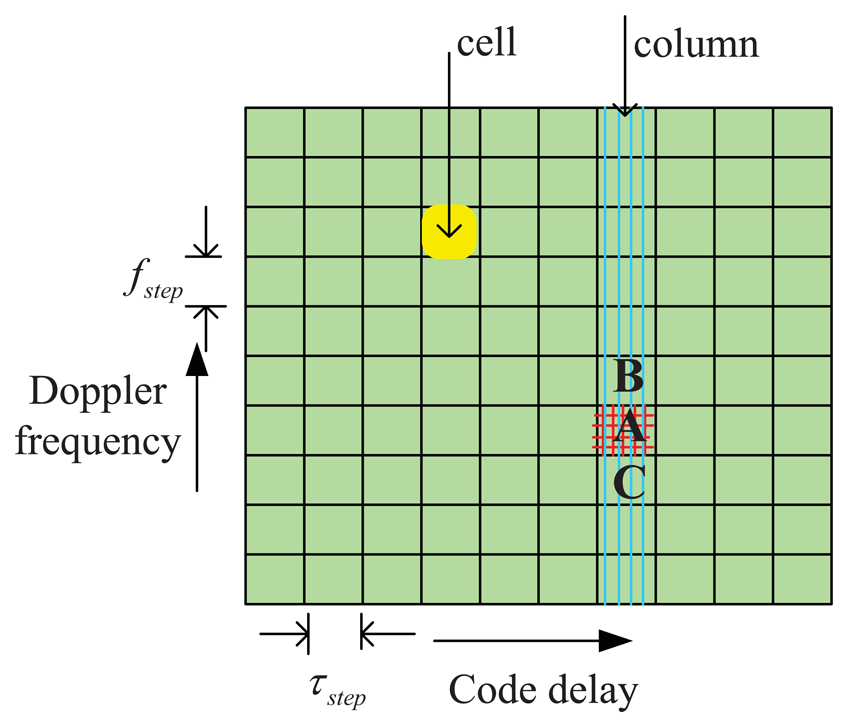
The signal acquisition process is basically a two dimensional search in a grid plane (commonly referred to as search space), as shown in Figure 4, where τ̅ ϵ (0, Tp) (X-axis range), and f̅d ∈ (−fdmax, fdmax) (Y-axis range). The variables under test τ̅ and f̅d are discretized with a step τsp for the code delay, and a step fsp for the Doppler frequency. The integration time is Td = LTs (where L is the total number of integrated samples). The number of trial points in the two axes are Nτ = Td/τsp, and Nf = 2fdmax/fsp. Therefore the grid plane contains Nτ × Nf cells, and each cell (marked by yellow color in Figure 4) corresponds to a parameter pair 〈τ̅, f̅d〉. Finally the decision variable for the acquisition is
The purpose of a traditional acquisition system is to find the coordinates of the peak cell of the grid plane when the satellite we want to detect is visible. To improve the accuracy of the estimates, the steps τsp and fsp must be decreased, at the expenses of the computational complexity, since the number of points of the search space increases. The empirical value fsp = 2/(3LTs) is a typical choice [8] for the Doppler frequency step.
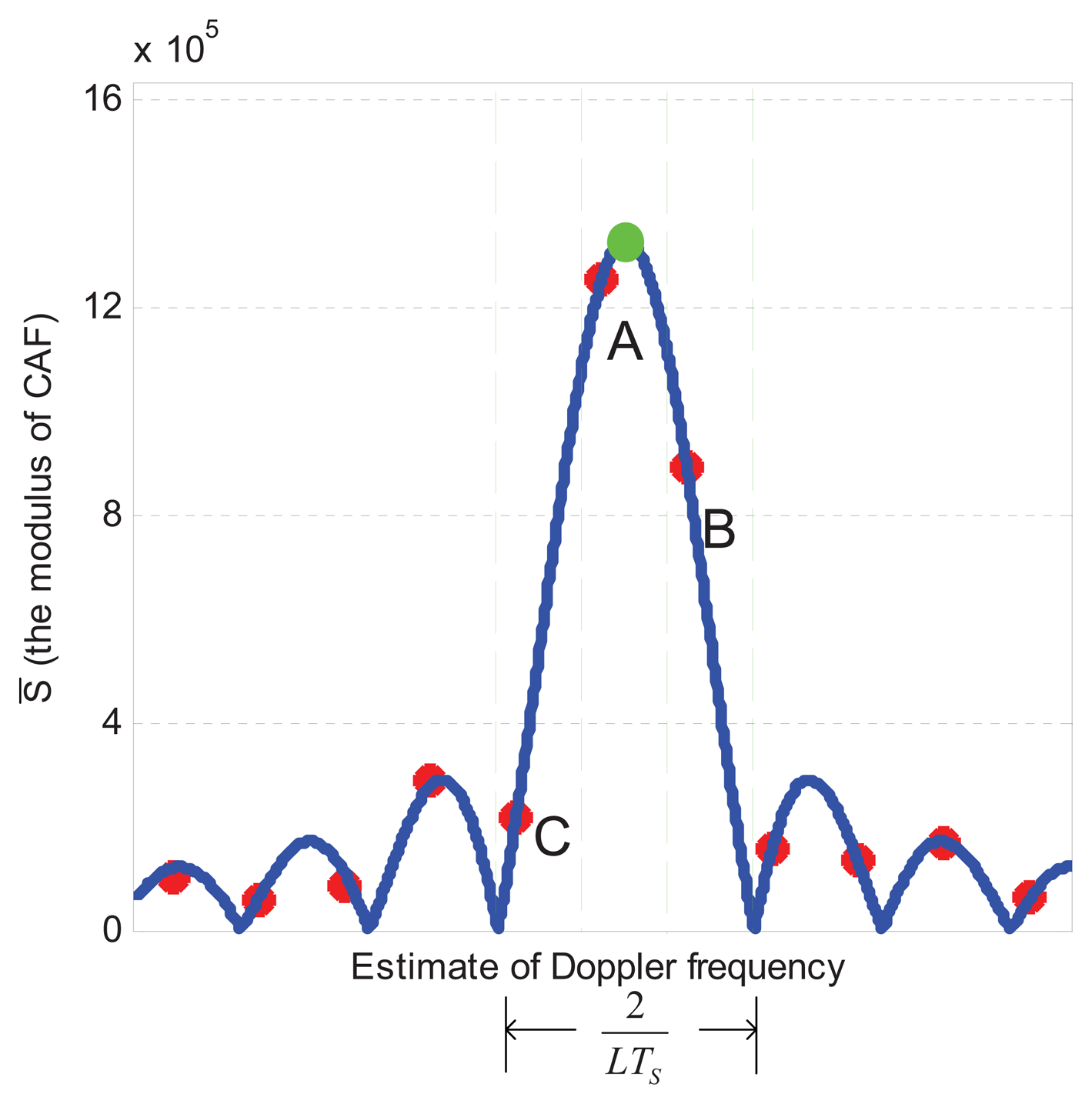
An example of search space is shown in Figure 4. The column (marked in green) crossing the peak cell (marked A) contains cells that share the same code delay. When the i-th satellite is visible, the function in this column is as shown in Figure 5, where the X-axis contains the variable Doppler frequency f̅d, while the Y-axis represents the absolute value of the acquisition test statistic S̅(τ̅, f̅d)ml. As indicated in Figure 3, the width of the main lobe is 2/Td = 2/(LTs). Since fsp = 2/(3LTs), this guarantees that three adjacent points of the frequency domain CAF (A, B, C) are located in the main lobe, and then we can assume that Equation (19) is always valid in these points.
The cells A, B and C are characterized by the triplete and (τ̅A,f̅AS̅a),(τ̅B,f̅BS̅B),and(τ̅C,f̅CS̅C), where the code delay is the same for all the cells in the same column (τ̅a=τ̅Bτ̅C) and we adopt the notation S̅X = S̅(τ̅X, f̅dX) ml, X = (A,B,C) for simplicity. In the case of no noise, these triplets can be used to find the true Doppler frequency fd, as it will be shown hereafter. This will be also the starting point of the estimation method proposed in this paper, when the measurements are affected by noise.
3.1. True Solution Based on the Absolute Value of CAF
In Reference [16], which is our initial work on this topic, we can also find the basic idea about the solution based on the absolute value of the CAF. Under the assumption that there is no data transition in the integration interval, based on Equations (19) and (20) we can write the following equations [16]
First of all we observe that, when the points are located in the main lobe (like points A, B and C in Figure 5), we can write |Sinc (πLTs(fd − f̅A))| = Sinc(πLTs(fd − f̅A)). Now, according to Equation (13) we write f̅ = fd − Δf, so
More in general, if we choose the Doppler frequency step as
When n̅ is odd, we take (n̅ − 1)/2 cells at each side of the peak cell, as shown in Figure 6(a).
When n̅ is even, we take n̅/2 cells at one side and [(n̅/2) − 1]cells on the other side of the peak cell, as Figure 6(b) shows.
No matter what value n̅ assumes (even or odd), there will be n̅ cells taken into the final calculation, and Equation (26) will become
For simplicity, hereafter we refer to solution Equation (27) as algorithm R-3 and solution Equation (30) as algorithm R-n̅.
3.2. True Solution Based on Complex Values of CAF
Based on References [7,10], we can obtain another similar solution by using the test statistic S̅(r̅,f̅d)ml in the complex form given in Equation (19). In fact it is possible to show that
At the same time, similarly to Equation (30), we can generalize this solution as
For simplicity, hereafter we refer to solution Equation (31) as algorithm C-3 and solution Equation (32) as algorithm C-n̅.
3.3. Test of Validity
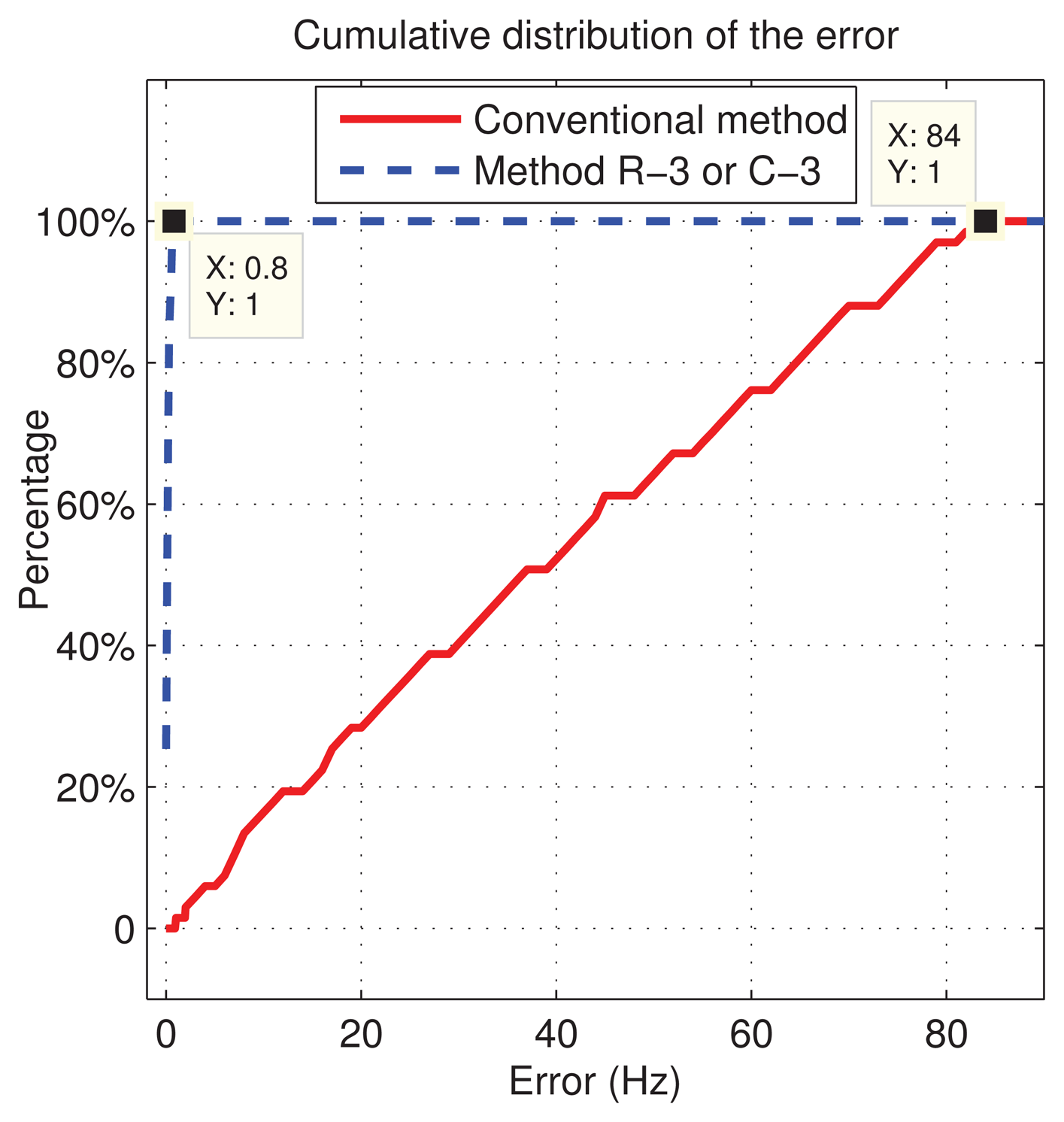
The formulas in the previous sections show that, in the absence of noise and other nuisances, the proposed equations are able to evaluate the true Doppler frequency, hence reducing the estimation error range from the traditional (−fsp/2, fsp/2) to theoretically zero. A possible residual error can arise due to the fact that the method is based on an approximate formulation of the test statistic Equation (19). Therefore to test its validity, we set up a simulated acquisition campaign, where the Doppler frequency estimation error due to the traditional acquisition method is compared with the residual error introduced by the algorithms R-3, R-n̅, C-3, and C-n̅. In the simulations, the GNSS signals are generated by using the signal simulator N-FUELS [20], and several instances of a Galileo E1-b signal are obtained. Firstly we tested the methods in an ideal scenario (i.e., noiseless), with parameters fIF = 4 MHz, fs = 17 MHz, τ = 0.11 ms.
The accumulation time of the acquisition stage is set to the minimum period (4 ms), assuming that no data transition occurs in this period, the Doppler frequency step is
Therefore, we can conclude that in the absence of noise, in experiments, the new methods eliminate the error in the evaluation of the Doppler frequency due to the discretization of the search space, just using three cells selected in the main lobe of the frequency-domain CAF The only constraint is that the Doppler frequency step has to be as given in Equation (28), with n̅ = 3. Moreover the obtained results show that the method is not affected by the code delay error Δτ.
The practical situation in which the noise is unavoidable is discussed in the next section.
4. Doppler Frequency Estimation in the Presence of Noise
In real scenarios, we have to consider the influence of noise, which can be modeled as an Additive White Gaussian Noise (AWGN), as commonly done in the literature. Then the received signal model becomes
Hereafter, we refer to Equation (40) as algorithm “Rn-3” and to Equation (41) as algorithm “Cn-3”. As before, they can be generalized to “Rn-n̅” and “Cn-n̅”
In the following two subsections, we discuss two terms of comparison worth to be considered for the frequency estimators proposed so far, firstly a least squares solution and secondly the CRLB on the variance of the estimator. Performance comparisons obtained in simulation are presented in Section 4.3.
4.1. Least-Square Method
Another approach to exploit the CAF points as defined in Equation (39) is to set up a least squares (LS) problem as follows.
Since we know that the main lobe of the CAF is a sinc function, it is possible to use the LS method in which the fitting curve is the sinc function Equation (21). The LS method requires that the sum of the squared residuals
4.2. Evaluation of the Cramer-Rao Lower Bound
Usually, a statistical estimator is characterized by its bias (mean error), variance (mean square error), and the threshold SNR (signal-to-noise ratio) [22]. Hence, here the Cramer-Rao lower bound (CRLB) is proposed as benchmark to compare the performance of different algorithms.
Without considering the data-transition problem and ignoring the influence of the code delay estimation error (which will be discussed in Section 5.2), the received samples Equation (34) can be mathematically expressed as
4.3. Simulation Experiments for Performance Assessment
To test the algorithms Rn-3, Cn-3 and LS, we performed several simulation experiments with different values of the carrier-to-noise density ratio (CNR), corresponding to a signal-to-noise ratio ρ given by:
The parameters used in the experiments are fIF = 4 MHz, fs = 17 MHz, τ = 0.11 ms, and fsp is set as in Equation (33). We use the root-mean-square error (RMSE) computed for the different algorithms as a metric of performance comparison:
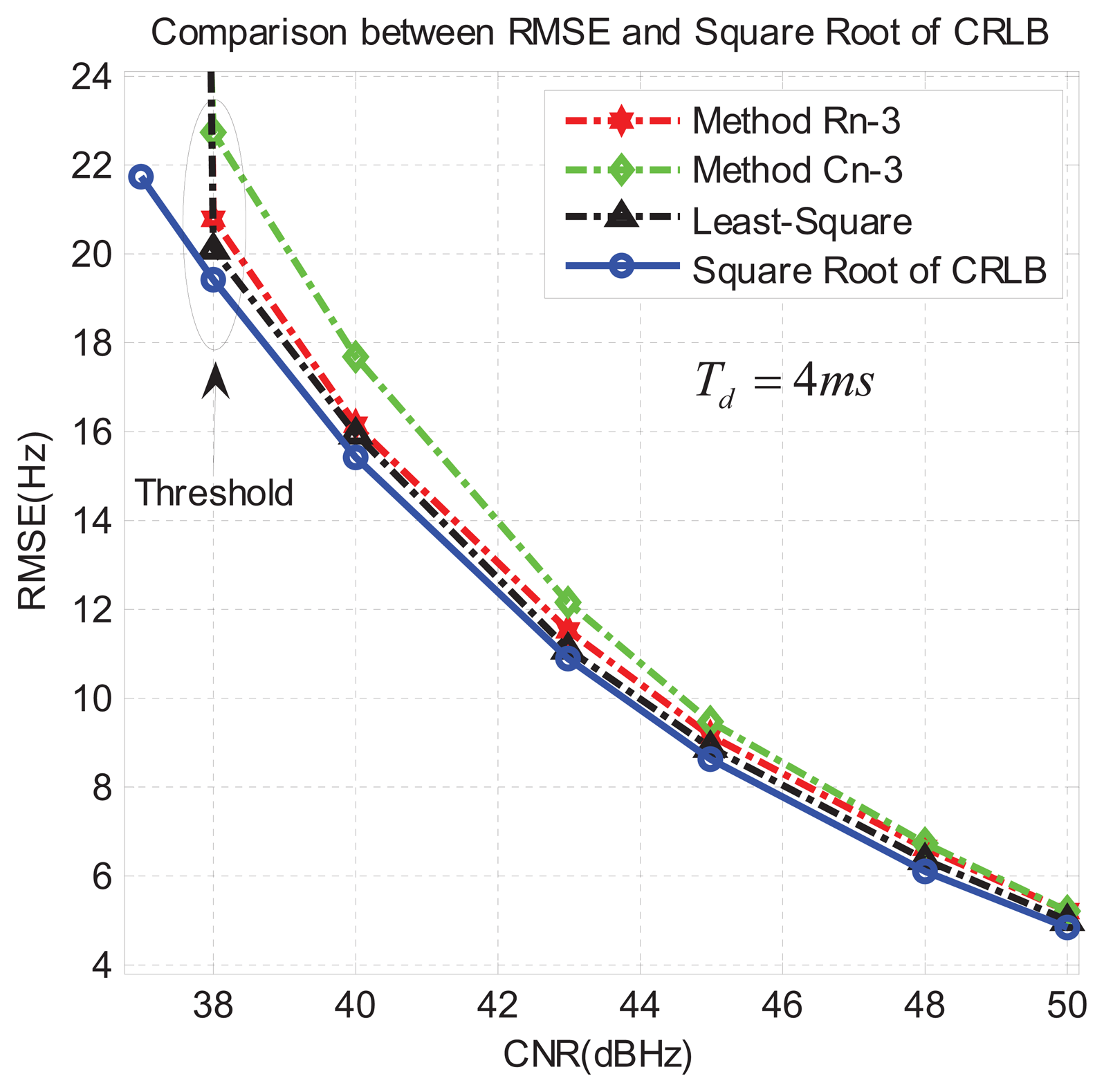
In the first group of experiments, we set Td = 4 ms and we executed 1000 runs for each CNR. Then, according to Equation (51), we calculated the corresponding RMSE. The results can be seen in Figure 8. We can see that in this case the algorithm Rn-3 is better than Cn-3, as it achieves a lower RMSE closer to the CRLB. At the same time we can see that the algorithm Rn-3 is very close to the least-square method, though the latter is slightly better. However, considering the computation complexity of the LS method, the algorithm Rn-3 appears really competitive with respect to the LS. Finally, the threshold CNR (below which the RMSE rapidly worsens) is around CNR = 38 dB-Hz in all the proposed methods.
In the second group of experiments, we changed the integration time to Td = 8ms. Similarly, we executed 1,000 runs for each CNR and obtained the results reported in Figure 9, where we can observe that, as expected, the RMSE is lower than in Figure 8, since a longer integration time reduces the effects of noise. Again, Rn-3 is the closest to the least-square method, and the threshold CNR decreases to around CNR = 35 dB-Hz in all three proposed methods.
Comparing Figures 8 and 9 we can observe that, first, at the same CNR, the RMSE in Figure 9 is decreased by about a factor of 2.8 with respect to Figure 8. This is in agreement with the theoretical CRLB given in Equation (49). In fact when Td = 4 ms is replaced with Td = 8 ms, the CRLB bound decreases by a factor of . Furthermore, when CNR is relatively high (like CNR≥ 45dB-Hz in Figure 8), the proposed three algorithms are very close to the CRLB and each other.
4.4. Averaging Method
Since noise is dominant in the acquisition process, in order to increase the robustness of the proposed approach in the presence of noise, the performance of a simple averaging method, based on the idea of non-coherent sums, is assessed here. The main steps of the method represented in Figure 10 are:
Find the initial code delay using a first period of data, then pick out the column (marked in blue color in Figure 4), and save (2J + 1) points (J points at each side of the peak point as illustrated in Figure 10)
Use the parameter 〈f̅d, τ̅〉 evaluated in the first step to calculate the new columns (as shown in Figure 10) of the next (M − 1) periods of data.
Calculate the average of the M columns into one single mean column.
Pick out the top n̅ cells in the mean column and use Equation (40) to calculate the final Doppler frequency.
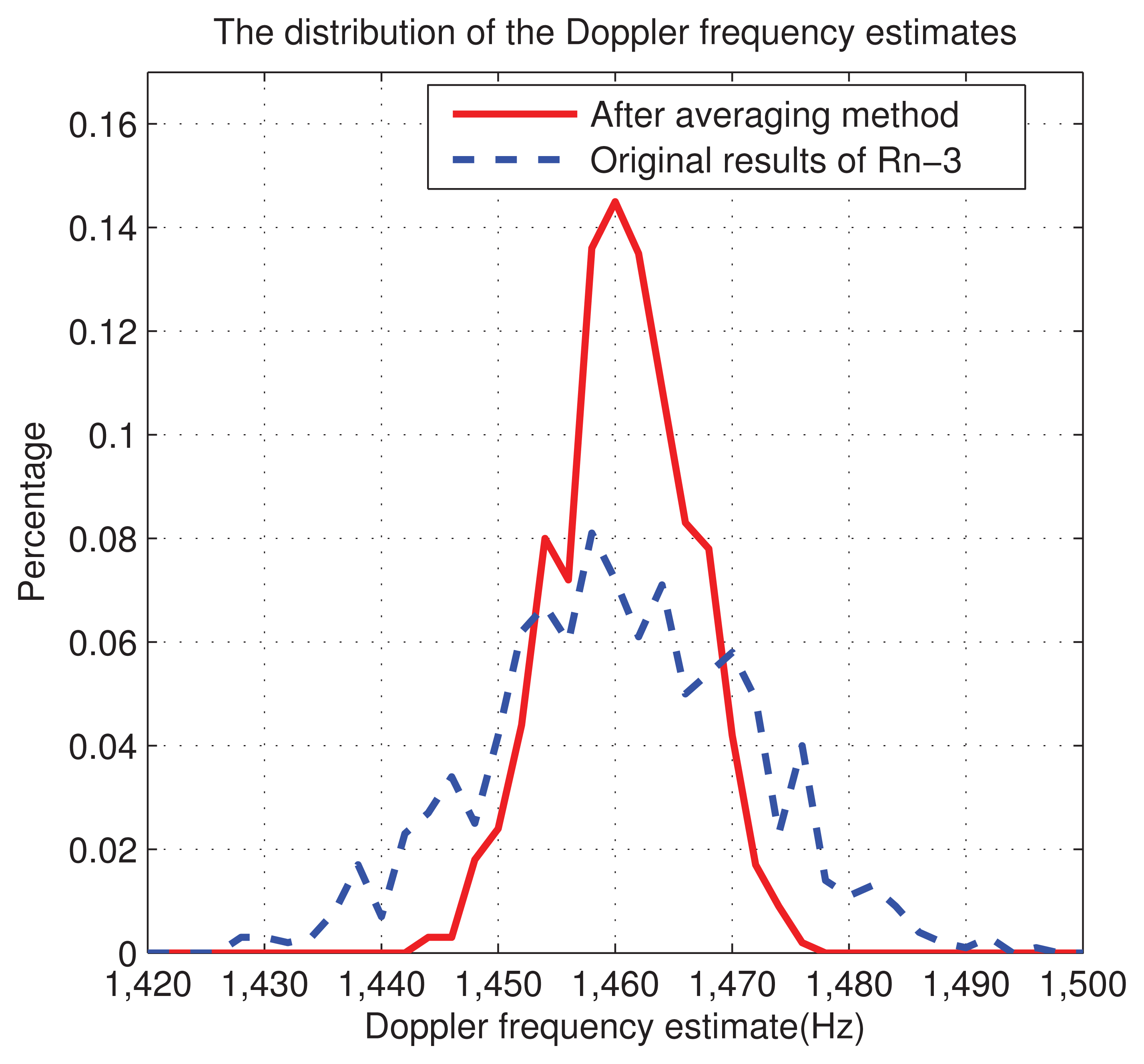
In the following simulation, we set CNR = 43 dB-Hz, n̅=3, J = 2, M = 4, and we execute 1,000 independent runs, for both averaging and non-averaging strategies. The result is shown in Figure 11, where we can see that the new averaging method decreases the error range from (−25,25) Hz to nearly (−15,15) Hz.
5. Analysis of Other Non-AWGN Nuisances
The performance of the algorithms presented so far depends not only on the additive noise but also on other nuisances, whose impact is analyzed in this section. In particular we observe that the methods Rn-3 and Cn-3 are based on the two measured vectors f = [f̅C, f̅A, f̅B] and S̅ = [SC, SA, SB] used in Equations (27) and (31), obtained by reading the peak cell and the adjacent cells in the same column (marked as C, A and B in Figure 4). In particular, the code delay τ̅p is kept constant in these three cells.
Since the search space is discretized, in general even in the absence of noise f̅p ≠ fd, and τ̅p ≠ τ. This can be seen as a quantization error Δ fq = f̅p −fd in the frequency domain, and Δ τq = τ̅p − τ in the time domain. We know that Equations (27) and (31) completely eliminate the quantization errors in the absence of noise. However, in the presence of noise, we experience an accuracy degradation due to the noise influence on vector S̅, as shown in the simulation results of the previous section. The purpose of the following analysis is to state the influence of the frequency and code delay quantization errors on the proposed frequency estimators, in the presence of noise.
5.1. The Influence of the Peak Point's Location
In this section we study the influence of the quantization error in the frequency domain, which can be re-elaborated as
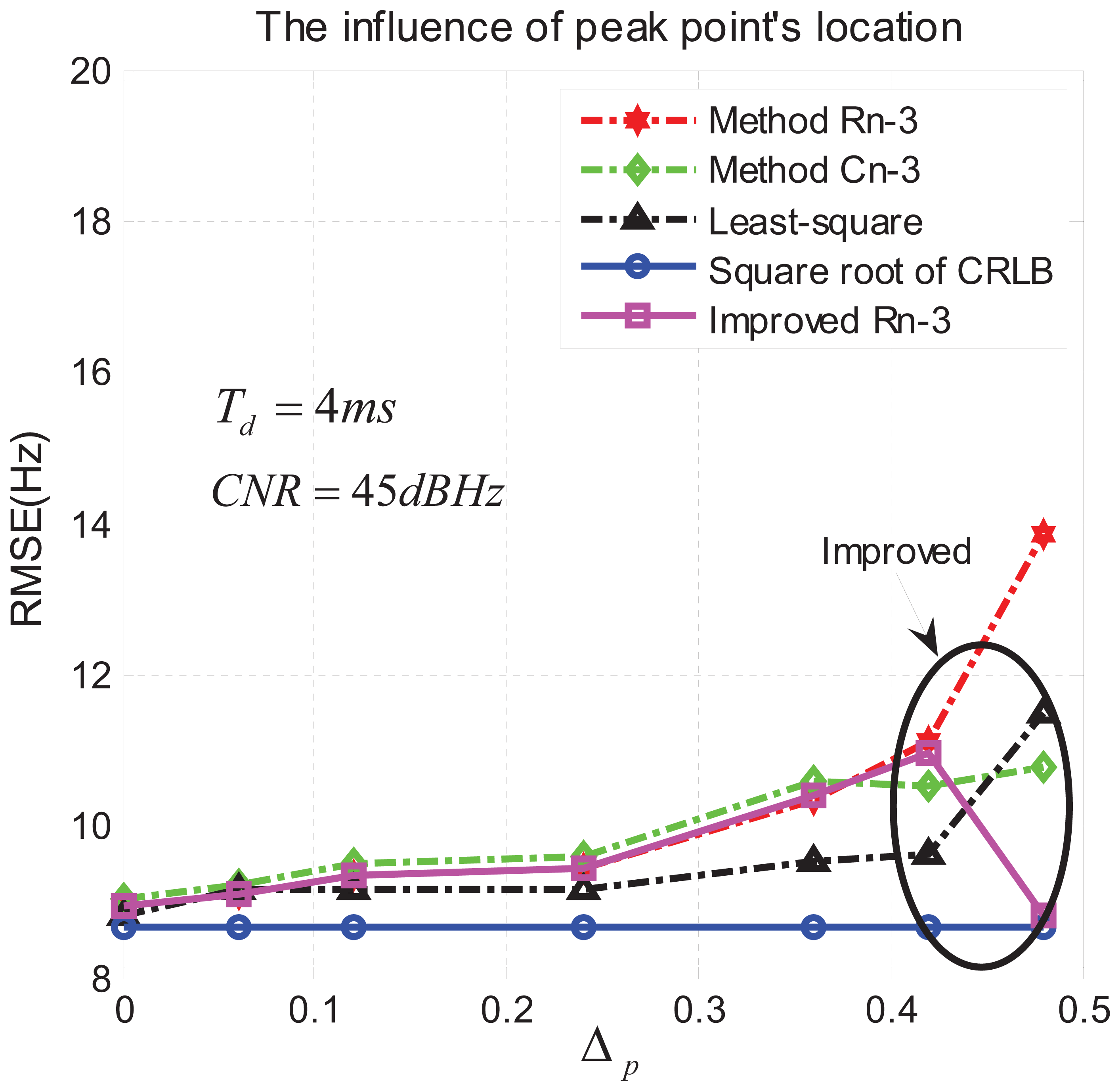
From Figure 12 we can see that Δp influences the accuracy of the proposed three methods, especially when it comes to the top limit 0.5. This result suggested us to adopt a strategy to mitigate this effect. Recalling Figure 4, in which “A” is the peak point, “B” is the second high point and “C” is the lowest point independently from their relative position on the frequency axis, we can easily observe that, when Δp is close to the limit 0.5, then S̅C is close to zero. In this case the residual error defined in Equation (39) introduces a significant error in the estimate Equation (40), since noise dominates in point “C”. This is experimentally proven in Figure 12, where the curves of Rn-3 and Cn-3 show an increasing RMSE as Δp increases, while the LS appears slightly more robust.
So when Δp is close to 0.5, to limit the accuracy degradation we changed the algorithm (40) as
To implement this method, a threshold control has to be added, as drawn in Figure 13. Here we use the empirical criterion to decide whether Δp is critically close to 0.5 or not. In Figure 12 we can observe the result of the method drawn in Figure 13 (continuous line with square markers), which is able to consistently reduce the RMSE when Δp is close to 0.5.
5.2. The Influence of the Code Delay Error
The peak column selected in the search space (marked in Figure 4) also depends on the resolution of the search space in the code delay domain. The mentioned quantization error Δτq = τ̅p − τ affects the CAF samples with an amplitude scale factor |R(Δτq) | as shown in Equation (21), where now Δτ = Δτq. This factor is expected to affect the performance of the estimators Cn-3, and Rn-3.
The influence of such a code delay error can be quantified by modifying the expression of the signal-to-noise ratio ρ in the CRLB Equation (49), so as to take into account the term R(Δτq). Thus, defining the modified Equation (49) becomes
From Equation (56), because R(Δτq ≤ 1), we can conclude that the CRLB value increases as the code delay Δτq increases; this increase will be also experienced by the RMSE of the proposed algorithms. In conclusion the effect of the quantization error Δτq is an attenuation, which does not modify the results of Figures 8 and 9, except for a scaling factor in the abscissa.
6. Conclusions
In this paper a new family of algorithms is proposed for the fine estimation of the Doppler frequency based on an approximate analytical expression of the CAF The proposed methods have been analyzed in both ideal (i.e., noiseless) and realistic (i.e., noisy) scenarios and compared with a similar LS approach. The CRLB has been derived and used as benchmark for performance assessment. The influences of non-AWGN nuisances are also analyzed under a theoretical perspective. In application, from the experiments, we can see that the method Rn-3 almost achieves the performance of LS, which is very close to CRLB, but the complexity of Rn-3 is notably lower. Moreover, performance can be improved by adopting a simple averaging method.
References
- Kaplan, E.D.; Hegarty, C.J. Understanding GPS: Principle and Applications; Artech House: Boston, MA, USA, 2006; pp. 166–173. [Google Scholar]
- Curran, J.T.; Lachapelle, G.; Murphy, C.C. Improving the design of frequency lock loops for GNSS receivers. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 850–868. [Google Scholar]
- Tsui, J.B. Fundamentals of Global Positioning System Receiver: A Software Approach; Wiley: New York, NY, USA, 2005; pp. 146–151. [Google Scholar]
- Borio, D.; Camoriano, L.; Lo Presti, L.; Fantino, M. DTFT-based frequency lock loop for GNSS applications. IEEE Trans. Aerosp. Electron. Syst. 2008, 44, 595–612. [Google Scholar]
- Ma, C.; Lachapelle, G.; Cannon, M.E. Implementation of a Software GPS Receiver. 142–149.
- Jacobsen, E.; Kootsookos, P. Fast, accurate frequency estimators. IEEE Signal Process. Mag. 2007, 24, 123–125. [Google Scholar]
- Quinn, B.G. Estimating frequency by interpolation using Fourier coefficients. IEEE Trans. Signal Process 1994, 42, 1264–1268. [Google Scholar]
- Quinn, B.G. Estimation of frequency, amplitude, and phase from the DFT of a time series. IEEE Trans. Signal Process. 1997, 45, 814–817. [Google Scholar]
- Macleod, M.D. Fast High Accuracy Estimation of Multiple Cisoids in Noise. In Signal Processing V: Theories and Applications; Torres, L., Masgrau, E., Eds.; Elsevier: New York, NY, USA, 1990; pp. 333–336. [Google Scholar]
- Macleod, M.D. Fast nearly ML estimation of the parameters of real or complex single tones or resolved multiple tones. IEEE Trans. Signal Process 1998, 46, 141–148. [Google Scholar]
- Jacobsen, E.A. On Local Interpolation of DFT Outputs. Available online: http://www.ericjacobsen.org/FTinterp.pdf (accessed on 2 January 2013).
- Kay, S.M. A fast and accurate single frequency estimator. IEEE Trans. Acoust. Speech Signal Process 1989, 37, 1987–1990. [Google Scholar]
- Candan, C. A method for fine resolution frequency estimation from three DFT samples. IEEE Signal Process. Lett. 2011, 18, 351–354. [Google Scholar]
- Parkinson, B.W.; Spilker, J.J., Jr. Global Positioning System: Theory and Application; American Institute of Aeronautics and Astronautic: Washington, WA, USA, 1996; pp. 330–368. [Google Scholar]
- Lo Presti, L.; Motella, B. The math of ambiguity. Inside GNSS 2010, 5, 20–28. [Google Scholar]
- Tang, X.; Falletti, E.; Lo Presti, L. Fine Doppler Frequency Estimation in GNSS Signal Acquisition Process.
- Lo Presti, L.; Xuefen, Z.; Fantino, M.; Mulassano, P. GNSS signal acquisition in the presence of sign tansition. IEEE J. Sel. Top. Signal Process 2009, 3, 557–570. [Google Scholar]
- European Union. European GNSS (Galileo) Open Service Signal in Space Interface Control Document. Available online: http://ec.europa.eu/enterprise/policies/satnav/galileo/open-service/ (accessed on 10 January 2013).
- John, J.B. A Software-Defined GPS and Galileo Receiver: A Single-Frequency Approach; Birkhauser: Boston, MA, USA, 2007; pp. 75–85. [Google Scholar]
- Falletti, E.; Margaria, D.; Motella, B. A complete educational library of GNSS signals and analysis functions for navigation studies. Coordinates 2009, 5, 30–34. [Google Scholar]
- Borio, D.; O'driscoll, C.; Lachapelle, G. Composite GNSS signal acquisition over multiple code periods. IEEE Trans. Aerosp. Electron. Syst. 2010, 46, 193–206. [Google Scholar]
- Kay, S.M. Fundamentals of Statistical Signal Processing Estimation Theory; Prentice-Hall PTR: New Jersey, NJ, USA, 1993; pp. 27–67. [Google Scholar]
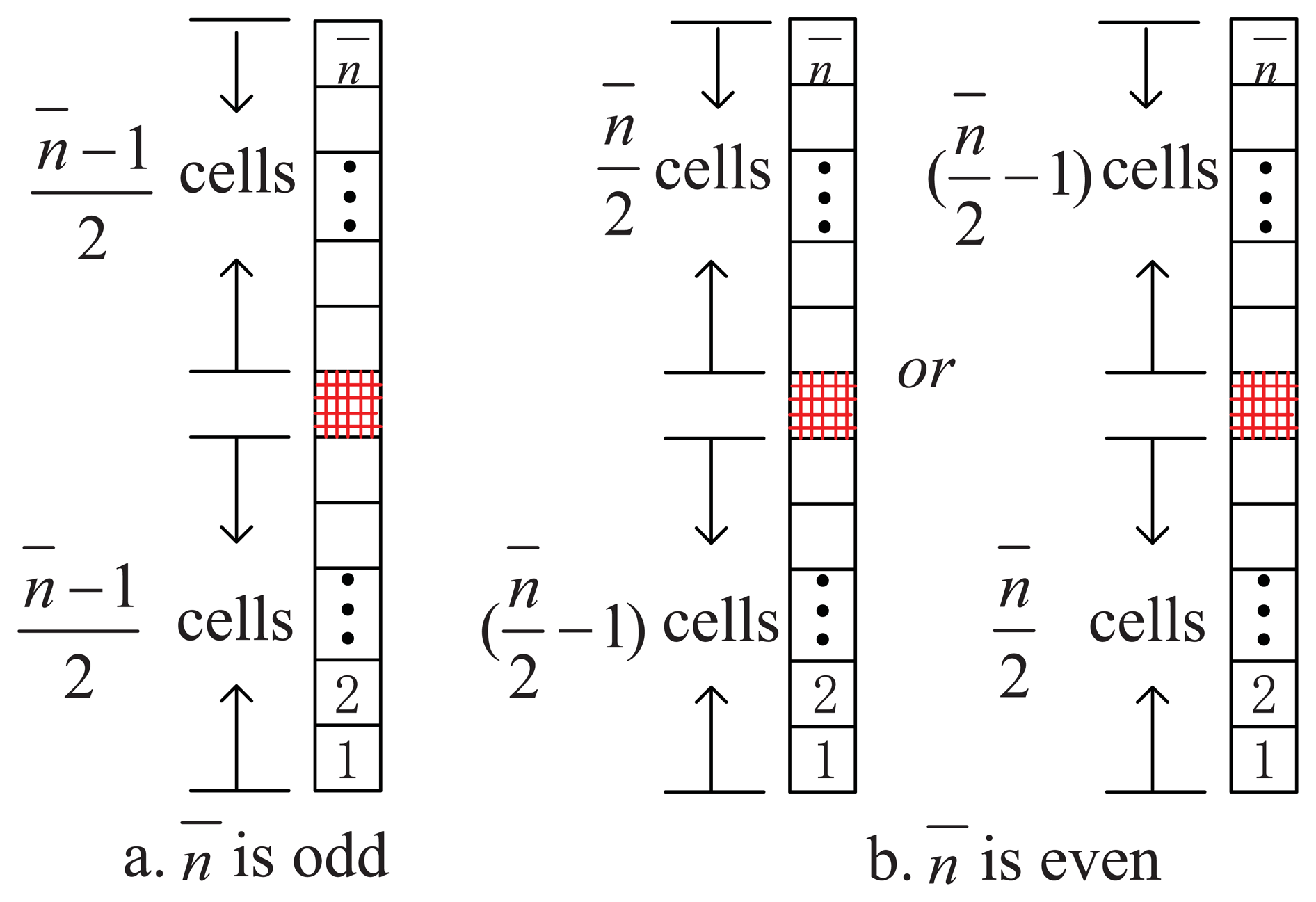



© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/
Share and Cite
Tang, X.; Falletti, E.; Lo Presti, L. Fast Nearly ML Estimation of Doppler Frequency in GNSS Signal Acquisition Process. Sensors 2013, 13, 5649-5670. https://doi.org/10.3390/s130505649
Tang X, Falletti E, Lo Presti L. Fast Nearly ML Estimation of Doppler Frequency in GNSS Signal Acquisition Process. Sensors. 2013; 13(5):5649-5670. https://doi.org/10.3390/s130505649
Chicago/Turabian StyleTang, Xinhua, Emanuela Falletti, and Letizia Lo Presti. 2013. "Fast Nearly ML Estimation of Doppler Frequency in GNSS Signal Acquisition Process" Sensors 13, no. 5: 5649-5670. https://doi.org/10.3390/s130505649
APA StyleTang, X., Falletti, E., & Lo Presti, L. (2013). Fast Nearly ML Estimation of Doppler Frequency in GNSS Signal Acquisition Process. Sensors, 13(5), 5649-5670. https://doi.org/10.3390/s130505649




