A PARALIND Decomposition-Based Coherent Two-Dimensional Direction of Arrival Estimation Algorithm for Acoustic Vector-Sensor Arrays
Abstract
: In this paper, we combine the acoustic vector-sensor array parameter estimation problem with the parallel profiles with linear dependencies (PARALIND) model, which was originally applied to biology and chemistry. Exploiting the PARALIND decomposition approach, we propose a blind coherent two-dimensional direction of arrival (2D-DOA) estimation algorithm for arbitrarily spaced acoustic vector-sensor arrays subject to unknown locations. The proposed algorithm works well to achieve automatically paired azimuth and elevation angles for coherent and incoherent angle estimation of acoustic vector-sensor arrays, as well as the paired correlated matrix of the sources. Our algorithm, in contrast with conventional coherent angle estimation algorithms such as the forward backward spatial smoothing (FBSS) estimation of signal parameters via rotational invariance technique (ESPRIT) algorithm, not only has much better angle estimation performance, even for closely-spaced sources, but is also available for arbitrary arrays. Simulation results verify the effectiveness of our algorithm.1. Introduction
Compared with traditional acoustic pressure sensor arrays, acoustic vector sensors can measure the acoustic pressure as well as all three orthogonal components of the acoustic particle velocity at a single point in space, which offers certain significant advantages in collecting more acoustic information and enhancing the system performance [1–6]. Since the measurement model of an acoustic vector sensor array was developed in [2], researchers mainly turned to the study of incoming signal direction of arrival (DOA) estimation and have proposed many DOA estimation algorithms, which include the Capon technique [4], estimation of signal parameters via rotational invariance technique (ESPRIT) [7–9], root multiple signal classification (MUSIC) [10], self-initiating MUSIC [11], hypercomplex [12], propagator method (PM) [13], trilinear decomposition or parallel factor (PARAFAC) [14], as well as others [15–21]. The subspace-based methods, such as ESPRIT [7–9] and MUSIC [10,11], require eigenvalue decomposition (EVD) of the cross correlation matrix and singular value decomposition (SVD) of the received data to obtain the signal subspace or noise subspace, which implies fairly high computational complexity, while the propagator method (PM) is considerably less demanding because the PM does not require any EVD of the cross correlation matrix and SVD of the received data [22]. However, only in high-snapshots situation and signal to noise ratio (SNR), can the PM algorithm provide a better estimation performance. In most current algorithms for DOA estimation, some precise a priori knowledge, including the sensor locations, gain, phase response and mutual coupling of the receiver array is needed, but in realistic situations this can seldom be pre-known. For example, Capon [4] and the MUSIC algorithm can be used for arbitrary arrays, however they need to pre-know the array geometry. Besides, peak searching is also required for Capon and MUSIC algorithms, which renders a heavier computational cost. EVD of the cross spectral matrix or SVD of the received data to obtain the signal subspace is needed for the ESPRIT algorithm [7], which has been used for two dimensional (2D) DOA estimation for arbitrarily spaced arrays at unknown locations based on the acoustic vector-sensor property. However, a problem existing in [7] is that the ESPRIT algorithm needs an extra pair matching which increases the computational load, and usually fails to work in lower SNR when it is used for 2D-DOA estimation. Reference [14] proposes a trilinear decomposition-based 2D-DOA estimation algorithm for acoustic vector sensor arrays, which provides DOA estimation for the arbitrarily spaced sensor arrays and doesn't require knowledge of sensor locations and extra pair matching.
The reflected signal of the same sources through different propagation paths will produce multipath signals. Therefore, it is of significant importance to study the coherent angle estimation problem. The angle estimation algorithms listed above are all proposed for incoherent sources. When it comes to coherent sources, the coherency of sources will result in serious degradation or invalidity of the above algorithms. Some conventional coherent angle estimation algorithms, including forward backward spatial smoothing (FBSS) [23,24], only work for uniform arrays.
This paper combines the acoustic vector-sensor array parameter estimation problem with the so-called PARAllel profiles with LINear Dependencies (PARALIND) model, and proposes a blind coherent 2D-DOA estimation algorithm for arbitrarily spaced acoustic vector-sensor arrays subject to unknown locations by exploiting the PARALIND decomposition approach. Our algorithm can provide coherent and incoherent two-dimensional angle estimation for arbitrary arrays, and it automatically archives paired azimuth and elevation angles, and the paired correlated matrix of the sources can also be acquired. Compared with conventional coherent angle estimation algorithms such as the FBSS-ESPRIT algorithm which only works for uniform arrays, our algorithm has much better angle estimation performance. Furthermore, our algorithm performs considerably well for angle estimation of closely spaced sources. We also derive the Cramér-Rao bound (CRB) of angle estimation for arbitrarily spaced acoustic vector-sensor arrays. Simulation results verify the effectiveness of the proposed algorithm.
The trilinear decomposition, also known as PARAFAC analysis [25,26], has been naturally related to angle estimation for arbitrarily spaced acoustic vector-sensor arrays at unknown locations [14]. However, the PARAFAC angle estimation solution is usually non-unique when the coherent sources exist. The PARALIND model [27,28] is a generalization of PARAFAC suitable for solving problems with linear dependent factors where PARAFAC analysis will fail to provide meaningful results. Our work links the coherent angle estimation problem to the PARALIND model, and proposes a PARALIND decomposition-based coherent angle estimation algorithm for arbitrary arrays, which can be regarded as an extension of the work presented in [14]. Reference [27] proposed the PARALIND model for application in biology and chemistry; the present paper expands this model to the acoustic vector-sensor array signal processing problem to estimate coherent DOA and automatically achieve paired two-dimensional angle estimations, which is an innovation.
Although the ESPRIT algorithm [7] and our algorithm can be used for DOA estimation for arbitrarily spaced acoustic vector-sensor arrays, there are some differences between our paper and Reference [7]. The latter proposed an ESPRIT algorithm for DOA estimation for arbitrarily spaced three-dimensional arrays of vector hydrophones, but it fails to work well for coherent sources. Our work exploits the PARALIND decomposition approach to estimate 2D-DOA in arbitrarily spaced acoustic vector-sensor arrays with unknown locations, and our algorithm is suitable for coherent sources.
The present paper is structured as follows: Section 2 develops the data model for arbitrarily spaced acoustic vector-sensor arrays at unknown locations; Section 3 establishes our PARALIND decomposition-based coherent 2D-DOA angle estimation algorithm in addition with the identifiability issues and complexity analysis; In Section 4, simulation results are presented to verify effectiveness of the proposed algorithm, while the final conclusions are made in Section 5.
2. Data Model
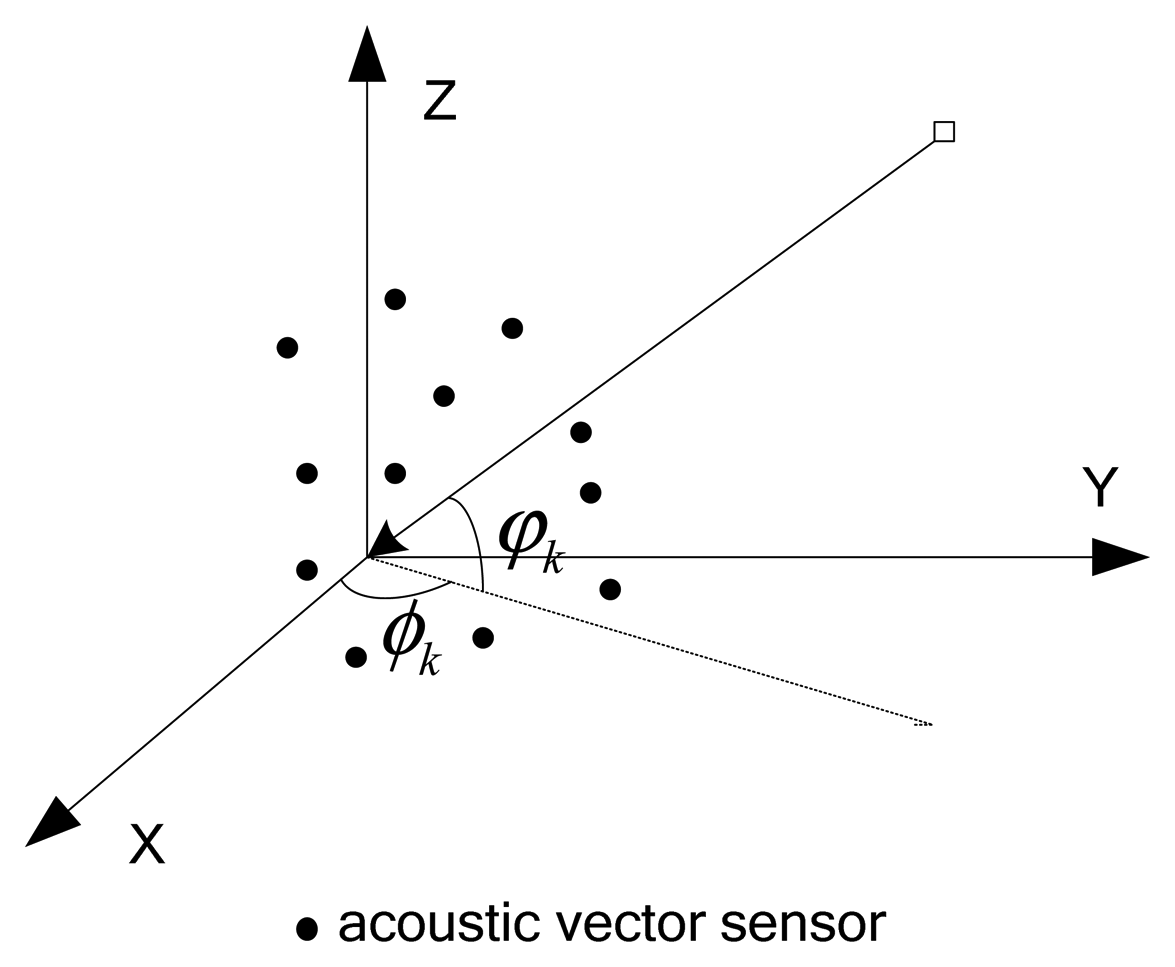
We assume that a total of K narrowband plane waves impinge on an array equipped with M acoustic vector sensors, which are all located at arbitrary unknown three dimensional positions as shown in Figure 1. We define the location of the mth vector sensor as rm = (xm, ym, zm).
We also assume the signals in the far-field. K sources, including K1 incoherent sources and K-K1 coherent sources, are considered. Assume that the noise is additive white Gaussian, which is independent of the sources. The kth signal arrives from direction (ϕk, φk), where ϕk and φk respectively stand for the azimuth angle and the elevation angle. Let θk = [ϕk, φk]T as the 2D-DOA of the kth source. According to [2], the output at the acoustic vector sensors array can be expressed as:
Therefore, the output of J snapshots can be given by:
X can be compactly expressed as:
3. The Coherent Two-Dimensional Angle Estimation
3.1. PARALIND Decomposition
Define Ỹ = XT, according to the signal model in Equation (4), Ỹ can be expressed as:
According to [27], least fitting for the signal model in Equation (5) amounts to:
In a no-noise case, according to Equation (5), we have:
According to [7], stacking these vectors leads to:
Equation (9) can be expressed compactly as:
According to Equation (10), we can obtain:
For attaining vec(ΓT), then Γ can be easily updated via transforming the column vector to its original column-wise matrix.
According to Equation (6), the least square (LS) update for ST is given by:
According to Equation (7), we have:
A has full column rank, so we can acquire A* via:
Similarly, we have:
Extracting the diagonal elements of the matrices in two sides of the equation, we get:
Then we get:
The matrix H can be straightforwardly obtained via diag−1(Dn(H)), n = 1,2,3,4.
According to Equations (11), (12), (14), and (17), we can show PARALIND algorithm applied in the data model established in this paper in detail as follows:
According to Equation (11), the update for vec(Γ̂T) is given by:
Define E = Ỹ × (Γ̂Ŝ)T (Ĥ ○ Â)T, where Â, Ĥ, Ŝ, and Γ̂ present estimates of A, H, Γ and S, respectively. The sum of squared residuals (SSR) in PARALIND model is defined as , where eji is the (j, i) element of the matrix E. According to Equations (18), (19), (20) and (21), the matrices A, H, Γ, and S are updated until the SSR ≤ 10−8, finally we obtain Â, Ĥ, Ŝ, and Γ̂.
3.2. Uniqueness of PARALIND Decomposition
According to [27], we derive the uniqueness of PARALIND decomposition in an acoustic vector-sensor array. The signal matrix in Equation (7) can be transformed to another equivalent matrix via column and row exchanging, which can be expressed as:
The two slices Zi and Zj (i ≠ j) in Equation (22) are represented as:
H being full row rank assures that , where U consists of largest K left singular vectors of the matrix . The matrix U can be denoted as:
Λ and G consist of the eigenvalues and the corresponding eigenvectors of the matrix R2R1−1. Λ is unique, and G is recovered with the scale ambiguity and permutation ambiguity. Then T = G−1R1, H = U1T−1, SE = H+Zi, AT = Di−1((ΓS)T) SE.
Notably, scale ambiguity and permutation ambiguity are inherent to the separation problem. However, the scale ambiguity can be resolved easily by normalization, while the existence of permutation ambiguity is not considered for angle estimation.
3.3. Two-Dimensional Angle Estimation
By imposing PARALIND decomposition for the received data matrix, we get the estimate of matrix Ĥ = [ĥ1,ĥ2, ⋯,ĥK]. According to Equation (2), ĥK can be expressed as:
Finally, the azimuth angle estimate of kth source can be attained via:
Obviously, the azimuth angle and elevation angle are automatically paired. We also obtain the estimate of the correlated matrix Γ from the PARALIND decomposition, because Γ is a matrix whose elements are 0 or 1, so we can easily decide it by a decision function to obtain accurate estimated Γ̂.
3.4. The Procedures of the Proposed Algorithm
Till now, we have achieved the proposal for the proposed coherent 2D-DOA estimation algorithm for the acoustic vector-sensor array. We show major steps of the proposed algorithm as follows:
- Step 1:
Obtain Ỹ from the received data matrix X, and then initialize for the matrices H, A, Γ, and S.
- Step 2:
According to Equations (18), (19), (20) and (21), update the matrices H, A, Γ, and S until SSR ≤ 10−8, finally obtain the corresponding estimated Ĥ, Â, Γ̂, and Ŝ.
- Step 3:
Estimate the two-dimensional DOA through Equations (28)-(30), then obtain accurate estimate Γ̂ by decision.
In our algorithm, the complexity of each iteration is O(4MJ(2K2K12 + 2KK1 + 2K + K1) + 4M(2K12 + K2 + KK1 + 2K) + K2(5J + M + 22) + K3K13 + 2K3+ K13 + 5KK1J). The average number of iterations required for our PARALIND decomposition algorithm is about a dozen.
Remark A: Our algorithm obtains the estimate of correlated matrix Γ from PARALIND decomposition, even for partly coherent sources, the correlated matrix Γ can be acquired as well.
Remark B: The PARALIND decomposition brings the same permutation ambiguity for the estimated Ĥ, Â, and Γ̂, so the elevation and azimuth angles and the correlated matrix are automatically paired.
Remark C: If the number of sources K is unknown, it can be estimated by performing SVD for a slice Zi in Equation (22) and finding the number of largest singular values.
3.5. CRB and Advantages of the Proposed Algorithm
According to [29], we can derive the CRB of coherent angle estimation for the acoustic vector-sensor array with unknown locations as:
The advantages of the proposed algorithm can be presented as follows, which can be verified by the simulation results in Section 4:
- (1)
The proposed algorithm is effective for coherent and incoherent two-dimensional angle estimation.
- (2)
The proposed algorithm does not require precise knowledge of the characteristics of the receiver array.
- (3)
The proposed algorithm can archive automatically paired angles and the corresponding correlated matrix.
- (4)
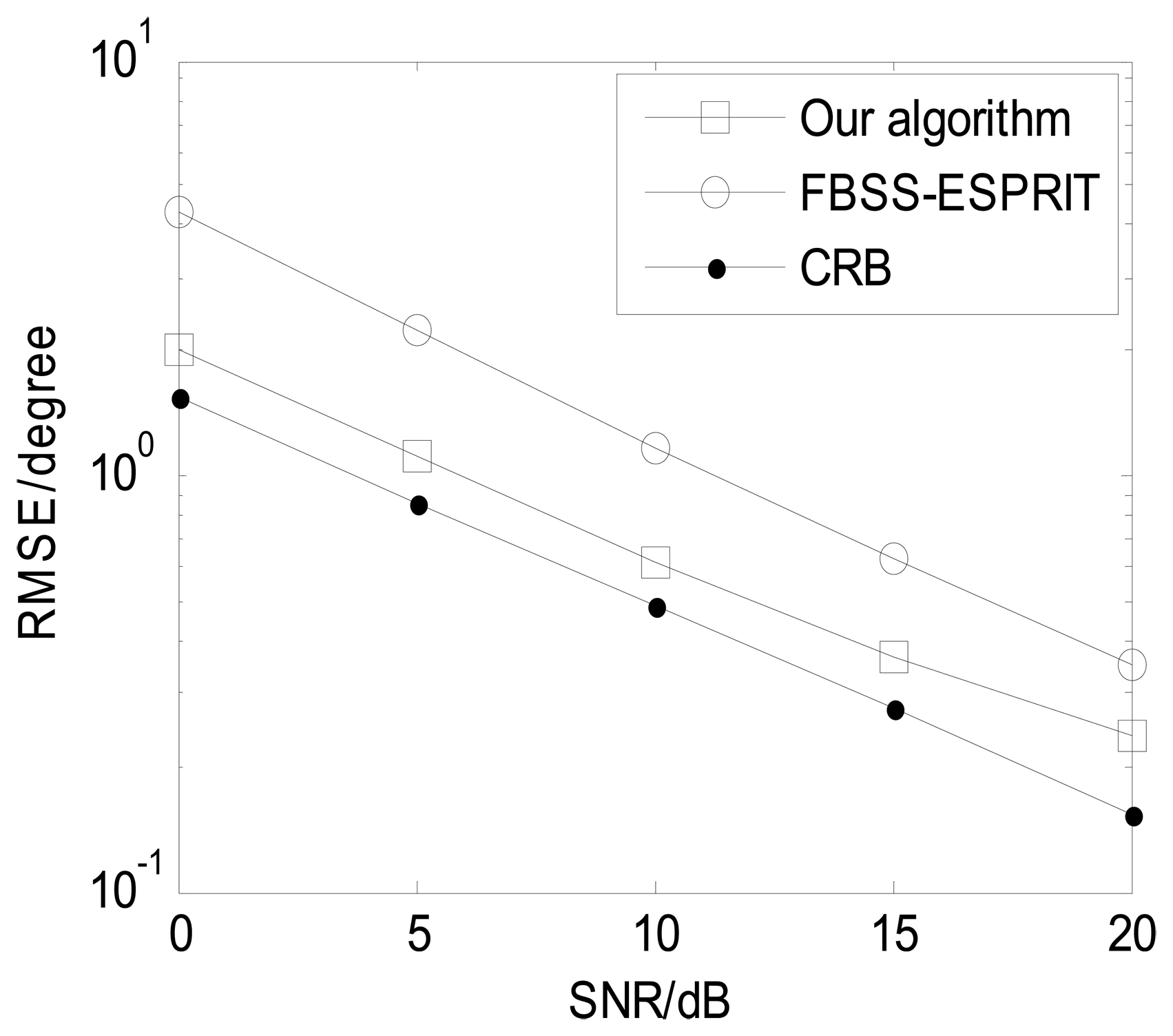
The proposed algorithm has much better angle estimation performance than conventional FBSS-ESPRIT algorithm which only works for uniform array.
- (5)
The proposed algorithm has considerably performance for angle estimation of closely spaced sources.
4. Simulation Results
In most of the following simulations, we assume that there are 3 sources in which only source 1 and source 3 are coherent, namely the correlated matrix is .
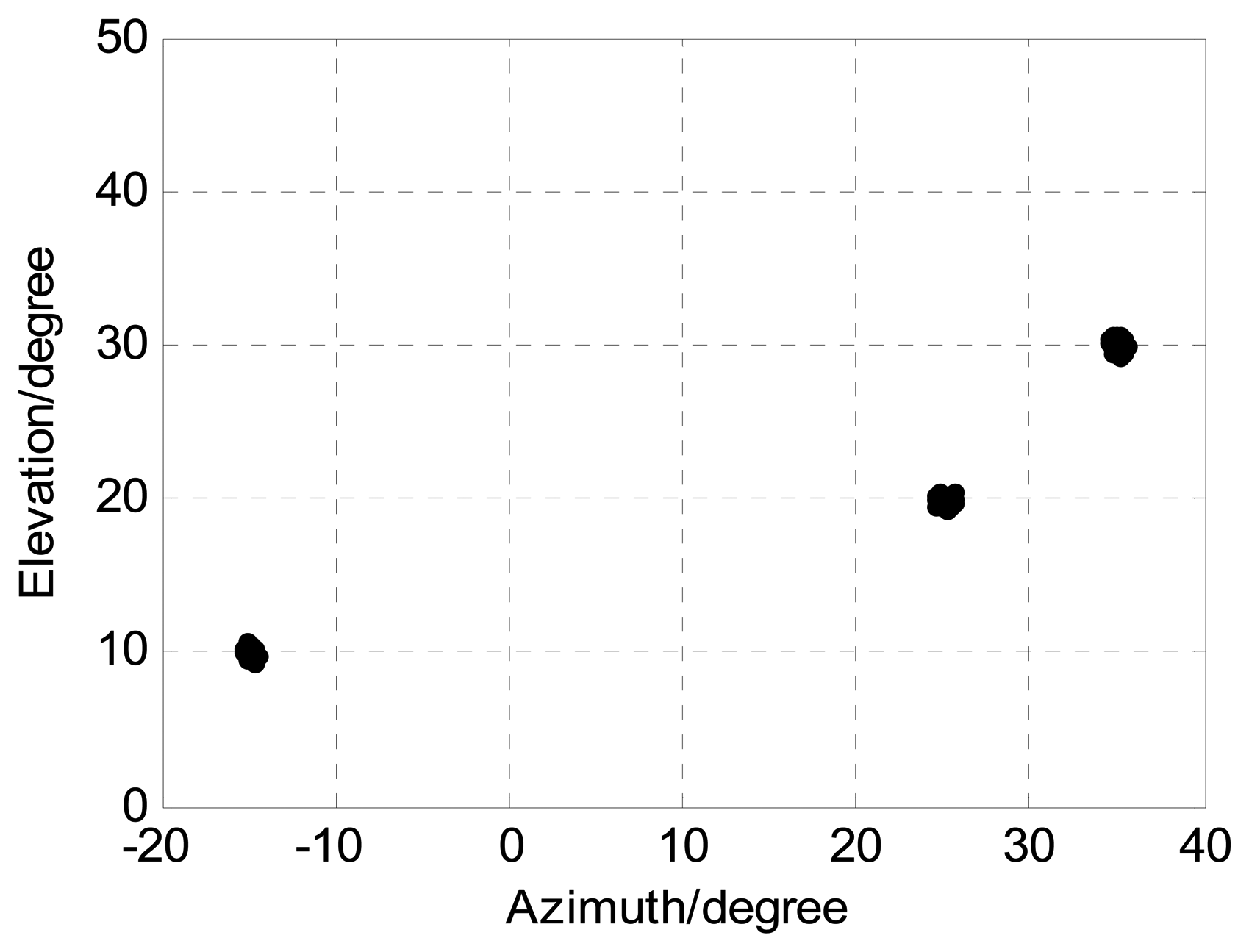
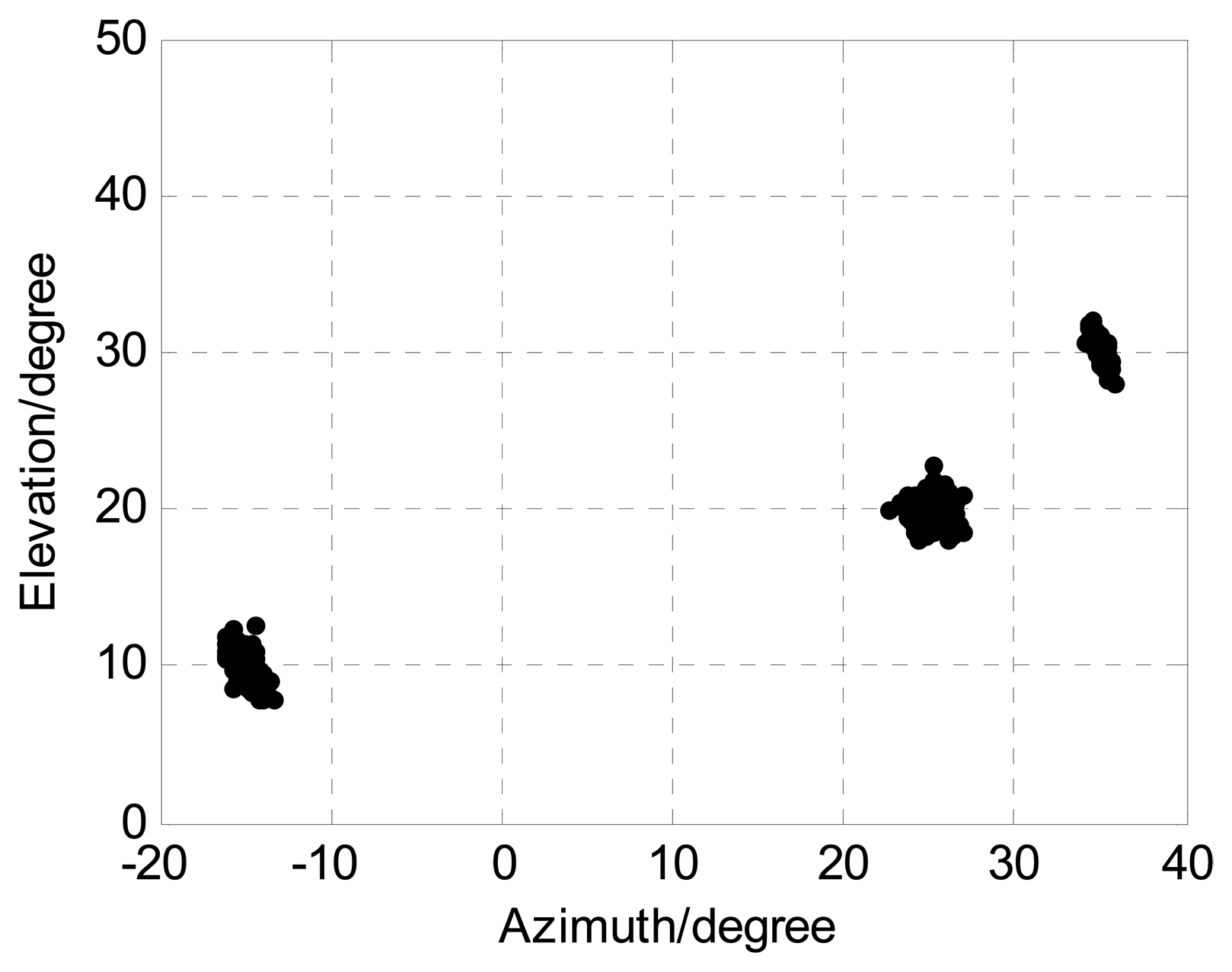
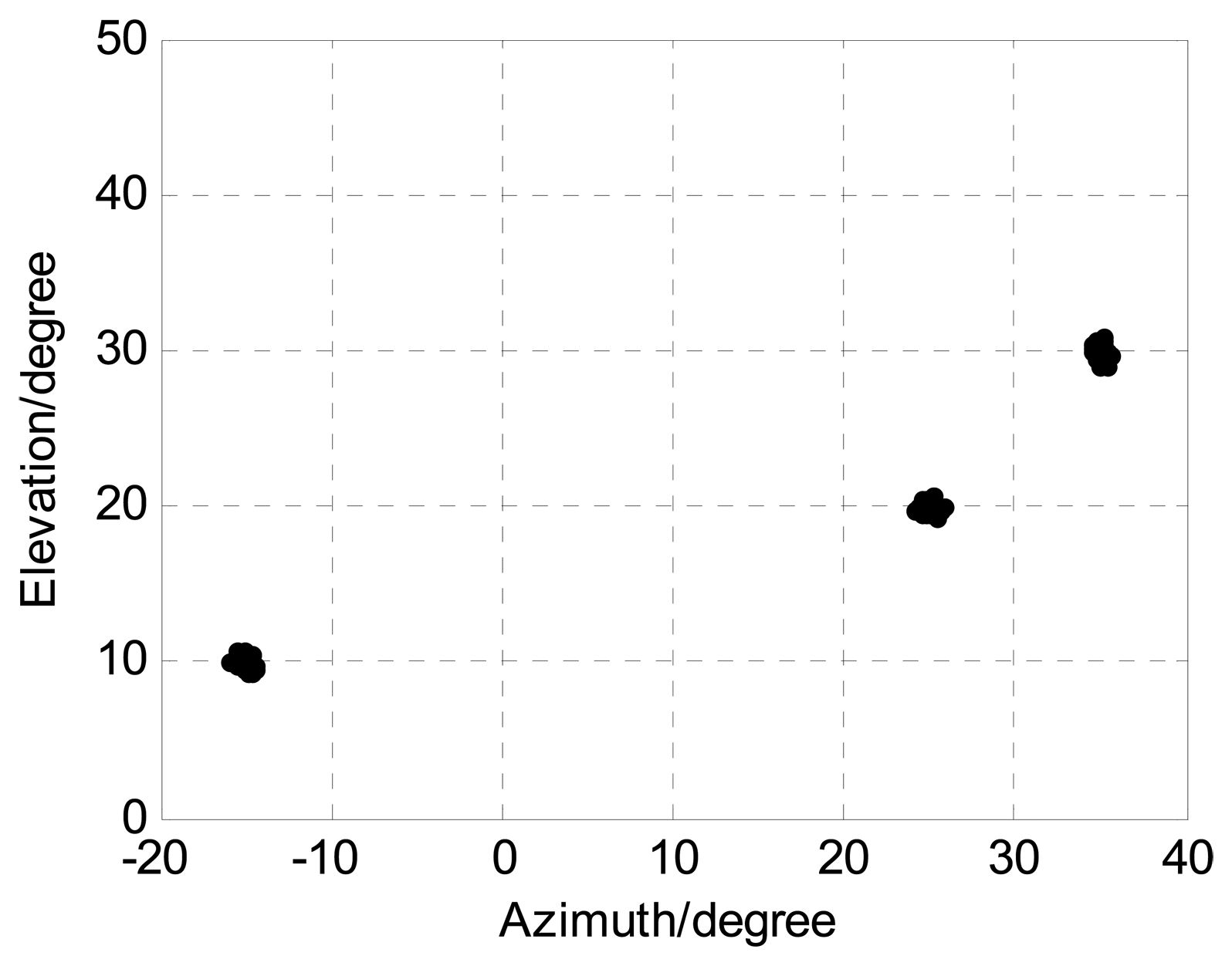
The sources are located at angles (ϕ1,φ1) = (−15°, 10°), (ϕ2,φ2) = (25°,20°), and (ϕ3,φ3) = (35°,30°), respectively. M, J, and K denote the number of receive sensors, snapshots, and sources, respectively. We present 1000 Monte Carlo simulations to assess the angle estimation performance of the proposed algorithm. Define root mean squared error (RMSE) as follows:
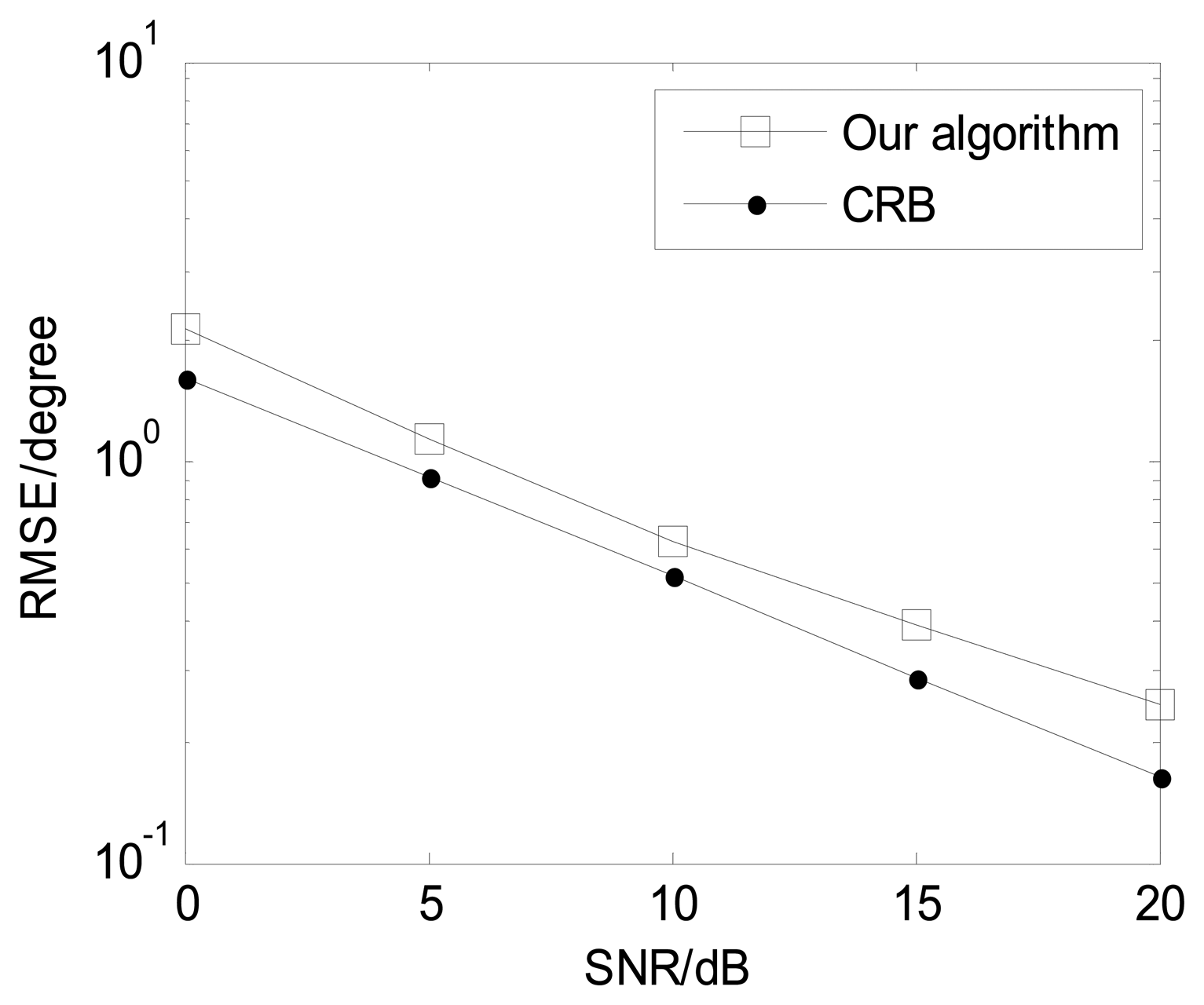
In order to present the angle estimation performance comparison of the proposed algorithm and FBSS-ESPRIT algorithm, we assume that the acoustic vector-sensor array is a uniform linear array (ULA) in Figures 2 and 3. Figure 2 depicts the two-dimensional angle estimation with M = 12, J = 100, K = 3, and SNR = 15 dB. It illustrates that our algorithm is effective for paired two-dimensional angle estimation using ULA. Figure 3 presents the angle estimation performance comparison of the proposed algorithm, FBSS-ESPRIT algorithm, and CRB with M = 12, J = 100, and K = 3. It is shown that our algorithm possesses much better angle estimation performance than the FBSS-ESPRIT algorithm in the ULA situation.
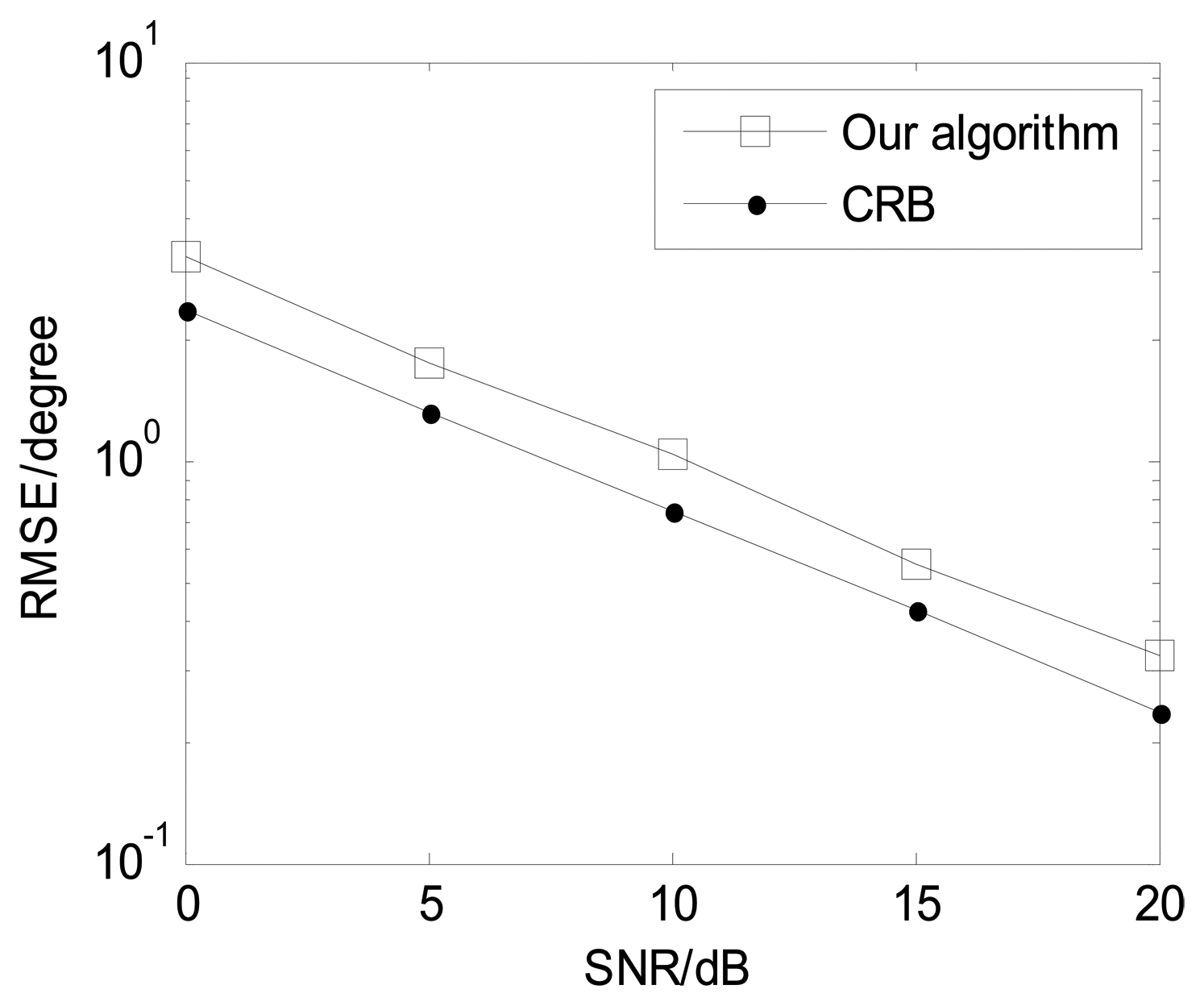
The following Figures 4, 5, 6, 7 and 8 are for the case of arbitrarily spaced acoustic vector-sensor arrays subject to unknown locations, and we assume that the column full rank receive direction matrix is generated randomly. Figure 4 presents the two-dimensional angle estimation of the proposed algorithm with M = 12, J = 100, K = 3, and SNR = 5 dB, and Figure 5 depicts the angle estimation with M = 12, J = 100, K = 3, and SNR = 15 dB. Figures 4 and 5 illustrate that our algorithm is effective for paired two-dimensional angle estimation using arbitrary acoustic vector-sensor arrays. Figure 6 presents the angle estimation performance comparison of the proposed algorithm and CRB with M = 12, J = 100, and K = 3, while Figure 7 depicts the angle estimation performance comparison with M = 10, J = 50, and K = 3.
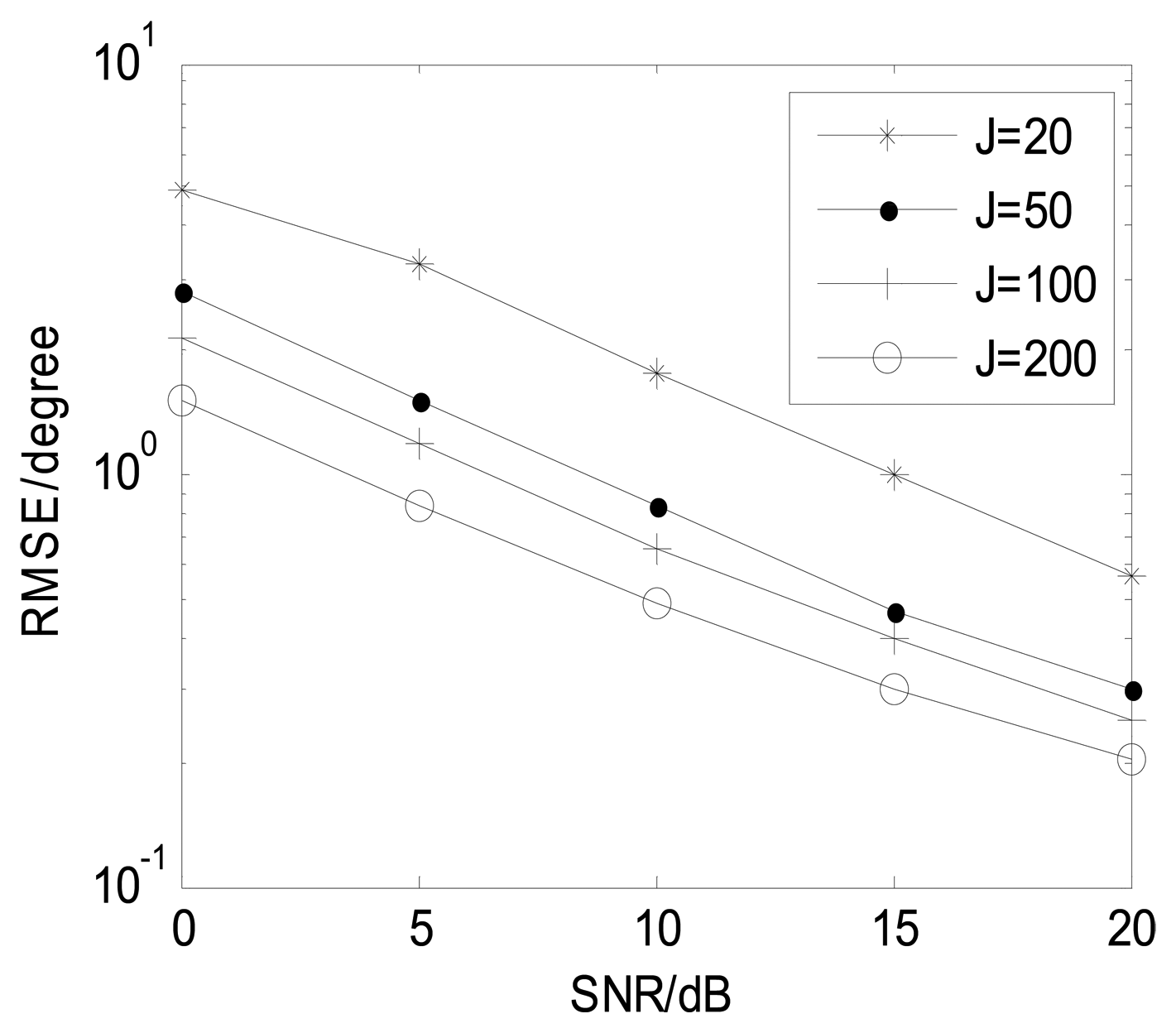
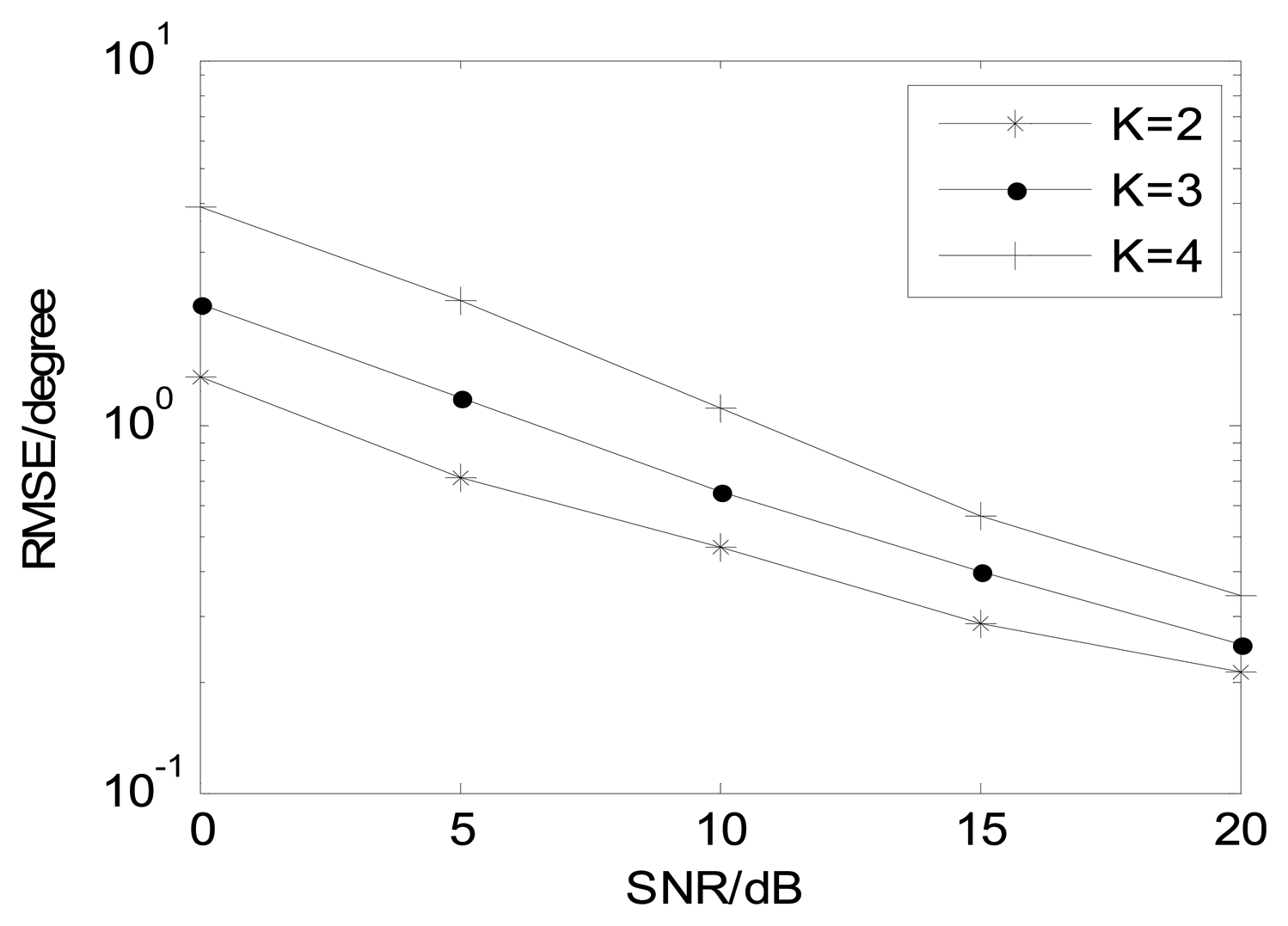
Figure 8 depicts the proposed algorithm estimation performance with different J (M = 12, and K = 3). It illustrates that the estimation performance becomes better in collaboration with J increasing and the proposed algorithm is effective in small snapshots. Figure 9 shows angle estimation performance of the proposed algorithm with different K (M = 12 and J = 100). It is indicated that the angle estimation performance of our algorithm is gradually improving as the number of sources is reduced.
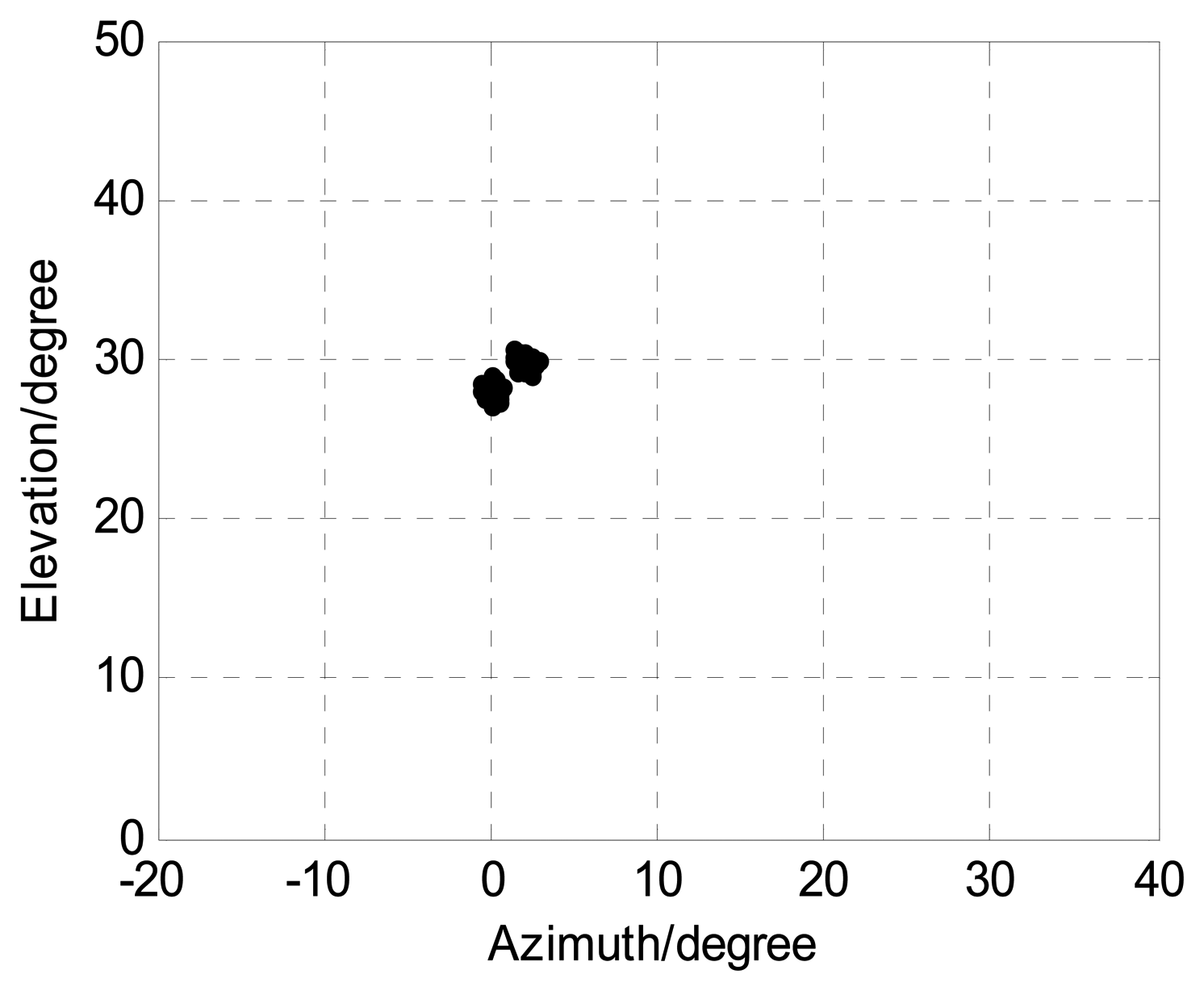
We assume two coherent closely spaced sources located at angles (ϕ1,φ1) = (0°,30°), (ϕ2,φ2) = (2°,28°). Figure 10 displays angle estimation of closely spaced sources exploiting the proposed algorithm with M = 12, J = 100, K = 2, and SNR = 15 dB. It implies that our angle algorithm has considerably good performance for angle estimation of closely spaced sources.
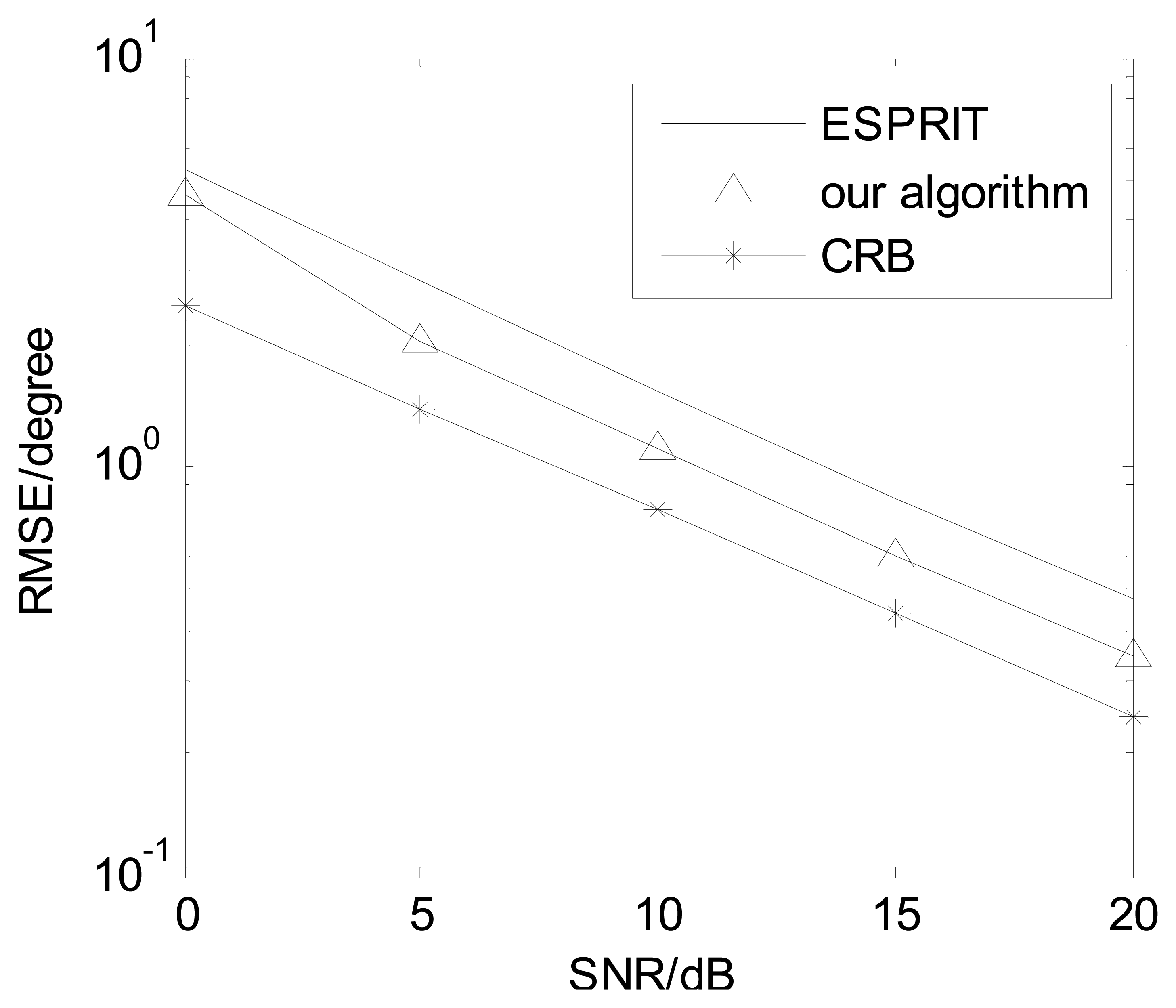
For non-coherent sources, the proposed algorithm becomes the PARAFAC algorithm [14]. In non-coherent sources, we compared our algorithm against the ESPRIT algorithm [7] and CRB. Figure 11 presents angle estimation performance comparisons with K = 3, M = 8 and L = 150. It is indicated our algorithm has better DOA estimation performance than the ESPRIT algorithm [7].
5. Conclusions
In the present paper we have expanded the PARALIND model, originally applied to biology and chemistry, to acoustic vector-sensor array signal processing. The PARALIND model is used for coherent 2D- DOA estimation for arbitrarily spaced acoustic vector-sensor arrays subject to unknown locations. We have derived the PARALIND decomposition and its uniqueness in acoustic vector-sensor arrays, which is convenient for simulation, performance analysis and further study. Our algorithm obtains automatically paired 2D-DOA estimation and the correlated matrix of the sources. Compared with the FBSS-ESPRIT algorithm which only works for uniform arrays, our algorithm has much better angle estimation performance. Furthermore, our algorithm has considerably good performance for angle estimation of closely spaced sources.
Acknowledgments
This work is supported by China NSF Grants (60801052), Jiangsu Planned Projects for Postdoctoral Research Funds (1201039C), China Postdoctoral Science Foundation (2012M521099), Open Project of Key Laboratory of Underwater Acoustic Communication and Marine Information Technology (Xiamen University), Hubei Key Laboratory of Intelligcnt Wireless Communications (IWC2012002), the Aeronautical Science Foundation of China(20120152001), Qing Lan Project and the Fundamental Research Funds for the Central Universities (NS2013024, NZ2012010, kfjj120115, kfjj20110215).
References
- Sun, G.; Li, Q.; Zhang, B. Acoustic vector sensor signal processing. Chin. J. Acoust. 2006, 25, 1–15. [Google Scholar]
- Nehorai, A.; Paldi, E. Acoustic vector-sensor array processing. IEEE Trans. Signal Process. 1994, 42, 2481–2491. [Google Scholar]
- Sun, G.; Yang, D.; Zhang, L. Maximum likelihood ratio detection and maximum likelihood DOA estimation based on the vector hydrophone. Acta Acustica 2003, 28, 66–72. [Google Scholar]
- Hawkes, M.; Nehorai, A. Acoustic vector-sensor beamforming and Capon direction estimation. IEEE Trans. Signal Process. 1998, 46, 2291–2304. [Google Scholar]
- Chen, H.; Zhao, J. Wideband MVDR beamforming for acoustic vector sensor linear array. IEE Proc. Radar Sonar. Navig. 2004, 151, 158–162. [Google Scholar]
- Hochwald, M.; Nehorai, A. Identifiability in array processing models with vector-sensor applications. IEEE Trans. Signal Process. 1996, 44, 83–95. [Google Scholar]
- Wong, K.T.; Zoltowski, M.D. Closed-form underwater acoustic direction-finding with arbitrarily spaced vector hydrophones at unknown locations. IEEE J. Ocean. Eng. 1997, 22, 566–575. [Google Scholar]
- Wong, K.T.; Zoltowski, M.D. Extended-Aperture underwater acoustic multisource azimuth/elevation direction-finding using uniformly but sparsely spaced vector hydrophones. IEEE J. Ocean. Eng. 1997, 22, 659–672. [Google Scholar]
- He, J.; Jiang, S.; Wang, J.; Liu, Z. Direction finding in spatially correlated noise fields with arbitrarily-spaced and far-separated subarrays at unknown locations. IET Radar Sonar Navigat. 2009, 3, 278–284. [Google Scholar]
- Wong, K.T.; Zoltowski, M.D. Root-MUSIC-based azimuth-elevation angle-of-arrival Estimation with uniformly spaced but arbitrarily oriented velocity hydrophones. IEEE Trans. Signal Process. 1999, 47, 3250–3260. [Google Scholar]
- Wong, K.T.; Zoltowski, M.D. Self-Initiating MUSIC-based direction finding in underwater acoustic particle velocity-field beamspace. IEEE J. Ocean. Eng. 2000, 25, 262–273. [Google Scholar]
- Wang, Y.; Zhang, J.; Hu, B.; He, J. Hypercomplex Model of Acoustic Vector Sensor Array with its Application for the High Resolution Two Dimensional Direction of Arrival Estimation. Proceedings of IEEE Instrumentation & Measurement Technology Conference (IMTC' 2008), Victoria, BC, Canada, 12–15 May 2008; pp. 1–5.
- He, J.; Liu, Z. Two-dimensional direction finding of acoustic sources by a vector sensor array using the propagator method. Signal Process. 2008, 88, 2492–2499. [Google Scholar]
- Zhang, X.; Li, J. Trilinear decomposition-based two-dimensional DOA estimation algorithm for arbitrarily spaced acoustic vector-sensor array subjected to unknown locations. Wirel. Pers. Commun. 2012, 67, 859–877. [Google Scholar]
- Liu, Z.; Ruan, X.; He, J. Efficient 2-D DOA estimation for coherent sources with a sparse acoustic vector-sensor array. Multidimens. Syst. Signal Process. 2013, 24, 105–120. [Google Scholar]
- Yuan, Y.; Zhang, B.; Fan, D.; Tong, G. DFT and PSD for Estimating DOA with an Active Acoustic Array. Proceedings of IEEE International Conference on Automation and Logistics, (ICAL'2008), Qingdao, China, 1–3 September 2008; pp. 694–699.
- Arunkumar, K.P.; Anand, G.V. Multiple Source Localization in Shallow Ocean Using a Uniform Linear Horizontal Array of Acoustic Vector Sensors. Proceedings of 2007 IEEE Intelligent Information Communication Technologies for Better Human Life (TENCON 2007), Taibei, Taiwan, 30 October–2 December 2007; pp. 1–4.
- Tam, P.K.; Wong, K.T. Cramer-rao bounds for direction finding by an acoustic vector sensor under nonideal gain-phase responses. IEEE Sens. J. 2009, 9, 969–982. [Google Scholar]
- Abdi, A.; Guo, H. Signal correlation modeling in acoustic vector sensor arrays. IEEE Trans. Signal Process. 2009, 57, 892–903. [Google Scholar]
- Hawkes, M.; Nehorai, A. Wideband source localization using a distributed acoustic vector-sensor array. IEEE Trans. Signal Process. 2003, 51, 1479–1491. [Google Scholar]
- Nan, Z.; Swee, C.C.; Chew, B.A.L. Vector hydrophone array development and its associated DOA estimation algorithms. Asia Pac. OCEANS 2006, 2006, 1–5. [Google Scholar]
- Marcos, S.; Marsal, A.; Benidir, M. The propagator method for source bearing estimation. Signal Process. 1995, 42, 121–138. [Google Scholar]
- Shan, T.J.; Wax, M.; Kailath, T. On spatial smoothing for direction-of-arrival estimation of coherent signals. IEEE Trans Acoust. Speech Signal Process. 1985, 33, 806–811. [Google Scholar]
- Pillai, S.U.; Kwon, B. Forward/backward spatial smoothing techniques for the coherent signal identification. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 8–15. [Google Scholar]
- Kruskal, J.B. Three-way arrays: Rank and uniqueness of trilinear decompositions with application to arithmetic complexity and statistics. Linear Algebra Applicat. 1977, 18, 95–138. [Google Scholar]
- Vorobyov, S.A.; Rong, Y.; Sidiropoulos, N.D.; Gershman, A.B. Robust Iterative. Fitting of Multilinear Models. IEEE Trans. Signal Proces. 2005, 53, 2678–2689. [Google Scholar]
- Bro, R.; Harshmab, R.A.; Sidiropoulos, N.D. Modeling multi-way data with linearly dependent loadings. J. Chemometr. 2009, 23, 324–340. [Google Scholar]
- Bahram, M.; Bro, R. A novel strategy for solving matrix effect in three-way data using parallel profiles with linear dependencies. Anal. Chim. Acta 2007, 584, 397–402. [Google Scholar]
- Stoica, P.; Nehorai, A. Performance study of conditional and unconditional direction-of-arrival estimation. IEEE Trans. Signal Process. 1990, 38, 1783–1795. [Google Scholar]
- Notation
(·)T, (·)H, (·)*, (·)−1 and (·)+ denote transpose, conjugate transpose, conjugate, matrix inversion and pseudo-inverse operations, respectively.
IP stands for a P × P identity matrix.
○, ⊗ and ⊙ denote Khatri-Rao, Kronecker, and Hadamard product, respectively.
E[.] is a expectation operator
Dm(.) is to take the nth row of the matrix to construct a diagonal matrix.
diag(v) stands for a diagonal matrix the diagonal of which is a vector v
diag−1(V) denotes a column vector consisted of the diagonal elements of matrix V.
vec(X) is to arrange matrix X column-wisely to be a column vector.
A(:,k) denotes the kth column of matrix A.
hk(n) is nth elements of vector hk.
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Zhang, X.; Zhou, M.; Li, J. A PARALIND Decomposition-Based Coherent Two-Dimensional Direction of Arrival Estimation Algorithm for Acoustic Vector-Sensor Arrays. Sensors 2013, 13, 5302-5316. https://doi.org/10.3390/s130405302
Zhang X, Zhou M, Li J. A PARALIND Decomposition-Based Coherent Two-Dimensional Direction of Arrival Estimation Algorithm for Acoustic Vector-Sensor Arrays. Sensors. 2013; 13(4):5302-5316. https://doi.org/10.3390/s130405302
Chicago/Turabian StyleZhang, Xiaofei, Min Zhou, and Jianfeng Li. 2013. "A PARALIND Decomposition-Based Coherent Two-Dimensional Direction of Arrival Estimation Algorithm for Acoustic Vector-Sensor Arrays" Sensors 13, no. 4: 5302-5316. https://doi.org/10.3390/s130405302




