Improving Fingerprint Verification Using Minutiae Triplets
Abstract
: Improving fingerprint matching algorithms is an active and important research area in fingerprint recognition. Algorithms based on minutia triplets, an important matcher family, present some drawbacks that impact their accuracy, such as dependency to the order of minutiae in the feature, insensitivity to the reflection of minutiae triplets, and insensitivity to the directions of the minutiae relative to the sides of the triangle. To alleviate these drawbacks, we introduce in this paper a novel fingerprint matching algorithm, named M3gl. This algorithm contains three components: a new feature representation containing clockwise-arranged minutiae without a central minutia, a new similarity measure that shifts the triplets to find the best minutiae correspondence, and a global matching procedure that selects the alignment by maximizing the amount of global matching minutiae. To make M3gl faster, it includes some optimizations to discard non-matching minutia triplets without comparing the whole representation. In comparison with six verification algorithms, M3gl achieves the highest accuracy in the lowest matching time, using FVC2002 and FVC2004 databases.1. Introduction
Fingerprints are the marks made by ridges and furrows in the fingers. They are formed during the sixth month of intrauterine life of human beings and do not disappear until some time after death. Since there are not two persons with the same fingerprints and they do not change naturally, they are an important element to identify people.
Due to the high complexity of fingerprint matching and the huge amount of existing fingerprints, it is necessary to build computer systems that automatically process fingerprints with high accuracy and low computational costs. Historically, fingerprint recognition systems were mostly used in forensic sciences, but the current popularity of these systems is mainly due to civilian applications such as the control of physical access to facilities, the control of logical access to software, and the control of voters during elections. A key component in fingerprint recognition systems is the fingerprint matching algorithm.
To measure the quality of a fingerprint matching algorithm, the evaluator must consider the context in which it is applied. For example, the algorithms based on microscopic characteristics are suitable for applications where fingerprints are acquired with high resolution sensors (1,000 dpi or higher); the quality of these algorithms dramatically decreases when the resolution is low [1]. The following quality parameters are proved to be important for evaluating general matchers:
Low computational cost: The algorithm satisfies memory and time restrictions for its application context [2].
Invariance to translation: The algorithm returns a high similarity value when comparing fingerprints from the same finger notwithstanding that fingerprints be translated horizontally and/or vertically [3].
Invariance to rotation: The algorithm returns a high similarity value when comparing fingerprints from the same finger in spite of fingerprints rotation [3].
Tolerance to non-linear distortion: The algorithm returns a high similarity value when comparing fingerprints from the same finger even when fingerprints are affected by non-linear distortion, as a result of fingerprint creation mechanisms [4].
Sensitivity to the individuality of fingerprints: The algorithm returns a high similarity value when comparing fingerprints from the same finger and returns a low similarity value when comparing fingerprints from different fingers [5].
Insensitivity to select a single alignment: The algorithm does not perform a single global alignment from the best local alignment. Maximizing the local similarity value does not guarantee to find a true matching local structure pair. Even if the selected local structure pair is a true matching pair, it is not necessarily the best pair to carry out fingerprint alignment [3].
Tolerance to partial fingerprints: The algorithm returns a high similarity value when comparing fingerprints from the same finger even when the fingerprints are not complete [5]. Partial fingerprints can be produced by the restrictions of the sensors, latent fingerprints in crime scenes, and different fingerprint creation mechanisms.
Tolerance to the low quality of fingerprints: The results of the algorithm are not significantly affected by low fingerprint quality [6]. Due to different skin conditions and/or the different fingerprint creation mechanisms, sometimes many details of the fingerprints do not appear clearly.
Tolerance to errors of the feature extractor: The algorithm returns a high similarity value when comparing fingerprints from the same finger even when the feature extractor has missed some features and/or has extracted some non-existent features [3].
Determinism: Two executions of the algorithm with the same parameters return the same results.
Modern technologies impose new challenges to fingerprint matching algorithms; new systems reside on light architectures, need standards for systems interoperability, and use small area sensors [3,4,7]. In these contexts, the algorithms with higher quality are those based on minutiae [2]. Minutiae are the points where the ridge continuity breaks and they are typically represented as (x, y, θ); where (x, y) represent the 2D point coordinates, and θ the ridge direction at that point.
As a minutia-based matcher should be invariant to translation and rotation, the process of minutia pairing is ambiguous [8]. Thus, most matchers in this family use local minutia structures (minutiae descriptors) to quickly establish the minutiae correspondences [4].
A simple and accurate minutiae descriptor is based on minutiae triplets [3]. Minutiae triplets are local structures represented by three minutiae. Algorithms based on minutiae triplets have the following advantages, which make them of higher quality than algorithms based on other representations:
They are tolerant to fingerprint deformations [9].
They are faster and more accurate, compared to algorithms based on other representations [10,11], especially in applications with partial fingerprints [12].
They are suitable for applications based on interoperability standards because the most popular standards are based only on minutiae [2].
They are appropriate for systems embedded on light architectures because the representation and comparison of minutiae triplets can be performed efficiently [13].
Minutiae triplets have higher discriminative power than minutiae pairs and single minutiae [10].
Some important quality parameters related to fingerprint matching algorithms based on minutiae triplets are:
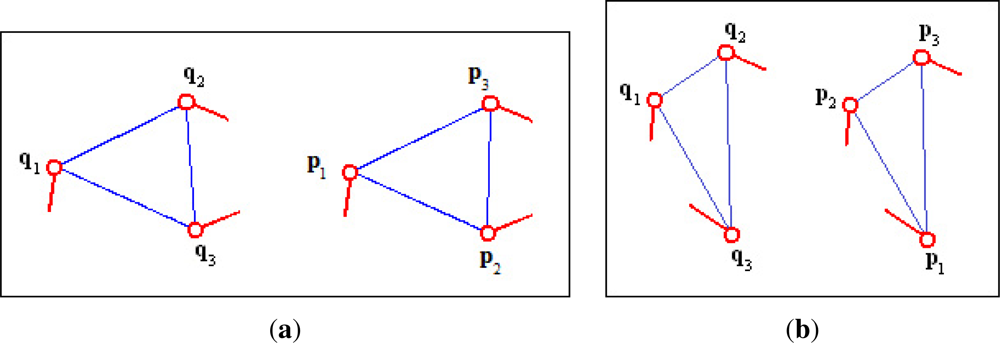
Invariance to the order of minutiae in the feature: No matter the minutiae order in the triplet, the algorithm finds the correct correspondences of minutiae when matching similar triplets (Figure 1).
Sensitivity to the reflection of minutiae triplets: The algorithm does not match a triplet with its reflected version (Figure 2).
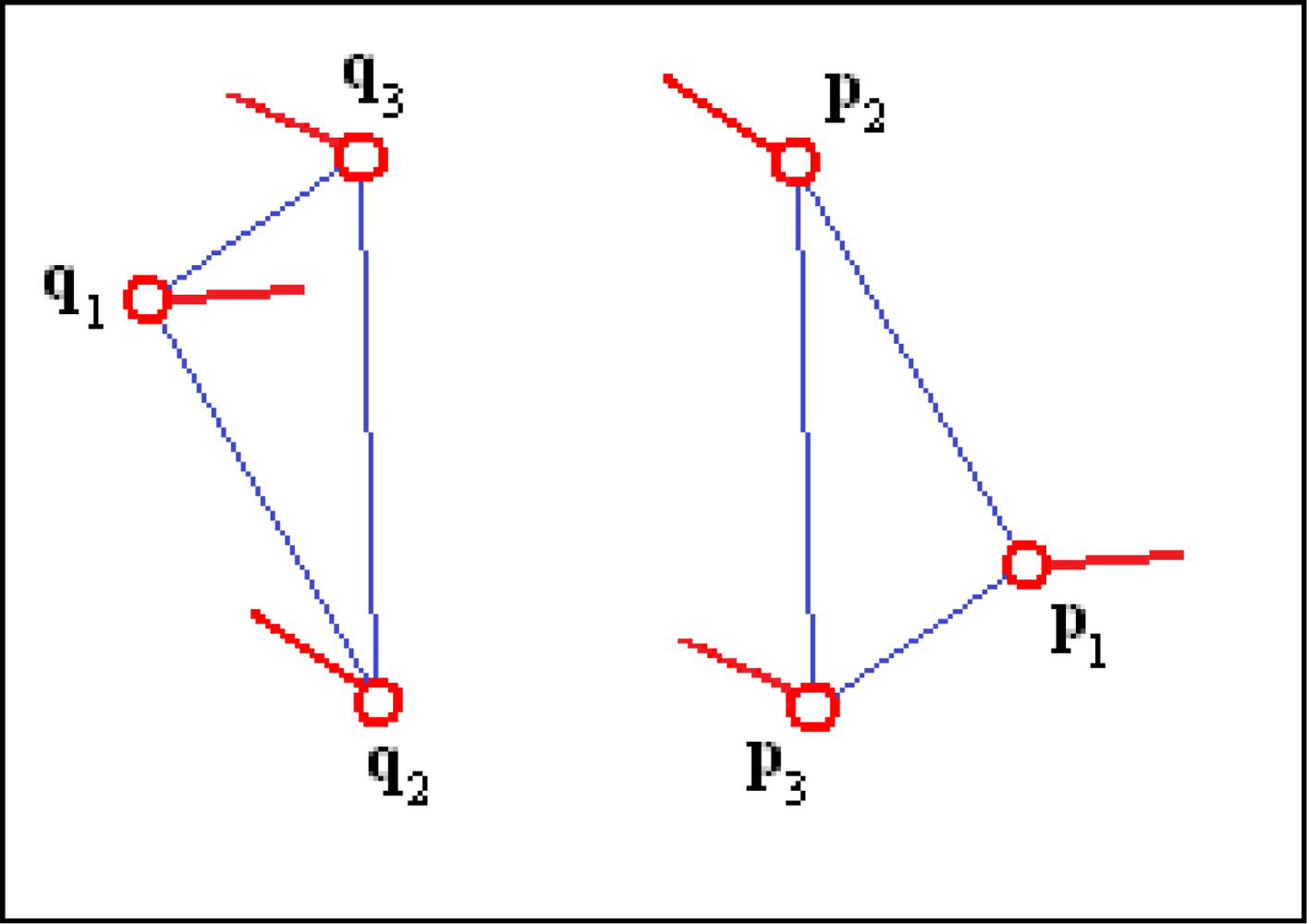
Sensitivity to the directions of the minutiae relative to the sides of the triangle: In order to find similar triplets, the algorithm takes into account the directions of the minutiae relative to the sides of the triangles formed by the triplets (Figure 3).
State-of-the-art algorithms based on minutiae triplets do not fulfil all the quality parameters, which has a negative impact on their accuracy. Table 1 shows the lacking quality parameter of all the reviewed matchers, according to the following parameters:
Invariance to the order of minutiae in the feature.
Sensitivity to the reflection of minutiae triplets.
Sensitivity to the directions of the minutiae relative to the sides of the triangle.
Insensitivity to select a single alignment.
Tolerance to errors of the feature extractor.
Determinism.
In this research, we introduce M3gl, a new fingerprint matcher that fulfils most quality parameters. M3gl is based on a new representation and a new comparison function for minutia triplets. An experimental comparison with algorithms based on different types of minutiae descriptors shows that M3gl is highly accurate and it has acceptable computational costs.
2. Definitions
This section defines some basic functions that we use throughout the paper. Given two minutiae pi = (xi, yi, θi) and pj = (xj, yj, θj), ed(pi, pj) represents the Euclidean distance between the coordinates of pi and pj Equation (1).
For two given angles α and β, adπ(α, β) computes the minimum angle required to superpose two vectors with the same origin and angles α and β respectively using Equation (2), while ad2π(α, β) computes the angle required to rotate a vector with angle β in clockwise sense to superpose it to another vector with the same origin and angle α using Equation (3).
Finally, for a given pair of minutiae pi and pj, ang(pi, pj) computes the angle of the vector with initial point at pi and terminal point at pj using Equation (4).
3. Feature Representation
In this section, we introduce m-triplets, a robust feature representation based on minutiae triplets. Provided that a fingerprint is described by the minutia set P, our representation is a tuple with the following components (see Figure 4):
minutiae pi ∈ P are clockwise arranged starting on p1.
di∈1...3, where di is the Euclidean distance between the minutiae different than pi.
dmax, dmid and dmin are the maximum, middle and minimum distances in the triplet, respectively. Although these components can be calculated based on distance values, we store them because they are a key point for the algorithm optimizations.
αi∈1...6 are the angles ad2π(ang(p, q),θ) required to rotate the direction θ of a minutia to superpose it to the vectors associated with the other two minutiae in the triplet.
βi = ad2π (θj, θk) is the angle required to rotate the direction of the minutia pk in order to superpose it to the direction of the minutia pj.
The m-triplets are sensitive to the directions of the minutiae relative to the sides of the triangle (angles α). The minutiae in this representation are arranged in clockwise direction without a central minutia. Therefore, in order to compare m-triplets, the similarity function considers the three minutiae rotations in clockwise sense (next section contains a formal definition of this procedure). This representation and the comparison function guarantee the invariance to the order of minutiae in the feature, and the sensitivity to the reflection of minutiae triplets.
4. M-Triplets Similarity
In this section, we introduce a new m-triplets similarity. It is designed to accurately distinguish between similar and non-similar m-triplets. Given two m-triplets t and r, we propose sinv(t, r) in Equation (5) to compare m-triplets.
The base similarity function spart is defined using functions sθ, sd, sα, and sβ, which consider different components of the m-triplets. According to Equation (6), two m-triplets are totally dissimilar if they have at least one component totally dissimilar. If all component similarities are above zero, the product rule makes the similarity hight if at least one component is close to 1.
The invariance to rotation is an important quality parameter for fingerprint recognition, especially for fingerprint identification. Nevertheless, for fingerprint verification, the rotation is usually restricted by sensors. The function sθ Equation (7) incorporates this information into the m-triplets similarity to increase minutia discrimination for such problems. Consequently, two m-triplets are dissimilar if their minutiae directions differ more than π/4.
The function sd Equation (8) compares m-triplets in terms of the side lengths of the triangle formed by the triplet minutiae. sd returns values in the interval [0,1], returning 0 if at least one length difference is greater than threshold tl. sd returns 1 if all length differences are 0; that is, the triangles formed by both m-triplets are identical.
The function sα Equation (9) compares m-triplets based on the angles formed by minutiae directions and the sides of the triangles (angles α on Figure 4).
The function sβ Equation (10) compares m-triplets based on relative minutiae directions (angles β on Figure 4
Equations (9) and (10) return values in the interval [0, 1]. They return 0 if at least two compared angles differ more than threshold ta. The less the angles differ, the higher is the value returned by the equations; therefore, they return 1 if the compared angles are identical.
In order to detect dissimilar m-triplets in advance, avoiding all costly shifts, we use Theorems 1, 2, and 3. Proofs for Theorems 1 and 2 appear in the appendixes. Proof of Theorem 3 is similar to the proof of Theorem 1 and is not stated.
Theorem 1. Given two m-triplets t and r, if then sinv(t, r) = 0.
Theorem 2. Given two m-triplets t and r, if then sinv(t, r) = 0.
Theorem 3. Given two m-triplets t and r, if then sinv(t, r) = 0.
Based on these theorems, we can modify sinv Equation (5). This way, our m-triplets similarity can be re-written as Equation (11).
Local distance threshold tl and angle threshold ta are parameters of the algorithm and must be tuned according to the image characteristics.
The function sinv, by means of spart, achieves the invariance to translation and the invariance to restricted rotation, the tolerance to non-linear distortion and the sensitivity to the directions of the minutiae relative to the sides of the triangle. The clockwise shifting makes function sinv invariant to the order of minutiae in the feature and sensitive to the reflection of minutiae triplets.
5. M3GL Algorithm
In this section, we introduce M3gl, a new fingerprint verification algorithm based on the proposed minutiae triplet representation and similarity measure.
Given a fingerprint described by the minutia set P we compute the m-triplets as follows. For each p ∈ P, find its c nearest minutiae in P and build all m-triplets that include p and two of its nearest minutiae, discarding duplicates. This way of computing m-triplets makes M3gl tolerant to the low quality of fingerprints and tolerant to errors of the feature extractor. Additionally, m-triplets in the fingerprint are sorted according to the length of the largest side to perform a binary search when looking for similar m-triplets; Theorem 1 guarantees the safety of this procedure.
M3gl consists of the following major steps: local minutiae matching, global minutiae matching, and similarity score computation.
5.1. Local Minutiae Matching
This step finds the similar m-triplets in the template fingerprint using binary search. Then, it sorts all matching pairs according to the similarity value and finds the local matching minutiae. Formally, the algorithm is the following:
Let Q and P be the query and template fingerprint minutiae sets respectively. Let R and T be the query and template fingerprint m-triplets sets respectively. Let A ← {} be the set that will contain local matching m-triplets pairs.
For each query m-triplet ri ∈ R perform binary search looking for the template m-triplets {t1, t2, …, tu} ⊂ T with similarity value higher than 0 and add the pairs (ri, t1), (ri, t2), …, (ri, tu) to A.
Sort in descendant order all matching pairs (r, t) in A according to the similarity value.
Let M ← {} be the set containing local matching minutiae pairs.
For each (r, t) ∈ A do
Let B ← {(q1, p1), (q2, p2), (q3, p3) } be the matching minutiae that maximizes sinv(r, t) where q1, q2, q3 ∈ Q and p1, p2, p3 ∈ P.
For each (qi, pi) ∈ B do:
If there is not any pair (qj, pj) ∈ M that qj = qi or pj = pi then M ← M ∪ {(qi, pi)}.
5.2. Global Minutiae Matching
This step uses every minutiae pair as a reference pair for fingerprint rotation and performs a query minutiae transformation for each reference pair. Later, it selects the transformation that maximizes the amount of matching minutiae. This strategy overcomes the limitations of the single alignment based matching. M3gl uses three criteria to determine if two minutiae match at global level and to achieve the tolerance to non-linear distortion. First, the Euclidean distance must not exceed threshold tg. Second, minutia directions must not exceed threshold ta. Third, the directions differences relative to reference minutiae pair must not exceed threshold ta. The formal algorithm is the following:
Let n ← 0 be the maximum number of matching minutiae computed after performing all fingerprint rotations.
For each (qi, pi) ∈ M do:
Let E ← {} be the set containing global matching minutiae pairs for the current iteration.
For each (qj, pj) ∈ M, if ∀(qk, pk) ∈ E [(qj ≠ qk) ∧ (pj ≠ pk)]
Compute q′ = (x′, y′, θ′) as where qi = (x1, y1, θ1), pi = (x2, y2, θ2), Δθ = θ2 − θ1, qj = (x3, y3, θ3).
Let pj = (x4, y4, θ4); if ed(q′, pj) ≤ tg ∧ adπ (ad2π(θ2, θ1), ad2π(θ4, θ3)) ≤ ta ∧ adπ(θ′, θ4) ≤ ta, then E ← E ∪ {(qj, pj)}.
if n < |E| then n ← |E|.
5.3. Similarity Score Computation
The similarity value is computed using the formula ; where P and Q are the template and query fingerprint minutiae sets respectively, and n is the amount of matching minutiae pairs.
Global distance threshold tg and angle threshold ta are parameters of the algorithm, and must be tuned based on the image characteristics.
6. Experimental Results
In order to evaluate the new fingerprint matching algorithm, we use databases DB1_A, DB2_A, DB3_A and DB4_A of FVC2002 and FVC2004 competitions. These databases are commonly used as benchmarks for evaluating fingerprint matchers in the context of fingerprint verification. We also use the FVC evaluation protocol [22]. Performance is measured by indicators EER, FMR100, FMR1000 and ZeroFMR. The indicator Time refers to the average matching time in milliseconds. We carry out all the experiments on a laptop with an Intel Core i7 740QM processor (1.73 GHz) and 4 GB of RAM.
We use the same parameters values for M3gl in all databases (tl = 12, tg = 12, ta = π/6, c = 4). We estimate these parameters through a few experiments using fingerprint databases DB1_B, DB2_B, DB3_B and DB4_B of FVC2004 competition.
In the experimental comparisons, we include the algorithm proposed by Jiang and Yau [9] (JY) because it is the most popular algorithm based on minutiae triplets in the literature. We implement the algorithm proposed by Parziale and Niel [11] (PN) because it is the algorithm based on minutiae triplets more similar to our proposal and we are interested in showing the difference in accuracy and speed. We also compare our proposal with algorithms based on other types of minutiae descriptors, that is why we implement the algorithms proposed by Wang et al. [23] (WLC), Qi et al. [24] (QYW), Tico and Kuosmanen [25] (TK), and Udupa et al. [26] (UGS).
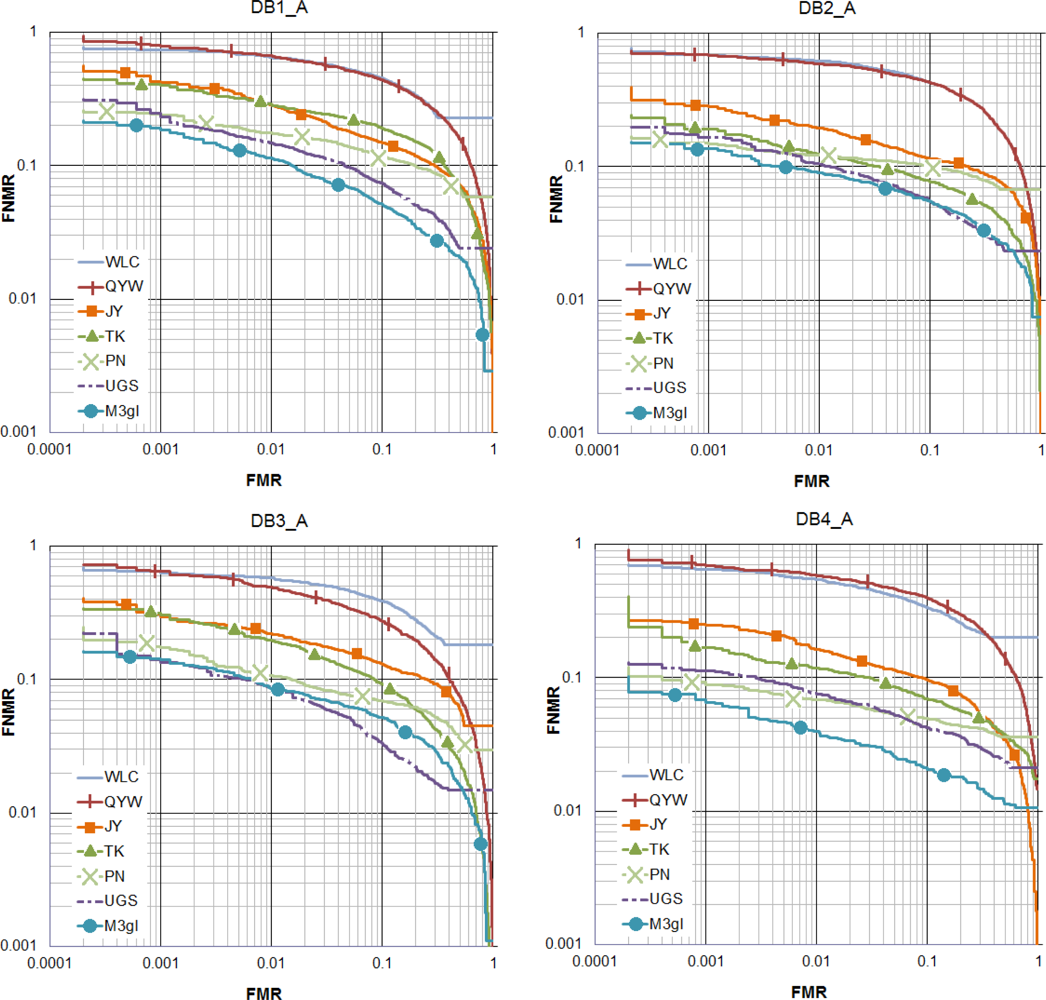
Figures 5 and 6 show that M3gl achieves lower FNMR for most of the FMR values. Tables 2 and 3 show that our algorithm achieves the best results for most of the performance indicators. Figure 7 shows examples where our algorithm is able to find true matching minutiae in difficult cases (partial fingerprints with low overlapping, non-linear distortion and low quality) where the other algorithms fail. M3gl is also the fastest algorithm due to the following reasons:
The m-triplets similarity function includes the properties demonstrated in Theorems 1, 2 and 3 to discard comparisons without performing all its operations.
The algorithm performs binary search when looking for similar m-triplets in the local minutiae matching step.
The similarity score computation of M3gl is simple but robust. In order to test this robustness we substitute the similarity score computation of M3gl for the strategies proposed by Wang et al. [23], Qi et al. [24], Jiang and Yau [9], and Tico and Kuosmanen [25]; we name the new algorithms M3gl1, M3gl2, M3gl3 and M3gl4 respectively. We test M3gl and its variations in the testing databases DB1_B, DB2_B, DB3_B and DB4_B of FVC2002 and FVC2004. The experimental results (Tables 4 and 5) do not show a clear superiority of any algorithm; nevertheless, when comparing M3gl with the other algorithms by pairs, we find that M3gl wins in most of the accuracy indicators.
Experimental results confirm that fulfilling the quality parameters discussed in Section 1 has a direct impact in the matcher accuracy.
7. Conclusions
Fingerprint matching algorithms based on minutiae triplets have proved to be fast and accurate. They are commonly used on light architectures and in systems based on interoperability standards for fingerprints represented by minutiae. However, existing algorithms have several limitations that affect their accuracy. In this paper, we identify the quality parameters that have a more significant impact on fingerprint matching accuracy in order to create M3gl, a more accurate matcher.
M3gl uses a new representation based on minutiae triplets and a new comparison function that achieves the invariance to the translation and rotation of fingerprints, and achieves the sensitivity to the directions of the minutiae relative to the sides of the triangle. The new representation arranges the minutiae in clockwise sense and the comparison function performs the three possible rotations of the triplets achieving the invariance to the order of minutiae in the feature and the sensitivity to the reflection of minutiae triplets. The components of the proposed representation are compared using thresholds that allow the tolerance to the non-linear distortion of fingerprints. Besides, the new comparison function includes optimizations that avoid comparing all the components of the triplets, increasing the matching speed in many cases.
M3gl is deterministic, insensitive to select a single alignment, and sensitive to the individuality of fingerprints. It uses a simple and effective procedure to compute minutiae triplets which makes the algorithm tolerant to the low quality of fingerprints and to errors of the feature extractor.
Experimental results in databases of the FVC2002 and FVC2004 competitions show that M3gl has low computational costs and is more accurate than other algorithms based on minutiae triplets and other algorithms based on different representations.
In the near future we plan to study the behaviour of the new algorithm for latent fingerprint identification.
Acknowledgments
The authors would like to thank Dania Yudith Suárez Abreu for her valuable contribution improving the grammar and style of this paper.
References
- Zhao, Q.; Zhang, D.; Zhanga, L.; Luoa, N. High resolution partial fingerprint alignment using pore-valley descriptors. Pattern Recogn 2010, 43, 1050–1061. [Google Scholar]
- Cappelli, R.; Ferrara, M.; Maltoni, D. Minutia cylinder-code: A new representation and matching technique for fingerprint recognition. IEEE Trans. Pattern. Anal. Mach. Intell 2010, 32, 2128–2141. [Google Scholar]
- Maltoni, D.; Maio, D.; Jain, A.K.; Prabhakar, S. Handbook of Fingerprint Recognition, 2nd ed; Springer-Verlag: London, UK, 2009. [Google Scholar]
- Jain, A.K.; Feng, J.; Nandakumar, K. Fingerprint matching. Computer 2010, 43, 36–44. [Google Scholar]
- Jea, T.Y. Minutiae-Based Partial Fingerprint Recognition. PhD Thesis,. State University of New York, NY, USA, 2005. [Google Scholar]
- Jain, A.K.; Feng, J. Latent fingerprint matching. IEEE Trans. Pattern. Anal. Mach. Intell 2011, 33, 88–100. [Google Scholar]
- Prabhakar, S.; Ivanisov, A.; Jain, A.K. Biometric recognition: Sensor characteristics and image quality. IEEE Instrum. Meas. Mag 2011, 14, 10–16. [Google Scholar]
- Feng, J. Combining minutiae descriptors for fingerprint matching. Pattern Recogn 2008, 41, 342–352. [Google Scholar]
- Jiang, X.; Yau, W.Y. Fingerprint Minutiae Matching Based on the Local and Global Structures. Proceedings of the 15th International Conference on Pattern Recognition, Barcelona, Spain, 3–7 September 2000; 2, pp. 1038–1041.
- Chen, X.; Tian, J.; Yang, X. A new algorithm for distorted fingerprints matching based on normalized fuzzy similarity measure. IEEE Trans. Image Process 2006, 15, 767–776. [Google Scholar]
- Parziale, G.; Niel, A. A Fingerprint Matching Using Minutiae Triangulation. Proceedings of the 1st International Conference on Biometric Authentication, Hong Kong, China, 15–17 July 2004; Volume LNCS 3072. pp. 241–248.
- Jea, T.Y.; Govindaraju, V. A minutia-based partial fingerprint recognition system. Pattern Recogn 2005, 38, 1672–1684. [Google Scholar]
- Reisman, J.; Uludag, U.; Ross, A. Secure Fingerprint Matching with External Registration. Proceedings of the 5th International Conference on Audio- and Video-Based Biometric Person Authentication (AVBPA ’05), Tarrytown, NY, USA, July 2005; Volume LNCS 3546. pp. 720–729.
- Kovcs-Vajna, Z.M. A fingerprint verification system based on triangular matching and dynamic time warping. IEEE Trans. Pattern. Anal. Mach. Intell 2000, 22, 1266–1276. [Google Scholar]
- Tan, X.; Bhanu, B. Fingerprint matching by genetic algorithms. Pattern Recogn 2006, 39, 465–477. [Google Scholar]
- Feng, Y.; Feng, J.; Chen, X.; Song, Z. A Novel Fingerprint Matching Scheme Based on Local Structure Compatibility. Proceedings of the 18th International Conference on Pattern Recognition, Hong Kong, China, 20–24 August 2006; 4, pp. 374–377.
- Chen, X.; Tian, J.; Yang, X.; Zhang, Y. An algorithm for distorted fingerprint matching based on local triangle feature set. IEEE Trans. Inf. Forensics Secur 2006, 1, 169–177. [Google Scholar]
- Xu, W.; Chen, X.; Feng, J. A Robust Fingerprint Matching Approach: Growing and Fusing of Local Structures. Proceedings of the 2nd International Conference on Biometrics, Seoul, Korea, 27–29 August 2007; Volume LNCS 4642. pp. 134–143.
- Zheng, J.D.; Gao, Y.; Zhang, M.Z. Fingerprint Matching Algorithm Based on Similar Vector Triangle. Proceedings of the 2nd International Congress on Image and Signal Processing (CISP ’09), Tianjin, China, 17–19 October 2009; pp. 1–6.
- Hoyle, K. Minutiae Triplet-Based Features with Extended Ridge Information for Determining Sufficiency in Fingerprints. Master Thesis,. Virginia Polytechnic Institute and State University, Burruss Hall Blacksburg, VA, USA, 2011. [Google Scholar]
- Ghazvini, M.; Sufikarimi, H.; Mohammadi, K. Fingerprint Matching Using Genetic Algorithm and Triangle Descriptors. Proceedings of the 19th Iranian Conference on Electrical Engineering, Tehran, Iran, 17–19 May 2011; pp. 1–6.
- Cappelli, R.; Maio, D.; Maltoni, D.; Wayman, J.L.; Jain, A.K. Performance evaluation of fingerprint verification systems. IEEE Trans. Pattern. Anal. Mach. Intell 2006, 28, 3–18. [Google Scholar]
- Wang, W.; Li, J.; Chen, W. Fingerprint Minutiae Matching Based on Coordinate System Bank and Global Optimum Alignment. Proceedings of the 18th International Conference on Pattern Recognition, Hong Kong, China, 20–24 August 2006; Volume 4,. pp. 401–404.
- Qi, J.; Yang, S.; Wang, Y. Fingerprint matching combining the global orientation field with minutia. Pattern Recogn. Lett 2005, 26, 2424–2430. [Google Scholar]
- Tico, M.; Kuosmanen, P. Fingerprint matching using an orientation-based minutia descriptor. IEEE Trans. Pattern. Anal. Mach. Intell 2003, 25, 1009–1014. [Google Scholar]
- Udupa, U. R.; Garg, G.; Sharma, P. Fast and Accurate Fingerprint Verification. Proceedings of the 3rd International Conference on Audio- and Video-Based Biometric Person Authentication (AVBPA ’01), Halmstad, Sweden, 6–8 June 2001; Volume LNCS 2091. pp. 192–197.
Appendix Theorem Proofs
Theorem A1. Given two m-triplets t and r, then sinv(t, r) = 0.
Proof. From the definition of m-triplet we have:
Assume, without loss of generality, that ; then, from the hypothesis of Theorem A1, we infer that:
From Equations (A5) and (A1) we have ; which is equivalent to:
From Equations (A4), (A6) and (A7) we conclude that differs more than threshold tl with respect to , and respectively. Therefore, sd(t, r) returns 0 for every clockwise shifting of r and consequently sinv(t, r) = 0.
Theorem A2. Given two m-triplets t and r, then sinv(t, r) = 0.
Proof. From the definition of m-triplet we have:
Assume, without loss of generality, that ; then, from the hypothesis of Theorem A2, we infer that:
From Equation (A10) and (A3) we have ; which is equivalent to:
From Equations (A9), (A11), (A12) and (A13) we conclude that and differ more than threshold tl with respect to both , . Therefore, sd(t, r) returns 0 for every clockwise shifting of r and consequently sinv(t, r) = 0.




| Algorithms | Lacking quality parameter | |||||
|---|---|---|---|---|---|---|
| I | II | III | IV | V | VI | |
| JY [9] | X | X | X | |||
| KV [14] | X | X | X | |||
| PN [11] | X | X | ||||
| JG1 [12] | X | X | X | X | ||
| JG2 [5] | X | X | ||||
| RUR [13] | X | X | ||||
| TB [15] | X | X | ||||
| FFCS [16] | X | X | ||||
| CTYZ [17] | X | X | ||||
| XCF [18] | X | X | X | X | ||
| ZGZ [19] | X | X | ||||
| HK [20] | X | X | ||||
| GSM [21] | X | X | ||||
| Database | Algorithm | EER | FMR100 | FMR1000 | ZeroFMR | Time(ms) |
|---|---|---|---|---|---|---|
| WLC | 29.5 | 57.2 | 63.6 | 66.9 | 123.0 | |
| D | QYW | 22.8 | 46.8 | 52.6 | 55.9 | 13.6 |
| B | JY | 5.1 | 10.6 | 23.9 | 31.9 | 3.3 |
| 1 | TK | 4.0 | 4.9 | 7.0 | 8.9 | 12.4 |
| - | PN | 1.9 | 2.5 | 3.4 | 5.8 | 20.3 |
| A | UGS | 2.2 | 2.8 | 4.1 | 5.9 | 1,239.4 |
| M3gl | 1.1 | 1.3 | 2.3 | 3.8 | 1.4 | |
| WLC | 34.0 | 63.6 | 69.3 | 72.6 | 269.6 | |
| D | QYW | 22.8 | 47.8 | 53.7 | 59.2 | 27.2 |
| B | JY | 4.5 | 8.3 | 17.3 | 27.6 | 4.6 |
| 2 | TK | 3.6 | 4.6 | 6.3 | 23.1 | 19.1 |
| - | PN | 1.4 | 1.6 | 2.4 | 3.5 | 44.4 |
| A | UGS | 1.9 | 2.3 | 4.9 | 5.6 | 2,846.1 |
| M3gl | 1.3 | 1.4 | 1.9 | 2.2 | 1.6 | |
| WLC | 29.8 | 57.4 | 62.7 | 65.0 | 27.1 | |
| D | QYW | 30.0 | 55.7 | 63.5 | 77.9 | 6.3 |
| B | JY | 9.4 | 16.4 | 26.1 | 33.1 | 1.5 |
| 3 | TK | 7.7 | 9.8 | 12.6 | 16.4 | 5.8 |
| - | PN | 5.6 | 6.9 | 10.2 | 12.8 | 5.6 |
| A | UGS | 5.3 | 8.0 | 12.2 | 26.4 | 96.0 |
| M3gl | 3.1 | 4.5 | 7.5 | 9.4 | 0.6 | |
| WLC | 22.9 | 51.7 | 61.0 | 63.5 | 37.0 | |
| D | QYW | 24.3 | 57.3 | 63.2 | 67.6 | 8.5 |
| B | JY | 7.4 | 13.0 | 23.0 | 28.3 | 2.1 |
| 4 | TK | 5.1 | 7.1 | 9.4 | 12.1 | 8.4 |
| - | PN | 3.1 | 3.9 | 5.6 | 10.3 | 10.3 |
| A | UGS | 4.2 | 7.1 | 12.6 | 16.8 | 463.0 |
| M3gl | 2.4 | 3.4 | 5.6 | 11.2 | 1.0 | |
| Database | Algorithm | EER | FMR100 | FMR1000 | ZeroFMR | Time(ms) |
|---|---|---|---|---|---|---|
| WLC | 27.3 | 64.8 | 73.9 | 77.3 | 150.0 | |
| D | QYW | 24.3 | 60.6 | 80.3 | 97.3 | 15.5 |
| B | JY | 13.5 | 28.5 | 42.8 | 55.9 | 4.2 |
| 1 | TK | 15.9 | 29.1 | 41.8 | 51.0 | 11.7 |
| - | PN | 11.4 | 17.7 | 24.4 | 25.9 | 20.9 |
| A | UGS | 7.9 | 14.8 | 24.9 | 31.3 | 1,649.4 |
| M3gl | 6.3 | 11.4 | 19.3 | 21.7 | 1.3 | |
| WLC | 28.1 | 62.1 | 68.9 | 78.0 | 103.0 | |
| D | QYW | 24.8 | 52.1 | 58.9 | 73.7 | 12.9 |
| B | JY | 11.0 | 19.4 | 28.4 | 39.2 | 3.0 |
| 2 | TK | 7.8 | 12.0 | 18.7 | 24.9 | 11.6 |
| - | PN | 10.0 | 12.1 | 15.1 | 16.9 | 14.9 |
| A | UGS | 6.4 | 10.5 | 16.7 | 19.9 | 1,210.8 |
| M3gl | 6.2 | 9.1 | 13.6 | 15.3 | 1.1 | |
| WLC | 24.5 | 57.9 | 64.9 | 69.5 | 312.0 | |
| D | QYW | 19.7 | 47.7 | 65.9 | 87.5 | 22.6 |
| B | JY | 12.0 | 22.1 | 32.3 | 41.4 | 6.4 |
| 3 | TK | 9.6 | 19.7 | 32.9 | 37.3 | 17.0 |
| - | PN | 7.1 | 10.7 | 17.6 | 24.9 | 38.0 |
| A | UGS | 5.1 | 8.6 | 14.1 | 22.4 | 6,510.9 |
| M3gl | 6.1 | 8.6 | 14.4 | 16.4 | 1.9 | |
| WLC | 23.6 | 54.9 | 65.0 | 70.0 | 108.8 | |
| D | QYW | 25.5 | 55.5 | 65.8 | 74.7 | 13.3 |
| B | JY | 9.7 | 16.3 | 25.3 | 28.6 | 3.2 |
| 4 | TK | 7.6 | 11.4 | 16.6 | 39.4 | 11.8 |
| - | PN | 5.2 | 6.9 | 9.3 | 11.9 | 17.2 |
| A | UGS | 5.1 | 7.6 | 11.2 | 13.1 | 1,687.1 |
| M3gl | 3.0 | 4.0 | 6.9 | 10.3 | 1.2 | |
| Database | Algorithm | EER | FMR100 | FMR1000 | ZeroFMR | Time(ms) |
|---|---|---|---|---|---|---|
| D | M3gl1 | 1.7 | 2.5 | 3.6 | 3.6 | |
| B | M3gl2 | 2.5 | 1.6 | 3.2 | 3.2 | |
| 1 | M3gl3 | 1.4 | 2.9 | 3.6 | 3.6 | |
| - | M3gl4 | 1.6 | 2.9 | 3.2 | 3.2 | |
| B | M3gl | 2.0 | 2.5 | 3.2 | 3.2 | |
| D | M3gl1 | 0.7 | 1.1 | 1.8 | 1.8 | |
| B | M3gl2 | 1.9 | 2.5 | 3.2 | 3.2 | |
| 2 | M3gl3 | 0.8 | 0.8 | 1.8 | 1.8 | |
| - | M3gl4 | 1.9 | 2.9 | 2.9 | 2.9 | |
| B | M3gl | 0.7 | 1.1 | 1.8 | 1.8 | |
| D | M3gl1 | 6.5 | 9.4 | 12.1 | 12.1 | |
| B | M3gl2 | 7.7 | 13.9 | 18.6 | 18.6 | |
| 3 | M3gl3 | 6.9 | 9.3 | 11.8 | 11.8 | |
| - | M3gl4 | 6.9 | 11.4 | 27.9 | 27.9 | |
| B | M3gl | 6.4 | 9.3 | 11.1 | 11.1 | |
| D | M3gl1 | 2.3 | 3.6 | 19.6 | 19.6 | |
| B | M3gl2 | 2.8 | 3.9 | 11.1 | 11.1 | |
| 4 | M3gl3 | 2.2 | 3.2 | 16.4 | 16.4 | |
| - | M3gl4 | 4.0 | 32.5 | 78.2 | 78.2 | |
| B | M3gl | 2.4 | 3.6 | 19.6 | 19.6 | |
| Database | Algorithm | EER | FMR100 | FMR1000 | ZeroFMR | Time(ms) |
|---|---|---|---|---|---|---|
| D | M3gl1 | 4.0 | 5.4 | 10.4 | 10.4 | |
| B | M3gl2 | 5.8 | 24.3 | 30.7 | 30.7 | |
| 1 | M3gl3 | 3.8 | 6.1 | 13.6 | 13.6 | |
| - | M3gl4 | 6.4 | 33.6 | 50.4 | 50.4 | |
| B | M3gl | 2.5 | 5 | 9.3 | 9.3 | |
| D | M3gl1 | 9.7 | 21.1 | 24.3 | 24.3 | |
| B | M3gl2 | 12.9 | 25.0 | 28.6 | 28.6 | |
| 2 | M3gl3 | 8.9 | 18.9 | 20.7 | 20.7 | |
| - | M3gl4 | 11.4 | 25.0 | 31.1 | 31.1 | |
| B | M3gl | 10.5 | 20.7 | 25.7 | 25.7 | |
| D | M3gl1 | 0.9 | 1.4 | 2.5 | 2.5 | |
| B | M3gl2 | 3.1 | 6.1 | 24.6 | 24.6 | |
| 3 | M3gl3 | 1.0 | 1.4 | 2.5 | 2.5 | |
| - | M3gl4 | 3.7 | 48.2 | 70.4 | 70.4 | |
| B | M3gl | 0.6 | 0.7 | 1.4 | 1.4 | |
| D | M3gl1 | 3.4 | 6.1 | 7.5 | 7.5 | |
| B | M3gl2 | 4.6 | 11.4 | 13.2 | 13.2 | |
| 4 | M3gl3 | 3.8 | 6.1 | 7.9 | 7.9 | |
| - | M3gl4 | 5.3 | 20.0 | 72.9 | 72.9 | |
| B | M3gl | 4.2 | 6.1 | 7.5 | 7.5 | |
© 2012 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Medina-Pérez, M.A.; García-Borroto, M.; Gutierrez-Rodríguez, A.E.; Altamirano-Robles, L. Improving Fingerprint Verification Using Minutiae Triplets. Sensors 2012, 12, 3418-3437. https://doi.org/10.3390/s120303418
Medina-Pérez MA, García-Borroto M, Gutierrez-Rodríguez AE, Altamirano-Robles L. Improving Fingerprint Verification Using Minutiae Triplets. Sensors. 2012; 12(3):3418-3437. https://doi.org/10.3390/s120303418
Chicago/Turabian StyleMedina-Pérez, Miguel Angel, Milton García-Borroto, Andres Eduardo Gutierrez-Rodríguez, and Leopoldo Altamirano-Robles. 2012. "Improving Fingerprint Verification Using Minutiae Triplets" Sensors 12, no. 3: 3418-3437. https://doi.org/10.3390/s120303418




