The Performance Analysis Based on SAR Sample Covariance Matrix
Abstract
: Multi-channel systems appear in several fields of application in science. In the Synthetic Aperture Radar (SAR) context, multi-channel systems may refer to different domains, as multi-polarization, multi-interferometric or multi-temporal data, or even a combination of them. Due to the inherent speckle phenomenon present in SAR images, the statistical description of the data is almost mandatory for its utilization. The complex images acquired over natural media present in general zero-mean circular Gaussian characteristics. In this case, second order statistics as the multi-channel covariance matrix fully describe the data. For practical situations however, the covariance matrix has to be estimated using a limited number of samples, and this sample covariance matrix follow the complex Wishart distribution. In this context, the eigendecomposition of the multi-channel covariance matrix has been shown in different areas of high relevance regarding the physical properties of the imaged scene. Specifically, the maximum eigenvalue of the covariance matrix has been frequently used in different applications as target or change detection, estimation of the dominant scattering mechanism in polarimetric data, moving target indication, etc. In this paper, the statistical behavior of the maximum eigenvalue derived from the eigendecomposition of the sample multi-channel covariance matrix in terms of multi-channel SAR images is simplified for SAR community. Validation is performed against simulated data and examples of estimation and detection problems using the analytical expressions are as well given.1. Introduction
Multi-channel systems with random nature appear in a wide range of fields in the literature. For several of them, the central limit theorem applies and their random behavior can be modeled by Gaussian statistics, being thus statistically fully described by the first and second order moments. In the case of multi-channel SAR systems, the assumption of zero-mean multivariate complex Gaussian distribution is frequently valid for geophysical media, being thus fully described by the complex Hermitian covariance matrix. This is the statistical case treated in this work.
Since a SAR signal corresponds to the superposition of the scattered fields from all scatters inside a resolution cell, physical parameter estimation may be performed by exploiting the multi-channel covariance matrix. For that, eigendecomposition theorems have been widely used in the literature, decomposing the whole covariance matrix into elementary quantities, in order to provide a better physical interpretation of the data.
The eigendecomposition of the multi-channel SAR covariance matrix leads to useful information in a large range of SAR applications, including Ground Moving Target Indication (GMTI) [1], polarimetric SAR (PolSAR) [2], interferometric SAR (InSAR) [3], polarimetric interferometric SAR (PolInSAR) [4], change detection [5], target detection [6] and filtering [7,8]. Particularly, the covariance matrix maximum eigenvalue has been proved to be a key parameter in various areas. In [5] and [9], the change detection problem was elaborated using the maximum eigenvalue of the interferometric covariance matrix. The eigendecomposition of the SAR covariance matrix with application to SAR GMTI is used in and to calculate the probability of moving target detection in homogeneous and heterogeneous terrain. Regarding polarimetry, the eigendecomposition of the coherency (which is also a covariance) matrix is the most common tool among incoherent target decomposition theorems for the interpretation of the earth’s surface. The maximum eigenvalue of the coherency matrix is also often used in polarimetry, due to the close relationship to the dominant scattering mechanism of the scattering process [2,10,11].
Although there is a wide area of applications regarding the maximum eigenvalue of the multi-channel covariance matrix, a certain lack of information in the literature concerning its statistical characterization in terms of multi-channel SAR may be verified. The statistical description can be useful to understand bias effects and to analyze estimation as well as detection problems. The estimated (sample) covariance matrix follows a Wishart distribution, which has been of interest along the years since its first derivation. In areas as communication systems, several works using such results have been published [12–16]. The application of the Wishart distribution in remote sensing was however considerably late introduced [17].
The cornerstone study considering the statistical description of the covariance matrix eigendecomposition in polarimetry has been carried out in [18]. The majority of the analysis in [18] was performed on the basis of numerical methods. In this paper the results of [18] is supported by addressing analytical solutions. Additionally, it is derived an exact closed form expressions for the Moment Generating Function (MGF) of the sample covariance matrix maximum eigenvalue.
The validation of the derived expressions is performed using simulated data, demonstrating its agreement with the theory. The effect of the number of samples and underlying correlation scenario of the sample covariance matrix on the bias in the estimation of the maximum eigenvalue is also investigated. Finally, examples of applications are as well given, in the fields of estimation and detection theory.
The next section reminds the basics of the statistical description of multi-channel SAR systems and of the covariance matrix eigendecomposition. It also includes the derived theorems presenting the statistical founds. Section 3 includes numerical examples validating the theorems as well as an analysis of their behavior. Sections 4 and 5 show their usage for the analysis of the estimation bias and for the elaboration of detection problems, respectively. Section 6 concludes the paper with discussions and directions for future work. The detailed statistical derivations can be found in the Appendix.
2. Statistical Characteristics of the Maximum Eigenvalue of the Multi-Channel Sample Covariance Matrix
2.1. Preliminaries
The individual elements of a m-dimensional multi-channel system may be organized in a m-dimensional vector k. As the elements are assumed to follow zero mean complex Gaussian distributions, the vector k is said to follow a m-dimensional multivariate normal distribution, with zero mean and true covariance matrix Σ among the vector elements, and is represented by [19,20]. For zero mean Gaussian statistics the covariance matrix fully describes the data, playing a key role in several application fields. In practical situations however, the true covariance matrix Σ is unknown and has to be estimated by its maximum likelihood estimator (MLE), the sample covariance matrix , where n is the number of estimation samples and † is the transpose conjugate operator. In the SAR context, the number of independent samples is also called looks. The elements of Z follow a m dimensional complex Wishart distribution with n degrees of freedom and true covariance matrix Σ, represented by and defined as [20]:
The spectral theorem from linear algebra allows the decomposition of the full rank m-dimensional covariance matrix in a set of m one-rank covariance matrices using its eigenvalues and eigenvectors. Accordingly, the decompositions of the true covariance matrix and its estimator are given by
2.2. Sample Maximum Eigenvalue Statistical Description
The following Theorem III concerns the derived Moment Generating Function (MGF) of the maximum eigenvalue of the sample covariance matrix Z of a multi-channel statistical system, which is a critical step in removing the bias of the largest eigenvalue. The Theorem III, which is derived due to the previous works (Theorems I and II), is the main result of the paper. It is detailed in the appendix and will be used for the elaboration of illustrative estimation and detection problems in Sections 4 and 5.
Throughout the paper, | · | is the matrix determinant, denotes the estimator of the random matrix X formed from a sample of size n.
Theorem I: Let be a m-dimensional complex vector whose elements follow zero mean Gaussian distributions with associated m × m covariance matrix Σ. Let Σ have lm ≤ .... ≤ l1 eigenvalues. Then the Cumulative Density Function (CDF) of the maximum eigenvalue λmax of the sample covariance matrix 〈kk†〉n, with the assumption m ≤ n, is given by
Proof: [14] gave the closed expression of CDF of the largest eigenvalue of the complex Wishart matrices. Here, it is written in the form of SAR covariance matrix after small continuation, see also Appendix A.
Theorem II: Let be a m-dimensional complex vector whose elements follow zero mean Gaussian distributions with associated m × m covariance matrix Σ. Let Σ have lm ≤ .... ≤ l1 eigenvalues. Then the Probability Density Function (PDF) of the maximum eigenvalue λmax of the sample covariance matrix 〈kk†〈n, with the assumption of m ≤ n, is given by
Proof: Equation (4) is obtained by differentiating Equation (3) with respect to x using (Equation (9) in [22])
Theorem III: Let be a m-dimensional complex vector whose elements follow zero mean Gaussian distributions with associated m × m covariance matrix Σ. Let Σ have lm ≤ .... ≤ l1 eigenvalues. Then for any positive integers s, the sth moment of the maximum eigenvalue λmax of the sample covariance matrix 〈kk†〉n, with the assumption of m ≤ n, is given by
Proof: See Appendix section B. In the appendix the moment of sample maximum eigenvalue is also given in more friendlier form for programming obtained by splitting the hypergeometric function of several variables into a sum of its variables.
2.3. Dependence of the Covariance Matrix Eigenvalues
Before starting the following analysis, it would be nice to illustrate the dependencies of the eigenvalues on the covariance matrix parameters, which is necessary for the further understanding of the addressed topics. For that, a two-dimensional covariance matrix is used, originated from the expected values of the outer product of the vector k = [k1 k2]T, i.e.,
The eigenvalues of the true covariance matrix can be shown to be given by [5]:
3. Validation and Analysis of the Theoretical Expressions
This section aims to validate the theorems mentioned in the previous section using simulated data. The simulated data have been generated using different multi-dimensional configurations, where the correlation between channels have been generated using the well known Mahalanobis transformation [24].
Figure 2(a) shows the comparison of the Equation (4) with simulations. The theoretical PDF curves clearly agree with the histograms obtained from simulated data. As expected, the PDFs become narrower with increasing n, indicating less variance around the true value of the maximum eigenvalue l1 = 1.8. This behavior can be better seen in Figure 2(b) where the distribution of λmax as a function of the number of estimation samples n is presented. Note also that the expected value of the distributions seems to change for different n.
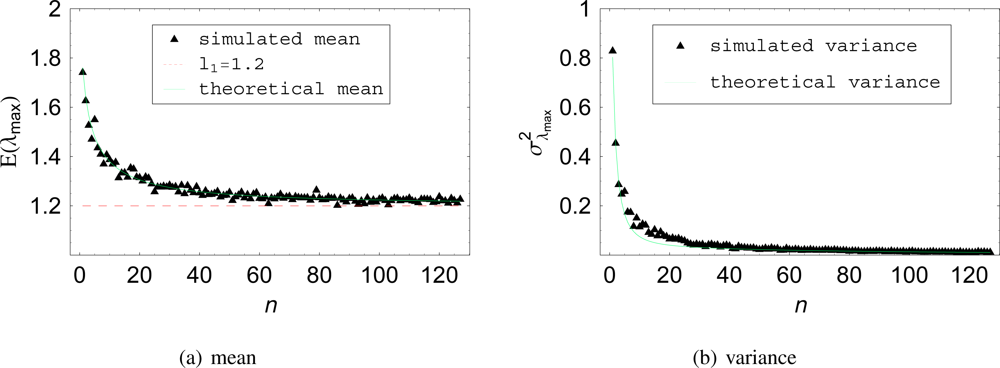
Figure 3(a) shows the variation of the histogram mean as a function of n for a two-dimensional case with fix correlation ρ = 0.2. In Figure 3(a), the theoretical expected value of λmax has been also over plotted for comparison. The curves match well, which validates Theorem III. The same has been carried out for the second order moment, i.e., the variance of λmax, and is presented in Figure 3(b). The agreement between the theoretical variance of λmax and the variance of the simulated data can again be confirmed. Also, as already observed in Figure 2(a), the lower the number of samples n, the higher the variance of λmax.
The impact of the correlation and the number of samples on the behavior of the third (skewness) and fourth (kurtosis) order moment of the maximum sample eigenvalue λmax is presented in Figure 4. Skewness is a measure of how symmetrical the distribution is with respect to its mean. Figure 4(a,b) indicates that the skewness of λmax converges to zero for increasing n and increasing ρ, expressing the tendency to a symmetrical distribution in that cases.
Kurtosis is a measure of the peakedness of the distribution. Figure 4(c,d) shows that for increasing n and ρ, the kurtosis of the λmax distribution tends to three, which corresponds to the kurtosis of the normal Gaussian distribution.
4. Estimation Bias
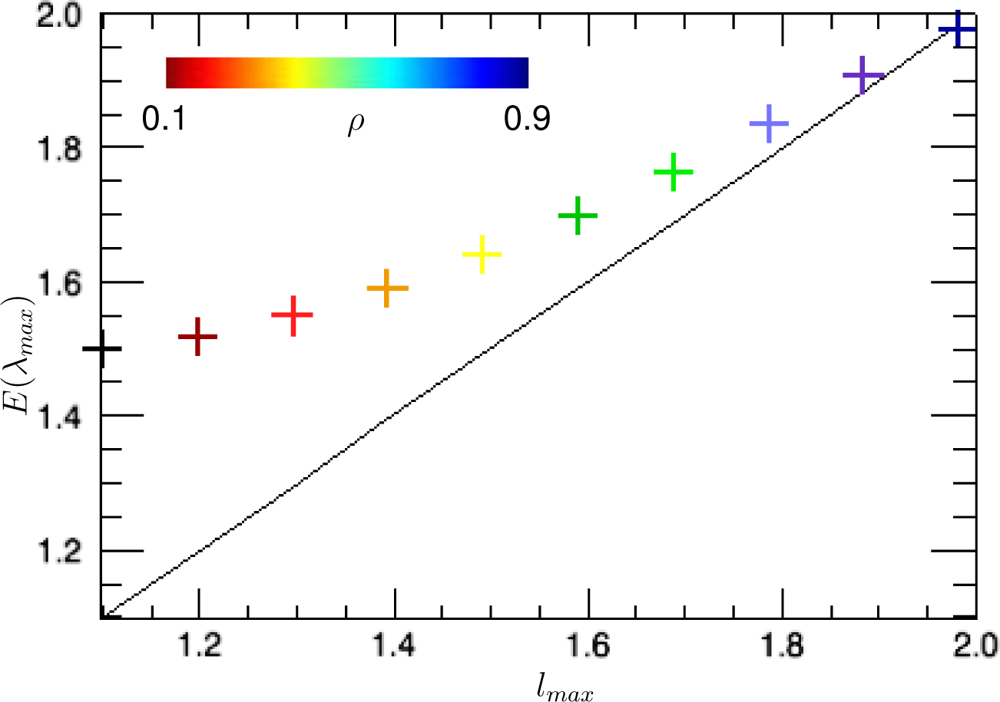
Figure 5 shows the expected value (first order moment) of the maximum sample eigenvalue λmax as a function of the true eigenvalues lmax for a fixed number of samples n = 3 and k = 1. The variation of the underlying correlation of the true covariance matrix ρ, which changes the values of lmax, has been as well indicated in a color code. Observe that the higher the correlation is, the higher lmax becomes.
The bias of the estimator of a certain parameter is defined as the difference between the expected value of the estimator and the true value of the parameter. In the present case, the bias is hence given by E[λmax] − lmax. Notice thus from Figure 5 that the bias of λmax becomes very strong for low values of the correlation lmax (or equivalently, low values of ρ).
The effect is emphasized in Figure 6(a,b), where the bias of λmax is presented as a function of lmax and l2, for n = 3 and n = 16, respectively. The values of the underlying correlation ρ have been also indicated. The bias is small either when the correlation is high or the number of samples is sufficiently large. When the correlation between channels is low, the bias becomes very significant and a large number of samples is necessary to decrease the estimation bias.
5. Analysis of Detection Problems
Detection theory is a means to quantify the ability of a procedure to detect a parameter (or signal) immersed in a noise environment. A decision has to be taken, in order to say yes, there is a signal, or no, there is no signal. Such decision is usually taken under the application of a decision threshold. Noise contributes off course negatively inducing wrong decisions. For the quantification of detection accuracy, some quantities are usually defined as the probability of detection (PD) and probability of false alarm (PFA), allowing a detection problem analysis.
The maximum eigenvalue of covariance matrices has been frequently used in the literature for the elaboration of certain detection problems. In the Ground Moving Target Indication (GMTI) area, for instance, the signal to clutter plus noise ratio has been studied under the distribution of the sample eigenvalues, which allowed the implementation of a constant false alarm rate detector [9]. The eigenvalues of the covariance matrix of a SAR image pair have been also used in order to formulate a problem in the change detection area [5]. Another example is the determination of the existence of just a single dominant scattering mechanism in a SAR polarimetric acquisition, which also has been evaluated using a threshold in the maximum sample eigenvalue of the polarimetric covariance matrix [11]. Target detection and polarimetric filtering represent other fields of application in which the maximum eigenvalue can be used.
Having the closed form expressions of the PDF (Equation (4)) and/or CDF (Equation (3)) of the maximum sample eigenvalue of the covariance matrix, the PD and PFA when applying a threshold in λmax can be analytically computed, allowing a complete detection problem analysis.
5.1. Detection of a Dominant Maximum Eigenvalue
Since several detection problems rely in fact on the choice of a dominant or non-dominant lmax by applying a threshold in λmax, the following problem with two hypotheses is elaborated
In one application area H0 may mean that just a single scattering mechanism is present inside a resolution cell of polarimetric SAR data, in other application H0 can mean that a change happened or a moving target is present in the scene.
Since lmax is not achievable, a threshold has to be used in λmax, originating the following PD and PFA
Hence, for a two-dimensional system configuration, the distribution pλmax (x; H0) is the distribution of λmax when l1 = 2 and l2 = 0. For a three-dimensional system, pλmax (x; H0) is determined evaluating the distribution of λmax when l1 = 3 and l2 = l3 = 0. Higher dimensional system configurations follow the same rule.
On the other hand, the distribution pλmax (x; H1) is given by l1 = l2 = 1 and l1 = l2 = l3 = 1 for a two- and three-dimensional system, respectively.
For each value of , there exists a pair (PFA, PD). The curves of PD versus PFA are called Receiver Operating Characteristic (ROC) curves and express the detection performance. The more a ROC curve bends toward the upper left, the better is the detection performance since a higher PD and lower PFA is achieved.
Figure 7(a) shows the detection performance as a function of the dimension of the multichannel system, i.e., m = 2, e.g., interferometric, m = 3, e.g., polarimetric and m = 6, e.g., polarimetric-interferometric system. For all cases, with fixed number of samples n = 6, one can realize that the performance of detection is significantly improved as the number of SAR images increases. Figure 7(b) shows the ROC curves for m = {2, 3} and for different number of samples n. It can be seen that for both multidimensional system configurations the number of samples increases the detection performance.
In order to state how correlation effects the detection performance, the detection problem is reformulated as follows
5.2. Target Detection Using Polarimetric Matched Filter
In this section the application of the expressions for the detection of specific targets using the Polarimetric Matched Filter (PMF) concept is illustrated. For that, a short review on PMF is required [6,7].
In a polarimetric acquisition, the dimension of the system corresponds to the number of channels, which are in general four, but three for the backscattering reciprocal case. The measured vector k is hence three- or four-dimensional. The elements of the vector k may be weighted in a given way, in order to satisfy a certain condition. The weighting can be accounted for by making y = h†k, where h is a complex vector with same dimension as k. A condition usually aimed to be satisfied in the literature is the maximization of the quadratic detector |y|2 (Equation (59) in [6]). The optimal weighting vector h in order to detect a distributed target with the target vector k is dependent on the target characteristics. Accordingly, the expected value of |y|2 is given by
The target vector k is a random sample and has alone no physical meaning. Therefore, usually multi-look processing is performed making, for n samples (or looks)
In the presence of target y̅2 is maximum, given by y̅2 = ||h̅||2λmax, where h̅ is the eigenvector of λmax. Hence, assuming without loss of generality that h̅ has unitary length (||h̅||2 = 1), detection performances can be made using the derivations given in this work, as done in the previous section, where a threshold has been used in order to detect a dominant maximum sample eigenvalue (λmax = y̅2 > ).
Note that the probabilities of detection and false alarm defined in last section can be more simply evaluated by
A three-dimensional polarimetric target detection problem was formulated making k = [SHH SHV SVV]T, where Si is the polarimetric scattering matrix element in channel i, and using the target covariance matrix structure
6. Conclusions and Discussion
In this paper a depth statistical analysis of the maximum eigenvalue of the eigendecomposition of the sample covariance matrix in terms of SAR applications is presented. The proposed analysis are supported by simulation results via several examples. The results are based on a exact closed-form expressions of PDF, CDF and MGF. In this study, existing density functions of the sample maximum eigenvalue were extended and/or implemented into multi-channel SAR system in order to obtain a simple expression of the sample eigenvalues giving a way to fruitful applications. From these closed-form expressions, it has been possible to develop new algorithms for unbiased calculations of parameters extracted from multi-channel SAR covariance matrix. In addition to these implementations, closed-form expressions were developed for the MGF of the sample maximum eigenvalue, which can be critical in the area of bias removal and detection performance analysis. This new closed-form expressions of the MGF can be also interesting for other application areas like MIMO systems (Multiple-Input Multiple-Output). Apart from estimation theory analysis including the MGF, the detection problem of the sample maximum eigenvalue has been also discussed.
References
- Sikaneta, I.; Gierull, C.; Chouinard, J.Y. Metrics for SAR-GMTI Based on Eigen-Decomposition of the Sample Covariance Matrix. Proceedings of the 2003 International Radar Conference, Adelaide, Australia, 3–5 September 2003; pp. 442–447.
- Hajnsek, I.; Pottier, E.; Cloude, S.R. Inversion of surface parameters from polarimetric SAR. IEEE Trans. Geosci. Remote Sens 2003, 4, 727–744. [Google Scholar]
- Li, Z.; Bao, Z.; Li, H.; Liao, G. Image autocoregistration and InSAR interferogram estimation using joint subspace projection. IEEE Trans. Geosci. Remote Sens 2006, 44, 288–297. [Google Scholar]
- Erten, E.; Reigber, A.; Ferro-Famil, L.; Hellwich, O. A new coherent similarity measure for temporal multichannel scene characterization. IEEE Trans. Geosci. Remote Sens 2011, 50, 1–13. [Google Scholar]
- Zandoná-Schneider, R.; Fernandes, D. Entropy Concept for Change Detection in Multitemporal SAR Images. Proceedings of EUSAR, Köln, Germany, 4–6 June 2002.
- Novak, L.M.; Sechtin, M.B.; Cardullo, M.J. Studies of target detection algorithms that use polarimetric radar data. IEEE Trans. Aerosp. Electon. Syst 1989, 25, 150–165. [Google Scholar]
- Liu, G.; Huang, S.; Torre, A.; Rubertone, F. The multilook polarimetric whitening filter (MPWF) for intensity speckle reduction in polarimetric SAR images. IEEE Trans. Geosci. Remote Sens 1998, 36, 1016–1020. [Google Scholar]
- Li, Z.; Bao, Z.; Suo, Z.A. Joint image coregistration, phase noise suppression, and phase unwrapping method based on subspace projection for multibaseline InSAR systems. IEEE Trans. Geosci. Remote Sens 2007, 54, 584–591. [Google Scholar]
- Nadarajah, S. Comments on Eigendecomposition of the multi-channel covariance matrix with applications to SAR-GMTI. Signal Process 2007, 87, 1534–1536. [Google Scholar]
- Lee, J.S.; Grunes, M.R.; Schuler, D.L.; Pottier, E.; Ferro-Famil, L. Scattering-model-based speckle filtering of polarimetric SAR data. IEEE Trans. Geosci. Remote Sens 2006, 44, 176–187. [Google Scholar]
- Touzi, R. Target scattering decomposition in terms of roll-invariant target parameters. IEEE Geosci. Remote Sens. Lett 2007, 45, 73–84. [Google Scholar]
- Khatri, C.G. Non-central distributions of ith largest characteristic roots of three matrices concerning complex multivariate normal populations. Ann. Inst. Stat. Math 1969, 21, 23–32. [Google Scholar]
- Hirakawa, F. Some distributions of the latent roots of a complex Wishart matrix variate. Ann. Inst. Stat. Math 1975, 27, 357–363. [Google Scholar]
- Kang, M.; Alouini, M.S. Largest eigenvalue of complexWishart matrices and performance analysis of MIMO MRC systems. IEEE J. Sel. Areas Commun 2003, 21, 418–426. [Google Scholar]
- McKay, M.R.; Grant, A.J.; Collings, I.B. Performance analysis of MIMO-MRC in double-correlated Rayleigh environments. IEEE Trans. Commun 2007, 55, 497–507. [Google Scholar]
- McKay, M.R. Random Matrix Theory Analysis of Multiple Antenna Communication Systems. Ph.D. Thesis,. The University of Sydney, Sydney, Australia, 2006. [Google Scholar]
- Lee, J.S.; Hoppel, K.W.; Mango, S.A.; Miller, A.R. Intensity and Phase Statistics of Multilook Polarimetric and Interferometric SAR Imagery. IEEE Trans. Geosci. Remote Sens 1994, 32, 1117–1028. [Google Scholar]
- Lopez-Martinez, C.; Pottier, E.; Cloude, S.R. Statistical assessment of eigenvector-based target decomposition theorems in radar polarimetry. IEEE Trans. Geosci. Remote Sens 2005, 43, 2058–2074. [Google Scholar]
- Muirhead, R.J. Aspects of Multivariate Statistic Theory; John Wiley&Sons: New York, NY, USA, 1982. [Google Scholar]
- Ferro-Famil, L. Télédetection multi-fréquentielle et multi-temporelle d’environnements naturels à partir de données SAR polarimétriques. Ph.D. Thesis,. Université de Nantes, Nantes, France, 2000. [Google Scholar]
- Andrews, L.C. Special Functions of Mathematics for Engineers; McGraw-Hill Publishing Co: New York, NY, USA, 1992. [Google Scholar]
- Golberg, M.A. The derivative of a determinant. Am. Math. Month 1972, 78, 1124–1126. [Google Scholar]
- Ermolaev, V.T.; Rodyushkin, K.V. The distribution function of the maximum eigenvalue of a sample correlation matrix of internal noise of antenna-array elements. Radiophys. Quantum El 1999, 42, 439–444. [Google Scholar]
- Peebles, P.Z. Probability, Random Variables, and Random Signal Principles; McGraw-Hill College, 1993. [Google Scholar]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series, and Products; Academic Press: Burlington, MA, USA, 2007. [Google Scholar]
- Li, J.-S.; Pottier, E. Polarimetric Radar Imaging from Basics to Applications; CRS Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Chiani, M.; Win, M.Z.; Zanella, A. On the capacity of spatially correlated MIMO Rayleigh-fading channels. IEEE Trans. Inform. Theory 2003, 49, 2363–2371. [Google Scholar]
- Mestre, X.; Lagunas, M.A. Finite sample size effect on minimum variance beamformers: Optimum diagonal loading factor for large arrays. IEEE Trans. Signal Process 2003, 54, 69–82. [Google Scholar]
Appendix
This Appendix starts with the reminder of some basic results from linear algebra and statistical theory to prove the Theorem III proposed in this manuscript.
Definition 1 (Theorem A3 in [19]): The determinant of a square m × m matrix A is
Definition 2 (Corollary 2 in [27]): Given two arbitrary m × m matrices Φ(x) and Ψ(x) with ijth elements Φi(xj) and Ψi(xj), and an arbitrary function ξ(·), the following identity holds:
Proof of Theorem I
In the case m ≤ n, the sample covariance matrix has full rank and follows a central Wishart distribution. It can be noted that [28] is an interesting work concerning the case n ≤ m. In Wishart history, the joint PDF of the real ordered sample eigenvalues ∞ ≥ λ1 ≥ . . . ≥ λm ≥ 0 of Z is given by Equation (36) in [18]
The CDF of the maximum eigenvalue λmax = λ1 is obtained using
Proof of Moments of the Sample Maximum Eigenvalue
For any positive integer s, the sth moment of the maximum eigenvalue is obtained using
It is desirable to write a friendlier expression for Equation (A11) to be useful for deriving the moments of the sample maximum eigenvalue. Due to the definition of the inverse of the m × m matrix , Equation (A11) can be written in the following form
Now the problem in Equation (A11) is the evaluation of the diagonal elements of the D(x). The matrix D(x) is the product of the two square matrices and the trace of the product of two matrices is shown as
Although Equation (A22) is an exact closed-form expression for the MGF of the sample maximum eigenvalue, the hypergeometric function of several variables is in general very difficult to evaluate, and it is better to express Equation (A22) in a more tractable form for future analysis. Regarding Equation (2.53) in [21], the incomplete gamma function can be written in the closed form
Applying the rule in Equation (A26) it yields:
The moments of the sample maximum eigenvalue regarding its PDF is solved. For larger m dimensional systems, such an approach may become complicated due to the need for a large number of calculation of cofactors. However, for applications where only a few eigenvalues, like polarimetry (m = 3) and interferometry (m = 2), are of interest, the numerical calculations are quite rapid and stable. For example, in the simplest case of m = 2, n ≥ 2, the MGF is given by






© 2012 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Erten, E. The Performance Analysis Based on SAR Sample Covariance Matrix. Sensors 2012, 12, 2766-2786. https://doi.org/10.3390/s120302766
Erten E. The Performance Analysis Based on SAR Sample Covariance Matrix. Sensors. 2012; 12(3):2766-2786. https://doi.org/10.3390/s120302766
Chicago/Turabian StyleErten, Esra. 2012. "The Performance Analysis Based on SAR Sample Covariance Matrix" Sensors 12, no. 3: 2766-2786. https://doi.org/10.3390/s120302766
APA StyleErten, E. (2012). The Performance Analysis Based on SAR Sample Covariance Matrix. Sensors, 12(3), 2766-2786. https://doi.org/10.3390/s120302766



