Simultaneous Monitoring of Soil Water Content and Salinity with a Low-Cost Capacitance-Resistance Probe
Abstract
: Capacitance and resistivity sensors can be used to continuously monitor soil volumetric water content (θ) and pore-water electrical conductivity (ECp) with non-destructive methods. However, dielectric readings of capacitance sensors operating at low frequencies are normally biased by high soil electrical conductivity. A procedure to calibrate capacitance-resistance probes in saline conditions was implemented in contrasting soils. A low-cost capacitance-resistance probe (ECH2O-5TE, 70 MHz, Decagon Devices, Pullman, WA, USA) was used in five soils at four water contents (i.e., from dry conditions to saturation) and four salinity levels of the wetting solution (0, 5, 10, and 15 dS·m−1). θ was accurately predicted as a function of the dielectric constant, apparent electrical conductivity (ECa), texture and organic carbon content, even in high salinity conditions. Four models to estimate pore-water electrical conductivity were tested and a set of empirical predicting functions were identified to estimate the model parameters based on easily available soil properties (e.g., texture, soil organic matter). The four models were reformulated to estimate ECp as a function of ECa, dielectric readings, and soil characteristics, improving their performances with respect to the original model formulation. Low-cost capacitance-resistance probes, if properly calibrated, can be effectively used to monitor water and solute dynamics in saline soils.1. Introduction
Coastal farmlands are often threatened by saltwater contamination that poses a serious risk for drinking water quality and agricultural activities. To control and evaluate the hazard of soil salinity, accurate measurements of soil water content and solute concentrations are needed. The term salinity refers to the presence of the major dissolved inorganic solutes (basically Na+, Mg2+, Ca2+, K+, Cl−, SO42−, HCO3−, NO3−, and CO32− ions) in the soil [1]. The salinity of a solution can be quantified in terms of its electrical conductivity (EC; dS·m−1), which is strictly related to the total concentration of dissolved salts, with 1 dS m−1 being approximately equivalent to 10 meq·L−1 at 25 °C [2]. Soil salinity is generally determined by measuring the electrical conductivity of aqueous extracts of saturated soil-pastes (ECe) or of other soil to water ratio extracts. However, such methods of investigation are destructive, time-consuming, and usually not representative of the real salinity status of soils in field conditions [1]. To determine the real (i.e., at actual soil water contents) stress conditions affecting crops and to monitor fluxes of salts (e.g., upward fluxes in the vadose zone) the electrical conductivity of the pore-water (ECp) should be measured instead. Multi-sensor probes have recently been developed in order to assess water content and electrical conductivity with continuous and non-destructive measurements.
2. Methodological Issues
2.1. Water Content Measurements
The capacitance (dielectric) technique has been widely used to estimate soil volumetric water content (θ) [3]. Capacitance sensors induce an alternating electric field in the surrounding medium. The total complex impedance is obtained by quantifying the voltage and the current induced by the electric field on the sensor electrodes. The impedance is related to the complex permittivity (or dielectric constant; εr) of the surrounding medium. The volume of the induced electric field depends mainly on the size and shape of the sensor electrodes. Moreover, the electric field decays rapidly, being inversely proportional to the square of the distance. Topp et al.[4] noticed a strict correlation between εr measured by time domain reflectometry (TDR) and soil water content. They therefore proposed an empirical third-degree polynomial in εr to calculate θ. The complex permittivity of the soil measured by dielectric sensors is the sum of soil real (ε’) and imaginary (ε″) permittivity (dielectric loss):
2.2. Pore-Water Electrical Conductivity Assessment
The determination of the pore-water electrical conductivity is a difficult task as it cannot be directly related to any sensor output. Typically sensors measure soil bulk (or apparent) electrical conductivity (ECa), which is the combination of the contributions of the three phases constituting soils: solid, water and air [9,13]. According to Corwin [14], three pathways of current flow contribute to the ECa measurement: current through the pore water solution (the liquid phase pathway); current through exchange complexes on the surface of soil colloids (the soil-liquid phase pathway); and current through the soil particles that are in direct contact (the solid pathway). ECa can be estimated from εr readings [15] or from the electrical resistance that soil opposes to an alternating electric current [13,14]. ECp and ECa are strictly correlated, indeed an increase of ions in the matrix solution leads to an increase of ECa values [8,16,17].
Several models to estimate ECp from ECa have been developed in the last sixty years, based on empirical relations as well as on theoretical assumptions. Models are usually based on the empirical relationship between ECa and θ at constant ECp values, where the magnitude of ECa varies according to the tortuosity of the electrical current paths (depending on soil texture, density and particle geometry, particle pore distribution, and organic matter content). Tortuosity can be expressed in terms of a soil transmission factor (π) [16,18,19] or soil-type-related parameters [20–22].
Recent development of low-cost multi-sensor probes could make such ECp models implementable for continuous monitoring purposes. However, since most of the ECp models are calibrated in limited soil conditions [9,23–25], new relationships between variables and soil properties must be defined to extend their applicability to a wider range of soils.
The general aim of this study was to calibrate a multi-sensor probe for monitoring soil volumetric water content and soil water electrical conductivity in a heterogeneous saline coastal area. The specific objectives were: (i) to develop a procedure to simultaneously calibrate θ and ECp; (ii) to test different models for ECp; and (iii) to develop general functions to extend ECp model application to a wide range of soils, even in critical saline conditions.
3. Materials and Methods
3.1. Decagon ECH2O-5TE Probe
The sensor used in this experiment was an ECH2O-5TE probe (hereafter simply referred to as 5TE). 5TE is a multifunction sensor measuring εr, ECa, and T (Decagon Devices Inc., Pullman, WA, USA). A detailed description of the 5TE can be found in Bogena et al.[26] and Campbell and Greenway [27]. The probe is a fork-type sensor (0.1 m in length, 0.032 m in height). Two of the three tines host the dielectric sensor. The capacitance sensor supplies a 70 MHz electromagnetic wave to the prongs that charge according to the dielectric of the soil surrounding the sensor. The reference soil volume is ca. 3 × 10−4·m3. A charge is consequently stored in the prongs and it is proportional to the soil dielectric. Previous versions of dielectric sensors by Decagon Devices operate at lower frequencies (e.g., ECHO10 probe, 5 MHz). The increase of operating frequency has led to a higher salinity tolerance [6,8,12]. In fact εr measurement with 5TE should not be affected by soil salinity up to ECe values of 10 dS·m−1[28].
The bulk electrical conductivity is measured with a two-sensor array. The array consists of two screws placed on two of the sensor tines. An alternating electrical current is applied on the two screws and the resistance between them is measured. The sensor measures electrical conductivity up to 23.1 dS m−1 with 10% accuracy; however a user calibration is suggested above 7 dS·m−1. Temperature is measured with a surface-mounted thermistor reading the temperature on the surface of one of the prongs.
3.2. Soil Sampling
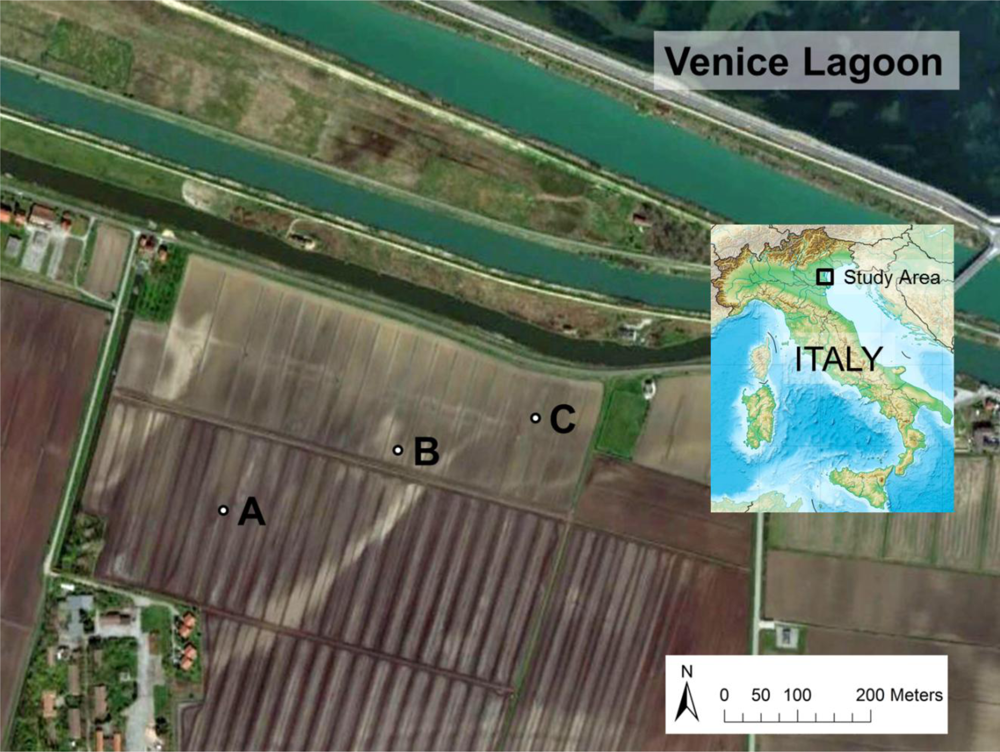
Soil samples from a coastal farmland affected by saltwater intrusion [29,30] were cored for the calibration of the 5TE probe. The site is located at Ca’ Bianca, Chioggia (12°13′55.218″E; 45°10′57.862″N), just south of the Venice Lagoon, North-Eastern Italy. The area has high spatial variability in soil characteristics due to its deltaic origins (Figure 1).
Three sampling locations were chosen in the basin (sites A, B, and C, Figure 1). At sites A and B both topsoil (0 to 0.4 m depth) and subsoil (0.4 to 0.8 m depth) were collected, while only the topsoil was cored at site C since the profile is uniform. The main physical and chemical properties of the samples were characterized. Soil texture was determined with a laser particle size analyzer (Mastersizer 2000, Malvern Instruments Ltd., Great Malvern, UK). Soil total carbon content and soil organic carbon (SOC) content were analyzed with a Vario Macro Cube CNS analyzer (Elementar Analysensysteme GmbH, Hanau, Germany). Cation exchange capacity (CEC) was measured at a pH value of 8.2 according to the BaCl extraction method [31]. Soil pH was measured with a 1:2 soil to water ratio with a pH-meter (S47K, Mettler Toledo, Greifensee, Switzerland). Particle density (ρr) was measured with an ethanol pycnometer [32]. Bulk density (ρb) was determined from undisturbed core samples. ECe was measured according to Rhoades et al.[1].
Soil samples show high variability in sand (from 174.7 to 905.2 g·kg−1), organic carbon content (from 15.4 to 147.8 g·kg−1), and ECe values (from 0.61 to 6.38 dS·m−1). Five soil types were selected: a sandy soil with low SOC content and low ECe, a silty-clay-loam with low SOC content and high ECe, two loam and one clay-loam with medium-high SOC content. Main soil properties are listed in Table 1.
3.3. Experimental Settings
The 5TE probe was used in a mixture of soil (preliminarily air-dried and sifted at 2 mm) and saline solution (54.92% Cl−; 30.82% Na+; 7.68% SO42−; 3.81% Mg2+; 1.21% Ca2+; 1.12% K+; 0.44%NaHCO4) to reproduce saline groundwater of the experimental site [33]. Soil samples were moistened to a relative saturation (S) of about 0, 0.35, 0.75, and 1.00 with a saline solution of 0, 5, 10, and 15 dS·m−1 (at 25 °C). The mixtures were prepared in a plastic container and then sealed and kept in a dark place at constant temperature 22 ± 1 °C for 48 hours. The soil was then packed uniformly in a 6 × 10−4·m3 beaker to reproduce the field bulk density. Output values for εr, ECa, and T were recorded by a datalogger (Em50, Decagon Devices) connected to the 5TE probe.
Electrical conductivity of the wetting solution (ECw) differs from the electrical conductivity of the pore-water (ECp) [21]. Pore-water solution was extracted from a portion of the soil sample by vacuum displacement [34] at −90 kPa and ECp was measured with a S47K conductivity meter. ECe was then measured on the remaining soil sample. Water content was determined gravimetrically (at 105 °C for 24 hours). Measures were replicated 3 times.
3.4. Calibration Procedure
A three-step procedure was implemented to calibrate the sensor output for the collected samples: (1) model calibration to convert εr and ECa readings to θ or ECp; (2) comparison and selection of the best models; (3) simultaneous calibration of the selected models for θ and ECp and evaluation of their robustness by applying a bootstrap procedure.
3.4.1. Models to Convert εr Readings to θ
Dielectric permittivity can be converted to volumetric water content using empirical models (e.g., [4]). However temperature and soil electrical conductivity affect the dielectric permittivity measurements of ECH2O sensors [5,35,36]. In one of their latest studies, Rosenbaum et al.[5] developed an empirical calibration to correct the temperature effect on εr measurements which performed very well in both liquid and soil media. Investigating the effect of temperature on εr, Bogena et al. [26] concluded that in a T range from 5 °C and 40 °C, εr varies up to 8% with respect to the reference liquid used (εr = 40 at 25 °C). As all the calibration experiments presented in this work took place at a controlled temperature of 22 ± 1 °C, the effect of T on εr was considered negligible. On the other hand, εr is much more sensitive to electrical conductivity changes [37].
Polynomial model-types as that proposed by Topp et al. [4] do not provide satisfactory θ estimates in the presence of high clay and organic contents or in saline soils, especially using sensors operating at low frequencies [12,38]. Indeed, application of the Topp model to the experimental data of Ca’ Bianca provided a large average error (∼0.11 m3·m−3).
Three models were tested to find a satisfactory empirical relationship between εr and θ data for each soil at different ECw values, namely:
logistic model:
hyperbolic model:
logarithmic model:
where θMAX is the volumetric content at saturation, a, b, and U are fitting parameters.
The three models were compared with the Akaike Information Criterion (AIC) [39] and the one with the higher Akaike weight (WAIC) [40] was selected for the subsequent simultaneous calibration of θ and ECp. The Akaike Information Criterion (AIC) is a measure of the goodness of fit of a specific model. It allows the direct comparison of different concurrent equations for model selection purposes. AIC accounts for the risk of over-parameterization as well as for the goodness of fit; several models can be ranked according to their AIC, with the one having the lower value being the best. From the AIC, the Akaike weight (ΣWAIC = 1) can be computed, which represents the probability that a specific model is the best, given the data and the set of candidate models. Note that the fitting parameters showed a high dependence on ECa and physico-chemical soil characteristics. To take this effect into account, the fitting parameters were expressed as a linear function of ECa and other selected soil properties yielding a “general” calibration equation usable on the various soils of the study site.
3.4.2. Models to Convert εr and ECa Readings to ECp
Four models were tested: the first is the Malicki and Walczak [21] model. They found that, when εr is higher than 6.2, the slope ∂ECa/∂εr depends only on salinity but not on water content, nor bulk density, nor dielectric permittivity. They developed an empirical relationship linearly linking ECa to εr for various values of ECw, i.e., ECa(εr,ECw). The validity of the linear relationships holds above a “converging point” characterized by εr0 = 6.2 and ECa0 = 0.08 dS·m−1. ECp was consequently defined as a function of ECa(εr,ECw) and soil texture:
On the basis of Equation (5), Hilhorst [20] developed the following theoretical model:
The third tested model is the one proposed by Rhoades et al.[16] (hereafter simply referred as Rhoades). They expressed the pore-water electrical conductivity as:
Archie’s law [22] (hereafter simply referred as Archie) was developed to assess the conductivity of pore-water in clay-free rocks and sediments, and it has been therefore used in soils containing neither clay minerals nor organic matter. According to Archie ECp can be derived as follows:
Archie has been modified in order to be used also in soils containing clay minerals [42] by simply considering the contribution of ECs in Equation (10). Hence, ECp was defined as:
Despite the fact that Archie was originally developed for deep sediments in oil research, it has been successfully applied in shallow groundwater systems to trace salinity. An example of such implementation is given by Monego et al.[43]. It is worth noticing that Archie and Rhoades show a similar formulation, being equal when m = 1 and n = 1 (then k = 1/π).
The four models apply for θ > 0.1 m3·m−3 (for Rhoades and Hilhorst), θ > 0.2 m3·m−3 (for Malicki and Walczak), and S > 0.3 (for Archie).
The models were tested with the experimental (ECa,εr) values and the chemical and physical properties of the five soil samples collected at Ca’ Bianca. In a first step, the original formulations were tested by calculating the parameters according to the methodologies proposed by the authors. Next, the models were optimized by relating the calibration parameters to the physical and chemical characteristics of the soils. ECp data at S ≈ 0.35 were excluded from the optimization as it was impossible to collect a sufficient amount of solution with the extraction method used in this experiment. ECp data at S ≈ 0 were assumed equal to 0 dS·m−1[8].
3.4.3. Simultaneous Calibration of Models for θ and ECp
The model parameters for the simultaneous quantification of θ and ECp were calibrated by minimizing the following objective function:
This weighted procedure prevents one data type (i.e., ECp or θ) from dominating the other, solely because of its higher numerical values.
In this study the limited dataset size (M = 80 and N = 55) did not allow a validation to be performed on an independent set of data. The models were thus validated through a bootstrap procedure [45]. A Y number of iterations were carried out. At each iteration, a subset of 60 points out of 80 for θ and 42 out of 55 for ECp were extracted, forming the calibration dataset. The remaining points were retained for validation.
At the end of the iterations, the root mean square error ( ), which provides the goodness of fit, the median, and the 5th and 95th percentiles of the distribution of each parameter were retained for further analysis. The probability distribution function of RMSE was compared using the Kolmogorov-Smirnov (KS) test to assess the significance of difference in the model predictions.
The calibration procedure described above was performed using the Generalized Reduced Gradient (GRG) Nonlinear Solving Method (Frontline Systems, Inc., Incline Village, NV, USA).
4. Results and Discussion
4.1. Converting εr Readings to θ
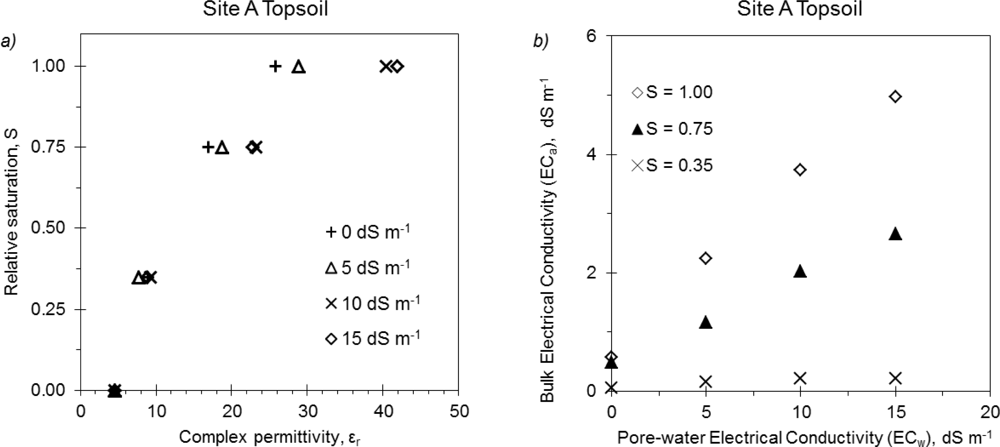
Dependence of 5TE on bulk electrical conductivity was observed to be similar in all the tested soil samples. εr readings were greatly affected by ECa: especially for high θ values, a small increase in ECw significantly raised the dielectric output of the probe, indicating that dielectric readings carried out in highly conductive media must be corrected. This finding confirms the results by Rosenbaum et al.[5] on the same probe and by Saito et al.[8] on other Decagon dielectric probes operating at lower frequencies. An example of the non-linear response of εr at different ECw and θ values is presented in Figure 2(a). Starting from a relative saturation of 0.75, the response of the probe significantly diverged at salinity solution with ECw > 10 dS m−1. Figure 2(b) evidences also the direct effect of the ECw on ECa readings and how the effect was amplified at higher water content. This observation, confirmed by Schwank et al.[11] and Rosenbaum et al.[5], suggests investigating the effect of ECa on θ estimation.
Between the tested θ models, Equation (4) showed the best performances, with an Akaike weight WAIC close to 1 (Table 2).
Parameters a and b of the logarithmic model were found to be significantly correlated with the ECa values at different water contents. Therefore the logarithmic model was reformulated as:
Equations (14) and (15) were compared with the AIC test. A WAIC = 0.99 was obtained for Equation (15), indicating that this formulation of the logarithmic model is to be preferred over Equation (14), mainly for the reduced number of parameters.
To identify a “general” equation, q was set as a constant (=−0.766), whereas parameters a′ and a″ were related to soil properties (Table 3). Parameters a′ and a″ were estimated according to the following empirical equations:
Equation (15) allows correcting of the effect of dielectric losses due to the high electrical conductivity of the medium [3] due to high organic carbon content, salinity, and clay/sand ratio. The RMSE of Equation (15) was 0.038 m3·m−3.
4.2. Converting εr and ECa Readings to ECp
The parameters of models (5), (6), (8), and (11) showed significant correlations with soil properties (Table 3).
The parameter l by Malicki and Walczak was confirmed to be mainly correlated to sand content. The calibrated parameters for Equation (5) are: ECa0 = 0.06 dS·m−1; εr0 = 7.1; l = 0.012 + 10−6× sand(%) yielding RMSE = 2.52 dS·m−1. In the original paper by Malicki and Walczak l varied from 0.0083 to 0.0127 while in this experiment the range was narrower, from 0.0117 to 0.0124.
The ε(ECa = 0) parameter by Hilhorst was expressed as a function of soil organic carbon content:
According to Equation (18), εECa = 0 ranged from 5.16 to 7.85, values close to the interval found by Hilhorst (from 3.76 to 7.6 in soils and synthetic media). The calibrated model yielded RMSE = 2.34 dS m−1.
Concerning the Rhoades and Archie models, the term ECs was neglected as the 5TE probe registered ECa = 0 in dry soil conditions. Please note that other Authors [41] demonstrated that ECs could assume a certain magnitude.
In contrast to Equation (9) by Rhoades et al.[16], π was found to be uncorrelated with soil water content. Nevertheless, π showed a linear correlation with soil porosity (π = e + f × ϕ), with e and f depending on CaCO3 as follows:
In the tested samples π ranged from 0.22 to 0.71, whereas Rhoades et al.[16] found a variation from 0.01 to 0.6. The inverse correlation of CaCO3 with the tortuosity factor evidenced in the Ca’ Bianca soils can be explained by the fact that here a low CaCO3 content corresponds to high clay and SOC percentages. Indeed, the higher clay and SOC contents (more complicated geometric arrangement), the higher is soil tortuosity [41]. The “general” formulation of the Rhoades model provided RMSE = 0.90 dS m−1.
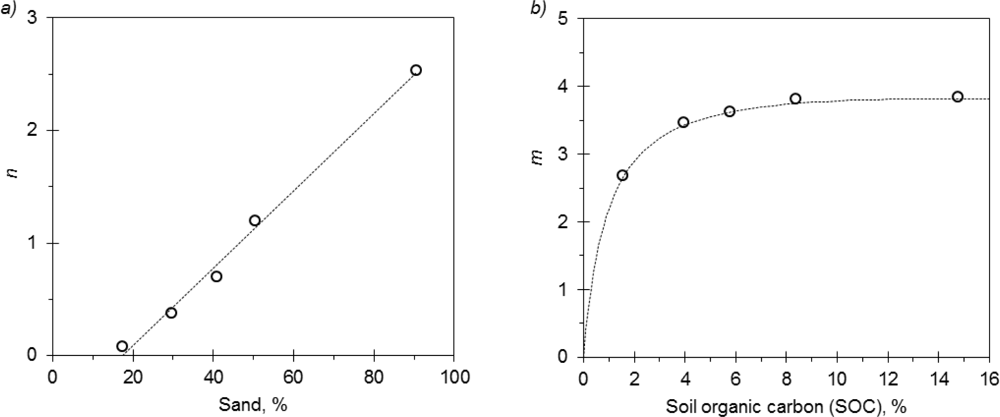
Several formulations were attempted for Archie in order to decrease the number of parameters related to soil properties. Here, the parameters k, m, and n were alternately fixed and kept independent from the soil type. The formulation with k = 0.487 provided the best fitting according to the AIC test. With fixed k, n showed a significant correlation with sand content:
It is worth noticing that with higher sand contents (Figure 3(a)) n ≅ 2.5, which is close to n values suggested for sandy media [13]. As shown in Table 3, n decreases with increasing clay values. For given S and ECa values, it is clearly derived from Equation (10) that the smaller the n the higher is ECp, i.e., with a large percentage of clay the influence of “the liquid phase pathway” on the ECa reading is reduced [14,41]. A non-linear relationship was detected between m and soil organic carbon (Figure 3(b)):
Values of m between 2.65 and 3.82 were derived. As reported by Archie, m becomes larger as the permeability of the porous medium decreases (increasing tortuosity). As shown in Figure 3(b) the magnitude of m rises with SOC. High organic contents decrease soil bulk density, possibly increasing soil tortuosity [46]. Archie calibration returned RMSE = 0.65 dS m−1.
Comparison between the RMSE values computed for the four ECp models showed that the “general” formulation of Archie provided the best estimates. Archie also had the highest WAIC (∼1.00). For the Malicki and Walczak, Hilhorst, and Rhoades models the WAIC were close to zero.
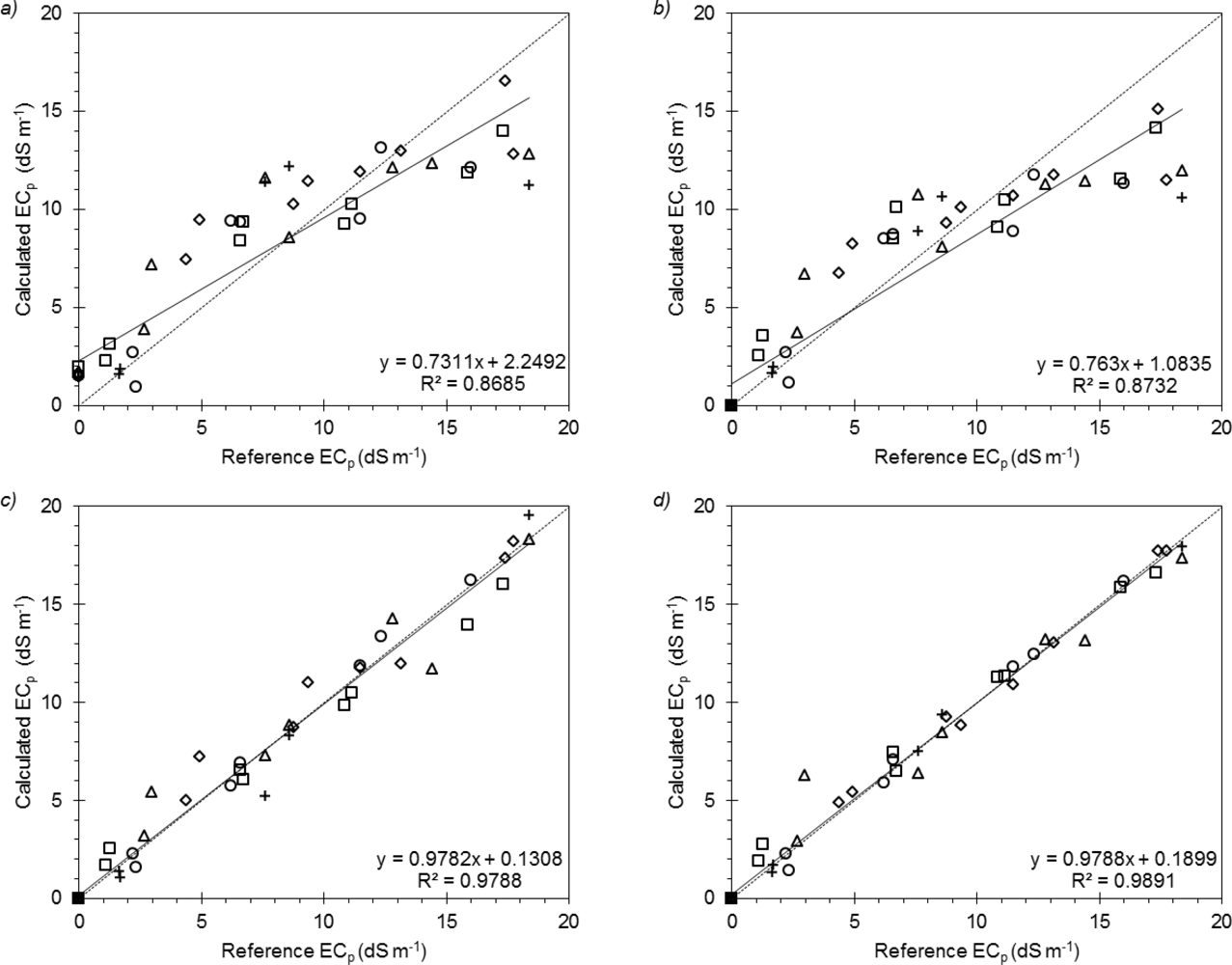
These results are also confirmed by the linear regressions between measured and estimated ECp (Figure 4). As displayed in this figure the models by Malicki and Walczak, and by Hilhorst did not show a good fitting, especially at high ECp values, as already observed by [23,25].
The different performances of the four models at various salinity ranges were tested resampling observed and estimated ECp 2,000 times, to compute average RMSEs and their confidence intervals at p = 0.05 as previously done by Giardini et al.[47]. The selected ranges were: (a) the 0–3 dS·m−1 and >3 dS·m−1; and (b) the 0–10 dS·m−1 and >10 dS·m−1.
At low ECp range (i.e., ECp < 3 dS·m−1) Rhoades showed the smallest RMSE (0.57 dS·m−1), nevertheless its performance was not significantly different from those by Hilhorst (RMSE = 0.93 dS·m−1) and Archie (RMSE = 0.72 dS·m−1). On the contrary, the model by Malicki and Walczak provided significantly higher errors (RMSE = 1.69 dS·m−1).
Above 3 dS·m−1, the models by Malicki and Walczak and by Hilhorst significantly differentiated from the other two. In fact they generally overestimated ECp in the range from 3 to 10 dS·m−1 with RMSE equal to 2.16 and 1.43 dS·m−1, respectively. On the other hand they underestimated ECp when the pore-water was very conductive (i.e., ECp > 10 dS·m−1), with RMSE = 3.28 dS·m−1 and RMSE = 3.83 dS·m−1, respectively.
In their work, Malicki and Walczak used TDR probes at fairly high frequencies, reducing the influence of ECa on εr. Moreover, their study was conducted using a wetting solution with a maximum conductivity of 11.7 dS·m−1. In the present work, calibrating the Malicki and Walczak model only for ECp < 10 dS·m−1 would provide satisfactory estimations (RMSE = 1.00 dS·m−1). Moreover, the metrics of fitting regression would have shown a slope and intercept of 0.837 and 0.680, yielding very similar results to those obtained by Malicki and Walczak in their work. With some limitations, the model by Malicki and Walczak might therefore be used in capacitance applications as well as TDR [21] and frequency-domain reflectometry [10].
Hilhorst validated his model in a much lower ECp range than the one used in this work. Hilhorst actually indicated the validity upper bound for the probe used in his work as 3 dS·m−1. Indeed, in the present study the model showed good performances in the 0–3 dS·m−1 range. Moreover, calibrating the model for ECp <10 dS·m−1 would suitably yield a RMSE of 0.68 dS·m−1 with an observed-estimated relationship having a slope and an intercept of 0.957 and 0.127, respectively. Most likely, the higher operating frequency of 5TE compared to the capacitive probe used by Hilhorst (i.e., 30 MHz) could have increased the range of model validity. However, as stated by Hilhorst, the model assumptions cease to be valid at higher salt concentrations as εp significantly deviates from that of free water (Equation (7)). From the experiment presented here this limit seems to be ECp ∼ 10 dS·m−1.
The comparison of the error distribution at different ECp ranges showed that Rhoades and Archie did not give significantly different performances. Nevertheless, the Rhoades model showed a larger RMSE at high ECp values than at low ones (ECp < 10 dS·m−1: RMSE = 0.78 dS·m−1; ECp > 10 dS·m−1: RMSE = 1.17 dS·m−1). On the other hand, the Archie model showed a greater consistency over the two salinity ranges (ECp < 10 dS·m−1: RMSE = 0.69 dS·m−1; ECp > 10 dS·m−1: RMSE = 0.54 dS·m−1).
4.3. Simultaneous Calibration of Models for θ and ECp
As reported above, the “general” formulations of Rhoades and Archie showed overall similar performances. As already stated experimental θ values were used in the two equations. A simultaneous calibration was then done estimating ECp and θ from ECa and εr readings by substituting the “general” logarithmic θ model (Equation (15)) within Rhoades and Archie “general” models. The W1 weight (Equation (12)) was set to 0.5, thus improving the ECp estimation without notably worsening the θ evaluation.
The combined logarithmic θ model and Rhoades reads:
Similarly, the combined logarithmic θ model and Archie becomes:
The calibration of Equation (22) yielded RSME values for θ and ECp of 0.048 m3·m−3 and 0.77 dS·m−1, respectively. Better overall results were obtained by Equation (26): RMSE = 0.046 m3·m−3 and RMSE = 0.63 dS·m−1 for θ and ECp, respectively. It is worth noting that the simultaneously calibrated parameters were very close to the independently calibrated ones.
A bootstrap validation was done on the simultaneous calibrations. A total of 5,000 iterations were operated for both Equations (22) and (26). Table 4 shows the variations of the slope and intercept of the fitting linear regression between observed and predicted values. Soil water content was correctly predicted by both the equations: the slope and intercept medians of the observed-estimated relationships were fairly close to 1 and 0, respectively. ECp predictions were less accurate, generally overestimated by Equation (22) and underestimated by Equation (26) (Table 4).
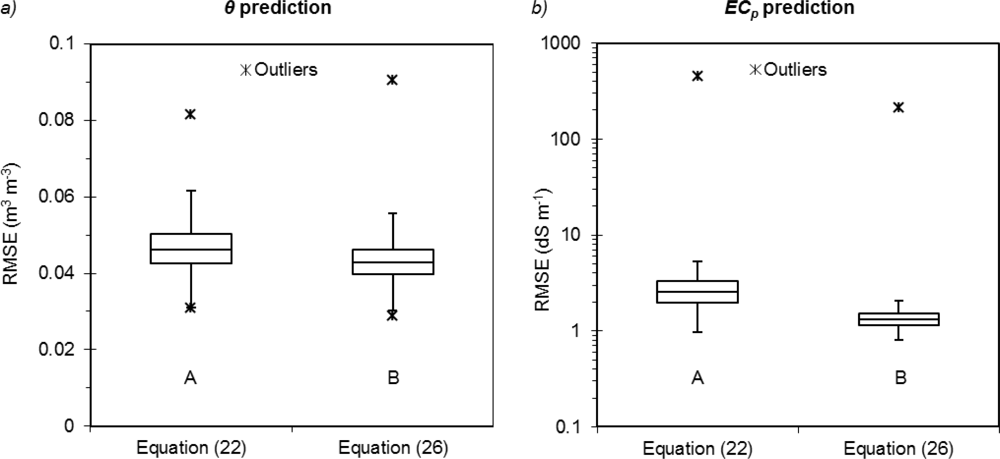
According to the Kolmogorov-Smirnov test, significant differences were observed between the two equations. The Archie-based model provided significantly lower RMSE values on the validation sets for both θ (p < 0.01) and ECp (p < 0.01) (Figure 5(a,b)). Equations (22) or (26) provided similar maximum errors for water content, with maximum RMSE of 0.08 m3·m−3 and 0.09 m3·m−3, respectively. On the other hand, Equation (22) produced a maximum ECp error higher than that of Equation (26) (451.42 dS·m−1vs. 211.26 dS·m−1). The overall more accurate prediction of the system implementing Archie can be justified by the more flexible functional form of the ECp model allowed by the two exponential parameters.
5. Summary and Conclusions
Low-cost capacitance-resistance multiprobe sensors are becoming popular for agro-environmental studies. In order to obtain reliable results, robust models for soil water content and pore-water electrical conductivity must be calibrated in different soil and climatic conditions, especially when these instruments are used in coastal areas with contrasting soils and affected by saltwater contamination.
This experiment verifies the possibility of simultaneously quantifying water content and pore-water electrical conductivity from complex permittivity, bulk electrical conductivity, and soil temperature measurements performed by the ECH2O-5TE (Decagon Devices, Inc.) probe. This result was achieved by improving empirical/theoretical reference models with the use of parameters dependent on physical and chemical soil properties, such as texture, soil organic carbon and soil carbonates. The improved models, in particular the one developed starting from Archie’s law, prove to be reliable and robust over a wide range of water content (from dry to saturated conditions), salinity conditions (pore-water electrical conductivity from 0 to ∼20 dS·m−1), and soil types (from sand with low SOC to clay-loam with high SOC).
Further studies performed in different soil and climatic environment coupled with improved dielectric sensors (e.g., with higher operating frequencies) will allow the accuracy of soil water content and pore-water salinity determination to be increased.
Symbols
| θ | volumetric water content |
| εr | soil complex permittivity |
| ECa | bulk electrical conductivity |
| ECp | pore-water electrical conductivity |
| ECw | electrical conductivity of the solution used to wet the soil |
| ECs | electrical conductivity of the solid phase |
| ECe | electrical conductivity of aqueous extract of saturated soil-paste |
Acknowledgments
This study was funded within the Research Programme “GEO-RISKS: Geological, Morphological and Hydrological Processes: Monitoring, Modelling and Impact in the North-Eastern Italy”, WP4, the University of Padova, Italy.
References
- Rhoades, J.D.; Chanduvi, F.; Lesch, S.M. Soil Salinity Assessment: Methods and Interpretation of Electrical Conductivity Measurements; Food & Agriculture Organization of the UN (FAO): Rome, Italy, 1999. [Google Scholar]
- Richards, L.A.; US Salinity Laboratory Staff. USDA Handbook No. 60. Diagnosis and Improvement of Saline and Alkali Soils; U.S. Government Printing Office: Washington, DC, USA, 1954. [Google Scholar]
- Fares, A.; Polyakov, V. Advances in Crop Water Management using Capacitive Water Sensors. Adv. Agron 2006, 90, 43–77. [Google Scholar]
- Topp, G.C.; Davis, J.L.; Annan, A.P. Electromagnetic Determination of Soil Water Content: Measurements in Coaxial Transmission Lines. Water Resour. Res 1980, 16, 574–582. [Google Scholar]
- Rosenbaum, U.; Huisman, J.A.; Vrba, J.; Vereecken, H.; Bogena, H.R. Correction of Temperature and Electrical Conductivity Effects on Dielectric Permittivity Measurements with ECH2O Sensors. Vadose Zone J 2011, 10, 582–593. [Google Scholar]
- Kelleners, T.J.; Soppe, R.W.O.; Robinson, D.A.; Schaap, M.G.; Ayars, J.E.; Skaggs, T.H. Calibration of Capacitance Probe Sensors Using Electric Circuit Theory. Soil Sci. Soc. Am. J 2004, 68, 430–439. [Google Scholar]
- Kelleners, T.; Soppe, R.; Ayars, J.; Skaggs, T. Calibration of Capacitance Probe Sensors in a Saline Silty Clay Soil. Soil Sci. Soc. Am. J 2004, 68, 770–778. [Google Scholar]
- Saito, T.; Fujimaki, H.; Inoue, M. Calibration and Simultaneous Monitoring of Soil Water Content and Salinity with Capacitance and Four-Electrode Probes. Am. J. Environ. Sci 2008, 4, 683–692. [Google Scholar]
- Friedman, S.P. Soil Properties Influencing Apparent Electrical Conductivity: A Review. Comput. Electron. Agric 2005, 46, 45–70. [Google Scholar]
- Wilczek, A.; Szypłowska, A.; Skierucha, W.; Cieśla, J.; Pichler, V.; Janik, G. Determination of Soil Pore Water Salinity Using an FDR Sensor Working at Various Frequencies up to 500 MHz. Sensors 2012, 12, 10890–10905. [Google Scholar]
- Schwank, M.; Green, T.R. Simulated Effects of Soil Temperature and Salinity on Capacitance Sensor Measurements. Sensors 2007, 7, 548–577. [Google Scholar]
- Pardossi, A.; Incrocci, L.; Incrocci, G.; Malorgio, F.; Battista, P.; Bacci, L.; Rapi, B.; Marzialetti, P.; Hemming, J.; Balendonck, J. Root Zone Sensors for Irrigation Management in Intensive Agriculture. Sensors 2009, 9, 2809–2835. [Google Scholar]
- Allred, B.J.; Groom, D.; Reza Eshani, M.; Daniels, J.J. Resistivity Methods. In Handbook of Agricultural Geophysics; Allred, B.J., Daniels, J.J., Reza Ehsani, M., Eds.; CRC Press, Taylor & Francis Group: New York, NY, USA, 2008; pp. 85–108. [Google Scholar]
- Corwin, D.L. Past, Present, and Future Trends of Soil Electrical Conductivity Measurements Using Geophysical Methods. In Handbook of Agricultural Geophysics; Allred, B.J., Daniels, J.J., Reza Eshani, M., Eds.; CRC Press, Taylor & Francis Group: New York, NY, USA, 2008; pp. 17–44. [Google Scholar]
- Dalton, F.N.; Herkelrath, W.N.; Rawlins, D.S.; Rhoades, J.D. Time-Domain Reflectometry: Simultaneous Measurement of Soil Water Content and Electrical Conductivity with a Single Probe. Science 1984, 224, 989–990. [Google Scholar]
- Rhoades, J.D.; Raats, P.A.C.; Prather, R.J. Effects of Liquid-Phase Electrical Conductivity, Water Content, and Surface Conductivity on Bulk Soil Electrical Conductivity. Soil Sci. Soc. Am. J 1976, 40, 651–655. [Google Scholar]
- Rhoades, J.; Manteghi, N.A.; Shouse, P.; Alves, W. Estimating Soil Salinity from Saturated Soil-Paste Electrical Conductivity. Soil Sci. Soc. Am. J 1989, 53, 428–433. [Google Scholar]
- Mualem, Y.; Friedman, S.P. Theoretical Prediction of Electrical Conductivity in Saturated and Unsaturated Soil. Water Resour. Res 1991, 27, 2771–2777. [Google Scholar]
- Heimovaara, T.J.; Focke, A.G.; Bouten, W.; Verstraten, J.M. Assessing Temporal Variations in Soil Water Composition with Time Domain Reflectometry. Soil Sci. Soc. Am. J 1995, 59, 689–698. [Google Scholar]
- Hilhorst, M.A. A Pore Water Conductivity Sensor. Soil Sci. Soc. Am. J 2000, 64, 1922–1925. [Google Scholar]
- Malicki, M.A.; Walczak, R.T. Evaluating Soil Salinity Status from Bulk Electrical Conductivity and Permittivity. Eur. J. Soil Sci 1999, 50, 505–514. [Google Scholar]
- Archie, G.E. The Electrical Resistivity Log as an Aid in Determining Some Reservoir Characteristics. Trans. AIME 1942, 5, 54–62. [Google Scholar]
- Persson, M. Evaluating the Linear Dielectric Constant-Electrical Conductivity Model Using Time-Domain Reflectometry. Hydrol. Sci. J 2002, 47, 269–277. [Google Scholar]
- Amente, G.; Baker, J.M.; Reece, C.F. Estimation of Soil Solution Electrical Conductivity from Bulk Soil Electrical Conductivity in Sandy Soils. Soil Sci. Soc. Am. J 2000, 64, 1931–1939. [Google Scholar]
- Hamed, Y.P.; Magnus Berndtsson, R. Soil Solution Electrical Conductivity Measurements Using Different Dielectric Techniques. Soil Sci. Soc. Am. J 2003, 67, 1071–1078. [Google Scholar]
- Bogena, H.R.; Herbst, M.; Huisman, J.A.; Rosenbaum, U.; Weuthen, A.; Vereecken, H. Potential of Wireless Sensor Networks for Measuring Soil Water Content Variability. Vadose Zone J 2010, 9, 1002–1113. [Google Scholar]
- Campbell, G.S.; Greenway, W.C. Moisture Detection Apparatus and Method. U.S. Patent 6904789. 14 June 2005. [Google Scholar]
- Kizito, F.; Campbell, C.S.; Campbell, G.S.; Cobos, D.R.; Teare, B.L.; Carter, B.; Hopmans, J.W. Frequency, Electrical Conductivity and Temperature Analysis of a Low-Cost Capacitance Soil Moisture Sensor. J. Hydrol 2008, 352, 367–378. [Google Scholar]
- Scudiero, E.; Deiana, R.; Teatini, P.; Cassiani, G.; Morari, F. Constrained Optimization of Spatial Sampling in Salt Contaminated Coastal Farmland Using EMI and Continuous Simulated Annealing. Proc. Environ. Sci 2011, 7, 234–239. [Google Scholar]
- Keesstra, S.; Geissen, V.; Mosse, K.; Piiranen, S.; Scudiero, E.; Leistra, M.; van Schaik, L. Soil as a Filter for Groundwater Quality. Curr. Opin. Environ. Sustain. 2012, 7. [Google Scholar] [CrossRef]
- Sumner, M.E.; Miller, W.P.; Sparks, D.L.; Page, A.L.; Helmke, P.A.; Loeppert, R.H.; Soltanpour, P.N.; Tabatabai, M.A.; Johnston, C.T. Cation Exchange Capacity and Exchange Coefficients. In Methods of Soil Analysis. Part 3-Chemical Methods; SSSA and ASA: Madison, WI, USA, 1996; pp. 1201–1229. [Google Scholar]
- Blake, G.; Hartge, K. Particle Density. In Methods of Soil Analysis. Part 1. Agronomy Monographs 9; Klute, A., Ed.; ASA: Madison, WI, USA, 1986; pp. 377–382. [Google Scholar]
- Gattacceca, J.C.; Vallet-Coulomb, C.; Mayer, A.; Claude, C.; Radakovitch, O.; Conchetto, E.; Hamelin, B. Isotopic and Geochemical Characterization of Salinization in the Shallow Aquifers of a Reclaimed Subsiding Zone: The Southern Venice Lagoon Coastland. J. Hydrol 2009, 378, 46–61. [Google Scholar]
- Wolt, J.G.; John, G. A Rapid Routine Method for Obtaining Soil Solution Using Vacuum Displacement. Soil Sci. Soc. Am. J 1986, 50, 602–605. [Google Scholar]
- Jones, S.B.; Blonquist, J.M., Jr.; Robinson, D.A.; Rasmussen, V.P.; Or, D. Standardizing Characterization of Electromagnetic Water Content Sensors: Part 1. Methodology. Vadose Zone J 2005, 4, 1048–1058. [Google Scholar]
- Saito, T.; Fujimaki, H.; Yasuda, H.; Inoue, M. Empirical Temperature Calibration of Capacitance Probes to Measure Soil Water. Soil Sci. Soc. Am. J 2009, 73, 1931–1937. [Google Scholar]
- Blonquist, J.M., Jr.; Jones, S.B.; Robinson, D.A. Standardizing Characterization of Electromagnetic Water Content Sensors: Part 2. Evaluation of Seven Sensing Systems. Vadose Zone J 2005, 4, 1059–1069. [Google Scholar]
- Seyfried, M.; Murdock, M. Response of a New Soil Water Sensor to Variable Soil, Water Content, and Temperature. Soil Sci. Soc. Am. J 2001, 65, 28–34. [Google Scholar]
- Akaike, H. A New Look at the Statistical Model Identification. IEEE Trans. Autom. Contr 1974, 19, 716–723. [Google Scholar]
- Burnham, K.P.; Anderson, D.R. Model Selection and Multi-Model Inference: A Practical Information-Theoretic Approach; Springer: New York, NY, USA, 2002. [Google Scholar]
- Rhoades, J.; Manteghi, N.; Shouse, P.; Alves, W. Soil Electrical Conductivity and Soil Salinity: New Formulations and Calibrations. Soil Sci. Soc. Am. J 1989, 53, 433–439. [Google Scholar]
- Waxman, M.; Smits, L. 1863-A-Electrical Conductivities in Oil-Bearing Shaly Sands. SPE 1968, 8, 107–122. [Google Scholar]
- Monego, M.; Cassiani, G.; Deiana, R.; Putti, M.; Passadore, G.; Altissimo, L. A Tracer Test in a Shallow Heterogeneous Aquifer Monitored via Time-Lapse Surface Electrical Resistivity Tomography. Geophysics 2010, 75, WA61. [Google Scholar]
- Van Genuchten, M.T.; Leij, F.; Yates, S. The RETC Code for Quantifying the Hydraulic Functions of Unsaturated Soils; EPA: Ada, OK, USA, 1991. [Google Scholar]
- Efron, B. Bootstrap Methods: Another Look at the Jackknife. Ann. Statist 1979, 7, 1–26. [Google Scholar]
- Barber, S.A. Soil Nutrient Bioavailability: A Mechanistic Approach; John Wiley & Sons Inc: New York, NY, USA, 1995. [Google Scholar]
- Giardini, L.; Berti, A.; Morari, F. Simulation of Two Cropping Systems with EPIC and CropSyst Models. Ital. J. Agron 1998, 1, 29–38. [Google Scholar]
| Soil Sample | Sand (%) | Silt (%) | Clay (%) | Total C (%) | SOC (%) | CEC (meq·g−1) | pH | ρr (g·cm−3) | ρb (g·cm−3) | ECe (dS·m−1) | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| A | Topsoil | 40.92 | 41.31 | 17.77 | 15.50 | 14.78 | 0.57 | 5.60 | 1.90 | 0.87 | 0.61 |
| A | Subsoil | 17.47 | 52.66 | 29.87 | 4.30 | 3.96 | 0.12 | 5.89 | 2.28 | 1.08 | 6.38 |
| B | Topsoil | 50.54 | 37.61 | 11.85 | 6.64 | 5.78 | 0.33 | 7.23 | 2.32 | 1.07 | 1.42 |
| B | Subsoil | 90.52 | 7.71 | 1.77 | 4.26 | 1.54 | 0.05 | 7.68 | 2.62 | 1.29 | 2.26 |
| C | Topsoil | 29.61 | 48.46 | 21.93 | 9.84 | 8.36 | 0.45 | 7.58 | 2.21 | 0.93 | 2.05 |
| Model | RMS | K | AIC | Di | WAIC |
|---|---|---|---|---|---|
| Hyperbolic | 0.015 | 21 | −301.61 | 104 | 2.11 × 10−23 |
| Logistic | 0.002 | 42 | −391.41 | 15 | 6.69 × 10−4 |
| Logarithmic | 0.001 | 41 | −406.03 | 0 | 1.000 |
| Equation (15) | Equation (5) | Equation (6) | Equation (19) | Equation (10) | ||||
|---|---|---|---|---|---|---|---|---|
| a′ | a″ | l | εECa = 0 | e | f | m | n | |
| Sand | 0.25 | 0.76 | 1.00 | −0.60 | −0.68 | 0.73 | −0.79 | 1.00 |
| Clay | −0.14 | −0.8 | −0.98 | 0.51 | 0.59 | −0.62 | 0.66 | −0.97 |
| Clay/Sand | 0.23 | −0.89 | −0.82 | 0.20 | 0.45 | −0.43 | 0.31 | −0.79 |
| SOC | −0.98 | 0.30 | −0.40 | 0.94 | 0.36 | −0.48 | 0.78 | −0.46 |
| CaCO3 | 0.26 | 0.58 | 0.85 | −0.73 | −0.95 | 0.96 | −0.75 | 0.84 |
| Slope | Intercept | |||||
|---|---|---|---|---|---|---|
| Median | 5% Limit | 95% Limit | Median | 5% Limit | 95% Limit | |
| θ | ||||||
| Rhoades (Equation (22)) | 0.97 | 0.89 | 1.02 | 0.01 | −0.01 | 0.04 |
| Archie (Equation (26)) | 0.98 | 0.91 | 1.04 | 0.01 | −0.01 | 0.03 |
| ECp | ||||||
| Rhoades (Equation (22)) | 1.15 | 0.98 | 1.31 | 0.13 | −0.13 | 0.39 |
| Archie (Equation (26)) | 0.93 | 0.88 | 1.03 | 0.32 | 0.11 | 0.53 |
© 2012 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Scudiero, E.; Berti, A.; Teatini, P.; Morari, F. Simultaneous Monitoring of Soil Water Content and Salinity with a Low-Cost Capacitance-Resistance Probe. Sensors 2012, 12, 17588-17607. https://doi.org/10.3390/s121217588
Scudiero E, Berti A, Teatini P, Morari F. Simultaneous Monitoring of Soil Water Content and Salinity with a Low-Cost Capacitance-Resistance Probe. Sensors. 2012; 12(12):17588-17607. https://doi.org/10.3390/s121217588
Chicago/Turabian StyleScudiero, Elia, Antonio Berti, Pietro Teatini, and Francesco Morari. 2012. "Simultaneous Monitoring of Soil Water Content and Salinity with a Low-Cost Capacitance-Resistance Probe" Sensors 12, no. 12: 17588-17607. https://doi.org/10.3390/s121217588
APA StyleScudiero, E., Berti, A., Teatini, P., & Morari, F. (2012). Simultaneous Monitoring of Soil Water Content and Salinity with a Low-Cost Capacitance-Resistance Probe. Sensors, 12(12), 17588-17607. https://doi.org/10.3390/s121217588





