The features are derived from the multilook coherence matrix of the PolSAR data [5]. Suppose: (1) S   =   [ S h h S h v S v h S v v ]   =   [ S h h S h v S h v S v v ]stands for the measured scattering matrix. Here S_qp represents the scattering coefficients of the targets, p the polarization of the incident field, q the polarization of the scattered field. S_hv equals to S_vh since reciprocity applies in a monostatic system configuration.

The Pauli decomposition expresses the scattering matrix S in the so-called Pauli basis, which is given by the following three 2 × 2 matrices: (2) S a   =   1 2 [ 1 0 0 1 ] ,   S b   =   1 2 [ 1 0 0 − 1 ] ,   S c   =   1 2 [ 0 1 1 0 ]

Thus, S can be expressed as: (3) S   =   a S a   +   b S b   +   c S cwhere: (4) a   =   S h h   +   S v v 2 ,   b   =   S h h   −   S v v 2 ,   c   =   2 S h v

An RGB image could be formed with the intensities |a|², |b|², |c|². The meanings of S_a, S_b, and S_c are listed in Table 1.

The coherence matrix is obtained as [16]: (5) T   =   [ a ,   b ,   c ] [ a ,   b ,   c ] T   =   [ T 11 T 12 T 13 T 12 * T 22 T 23 T 13 * T 23 * T 33 ]

The average of multiple single-look coherence matrices is the multi-look coherence matrix. (T₁₁, T₂₂, T₃₃) usually are regarded as the channels of the PolSAR images.

The span or total scattered power is given by: (6) M   =   | S h h | 2   +   | S v v | 2   +   2 | S h v | 2which indicates the power received by a fully polarimetric system.

H/A/α decomposition is designed to identify in an unsupervised way polarimetric scattering mechanisms in the H-α plane [5]. The method extends the two assumptions of traditional ways [17]: (1) azimuthally symmetric targets; (2) equal minor eigenvalues λ₂ and λ₃. T can be rewritten as: (7) T   =   U 3   [ λ 1 0 0 0 λ 2 0 0 0 λ 3 ]   U 3 Hwhere: (8) U 3   =   [ cos   α 1 cos   α 2 cos   α 3 sin   α 1   cos   β 1   exp ( i δ 1 ) sin   α 2   cos   β 2   exp ( i δ 2 ) sin   α 3   cos   β 3   exp ( i δ 3 ) sin   α 1   sin   β 1   exp ( i γ 1 ) sin   α 2   sin   β 2   exp ( i γ 2 ) sin   α 3   sin   β 3   exp ( i γ 3 ) ]

Then, the pseudo-probabilities of the T matrix expansion elements are defined as: (9) P i   =   λ ∑ j = 1 3 λ j

The entropy [18] indicates the degree of statistical disorder of the scattering phenomenon. It can be defined as: (10) H   =   ∑ i = 1 3 − P i   log 3   P i   0   ≤   H   ≤   1

For high entropy values, a complementary parameter (anisotropy) [1] is necessary to fully characterize the set of probabilities. The anisotropy is defined as the relative importance of the second scattering mechanisms [19]: (11) A   =   P 2   −   P 3 P 2   +   P 3   0   ≤   A   ≤   1

The four estimates of the angles are easily evaluated as: (12) [ α ¯ ,   β ¯ ,   δ ¯ ,   γ ¯ ]   =   ∑ i = 1 3 P i [ α ,   β ,   δ ,   γ ]

Thus, vectors from coherence matrix can be represented as (H, A, ᾱ, β̄, δ̄, γ̄).

Gray level co-occurrence matrix (GLCM) is a text descriptor which takes into account the specific position of a pixel relative to another. The GLCM is a matrix whose elements correspond to the relative frequency of occurrence of pairs of gray level values of pixels separated by a certain distance in a given direction [20]. Formally, the elements of a GLCM G(i,j) for a displacement vector (a,b) is defined as: (13) G   ( i ,   j )   =   | { ( x ,   y ) ,   ( t ,   v )   :   I ( r ,   s )   =   i   &   I ( t ,   v )   =   j } |where (t,v) = (x + a, y + b), and |•| denotes the cardinality of a set. The displacement vector (a,b) can be rewritten as (d, θ) in polar coordinates.

GLCMs are suggested to be calculated from four displacement vectors with d = 1 and θ = 0°, 45°, 90°, and 135° respectively. In this study, the (a, b) are chosen as (0,1), (−1,1), (−1,0), and (−1,–1) respectively, and the corresponding GLCMs are averaged. The four features are extracted from normalized GLCMs, and their sum equals to 1. Suppose the normalized GLCM value at (i,j) is p(i,j), and their detailed definition are listed in Table 2.

The texture features consist of 4 GLCM-based features, which should be multiplied by 3 since there are three channels (T₁₁, T₂₂, T₃₃). In addition, there are one span feature, and six H/α parameters. In all, the number of total features is 1 + 6 + 4 × 3 = 19.

PCA is an efficient tool to reduce the dimension of a data set consisting of a large number of interrelated variables while retaining most of the variations. It is achieved by transforming the data set to a new set of ordered variables according to their variances or importance. This technique has three effects: It orthogonalizes the components of the input vectors so that uncorrelated with each other, it orders the resulting orthogonal components so that those with the largest variation come first, and eliminates those components contributing the least to the variation in the data set [21].

More specifically, for a given n-dimensional matrix n × m, where n and m are the number of variables and the number of temporal observations, respectively, the p principal axes (p ≪ n) are orthogonal axes, onto which the retained variance is maximal in the projected space. The PCA describes the space of the original data projecting onto the space in a base of eigenvectors. The corresponding eigenvalues account for the energy of the process in the eigenvector directions. It is assumed that most of the information in the observation vectors is contained in the subspace spanned by the first p principal components. Considering data projection restricted to p eigenvectors with the highest eigenvalues, an effective reduction in the input space dimensionality of the original data can be achieved with minimal information loss. Reducing the dimensionality of the n dimensional input space by projecting the input data onto the eigenvectors corresponding to the first p eigenvalues is an important step that facilitates subsequent neural network analysis [22].

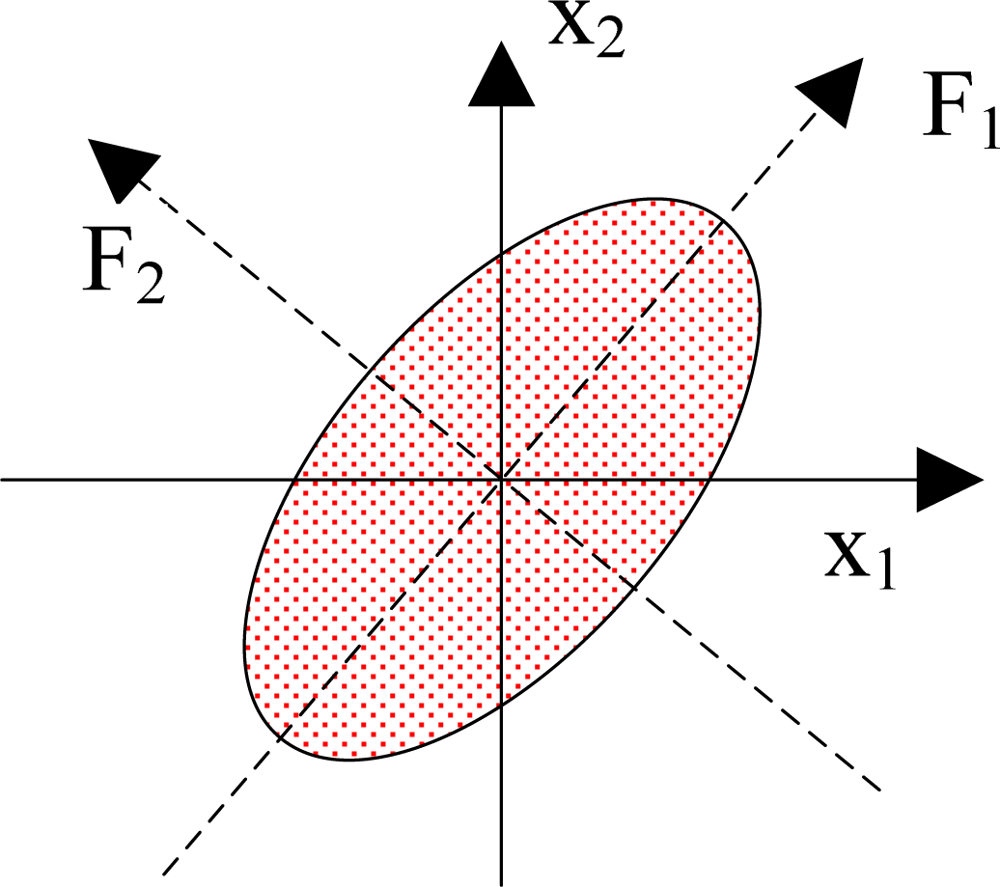
The detailed steps of PCA are as follows: (1) organize the dataset; (2) calculate the mean along each dimension; (3) calculate the deviation; (4) find the covariance matrix; (5) find the eigenvectors and eigenvalues of the covariance matrix; (6) sort the eigenvectors and eigenvalues; (7) compute the cumulative energy content for each eigenvector; (8) select a subset of the eigenvectors as the new basis vectors; (9) convert the source data to z-scores; (10) project the z-scores of the data onto the new basis. Figure 1 shows a geometric illustration of PCA. Here the original basis is {x₁, x₂}, and the new basis is {F₁, F₂}. After the data was projecting onto the new basis, we can find that the data focused along the first dimension of the new basis.

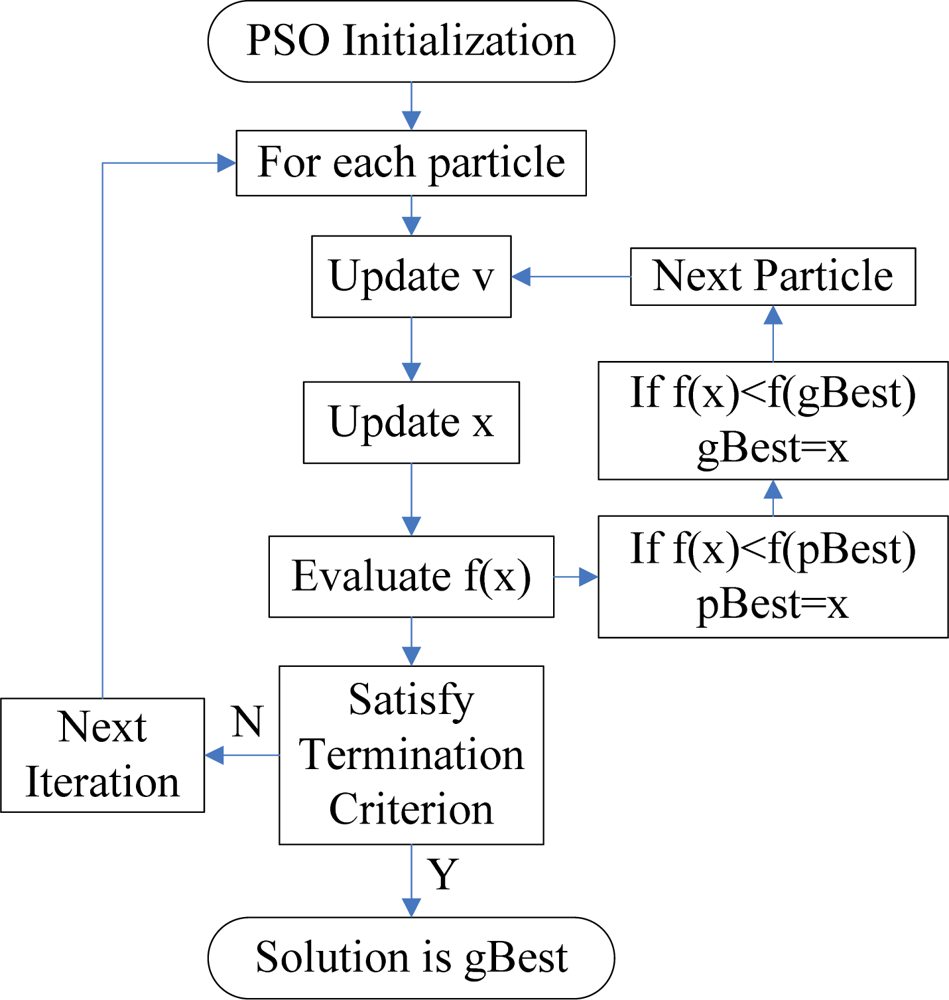
The traditional NN training method can easily be trapped into the local minima, and the training procedures take a long time [24]. In this study, PSO is chosen to find the optimal parameters of the neural network. PSO is a population based stochastic optimization technique, which is based on simulating the social behavior of swarm of bird flocking, bees, and fish schooling. By randomly initializing the algorithm with candidate solutions, the PSO successfully leads to a global optimum [25]. This is achieved by an iterative procedure based on the processes of movement and intelligence in an evolutionary system. Figure 3 shows the flow chart of a PSO algorithm.

In PSO, each potential solution is represented as a particle. Two properties (position x and velocity v) are associated with each particle. Suppose x and v of the ith particle are given as [26]: (14) x   =   ( x i 1 ,   x i 2 ,   ⋯ ,   x i N ) (15) v   =   ( v i 1 ,   v i 2 ,   ⋯ ,   v i N )where N stands for the dimensions of the problem. In each iteration, a fitness function is evaluated for all the particles in the swarm. The velocity of each particle is updated by keeping track of two best positions. One is the best position a particle has traversed so far. It is called “pBest”. The other is the best position that any neighbor of a particle has traversed so far. It is a neighborhood best and is called “nBest”. When a particle takes the whole population as its neighborhood, the neighborhood best becomes the global best and is accordingly called “gBest”. Hence, a particle’s velocity and position are updated as follows: (16) v   =   ω ⋅ v   +   c 1 r 1   ( p Best   −   x )   +   c 2 r 2   ( n Best   −   x ) (17) x   =   x   +   v Δ twhere ω is called the “inertia weight” that controls the impact of the previous velocity of the particle on its current one. c₁ and c₂ are positive constants, called “acceleration coefficients”. r₁ and r₂ are random numbers that are uniformly distributed in the interval [0,1]. These random numbers are updated every time when they occur. Δt stands for the given time-step and usually equals to 1.

The population of particles is then moved according to Equations (16) and (17), and tends to cluster together from different directions. However, a maximum velocity v_max, should not be exceeded by any particle to keep the search within a meaningful solution space. The PSO algorithm runs through these processes iteratively until the termination criterion is satisfied.

Let NP denotes the number of particles, each having a position x_i and a velocity v_i. Let p_i be the best known position of particle i and g be the best known position of the entire swarm. A basic PSO algorithm can be described as follows:

Step 1 Initialize every particle’s position with a uniformly distributed random vector;

In order to enhance the performance of canonical PSO, two improvements are proposed as follows. The inertia weight ω in Equation (16) affects the performance of the algorithm. A larger inertia weight pressures towards global exploration, while a smaller one pressures towards fine-tuning of current search area [27]. Thus, proper control of ω is important to find the optimum solution accurately. To deal with this shortcoming, an “adaptive inertia weight factor” (AIWF) was employed as follow: (18) ω   =   ω max   −   ( ω max   −   ω min ) / k max   ×   k

Here, ω_max denotes the maximum inertial weight, ω_min denotes the minimum inertial weight, k_max denotes the epoch when the inertial weight reaches the final minimum, and k denotes current epoch.

The parameters (r₁, r₂) were generated by pseudo-random number generators (RNG) in classical PSO. The RNG cannot ensure the optimization’s ergodicity in solution space because they are pseudo-random; therefore, we employed the Rossler chaotic operator [28] to generate parameters (r₁, r₂). The Rossler equations are as follows: (19) { d x d t   =   − ( y   +   z ) d y d t   =   x   +   a y d z d t   =   b   +   x z   −   c z

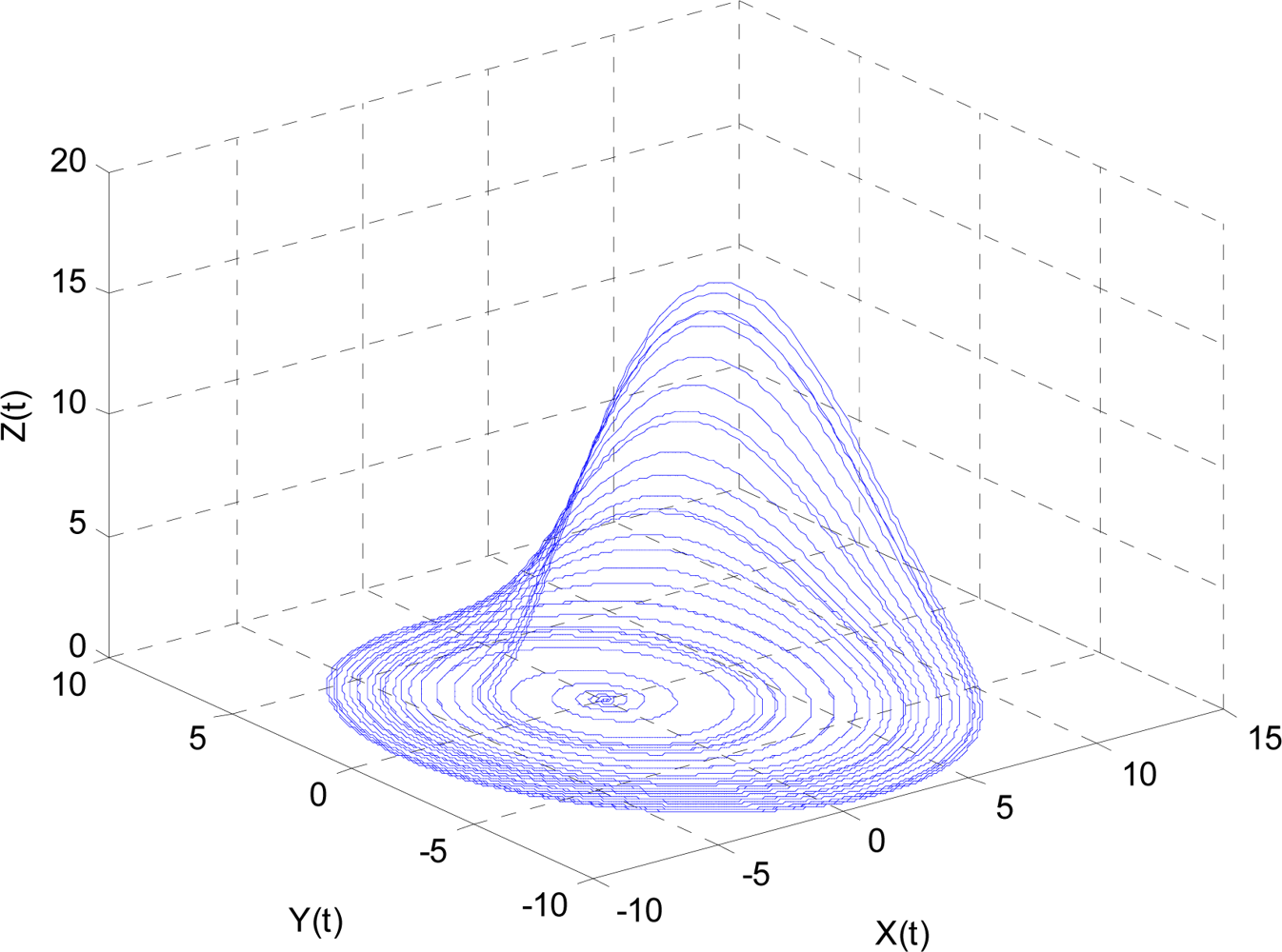
Here a, b, and c are parameters. In this study, we chose a = 0.2, b = 0.4, and c = 5.7. The results are shown in Figure 4, where the line in the 3D space exhibits a strong chaotic property called “spiral chaos”.

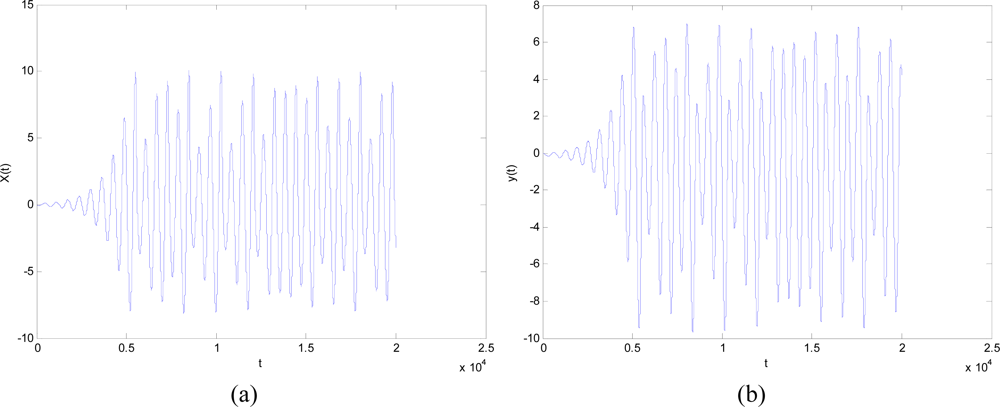
The dynamic properties of x(t) and y(t) are shown in Figure 5, where x(t) and y(t) satisfy both ergodicity and randomness. Therefore, we let r₁ = x(t) and r₂ = y(t) to embed the chaotic operator into the canonical PSO method.

There are some other chaotic PSO methods proposed in the past. Wang et al. [29] proposed a chaotic PSO to find the high precision prediction for the grey forecasting model. Chuang et al. [30] proposed a chaotic catfish PSO for solving global numeric optimization problem. Araujo et al. [31] intertwined PSO with Lozi map chaotic sequences to obtain Takagi-Sugeno fuzzy model for representing dynamic behaviors. Coelho [32] presented an efficient PSO algorithm based on Gaussian distribution and chaotic sequence to solve the reliability–redundancy optimization problems. Coelho et al. [33] presented a quantum-inspired version of the PSO using the harmonic oscillator well to solve the economic dispatch problem. Cai et al. [34] developed a multi-objective chaotic PSO method to solve the environmental economic dispatch problems considering both economic and environmental issues. Coelho et al. [35] proposed three differential evolution approaches based on chaotic sequences using logistic equation for image enhancement process. Sun et al. [36] proposed a drift PSO and applied it in estimating the unknown parameters of chaotic dynamic system.

The main difference between our ACPSO and popular PSO lies in two points: (1) we introduced in the adaptive inertia weight factor strategy; (2) we used the Rossler attractor because of the following advantages [37]: the Rossler is simpler, having only one manifold, and easier to analyze qualitatively. In total, the procedures of ACPSO are listed as follows:

Step 1 Initialize every particle’s position with a uniformly distributed random vector;

Let ω₁, ω₂, ω₃ represent the connection weight matrix between the input layer and the first hidden layer, between the first and the second hidden layer, and between the second hidden layer and the output layer, respectively. When the ACPSO is employed to train the multi-layer neural network, each particle is denoted by: (20) ω   =   [ ω 1 ,   ω 2 ,   ω 3 ]

The outputs of all neurons in the first hidden layer are calculated by following steps: (21) y 1 j   =   f H   ( ∑ i = 1 N I ω 1   ( i ,   j ) x i )   j   =   1 , 2 ,   ⋯ ,   N H 1

Here x_i denotes the ith input value, y_1j denotes the jth output of the first hidden layer, and f_H is referred to as the activation function of hidden layer. The outputs of all neurons in the second hidden layer are calculated as: (22) y 2 k   =   f H   ( ∑ j = 1 N H 1 ω 2   ( j ,   k ) y 1 j )   k   =   1 , 2 ,   ⋯ ,   N H 2where y_2j denotes the jth output of the second hidden layer.

The outputs of all neurons in the output layer are given as follows: (23) O l   =   f O   ( ∑ k = 1 N H 2 ω 3   ( k ,   l ) y 2 k )   l   =   1 ,   2 , … ,   N O

Here f_O denotes the activation function of output layer, usually a line function. All weights are assigned with random values initially, and are modified by the delta rule according to the learning samples traditionally.

The error of one sample is expressed as the MSE of the difference between its output and the corresponding target value: (24) E m   =   mse ( ∑ l = 1 N O ( O l   −   T l ) )   m   =   1 ,   2 , … N Swhere T_k represents the kth value of the authentic values which are already known to users, and N_S represents the number of samples. Suppose there are N_S samples, then the fitness value is written as: (25) F   ( ω )   =   ∑ m = 1 N S E mwhere ω represents the vectorization of the (ω₁, ω₂, ω₃). Our goal is to minimize this fitness function F(ω) by the proposed ACPSO method, viz., force the output values of each sample approximate to corresponding target values.

Cross validation methods consist of three types: Random subsampling, K-fold cross validation, and leave-one-out validation. The K-fold cross validation is applied due to its properties as simple, easy, and using all data for training and validation. The mechanism is to create a K-fold partition of the whole dataset, repeat K times to use K-1 folds for training and a left fold for validation, and finally average the error rates of K experiments. The schematic diagram of 5-fold cross validation is shown in Figure 6.

A challenge is to determine the number of folds. If K is set too large, the bias of the true error rate estimator will be small, however, the variance of the estimator will be large and the computation will be time-consuming. Alternatively, if K is set too small, the computation time will decrease, the variance of the estimator will be small, but the bias of the estimator will be large. The advantages and disadvantages of setting K large or small are listed in Table 3. In this study, K is determined as 10 through trial-and-error method.

If the model selection and true error estimation are computed simultaneously, the data needs to be divided into three disjoint sets [38]. In another word, the validation subset is used to tune the parameters of the neural network model, so another test subset is needed only to assess the performance of a trained neural network, viz., the whole dataset is divided into three subsets with different purposes listed in Table 4. The reason why the validation set and testing set cannot merge with each other lies in that the error rate estimation via the validation data will be biased (smaller than the true error rate) since the validation set is used to tune the model [39].

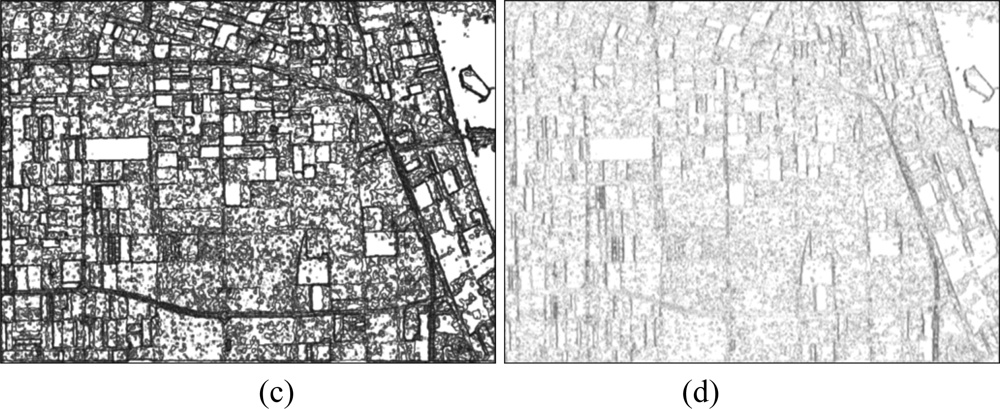
The Pauli image of Flevoland is shown in Figure 7(a), and the refine Lee filtered image (Window Size = 7) is shown in Figure 7(b).

The basic span image and three channels (T₁₁, T₂₂, T₃₃) are easily obtained and shown in Figure 8. The parameters of H/A/Alpha decomposition are shown in Figure 9. The GLCM-based parameters of T₁₁, T₂₂, T₃₃ are shown in Figures 10–12.

The curve of cumulative sum of variance with dimensions of reduced vectors via PCA is shown in Figure 13. The detailed data are listed in Table 5. It shows that only 13 features, which are only half the original features, could preserve 98.06% of variance.

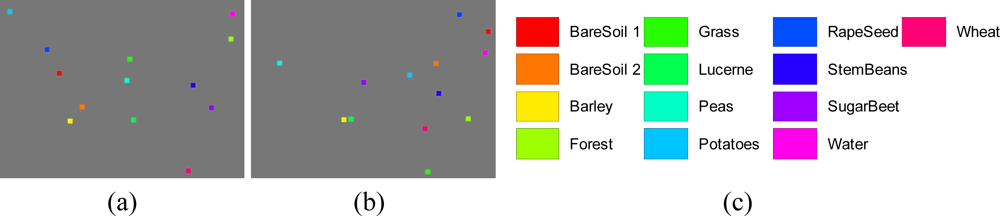
The classification is run over 13 classes, bare soil 1, bare soil 2, barley, forest, grass, lucerne, peas, potatoes, rapeseed, stem beans, sugar beet, water, and wheat. Our strategy is a semiautomatic method, viz. the training area was chosen and labeled manually. For each crop type, we choose a square of size 20 × 20, which is easy to perform since the training area size is 13 × 20 × 20 = 5,200 compared to the size of the whole image is 1,024 × 750 = 768,000. In order to reduce the complexity of experiment, the test areas are chosen randomly from rest areas [40,41], with the same square size as the training area.

The final manually selected training areas are shown in Figure 14(a). Each square corresponds to a crop type with the size of 20 × 20. In total, there are 5,200 pixels for our training. The cross validation procedures loop 10 times, therefore, each loop we use 4,680 pixels for training and the left 520 pixels for validation. The final randomly selected test areas are shown Figure 14(b). The samples numbers of training and test area are shown in Table 6.

N_I is determined as 13 due to the 13 features obtained by PCA. No is determined as 13 due to the 13 classes shown in Figure 14. Both N_H1 and N_H2 are set as 10 via the information entropy method [42]. Therefore, the number of unknown variables of the neural network is 13 × 10 + 10 + 10 × 10 + 10 + 10 × 13 + 13 = 393.

The network was trained by the proposed ACPSO algorithm, of which the parameters are obtained via trial-and-error method and shown in Table 7. Besides, BP algorithm [8], BP with momentum (MBP) [43], adaptive BP algorithm (ABP) [44], and PSO [45] are employed as comparative algorithms.

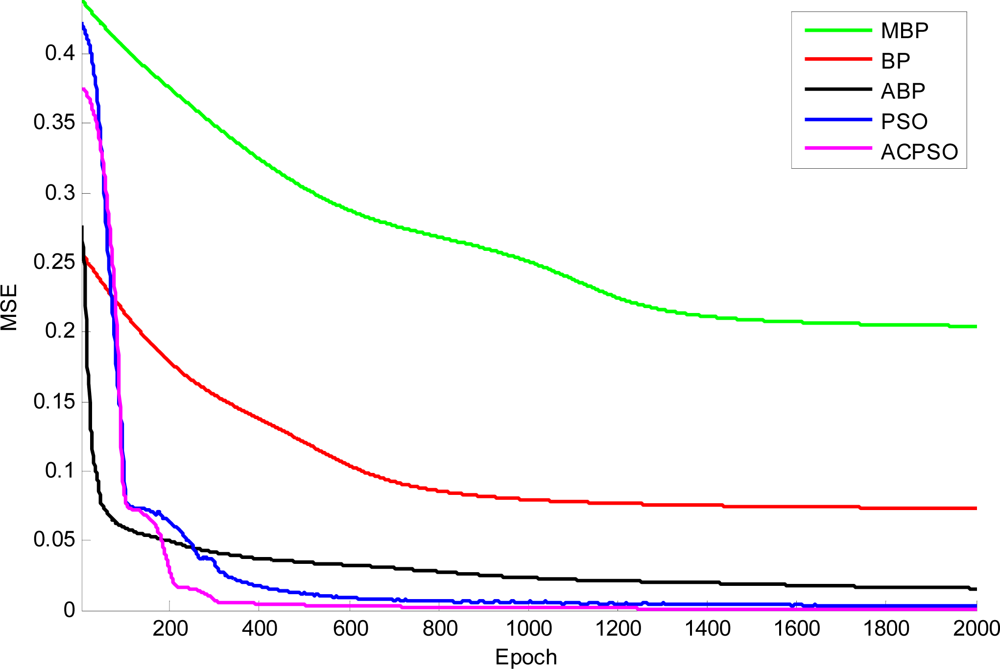
The curves of function fitness versus versus epoch of different algorithms are shown in Figure 15, indicating that the proposed ACPSO converges the most quickly and is capable of finding global minimum point.

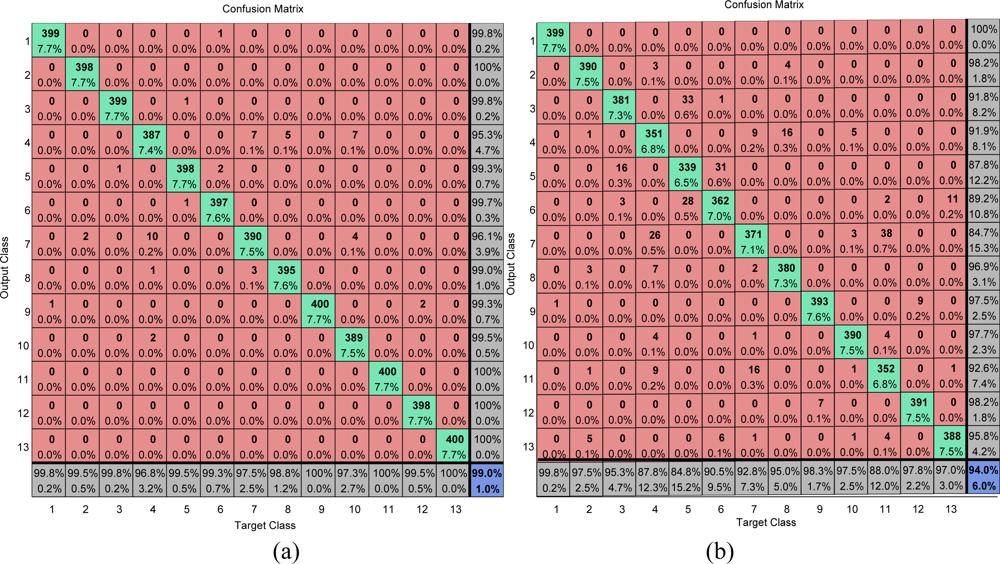
The confusion matrices on training area of our method are calculated and shown in Figure 16. The overall accuracies of our method on the training area (combining training and validation subsets) and test area are 99.0% and 94.0%, respectively. The main drawbacks are around the following four misclassifications: (I) forest zones are easily misclassified as peas; (II) grasses are easily misclassified as barley and lucerne; (III) lucerne are easily misclassified as grasses; (IV) sugarbeets are easily misclassified as peas.

A typical classification accuracy of both training area and test area by BP, ABP, MBP, and PSO are listed in Table 8, indicating that the proposed algorithm achieves the highest classification accuracy on both training (99.0%) and test area (94.0%). The random classifier disregards the information of the training data and returns random predictions, so it is usually employed to find the lowest classification rate.

Yudong also used Resilient back-propagation (RPROP) algorithm to train the neural network to classify the same Flevoland area [41], and obtains 98.62% on training area and 92.87% on test area. The PSO ranks the third with 98.1% on training area and 88.7% on test area. The ABP ranks the fourth with 90.7% and 86.4% on both training and test area, respectively. The BP and MBP performs the worst with the classification accuracy only a bit higher than the random classifier of 1/131 = 37. 69%, indicating that only 2,000 iterations are not enough for these two training strategies. Besides, the classification accuracy of the proposed algorithm was extremely high on the test area due to the 10-fold cross validation.

In order to compare the robustness of each algorithm, we perform each algorithm 50 runs and calculated the minimum, the average, and the maximum of the classification rates. The results are listed in Table 9. It indicates that the results of each algorithm changed at each run, but the variation is limited, so the rank of the performance of all algorithms is the same as that in Table 8.

Computation time is another important factor used to evaluate the classifier. The time for network training of our algorithm costs about 120 s, which can be ignored since the weights/biases of the NN remain fixed after training unless the property of images changes greatly. For example, the main crops in Flevoland are involved in the 13 types shown in Figure 14(c), therefore, the classifier can be directly used to other remote-sensing images of Flevoland without retrain. It will cost about 0.131 + 30, 0.242 + 40, 0.232 + 30, 0.181 + 80, 0.048 = 0.83 s from the input of Flevoland images (size 1,024 × 750) to the output of final classification results as shown in Table 10. For each pixel, it costs only 1.08 × 10⁻⁷s, which is fast enough for real time applications.