Secure Chaotic Map Based Block Cryptosystem with Application to Camera Sensor Networks
Abstract
: Recently, Wang et al. presented an efficient logistic map based block encryption system. The encryption system employs feedback ciphertext to achieve plaintext dependence of sub-keys. Unfortunately, we discovered that their scheme is unable to withstand key stream attack. To improve its security, this paper proposes a novel chaotic map based block cryptosystem. At the same time, a secure architecture for camera sensor network is constructed. The network comprises a set of inexpensive camera sensors to capture the images, a sink node equipped with sufficient computation and storage capabilities and a data processing server. The transmission security between the sink node and the server is gained by utilizing the improved cipher. Both theoretical analysis and simulation results indicate that the improved algorithm can overcome the flaws and maintain all the merits of the original cryptosystem. In addition, computational costs and efficiency of the proposed scheme are encouraging for the practical implementation in the real environment as well as camera sensor network.1. Introduction
Camera Sensor Networks (CSNs) are usually built with a large number of inexpensive, small and battery-powered devices. They have been used for a wide variety of applications such as environment monitoring, health monitoring, military sensing and tracking, etc. [1]. As CSNs are widely deployed in remote and hostile environments to transmit sensitive information by broadcast, sensor nodes are prone to node compromise attacks and security issues such as data confidentiality and integrity are extremely important. Hence, security becomes a very serious concern in wireless CSN protocols. Unfortunately, the sensors have limited power, computation, storage and communication capabilities, they impose several constraints on the algorithms and protocols that can be effectively deployed for such systems. In this scenario, most of the traditional security mechanisms are useless. Thus, the research of new efficient security techniques such as block and stream cipher [2,3] is needed.
As a very complicated phenomenon of nonlinear system, chaos has inherent analogous cryptographic properties such as sensitive to parameter and initial state, which inspires people to apply it into cryptography [4,5] are representative works. Since Baptista proposed a novel cryptosystem based on the property of ergodicity of chaotic systems [5], a number of new algorithms based on variations of Baptista’s one have been published [6,7]. However, most of those modified methods can’t possess both fast encryption speed and flat ciphertext distribution. To solve these problems, Xiang et al. [8] proposed a novel chaotic block cryptosystem based on [5,9,10]. Unfortunately, the sub-keys of this scheme are independent of the plaintext and are determined only by the secret key, which will cause chosen plaintext attack and differential known-plaintext attack [11,12]. Wang et al. [11] put forward an improved version by utilizing ciphertext feedback.
This paper studies the security of Wang et al. scheme and reports the following findings: (1) Without the secret key, any ciphertext can be decrypted by using only two identical length of chosen ciphertext sequences; (2) It is vulnerable to key stream attack (KSA), i.e., the underlying chaotic key stream sequence of any key (μ, x0) can be deduced from some chosen plaintext and ciphertext pairs. By utilizing the calculated chaotic key stream sequence, any ciphertext encrypted by key (μ, x0) can be decrypted efficiently. To provide an efficient cryptographic primitive and eliminate the weaknesses of Wang et al. scheme, this paper presents a modified chaotic block cryptographic algorithm on CSN. Security analysis shows that the proposed scheme is more secure than the original one. In addition, the high computational efficiency promotes its application in CSN.
The rest of this paper is organized as follows. Section 2 briefly reviews the Wang et al. scheme. Section 3 elaborates the chosen ciphertext attack (CCA) and the key stream attack (KSA). A secure chaotic block cipher in camera sensor network and its performance analysis are given in Section 4 and 5. Conclusions are drawn in Section 6.
2. Review of Wang et al. Cryptosystem
In this cryptosystem, the secret key is (μ, x0), where μ and x0 is the initial condition and control parameter of the following chaotic logistic map, respectively:
Writing the value of x in a binary representation:
A binary sequence , where n is the length of the sequence and τn (x) is the nth iteration of the logistic map, can be obtained by iterating the logistic map. The whole procedure of this scheme can be described in the following steps and an illustration is given in Figure 1.
Step 1. Get the start point ω which denotes the real value of x from the last N0 transient iterations, i.e., ω = τN0 (x0). Note that we set N0 = 100 in all the following simulations.
Step 2. Divide the plaintext P into subsequences Pj of length l bytes (here l = 8):
Step 3. Set j = 1;
Step 4. Based on the method to generate binary sequences by iterating the logistic map, obtain a 64-bit binary sequence and a 6-bit binary sequence formed by all the third bits, i.e., i = 3 in Equation (2), through 70 iterations of the logistic map. Dj is the decimal value of .
Step 5. Compute the jth ciphertext block:
where <<< and ⊕ denote the left cyclic shift and XOR operation, respectively.Step 6. Dividing the ciphertext block Cj into 8-bit partitions and obtain the ciphertext .
Step 7. If all the plaintexts have already been encrypted, the encryption process is finished. Otherwise, calculate:
and go to Step 4.
The decryption process is almost the same as the encryption one. Just need to replace Equation (4) with:
3. Cryptanalysis of Wang et al. Cryptosystem
According to Kerchoff ’s principle [13], the cryptanalyst knows exactly the design and working of the cryptosystem under study except the secret key. The general types of cryptanalytic attacks [14] are enumerated as follows, ordered from the hardest type of attack to easiest: ciphertext only attack, known plaintext attack, chosen plaintext attack and chosen ciphertext attack. In each of these four attacks, the objective is to determine the key that was used. It suffices that one of the attacks is feasible to consider an algorithm insecure.
In the following subsections, we will perform a chosen ciphertext attack (CCA) and a key stream attack (KSA) on Wang et al. scheme. For convenient illustration, suppose P = P1P2⋯Pj⋯ and C = C1C2⋯Cj⋯ are the plaintext and ciphertext pairs, (μ, x0) and K = (A1D1)(A2D2)⋯(AjDj)⋯ denote the corresponding secret key and key stream, respectively.
3.1. Chosen Ciphertext Attack
A chosen-ciphertext attack [15] operates under the following model: an adversary is allowed access to plaintext-ciphertext pairs for some number of ciphertexts of his choice, and thereafter attempts to use this information to recover the key (or plaintext corresponding to some new ciphertext).
In the Wang et al. scheme, Equations (5–7) indicate that the space of the feedback message is only 64, i.e., once the secret key (μ, x0) is determined, the key stream Dj+1 and Aj+1 are determined only by the former ciphertext f(Cj) mod 64. To illustration this security loophole, we set the secret keys μ = 4, x0 = 0.1777 and decrypt two different ciphertext sequences. They are C1=“EAFA4D22D326D40C2960D4C5E76…” and C2=“F11ED8CA5F72155E8A99683495F…” in hexadecimal format. Each block of Cj, f(Cj) mod 64, Dj and Aj are filled into Tables 1 and 2, respectively.
The simulation results indicate that once μ, x0 and all the former ciphertext blocks have equal f(Cj)mod 64, any ciphertext has identical sub-key Dj+1 and Aj+1. This loophole is vulnerable to CCA, one of CCA illustration can be played as follows: (they cannot be showed completely).
(1) Let denotes the 6-bit length of f(Cj)mod 64 in binary representation. For j = 1,2,⋯ select two cipher blocks:
From Equation (5), it is not difficult to see that:
To demonstrate this procedure, we fill the chosen corresponding C1 and C2 of a random selected ciphertext C = 218A916626 E5DA55… (in hexadecimal format) into Table 3.
(2) Decrypt and using the same key (μ, x0) of C = C1C2 ⋯Cj ⋯, then we can get the corresponding plaintext and . From Equations (6) and (12) we can deduce that Cj, and have the identical corresponding sub-keys Dj and Aj.
(3) Calculate
From Equations (10) and (11), we can obtain that:
Therefore, we can determine the value of Dj by searching the position of in .
(4) Using Equation (4) and the conquered Dj, we can calculate . To demonstrate these procedures, the chosen C1 and C2 of Table 3 are decrypted using μ = 4, x0 = 0.1777. The corresponding plaintext blocks and sub-keys are filled into Table 4.
(5) By utilizing Dj and Aj, it is easy to figure out the plaintext
Some simulations are utilized to prove the validity of CCA. Figure 2(a–c) are the original image, the encrypted image with Wang et al’s scheme and the analyzed image of a 128 × 128 bitmap image file named Boat, where the secret key μ = 4, x0 = 0.1777 and N0 = 100.
3.2. Key Stream Attack
In the Wang et al. scheme [11], although a ciphertext feedback model is employed to ensure sub-keys depend on both secret key and plaintext, a fundamental flaw is unaware, i.e., the first sub-key D1 and A1 are independent of the plaintext and are determined only by the secret key (μ, x0). An adversary can reconstruct the key stream sequence as an equivalent key (μ, x0) as follows:
Choose two pair of special messages (Pz, Cz) and (Ps, Cs), where Pz is composed of 64-bit zeros, Ps is 011…11 in binary representation, Cz and Cs are the corresponding ciphertext of Pz and Ps, respectively.
Set Pz as the first plaintext block, then can get Cz = (Pz <<< D1) ⊕ A1 = A1.
Similarly, when set Ps as the first plaintext block, Cs = (Ps <<< D1) ⊕ A1, i.e., Cs ⊕ A1 = Ps <<< D1. Thus the position of zero in Cs ⊕ A1 counting from rightmost bit is equal to D1.
Set k = 0, and define a plaintext sequence Pu = ϕ, where ϕ is a null string.
k = k + 1. By utilizing Dk, choose to make sure
From Equation (7), it can be seen that the sub-keys of , , and are continuous state bit of logistic map.
Decrypt Ck with Dk and Ak:
Set Pu = PuPk, i.e., add Pk as the last 64 bits of Pu.
Encrypt the 64(k + 1)-bit length plaintext sequence Pz = PuPz, and then obtain the corresponding ciphertext:
Obviously, is equal to C1 ⋯Ck when k > 1, and . Therefore, it can be calculated that .
Encrypt another 64(k + 1)-bit length plaintext sequence Ps = PuPs, and then obtain the corresponding ciphertext:
Similarly, is equal to C1 ⋯Ck when k > 1, and , i.e., . Utilizing the computed Ak+1, the adversary can obtain Dk+1 by counting the position of zero in from rightmost bit.
Go to (5) if the length of the key stream sequence is not enough; otherwise, finish the attack.
For j = 1,2,⋯,k, translate decimal value Dj to the corresponding 6-bit length binary sequence , and then the adversary can acquire a 70j-bit length binary key stream sequence K = (A1A1′) (A2A2′) ⋯ AjAj′ of secret key (μ, x0). We denote K = B1B2 ⋯ B70j.
The key stream K can be utilized to decrypt any ciphertext encrypted by (μ, x0). To demonstrate this circumstance, ciphertext C = C1C2 ⋯ Ci is decrypted as follows:
Define k = 1. Set the start point of kth sub-key in K = B1B2 ⋯ B70j as n = 1.
Obviously, the kth sub-key of Ck is BnBn+1 ⋯ Bn+69, i.e., Ak = BnBn+1 ⋯ Bn+63, Dk is the decimal value of A′k = Bn+64Bn+65 ⋯ Bn+69. And then we can obtain the kth plaintext block:
If k < i, continue; otherwise, finish the decryption process.
By utilizing the known Ck, Dk and Equations (5) and (6), it is easy to obtain the value of . Thus, we can utilize Equation (7) to calculate the start point of (k+1)th sub-key in K = B1B2 ⋯ B70j:
Compute k = k +1and go to (2).
As a result, C = C1C2 ⋯ Ci is decrypted effectively with key stream sequence K = B1B2 ⋯ B70j.
4. Proposed Secure Block Cipher for Camera Sensor Networks
4.1. Secure Block Cipher Algorithm
The Wang et al. cryptosystem is cryptographically weak because information about the feedback value leaks into the ciphertext and the first sub-key is independent of plaintext. Except these flaws, it has some excellent benefits, such as flat ciphertext, fast encryption speed and prominent diffusion and confusion. Therefore it is valuable to propose an improved version to get rid of above flaws. As for the first flaw, it can be remedied via hiding from ciphertext, and the latter can be conquered by pretreating of the first plaintext block. Detail of the improvement is described as follows:
Steps 1–4. They are the same as Wang et al. scheme described in Section 2.
Step 5. Compute:
Step 6. Obtain the jth ciphertext block (j ≥ 1):
Obviously, after the modified process, the feedback value is hidden from ciphertext. Encrypt Pz and Ps, then one can obtain:
Equations (26) and (27) leak noting about the key stream A1 and D1, so the security is enhanced in the improvement. Though it involves some computations, they are not time consuming operations. Therefore, the improved scheme does not lose the original efficiency advantage.
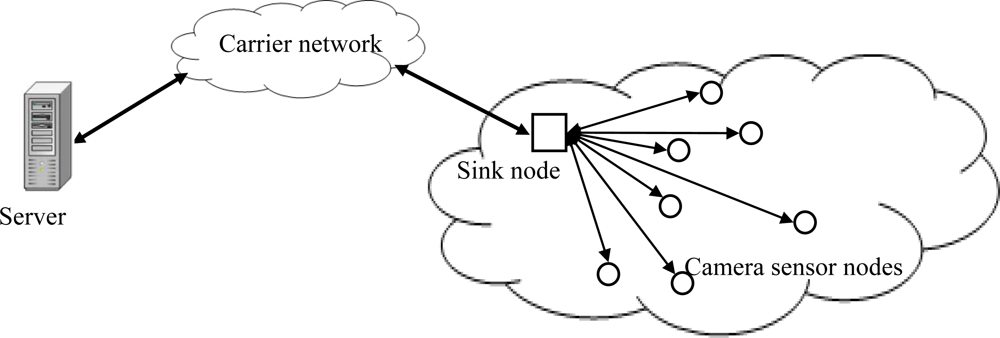
4.2. Architecture of Wireless Camera Sensor Networks
In this section, we introduce the developed architecture of the secure wireless camera sensor networks by utilizing the proposed chaotic block cipher. Each camera sensor node in the networks is battery-powered and has limited computation and wireless communication capabilities. The sink is a data collection center equipped with sufficient computation and storage capabilities. Camera sensor nodes periodically send the captured images to the sink node. Then the sink nodes transport this information secretly with the data process server via carrier networks. The proposed block cipher is mounting at the carrier network. Figure 3 shows the system architecture of the camera sensor network.
5. Performance Analysis
5.1. Information Entropy Analysis
It is known that the entropy H(m) of a message source m can be calculated by Equation (28) [8]:
When a cipher emits symbols with entropy less than N, there exists a certain degree of predictability, which threatens its security. Let us consider the ciphertext of a random text file, a Lena’s image of size 256 × 256 and a random video file encrypted using the proposed scheme. The number of occurrence of each ciphertext pixel mi is recorded and the probability of occurrence is computed for the three files. The corresponding entropies are filled into Table 5. The test values obtained are very close to the theoretical value N = 8 for the three kinds of files. This means that information leakage in the encryption process is negligible and the encryption system is secure against the entropy attack.
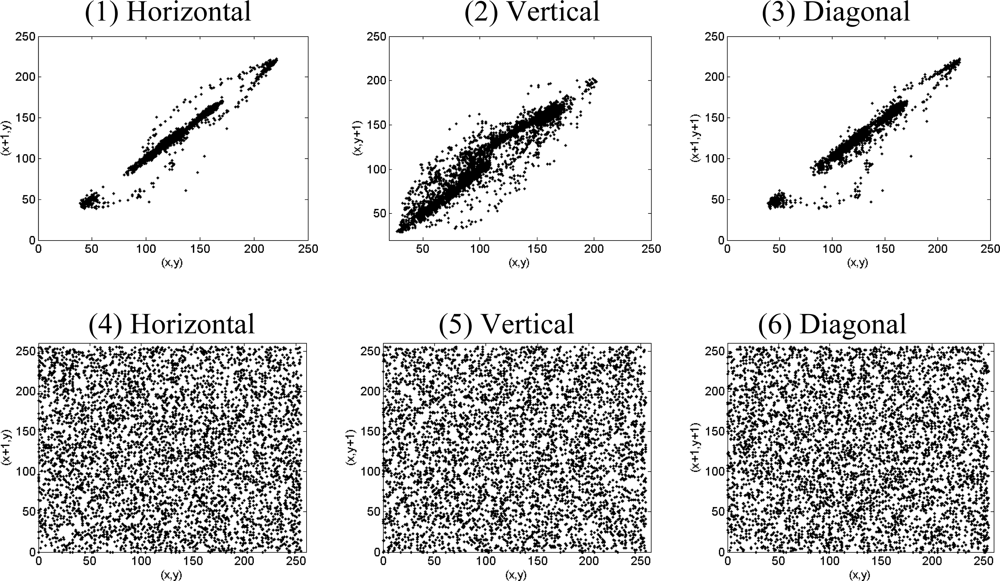
5.2. Correlation of Adjacent Pixels in Encrypted Image
In order to resist statistical attacks, the ciphertext should possess certain random properties. A detail study has been explored and the results are summarized. The results of the Lena.bmp are used for illustration. For an ordinary image, each pixel is usually highly correlated with its adjacent pixels either in horizontal, vertical or diagonal directions. These high-correlation properties can be quantified as their correlation coefficients for comparison. To calculate the correlation coefficients, the following formulas are used:
It is clear that there is negligible correlation between these two adjacent pixels in the encrypted image. However, the two adjacent pixels in the original image are highly correlated. The results indicate that the proposed algorithm has successfully removed the correlation of adjacent pixels in the plain-image so that neighbor pixels in the cipher-image virtually have no correlation. That is to say, the new scheme possesses prominent diffusion property.
5.3. Sensitivity Analysis
From the cryptographical point of view, given two distinct keys, even if their difference is the minimal value under the current finite precision, the encryption and decryption results of a good cryptosystem should still be completely different. In other words, this cryptosystem should have a very high sensitivity to the secret key [14]. For testing the key sensitivity of the proposed block encryption procedure, we use the grayscale image Lena.bmp of size 256 × 256 as the test image to illustrate the result and perform the following steps:
Lena.bmp is encrypted by using the secret key (μ = 3.998, x0 = 0.21745) and the resultant image is referred as Ciphertext A;
The same image is encrypted by making the slight modification in the secret key i.e., (μ = 3.998 + 10−15, x0 = 0.21745) and the resultant image is referred as Ciphertext B;
Again, the same original image is encrypted by making the slight modification in the secret key i.e., (μ = 3.998, x0 = 0.21745 + 10−15) and the resultant image is referred as Ciphertext C;
The same original image is encrypted by making the slight modification in the secret key i.e., (μ = 3.998, x0 = 0.21745 − 10−15) and the resultant image is referred as Ciphertext D.
Finally, the correlation coefficients between the corresponding pixels of the four ciphertexts A, B, C and D are computed and filled into Table 7.
It is clear from the Table 7 that no correlation exists among four encrypted images even though these have been produced by using slightly different secret keys. These results sufficiently demonstrate the proposed cryptosystem is highly key sensitive.
Another cryptographical property required by a good cryptosystem is that the encryption should be very sensitive to plaintext, i.e., the ciphertexts of two plaintexts with a slight difference should be very different [14]. Figure 5 is the bit-wise XOR of two ciphertexts when encrypting two image plaintexts with only the first bit different based on the proposed cryptosystem. The result of Figure 5 showing that the proposed encryption scheme is very sensitive with respect to small changes in the plaintext.
From the above investigation and study, we can conclude that the lack of security will discourage the use of these algorithms for secure applications. It is advisable that new chaotic cryptosystems take into account some important things: (1) the distribution of the ciphertext should be sufficiently flat in order to resist the statistics attack [8]; (2) the sub keys should depend on not only the secret key but also the plaintext to avoid key stream attack [11]; (3) the first block or sub key should be pretreated to resist some existing attacks; (4) the ciphertext should not leak out any information of the sub keys to eliminate corresponding utilizing ciphertext attacks.
6. Conclusions
This paper has analyzed the security of a block cipher based on logistic map proposed in [11]. It demonstrated that [11] is vulnerable to chosen ciphertext attack and key stream attack. Then it gave an enhancement version on wireless camera sensor network. Performance analysis demonstrates that the proposed scheme possesses the original benefits as well as enhancing its security. The sample procedure and efficiency of the new scheme are encouraging for the practical implementation in wireless camera sensor network.
Acknowledgments
This work described here was supported in part by the National Natural Science Foundation of China (No.60971104), the Fundamental Research Funds for the Central Universities (No. SWJTU09ZT16), the Science & Technology Key Plan Project of Chengdu (No.10GGYB649GX-023) and the Foundation of Southwest University for Nationalities (No.09NYB002 and Y-2010-08).
References and Notes
- Yick, J.; Mukherjee, B.; Ghosal, D. Wireless sensor network survey. Comp. Netw 2008, 52, 2292–2330. [Google Scholar]
- Yang, J.; Xiao, D.; Xiang, T. Cryptanalysis of a chaos block cipher for wireless sensor network. Commun. Nonlinear Sci. Numer. Sim 2011, 16, 844–850. [Google Scholar]
- Khan, M.K.; Alghathbar, K. Cryptanalysis and security improvements of “Two-Factor User Authentication in Wireless Sensor Networks”. Sensors 2010, 10, 2450–2459. [Google Scholar]
- Khan, M.K.; Xie, L.; Zhang, J. Chaos and NDFT-based concealing of fingerprint-biometric data into audio signals for trustworthy Person Authentication. Digit. Signal Process 2010, 20, 179–190. [Google Scholar]
- Baptista, M.S. Cryptography with chaos. Phy. Lett. A 1998, 240, 50–54. [Google Scholar]
- Wong, W.-K.; Lee, L.-P.; Wong, K.-W. A modified chaotic cryptographic method. Comp. Phys. Commun 2001, 138, 234–236. [Google Scholar]
- Rhouma, R.; Belghith, S. Cryptanalysis of a spatiotemporal chaotic image/video cryptosystem. Phys. Lett. A 2008, 372, 5790–5794. [Google Scholar]
- Xiang, T.; Liao, X.; Tang, G.; Chen, Y.; Wong, K. A novel block cryptosystem based on iterating a chaotic map. Phys. Lett. A 2006, 349, 109–115. [Google Scholar]
- García, P.; Jiménez, J. Communication through chaotic map systems. Phys. Lett. A 2002, 298, 35–40. [Google Scholar]
- Wong, K. A combined chaotic cryptographic and hashing scheme. Phys. Lett. A 2003, 307, 292–298. [Google Scholar]
- Wang, Y.; Liao, X.; Xiang, T.; Wong, K.; Yang, D. Cryptanalysis and improvement on a block cryptosystem based on iteration a chaotic map. Phys. Lett. A 2007, 363, 277–281. [Google Scholar]
- Li, C.; Li, S.; Alvarez, G.; Chen, G.; Lo, K. Cryptanalysis of two chaotic encryption schemes based on circular bit shift and XOR operations. Phys. Lett. A 2007, 369, 23–30. [Google Scholar]
- Stinson, D.R. Cryptography: Theory and Practice; CRC Press: Boca Raton, FL, USA, 1995. [Google Scholar]
- Schneier, B. Applied Cryptography-Protocols, Algorithms, and Source Code in C, 2nd ed; John Wiley Sons: New York, NY, USA, 1996. [Google Scholar]
- Menezes, A.; VanOorschot, P.; Vanstone, S. Handbook of Applied Cryptography; CRC Press: Boca Raton, FL, USA, 1996. [Google Scholar]



| j | Cj | f(Cj) mod 64 | Dj | Aj |
|---|---|---|---|---|
| 1 | EAFA4D22D326D40C | 35 | 10 | 5E0AEF19A566A729 |
| 2 | 2960D4C5E768138D | 36 | 03 | D6E5053AF966B07E |
| 3 | C716165410ACD847 | 12 | 1D | EF5FCAE1DB5FA883 |
| 4 | 3C991CA5F1E8FCC6 | 20 | 2E | 4246A2AAADA975E2 |
| j | Cj | f(Cj) mod 64 | Dj | Aj |
|---|---|---|---|---|
| 1 | F11ED8CA5F72155E | 35 | 10 | 5E0AEF19A566A729 |
| 2 | 8A99683495FDBAAB | 36 | 03 | D6E5053AF966B07E |
| 3 | CC1E07D524E0E7A1 | 12 | 1D | EF5FCAE1DB5FA883 |
| 4 | D9D58D603B600C1E | 20 | 2E | 4246A2AAADA975E2 |
| j | Cj | f(Cj) mod 64 | Chosen | Chosen |
|---|---|---|---|---|
| 1 | 218A916626E5DA55 | 28 | 00000000000000DC | 0000000000001C00 |
| 2 | BA53340E52524733 | 45 | 00000000000000ED | 0000000000002D00 |
| 3 | 2C2CE7EEB40BA7EC | 63 | 00000000000000FF | 0000000000003F00 |
| 4 | B19F2A8A8BBAB8BD | 62 | 00000000000000FE | 0000000000003E00 |
| j | Dj | Aj | |||
|---|---|---|---|---|---|
| 1 | A7F55E0AEF19A566 | BB295E0AEF19A566 | 1CDC000000000000 | 16 | 5E0AEF19A566A729 |
| 2 | ABA16BD9AC1F83AC | ABB79D59AC1F83AC | 0016F68000000000 | 25 | B3583F075957423A |
| 3 | 2B876D414E8FBD7F | 2B8762BE8E8FBD7F | 00000FFFC0000000 | 34 | 3A3EF5FCAE1DB5FA |
| 4 | 6A2A9568E24C2424 | 6A252AE8E24C2424 | 000FBF8000000000 | 26 | A389309091A8AAAB |
| Test file | Lena | Text file | Video file |
|---|---|---|---|
| Ciphertext entropy | 7.9923 | 7.9981 | 7.9919 |
| Positions | Plaintext image | Ciphertext image |
|---|---|---|
| Horizontal | 0.98448 | 0.0031261 |
| Vertical | 0.94878 | 0.0057563 |
| Diagonal | 0.96787 | 0.0130690 |
| Ciphertext 1 | Ciphertext 2 | Correlation Coefficient |
|---|---|---|
| Ciphertext A | Ciphertext B | 0.00296 |
| Ciphertext A | Ciphertext C | 0.00137 |
| Ciphertext A | Ciphertext D | 0.00429 |
| Ciphertext B | Ciphertext C | 0.00153 |
| Ciphertext B | Ciphertext D | 0.00194 |
| Ciphertext C | Ciphertext D | 0.00296 |
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Guo, X.; Zhang, J.; Khan, M.K.; Alghathbar, K. Secure Chaotic Map Based Block Cryptosystem with Application to Camera Sensor Networks. Sensors 2011, 11, 1607-1619. https://doi.org/10.3390/s110201607
Guo X, Zhang J, Khan MK, Alghathbar K. Secure Chaotic Map Based Block Cryptosystem with Application to Camera Sensor Networks. Sensors. 2011; 11(2):1607-1619. https://doi.org/10.3390/s110201607
Chicago/Turabian StyleGuo, Xianfeng, Jiashu Zhang, Muhammad Khurram Khan, and Khaled Alghathbar. 2011. "Secure Chaotic Map Based Block Cryptosystem with Application to Camera Sensor Networks" Sensors 11, no. 2: 1607-1619. https://doi.org/10.3390/s110201607




