Abstract
Most portable systems like smart-phones are equipped with low cost consumer grade sensors, making them useful as Pedestrian Navigation Systems (PNS). Measurements of these sensors are severely contaminated by errors caused due to instrumentation and environmental issues rendering the unaided navigation solution with these sensors of limited use. The overall navigation error budget associated with pedestrian navigation can be categorized into position/displacement errors and attitude/orientation errors. Most of the research is conducted for tackling and reducing the displacement errors, which either utilize Pedestrian Dead Reckoning (PDR) or special constraints like Zero velocity UPdaTes (ZUPT) and Zero Angular Rate Updates (ZARU). This article targets the orientation/attitude errors encountered in pedestrian navigation and develops a novel sensor fusion technique to utilize the Earth’s magnetic field, even perturbed, for attitude and rate gyroscope error estimation in pedestrian navigation environments where it is assumed that Global Navigation Satellite System (GNSS) navigation is denied. As the Earth’s magnetic field undergoes severe degradations in pedestrian navigation environments, a novel Quasi-Static magnetic Field (QSF) based attitude and angular rate error estimation technique is developed to effectively use magnetic measurements in highly perturbed environments. The QSF scheme is then used for generating the desired measurements for the proposed Extended Kalman Filter (EKF) based attitude estimator. Results indicate that the QSF measurements are capable of effectively estimating attitude and gyroscope errors, reducing the overall navigation error budget by over 80% in urban canyon environment.1. Introduction
The provision to pedestrians of location and orientation information, which in some way can be used for simplifying the task of reaching a particular destination, is called pedestrian navigation. The versatility of environments in which the pedestrian navigation system has to work, differentiates it from land vehicle, sea vessel and aircraft navigation. Of all the possible environments in which the PNS has to work, the urban and indoor environments are the most challenging ones. These challenges arise from the amount and reliability of information available for estimating the navigation parameters. This diversity of environment for pedestrian navigation imposes the use of self-contained sensors for navigation that can provide users with navigation parameters irrespective of the availability of external aids.
2. The Earth’s Magnetic Field
The Earth’s magnetic field is a naturally occurring planetary phenomenon, which can be modeled as a dipole and follows the basic laws of magnetic fields summarized and corrected by Maxwell [13,14]. It is a three dimensional vector originating at the positive pole of the dipole, the magnetic South and ends at the magnetic North pole. For centuries, the Earth’s magnetic field has been successfully used for navigation purposes.
With the advancements in sensor technology, this field can now be precisely measured with the help of a sensor commonly known as the magnetometer. With the proper transformation of the field components to the horizontal plane and knowing the declination angle specific to the measurement area and time, a simple trigonometric operation estimates the geographic heading. The magnetic field vector is elaborated in Figure 1. Here H is the horizontal field component. The angle between the True North and H is called the declination angle D whereas the angle between the magnetic field B and horizontal plane is called the inclination angle I. Bx, Bv and Bz are the three orthogonal magnetic field components.
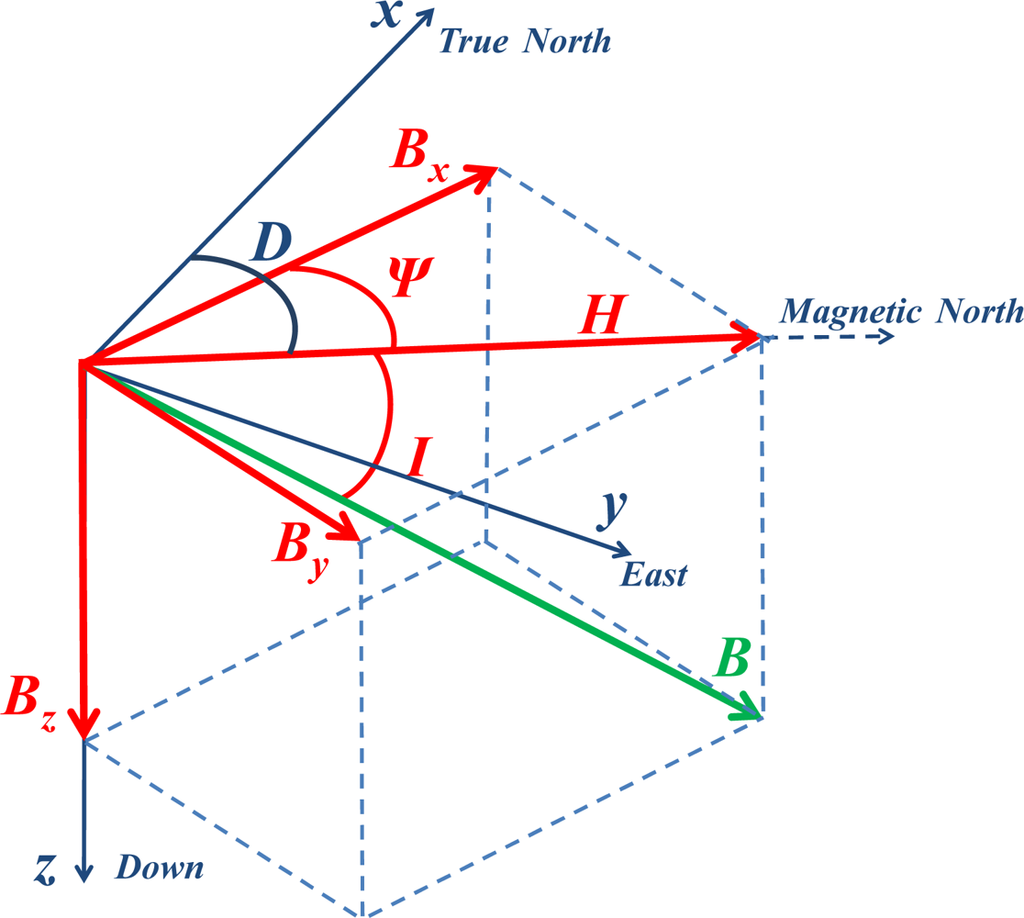
2.1. Heading Estimation Using the Earth’s Magnetic Field
The orthogonal components of the horizontal magnetic field are used for estimating the heading. Thus the field components must first be transformed to a local level in order to find the horizontal field component of the measured Earth’s magnetic field. For estimating the heading with respect to true North instead of the magnetic North, the declination angle also needs to be predicted using one of the Earth’s magnetic field models [15]. After resolving the magnetic field to the local level and estimating the declination angle, a simple trigonometric relationship is used for estimating the heading from the measured Earth’s magnetic field:
2.2. Effects of Indoor Environment on Earth’s Magnetic Field
Modeling of the Earth’s magnetic field is possible in an indoor environment in the presence of magnetic dipoles known as magnetic perturbations [12]. These perturbations are due either to electromagnetic devices or magnetization of manmade structures in the presence of an external magnetic field, which is mostly constituted of the Earth’s magnetic field. Figure 2 depicts the heading estimates for a clean and a perturbed environment, while the user walks along a straight line path. A perturbation source is modeled at around the 20 s time mark. Here it can be observed that in the close vicinity of a perturbation source, the heading estimate deviates from the nominal heading with respect to the Earth’s magnetic field, which results from the change in the local magnetic field components due to the perturbation source. If one uses the magnetic heading estimates obtained using the perturbed magnetic field, the effects on pedestrian navigation solution would be adverse.
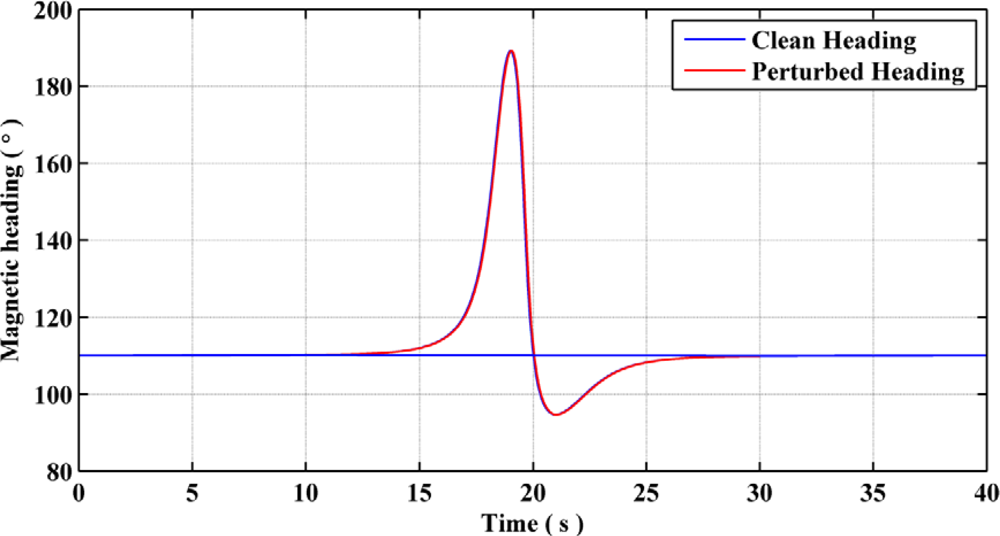
For better understanding the nature of artificial magnetic perturbations and their influence on Earth’s magnetic field measurements, an exhaustive assessment of the magnetic field was conducted by surveying different indoor and outdoor environments [16]. From these surveys, it has been observed that the effects of perturbation sources on the magnetic heading estimates can cause errors reaching up to 130° in some cases. Thus the urban and indoor magnetic field information cannot be used for effectively estimating ones absolute orientation and new approaches need to be investigated in order to utilize the perturbed magnetic field for pedestrian navigation applications.
4. Extended Kalman Filter for Attitude and Angular Rate Error Estimation
Attitude and its error estimation constitute a non linear problem [21], which can be solved by using a number of estimation approaches. In this article, an extension of a Kalman filter based estimator, namely an Extended Kalman Filter (EKF) is used [22]. The main purpose of this estimator is to model the effects of the gyroscope errors on attitude estimates and use the magnetic field information as corrective measurements to estimate the attitude errors in general and gyroscope errors in particular, which can then be compensated from the present epoch and remodeled for the proceeding ones until new measurements are available. Detailed derivation of the said estimator can be found in a number of books [6,20–25]. Only the appropriate states, measurements and their respective system and measurement error models are detailed herein.
4.1. The State Vector
As only the attitude/orientation estimation for pedestrian navigation is targeted herein, the main states to be estimated are the three attitude angles. The attitude is primarily determined using the angular rates obtained using the rate gyroscopes. The deterministic errors associated with this sensor can be compensated for using the calibration parameters [12], leaving the time varying biases as the residual errors. Thus the state vector becomes:
Here, ϕ is the roll angle, θ is the pitch angle and Ψ is the heading angle. The time varying biases associated with the three gyroscopes are represented by bωx, bωy and bωz.
4.2. System Error Model
The perturbed state vector representing errors in Equation (4) is given by:
From Equation (6), it can be shown that:
The matrix is defined by the uncompensated gyroscope measurements. Let be the skew symmetric matrix for the gyroscope measurement errors. By definition of the different matrices, can now be written as:
Substituting Equation (11) in Equation (10), simplifying and neglecting the second order terms to get a relationship for Ė yields:
In Equation (13):
The time varying gyroscope bias is modeled as an exponentially correlated noise term, resulting in the derivative of perturbations in the time varying gyroscope bias δbω given by [20]:
4.3. Measurement Error Models
The measurements used for compensating the errors associated with the attitude vector in general and gyroscope biases in particular are herein solely based on the magnetic field vector measurements. In order to utilize the clean as well as perturbed magnetic field measurements, a novel technique for estimating the sensor frame’s angular rates using a tri-axis magnetometer was developed and is detailed in the following section.
5. Quasi-Static Field (QSF) Based Attitude and Angular Rate Measurements (Patent Pending)
The novel idea for estimating attitude and gyroscope errors using magnetic field measurements for pedestrian navigation environments mainly involves detecting quasi-static total magnetic field periods during pedestrian motion and utilizing them as measurements for estimating attitude and gyroscope errors. Indeed when the local magnetic field is quasi-static, the rate of change of the magnetic field is combined with the rotational rate of change of the inertial device generating an estimated gyroscope error, which can be further used to correct for time-varying inherent gyroscope errors [12]. Contrary to existing solutions, this technique is working in magnetically perturbed environments as long as the field is identified as constant over a selective period of time. Further, in order to successfully detect the presence of QSF periods, proper pre-calibration of the magnetic field sensors is necessary. This is achieved by utilizing a calibration algorithm developed by the authors [26]. The QSF detector, developed using statistical signal processing techniques, is now presented.
The Earth’s magnetic field, though a good source of information for estimating heading outdoor, suffers severe degradations in the indoors caused by magnetic field perturbations [16]. These perturbations are of changing magnitudes and directions, which induce random variations in the total magnetic field. These variations render the magnetic field information useless for absolute orientation estimation with respect to the magnetic North in indoor environments. Although the magnetic field indoor is not spatially constant due to changing perturbation sources, depending on the pedestrian’s speed and surroundings, it is possible to have locations as well as short periods (user not moving) when the perturbed magnetic field is constant in magnitude as well as in direction. The rate of change of the total magnetic field in such situations will be ideally zero. It is possible to have very slight changes in the magnitude and direction of the total magnetic field (due to sensor noise) that can still be considered as quasi-static. Thus information to be considered for detecting a QSF is the rate of change of the total magnetic field ||Ḃ||, which is referred to as the field gradient and is computed using:
Let the hypothesis for a non-static field be H0 and that for a quasi-static field be H1 respectively. The Probability Density Functions (PDFs) associated with these two hypotheses are:
The rate of change of the total magnetic field is also contaminated by white Gaussian noise vk, which, when modeled with the measurements, gives:
As the complete knowledge about ||Ḃk|| is unknown for H0, the PDF in this case is given by:
Let the Maximum Likelihood Estimator (MLE) for the unknown parameter in case of H0 be , which is given by the mean of the signal as:
Now the PDF for H0 becomes:
For hypothesis H1, the rate of change of the total magnetic field is known (it will be zero), therefore the PDF in this case becomes:
The Generalized Likelihood Ratio Test (GLRT) for detecting a quasi-static field is given by:
Substituting for the PDFs in Equation (30) and simplifying, one gets:
Taking the natural log on both sides and simplifying yields:
6. Use of QSF Detected Periods for Attitude and Gyroscope Error Estimation
Once the QSF periods are detected during pedestrian motion, the next step is to utilize the magnetic field information during such periods for estimating the attitude angles and the gyroscope errors. This section derives the equations required for using QSF magnetic field measurements, even perturbed, in the EKF developed in Section 4. It principally consists of a measurement error model that is used for updating the state vector of the navigation filter.
6.1. QSF Measurement Error Model Using the Local Magnetic Field
Let the magnetic field measurement in the sensor frame at the start, i.e., the kth epoch, of the quasi-static field period be given by:
Considering the attitude at the start of quasi-static period as the reference for the measurement model, the magnetic field measurement can be transformed to the navigation frame using:
is considered as a measurement during quasi-static field periods. Indeed in the novel approach the magnetic field information extracted from a geomagnetic field model is not considered as a measurement of the truth but rather the field is considered as a reference over the QSF period. As the inaccuracies in the sensor will bias the estimated attitude, the transformations of proceeding magnetic field measurements from body to navigation frame using the updated would be different from hence introducing the measurement error. This gives the relationship for the first measurement error model:
At the kth epoch, Equation (35) would equal to zero as is obtained using . Thus the magnetic field information from the proceeding epoch along with new attitude estimate for are needed. Let be the next magnetometer measurement while the QSF period lasts. Substituting the new magnetic field measurement, at epoch k + 1, in Equation (35), the measurement error model becomes:
Ideally, as the magnetic field during QSF period is locally static (magnetic field vector not changing its magnitude or direction), Equation (36) should be equal to zero. But due to errors in rate gyroscope measurements, which are used for estimating the rotation matrix, the following perturbed model is obtained:
Simplifying (37) to get a relationship between measurements and states, one obtains:
Because the last term in Equation (38) is of the second order in errors, neglecting it results in:
From Equation (39), the first QSF measurement error model becomes:
6.2. QSF Measurement Error Model Using the Rate of Change of the Local Magnetic Field
During the quasi-static field periods, the rate of change of the reference magnetic field is zero. Using this information as a measurement, one gets:
Taking the derivative of Equation (41) to get the relationship between the rate of change of a vector in two different frames [28], one gets:
During user motion, the magnetic field components in the body frame will encounter changes, which can be modeled by Equation (43). But due to errors in gyroscopes angular rates, the predicted changes in magnetic field will be different from the measured ones given by:
The first two terms give the rate of change of the reference magnetic field, which, during QSF periods, is zero. is the error in caused by the gyroscope biases. Thus Equation (45) reduces to:
6.3. Full QSF Measurement Error Model
Combining Equations (40) and (48), the complete measurement error model using QSF is:
7. Statistical Analysis of the QSF Detector
In order to quantify the performance of the proposed quasi-static magnetic field detector, statistical analysis was conducted. From Equation (32), it can be observed that there are a number of tuning parameters that need to be evaluated for effectively using the QSF detector. These are the threshold, noise variance and the number of samples (window size) required for the detection test statistics.
7.1. Measurement Noise Variance
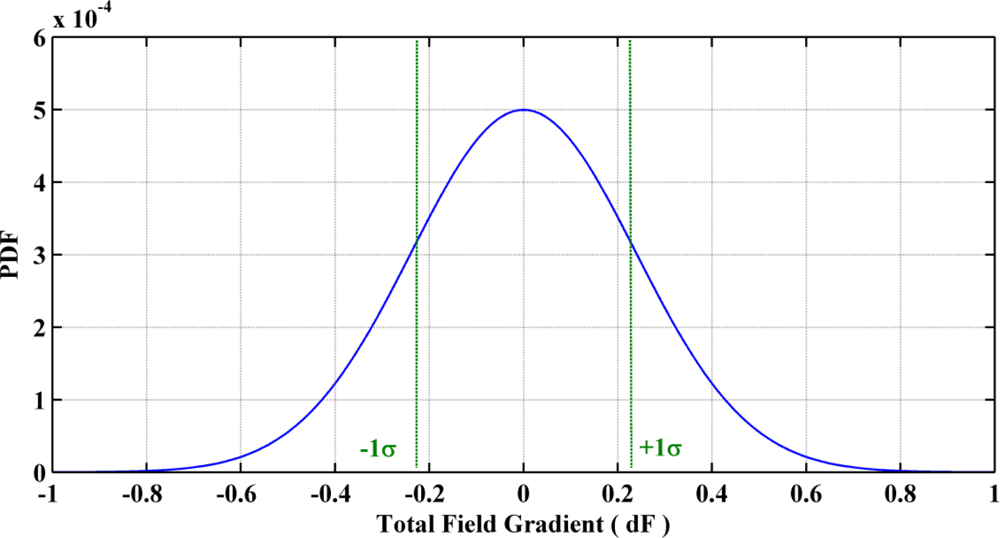
This factor corresponds to the variance of the total field gradient when the field itself is not changing. This gives a measure of the gradient noise that is encountered during quasi-static field periods. More than seven hours of data in five different environments that are common for pedestrian navigation have been collected and analyzed for evaluating this parameter [16,27]. The magnetic field survey was conducted using a tri-axis Bartington high resolution and high sensitivity fluxgate magnetometer. The magnetically derived heading was compared with the true heading estimated by post-processing synchronous measurements collected with the tactical grade inertial system (INS): the SPAN-CPT HG1700 from NovAtel. As shown in Figure 3, all devices were rigidly mounted on a plastic cart. The complete hardware setup was calibrated by performing 3D rotational maneuvers in a perturbation free environment and applying the complete calibration algorithm detailed in [26] to the recorded data. Figure 4 depicts the derived field gradient noise distribution, which is used for estimating the noise variance at 1σ. This comes out to be 0.057 μT2.

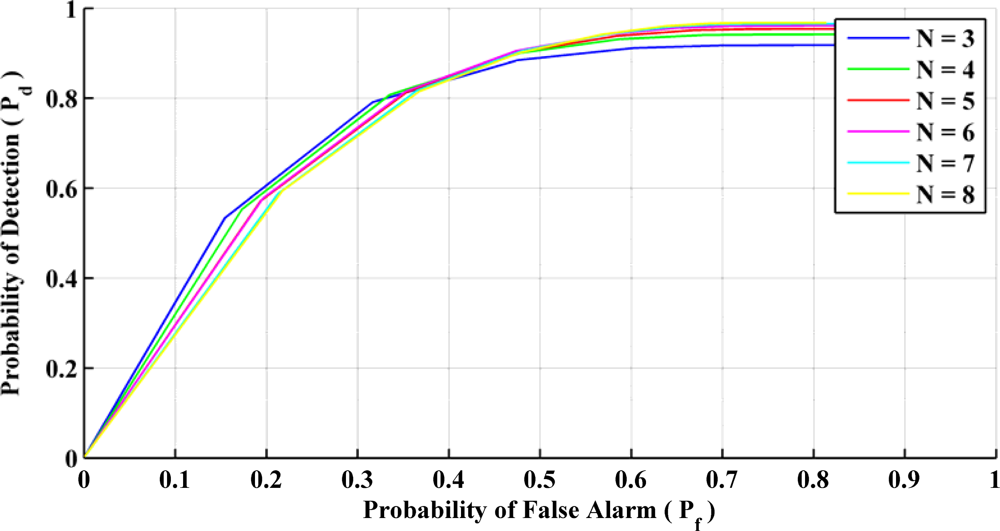
7.2. Selection of Threshold and Window Size Using Receiver Operating Characteristics
The Receiver Operating Characteristics (ROC) curve allows one to select the test statistics acceptance threshold based on the required probability of detection Pd and the acceptable probability of false alarm Pf. Figure 5 shows the ROC for the QSF detector for different sample window sizes. The sensor sampling rate is 0.04 s, which gives a minimum window size of 0.12 s and a maximum of 0.32 s in this case. It can be observed that the ROC tends to flatten out after Pd = 0.8. Thus selecting a Pd any larger than this value will cause more false alarms. Hence a Pd of approximately 0.8 is selected for this detector. The effect of the window size on the detector’s performance is negligible at the selected Pd. Therefore a window size of three samples is selected to reduce the processing burden. Table 1 summarizes the parameters selected for the QSF detector.

7.3. Occurrence and Durations of QSF Periods in Magnetically Perturbed Environments
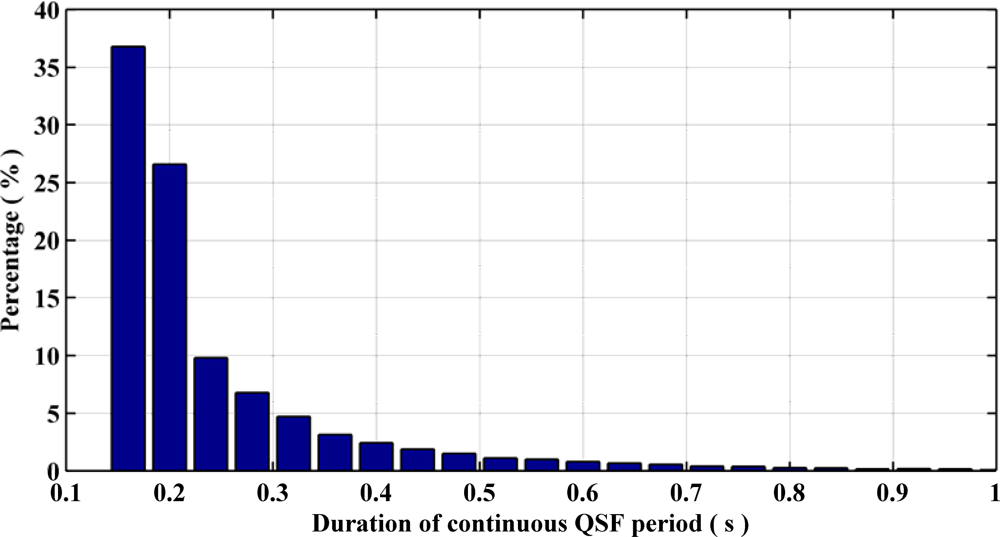
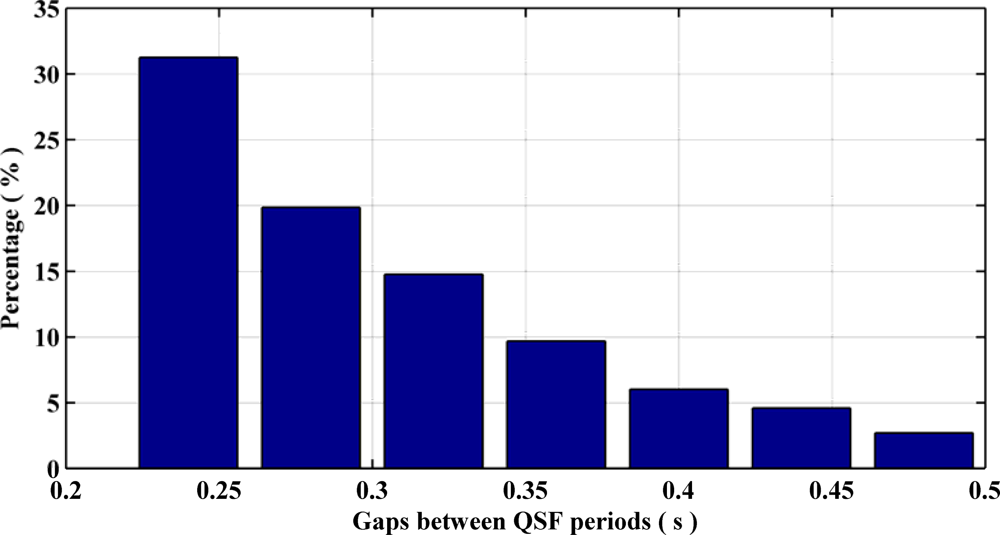
Figure 6 summarizes the QSF detection periods and their respective durations for different pedestrian navigation environments surveyed. Most of the detection periods have a duration of 120 ms to 300 ms. Figure 7 depicts the shortest and longest gaps between two consecutive QSF periods and their percentages of occurrence respectively. The minimum gap, i.e., 240 ms, occurs more frequently as compared with the maximum gap of 480 ms. Therefore it can be concluded that the QSF periods are encountered frequently and hence may allow for estimation of angular rate errors. It is worth mentioning here that unlike some pedestrian navigation applications where Zero Velocity Updates (ZUPT) occur frequently during a pedestrian’s walk (e.g., shoe mounted sensors), when the sensor block is in the hand or in a pocket/purse, these may not be encountered at all. In such scenarios, QSF periods can still be used effectively for providing regular measurements for sensor error estimation.
8. Experimental Assessment of the Proposed Attitude Computer
In order to assess the performance of the proposed QSF based orientation/attitude estimation algorithm, test data was collected in a real world environment, which is most common for pedestrian navigation applications: downtown. The test setup used for analyzing the impact of the proposed algorithm on attitude estimation comprised a Multiple Sensor Platform (MSP) and an optical wheel encoder developed by the author [12]. The MSP comprises a tri-axis gyroscope made of a dual-axis ST Microelectronics’ LPR530AL and a single-axis LY530ALH from the same manufacturer. It includes a HMC5843 tri-axis Anisotropic Magneto-Resistive (AMR) sensor for magnetic field measurements. Finally a tri-axis Analog Devices’ ADXL335 accelerometer completes the inertial measurement unit. The wheel encoder is used here for measuring the pedestrian’s walking speed so as to bring the outcome of the proposed algorithm from attitude domain to the position domain and provide better insight into the performance of the system. The wheel encoder is capable of computing the pedestrian’s walking speed with an accuracy of ±4 × 10−3 m/s. This walking speed is later resolved into North and East components using the estimated attitude to compute the position, the latter being obtained by integrating the velocity components. As this article focuses only on attitude estimation, the wheel encoder provides accurate speed measurements, which are necessary for de-correlating the velocity error budget from the attitude one, allowing the assessment of attitude accuracies only.
In an actual portable device such as a smart-phone, the walking speed would be measured by accelerometers. Although smart-phones of today are equipped with accelerometers, performing gait analysis with a handheld device is a challenging task and constitutes a research topic in itself. Thus with the use of wheel encoder, the experimental assessments of the proposed attitude estimator in the position domain as described herein, can be considered free of errors induced by speed sensors (accelerometers), providing a better insight into attitude accuracy. However the MSP developed for this research is hosting a tri-axis of accelerometers, which can be used in future for investigating different methods to estimate stride length and speed. This work targets the implementation of a complete pedestrian navigation system.
The MSP was rigidly mounted on a plastic plate, which can be easily carried in a hand. The wheel encoder is mounted on a pole that can be held by a pedestrian and pushed along the ground for measuring the walking speed. Figure 8(a) shows the handheld arrangement of the sensor module used for the test data collection. Here the pedestrian and body frames are also identified to clarify in which frame (body frame) the attitude is estimated. Figure 8(b) shows the overall test data collection setup including the wheel encoder. It is assumed that the body frames x–z plane is aligned with that of the pedestrian frame in order to account for the ambiguity between sensor frame’s orientation and users walking direction. This is achieved with the help of the hand held plastic plate. Thus the sensor’s frame is effectively aligned with the body frame.

8.1. Assessment Criterion
In order to assess the impact of the proposed algorithm on attitude estimation for pedestrian navigation, the solution repeatability criterion is chosen. Multiple paths of the same trajectory were followed in different environments keeping the same starting and ending point to assess the performance. The paths were followed so as to keep the separation between them within one metre if possible. This is achieved by following prominent patterns on the ground (tiles boundaries, pavement markings/intersections etc.).
8.2. Test Environment
In order to assess the impact of the proposed algorithms on attitude estimation for pedestrian applications, a urban canyon was selected.
Urban canyons can be considered as one of the regions where pedestrian navigation applications have a lot of commercial significance. Also before moving indoor, one often ends up being in an urban canyon for some time. Hence detailed analysis of the proposed algorithm in this environment is very important. Figure 9 gives the bird’s eye view of the test region selected in downtown Calgary for the assessment. The block selected is newly constructed with a walkway filled with ferrous infrastructure all around including phone booths, newspaper dispensers, street light poles and manholes. The walking trajectory around this block was approximately 370 m and was traversed thrice for repeatability testing.
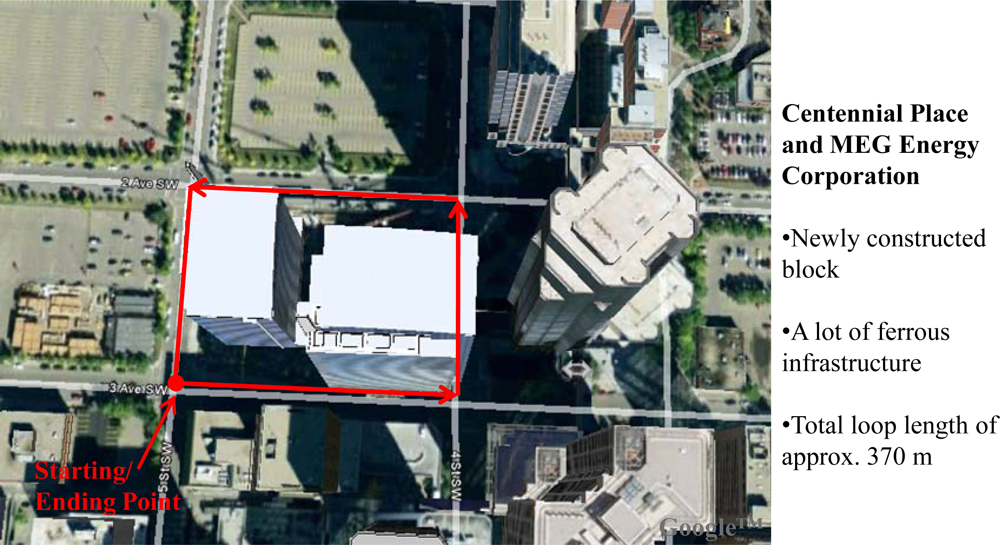
Figure 10(a) shows the same starting and ending point for each loop around the block with a traffic signal control panel right beside it. The last was made out of metal and hence contributed to the magnetic field perturbations in this region. Figure 10(b) shows one of the paths traversed in the selected region with high rise buildings and metallic infrastructure all around. Indeed this environment includes numerous magnetic field perturbation sources and hence can be considered a good test area for assessing the attitude estimation algorithms presented in this article.

8.3. Urban Canyon Test Results
Figure 11 shows the total field observed in the urban canyon environment along with the QSF detections. It can be observed that the overall signatures of the total field as well as the detection of QSF periods are temporally very similar for different paths. This is because the paths traversed were kept within 1 m of one another for assessing the repeatability of the results.
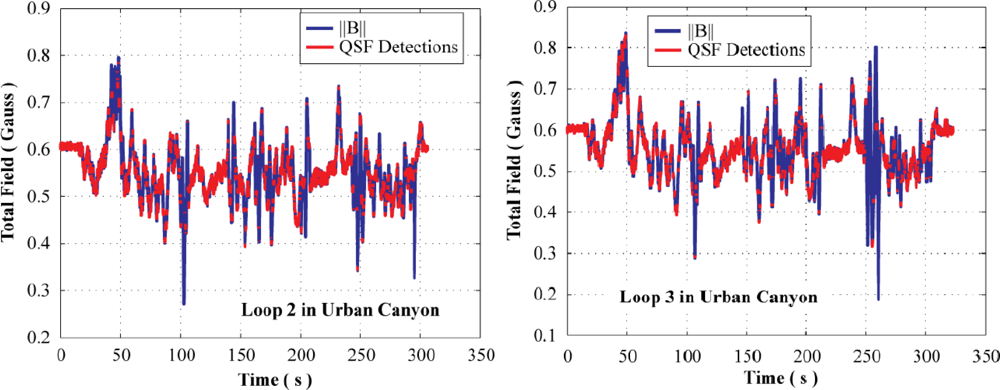
Figure 12 shows the trajectories obtained using raw heading versus QSF measurements for estimating gyroscope errors. It can be observed that due to severe magnetic field perturbations, the trajectory obtained using raw heading estimates has a maximum error of 43 m as compared to 5 m in case of QSF measurements.
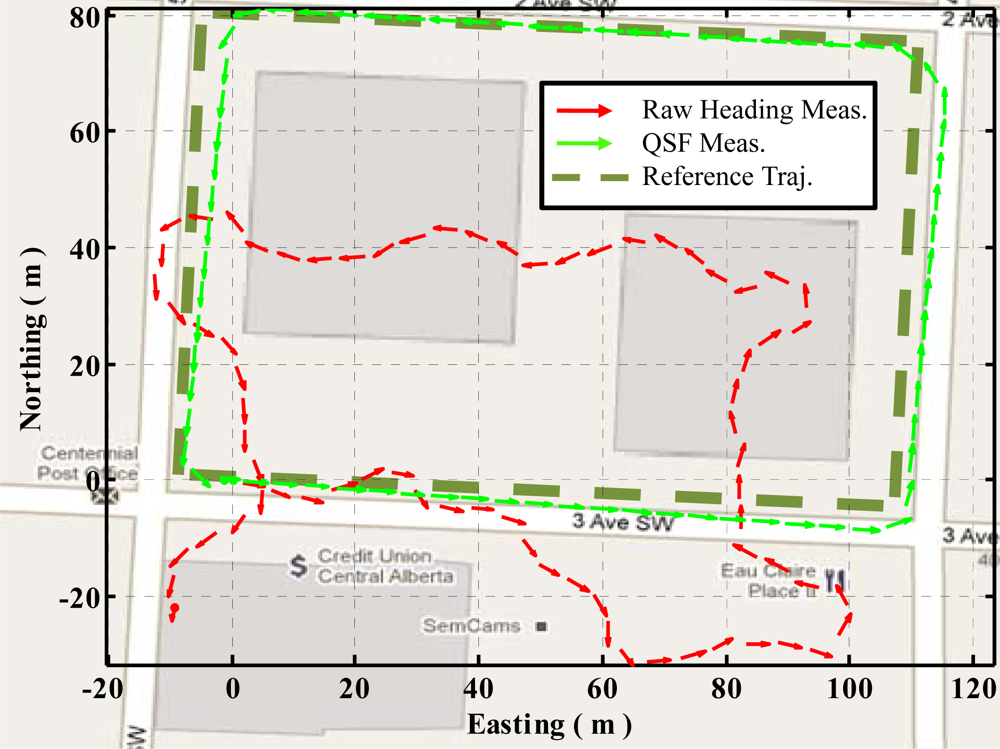
The observability of gyroscope biases using QSF measurements is presented graphically in Figures 13 and 14. Using Equation (43), one can obtain the estimates of the rate of change of magnetic field components using gyroscopes during a QSF period. Due to presence of biases in the gyroscope measurements, these estimates are different from the actual rate of change of magnetic field as shown in Figure 13. Upon utilizing Equation (44) as measurement errors for the EKF, the gyroscope biases are successfully estimated and compensated from the gyroscope measurements bringing the estimated rate of change of magnetic field components in harmony with the actual ones, as shown in Figure 14.
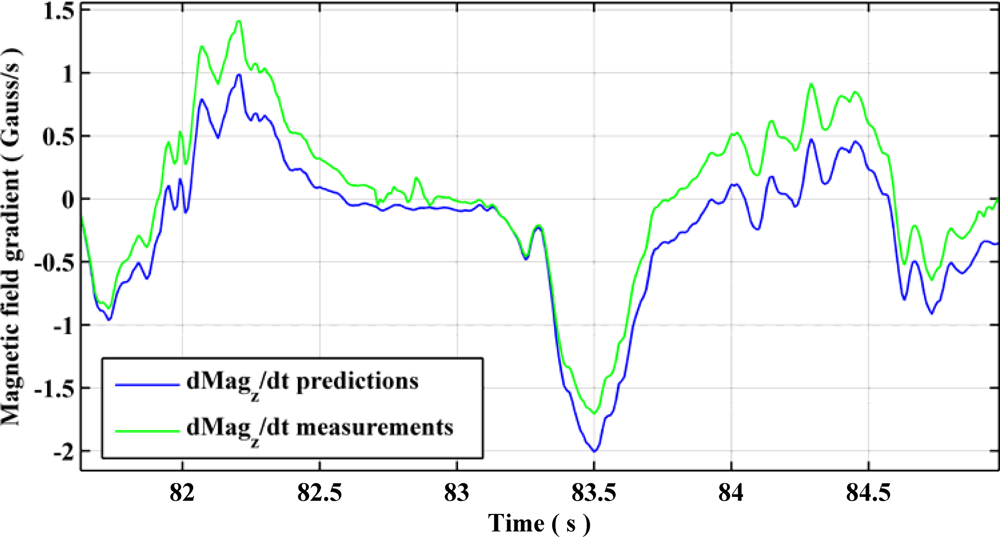
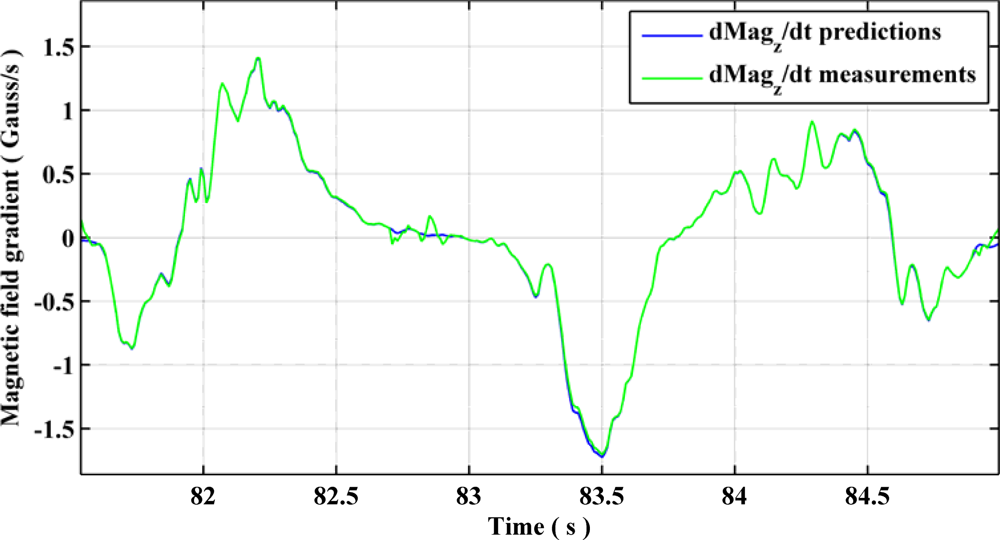
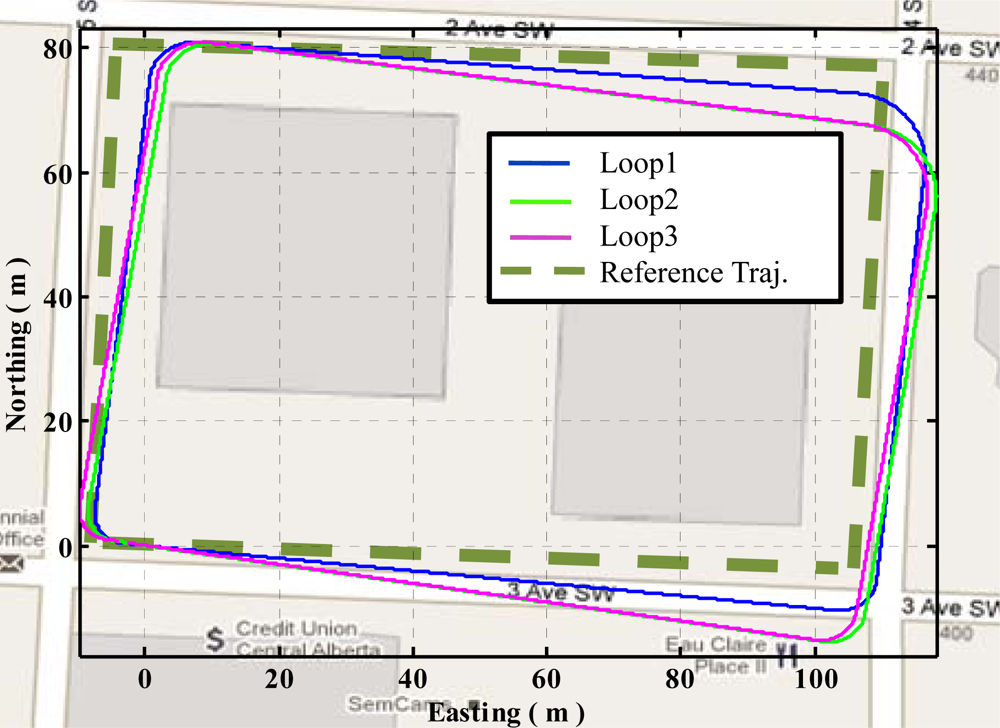
Figure 15 shows the three trajectories obtained using QSF measurements in the urban canyon. These trajectories are obtained by initializing the starting position and orientation for each loop. The first observation is the consistency of the ending locations. These are within 2 m of one another showing the effectiveness of QSF in estimating the rate gyroscope errors. The other observation is the random skewing of the three trajectories with respect to one another. This is because the QSF measurements can completely observe the rate gyroscope errors, but are not capable of observing the actual attitude errors. The attitude error growth is constrained using QSF measurements as is evident from Equation (49). As the rate gyroscope errors are randomly varying, these cause random errors in the attitude at the beginning of each path while the gyroscope errors are being estimated, which results in a random orientation error. Once the rate gyroscope errors are completely estimated, the attitude error growth is constrained. Thus the accuracy of the estimated trajectory is improved through the use of the QSF detections.
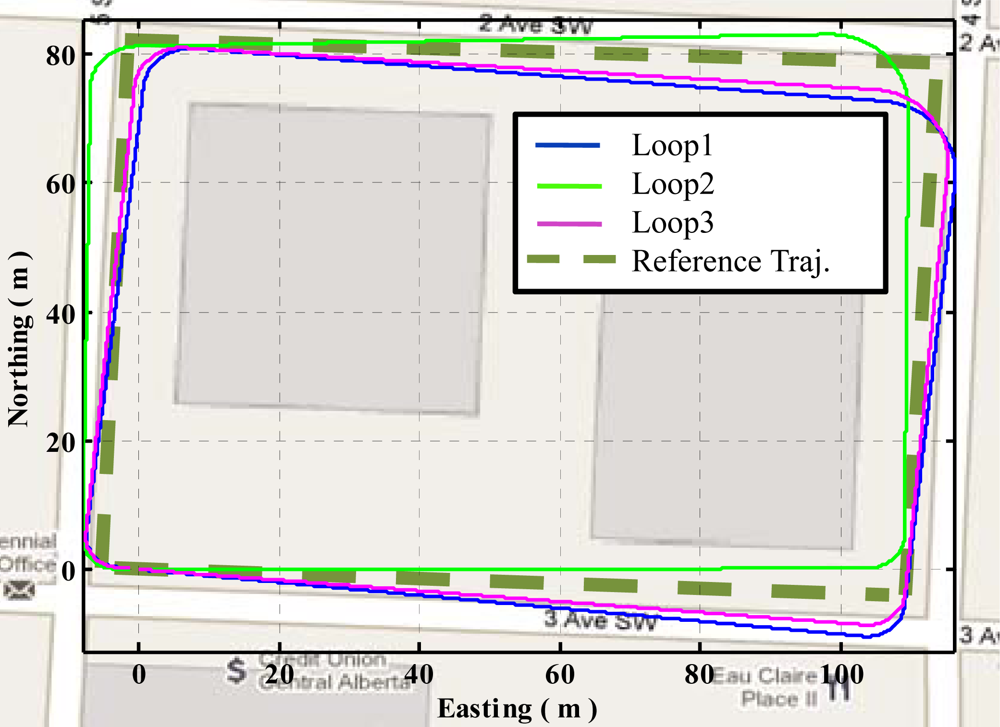
Figure 16 shows the trajectory obtained using the three loops in a continuous fashion. It is quite evident that Loop2 and Loop3 are very similar in this case. This is because the rate gyroscope errors have been properly estimated resulting in trajectories with a steady skew, which means that the orientation errors are now effectively constrained.
8.4. Performance of Attitude Estimator in Urban Environment
The maximum trajectory error obtained using raw magnetic heading based on measurement models for estimating continuous trajectory, whose length was longer than 1 km (for the three loops) is approximately 87 m whereas that for the QSF measurement model is approximately 16 m. Thus the trajectory errors are reduced by 80% by utilizing QSF measurements for constraining the attitude error growth and estimating the gyroscopes’ errors.
9. Conclusions and Future Work
This article investigated the use of handheld devices (smart-phones) equipped with low cost consumer grade sensors for pedestrian navigation. As the attitude/orientation errors play a major role in the overall navigation error budget, the focus was on improving the attitude estimates in environments where GPS is denied. For this purpose, the use of the Earth’s magnetic field as a measurement source for estimating the errors associated with low cost inertial sensors was investigated.
A novel method for utilizing the Quasi-Static magnetic Field (QSF), regardless of perturbation, to mitigate gyroscope errors has been developed and the corresponding equations have been presented. The novel estimation technique proved to deliver a high level of performance, reducing the trajectory errors by 80% for a distance of more than 1 km. This method detected the QSF periods during pedestrian’s motion and related the changes in the magnetic field components during these periods with the angular rates of the sensor block, thus providing measurements for directly assessing the errors associated with the rate gyroscopes. Development of an Extended Kalman Filter (EKF) for modeling the attitude and gyroscope errors as well as relating these to the magnetic field measurements have been conducted. They gave an insight into the interdependence of different parameters, which proved beneficial in identifying the limitations of the proposed model.
Selection of an urban canyon (magnetically disturbed outdoor field) for the experimental assessments provided data sets for a realistic and detailed analysis of the performance of the proposed algorithm. Analyzing the results in the position domain with the sensor platform carried in a hand gave detailed insight into the impact of the attitude estimator on the position error budget. A high accuracy wheel encoder made it possible to isolate the attitude errors from the position ones.
Even with an 80% error reduction in the positioning domain as compared with classical integration of magnetometers and gyroscopes in attitude estimation filter, the use of QSF measurements to successfully estimate the gyroscope errors resulted in constant orientation errors. This showed that this scheme is not sufficient for observing the absolute attitude errors. The position errors reached 16 m for a traversed trajectory of more than 1 km.
The use of accelerometers and pressure sensors for estimating pedestrian’s position as well as speed is necessary to completely assess the impact of this research in real world navigation scenarios. Both of these sensors are already incorporated in the MSP developed for this research and will form the basis for the above suggested research.
Research into the resolution of the ambiguity between sensor and body frames, which was constrained to be zero for the experiment herein, is needed. This can be achieved by using the accelerometers, but requires detailed modeling of the pedestrian’s walk related to arm swing or hip joint motion. The algorithm developed herein is self-contained and assumed a fully denied GNSS environment. However, GNSS is partly available in urban canyons and in numerous indoor environments. Hence research into the integration of the two approaches to maximize availability and accuracy is in order.
Acknowledgments
The financial support of Research In Motion (RIM), the Natural Science and Engineering Research Council of Canada, Alberta Advanced Education and Technology and Western Economic Diversification Canada is acknowledged.
References
- Alonso, J.M.; Ocana, M.; Sotelo, M.A.; Bergasa, L.M.; Magdalena, L. Wifi Localization System Using Fuzzy Rule-Based Classification. In Computer Aided Systems Theory—Eurocast 2009; MorenoDiaz, R., Pichler, F., Quesada Arencibia, A., Eds.; Springer-Verlag: Berlin, Germany, 2009; Volume 5717, pp. 383–390. [Google Scholar]
- Inoue, Y.; Sashima, A.; Kurumatani, K. Indoor Positioning System Using Beacon Devices for Practical Pedestrian Navigation on Mobile Phone. Proceedings of the 6th International Conference on Ubiquitous Intelligence and Computing, UIC'09, Brisbane, Australia, 7–9 July 2009; pp. 251–265.
- Luimula, M.; Saaskilahti, K.; Partala, T.; Pieska, S.; Alaspaa, J. Remote navigation of a mobile robot in an rfid-augmented environment. Pers. Ubiquitous Comput 2010, 14, 125–136. [Google Scholar]
- Shen, G.W.; Zetik, R.; Hirsch, O.; Thoma, R.S. Range-based localization for uwb sensor networks in realistic environments. EURASIP J. Wirel. Commun. Netw 2010, 2010, 476598:1–476598:9. [Google Scholar]
- Ramalingam, R.; Anitha, G.; Shanmugam, J. Microelectromechnical systems inertial measurement unit error modelling and error analysis for low-cost strapdown inertial navigation system. Def. Sci. J 2009, 59, 650–658. [Google Scholar]
- Bekir, E. Introduction to Modern Navigation Systems; World Scientific: Hackensack, NJ, USA, 2007; p. xiv. [Google Scholar]
- Renaudin, V.; Merminod, B.; Kasser, M. Optimal Data Fusion for Pedestrian Navigation Based on UWB and MEMS. Proceedings of the 2008 IEEE/ION Position, Location And Navigation Symposium, Monterey, CA, USA, 5–8 May 2008; 1–3, pp. 753–761.
- Suh, Y.S.; Park, S. Pedestrian Inertial Navigation with Gait Phase Detection Assisted Zero Velocity Updating. Proceedings of the Fourth International Conference on Autonomous Robots and Agents, Wellington, New Zealand, 10–12 February 2009; pp. 505–510.
- Steinhoff, U.; Schiele, B. Dead Reckoning from the Pocket—An Experimental Study. Proceedings of 2010 IEEE International Conference on Pervasive Computing and Communications (PerCom), Mannheim, Germany, 29 March–2 April 2010; pp. 162–170.
- Kamisakata, D.; Muramatsu, S.; Iwamoto, T.; Yokoyama, H. Design and implementation of pedestrian dead reckoning system on a mobile phone. IEICE Trans. Inf. Syst 2011, E94D, 1137–1146. [Google Scholar]
- Farrell, J.; Barth, M. The Global Positioning System and Inertial Navigation; McGraw-Hill: New York, NY, USA, 1999. [Google Scholar]
- Afzal, M.H. Use of Earth’s Magnetic Field for Pedestrian Navigation. Ph.D. Thesis,. University of Calgary, Calgary, AB, Canada, 2011. [Google Scholar]
- Knoepfel, H. Magnetic Fields: A Comprehensive Theoretical Treatise for Practical Use; Wiley: New York, NY, USA, 2000; p. xxi. [Google Scholar]
- Milsom, J. Field Geophysics, 3rd ed; Wiley: New York, NY, USA, 2003. [Google Scholar]
- Haines, G.V.; Newitt, L.R. The Canadian geomagnetic reference field 1995. J. Geomagn. Geoelectr 1997, 49, 317–336. [Google Scholar]
- Afzal, M.H.; Renaudin, V.; Lachapelle, G. Assessment of Indoor Magnetic Field Anomalies Using Multiple Magnetometers. Proceedings of ION GNSS10, Portland, OR, USA, 21–24 September 2010; pp. 1–9.
- Wertz, J.R. Space Attitude Determination and Control; Kluwer Academic Publishers: Dordrecht The Netherlands, 1990. [Google Scholar]
- Wahba, G. Problem 65-1: A least squares estimate of spacecraft attitude. SIAM Rev 1965, 7, 409. [Google Scholar]
- Shuster, M.D.; Oh, S.D. Three-axis attitude determination from vector observations. J. Guid. Control 1981, 4, 70–77. [Google Scholar]
- Farrell, J. Aided Navigation: GPS with High Rate Sensors; McGraw-Hill: New York, NY, USA, 2008; p. xxi. [Google Scholar]
- Bak, T. Spacecraft Attitude Determination—A Magnetometer Approach. Ph.D. Thesis,. Department of Control Engineering, Aalborg University, Aalborg, Denmark, 1999. [Google Scholar]
- Brown, R.G.; Hwang, P.Y.C. Introduction to Random Signals and Applied Kalman Filtering, 3rd ed; John Wiley & Sons: New York, NY, USA, 1997. [Google Scholar]
- Britting, K.R. Inertial Navigation Systems Analysis; Wiley-Interscience: New York, NY, USA, 1971; p. 249. [Google Scholar]
- Cohen, C.E. Attitude Determination Using GPS. Ph.D. Thesis,. Stanford University, Stanford, CA, USA, 1992. [Google Scholar]
- Grewal, M.S.; Weill, L.R.; Andrews, A.P. Global Positioning Systems, Inertial Navigation, and Integration; John Wiley & Sons: New York, NY, USA, 2001. [Google Scholar]
- Renaudin, V.; Afzal, H.; Lachapelle, G. Complete tri-axis magnetometer calibration in the magnetic field domain. J. Sens 2010, 2010, 967245:1–967245:10. [Google Scholar]
- Afzal, M.H.; Renaudin, V.; Lachapelle, G. Magnetic Field Based Heading Estimation for Pedestrian Navigation Environments. Proceedings of International Conference on Positioning and Indoor Navigation (IPIN), Guimaraes, Portugal, 21–23 September 2011; pp. 1–10.
- Natanson, G.A.; Challa, M.S.; Deutschmann, J.; Baker, D.F. Magnetometer-Only Attitude and Rate Determination for a Gyro-Less Spacecraft. Proceedings of Third International Symposium on Space Mission Operations and Ground Data Systems, Greenbelt, MD, USA, 1994; pp. 791–798.
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).