Wavelet Analysis for Wind Fields Estimation
Abstract
:1. Introduction
2. SAR Images and QuikSCAT Data
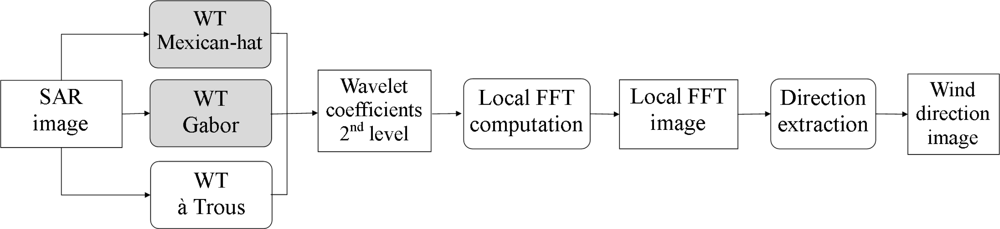
3. Methods
3.1. The WDWaT Method for Wind Direction Estimation
3.2. The LG-method for Wind Direction Estimation
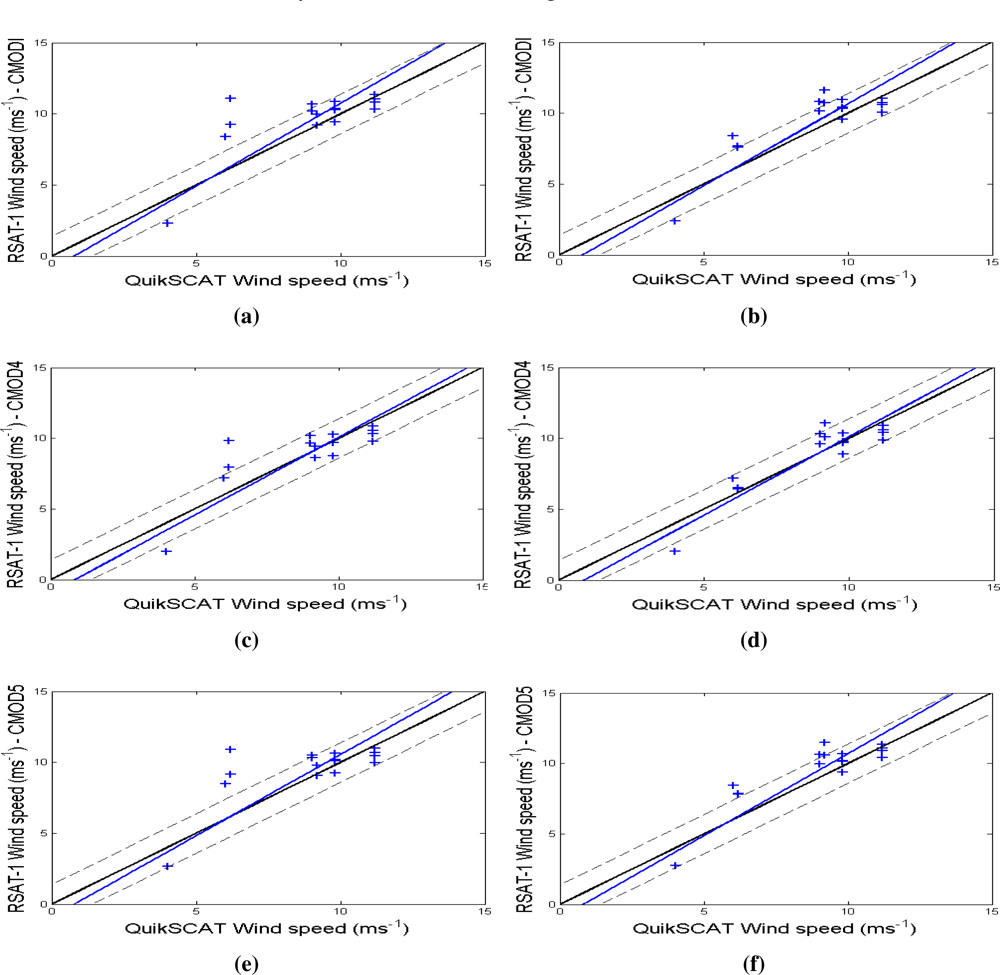
3.3. Wind Speed Retrieval Models for Assessment and Comparison Purposes
3.4. Undecimated Wavelets
(A) The à Trous Wavelet Transform
(B) The Gabor Wavelet Transform
(C) The Mexican-hat Wavelet Transform
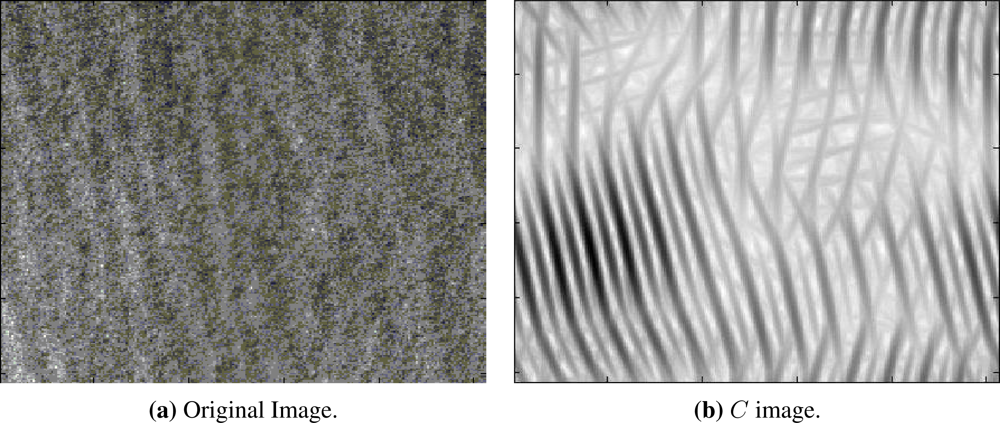
3.5. Proposed Spectral Algorithm for Wind Direction Estimation
4. Results
5. Conclusions
Acknowledgments
References
- Adamo, M.; De Carolis, G.; Morelli, S.; Parmiggiani, F. Synergic use of SAR imagery and high-resolution atmospheric model to estimate wind vector over the Mediterranean Sea. Proc. SPIE 2004, 5574, 470–481. [Google Scholar]
- Portabella, M.; Stoffelen, A.; Johannessen, J.A. Toward an optimal inversion method for synthetic aperture radar wind retrieval. J. Geophys. Res 2002, 107, 1–13. [Google Scholar]
- Cameron, I.; Lumsdon, P.; Walker, N.; Woodhouse, I. Synthetic aperture radar for offshore wind resource assessment and wind farm development in the UK. Proceedings of SEASAR 2006: Advances in SAR Oceanography from ENVISAT and ERS Missions, Frascati, Italy, 2006; 613, pp. 1–6.
- Girard-Ardhuin, F.; Mercier, G.; Collard, F.; Garello, R. Operational oil-slick characterization by SAR imagery and synergistic data. IEEE J. Oceanic Eng 2005, 30, 487–495. [Google Scholar]
- Brekke, C.; Solberg, A.H.S. Oil spill detection by satellite remote sensing. Remote Sens. Environ 2005, 95, 1–13. [Google Scholar]
- Solberg, A.H.S.; Brekke, C.; Husøy, P.O. Oil spill detection in RADARSAT and ENVISAT SAR images. IEEE Trans. Geosci. Remote Sens 2007, 45, 746–755. [Google Scholar]
- Du, Y.; Vachon, P.W.; Wolfe, J. Wind direction estimation from SAR images of the ocean using wavelet analysis. Canadian J. Remote Sens 2002, 28, 498–509. [Google Scholar]
- Fichaux, N.; Ranchin, T. Combined extraction of high spatial resolution wind speed and wind direction from SAR images: A new approach using wavelet transform. Canadian J. Remote Sens. 2002, 28, 510–516. [Google Scholar]
- Wackerman, C.C.; Rufenach, C.L.; Shuchman, R.A.; Johannessen, J.A.; Davidson, K.L. Wind vector retrieval using ERS-1 synthetic aperture radar imagery. IEEE Trans. Geosci. Remote Sens 1996, 34, 1343–1352. [Google Scholar]
- Zecchetto, S.; De Biasio, F. On shape, orientation, and structure of atmospheric cells inside wind rolls in two SAR images. IEEE Trans. Geosci. Remote Sens 2002, 40, 2257–2262. [Google Scholar]
- Ceccarelli, M.; De Filippo, M.; Di Bisceglie, M.; Galdi, C. A texture based approach for ocean surface wind detection in SAR images. Proceedings of IEEE International Workshop on Imaging Systems and Techniques, IST 2008, Chania, Greece, 2008; pp. 193–197.
- Koch, W. Directional analysis of SAR images aiming at wind direction. IEEE Trans. Geosci. Remote Sens 2004, 42, 702–710. [Google Scholar]
- Horstmann, J.; Koch, W. Measurement of ocean surface winds using synthetic aperture radars. IEEE J. Oceanic Eng 2005, 30, 14–23. [Google Scholar]
- Monaldo, F.M.; Thompson, D.R.; Beal, R.C.; Pichel, W.G.; Clemente-Colon, P. Comparison of SAR-derived wind speed with model predictions and ocean buoy measurements. IEEE Trans. Geosci. Remote Sens 2001, 39, 2587–2600. [Google Scholar]
- Zecchetto, S.; De Biasio, F. A wavelet-based technique for sea wind extraction from SAR images. IEEE Trans. Geosci. Remote Sens 2008, 46, 2983–2989. [Google Scholar]
- Horstmann, J.; Koch, W.; Lehner, S.; Tonboe, R. Wind retrieval over the ocean using synthetic aperture radar with C-band HH polarization. IEEE Trans. Geosci. Remote Sens 2000, 38, 2122–2131. [Google Scholar]
- Agency, C.S. Satellite RADARSAT-1, Canadian Space Agency. Available online: http://www.asc-csa.gc.ca/eng/satellites/radarsat1 (accessed on 12 August 2005).
- Isoguchi, O.; Shimada, M. An L-band ocean geophysical model function from PALSAR. IEEE Trans. Geosci. Remote Sens 2009, 47, 1925–1936. [Google Scholar]
- Choisnard, J.; Power, D.; Davidson, F.; Stone, B.; Howell, C.; Randell, C. Comparison of C-band SAR algorithms to derive surface wind vectors and initial findings in their use marine search and rescue. Canadian J. Remote Sens 2007, 33, 1–11. [Google Scholar]
- QuikSCAT data are produced by Remote Sensing Systems and sponsored by the NASA Ocean Vector Winds Science Team. Available online: www.remss.com/ (accessed on 5 June 2010).
- Daubechies, I. Orthonormal bases of wavelets with finite support–connection with discrete filters. In Wavelets, Proceedings of the International Conference on Time-Frequency Methods and Phase Space, Marseille, France, December, 1989; Combes, J.M., Grossmann, A., Tchamitchian, P., Eds.; Springer-Verlag, Berlin: Germany, 1989; pp. 38–39. [Google Scholar]
- Koch, W.; Feser, F. Relationship between SAR-derived wind vectors and wind at 10-m height represented by a meososcale model. Amer. Meteor. Soc 2006, 26, 1505–1517. [Google Scholar]
- Stoffelen, A.; Anderson, D. Scatterometer data interpretation: measurement space and inversion. J. Atmos. Oceanic Tech 1997, 14, 1298–1313. [Google Scholar]
- Guiting, S.; Yijun, H.; Yijun, H. Comparison of two wind algorithms of ENVISAT ASAR at high wind. Chin. J. Oceanol. Limnol 2006, 24, 92–96. [Google Scholar]
- Hersbach, H.; Stoffelen, A.; de Haan, S. The improved C-band geophysical model function CMOD5. Proceedings of the 2004 ENVISAT & ERS Symposium, Salzburg, Austria, September, 2004; pp. 1–8.
- Horstmann, J.; Koch, W.; Lehner, S. Ocean wind fields retrieval from the advanced synthetic aperture radar aboard ENVISAT. IEEE Trans. Geosci. Remote Sens 2004, 42, 702–710. [Google Scholar]
- Kim, D.; Moon, W.M. Estimation of sea surface wind vector using RADARSAT data. 2002, 80, 55–64. [Google Scholar]
- Thompson, D.R.; Elfouhaily, T.M.; Chapron, B. Polarization ratio for microwave backscattering from the ocean surface at low to moderate incidence angles. Proceedings of IEEE International Geoscience and Remote Sensing Symposium, IGARSS ’98, Seattle, WA, USA, 1998; 3, pp. 1671–1673.
- Mallat, S.G. A Wavelet Tour of Signal Processing, 2nd ed; Academic Press: Orlando, FL, USA, 1998. [Google Scholar]
- Holschneider, M.; Kronland-Martinet, R.; Morlet, J.; Tchamitchian, P. A real-time algorithm for signal analysis with the help of the wavelet transform. In Wavelets, Time-Frequency Methods and Phase Space; Combes, J.M., Grossmann, A., Tchamitchian, P., Eds.; Springer-Verlag, Berlin: Germany, 1989; pp. 286–297. [Google Scholar]
- Shensa, M. The discrete wavelet transform: wedding the à trous and Mallat algorithms. IEEE Trans. Signal Process 1992, 40, 2464–2482. [Google Scholar]
- Dutilleux, P. An implementation of the “algorithme à trous” to compute the wavelet transform. In Wavelets. Time-Frequency Methods and Phase Space; Combes, J.M., Grossmann, A., Tchamitchian, P., Eds.; Springer-Verlag: Berlin, Germany, 1989; pp. 298–304. [Google Scholar]
- Bijaoui, A.; Starck, J.L.; Murtagh, F. Image Processing and Data Analysis: The Multiscale Approach, 1st ed; Cambridge University Press: New York, NY, USA, 1998. [Google Scholar]
- Hong, L.; Guan, Y.; Zhang, L. An à trous algorithm based threshold shrinkage denoising method for blood oxygen signal. Proceedings of International Conference on Wavelet Analysis and Pattern Recognition, ICWAPR07, Beijing, China, 2007; 4, pp. 1669–1673.
- Lee, T.S. Image representation using 2D Gabor wavelets. IEEE Trans. Pattern Anal. Machine Intell 1996, 18, 959–971. [Google Scholar]
- Cheng, Y.S.; Liang, T.C. Rotational invariant pattern recognition using a composite circular harmonic and 2D isotropic Mexican-hat wavelet filter. Optics Commun 1994, 112, 9–15. [Google Scholar]
- Kutter, M.; Bhattacharjee, S.K.; Ebrahimi, T. Towards second generation watermarking schemes. Proceedings of IEEE International Conference Image Processing, ICIP99, Kobe, Japan, 1999; pp. 320–323.
- Horstmann, J.; Koch, W.; Lehner, S.; Tonboe, R. Ocean winds from RADARSAT-1 ScanSAR. Canadian J. Remote Sens 2002, 28, 524–533. [Google Scholar]
- Oliveira, J.G., Jr.; Medeiros, W.E.; Tabosa, W.F.; Vital, H. From barchan to domic shape: evolution of a coastal sand dune in Northeastern Brazil based on GPR survey. Brazilian J. Geophy 2008, 26, 5–20. [Google Scholar]
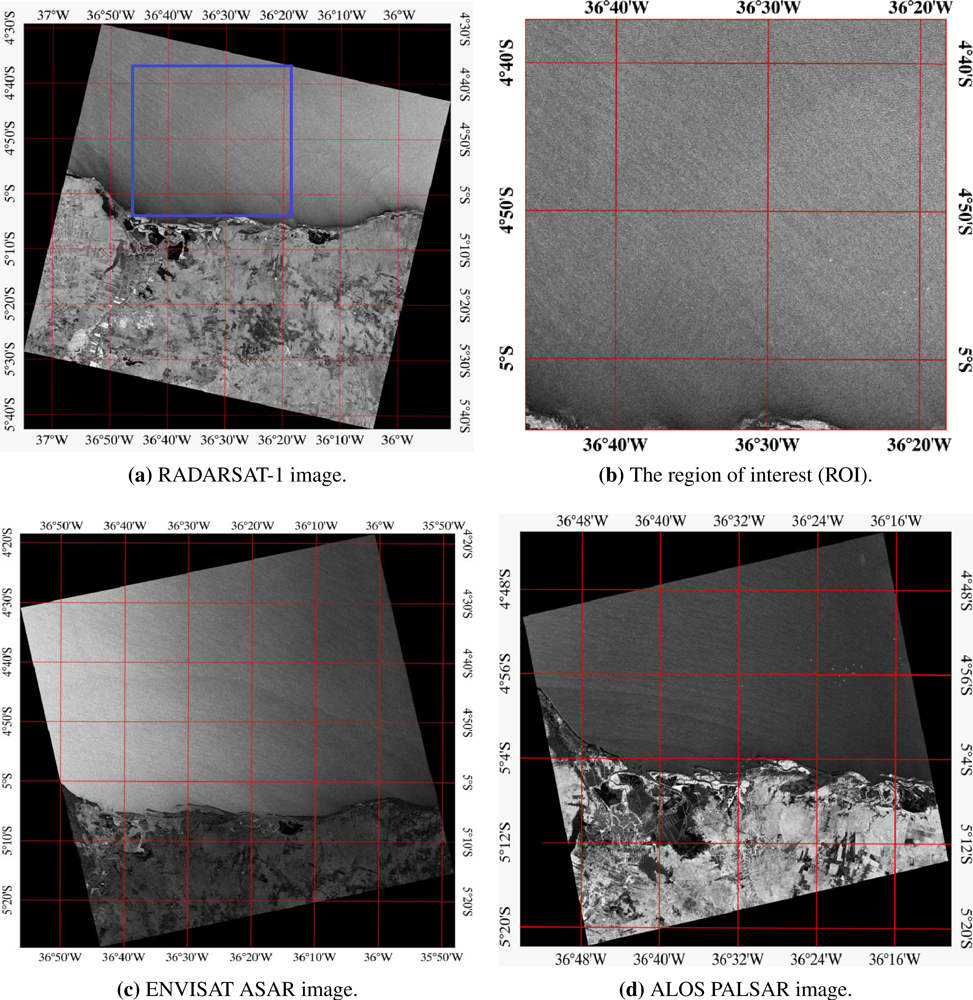
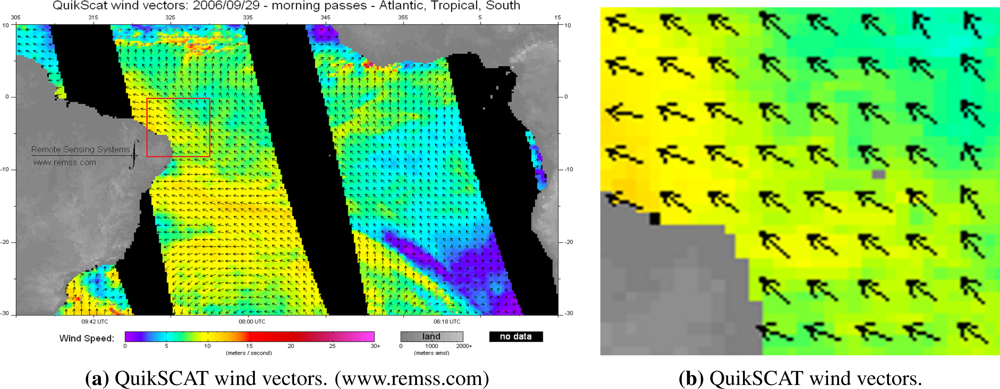


| Satellite | Mode Beam | Orbit | Image Time UTC | Wind Conditions 1 |
|---|---|---|---|---|
| RADARSAT-1 | Standard 7 | 39713 | 2003/06/14 07:56 | M/9.1 |
| RADARSAT-1 | Standard 2 | 39756 | 2003/06/17 08:09 | M/6.3 |
| RADARSAT-1 | Standard 7 | 56863 | 2006/09/26 07:55 | H/11.2 |
| RADARSAT-1 | Standard 2 | 56906 | 2006/09/29 08:07 | M/9.8 |
| RADARSAT-1 | Standard 3 | 56906 | 2001/02/03 20:42 | M/6.1 |
| RADARSAT-1 | Standard 6 | 56906 | 2001/02/07 07:53 | L/4.0 |
| ENVISAT | IMG | 11779 | 2004/06/01 00:39 | M/9.4 |
| ENVISAT | IMG | 15286 | 2005/02/01 00:38 | M/9.8 |
| ENVISAT | IMP | 19566 | 2005/11/29 00:41 | H/11.0 |
| ENVISAT | IMP | 25342 | 2007/01/04 12:13 | M/6.9 |
| ALOS | FBS8 | 7905 | 2007/07/20 01:16 | M/10 |
| ALOS | FBS8 | 12602 | 2008/06/06 01:13 | M/8.2 |
| ALOS | FBS8 | 18641 | 2009/07/25 01:18 | H/10.5 |
| ALOS | FBS8 | 19064 | 2009/08/23 01:16 | M/9.7 |
| FFT | WDWaT | LG | ||||||
|---|---|---|---|---|---|---|---|---|
| SAR images | Measures | à trous | Gabor | Hat | Haar | Gradient | QuikSCAT | |
| Triangular | B3-spline | |||||||
| 2003/06/14 | Mean (°) | 352.6 | 306.2 | 270 | 287.66 | 355.0 | 294 | 314.2 |
| Std. dev. (°) | 0.3 | 2.1 | 0 | 20.4 | 5.8 | 4.8 | 2.6 | |
| 2006/09/26 | Mean (°) | 334.3 | 328.5 | 270.0 | 180.84 | 335.0 | 264.3 | 277.5 |
| Std. dev. (°) | 22.2 | 1.9 | 0 | 169.1 | 5.8 | 10.4 | 10.4 | |
| 2006/09/29 | Mean (°) | 322.6 | 316.3 | 279.0 | 311.61 | 295.0 | 279.4 | 316.5 |
| Std. dev. (°) | 11.1 | 0.07 | 10.6 | 2.3 | 5.7 | 4.7 | 0.0 | |
| 2001/02/03 | Mean (°) | 275.76 | 246.33 | 272.33 | 225.12 | 303.33 | 270.46 | 259.5 |
| Std. dev. (°) | 58.26 | 15.84 | 76.96 | 7.42 | 56.86 | 0.09 | 2.59 | |
| 2001/02/07 | Mean (°) | 328.57 | 327.99 | 327.53 | 321.67 | 190 | 270.35 | 292.5 |
| Std. dev. (°) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 2005/11/29 | Mean (°) | 270 | 275.53 | 360 | 270 | 360 | 241.89 | 283.5 |
| Std. dev. (°) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 2007/01/04 | Mean (°) | 252.66 | 290.39 | 317.03 | 217.28 | 280 | 254.84 | 235.5 |
| Std. dev. (°) | 152.9 | 6.13 | 46.03 | 13.94 | 58.06 | 11.33 | 5.01 | |
| 2005/02/01 | Mean (°) | 284.51 | 284.83 | 237.83 | 325.74 | 287.5 | 309.49 | 282 |
| Std. dev. (°) | 1.18 | 1.22 | 64.8 | 1.77 | 39.55 | 40.95 | 7.94 | |
| 2007/07/20 | Mean (°) | 316.58 | 286.04 | 270 | 326.54 | 240 | 241.81 | 268.5 |
| Std. dev. (°) | 47.25 | 9.30 | 0 | 1.30 | 42.43 | 21.73 | 6.36 | |
| 2008/06/06 | Mean (°) | 294.44 | 335.56 | 270 | 264.92 | 230 | 209.79 | 328.5 |
| Std. dev. (°) | 16.57 | 16.57 | 0 | 73.59 | 0 | 8.59 | 0 | |
| 2009/07/25 | Mean (°) | 342.17 | 340.34 | 315 | 321.89 | 320 | 224.99 | 330 |
| Std. dev. (°) | 4.37 | 4.19 | 63.64 | 1.4 | 28.28 | 15.34 | 0 | |
| 2009/08/23 | Mean (°) | 344.64 | 285.99 | 270 | 243.2 | 340 | 263.75 | 282.75 |
| Std. dev. (°) | 0.4 | 1.31 | 0 | 37.89 | 28.28 | 6.05 | 1.06 | |
| Measures | Total data set (41 imagettes) | Only imagettes with wind speed values < 10 ms−1 | ||||||
|---|---|---|---|---|---|---|---|---|
| Triangular | B3-spline | Gabor | Hat | Triangular | B3-spline | Gabor | Hat | |
| bias (°) | 19.75 | 17.01 | −0.13 | −12.24 | 19.90 | 16.39 | −1.82 | −10.25 |
| RMSE (°) | 72.13 | 31.15 | 60.68 | 63.66 | 82.60 | 31.24 | 69.00 | 38.82 |
| correlation | 0.35 | 0.57 | −0.11 | 0.47 | 0.35 | 0.61 | −0.22 | 0.62 |
| std. dev. (°) | 73.92 | 24.57 | 49.24 | 70.61 | 85.50 | 23.31 | 53.22 | 47.44 |
| mean (°) | 301.39 | 298.65 | 281.50 | 269.39 | 298.23 | 294.71 | 276.51 | 268.07 |
| maximum (°) | 353.54 | 347.28 | 360 | 328.28 | 353.39 | 347.28 | 360 | 327.46 |
| QuikSCAT parameters | ||||||||
| mean (°) | 281.63 | 278.33 | ||||||
| std. dev. (°) | 30.54 | 33.50 | ||||||
| maximum (°) | 330 | 328.5 | ||||||
| Measures | B3-spline | Mexican-hat | ||||
|---|---|---|---|---|---|---|
| CMOD-IFR2 | CMOD4 | CMOD5 | CMOD-IFR2 | CMOD4 | CMOD5 | |
| bias (ms−1) | 0.79 | 0.12 | 0.64 | 0.63 | 0.06 | 0.68 |
| RMSE (ms−1) | 1.75 | 1.34 | 1.71 | 1.34 | 0.99 | 1.26 |
| correlation | 0.72 | 0.79 | 0.69 | 0.85 | 0.90 | 0.87 |
| std. dev. (ms−1) | 2.06 | 2.05 | 1.91 | 2.17 | 2.29 | 2.09 |
| mean (ms−1) | 9.71 | 9.05 | 9.57 | 9.56 | 8.98 | 9.60 |
| maximum (ms−1) | 11.33 | 10.87 | 10.97 | 11.61 | 11.07 | 11.48 |
| QuikSCAT parameters | ||||||
| mean (ms−1) | 8.92 | |||||
| std. dev. (ms−1) | 2.11 | |||||
| maximum (ms−1) | 11.2 | |||||
© 2010 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Leite, G.C.; Ushizima, D.M.; Medeiros, F.N.S.; De Lima, G.G. Wavelet Analysis for Wind Fields Estimation. Sensors 2010, 10, 5994-6016. https://doi.org/10.3390/s100605994
Leite GC, Ushizima DM, Medeiros FNS, De Lima GG. Wavelet Analysis for Wind Fields Estimation. Sensors. 2010; 10(6):5994-6016. https://doi.org/10.3390/s100605994
Chicago/Turabian StyleLeite, Gladeston C., Daniela M. Ushizima, Fátima N. S. Medeiros, and Gilson G. De Lima. 2010. "Wavelet Analysis for Wind Fields Estimation" Sensors 10, no. 6: 5994-6016. https://doi.org/10.3390/s100605994
APA StyleLeite, G. C., Ushizima, D. M., Medeiros, F. N. S., & De Lima, G. G. (2010). Wavelet Analysis for Wind Fields Estimation. Sensors, 10(6), 5994-6016. https://doi.org/10.3390/s100605994





