A Multipath Routing Protocol Based on Clustering and Ant Colony Optimization for Wireless Sensor Networks
Abstract
:1. Introduction
- A novel distributed algorithm based on some parameters (such as signal strength, residual energy of node) is designed to form clusters among the nodes located in the event area.
- An extended ACO algorithm based on many metrics (such as residual energy, path length, energy consumption of communication) is applied to search for the multiple paths between the cluster head (CH) and sink node.
- A load balancing function is further proposed to distribute the traffic over discovered multiple paths.
2. Related Work
2.1. Hierarchical Routing
2.2. Multipath Routing
2.3. Ant Routing
3. System Model and Problem Statement
3.1. System Model
Network Model
- N sensor nodes are uniformly distributed within a square field. Each sensor nodes has a unique ID. Sensor nodes in the event area are grouped into clusters.
- All sensor nodes keep static or less movement after being deployed.
- The energy of the sensor nodes cannot be recharged.
- Sensor nodes are location-unaware, i.e., a sensor node need not rely on the expensive devices, such as Global Positioning System (GPS), to receive the position information for finding the shortest path routing to the sink.
- Communication is symmetric. Nodes can estimate distance based on the signal strength of each other, and at the same time the radio power can be controlled.
- We assume ideal MAC layer conditions, that is, perfect transmission of data on a node-to-node link.
Radio Model
3.2. Problem Statement
4. Description of MRP
4.1. Phase I: Cluster Formation
- Nodes located in the event area can sense the distance to the event according to RSS.
- Nodes know the residual energy of neighbor nodes in the event area.
- If RSSi ≥ Threshold Value [29], node i locates in the event area. (RSSi is the received signal strength of node i)
| Begin |
| 1: Schedule each node wait time with Ta sec. delay |
| 2: while (Ta ≠ 0) |
| 3: if Threshold ≤ RSSi then |
| 4: if node j is in the event area and Threshold ≤ RSSj |
| 5: Ki = Ki+1; |
| 6: end-if |
| 7: end-if |
| 8: end-while |
| 9: if Threshold ≤ RSSi then |
| 10: node i calculates qi and Ti; |
| 11: if Ti ≠ 0 then |
| 12: wait; |
| 13: collect the sender of any other incoming CH advertisement in K; |
| 14: else |
| 15: if K = 0 then |
| 16: send CH advertisement message; |
| 17: else |
| 18: send a join-request to the node j (qj is the biggest); |
| 19: end-if |
| 20: end-if |
| 21: end-if |
| 22: broadcast TDMA schedule to members; |
| End |
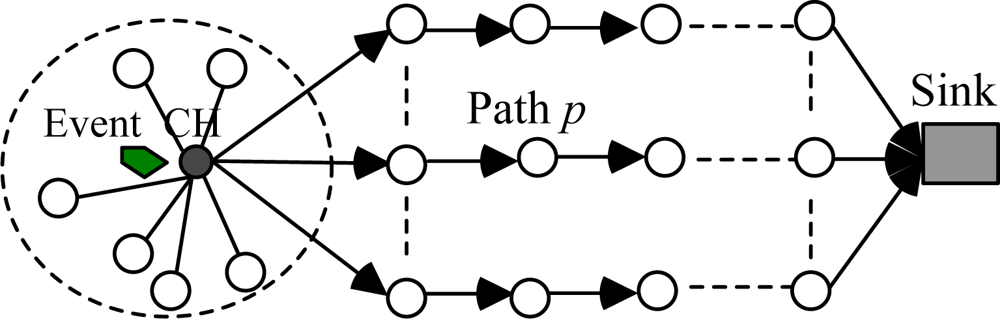
4.2. Phase II: Constructing Multipath
- The CH creates several SANTs to search for sink. The SANTs gather path information as they travel along the paths.
- The sink creates a BANT when a SANT arrives. The BANT is sent back following the reverse path. When a BANT moves, it need to update the pheromone on the link (i,j) at the reverse path.
- When a SANT arrives at an intermediate node, whether or not a AANT is generated according to a small probability.
Search Ant (SANT)
| Begin |
| 1: if TTL<>0 then |
| 2: if a SANT arrives at sink then |
| 3: create and release a new BANT; |
| 4: else |
| 5: if RAND (x)<0.001 then |
| 6: create a AANT; |
| 7: the AANT randomly chooses a node as the next hop node; |
| 8: else |
| 9: choose the next hop node j according to (26)–(29); |
| 10: refresh the residual energy of i and j; |
| 11: if selected node visited then |
| 12: back to the previous hop node; |
| 13: re-elect another node as the next hop node; |
| 14: end-if |
| 15: using (30), (31) to refresh pheromone value of link (i,j); |
| 16: end-if |
| 17 end-if |
| 18 end-if |
| End |
Backward ant (BANT)
| Begin |
| 1: if sink is reached then |
| 2: a new BANT is generated; |
| 3: while the CH is not reached |
| 4: the BANT moves along the reverse path; |
| 5: the BANT using (30), (32) to update pheromone value of link (i,j); |
| 6: |
| 7: calculate Emin, Ep and Length; |
| 8: update the residual energy of i and j; |
| 9: end-while |
| 10: end-if |
| End |
4.3. Phase III: Data Transmission
4.4. Route Maintenance
- When the residual energy of the current CH is lower than 50% the average energy of all nodes in the cluster, a new CH will be selected according to (24). If there are more than two paths to sink, the new CH will send the packets via these paths. Otherwise, the new CH will initiate a new route discovery process.
- When the number of multiple paths is less than two, that means the reliability of path decreased seriously. The current CH will initiate a new route discovery process.
5. Performance Evaluation
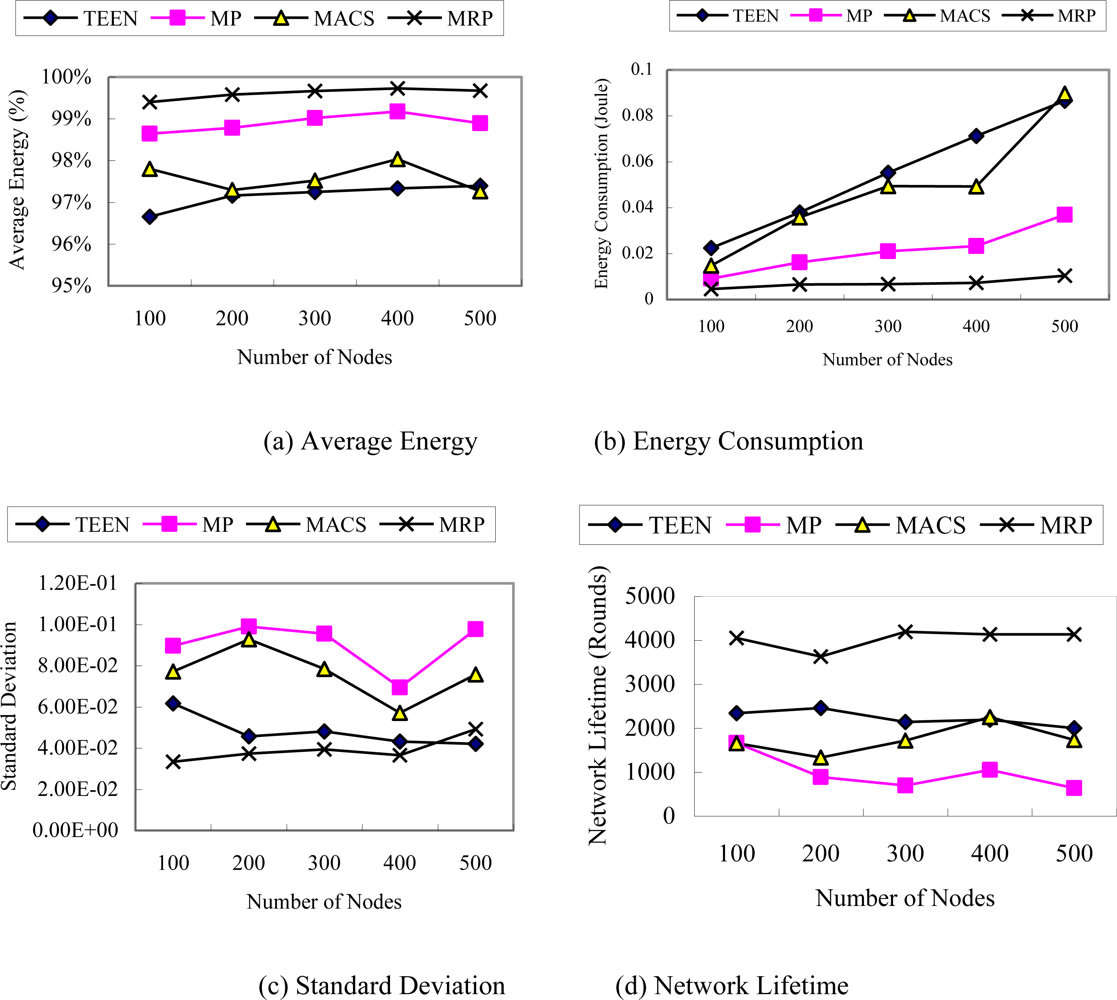
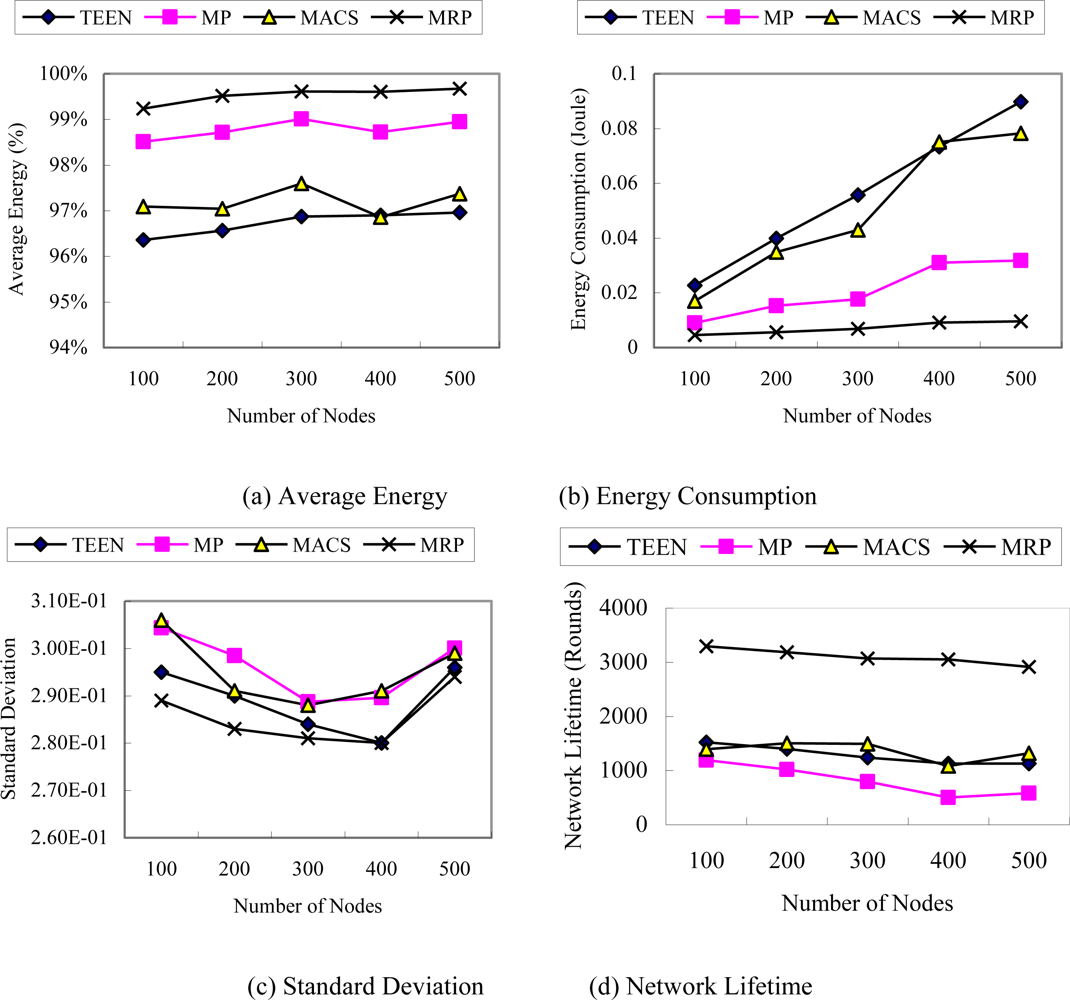
- Average Energy: The metric gives the average of energy of all nodes at the end of simulation.
- Energy consumption: The metric gives the energy consumption of nodes in the event area for transmitting a data packet to sink.
- The standard deviation of energy: The metric gives the average variance between energy levels on all nodes.
- Network lifetime: This metric gives the time of the first node running out of its energy.
6. Conclusion
Acknowledgments
References and Notes
- Hsieh, T.T. Using Sensor Networks for Highway and Traffic Applications. IEEE Potentials 2004, 3, 13–16. [Google Scholar]
- Ren, F.; Huang, H.; Lin, C. Wireless Sensor Networks. J. Softw 2003, 14, 1282–1291. [Google Scholar]
- Estrin, D. Wireless Sensor Networks Tutorial Part IV: Sensor Network Protocols. Proceedings of the 8th Annual International Conference on Mobile Computing and Networking (Mobicom 2002), Atlanta, GA, USA; 2002; pp. 23–28. [Google Scholar]
- Liu, M.; Cao, J.; Chen, G.; Wang, X. An Energy-Aware Routing Protocol in Wireless Sensor Networks. Sensors 2009, 9, 445–462. [Google Scholar]
- Schurgers, C.; Srivastava, M.B. Energy Efficient Routing in Wireless Sensor Networks. Proceedings of IEEE MILCOM, Vienna, VA, USA; 2001; pp. 357–361. [Google Scholar]
- Kalantari, M.; Shayman, M. Energy Efficient Routing in Wireless Sensor Networks. Proceedings of Conference on Information Sciences and System, Princeton, NJ, USA; 2004. [Google Scholar]
- Sun, L.; Li, J.; Chen, Y.; Zhu, H. Wireless Sensor Networks, 1st ed; Tsinghua Univ. Press: Beijing, China, 2005; pp. 28–49. [Google Scholar]
- Bonabeau, E.; Dorigo, M.; Theraulaz, G. Inspiration for Optimization from Social Insect Behavior. Nature 2000, 406, 39–42. [Google Scholar]
- Dorigo, M.; Stützle, T. Ant Colony Optimization, 1st ed.; MIT Press: Cambridge, MA, USA, 2004; pp. 1–319. [Google Scholar]
- Dorigo, M.; Gambardella, L.M. Ant Colony System: A Cooperative Learning Approach to the Traveling Salesman Problem. IEEE Trans. Evol. Comput 1997, 1, 53–66. [Google Scholar]
- Heinzelman, W.R.; Chandrakasan, A.; Balakrishnan, H. Energy-efficient Communication Protocol for Wireless Microsensor Networks. Proceedings of the 33rd Hawaii International Conference on System Sciences, Maui, HI, USA; 2000; pp. 1–10. [Google Scholar]
- Lindsey, S.; Raghavendre, C. PEGASIS: Power-efficient Gathering in Sensor Information Systems. Proceedings of IEEE Aerospace Conference, Big Sky, MT, USA; 2002; pp. 1125–1130. [Google Scholar]
- Selvakennedy, S.; Sinnappan, S.; Shang, Y. Data Dissemination Based on Ant Swarms for Wireless Sensor Networks. Proceedings of IEEE Consumer Communications and Networking Conference (CCNC 2006), Las Vegas, NV, USA; 2006; pp. 132–136. [Google Scholar]
- Ganesan, D.; Govindan, R.; Shenker, S.; Estrin, D. Highly-resilient, Energy-Efficient Multipath Routing in Wireless Sensor Networks. ACM Mob. Comput. Commun. Rev. (MC2R) 2001, 5, 11–25. [Google Scholar]
- De, S.; Qiao, C.; Wu, H. Meshed Multipath Routing with Selective Forwarding: An Efficient Strategy in Wireless Sensor Networks. Wirel. Sensor Netw 2003, 43, 481–497. [Google Scholar]
- Okdem, S.; Karaboga, D. Routing in Wireless Sensor Networks Using Ant Colony Optimization. Proceedings of the 1st NASE/ESA Conference on Adaptive Hardware and System-AHS, Istanbul, Turkey; 2006; pp. 401–404. [Google Scholar]
- Caro, G.D.; Dorigo, M. AntNet: Distributed Stigmergetic Control for Communications Networks. J. Artif. Intell. Res 1998, 9, 317–365. [Google Scholar]
- Günes, M.; Sorges, U.; Bouazizi, I. ARA-the Ant-Colony Based Routing Algorithm for MANETs. Proceedings of International Workshop on AD Hoc Networking (WAHN 2002), Vancouver, BC, Canada; 2002; pp. 79–85. [Google Scholar]
- Liu, C.; Li, L.; Xiang, Y. Research of Multi-Path Routing Protocol Based on Parallel Ant Colony Algorithm Optimization in Mobile Ad Hoc Networks. Proceedings of International Conference on Information Technology: New Generations (ITNG 2008), Las Vegas, NV, USA; 2008; pp. 1006–1010. [Google Scholar]
- Zhang, Y.; Kuhn, L.; Fromherz, M. Improvements on Ant Routing for Sensor Networks. Proceedings of ANTS 2004-the 4th International Workshop on Ant Colony Optimization and Swarm Intelligence, Brussels, Belgium; 2004; pp. 154–165. [Google Scholar]
- Camilo, T.; Carreto, C.; Silva, J.S.; Boavida, F. An Energy-efficient Ant-Based Routing Algorithm for Wireless Sensor Networks. Proceedings of ANTS 2006-the 5th International Workshop on Ant Colony Optimization and Swarm Intelligence, Brussels, Belgium; 2006; pp. 49–59. [Google Scholar]
- Liu, Y.; Zhu, H.; Xu, K.; Jia, Y. A Routing Strategy Based on Ant Algorithm for WSN. Proceedings of the 3rd International Conference on Natural Computation (ICNC 2007), Haikou, Hainan, China; 2007; pp. 685–689. [Google Scholar]
- GhasmAghaei, R.; Rahman, A.; Gueaieb, W.; Saddik, A.E. Ant Colony-Based Reinforcement Learning Algorithm for Routing in Wireless Sensor Networks. Proceedings of IEEE Instrumentation and Measurement Technology (IMTC 2007), Warsaw, Poland; 2007; pp. 1–6. [Google Scholar]
- Tu, Z.; Wang, Q.; Shen, Y. Optimal Mobile Agent Routing for Data Fusion in Distributed Sensor Networks Using Improved Ant Colony Algorithm. Proceedings of IEEE International Instrumentation and Measurement Technology Conference (I2MTC, 2008), Victoria, BC, Canada; 2008; pp. 155–159. [Google Scholar]
- Ren, X.; Liang, H.; Wang, Y. Multipath Routing Based On Ant Colony System in Wireless Sensor Networks. Proceedings of International Conference on Computer Science and Software Engineering (CSSE 2008), Wuhan, Hubei, China; 2008; pp. 202–205. [Google Scholar]
- Okdem, S.; Karaboga, D. Routing in Wireless Sensor Networks Using An Ant Colony Optimization (ACO) Router Chip. Sensors 2009, 9, 909–921. [Google Scholar]
- Heinzelman, W.R.; Chandrakasan, A.; Balakrishnan, H. An Application-Specific Protocol Architecture for Wireless Micro-Sensor Networks. IEEE Trans. Wirel. Commun 2002, 1, 660–670. [Google Scholar]
- Bahl, P.; Padmanabhan, V.N. RADAR: An In-Building RF-Based User Location and Tracking System. Proceedings of IEEE Infocom, Tel Aviv, Israel; 2000; pp. 775–784. [Google Scholar]
- Manjeshwar, A.; Agrawal, D.P. TEEN: A Routing Protocol for Enhanced Efficiency in Wireless Sensor Networks. Proceedings of the 15th International Parallel and Distributed Symposium, San Francisco, CA, USA; 2001; pp. 2009–2015. [Google Scholar]


| Neighbor ID | Pheromone Value | Residual Energy | Distance to Sink | Hop count | Tag |
|---|---|---|---|---|---|
| i | τci | Ei | Dis | hi | 0 |
| j | τcj | Ej | Djs | hj | 0 |
| … | … | … | … | … | 0 |
| Parameter | Value |
|---|---|
| α | 2 |
| β | 2 |
| ρ | 0.2 |
| τini(i, j) | k |
| the number of event | 1 |
| packet size | 512 bytes |
| broadcast packet size | 20 bytes |
| the coordinate of sink | (0,200) |
| event radius | 20 m |
© 2010 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Yang, J.; Xu, M.; Zhao, W.; Xu, B. A Multipath Routing Protocol Based on Clustering and Ant Colony Optimization for Wireless Sensor Networks. Sensors 2010, 10, 4521-4540. https://doi.org/10.3390/s100504521
Yang J, Xu M, Zhao W, Xu B. A Multipath Routing Protocol Based on Clustering and Ant Colony Optimization for Wireless Sensor Networks. Sensors. 2010; 10(5):4521-4540. https://doi.org/10.3390/s100504521
Chicago/Turabian StyleYang, Jing, Mai Xu, Wei Zhao, and Baoguo Xu. 2010. "A Multipath Routing Protocol Based on Clustering and Ant Colony Optimization for Wireless Sensor Networks" Sensors 10, no. 5: 4521-4540. https://doi.org/10.3390/s100504521





