Abstract
Generally, quartz crystal inductance frequency pulling in oscillators is very low and therefore is not often used in practice. The new method of improving frequency pullability uses inductance to compensate for quartz stray capacitances. To this end, a special AT fundamental quartz crystal working near the antiresonance frequency is selected. By modifying its equivalent circuit with load inductance and series tuning capacitance, the magnetic sensing of the circuit can be highly improved. The experimental results show that the new approach using the quartz crystal stray capacitance compensation method increases the frequency pulling range (from ≅ 2 kHz/μH to ≅ 600 kHz/μH) by × 300 depending on the type of oscillator, making possible the measurement of nano-magnetic changes.
1. Introduction
The high precision measurement of small inductance changes has become increasingly important in sensor techniques, particularly for the measurement of nano extensions, hollow nano-sphere magnetic properties, novel magnetic nano-adsorbents, displacement field forces, etc. The equivalent circuits of coreless inductive elements at low frequencies contain only inductances and series resistances. At high frequencies, parallel and coupling equivalent capacitances are included. Calculation of LCR values of complicated equivalent circuits (with many LCR elements) are very tedious, so often for that purpose a special dedicated processor with appropriate software is provided in the measuring device. In metrology, complex notation is frequently used to describe linear models of inductive elements. The presented models with lumped inductance are not always a sufficiently good approximation of the real properties of electric circuits. This applies particularly to circuits made with geometrically large wires (i.e., of a significant length, surface area, or volume). In such cases, the models applied use an adequately distributed inductance (linearly, over the surface, or throughout the volume) [–].
Impedance measurement methods for inductors are divided into three basic groups: current and voltage methods based on impedance determination, bridge and differential methods based on comparison of the voltage and currents of the measured and reference impedances until a state of balance is reached, and resonance methods based on physical connection of the measured inductor and a capacitor to create a resonant system [].
The advantage of the current and voltage method lies in limiting the influence of stray capacitances as a result of attaching one of the terminals of the measured impedance to a point of “virtual ground”. However, to obtain small measurement errors, especially at high frequencies, amplifiers with very good dynamic properties must be used. Combined inductance measurement errors obtained by current and voltage methods depend on the following factors: voltmeter errors, errors in calculating resistance, system factors (residual and leakage inductances, resistances and capacitances), and the quality of approximation of the measured impedances by the equivalent circuit [].
For correct measurements when using ac bridges, it is essential to minimize the influence of harmful coupling among the bridge elements and connection wires, between each other and the environment. These couplings are produced by the capacitances, inductances, and parasitic resistances of bridge elements to the environment and among themselves. The joint error of the inductance measurement results depends then on: the accuracy of the standards used as the bridge elements, mainly standard resistors and capacitors; errors in determining the frequency of the bridge supplying voltage; errors of the resolution of the zero detection systems; errors caused by the influence of residual and stray inductances; resistances and capacitances of the bridge elements and wiring; and the quality of approximation of the measured impedances in the equivalent circuit [].
Resonance methods are a third type of inductance measurement method. They are based on the application of a series or parallel resonance LC circuit as elements of either a bridge circuit or a two-port (four-terminal) “T”-type network. The joint error of the inductance measurement results are similar as when using ac bridge method (depending on the quality of the elements) [].
Instruments commonly used for inductance measurements are built as universal and multifunctional devices. The results of inductance measurements depend on how the measurements are preformed, including how the measured inductor is connected to the meter. Care should be taken to limit such influences as inductive and capacitive coupling of the inductive element to the environment, sources of distortion, and the choice of operating frequency (Hewlett-Packard 4284A—Precision LCR meter, 0.01 nH–99.9999 kH, 20 Hz–1 MHz, 0.05%) [].
The quartz crystal method is another possible method. A prior study of the quartz crystal pulling increase has shown that it is also possible to increase the inductive frequency pulling []. The latter is usually a lot smaller than the capacitive one and is as such not often used in practice. However, the great advantage of this method is smaller parasitic capacitance, inductance and resistance, on the one hand, and high sensitivity and stability of small inductance change measurements, on the other. The usual inductance pulling is in the range up to 2 kHz/μH, but through an appropriate compensation of the stray capacitance of the housing and the crystal element (which is a novelty in this research), inductance pulling can be greatly improved. This research focuses on the inductance pulling sensitivity of the AT fundamental quartz crystals operating over the measurement temperature range of 10°C to 40 °C. Crystals fabricated in this manner exhibit excellent frequency versus temperature stability. They have fundamental resonant frequencies between 3.5 and 10 MHz [].
2. Inductance Compensation of Quartz Parasitic Capacitance
In the equivalent circuit of an electrical representation of the quartz crystal’s parasitic capacitance Co represents the capacitance of the crystal element and holder (Figure 1). Oscillator crystals are normally designed with Co less than 5 pF. One possible way of increasing the inductance pulling sensitivity is to compensate Co using an inductance Lm. By decreasing the values of k = (1, 0.5, 0.33), Co in (1/k) · Co increases, changing the value of Lm into k · Lm (Equation 1) [–]:
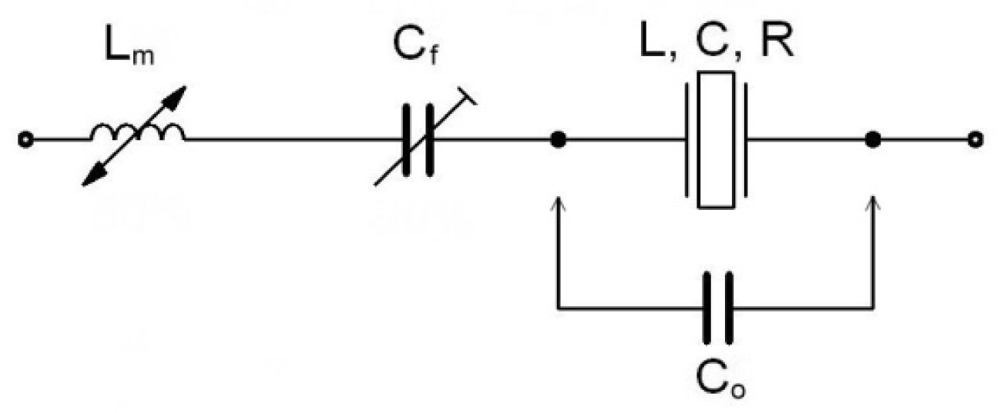
Figure 1.
Compensation inductance Lm (sensing inductance) and fine tuning capacitance Cf in series with the quartz crystal.
The special value of the chosen compensated Lm (sensing very small magnetic changes) due to high sensitivity represents a novelty in this research. Due to the small inductance Lm, the real resistance Rm can be ignored. The series capacitance Cf is using for fine (quartz resonsant) frequency tuning. The components L, C, and R represent the mechanical behavior of the crystal element [,].
Using the compensation criterion (Equation 1) we get Equation 2, which represents a new series resonant frequency for the circuit (Figure 1). The quartz series resonant frequency without Lm is represented with ω0. Depending on the selected value of k (k = 1, 0.5, 0.33), the value of Co changes producing three different resonance curves (Figure 2), for the Lm inductance range (450–750 μH). A more detailed theoretical background explaining Equation 2 is provided in references [] and [].
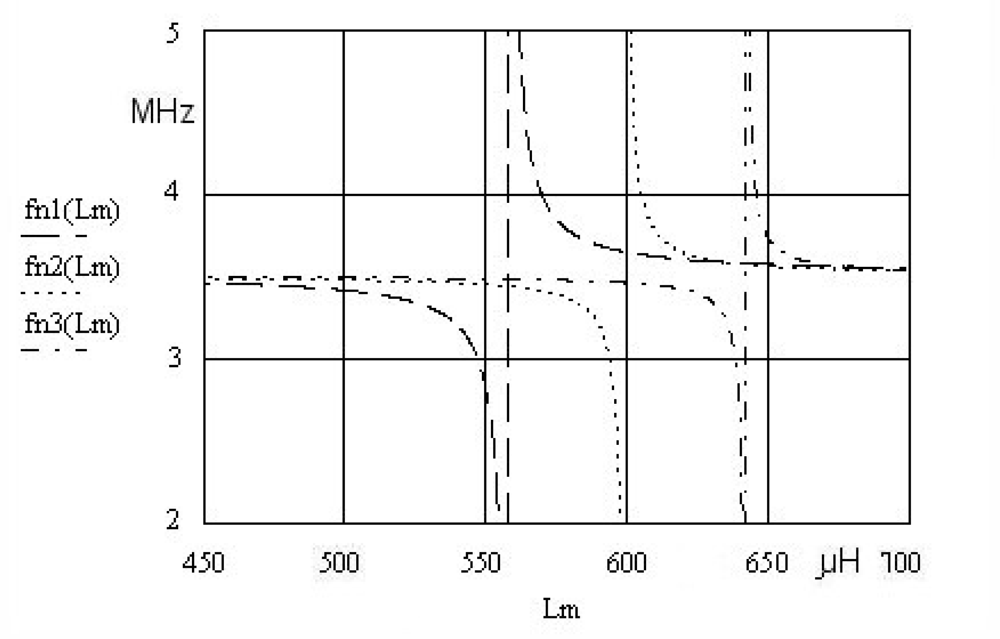
Figure 2.
Frequency pulling for fn1 (Lm) for k = 1, fn2 (Lm) for k = 0.5 and fn3 (Lm) for k = 0.33 in relation to the change of Lm.
Equation 2 contains the criterion (Equation 1) with a factor k determining the value of Lm in relation to the given C0.
3. Experimental Results
The experimental data values in the quartz crystal equivalent circuit were measured by a HP 4194A impedance/gain-phase analyzer. The quartz crystal (in a HC-49/U housing) was selected due to its high Q value (Table 1) and consequently, its stable oscillation []

Table 1.
Quartz data for resonant frequency 3.5 MHz [].
The frequency fr represents a fundamental quartz crystal resonant frequency (Table 1). The value k (Equation 2) determines the ratio between the compensation inductance Lm and C0. Figure 2 shows Equation 2 for three different k values (k = 1, 0.5, 0.33) at the constant value of Cf = 50 pF.
In the case of fn3 (Lm), where k = 0.33 and Lm = 640 μH, the most steep change of the resonant frequency close to quartz crystal antiresonance frequency can be observed. For the range of inductance change 1μH at Lm = 640 μH the oscillator frequency change is approximately 600 kHz (Figure 2 and Figure 3). The change is non-linear, but with an appropriate approximation method it can be linearized. To get a steeper change, C0 should be < 1 pF, which practically does not exist in the currently manufactured crystals.
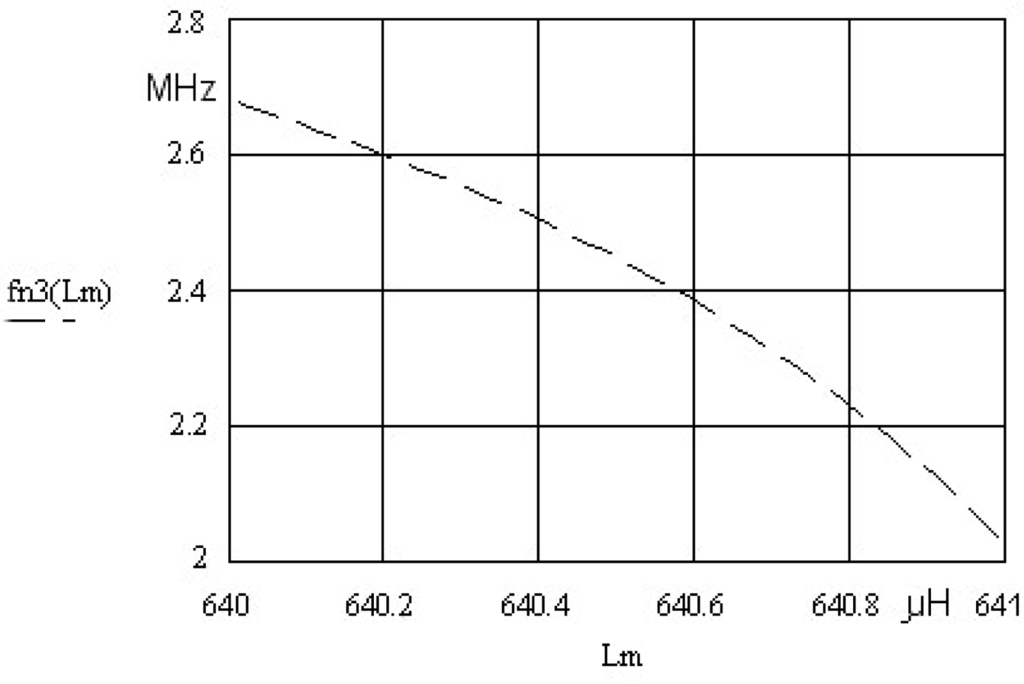
Figure 3.
Frequency pulling fn3 (Lm) for k = 0.33.
The capacitance Cf in the circuit (Figure 1) is used to set the frequency working point at a given chosen inductance (Figure 4). By setting the inductance working point, greater or smaller frequency sensitivity can be achieved. The capacitor Cf must be of high-quality (made of ceramics).
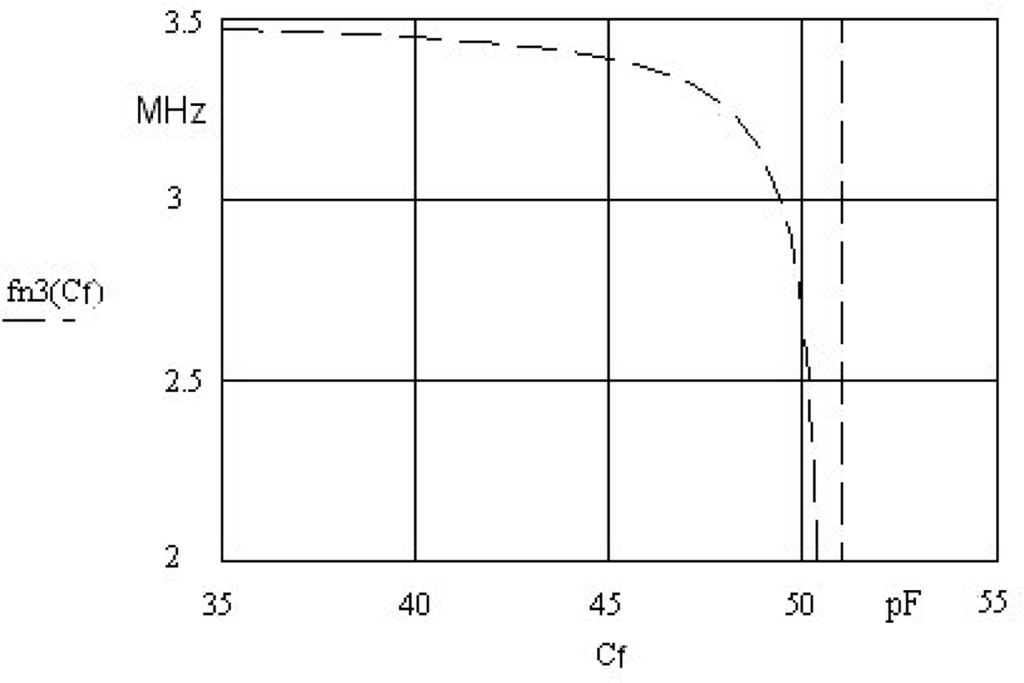
Figure 4.
Fine-tuning of the working frequency using Cf (35 up to 55 pF) at constant value Lm = 640 μH.
4. Frequency Sensitivity and Stability
Experimental results show the quartz crystal frequency sensitivity in relation to the applied use of circuits and increased inductance frequency pulling. Taking into account the long-term quartz crystal frequency stability (0.1 Hz) (described in reference []), the frequency pulling increase (at the frequency change of 600 kHz/1μH) (Figure 3) gives the lowest inductance change 100 fH/0.1Hz. If, however, the short-term (one day) crystal frequency stability (0.01Hz) is taken into account, the lowest inductance change is 10 fH/0.01Hz [–].
The most common factors affecting frequency stability such as operating temperature range, aging, hysteresis and drive level as well as all other crystal characteristics influencing the stability should also be considered because a stable oscillator circuit plays an important role in the increase of pulling and linear frequency dependence. As a consequence of hysteresis, the frequency versus temperature curves obtained by slowly increasing the temperature from, say, 10 °C to 40 °C will not coincide with the curve obtained by slowly decreasing the temperature from 40 °C to 10 °C. Frequency stability also depends on the temperature coefficient of the inductance material used of Lm. In general, the oscillator’s circuit long-term stability also depends upon the crystal aging. Cold weld packages which are specially processed and welded under a high vacuum offer better aging rates and typically the aging rates of cold weld crystals is less than ±1 ppm/year (10 °C to 40 °C). Stability of the electronic circuit depends upon the circuit type and quality of its elements. Also, it is important that the drive level in the oscillator application not exceed 30 μW [,,–].
5. Conclusions
Experimental results show that the use of series inductance compensated crystals with a special determined value of Lm increases the pulling range by ×300 for k = 0.33, depending on the circuit used. This high pulling increase represents a novelty and a major advantage of the method discussed in the measurement of femto-Henry ranges. With fine tuning a series load capacitance connected in series with the crystal, the frequency of the oscillator is set to an appropriate output circuit frequency. It should also be emphasized that the exact pulling limits depend on the crystal’s Q value as well as associated stray capacitances and the factor k. The inductance Lm is determined from known stray capacitances and the known factor k. Given the higher Q value, the frequency range below 10 MHz is very favorable because it influences high quartz oscillation stability. The increased pulling range obtained experimentally can be used for determination of many different measurements such as nano inductance, nano-extension and compression, nano-positioning, angle, pressure, nano-force and other non-electrical quantities [–].
References and Notes
- Dorf, R.C. Introduction to Electric Circuits; John Wiley & Sons: New York, NY, USA, 1989; pp. 100–200. [Google Scholar]
- Webster, J.G. The Measurement, Instrumentation, and Sensors, Inductance Measurement; CRC Press: Boca Raton, FL, USA, 1999; p. 50. [Google Scholar]
- Miller, G.L.; Wagner, E.R. Resonant Phase Shift Technique for the Measurement of Small Changes in Grounded Capacitors. Rev. Sci. Instrum 1990, 61, 1267. [Google Scholar]
- Matko, V.; Šafarič, R. Major Improvements of Quartz Crystal Pulling Sensitivity and Linearity Using Series Reactance. Sensors 2009, 9, 8263–8270. [Google Scholar]
- Matko, V. A Comparison of Frequency Pullability in Oscillators Using a Single AT-Cut Quartz Crystal and Those Using Two Single AT Cut Crystals Connected in Parallel with a Series Load Capacitance or Series Load Inductance. Sensors 2006, 6, 746–755. [Google Scholar]
- Jauch Quartz GmbH. Quartz Crystal Theory. Available online: http://www.jauch.de/ablage/med_00000619_1193753698_Quartz%20Crystal%20Theory%202007.pdf (accessed on 28 September 2009).
- Stanford Research Systems. Quartz Crystal Microbalance Theory. Available online: http://www.thinksrs.com/downloads/PDFs/ApplicationNotes/QCMTheoryapp.pdf (accessed on 28 September 2009).
- Brice, J.C. Crystals for Quartz Resonators. Rev. Mod. Phys 1985, 57, 105–138. [Google Scholar]
- Euroquartz. Quartz Oscillator Theory. Available online: http://www.euroquartz.co.uk (accessed on 28 September 2009).
- Schrüfer, E. Electrical Measurement: Quartz as a Frequency Reference; Carl Hanser Verlag: München, Germany, 1992; pp. 405–412. [Google Scholar]
- ATMEL. Analyzing the Behavior of an Oscillator and Ensuring Good Start-up. Available online: http://www.atmel.com/dyn/resources/prod_documents/doc4363.pdf (accessed on 28 September 2009).
- Kusters, J.A.; Vig, J.R. Thermal Hysteresis in Quartz Resonators. Proceedings of 44th Annual Symposium on Frequency Control, Baltimore, MD, USA; 1990; pp. 165–175. [Google Scholar]
- Rutman, J.; Walls, F.L. Characterization of Frequency Stability in Precision Frequency Sources. IEEE Trans. Instrum. Meas 1991, 79, 952–960. [Google Scholar]
- Lap-Tech Inc. Standard Frequency Components. Available online: http://www.laptech.com/ (accessed on 28 September 2009).
- Matko, V. Determination of Porosity Using a Water Pycnometer with Capacitive Level Detection. Sensor. Mater 2004, 16, 1–12. [Google Scholar]
- Gotlih, K.; Troch, I. Base Invariance of the Manipulability Index. Robotica 2004, 22, 455–462. [Google Scholar]
- Rajh, M.; Gotlih, K.; Kramberger, J.; Glodež, S. Improving Haptic Properties Using Manipulability Visualization. Gép 2008, 58, 123–126. [Google Scholar]
© 2010 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).