Quantitative Modeling of Coupled Piezo-Elastodynamic Behavior of Piezoelectric Actuators Bonded to an Elastic Medium for Structural Health Monitoring: A Review
Abstract
:1. Introduction
2. Review of the Bonded Piezo-Actuator Models
2.1. Analytical Approaches
2.1.1. The shear-lag theory based on the Euler-Bernoulli model
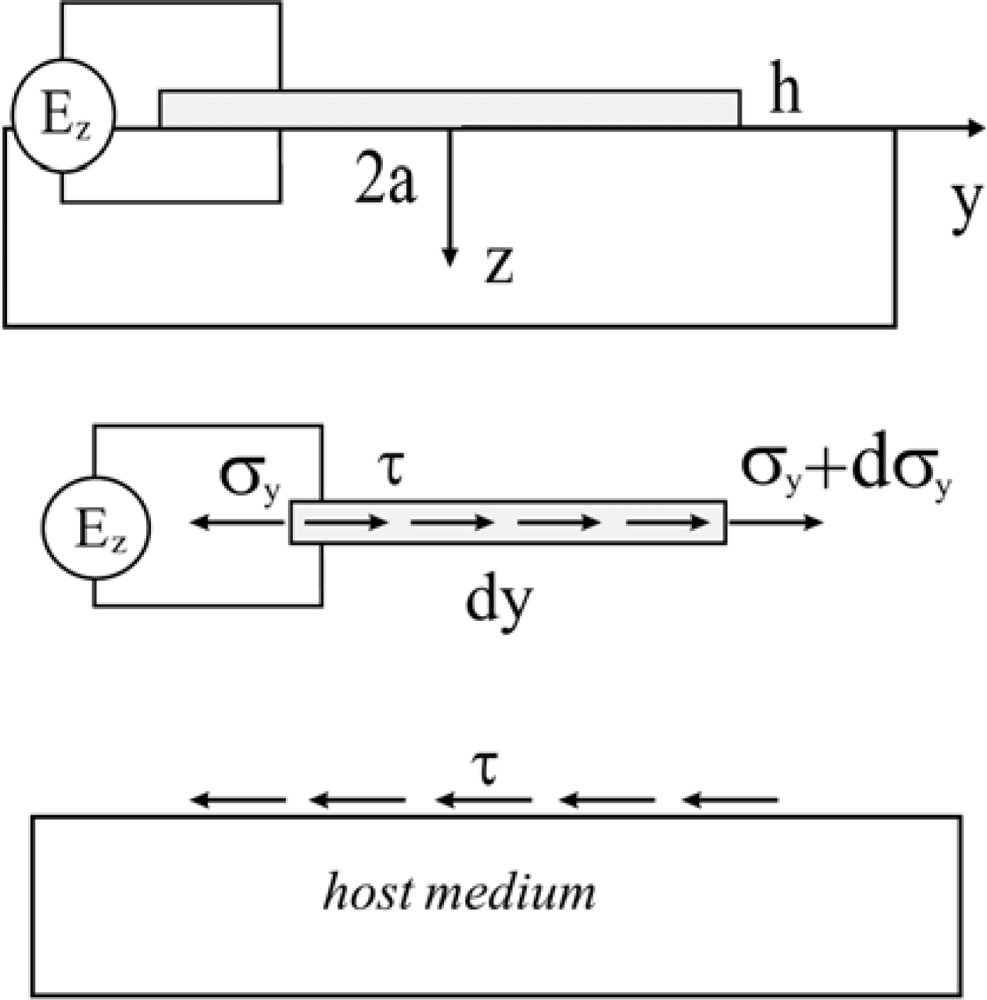
2.1.2. The simplified pin-force model
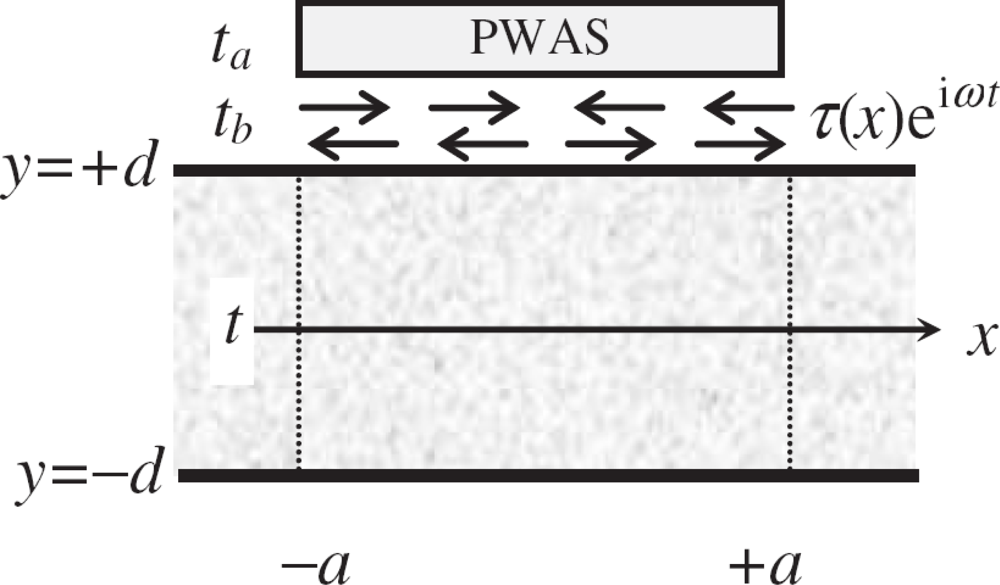
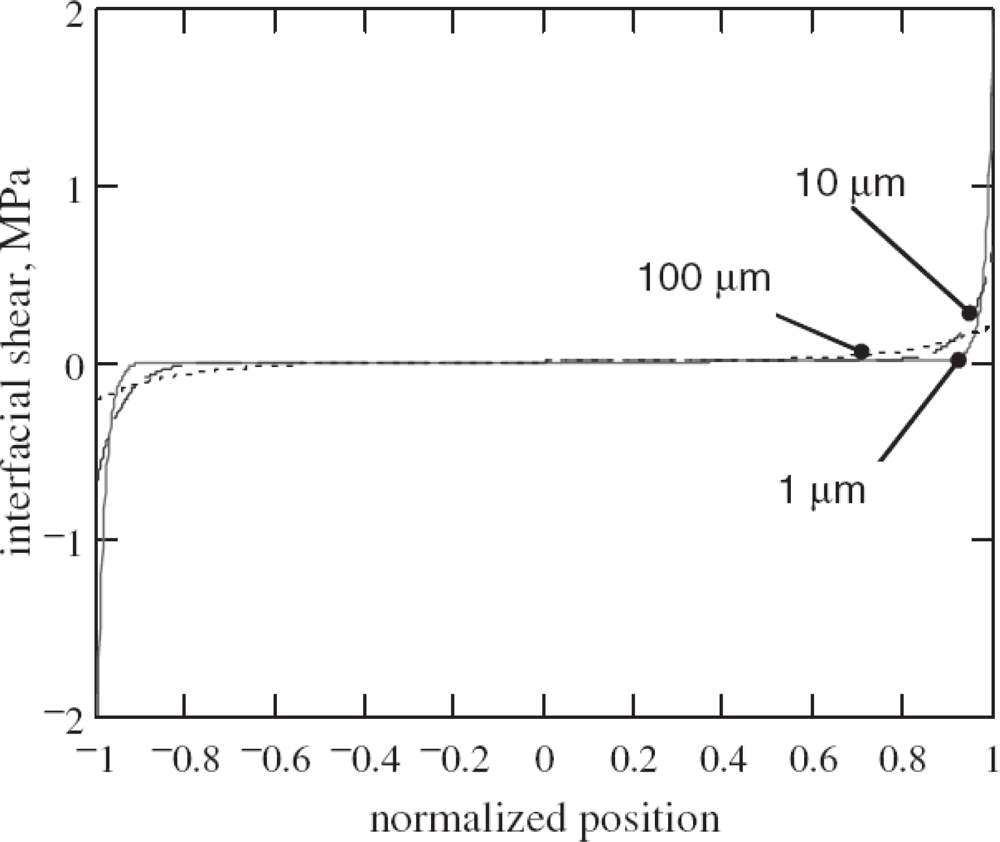
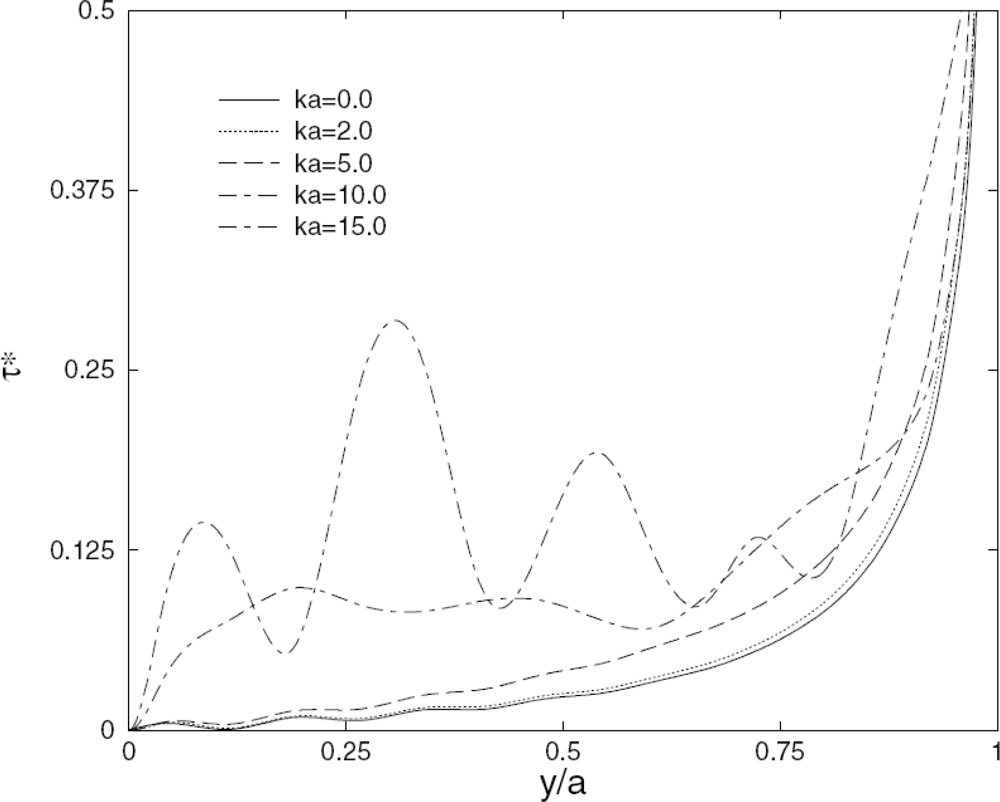
2.1.3. The elasticity equation-based model
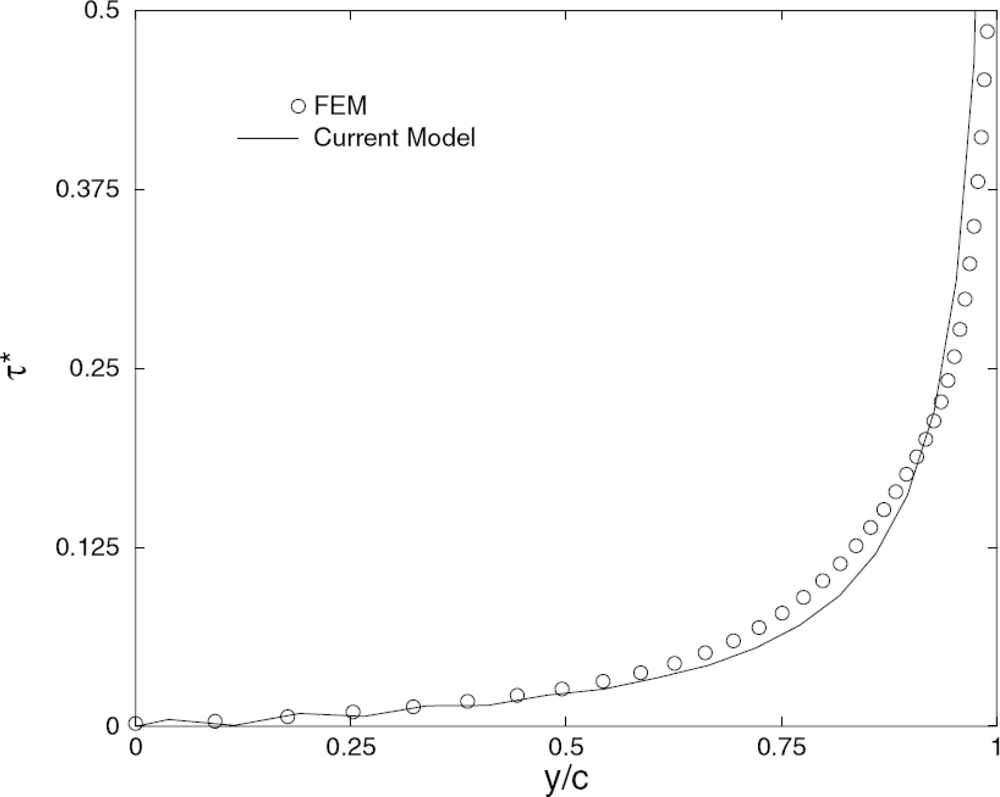
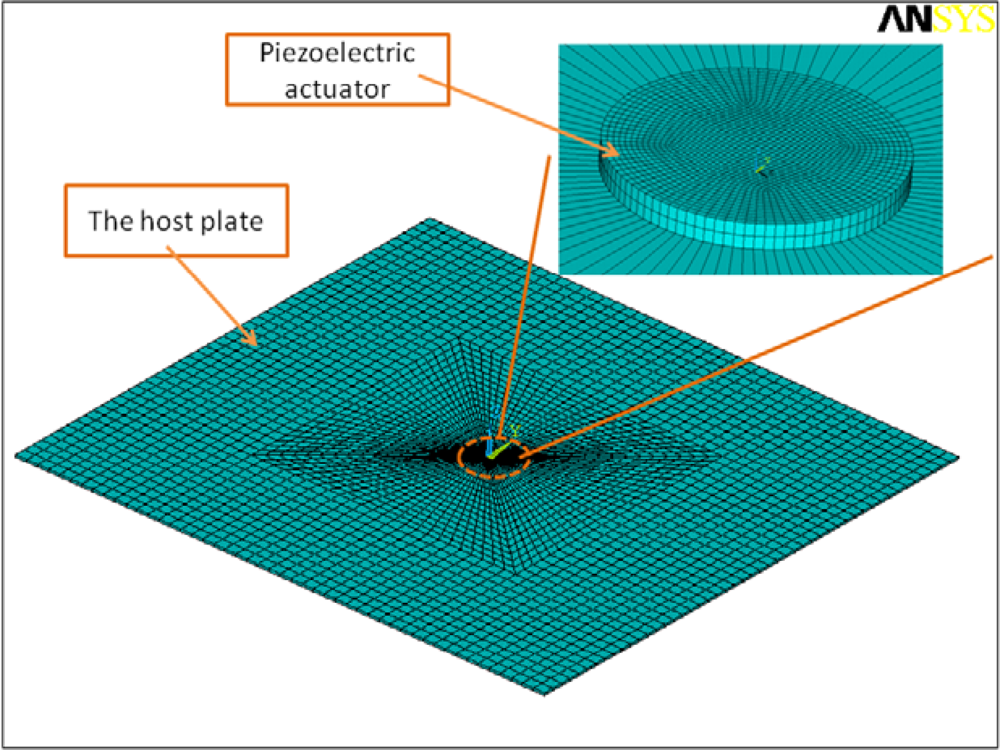
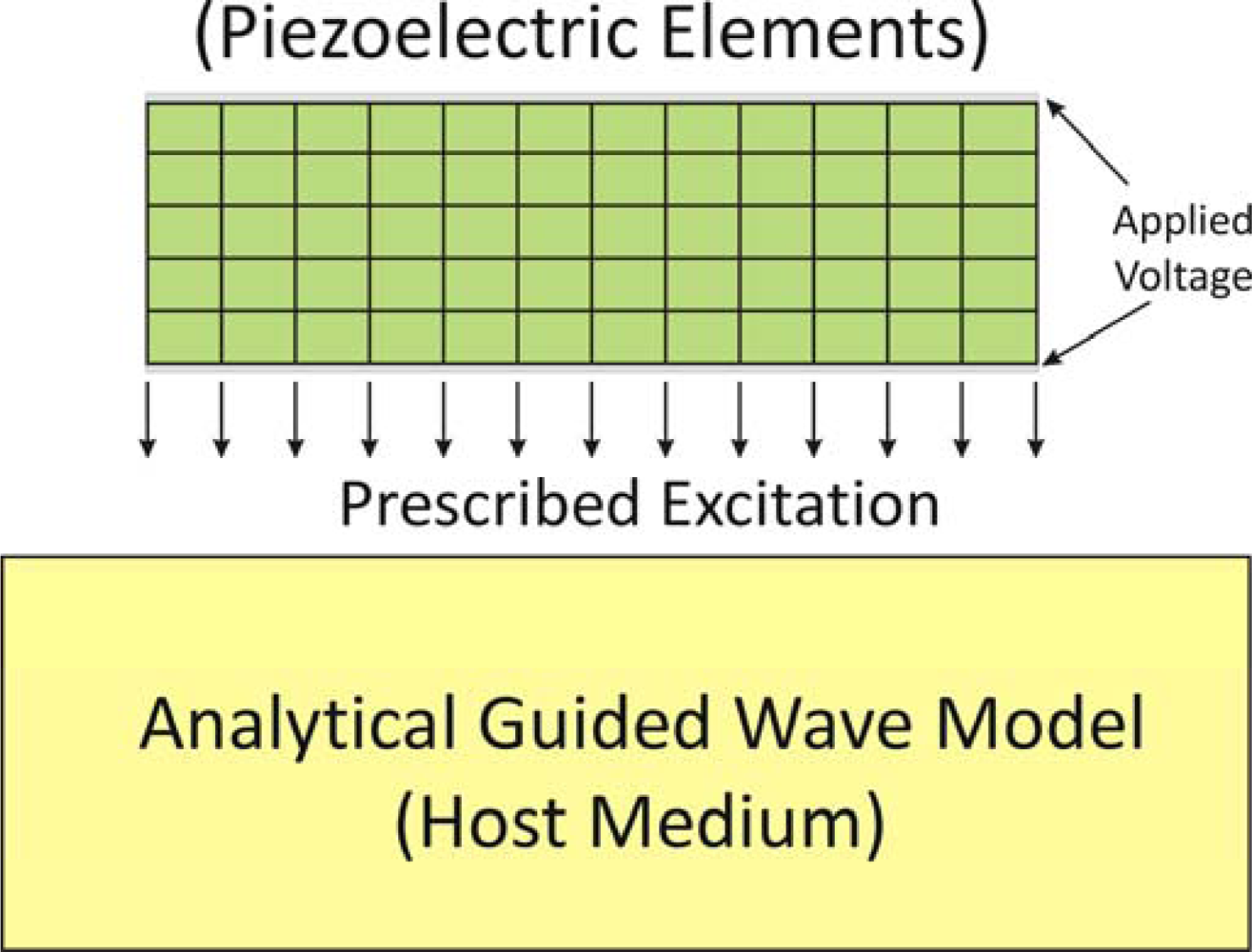
2.2. Numerical and Hybrid Approaches
3. Structural Health Monitoring Application
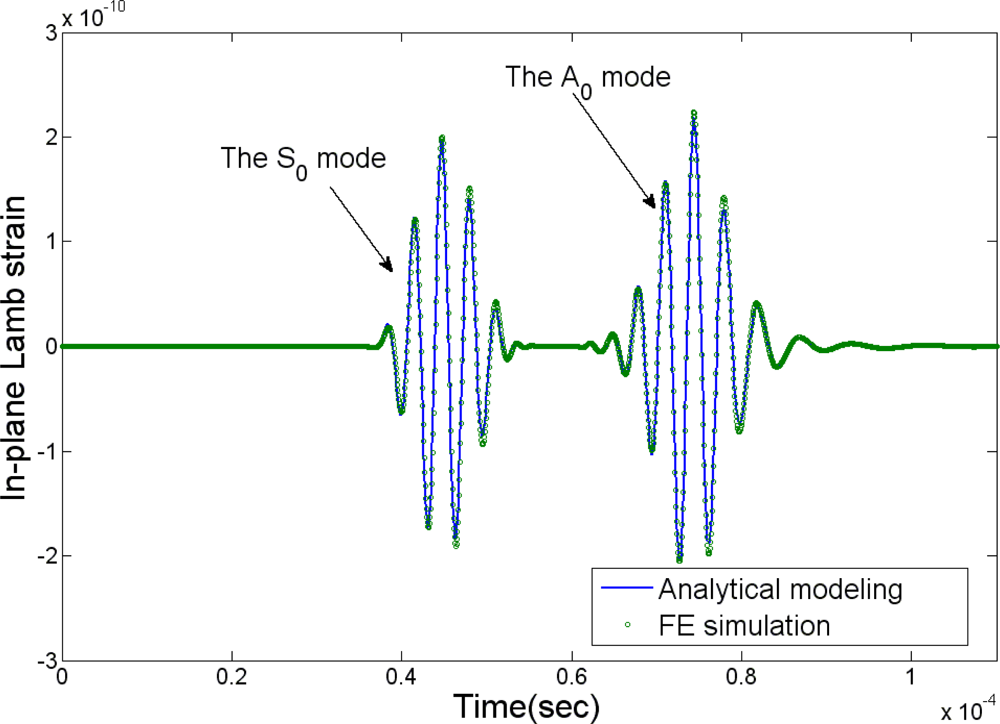
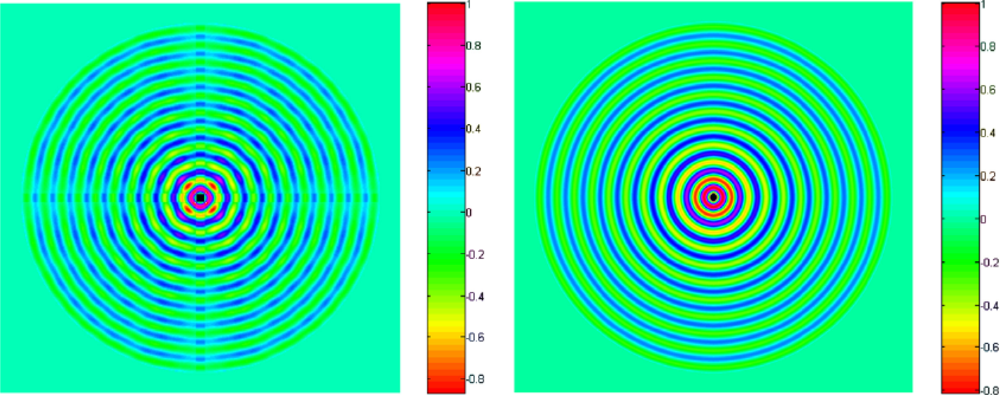
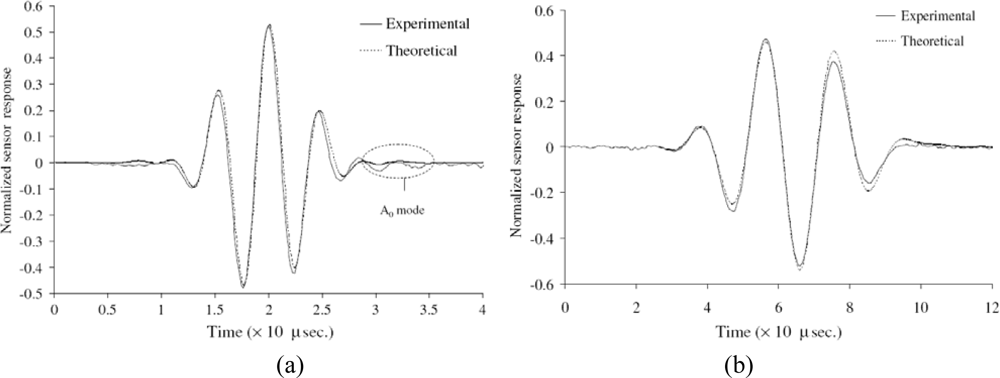
3.1. Dynamic Responses of the Host Structure Induced by the Piezo-Actuator
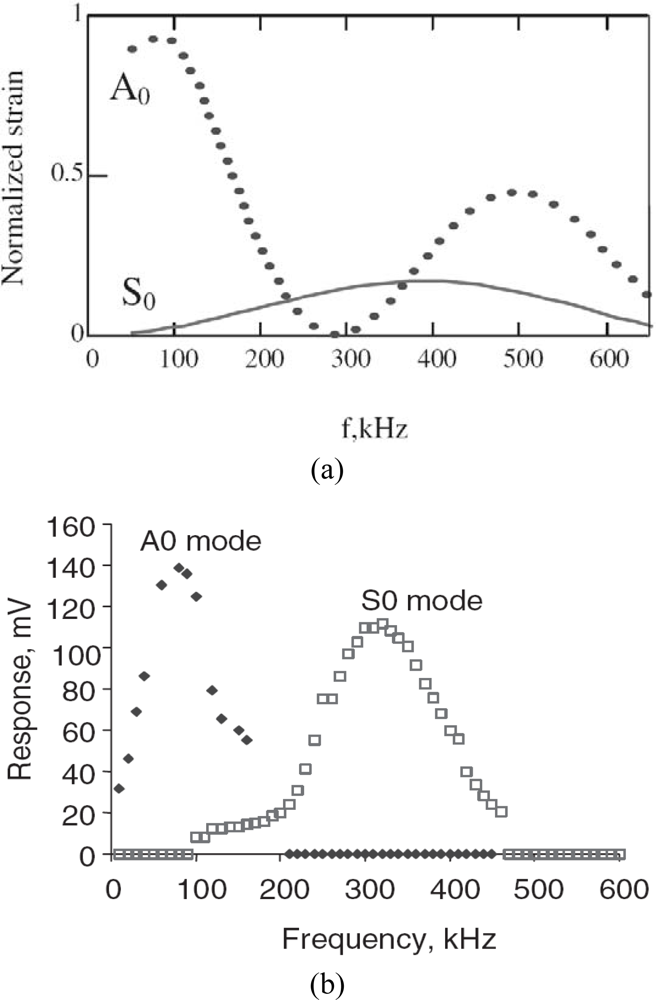
3.2. Wave Mode Tuning with Piezo-Actuators
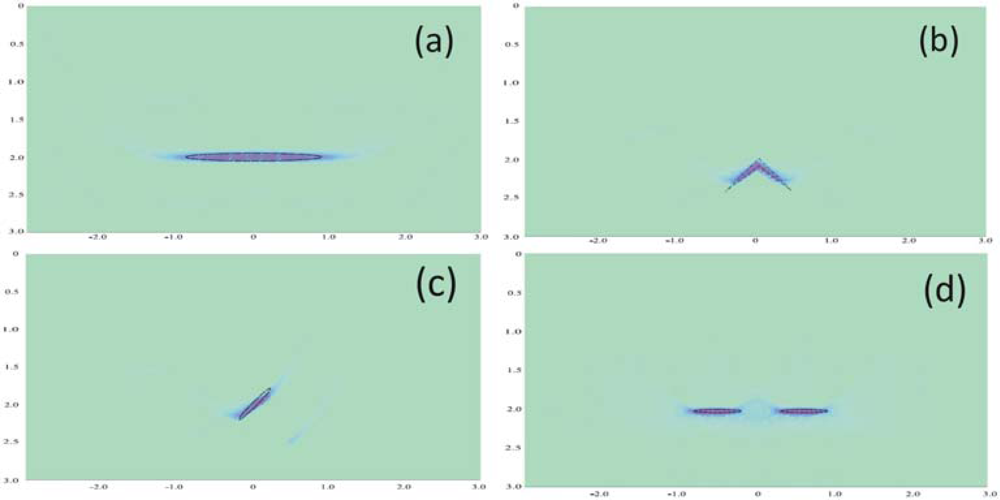
3.3. Quantitative Evaluation of Damage Using Elastic Waves
4. Conclusions and Summary
Acknowledgments
References
- Su, Z.; Ye, L.; Lu, Y. Guided Lamb waves for identification of damage in composite structures: a review. J. Sound Vibrat 2006, 295, 753–780. [Google Scholar]
- Song, F.; Huang, G.L.; Kim, J.H.; Haran, S. On the study of surface wave propagation in concrete structures using a piezoelectric actuator/sensor system. Smart Mater. Struct 2008, 17, 055024. [Google Scholar]
- Staszewski, W. J.; Mahzan, S.; Traynor, R. Health monitoring of aerospace composite structures–active and passive approach. Compos. Sci. Technol 2009, 69, 1678–1685. [Google Scholar]
- Giurgiutiu, V. Structural Health Monitoring with Piezoelectric Wafer Active Sensors; Academic Press: Burlington, MA, USA, 2007. [Google Scholar]
- Crawley, E.F. Intelligent structures for aerospace: a technology overview and assessment. AIAA J 1994, 32, 1689–1699. [Google Scholar]
- Song, G.; Qiao, P.Z.; Binienda, W.K.; Zou, G.P. Active vibration damping of composite beam using smart sensors and actuators. J. Aerosp. Eng 2002, 15, 97–103. [Google Scholar]
- Yu, L.; Santoni-Bottai, G.; Xu, B.; Liu, W.; Giurgiutiu, V. Piezoelectric wafer active sensors for in situ ultrasonic-guided wave SHM. Fatigue Fract. Eng. Mater. Struct 2008, 31, 611–628. [Google Scholar]
- Liu, Y.J.; Fan, H.; Yang, J.S. Analysis of the shear stress transferred from a partially electroded piezoelectric actuator to an elastic substrate. Smart Mater. Struct 2000, 9, 248–254. [Google Scholar]
- Yang, Z.T.; Hu, Y.T.; Yang, J.S. Thin film piezoelectric actuators with nonuniform thickness for reducing actuating shear stress concentration. J. Intelligent Mater. Syst. Struct 2009, 20, 729–731. [Google Scholar]
- Lanzara, G.; Yoon, Y.; Kim, Y.; Chang, F.-K. Influence of interface degradation on the performance of piezoelectric actuators. J. Intelligent Mater. Syst. Struct 2009, 20, 1699–1710. [Google Scholar]
- Bailey, T.; Hubbard, J.E. Distributed piezoelectric polymer active vibration control of a cantilever beam. AIAA J. Guid. Control Dyn 1985, 9, 605–611. [Google Scholar]
- Crawley, E.F.; de Luis, J. Use of piezoelectric actuators as elements of intelligent structures. AIAA J 1987, 25, 1373–1385. [Google Scholar]
- Crawley, E.F.; Anderson, E.H. Detailed models of piezoceramic actuation of beams. J. Intelligent Mater. Syst. Struct 1990, 1, 4–25. [Google Scholar]
- Im, S.; Atluri, S.N. Effects of a piezo-actuator on a finite deformation beam subjected to general loading. AIAA J 1989, 27, 1801–1807. [Google Scholar]
- Lin, M.W.; Rogers., C.A. Modeling of the actuation mechanism in a beam structure with induced strain actuators. Proceedings of the 34th AIAA/ASME/ASC/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Atlanta, GA, USA, 1993.
- Lin, M.W.; Rogers., C.A. Actuation response of a beam structure with induced strain actuators. Adaptive Struct. Mater. Syst 1993, 35, 129–139. [Google Scholar]
- Richard, J.S.; Cudney, H.H. Modeling multiple layer piezoelectric actuators in active structural control. Proceedings of SPIE Smart Structures and Materials, Albuquerque, NM, USA, 1993.
- Lee, S.S.; Sun, S.W. Vibrational formulation for Timoshenko beam element by separation of deformation mode. Commun. Num. Meth. Eng 1994, 10, 599–610. [Google Scholar]
- Lee, C.K.; Moon, F.C. Laminated piezopolymer plates for torsion and bending sensors and actuators. J. Acoust. Soc. Am 1989, 85, 2432–2439. [Google Scholar]
- Tzou, H.S.; Gadre, M. Theoretical analysis of a multi-layered thin shell coupled with piezoelectric shell actuators for distributed vibration control. J. Sound Vibrat 1989, 132, 433–450. [Google Scholar]
- Crawley, E.F.; Lazarus, K.B. Induced strain actuation of isotropic and anisotropic plates. AIAA J 1991, 29, 944–951. [Google Scholar]
- Wang, B.T.; Rogers, C.A. Laminated plate theory for spatially distributed induced strain actuators. J. Compos. Mater 1991, 25, 433–452. [Google Scholar]
- Batra, R.C.; Liang, X.Q.; Yang, J.S. The vibration of a simply supported rectangular elastic plate due to piezoelectric actuators. Int. J. Solids Struct 1996, 33, 1597–1618. [Google Scholar]
- Tzou, H.S.; Zhong, J.P. Electromechanics and vibrations of piezoelectric shell distributed systems: theory and applications. Trans. ASME J. Dyn. Syst. Meas. Control 1993, 115, 506–517. [Google Scholar]
- Hagood, N.W.; Chung, W.H. Modeling of piezoelectric actuator dynamics for active structural control. J. Intelligent Mater. Syst. Struct 1990, 1, 327–354. [Google Scholar]
- Tauchert, T.R. Piezothermalelastic behavior of a laminated plate. J. Therm. Stresses 1992, 15, 25–37. [Google Scholar]
- Mitchell, J.A.; Reddy, J.N. A study of embedded piezoelectric layers in composite cylinders. Trans. ASME J. Appl. Mech 1995, 62, 166–173. [Google Scholar]
- Banks, H.T.; Smith, R.C. The modeling of piezoelectric patch interactions with shells, plates and beams. Quart. Appl. Math 1995, 53, 353–381. [Google Scholar]
- Reddy, J.N. On laminated composite plates with integrated sensors and actuators. Eng. Struct 1997, 21, 568–593. [Google Scholar]
- Han, J.H.; Lee, I. Analysis of composite plates with piezoelectric actuators for vibration control using layerwise displacement theory. Compos. B: Eng 1998, 29, 519–672. [Google Scholar]
- Yang, S.; Ngol, B. General sensor equation and actuator equation for the theory of laminated piezoelectric plates. Smart Mater. Struct 1999, 8, 411–415. [Google Scholar]
- Wang, D.H.; Huang, S.L. Health monitoring and diagnosis for flexible structures with PVDF piezoelectric film sensor array. J. Intelligent Mater. Syst. Struct 2000, 11, 482–491. [Google Scholar]
- Benjeddou, A.; Trindade, M.A.; Ohayon, R. Piezoelectric actuation mechanism for intelligent sandwich structures. Smart Mater. Struct 2000, 9, 328–335. [Google Scholar]
- Wang, X.M.; Shen, Y.P. On the characterization of piezoelectric actuators attached to structures. Smart Mater. Struct 2001, 7, 389–395. [Google Scholar]
- Wang, Q.; Quek, S.T. A model for the analysis of beams with embedded piezoelectric layers. J. Intelligent Mater. Syst. Struct 2002, 11, 61–70. [Google Scholar]
- Ryu, D.H.; Wang, K.W. Characterization of surface bonded piezoelectric actuators on curved beams. Smart Mater. Struct 2002, 11, 377–388. [Google Scholar]
- Zhuk, Y.A.; Senchenkov, I.K. Modeling the stationary vibration and dissipative heating of thin-walled inelastic elements with piezoactive layers. Int. Appl. Mech 2004, 40, 546–556. [Google Scholar]
- Qiu, Z.C.; Zhang, X.M.; Wu, H.X.; Zhang, H.H. Optimal placement and active vibration control for piezoelectric smart flexible cantilever plate. J. Sound Vibrat 2007, 301, 521–543. [Google Scholar]
- Kumar, R.; Mishra, B.K.; Jain, S.C. Static and dynamic analysis of smart cylindrical shell. Finite Elem. Anal. Des 2008, 45, 13–24. [Google Scholar]
- Zheng, S.J.; Dai, F.; Song, Z. Active control of piezothermalelastic FGM shells using integrated piezoelectric sensor/actuator layers. Int. J. Appl. Electromagn 2009, 30, 107–124. [Google Scholar]
- Giurgiutiu, V. Tuned Lamb wave excitation and detection with piezoelectric wafer active sensors for structural health monitoring. J. Intelligent Mater. Syst. Struct 2005, 16, 291–305. [Google Scholar]
- Raghavan, A.; Cesnik, C.E.S. Finite-dimensional piezoelectric transducer modeling for guided wave based structural health monitoring. Smart Mater. Struct 2005, 14, 1448–1461. [Google Scholar]
- Nieuwenhuis, J.H.; Neumann, J.J., Jr; Greve, D.W.; Oppenheim, I.J. Generation and detection of guided waves using PZT wafer transducers. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2005, 52, 2103–2111. [Google Scholar]
- Moulin, E.; Assaad, J.; Delebarre, C.; Grondel, S.; Balageas, D. Modeling of integrated Lamb waves generation systems using a coupled finite element–normal modes expansion method. Ultrasonics 2000, 38, 522–526. [Google Scholar]
- Moulin, E.; Grondel, S.; Baouahi, M.; Assaad, J. Pseudo-3D modeling of a surface-bonded Lamb wave source (L). J. Acoust. Soc. Am 2006, 119, 2575–2578. [Google Scholar]
- Moulin, E.; Grondel, S.; Baouahi, M.; Assaad, J.; Duquenne, L. Modeling a surface-mounted Lamb wave emission-reception system: Applications to structural health monitoring. J. Acoust. Soc. Am 2008, 124, 3521–3527. [Google Scholar]
- Glushkov, E.; Glushkova, N.; Kvasha, O.; Seemann, W. Integral equation based modeling of the interaction between piezoelectric patch actuators and an elastic substrate. Smart Mater. Struct 2007, 16, 650–664. [Google Scholar]
- Dunn, C.T.; Raghavan, A.; Kessler, S.S. Analytical axisymmetric coupled piezo-elastodynamic models for guided-wave structural health monitoring. Proceedings of the 7th International Workshop on Structural Health Monitoring, Stanford, CA, USA, 2009.
- Wang, X.D.; Meguid, S.A. On the electroelastic behavior of a thin piezoelectric actuator attached to an infinite host structure. Int. J. Solids Struct 2000, 37, 3231–3251. [Google Scholar]
- Wang, X.D.; Huang, G.L. Wave propagation in electromechanical structures: induced by surface-bonded piezoelectric actuators. J. Intelligent Mater. Syst. Struct 2001, 12, 105–115. [Google Scholar]
- Chaudhry, Z.; Rogers, C.A. The pin-force model revisted. J. Intelligent Mater. Syst. Struct 1994, 5, 347–354. [Google Scholar]
- Yang, J.S. Equations for thick elastic plates with partially electroded piezoelectric actuators and higher mode electric fields. Smart Mater. Struct 1999, 8, 73–82. [Google Scholar]
- Kusculuoglu, Z.K.; Behrooz, F.; Rovston, T.J. New constitutive models for vibrations of a beam with piezoceramic patch actuator. Proceedings of SPIE Modeling, Signal processing and Control, San Diego, CA, USA, 2002.
- Ikeda, T.; Raja, S.; Ueda, T. Deformation of a beam with partially debonded piezoelectric actuators. J. Intelligent Mater. Syst. Struct 2009, in press.. [Google Scholar]
- Giugiutiu, V.; Santoni, G.B. Extension of the shear-lag solution for structurally attached ultrasonic active sensors. AIAA J 2009, 47, 1980–1983. [Google Scholar]
- Rose, J.L. Ultrasonic Waves in Solid Media; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Lin, X.; Yuan, F.G. Diagnostic Lamb waves in an integrated piezoelectric sensor/actuator plate: analytical and experimental studies. Smart Mater. Struct 2001, 10, 907–913. [Google Scholar]
- Giurgiutiu, V. Zagrai, Characterization of piezoelectric wafer active sensors. J. Intelligent Mater. Syst. Struct 2000, 11, 959–975. [Google Scholar]
- Wilcox, P.D.; Lowe, M.J.S.; Cawley, P. Mode and transducer selection for long range Lamb wave inspection. J. Intelligent Mater. Syst. Struct 2001, 12, 553–565. [Google Scholar]
- Santoni, G.B.; Yu, L.; Xu, B.; Giurgiutiu, V. Lamb wave-mode tuning of piezoelectric wafer active sensors for structural health monitoring. Trans. ASME J. Vib. Acoust 2007, 129, 752–762. [Google Scholar]
- Lanza di Scalea, F.; Salamone, S. Temperature effects in ultrasonic Lamb wave structural health monitoring systems. J. Acoust. Soc. Am 2008, 124, 161–174. [Google Scholar]
- Wang, X.D.; Huang, G.L. Wave propagation induced by multiple piezoelectric actuators in electromechanical structures. Trans. ASME J. Pressure Vessel Technol 2001, 124, 311–318. [Google Scholar]
- Wang, X.D.; Huang, G.L. Wave propagation in electromechanical structures: induced by embedded piezoelectric actuators. J. Intelligent Mater. Syst. Struct 2001, 12, 117–125. [Google Scholar]
- Wang, X.D.; Huang, G.L. On elastic wave propagation induced by a network of piezoelectric actuators. Acta Mech 2003, 160, 1–18. [Google Scholar]
- Wang, X.D.; Huang, G.L. Wave propagation generated by piezoelectric actuators attached to elastic substrates. Acta Mech 2006, 183, 155–176. [Google Scholar]
- Huang, G.L.; Sun, C.T. The dynamic behavior of a piezoelectric actuator bonded to an anisotropic elastic medium. Int. J. Solids Struct 2006, 43, 1291–1307. [Google Scholar]
- Sekouri, E.M.; Hu, Y.R.; Ngo, A.D. Modeling of a circular plate with piezoelectric actuators. Mechatronics 2004, 14, 1007–1020. [Google Scholar]
- Liu, W.P.; Giurgiutiu, V. Finite element simulation of piezoelectric wafer active sensors for structural health monitoring. Proceedings of SPIE Sensors and Smart Structures Technologies for Civil, Mechanical, and Aerospace Systems, San Diego, CA, USA, 2007.
- Han, S.; Palazotto, A.N.; Leakeas, C.L. Finite element analysis of Lamb wave propagation in a thin aluminum plate. J. Aerosp. Eng 2009, 22, 185–197. [Google Scholar]
- Ende, S. V.; Lammering, R. Modeling and simulation of Lamb wave generation with piezoelectric plates. Mech. Adv. Mater. Struct 2009, 16, 188–197. [Google Scholar]
- Raghavan, A.; Cesnik, CES. Modeling guided wave excitation by finite-dimensional piezoelectric transducers in composite plates. Proceedings of the 48th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Honolulu, HI, USA; 2007. [Google Scholar]
- Ihn, J.-B.; Chang, F.-K. Pitch-catch active sensing methods in structural health monitoring for aircraft structures. Struct. Health Monit 2008, 7, 5–19. [Google Scholar]
- Kessler, S.S.; Spearing, S.M.; Soutis, C. Damage detection in composite materials using Lamb wave methods. Smart Mater. Struct 2002, 11, 269–278. [Google Scholar]
- Giurgiutiu, V.; Zagrai, A.; Bao, J. Piezoelectric wafer embedded active sensors for aging structural health monitoring. Struct. Health Monit 2002, 1, 41–61. [Google Scholar]
- Mal, A.; Ricci, F.; Banerjee, S.; Shih, F. A conceptual structural health monitoring system based on vibration and wave propagation. Struct. Health Monit 2005, 4, 283–293. [Google Scholar]
- Zhao, X.L.; Gao, H.D.; Zhang, G.F.; Ayhan, B.; Yan, F.; Kwan, C.; Rose, J.L. Active health monitoring of an aircraft wing with embedded piezoelectric sensor/actuator network: I. Defect detection, localization and growth monitoring. Smart Mater. Struct 2007, 16, 1208–1217. [Google Scholar]
- Petculescu, G.; Krishnaswamy, S.; Achenbach, J.D. Group delay measurements using modally selective Lamb wave transducers for detection and sizing of delaminations in composites. Smart Mater. Struct 2008, 17, 015007. [Google Scholar]
- Kundu, T.; Das, S.; Jata, K.V. Health monitoring of a thermal protection system using Lamb waves. Struct. Health Monit 2009, 8, 25–49. [Google Scholar]
- Su, Z.; Li, C.; Wang, X.M.; Yu, L.; Zhou, C. Predicting delamination of composite laminates using an imaging approach. Smart Mater. Struct 2009, 18, 074002. [Google Scholar]
- Ng, C.T.; Veidt, M. A Lamb-wave-based technique for damage detection in composite laminates. Smart Mater. Struct 2009, 18, 074006. [Google Scholar]
- Michaels, J.E. Detection, Localization and characterization of damage in plates with an in situ array of spatially distributed ultrasonic sensors. Smart Mater. Struct 2008, 17, 035035. [Google Scholar]
- Giurgiutiu, V.; Roger, C.A. Modeling of the electro-mechanical (E/M) impedance response of a damaged composite beam. Adaptive Struct. Mater. Syst 1999, 87, 39–46. [Google Scholar]
- Su, Z.; Ye, L. Fundamental Lamb mode-based delamination detection for CF/EP composite laminates using distributed piezoelectrics. Struct. Health Monit 2004, 3, 43–68. [Google Scholar]
- Achenbach, J.D.; Sotiropoulos, D.A.; Zhu, H. Characterization of cracks from ultrasonic scattering data. Trans. ASME J. Appl. Mech 1987, 54, 754–760. [Google Scholar]
- Fink, M. Time reversal of ultrasonic field. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1992, 39, 555–592. [Google Scholar]
- Kuo, J.T.; Dai, T. Kirchhoff elastic wave migration for the case of noncoincident source and receiver. Geophysics 1984, 49, 1223–1238. [Google Scholar]
- Docherty, P. A brief comparison of some Kirchhoff integral formulas for migration and inversion. Geophysics 1991, 56, 1164–1169. [Google Scholar]
- Lin, X.; Yuan, F.G. Damage detection of a plate using migration technique. J. Intelligent Mater. Syst. Struct 2001, 12, 469–482. [Google Scholar]
- Lin, X.; Yuan, F.G. Experimental study applying a migration technique in structural health monitoring. Struct. Health Monit 2005, 4, 341–353. [Google Scholar]
- Wang, L.; Yuan, F.G. Damage identification in a composite plate using prestack reverse-time migration technique. Struct. Health Monit 2005, 4, 195–211. [Google Scholar]
- Wang, X.D.; Huang, G.L. Identification of embedded cracks using back-propagating elastic waves. Inverse Probl 2004, 20, 1393–1409. [Google Scholar]
- Wang, X.D.; Huang, G.L. Study of elastic wave propagation induced by piezoelectric actuators for crack identification. Int. J. Fract 2004, 126, 287–306. [Google Scholar]

© 2010 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Huang, G.; Song, F.; Wang, X. Quantitative Modeling of Coupled Piezo-Elastodynamic Behavior of Piezoelectric Actuators Bonded to an Elastic Medium for Structural Health Monitoring: A Review. Sensors 2010, 10, 3681-3702. https://doi.org/10.3390/s100403681
Huang G, Song F, Wang X. Quantitative Modeling of Coupled Piezo-Elastodynamic Behavior of Piezoelectric Actuators Bonded to an Elastic Medium for Structural Health Monitoring: A Review. Sensors. 2010; 10(4):3681-3702. https://doi.org/10.3390/s100403681
Chicago/Turabian StyleHuang, Guoliang, Fei Song, and Xiaodong Wang. 2010. "Quantitative Modeling of Coupled Piezo-Elastodynamic Behavior of Piezoelectric Actuators Bonded to an Elastic Medium for Structural Health Monitoring: A Review" Sensors 10, no. 4: 3681-3702. https://doi.org/10.3390/s100403681



