Optimal Filters with Multiple Packet Losses and its Application in Wireless Sensor Networks
Abstract
:1. Introduction
2. Problem Formulation
3. Linear Minimum Variance Filters with Multiple Packet Losses
3.1. Design of Linear Filter with Multiple Packet Losses
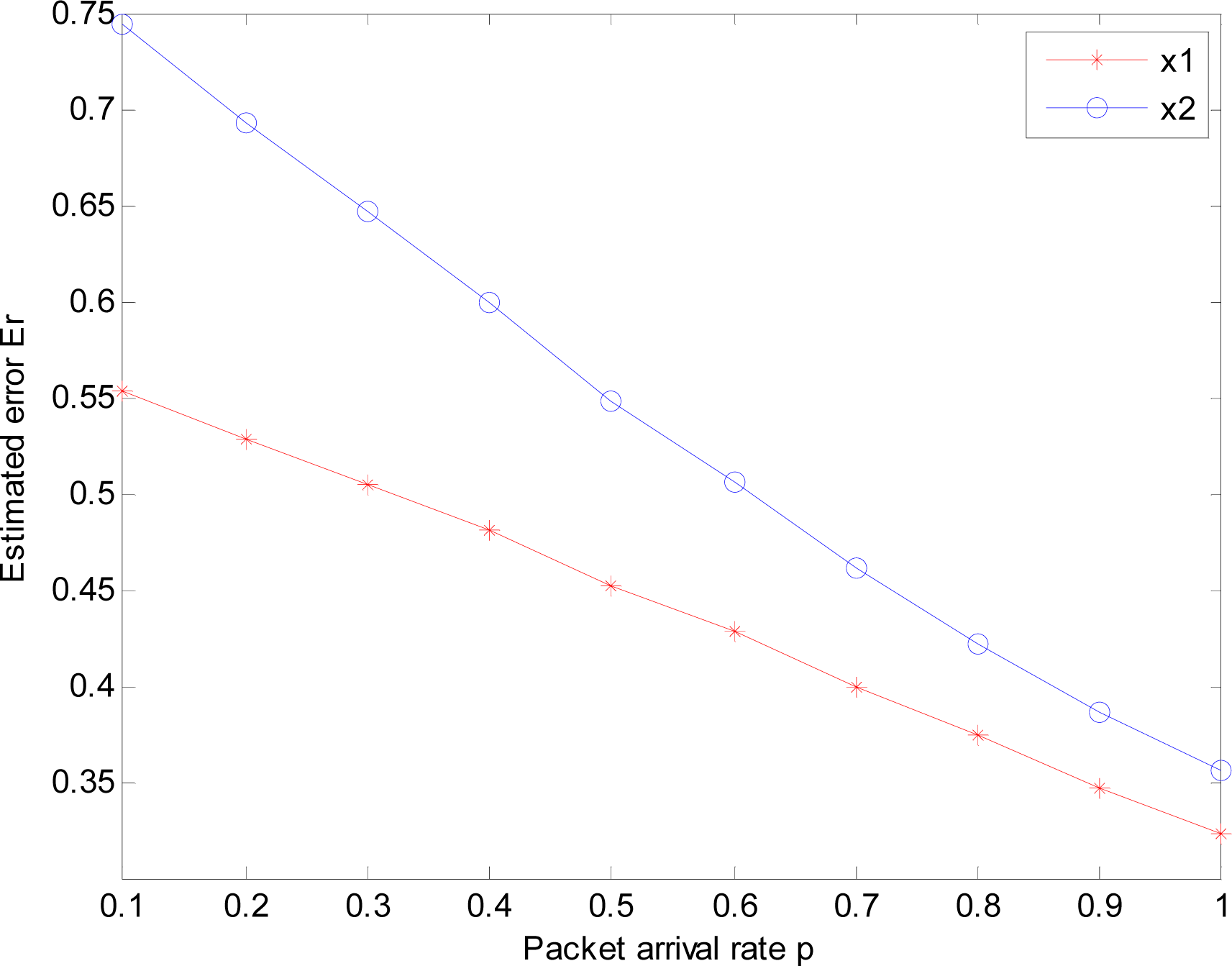
3.2. An example for LMVF
4. Extended Minimum Variance Filter with Multiple Packet Losses
4.1. Design of Extended Minimum Variance Filter with Multiple Packet Losses
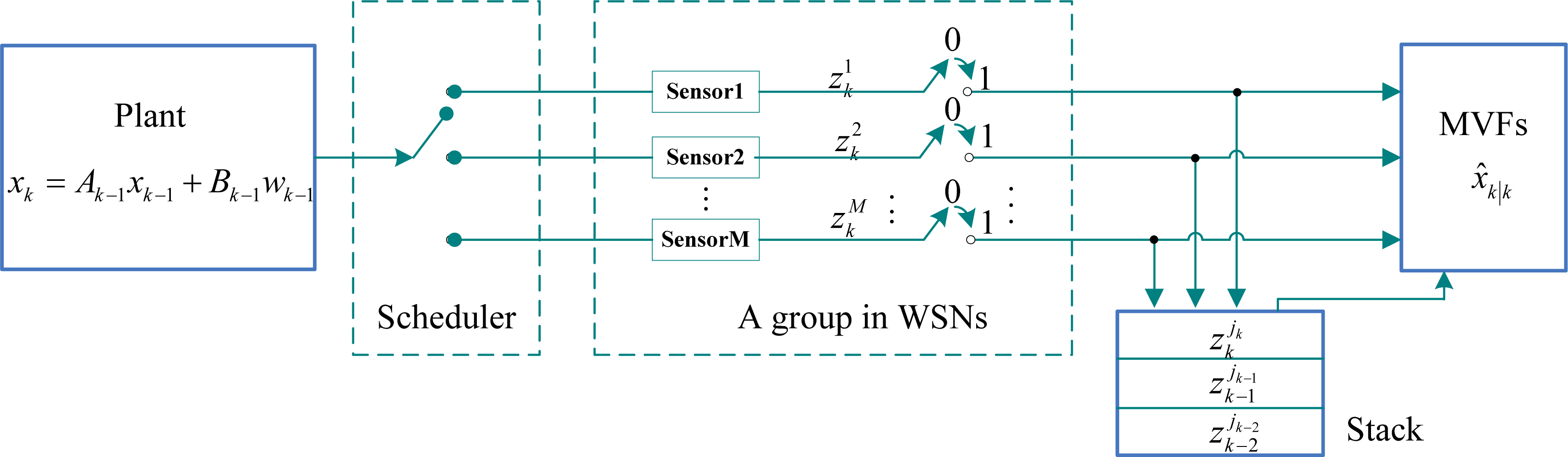
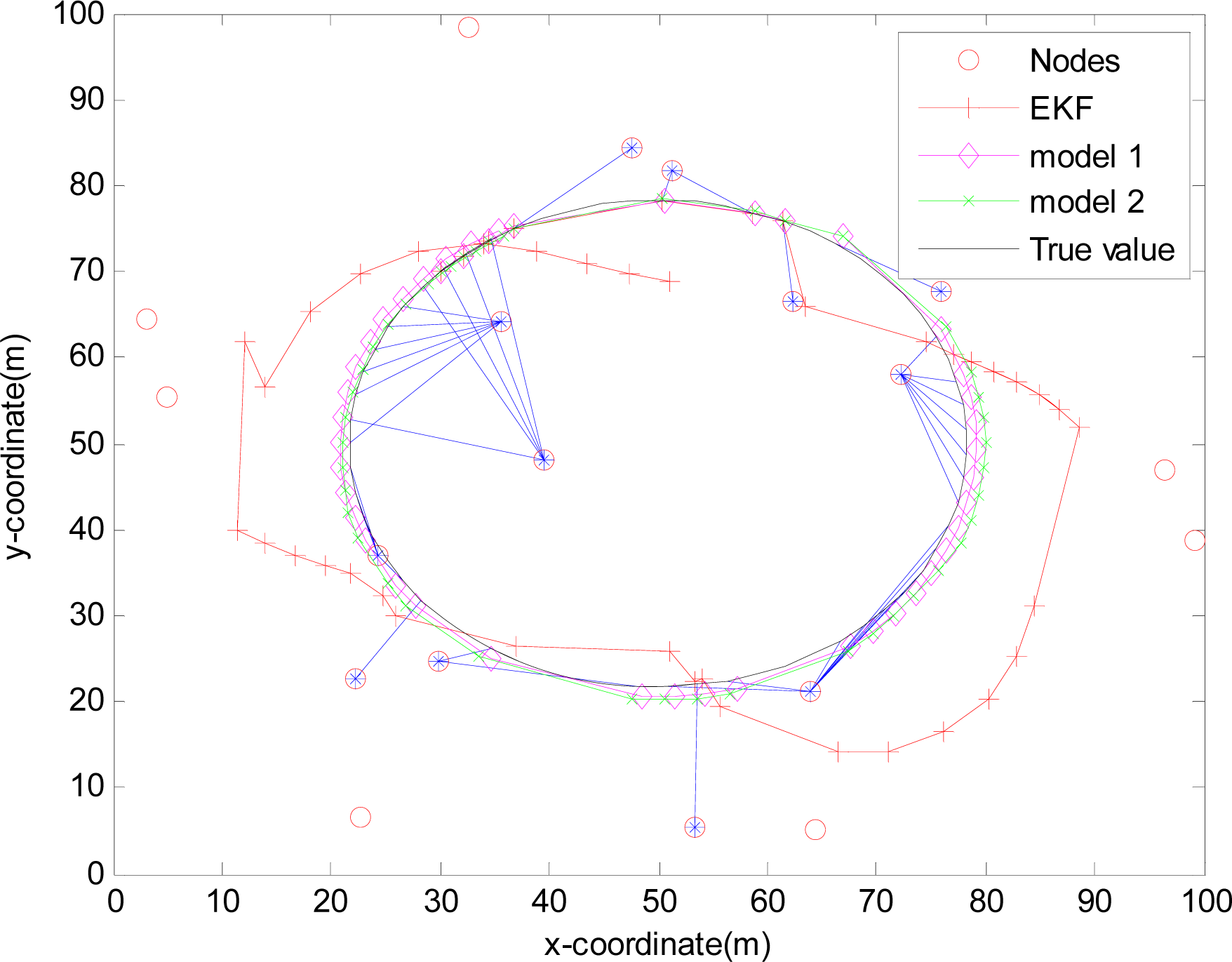
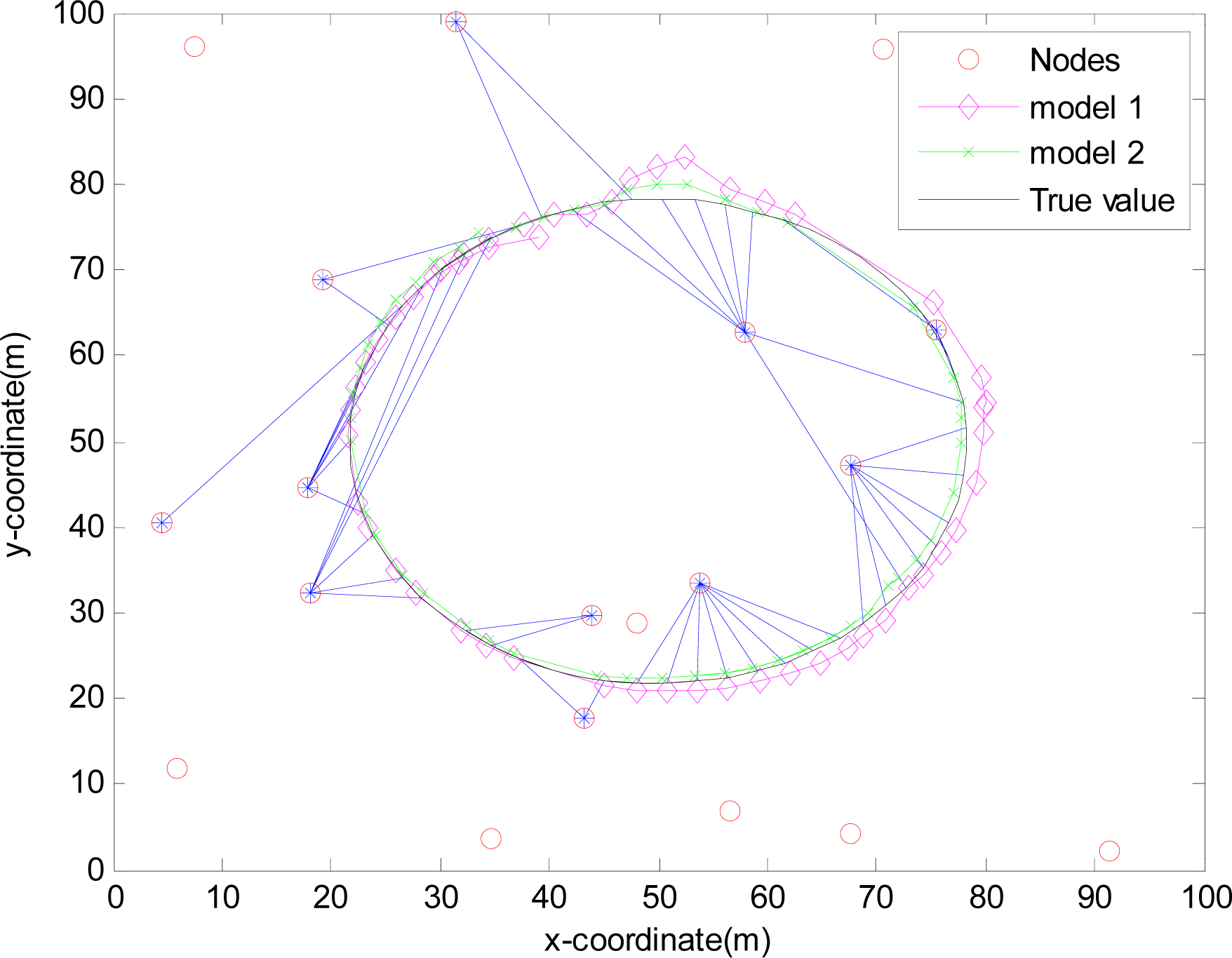
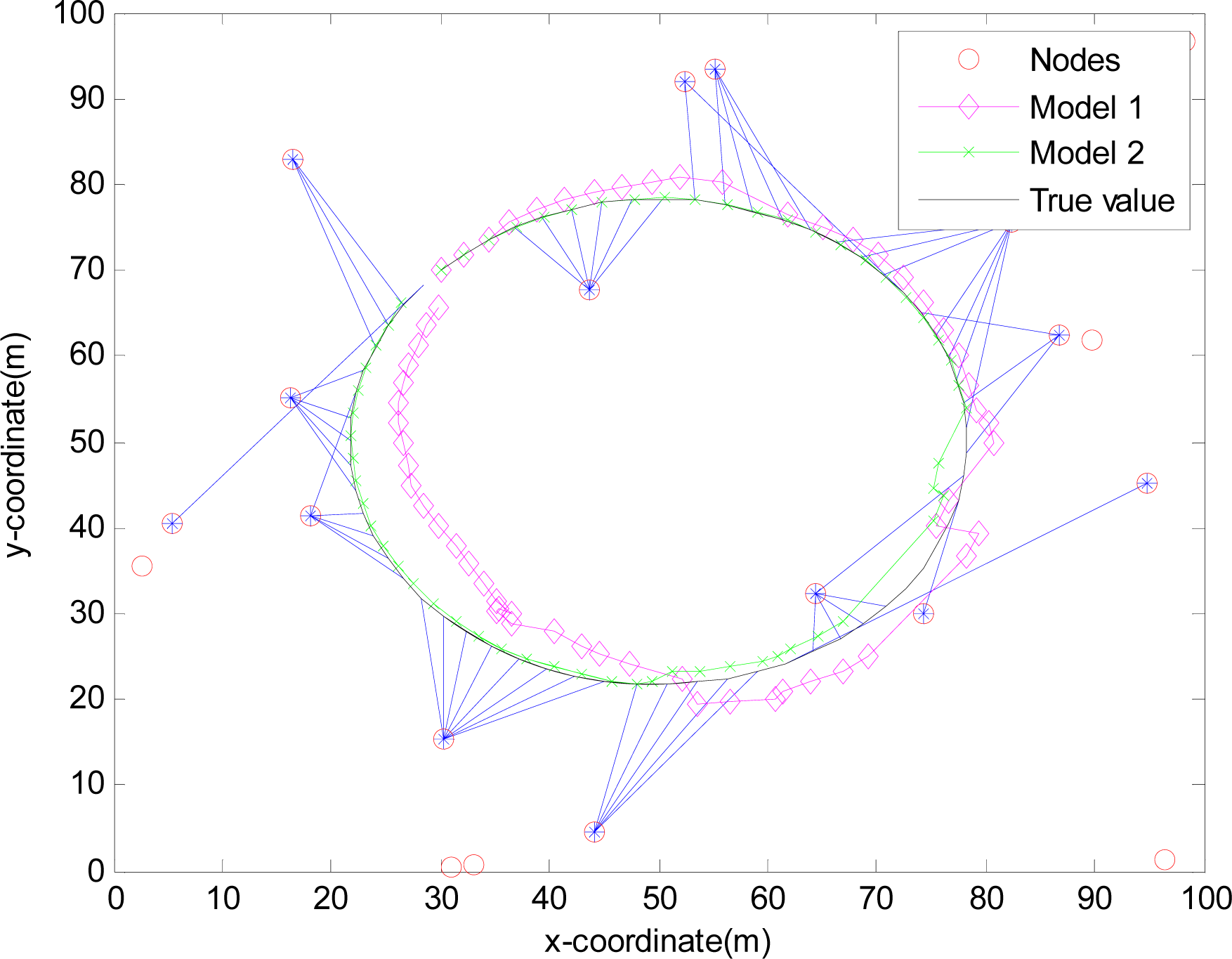
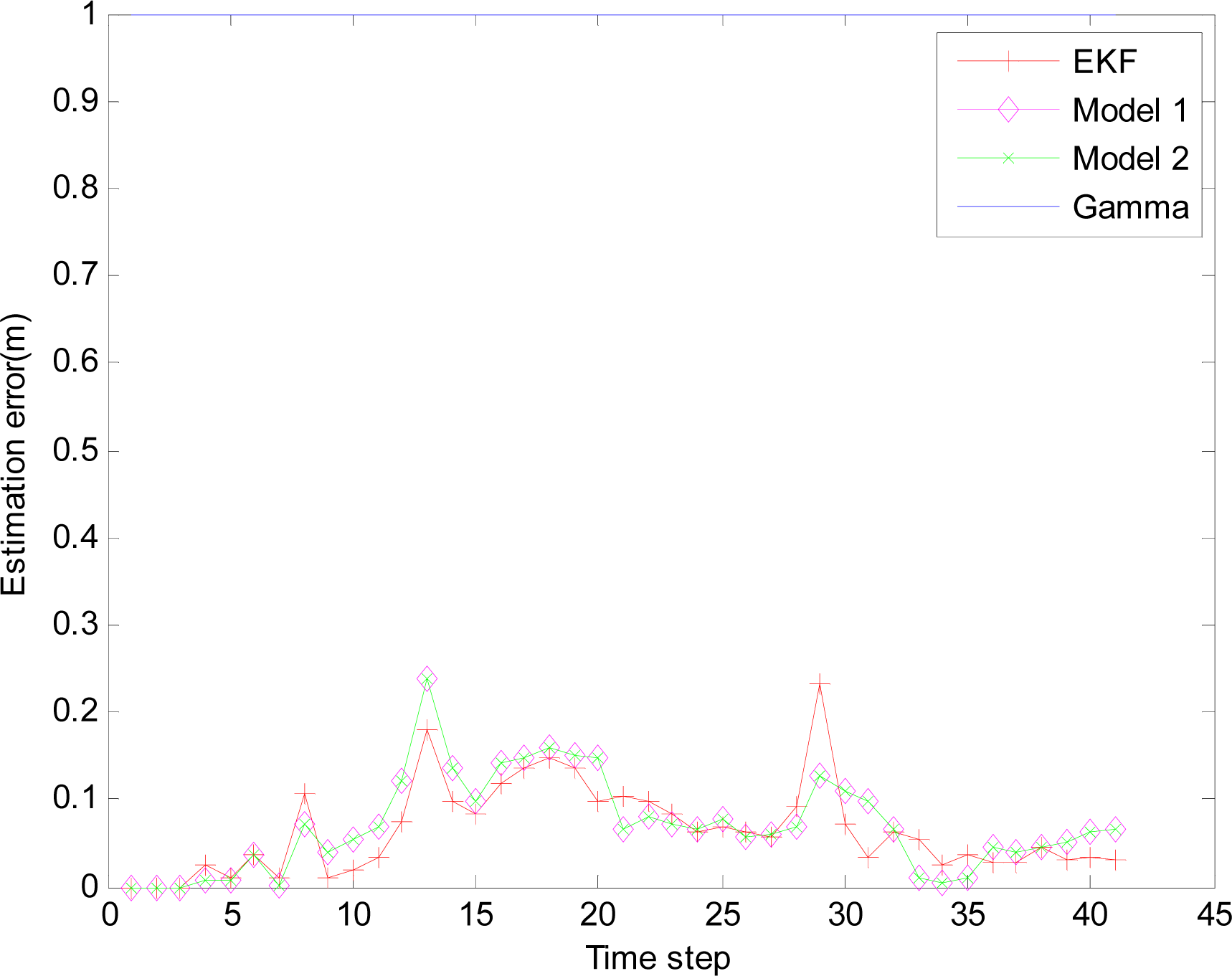
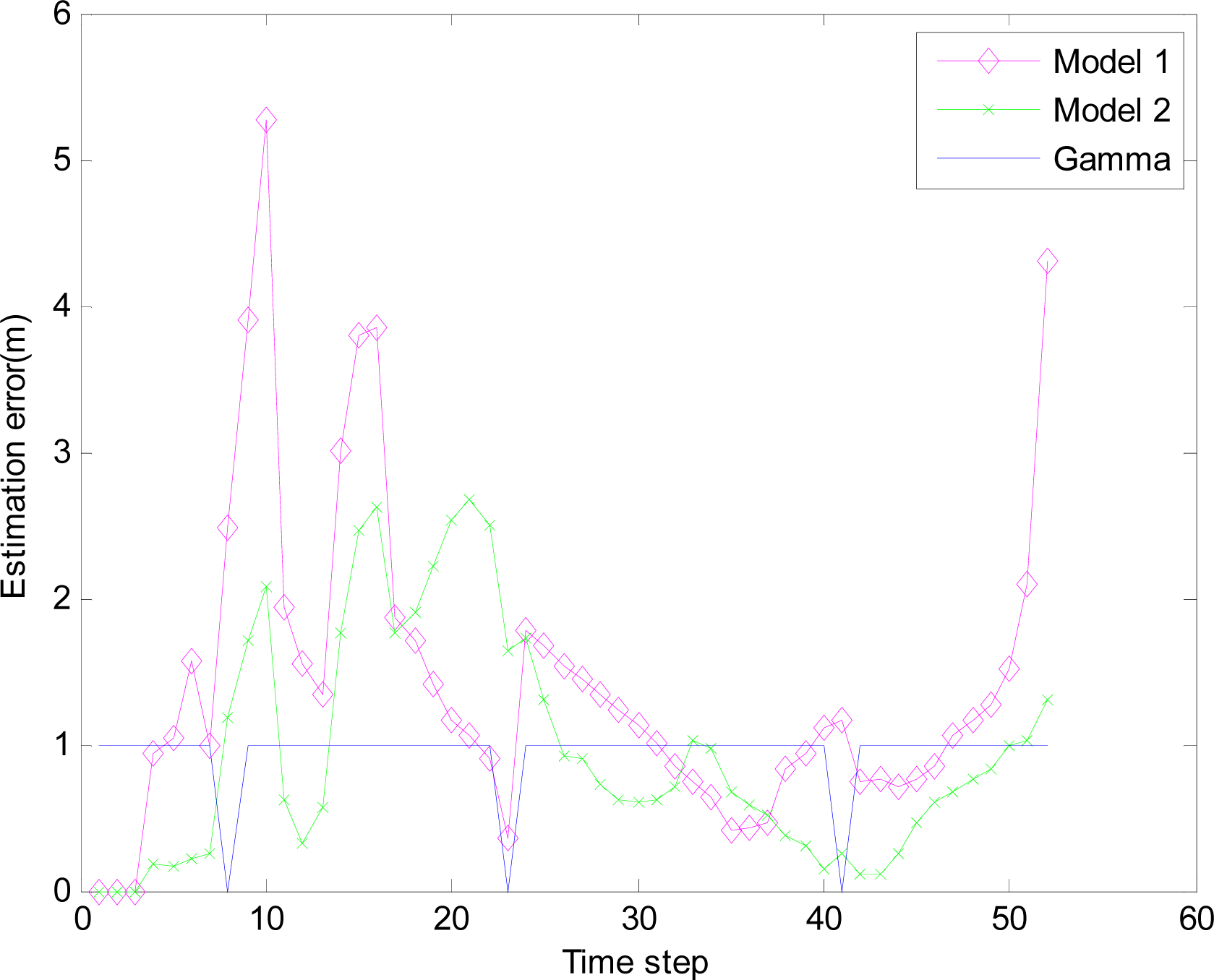
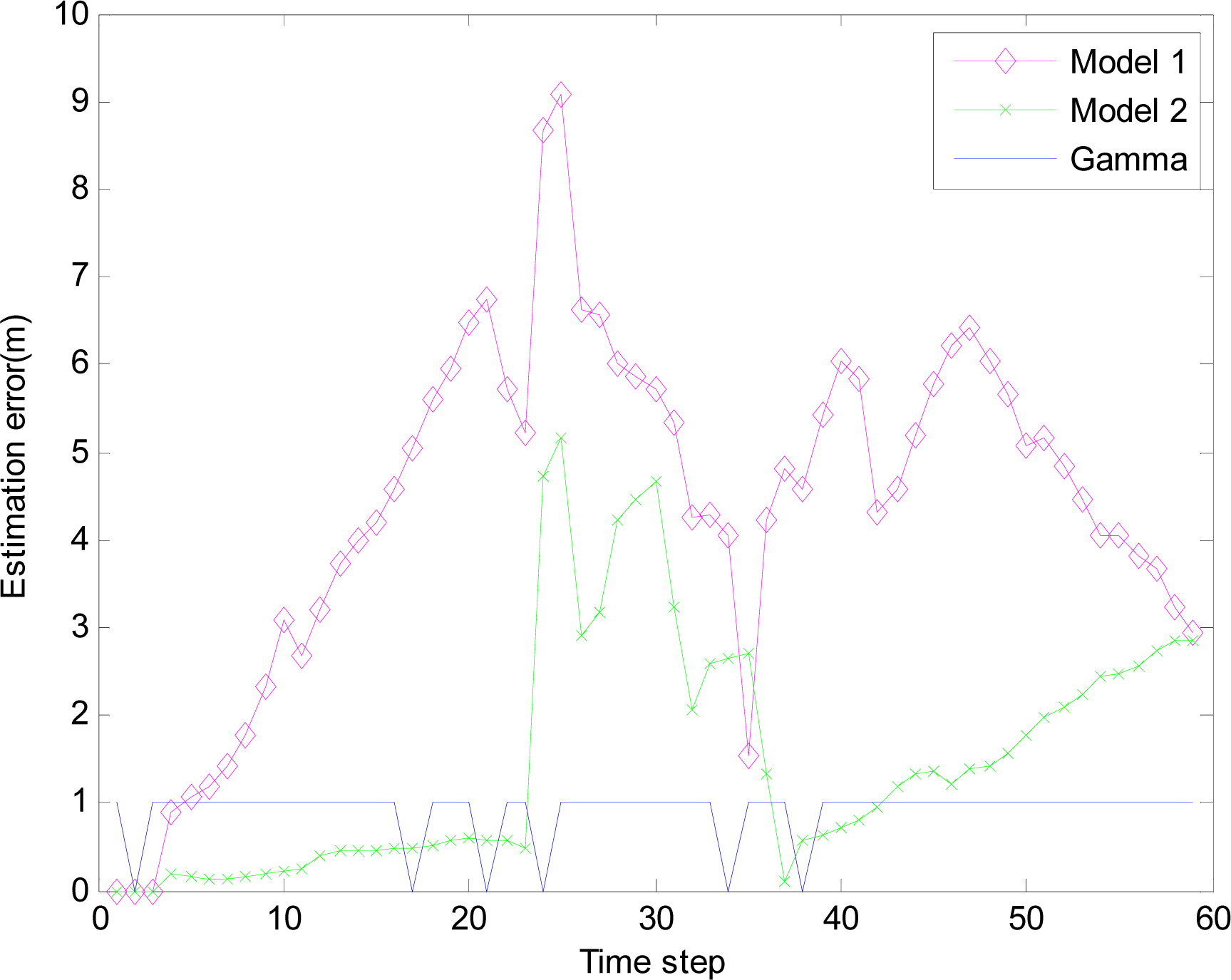
4.2. Application of EMVF in WSNs
4.2.1 Nonlinear state model
4.2.2. Nonlinear measurement model
4.2.3. Distributed wireless sensor scheduling
- Measuring the distance between the motion target and the current sensor node jk at the current time k, where (41) is used;
- Performing extended minimum variance filtering algorithm with packet losses by Theorem 2 in WSNs, and calculating the prediction accuracy according to ;
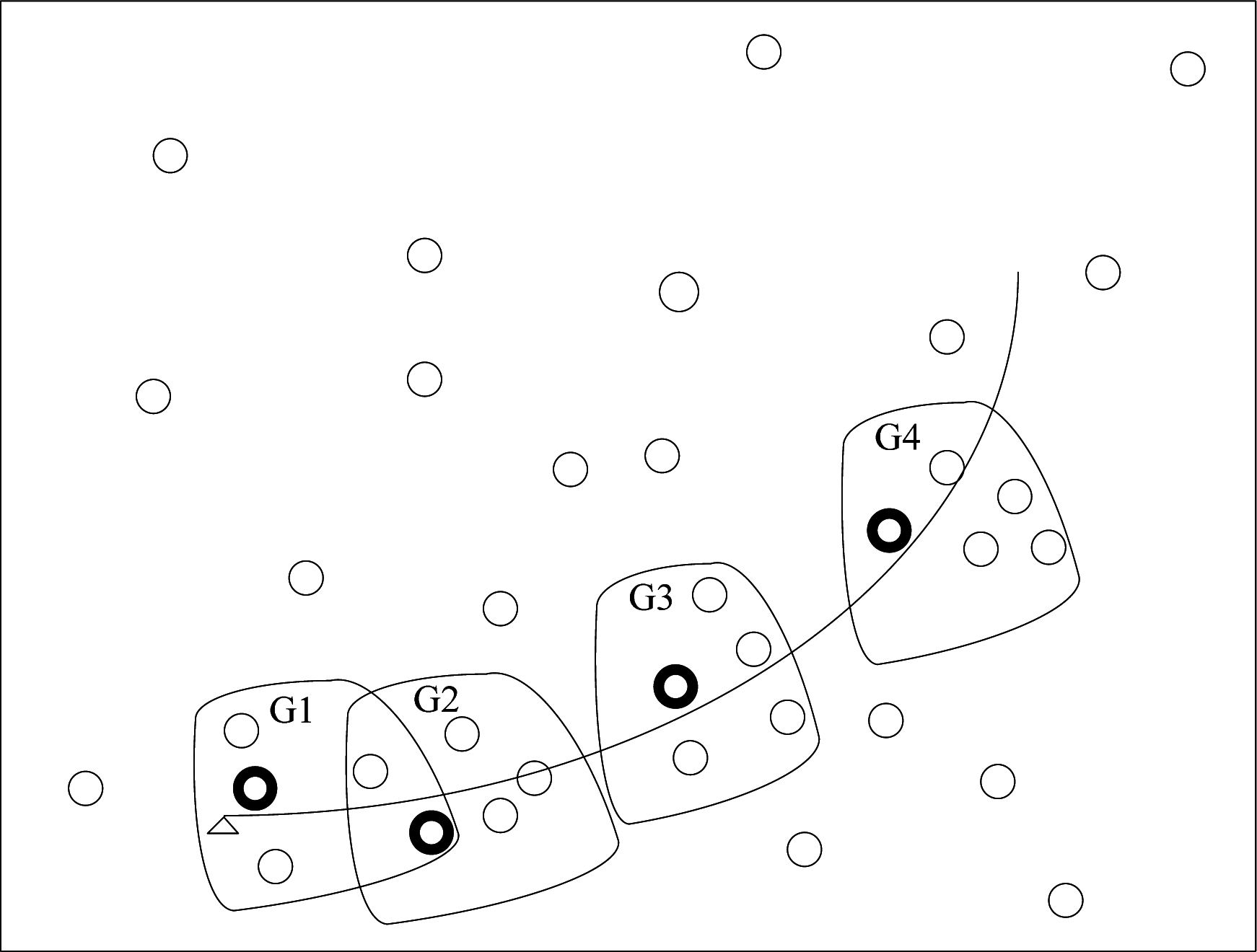
- First, the nearest node to the target (such as bold small circle in the group G1 in Figure 3) is awaked from sleep state and regarded as the task node at current time step k in the neighbor region;
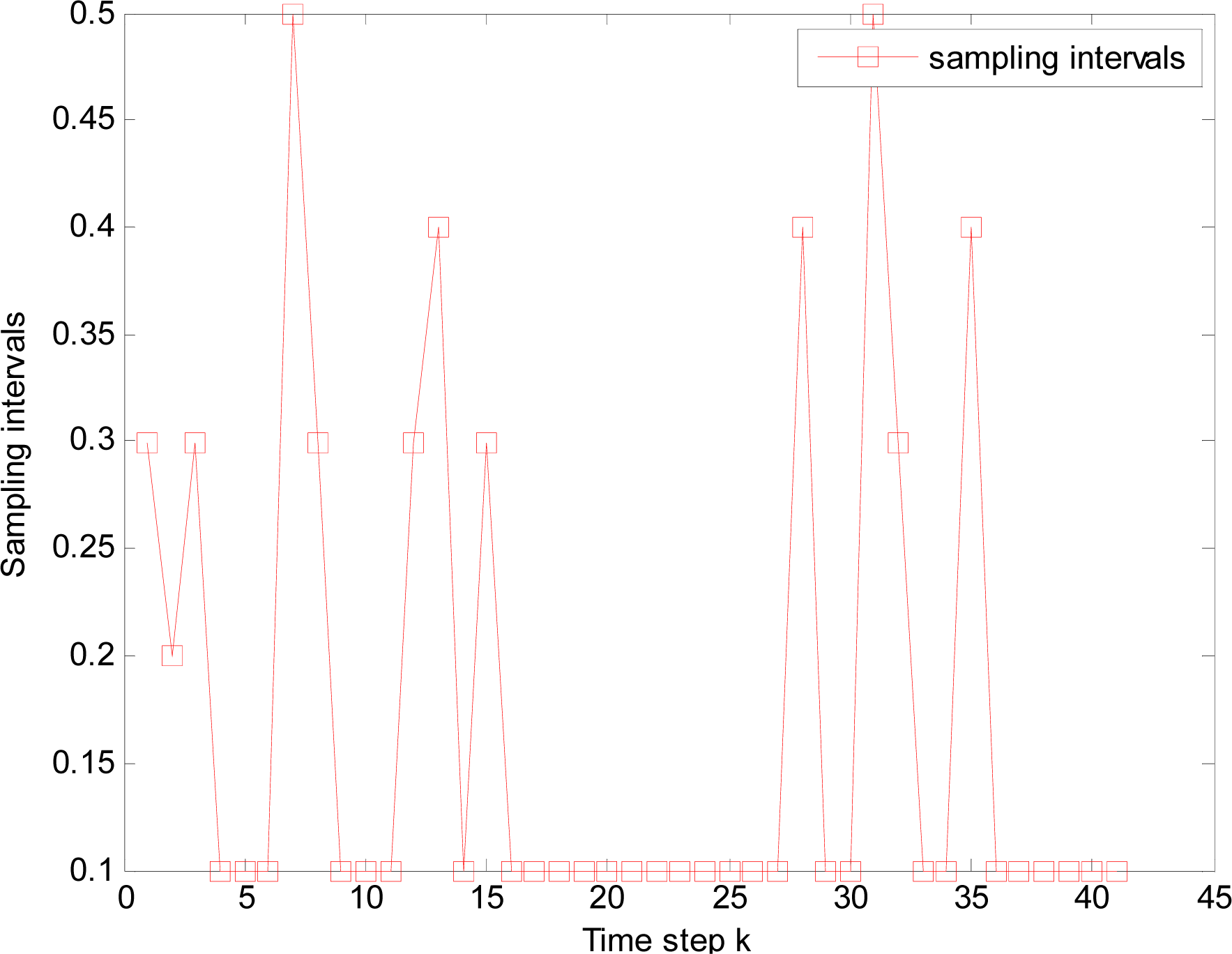
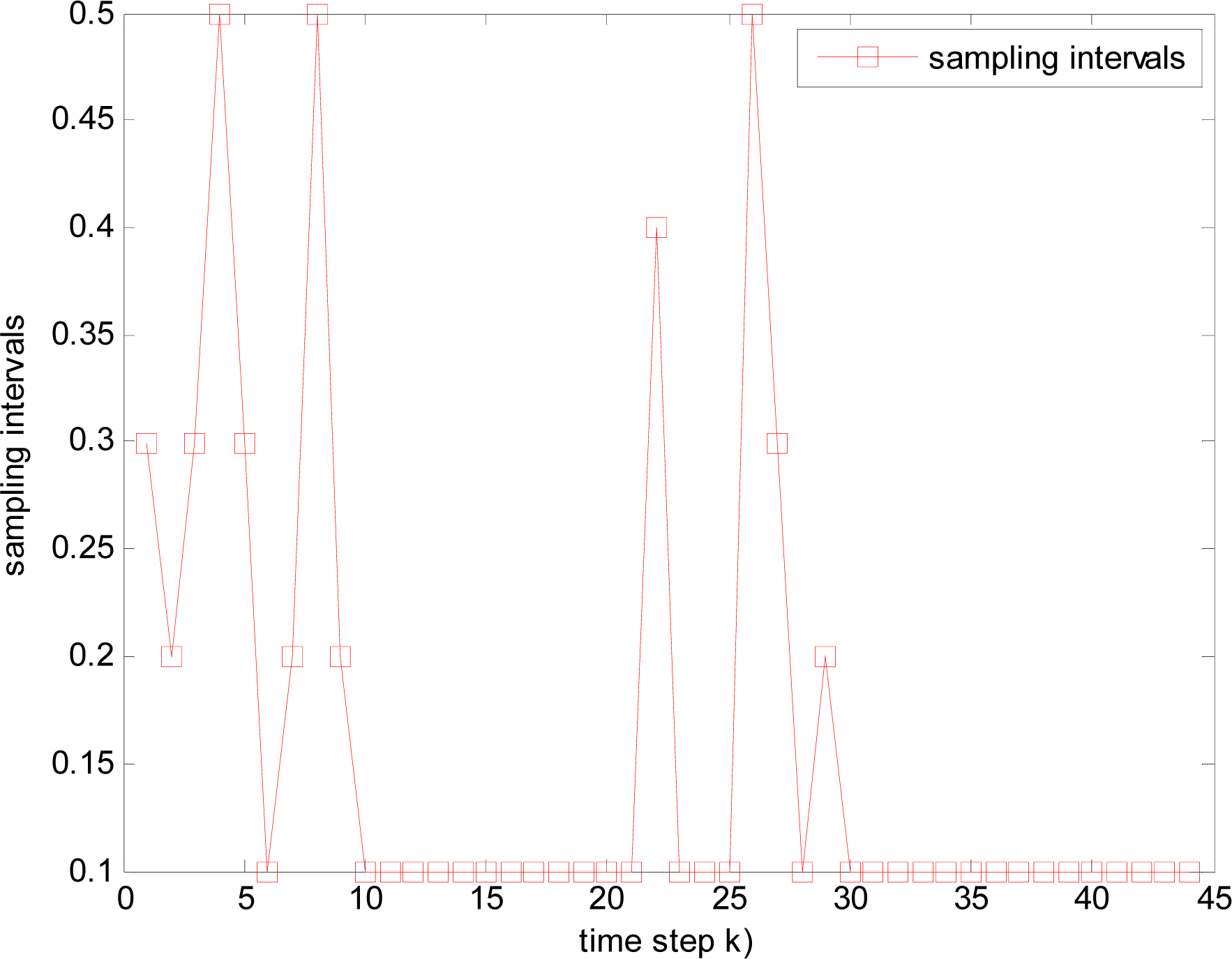
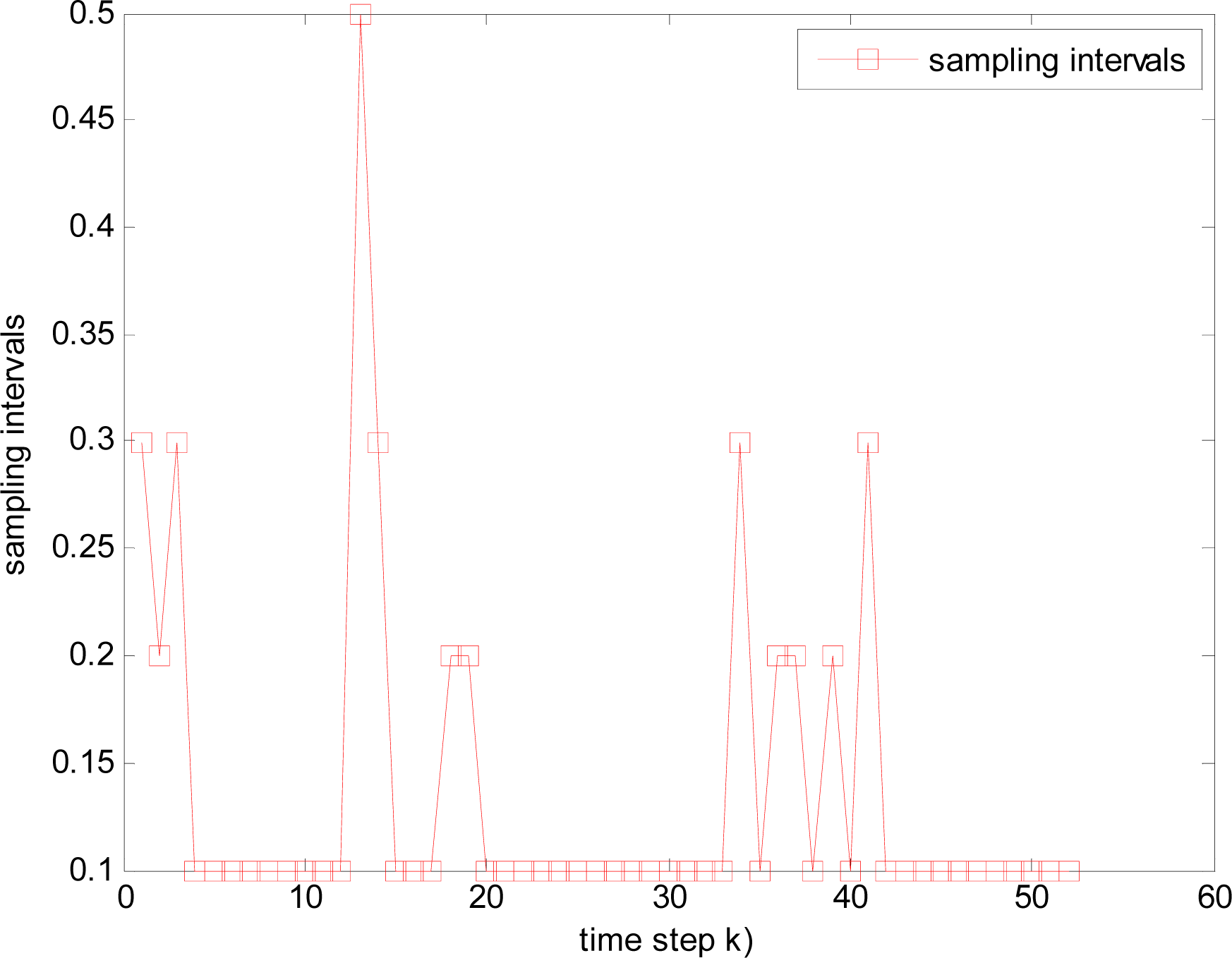
- The nearest sensor node is considered as the center node in a local neighbor area, total M nearest nodes to the target are awaked to form a group. When the target lies in the group, we consider both estimation accuracy and energy. If estimation accuracy is satisfactory, the sensor node, whose consumption energy is least, is selected to track the target by (44) at the next time step k+1, and changed sample interval Δtk is used in order to save energy; If estimation accuracy is not satisfactory, (43) is used to select next task node jk and Tmin is used as sample interval;
- When the target moves out of the group, the sensor nodes in the group return sleep state, and a new task node is awaked from the sleep state in a new local neighbor region. Similarly, a new dynamic group is formed again, as seen from Figure 3, such as G2, G3, G4,…
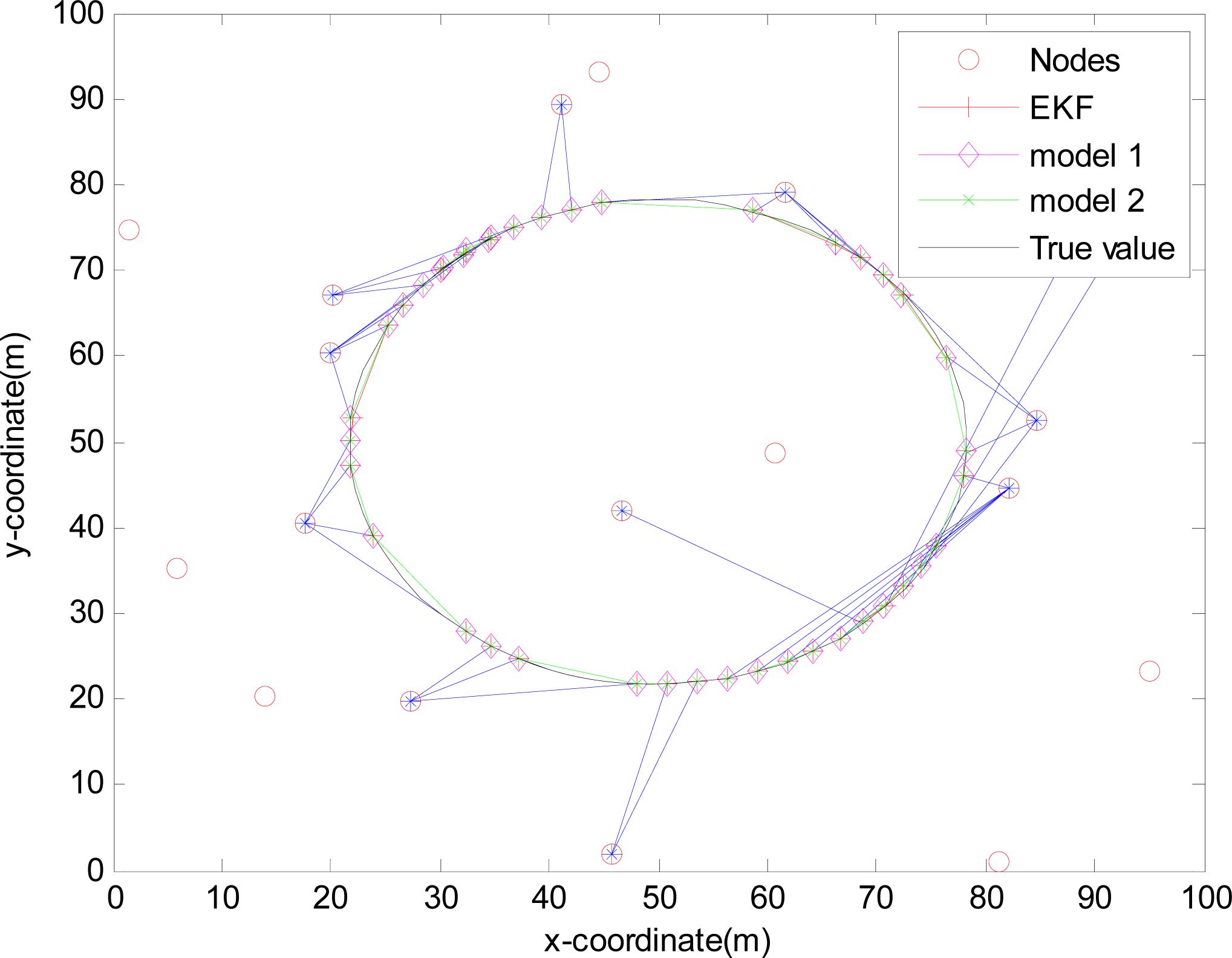
4.2.4. Simulation results
5. Conclusions
Acknowledgments
References and Notes
- Nahi, N. Optimal recursive estimation with uncertain observation. Inf. Theory IEEE Trans. 1969, 15, 457–462. [Google Scholar]
- Hadidi, M.; Schwartz, S. Linear recursive state estimators under uncertain observations. IEEE Trans. Inf. Theory 1979, 24, 944–948. [Google Scholar]
- Costa, O. Stationary filter for linear minimum mean square error estimator of discrete-time markovian jump systems. IEEE Trans. Automat. Contr. 2002, 48, 1351–1356. [Google Scholar]
- Nilsson, J. Real-time Control Systems with Delays, Ph.D. dissertation,; Department of Automatic Control, Lund Institution of Technology: Lund, Sweden, 1998.
- Nilsson, J.; Bernhardsson, B.; Wittenmark, B. Stochastic analysis and control of real-time systems with random time delays. Automatica 1998, 34, 57–64. [Google Scholar]
- Ling, Q.; Lemmon, M. Soft real-time scheduling of networked control systems with dropouts governed by a Markov chain. American Control Conference, Denver, June, 2003; 6, pp. 4845–4550.
- Sinopoli, B.; Schenato, L.; Franceschetti, M.; Poolla, K.; Jordan, M.; Sastry, S. Kalman filtering with intermittent observations. IEEE Trans. Autom. Control. 2004, 49, 1453–1464. [Google Scholar]
- Liu, X. H.; Goldsmith, A. Kalman filtering with partial observation losses. 43rd IEEE Conference on Decision and Control, Atlantis, Paradise Islands, Bahamas, December 14–17, 2004; pp. 4180–4186.
- Epstein, M.; Shi, L.; Tiwari, A.; Murray, R.M. Probabilistic performance of state estimation across a lossy network. Automatic. 2008, 44, 3046–3053. [Google Scholar]
- Sun, S.L.; Xie, L.H.; Xiao, W.D. Optimal full-order and reduced-order estimators for discrete-time systems with multiple packet dropouts signal processing. IEEE Trans. Signal Proc. 2008, 56, 4031–4038. [Google Scholar]
- Sun, S.L.; Xie, L.H.; Xiao, W.D.; Soh, Y.C. Optimal linear estimation for systems with multiple packet dropouts. Automatic 2008, 44, 1333–1342. [Google Scholar]
- Sahebsara, M.; Chen, T.; Shah, S.L. Optimal H2 filtering with random sensor delay, multiple packet dropout and uncertain observations. Int. J. Contr. 2007, 80, 292–301. [Google Scholar]
- Sun, S.L. Linear minimum variance estimators for systems with bounded random measurement delays and packet dropouts. Signal Proc. 2009, 89, 1457–1466. [Google Scholar]
- Schenato, L. Optimal Estimation in Networked Control Systems Subject to Random Delay and Packet Drop. IEEE Trans. Automat. Contr 2008, 53, 1311–1317. [Google Scholar]
- Speranzon, A.; Fischione, C. Adaptive distributed estimation over wireless sensor networks with packet losses. Proceedings of the 46th IEEE Conference on Decision and Control, New Orleans, LA, USA, December 12–14, 2007.
- Schenato, L. Optimal sensor fusion for distributed sensors subject to random delay and packet loss. Proceeding of the 46th IEEE conference on Decision and Control, New Orleans, LA, USA, December 12–14, 2007.
- Yang, X.; Xing, K.; Shi, K.; Pan, Q. Dynamic collaborative algorithm for maneuvering target tracking in sensor netwoks. Acta Automatica Sinica 2007, 33, 1029–1035. [Google Scholar]
- Xiao, W.; Zhang, S.; Lin, J.; Tham, C.K. Energy-efficient adaptive sensor scheduling for target tracking in wireless sensor networks[J]. J. Contr. Theor. Appl. 2010, 2, 86–92. [Google Scholar]
- Liu, Y.G.; Xu, B.G.; Feng, L.F. Distributed IMM filter based dynamic-group scheduling scheme for maneuvering target tracking in wireless sensor Network. Proceedings of 2nd International Congress on Image and Signal Processing, Tianjin, Chian, October 17–19, 2009.
- Shalom, Y.B.; Li, X.R.; Kirubarajan, T. Estimation with Applications to Tracking and Navigation; John Wiley & Sons: New York, NY, USA, 2001. [Google Scholar]


| Sampling interval (s) | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | IDGSS |
| Consumed energy (mJ) | 14.8564 | 9.1176 | 7.0780 | 6.1009 | 5.6857 | 6.0649 |
| Estimation accuracy(m) | 0.3161 | 0.4407 | 0.4973 | 0.6450 | 0.7114 | 0.6729 |
© 2010 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Liu, Y.; Xu, B.; Feng, L.; Li, S. Optimal Filters with Multiple Packet Losses and its Application in Wireless Sensor Networks. Sensors 2010, 10, 3330-3350. https://doi.org/10.3390/s100403330
Liu Y, Xu B, Feng L, Li S. Optimal Filters with Multiple Packet Losses and its Application in Wireless Sensor Networks. Sensors. 2010; 10(4):3330-3350. https://doi.org/10.3390/s100403330
Chicago/Turabian StyleLiu, Yonggui, Bugong Xu, Linfang Feng, and Shanbin Li. 2010. "Optimal Filters with Multiple Packet Losses and its Application in Wireless Sensor Networks" Sensors 10, no. 4: 3330-3350. https://doi.org/10.3390/s100403330
APA StyleLiu, Y., Xu, B., Feng, L., & Li, S. (2010). Optimal Filters with Multiple Packet Losses and its Application in Wireless Sensor Networks. Sensors, 10(4), 3330-3350. https://doi.org/10.3390/s100403330




