A Method for Clustering and Cooperation in Wireless Multimedia Sensor Networks
Abstract
:1. Introduction
- A node clustering algorithm based on overlapping camera FoVs. Finding the intersection polygons and in particular computing the overlapped areas is the key issue to establish clusters and determine cluster membership.
- Scheduling members of clusters in order to perform object detection in a planned manner.
- Energy conservation in scheduled cluster members, compared to energy consumption in ordinary un-clustered object detection and thus greater network lifetime.
2. Related Work
3. Node Clustering for WMSNs
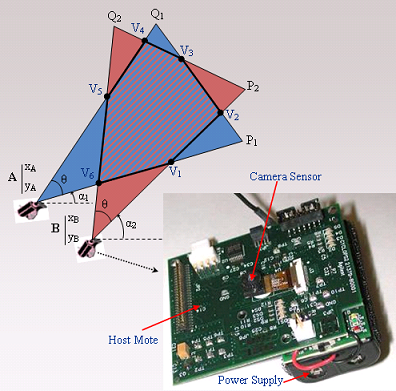
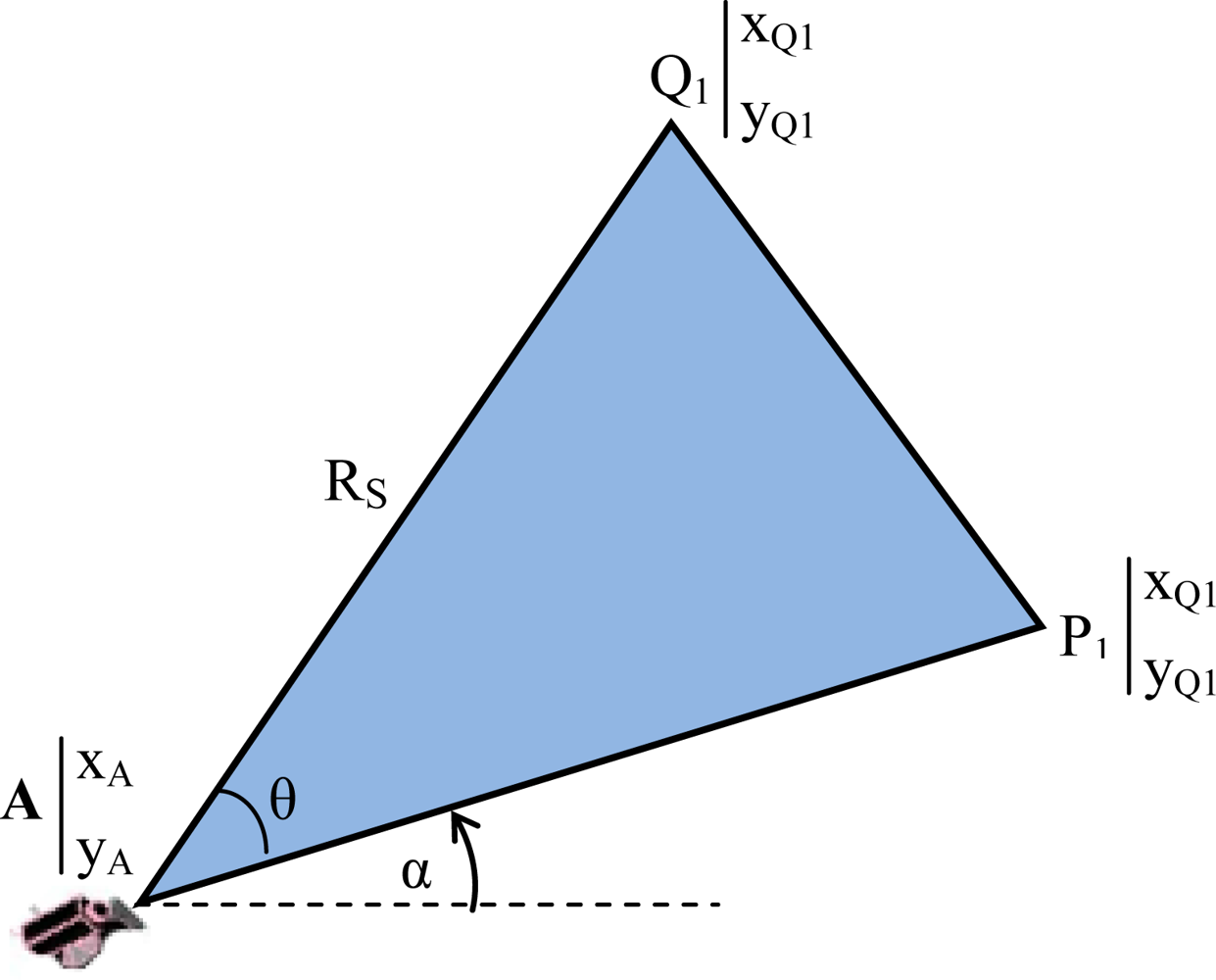
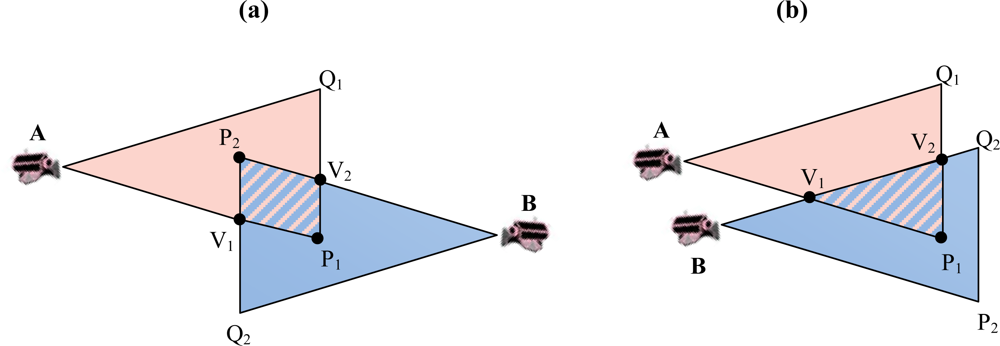
- ▪ Field of View (FoV): refers to the directional view (see Figure 1) of a multimedia sensor and it is assumed to be an isosceles triangle (two-dimensional approximation) with vertex angle θ, length of congruent sides Rs (sensing range) of the sensor and orientation α. The sensor is located at point A (xA,yA).
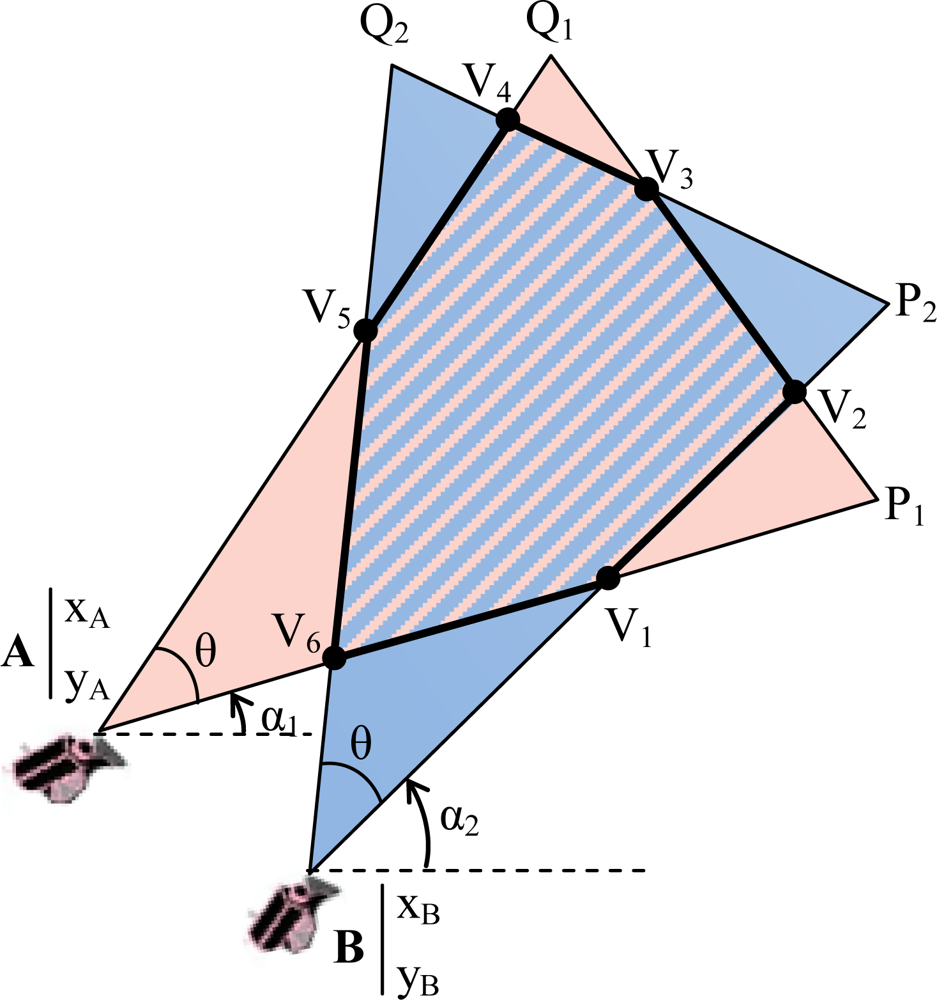
- ▪ Cluster (Cj, j = 1,…,M): consists of a subset of multimedia nodes with high overlapping FoV areas. The size of the overlapping area between FoVs of two nodes determines whether they can be in the same cluster.
- ▪ Overlapping scale (γ): defines the minimum percentage of node’s FoV area that is required to be overlapped for membership in a cluster.
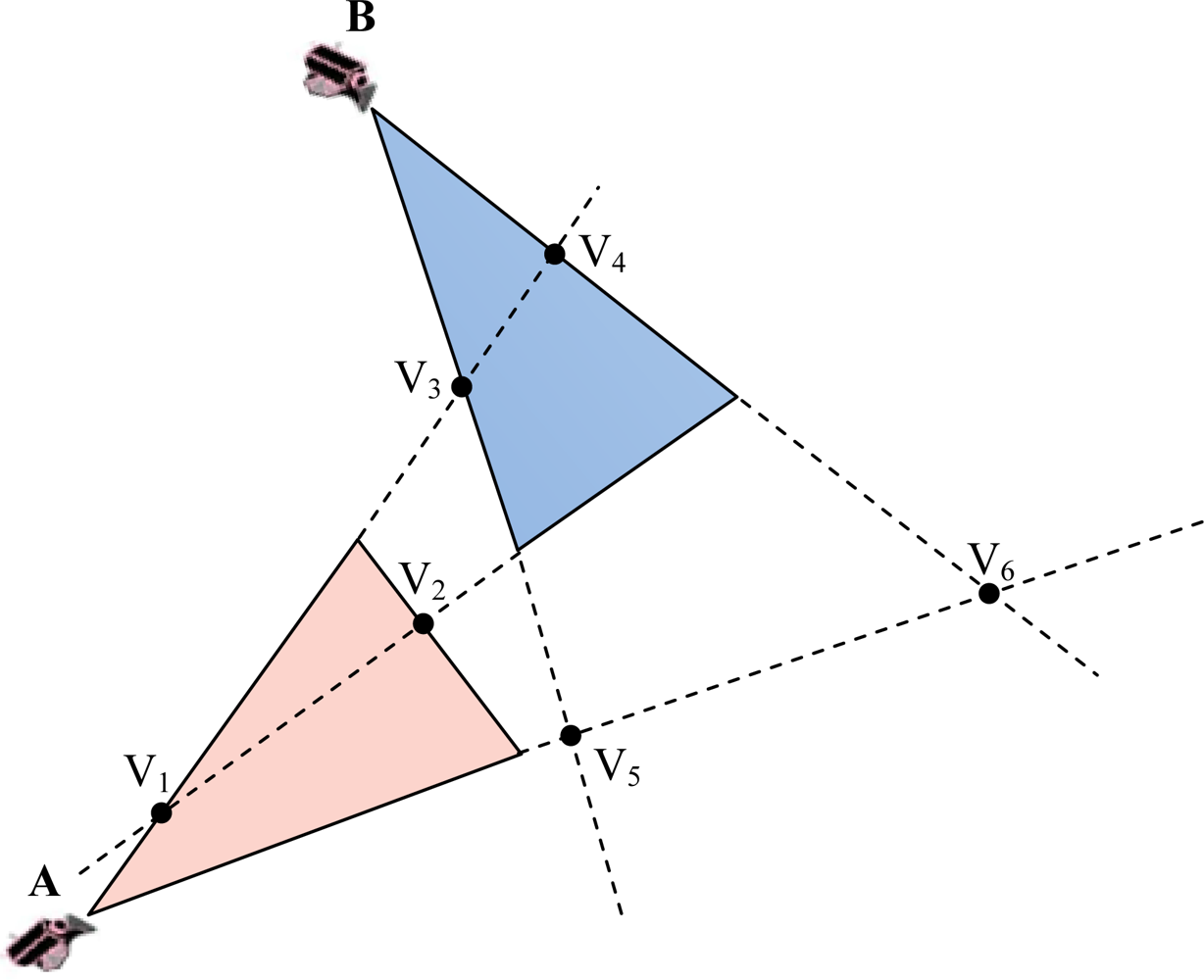
3.1. Overlapping Areas between FoV of Multimedia Nodes
3.2. Cluster Formation and Cluster Membership
- ▪ Bootstrap: At node bootstrap, each sensor {Si, i = 1,…,N} transmits its position (xi,yi) and orientation αi to the sink. To accomplish this step any efficient sensor routing algorithm can be used. Thus, the clustering algorithm is not bound to how the sink receives this information. If there is an un-connected node in the network, it cannot announce itself and thus will not be considered in the algorithm.
- ▪ Cluster Formation: (i) Initially, the sink creates an empty cluster associated with an un-clustered multimedia node of S. Thus, that node will be clustered as the first member (i.e., cluster-head) of the established cluster. (ii) Then, the sink finds the qualified un-clustered nodes for joining to that first member by computing the area of overlapped polygons of their FoV. From position and orientation of nodes, the sink computes the overlapped polygon area (Dij) between each un-clustered multimedia node and the first member of the established cluster as discussed in Section 3.1. If the computed overlapped area is equal or greater than the area determined by the overlapping scale (γ), the un-clustered node will be clustered as a member of the established cluster. (iii) When no more nodes can be added to the cluster, the sink takes a new un-clustered node, begins a new cluster and goes to step (ii). Table 1 indicates the formation procedure.
- ▪ Membership notification: we assume that the sink uses any energy-efficient sensor routing algorithm to notify to each first-member of every cluster about its cluster-ID and what are the members of the cluster. Then, each first-member sends a packet to the members of his cluster notifying them about the cluster which they belong to.
3.3. Cooperative Monitoring in Clusters
4. Cluster Formation Algorithm Evaluation
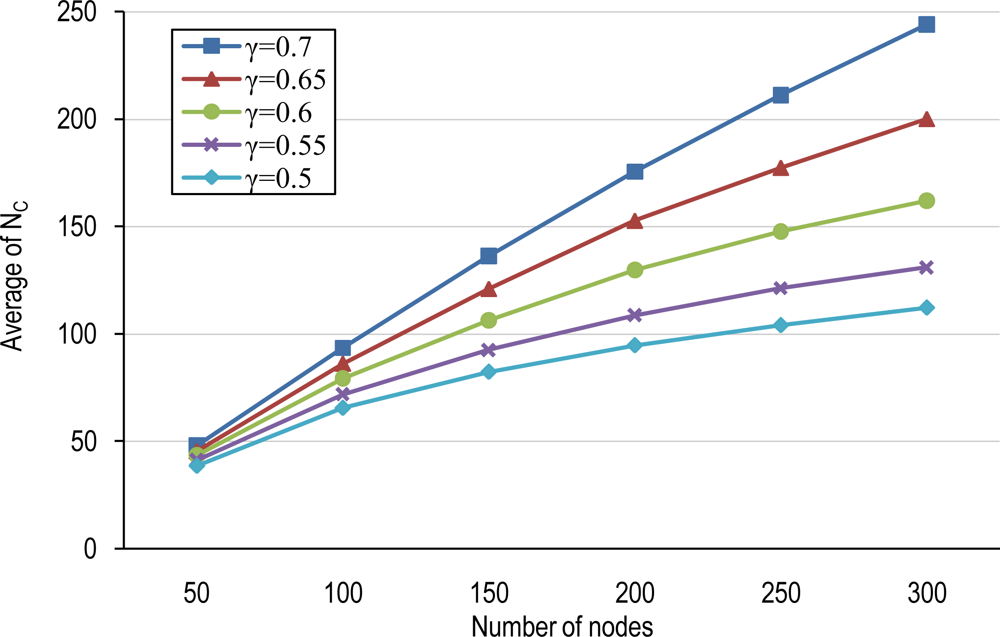
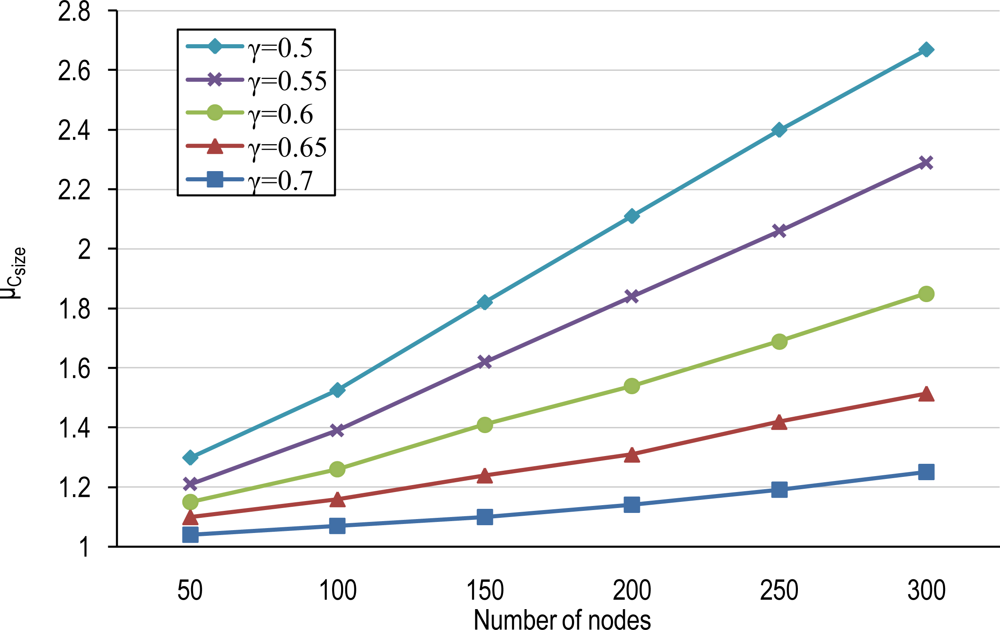
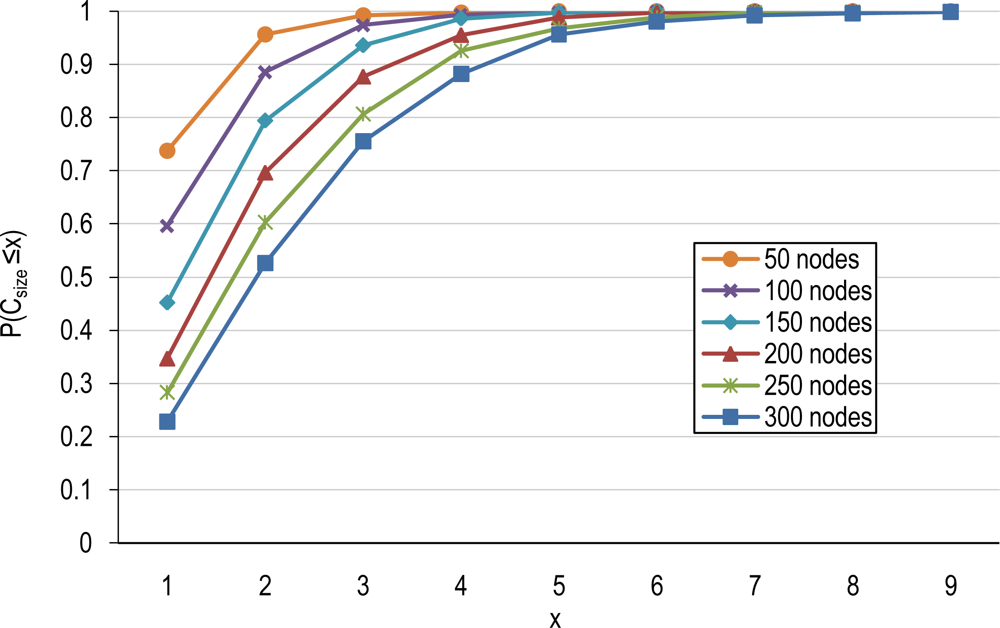
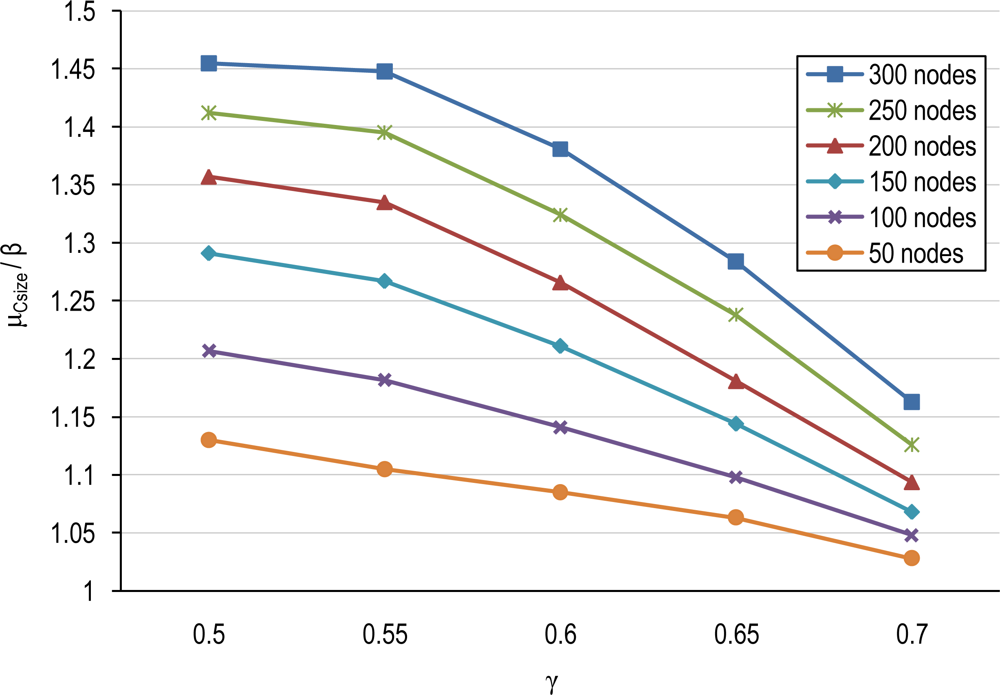
4.1. Number of Clusters and Average Cluster-Size
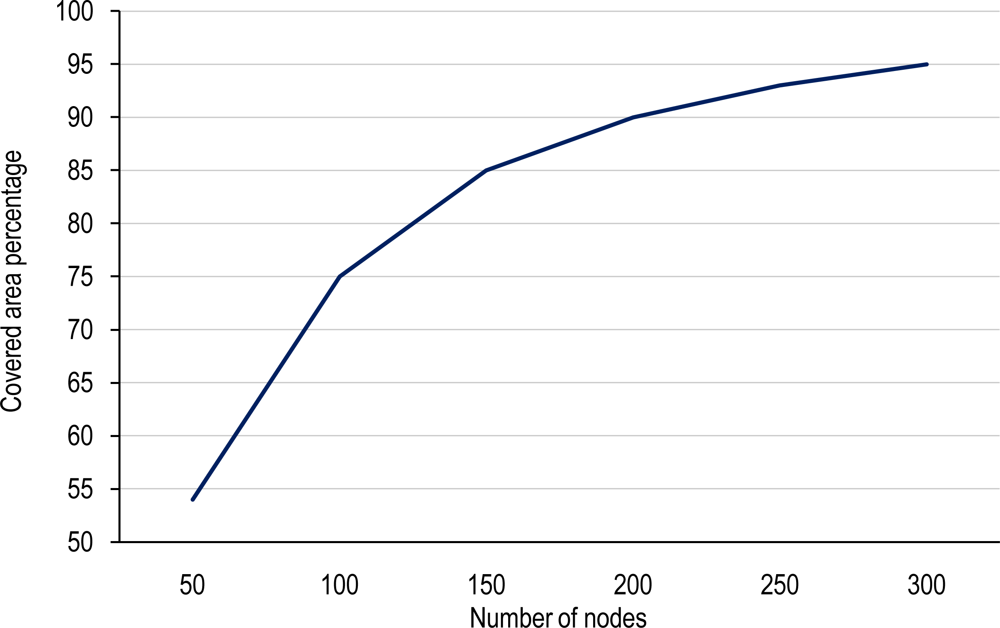
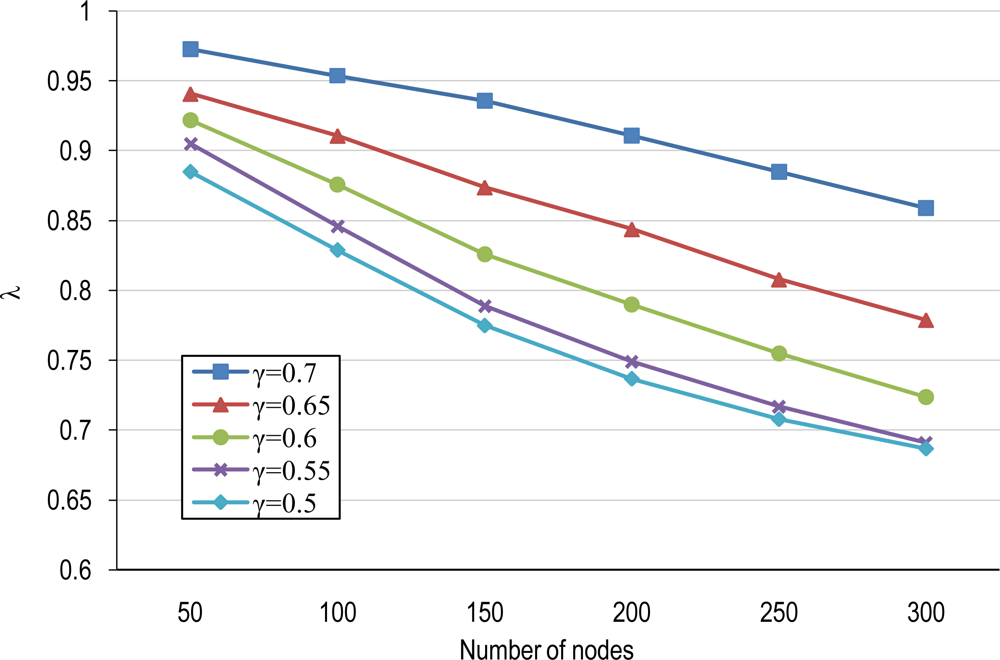
4.2. Covering Domain
5. Cooperative Scheduling for Object Detection in Cluster-Based WMSN
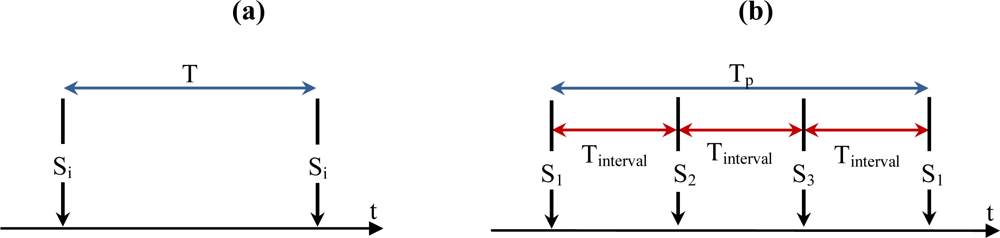
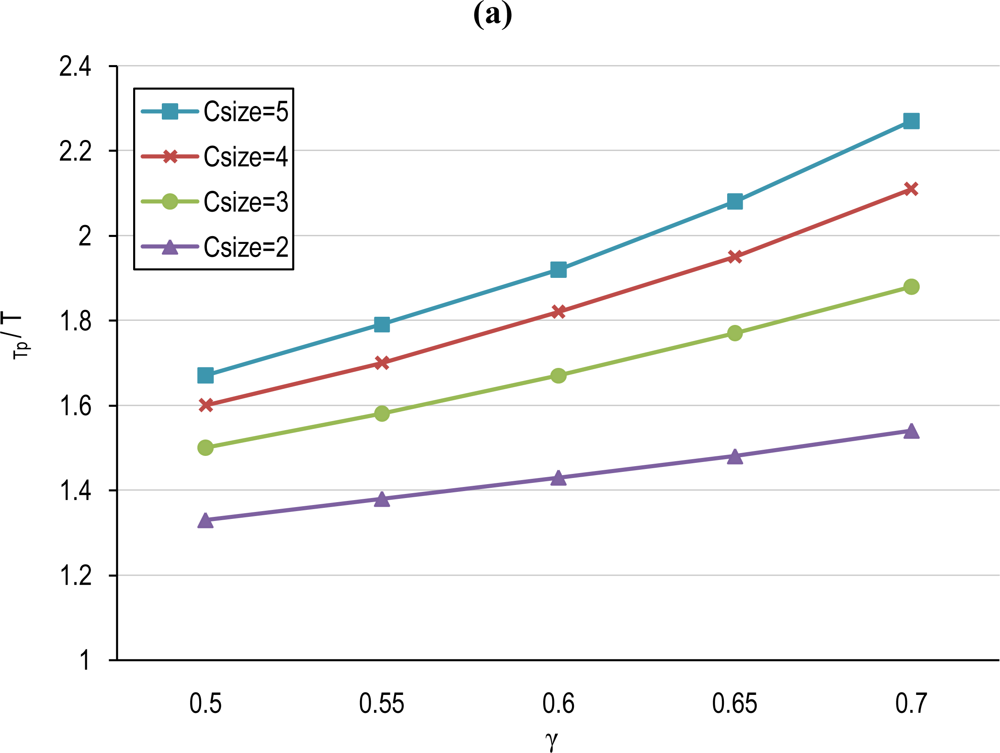
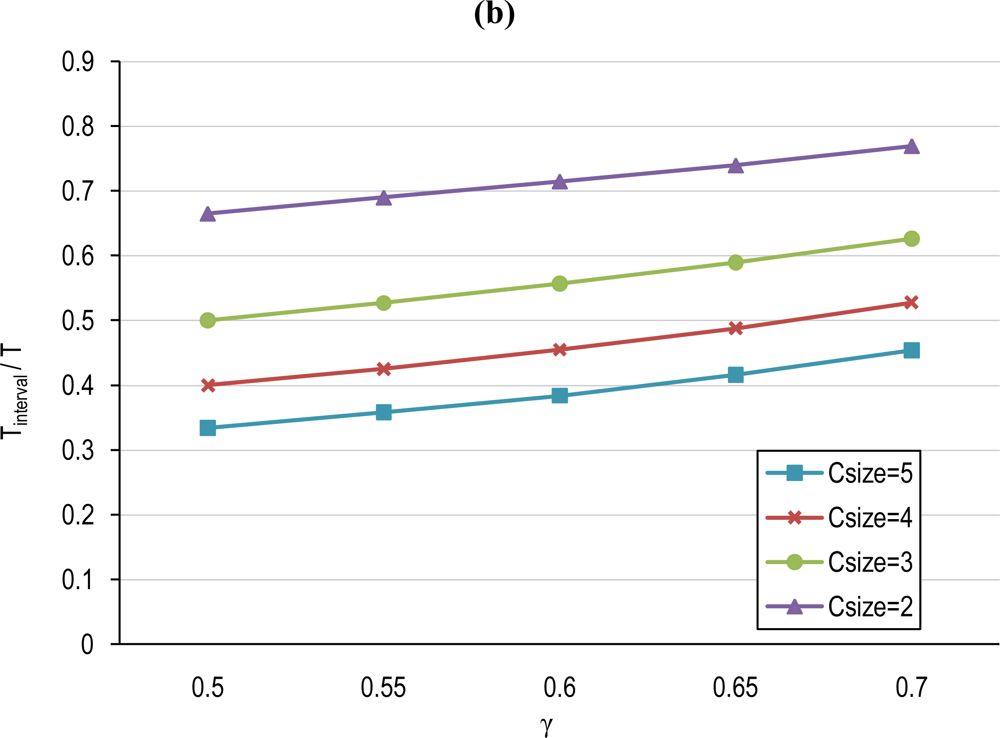
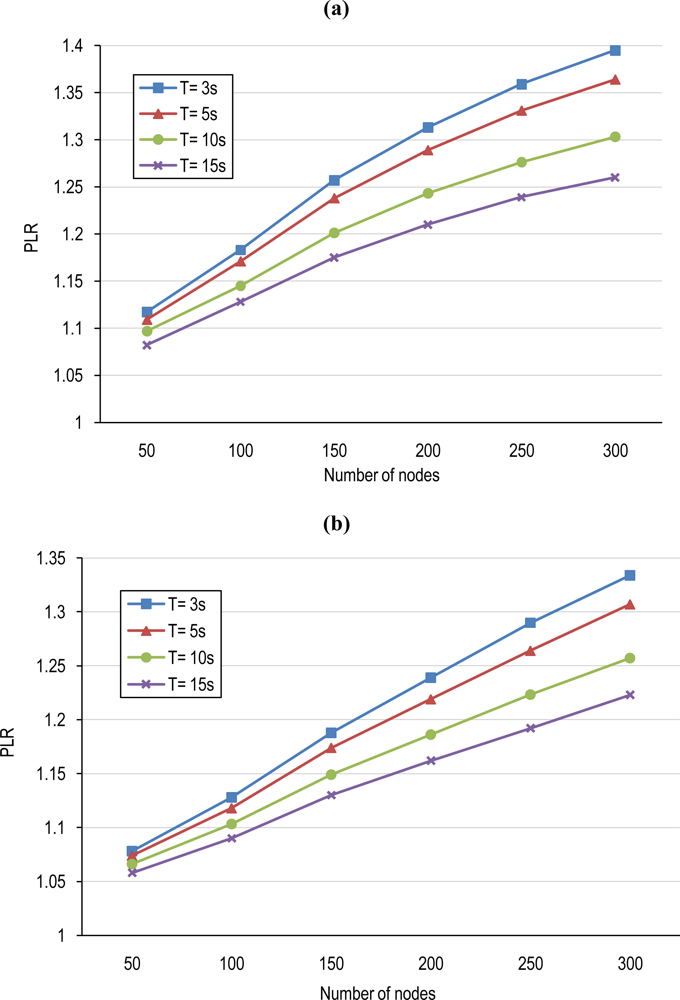
5.1. Cluster-based TP and Tinterval Computation
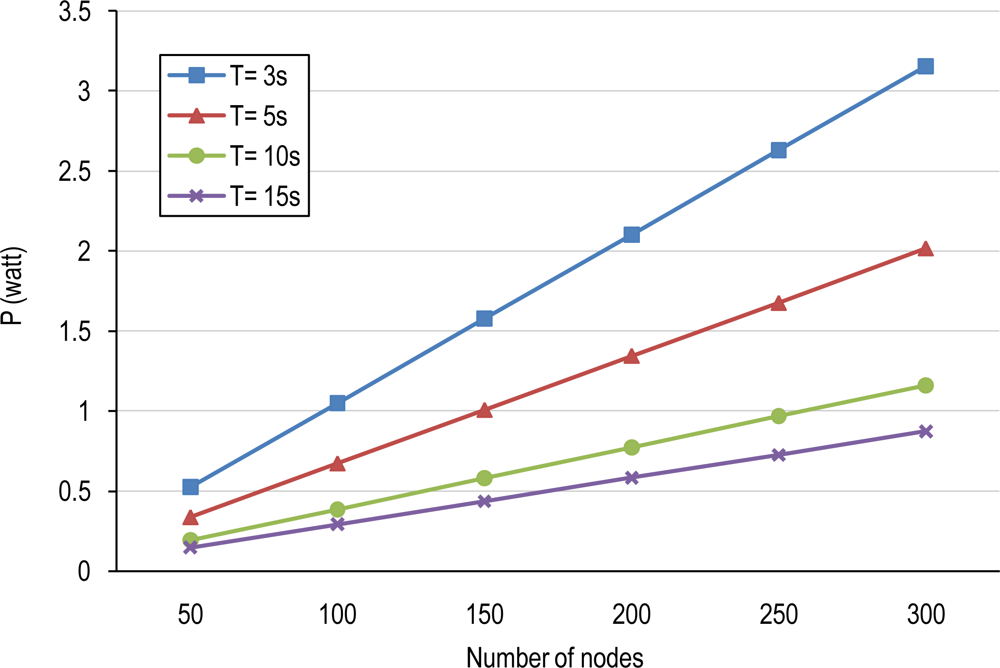
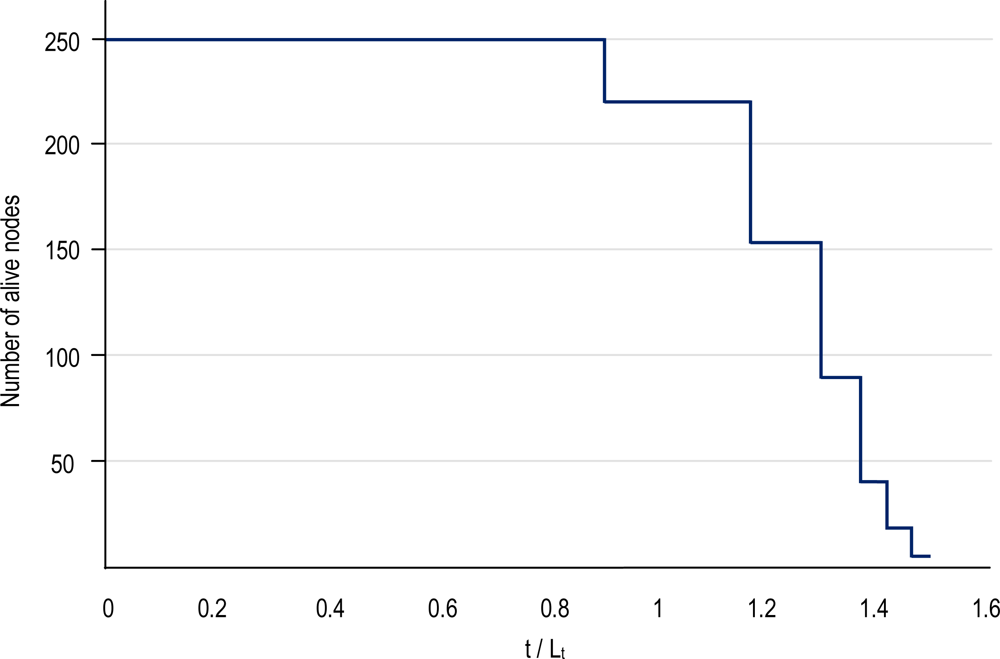
5.2. Power Conservation Evaluation
6. Conclusions
Acknowledgments
References and Notes
- Akyildiz, I.F; Su, W.; Sankarasubramaniam, Y.; Cayirci, E. Wireless sensor networks: A survey. Comput. Netw 2002, 38, 393–422. [Google Scholar]
- Chong, Y.; Kumar, S.P. Sensor networks: Evolution, opportunities, and challenges. Proc. IEEE 2003, 91, 1247–1256. [Google Scholar]
- Akyildiz, I.F; Melodia, T.; Chowdhury, K.R. A survey on wireless multimedia sensor networks. Comput. Netw 2007, 51, 921–960. [Google Scholar]
- Akyildiz, I.F; Melodia, T; Chowdhury, K.R. Wireless multimedia sensor networks: applications and testbeds. Proc. IEEE 2008, 96, 1588–1605. [Google Scholar]
- Abbasi, A.A; Younis, M. A survey on clustering algorithms for wireless sensor networks. Comput. Commun 2007, 30, 2826–2841. [Google Scholar]
- Soro, S.; Heinzelman, W. On the coverage problem in video-based wireless sensor networks. Proceedings of the 2nd IEEE International Conference on Broadband Communications and Systems (BroadNets), Boston, MA, USA, October 3–7, 2005; pp. 932–939.
- Tezcan, N.; Wang, W. Self-orienting wireless multimedia sensor networks for occlusion-free viewpoints. Comput. Netw 2008, 52, 2558–2567. [Google Scholar]
- Adriaens, J.; Megerian, S.; Potkonjak, M. Optimal worst-case coverage of directional field-of-view sensor networks. Proceedings of the 3rd IEEE Communication Society Conference on Sensor, Mesh and Ad Hoc Communications and Networks (IEEE SECON), Reston, VA, USA, September 25–28, 2006; pp. 336–345.
- Obraczka, K.; Manduchi, R.; Garcia-Luna-Aveces, J.J. Managing the Information Flow in Visual Sensor Networks. Proceedings of the 5th International Symposium on Wireless Personal Multimedia Communications, Honolulu, HI, USA, October 27–30, 2002; pp. 1177–1181.
- Tropp, O.; Tal, A.; Shimshoni, L. A fast triangle to triangle intersection test for collision detection. Comput. Anim. Virtual Worlds 2006, 17, 527–535. [Google Scholar]
- Shen, H.; Heng, P.A.; Tang, Z. A fast triangle-triangle overlap test using signed distances. J. Graph. Tools 2003, 8, 17–24. [Google Scholar]
- Guigue, P.; Devillers, O. Fast and robust triangle-triangle overlap test using orientation predicates. J. Graph. Tools 2003, 8, 25–42. [Google Scholar]
- Moller, T. A fast triangle-triangle intersection test. J. Graph. Tools 1997, 2, 25–30. [Google Scholar]
- Rahimi, M.; Baer, R.; Iroezi, O.I.; Garcia, J.C.; Warrior, J.; Estrin, D.; Srivastava, M. Cyclops: in situ image sensing and interpretation in wireless sensor networks. Proceeding of the 3rd ACM Conference on Embedded Networked Sensor Systems (SenSys 05), San Diego, CA, USA, November 2–4, 2005; pp. 192–204.
- Kulkarni, P.; Ganesan, D.; Shenoy, P.; Lu, Q. SensEye: A multi tier camera sensor network. Proceedings of the 13th ACM International Conference on Multimedia (ACM MM 2005), Singapore, November 6–11, 2005; pp. 229–238.
- Kerhet, A.; Magno, M.; Leonardi, F.; Boni, A.; Benini, L. A low-power wireless video sensor node for distributed object detection. J. Real-Time Image Process 2007, 2, 331–342. [Google Scholar]
- P. Chen, P.; Ahammed, P.; Boyer, C.; Huang, S.; Lin, L.; Lobaton, E.; Meingast, M.; Oh, S.; Wang, S.; Yan, P.; Yang, A.Y.; Yeo, C.; Chang, L.C.; Tygar, D.; Sastry, S.S. CITRIC: A low-bandwidth wireless camera network platform. Proceedings of the 2nd ACM/IEEE International Conference on Distributed Smart Cameras (ICDSC 2008), Palo Alto, CA, USA, September 7–11, 2008; pp. 1–10.
- Feng, W.C.; Kaiser, E.; Shea, M.; Feng, W.C; Baillif, L. Panoptes: scalable low-power video sensor networking technologies. ACM Trans. Multimed. Comput. Commun. Appl 2005, 1, 151–167. [Google Scholar]
- Margi, C.B.; Lu, X.; Zhang, G.; Stanek, G.; Manduchi, R.; Obraczka, K. Meerkats: A power-aware, self-managing wireless camera network for wide area monitoring. Proceedings of International Workshop on Distributed Smart Cameras (DSC 06) in Conjunction with SenSys06, Boulder, CO, USA, October 31, 2006; pp. 26–30.
- Xiao, S.; Wei, X.; Wang, Y. Energy-efficient Schedule for Object Detection in Wireless Sensor Networks. Proceedings of the IEEE International Conference on Service Operations and Logistics, and Information (IEEE SOLI 2008), Beijing, China, October 12–15, 2008; pp. 602–605.
- Liu, L.; Zhang, X.; Ma, H. Dynamic node collaboration for mobile target tracking in Wireless Camera Sensor Networks. Proceedings of The IEEE 28th Conference on Computer Communications (IEEE INFOCOM 2009), Rio de Janeiro, Brazil, April 19–25, 2009; pp. 1188–1196.
- Area of Triangles and Polygons (2D &3D). Available online: http://www.softsurfer.com/algorithm_archive.htm (accessed on 5 January 2009).
- Anastasi, G.; Conti, M.; di Francesco, M.; Passarella, A. Energy conservation in wireless sensor networks: A survey. Ad Hoc Netw 2009, 7, 537–568. [Google Scholar]
- Pereira, F.; Torres, L.; Guillemot, C.; Ebrahimi, T.; Leonardi, R.; Klomp, S. Distributed video coding: Selecting the most promising application scenarios. Signal Process.: Image Commun 2008, 23, 339–352. [Google Scholar]
| The Algorithm |
|---|
| 1: k = 1, i = 1 // k is index of clusters, i is index of sensors // |
| 2: C_S = {0,...0}, F_S = {0,...,0) // Mask vectors of size N indicating whether node Si is clustered and whether node Si is a first-member // |
| 3: Repeat: |
| 4: Create an empty cluster (Ck): Ck = Ø |
| 5: Set C_Si as a clustered multimedia node, member of Ck |
| 6: Set F_Si as the first member of the cluster Ck |
| 7: For all C_Sj// un-clustered multimedia nodes // |
| 8: If (C_Sj = 0) |
| 9: Find intersection polygon of FoVs of Si, Sj |
| 10: Compute Dij //overlapped area between Si, Sj // |
| 11: If (Dij ≥ γ.AFoV) |
| 12: Set C_Sj as a clustered multimedia node |
| 13: Set C_Sj as a member of Ck |
| 14: End-If |
| 15: End-If |
| 16: End-For |
| 17: i ← next i //next un-clustered node// |
| 18: K = K + 1 |
| 19: Until (all nodes are clustered) |
| The Algorithm |
|---|
| 1: For all Cj // all clusters in parallel // |
| 2: i = 0 // start with the first member of each cluster // |
| 3: Wake up member number i |
| 4: Capture an image and then call object detection |
| 5: If (detection==true) |
| 6: Send the image to sink |
| 7: End-If |
| 8: Delay (Tinterval) // each cluster has a proprietary Tinterval // |
| 9: i = i + 1(mod Csize) // select next node of the cluster // |
| 10: Goto 3 |
| 11: End-For |
© 2010 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Alaei, M.; Barcelo-Ordinas, J.M. A Method for Clustering and Cooperation in Wireless Multimedia Sensor Networks. Sensors 2010, 10, 3145-3169. https://doi.org/10.3390/s100403145
Alaei M, Barcelo-Ordinas JM. A Method for Clustering and Cooperation in Wireless Multimedia Sensor Networks. Sensors. 2010; 10(4):3145-3169. https://doi.org/10.3390/s100403145
Chicago/Turabian StyleAlaei, Mohammad, and Jose M. Barcelo-Ordinas. 2010. "A Method for Clustering and Cooperation in Wireless Multimedia Sensor Networks" Sensors 10, no. 4: 3145-3169. https://doi.org/10.3390/s100403145
APA StyleAlaei, M., & Barcelo-Ordinas, J. M. (2010). A Method for Clustering and Cooperation in Wireless Multimedia Sensor Networks. Sensors, 10(4), 3145-3169. https://doi.org/10.3390/s100403145