For the target surveillance purpose, a totally distributed WMSN will be discussed to provide flexible and adaptive capability. As stated in Section 3, the sensor nodes are randomly deployed. It would be a waste of energy to keep all the sensor nodes in active mode. Thus, an energy-aware sensor scheduling method is exploited here. It mainly involves three activities: target forecasting, target localization and data report. The future target position is obtained by target forecasting. Thus, the sensor nodes with potential sensing tasks can be awakened while the other sensor node can keep asleep to save energy. These sensor nodes are adaptively grouped with a fuzzy control approach. With the signal energy feature provided by sensor nodes, target localization is implemented with PSO algorithm. Besides, when any observer queries for the target trajectory information, it should be forwarded to the observer. A local routing scheme will be considered to reduce the computational cost.
4.1. HMM-based Target Forecasting
In WMSN, target localization is performed with constant sensing period T. For each sensing period, a data collection node which is randomly chosen from the awakened sensor nodes performs target forecasting after calculate the current target position. The historical target trajectory is delivered from one data collection node to another during the target surveillance procedure. The historical target trajectory and the current target position are utilized to estimate the prior target motion information. As the target localization task is time-critical and the computation resource of sensor node is limited, the forecasting algorithm should be light-weight. Here, a novel HMM-based algorithm is proposed.
HMM is built on the probabilistic framework for modeling a time series of multivariate observations [
33]. It has strong statistical foundation, computational efficiency to develop and ability to predict similar patterns efficiently.
In the two dimensional field, the time series of historical target position is presented by Descartes coordinates. One direction of the target trajectory {
yk |
k = 1,2,⋯,
Na} is taken for discussion. The problem is to estimate the target position
yNa+1 at the next sensing period. The same forecasting approach can be implemented on the other direction. Here, the observation vector sequence is considered as follows:
where ∇ is the differencing operator, which is defined as:
Thus, ∇yk denotes the target velocity factor, ∇2yk denotes the target acceleration factor, and ∇2yk denotes the varying factor of target acceleration. The hidden state set is denoted by
, where Nm is the number of hidden states.
Then a HMM can be constructed as:
where
Am is the transition matrix of the hidden state,
Bm = {
bm} is the observation emission matrix and
πm is the prior probability matrix. The parameter estimation of HMM can be approached as a maximum likelihood estimation (MLE) problem.
The Viterbi algorithm [
34] is adopted to estimate optimal hidden state sequence
. According to the Markovian process, if
, then the forecasting can be performed as:
where the
bi is probability distribution of observation vector for the hidden state
and
E(·) means the expected value. Then,
is forecasting result for target position.
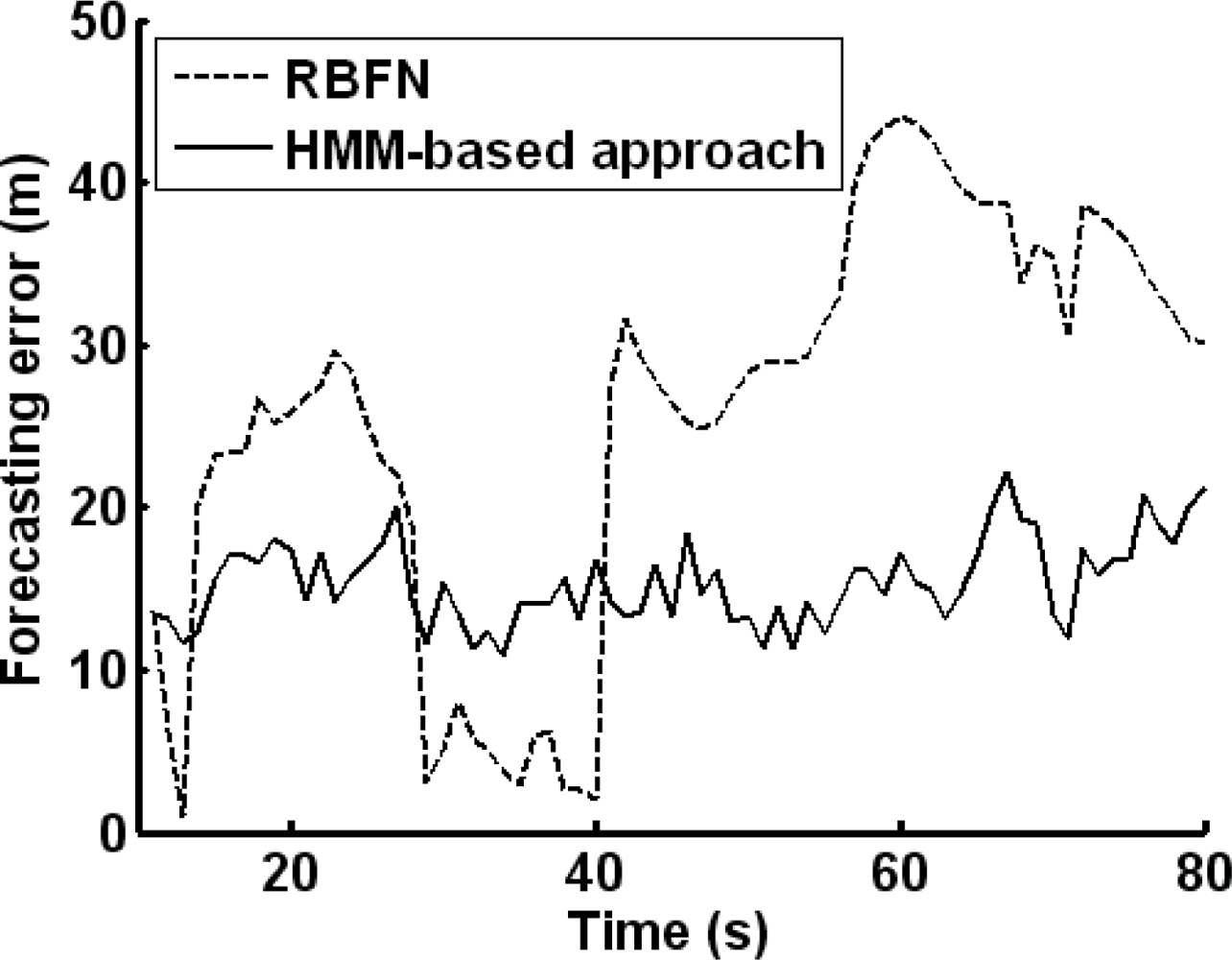
For comparison, another forecasting approach of RBFN is considered. RBFN is a three-layer feed-forward neural network which is embedded with several radial-basis functions. Such a network is characterized by an input layer, a single layer of nonlinear processing neurons, and an output layer. The output of the RBFN is calculated according to [
35]:
where
zin is an input vector,
χj is a basis function, ‖ · ‖
2 denotes the Euclidean norm,
ωj are the weights in the output layer,
M is the number of neurons in the hidden layer, and
cj are the centers of RBF in the input vector space. The functional form of
χj is assumed to have been given, which is always assumed as Gaussian function:
where
σ is a constant.
Here, the target position is usually forecasted as:
The performance of the two approaches will be compared with the experiments.
4.2. Energy-aware Target Localization
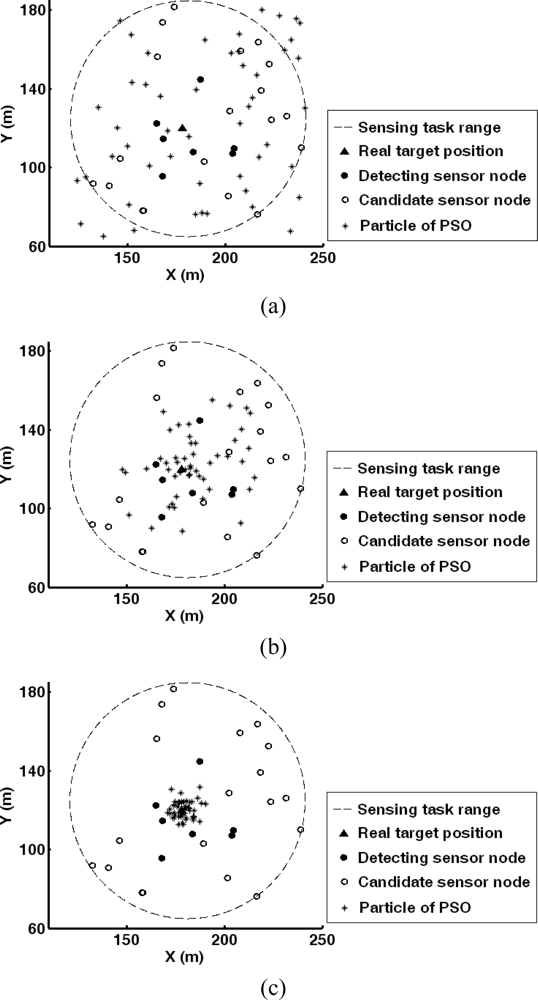
Given the future target position, the sensor nodes with potential sensing tasks are known. As shown in
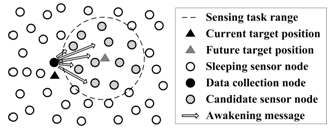
Figure 2, the current data collection node multicasts an awakening message to the sensor nodes which are located in the sensing task range. The architecture is similar to the cross-layer architecture proposed in [
36]. These sensor nodes are defined as candidates for target detection. Meanwhile, the other sensor nodes remain in sleep mode. The awakening message involves the time information. Thereby, the sensor nodes wake up for detection after the same time interval so that time synchronization can be easily achieved. Here, the communication energy consumption for awakening and time synchronization is ignored as the size of these messages is small.
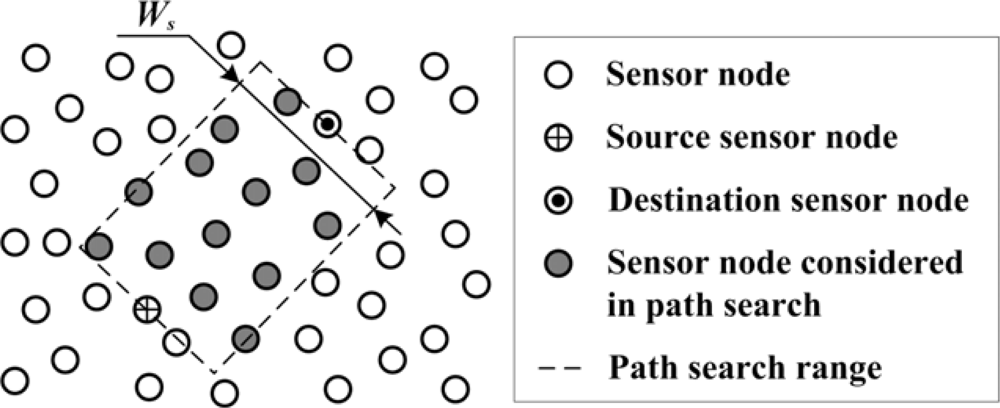
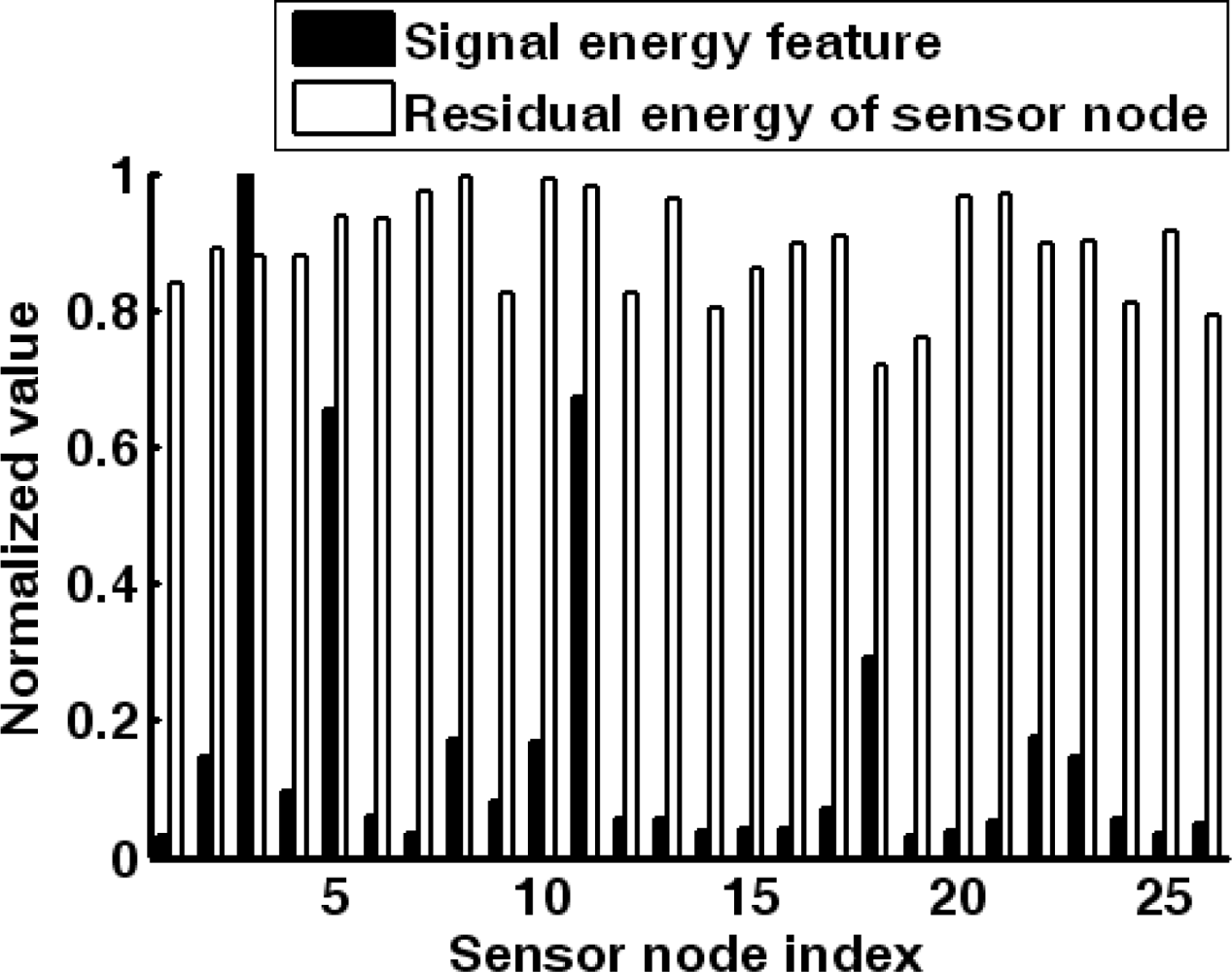
As sensor nodes are usually deployed with high density, it is not necessary for all the sensor nodes to acquire the target information. Thus, the sensor nodes might be grouped in the sensing task range. As shown in
Figure 3, two metrics of sensor nodes in the sensing range is concerned: residual energy of sensor node and the energy of acquired acoustic signal. The problem is to select a group of sensor nodes to implement the target localization [
37]. In [
37], a target direction-based sleep scheduling (TDSS) algorithm was proposed to achieve sensor nodes selection in the process of target tracking, and it was also proved that TDSS algorithm can minimize the energy consumption and guarantee the tracking accuracy. However, TDSS is a centralized algorithm, and it depends on a special assumption of the sensor node’s working mode. Obviously, centralized decision approach will lead heavy communication overheads. Thus, it is not applicable in resource-constrained WSN. To solve this problem, a fuzzy control approach is proposed to select the sensor nodes in a distributed way.
Fuzzy control is viewed as a branch of intelligent control which serves as an emulator of human decision-making behavior that is approximate rather than exact [
38]. It will provide robustness for the sensor node selection. The fuzzy control approach includes three stages: receipt, judgment and action.
In the receipt stage, sensor nodes in the awakening range obtain global information from the awakening message. It is assumed that there are
Nc candidate sensor nodes in the sensing task range. The awakening message which the data collection node multicast should contains three values: the first one is the average residual energy
ĒR of sensor nodes in WMSN; the second one is the normalized signal energy feature
(
i = 1,2,⋯,
Nc); the third one is the average signal energy feature
ĒA. The average residual energy
ĒR is delivered together with the historical target trajectory from one data collection node to another. As the data collection node has the knowledge of the detecting sensor node number, the average residual energy
ĒR can be updated as:
where
N′
s is an estimation of required detecting sensor node number,
N is the total sensor node number in WMSN, and Δ
E is the energy consumption for one detecting sensor node in one sensing period. Here,
N′
s is a predefined parameter to denote that the target can be well localized with a certain number of sensor nodes. It is experientially determined by a large number of results of target localization. The total sensor node number is a constant recorded by each sensor node in the initialization of sensor network. And Δ
E can be estimated according to the energy consumption model of sensor node. The normalized signal energy feature
(
i = 1,2,⋯,
Nc) is calculated by the data collection node according to the future target position and the energy attenuation model:
where
ps is the future target position and
is the position of candidate sensor node
i.
belongs to the interval (0,1]. Beside, the average signal energy feature is calculated as:
where
Rs is the sensing range of microphone sensor.
The fuzzy control system is constructed on each candidate sensor node in the judgment stage. The inputs of the fuzzy control system are the residual energy
and the signal energy feature
, which are already known by the according candidate sensor node
i. The output of the fuzzy control system is the awakening probability
of candidate sensor node
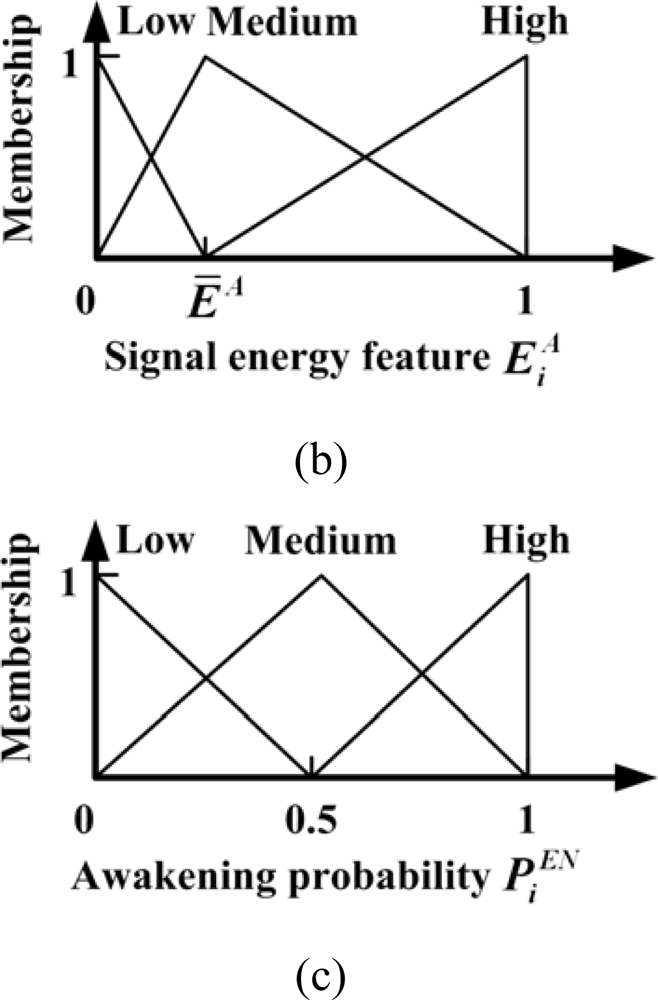
i. The fuzzy division of the inputs and output is shown in
Figure 4.
There are three linguistic variables (
low,
medium and
high) for the residual energy
, the signal energy feature
and the awakening probability
respectively. The triangle membership functions are utilized here. Especially, the linguistic variable
medium for residual energy
and signal energy feature
depends on the average residual energy
ĒR and average signal energy feature
ĒA, respectively. That is because they are relative values which vary during the target application of WMSN. Then the fuzzy rules should be designed. Energy and accuracy factors should be considered in the rules. For example, a sensor node with too little residual energy should remain in sleep mode although it is close to the target (such as sensor node 11 in
Figure 3), and the sensor node which has medium residual energy and low signal energy feature should also keep in the sleep mode (such as sensor node 1 in
Figure 3). Thus, the fuzzy rules are defined in
Table 3. With the inputs and the fuzzy rules, each candidate sensor node can obtain an output of awakening probability
.
In the action stage of the fuzzy control approach, each candidate sensor node easily generates an random number RANDi. If
, then it will participate in target detection at the next sensing instant; otherwise, it keep in the sleep mode.
In this way, the fuzzy control approach selects a group of sensor node adaptively, which will accomplish the target localization task. Moreover, one sensor node is chosen randomly from among them to act as the new data collection node. The old data collection node will deliver the historical target trajectory and average residual energy of the sensor nodes to the new one. Meanwhile, the other sensor nodes act as data acquisition node. Actually, the data collection node is used for collecting the data from the selected detecting sensor nodes and analyzing the position of target, then predicting the next position of target and sending out the awakening messages. All of the operations will consume overhead energy cost and network usage. Thus, if the data collection node is fixedly appointed, it will die out more quickly then other detecting sensor nodes. Random selection of data collection node can avoid this problem, and random selection will not bring in overhead cost. Compared to the purposeful selection, random selection of data collection node seems a little opportunistic without explicit performance guarantee. But the process of the selection of detecting sensor node can provide a guarantee for the lifetime of sensor network, because the data collection node is selected from the detecting sensor node. To achieve the tradeoff between the cost and the performance, random selection is preferred in this process. Furthermore, in the future work, a self-recommendation of data collection node will be investigated to improve this process.
It is assumed that there are
Ns detecting sensor nodes selected in the fuzzy control approach, which calculate the energy feature of acoustic signals according to (5) and send it to the data collection node. Thus, the data collection node keeps the signal energy feature
and the corresponding sensor node positions
, where
i = 1,2,⋯,
Ns. Then, target localization is carried out. In fact, there are many related works in the research field of target localization. However, depending on different motivations, different approaches carry out target localization with different sensing models, such as the center of gravity and DV-hop, and so on. In this paper, target localization is achieved by multiple acoustic sensor nodes. According to the analysis of the acoustic target localization in Section 3.1, this problem can be denoted by the over-determined equations in
Equation (9). Although target localization can also be implemented by other approaches, the specific assumptions of signal models determine that PSO is an appropriate choice for our application. Moreover, compare to other solutions for over-determined equations, PSO is easy to implement and it is also a well known tool for combinatorial and dynamic optimization problems. By transforming the target localization problem into a two dimensional search problem, PSO can convincingly provide accurate localization results. Importantly, PSO is easy to implement in distributed computing paradigm, which implies that it is more suitable and scalable for resource-constrained WSN.
Kennedy et al. developed PSO based on the analogy of swarming of birds and fish schools in 1995. It is an efficient tool for solving combinatorial optimization and dynamic optimization problems in multidimensional space, which implements fast convergence and good robust.
The population of particles is set as
m. For the particle
i,
Xi = (
xi1,
xi2) represents its current position, where the elements present ordinates of potential target position and
Vi =(
vi1,
vi2) represents its current velocity; furthermore,
Pi = (
pi1,
pi2) represents the best position it has achieved so far (
i = 1,2,⋯
m). As the optimization purpose is to solve (9), the minimization objective function
f(
X) is defined as follows:
where var is a function to compute variance.
The overall best position of the particle
i can be calculated as follows:
where
t is the iteration index.
The overall best position of particle
i is calculated as follows:
Velocity and position of particle
i are updated according to
equations (25) and
(26) respectively.
where the index
j = 1,2;
c1 and
c2 are acceleration constants, representing the weight of the stochastic acceleration terms that pull each particle toward the local best position and global best position;
r1j ∼
U(0,1) and
r2j ∼
U(0,1) are two separate random functions;
ω(
t) is the inertia weight, used to balance the global and local search ability. Here, a large inertia weight facilitates a global search while a small inertia weight facilitates a local search. As shown in (27), inertia weight linearly decreases through the course of the run. Accordingly, the optimization process can converge to the neighborhood of the global optimal solution smoothly at the prophase, and converge to the global optimal solution quickly at the anaphase.
where
MaxNumber is the number of maximum iterations. After
MaxNumber iterations, the optimal particle position presents the target localization result.
4.3. Local Data Report Routing Between Appointed Source Sensor Node and Destination Sensor Node
The purpose of target surveillance is to provide the target trajectory information for the observers. The observer might be located in any position of the sensing field. It injects a query message into the network through the closest sensor node, which is called destination sensor node. Then the destination sensor node will spread the query message simply by flooding. After the current data collection node receives the query message, it acquires the position of the destination sensor node. Here, the data collection node is called the source sensor node. The target trajectory data should be forwarded from the source sensor node to the destination sensor node and finally sent to the observer. Moreover, the data transmission between two data collection nodes and between the data collection node and detecting sensor node also needs the local data report routing. How to determine an efficient routing solution between the appointed source and destination sensor node is important for the cost of sensor network.
To obtain the optimal communication path, Dijkstra’s algorithm is usually considered [
39]. However, the computation cost will grow fast when the sensor node number increases. Hence, improvements should be made in the search procedure and a local routing scheme is introduced here.
As shown in
Figure 5, only the sensor nodes within the path search range are considered in the local routing scheme. The path search range is a rectangular area. Its length is equal to the distance between the source sensor node and the destination sensor node, while its width is denoted by
Ws. The direction of the long side of the rectangle is parallel to the orientation of a line segment from the source sensor node to the destination sensor node. The source sensor node and the destination sensor node are the midpoints of two rectangle short sides. Then, the path search is constrained in the local area. Here,
Ws should be well designed; this will be discussed in the experiment.
Then, the Dijkstra’s algorithm is performed on the path search area. The problem is formulated as:
The destination sensor node is denoted by p0 and the set of sensor nodes within the path search range is denoted by P = {p1,p2,⋯,pn};
According to
equation (11), the edge weight between
pi and
pj is:
where
Gt is the data packet size,
αt is the data rate, and Δ
Ec is the energy consumption for awakening a sensor node.
Variable Di represents estimate of the lowest cost from pi to p0, and converges to the real value after iterations.
The set of nodes that find the lowest cost paths is denoted by Q.
Searching procedure for the optimal data report path is described as follows:
Search for the next node with the lowest cost path to
p0. For
pi ∉ Q, if
Di satisfies:
The lowest cost path of
pi is found, update
Q:
If
Q =
P, then search is completed. Oppositely, if
Q ≠
P, continue searching.
Update
Dj for all
pj ∉
Q according to the result of step (ii):
Continue to execute step (ii).
Iterate the step (ii) and (iii) until the lowest cost path from the source sensor node to the destination sensor node is determined. Hence, the data of target trajectory information is reported to the observer along the path which consists of several intermediate sensor nodes.
In conclusion, in the proposed algorithm, the process of target tracking, position prediction and new sensor nodes selection are implemented in turn. That is, the selected detecting sensor nodes and data collection sensor nodes are awaked after receiving the awakening message. Then they implement the signal acquisition and send the local results to data collection sensor nodes. After receiving the results of all detecting sensor nodes, the data collection sensor nodes carry out target localization by PSO algorithm. With the historical target trajectory and current estimated position, the future target position is predicted by HMM algorithm. Then the data collection sensor node sends out the awakening message to the sensor nodes which are located in the sensing task range. Then, a new circulation is started by selecting new detecting sensor nodes and data collection sensor nodes. From the above process, the working sensor nodes in each tracking step and sensing period can be determined according to the requirements of low energy consumption and high tracking accuracy.