Efficiency of Event-Based Sampling According to Error Energy Criterion
Abstract
:1. Introduction
2. Event-Based Sampling according to Energy Criterion
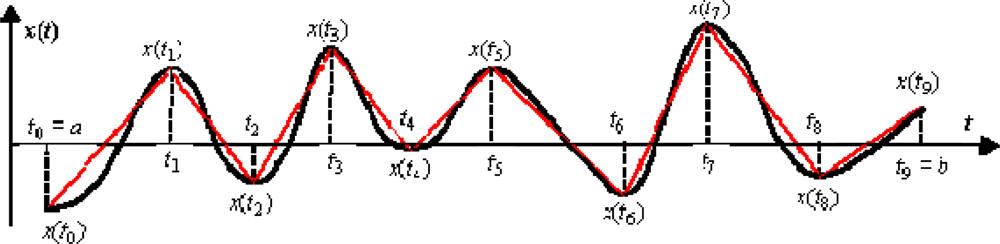
2.1. Sampled Signal Definition
2.2. Definition of Energy Criterion
2.3. Motivation
3. Analytical Modeling of Sampling according to Energy Criterion
3.1. Mean Sampling Rate Approximation
- - the mean of the cubic root of the signal derivative square , which is a measure of the sampled signal x(t),
- - the resolution ζ of the energy sampling (threshold).
3.2. Selection of Sampling Period in Uniform Scheme
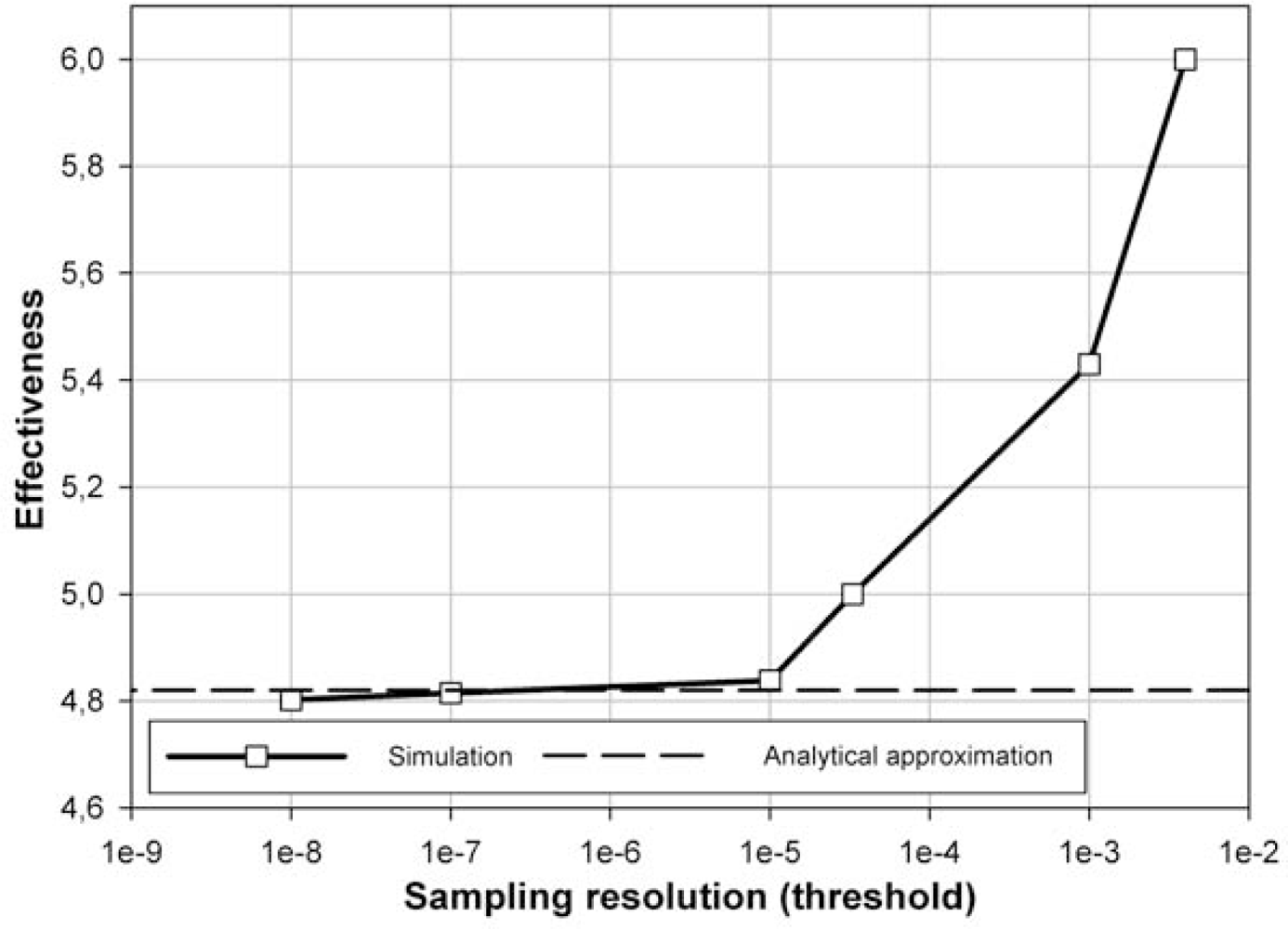
3.3. Effectiveness of Event-Based Sampling according to Energy Criterion
3.5. Comparing Sampling in Energy Domain to Integral Sampling and to Send-on-Delta Scheme
3.6. Generalized Event-Based Sampling Criteria
4. Event-Based Spatial Sampling
4.1. Event-Based Spatial Reporting Strategy
4.2. Modelling Event-Based Spatial Sampling Density
- - spatial (linear) sampling error [x(s) − x(si−1)] in the spatial send-on-delta sampling scheme,
- - integral of the spatial sampling error in the spatial integral sampling,
- - energy of the spatial sampling error in the spatial sampling according to the energy criterion.
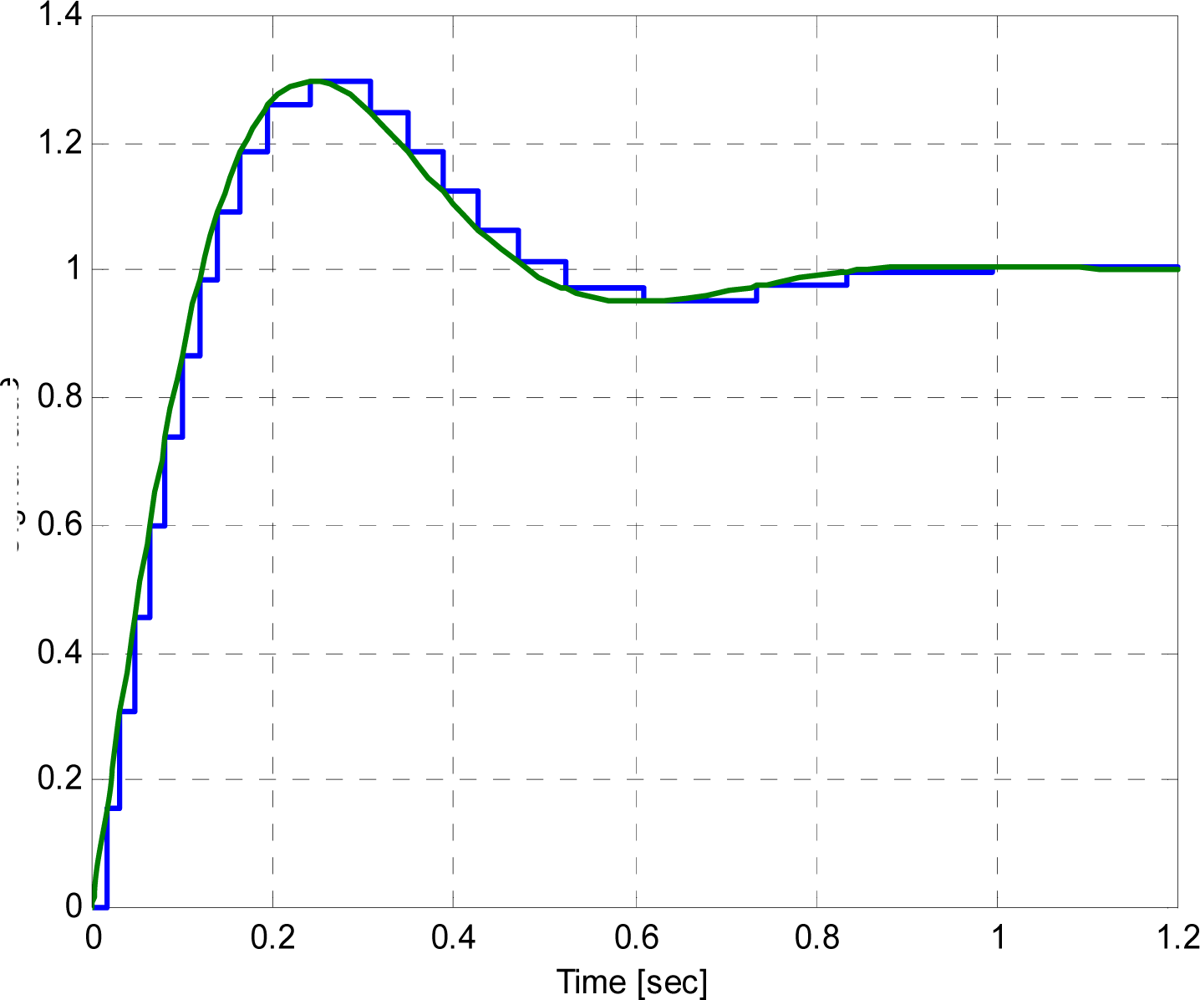
5. Simulation Results
6. Asymptotic Effectiveness of Event-Based Sampling in Dynamic Systems
- - step responses of the first-order system, of the differentiation circuit, and of the integration circuit,
- - critically damped step responses of the second-order and the nth-order systems,
- - second-order overdamped step response,
- - undamped step response (harmonic signal).
7. Conclusions
Acknowledgments
References and Notes
- Miśkowicz, M. Send-on-Delta Concept: an Event-Based Data Reporting Strategy. Sensors 2006, 6, 49–63. [Google Scholar]
- Pawlowski, A.; Guzman, J.L.; Rodríguez, F.; Berenguel, M.; Sánchez, J.; Dormido, S. Simulation of Greenhouse Climate Monitoring and Control with Wireless Sensor Network and Event-Based Control. Sensors 2009, 9, 232–252. [Google Scholar]
- Allier, E.; Sicard, G.; Fesquet, L.; Renaudin, M. A New Class of Asynchronous A/D Converters Based on Time Quantization. Proceedings of IEEE International Symposium on Asynchronous Circuits and Systems ASYNC 2003, Vancouver, Canada, 2003; pp. 196–205.
- Manohar, R.; Apsel, A.B.; Akopyan, F. A Level-Crosing Flash Asynchronous Analog-to-Digital Converter. Proceedings of IEEE International Symposium on Asynchronous Circuits and Systems ASYNC 2006, Grenoble, France, 2006; pp. 12–22.
- Kościelnik, D.; Miśkowicz, M. Asynchronous Sigma-Delta Analog-to-Digital Converter Based on the Charge Pump Integrator. Analog Integr. Circuit. Sig 2008, 55, 223–238. [Google Scholar]
- MalmirChegini, M.; Marvasti, F. Performance Improvement of Level-Crossing A/D Converters. Proceedings of IEEE International Conference on Telecommunications ICT-MICC 2007, Penang, Malaysia, 2007; pp. 438–441.
- Guan, K.M.; Kozat, S.S.; Singer, A.C. Adaptive Reference Levels in a Level-Crossing Analog-to-Digital Converter. EURASIP J. Adv. Sign. Proc 2008. Article No. 183.. [Google Scholar]
- Miśkowicz, M. Asymptotic Effectiveness of the Event-Based Sampling according to the Integral Criterion. Sensors 2007, 7, 16–37. [Google Scholar]
- Suh, Y.S. Send-on-Delta Sensor Data Transmission with a Linear Predictor. Sensors 2007, 7, 537–547. [Google Scholar]
- Ellis, P.H. Extension of Phase Plane Analysis to Quantized Systems. IRE Trans. Automat. Contr 1959, 4, 43–59. [Google Scholar]
- Dorf, R.C.; Farren, M.C.; Phillips, C.A. Adaptive Sampling for Sampled-Data Control Systems. IEEE Trans. Automat. Contr 1962, 7, 38–47. [Google Scholar]
- Mitchell, J.R.; McDaniel, W.L. Adaptive Sampling Technique. IEEE Trans. Automat. Contr 1969, 14, 200–201. [Google Scholar]
- Gupta, S.C. Increasing the Sampling Efficiency for a Control System. IEEE Trans. Automat. Contr 1963, 8, 263–264. [Google Scholar]
- Hsia, T.C. Comparisons of Adaptive Sampling Control Laws. IEEE Trans. Automat. Contr 1972, 17, 830–831. [Google Scholar]
- Hsia, T.C. Analytic Design of Adaptive Sampling Control Laws. IEEE Trans. Automat. Contr 1974, 19, 39–42. [Google Scholar]
- De la Sen, M.; Almansa, A. Adaptive Stable Control of Manipulators with Improved Adaptation Transients by Using On-Line Supervision of the Free-Parameters of the Adaptation Algorithm and Sampling Rate. Inform. Lith. Acad. Sci 2002, 13, 345–368. [Google Scholar]
- De la Sen, M. Non-Periodic and Adaptive Sampling. A Tutorial Review. Inform. Lith. Acad. Sci 1996, 7, 175–228. [Google Scholar]
- Dormido, S.; de la Sen, M.; Mellado, M. Criterios Generales de Determinación de Leyes de Maestro Adaptivo (in Spanish). Revista de Informática y Automática 1978, 38, 13–29. [Google Scholar]
- Xia, F.; Zhao, W. Flexible Time-Triggered Sampling in Smart Sensor-Based Wireless Control Systems. Sensors 2007, 7, 2548–2564. [Google Scholar]
- Henriksson, D.; Cervin, A. Optimal On-line Sampling Period Assignment for Real-Time Control Tasks Based on Plant State Information. Proceedings of IEEE Conference on Decision and Control and European Control Conference CDC-ECC’05, Seville, Spain, 2005; pp. 4469–4474.
- Manjeshwar, A.; Agrawal, D.P. TEEN: A Routing Protocol for Enhanced Efficiency in Wireless Sensor Networks. Proceedings of International Parallel Distributed Processing Symposium IPDPS’2001, San Francisco, CA, USA, 2001; pp. 189–199.
- Nguyen, V.H.; Suh, Y.S. Networked Estimation for Event-Based Sampling Systems with Packet Dropouts. Sensors 2009, 9, 3078–3089. [Google Scholar]
- Nguyen, V.H.; Suh, Y.S. Networked Estimation with an Area-Triggered Transmission Method. Sensors 2008, 8, 897–909. [Google Scholar]
- Vasyutynskyy, V.; Kabitzsch, K. Towards Comparison of Deadband Sampling Types. Proceedings of IEEE International Symposium on Industrial Electronics ISIE, Vigo, Spain, 2007; pp. 2899–2904.
- Ploennigs, J.; Vasyutynskyy, V.; Kabitzsch, K. Comparison of Energy-Efficient Sampling Methods for WSNs in Building Automation Scenarios. Proceedings of IEEE International Conference on Emerging Techonologies and Factory Automation ETFA, Palma de Mallorca, Spain, 2009; pp. 1–8.
- Sánchez, J.; Guarnes, M.Á.; Dormido, S. On the Application of Different Event-Based Sampling Strategies to the Control of a Simple Industrial Process. Sensors 2009, 9, 6795–6818. [Google Scholar]
- de la Sen, M. About Optimal Fractional Hold Circuits for Inter-Sample Output Reconstruction in Sampled-Data Systems. Sensors 2007, 7, 3146–3155. [Google Scholar]
- de la Sen, M. On the Properties Of Reachability, Observability, Controllability, and Constructibility of Discrete-Time Positive Time-Invariant Linear Systems with Aperiodic Choice of the Sampling Instants. Disc. Dynam. Nat. Soc 2007. [Google Scholar] [CrossRef]
- Layer 7 LonMark Interoperability Guidelines; Ver. 3.2; LonMark Interoperability Association: San Jose, CA, USA, 2002.
- Miśkowicz, M.; Golański, R. LON Technology in Wireless Sensor Networking Applications. Sensors 2006, 6, 30–48. [Google Scholar]
- Neugebauer, M.; Kabitzsch, K. A New Protocol for a Low Power Sensor Network. Proceedings of IEEE International Performance, Computing and Communications Conference IPCCC’2004, Phoenix, AZ, USA, 2004; pp. 393–399.
- Plönnigs, J.; Neugebauer, M.; Kabitzsch, K. A Traffic Model for Networked Devices in the Building Automation. Proceedings of IEEE International Workshop on Factory Communication Systems WFCS’2004, Vienna, Austria, 2004; pp. 137–145.
- Aström, K.J.; Bernhardsson, B. Systems with Lebesgue Sampling. In Directions in Mathematical Systems Theory and Optimization; Rantzer, A., Byrnes, C.I., Eds.; Springer: Berlin, Germany, 2003; pp. 1–13. [Google Scholar]
- Sayiner, N.; Sorensen, H.V.; Viswanathan, T.R. A Level-Crossing Sampling Scheme for A/D Conversion. IEEE Trans. Circuits Syst. II Analog Digit. Sig. Proc 1996, 43, 335–339. [Google Scholar]
- Mark, J.; Todd, T. A Nonuniform Sampling Approach to Data Compression. IEEE Trans. Commun 1981, 29, 24–32. [Google Scholar]
- Otanez, P.; Moyne, J.; Tilbury, D. Using Deadbands To Reduce Communication in Networked Control Systems. Proceedings of American Control Conference ACC’2002, Anchorage, AK, USA, 2002; pp. 3015–3020.
- Cogill, R. Event-Based Control Using Quadratic Approximate Value Functions. Proceedings of IEEE Conference on Decision and Control CDC 2009, Shanghai, China, 2009.
- Cogill, R.; Lall, S.; Hespanha, J.P. A Constant Factor Approximation Algorithm for Optimal Estimation Subject to Communication Costs. Proceedings of the 2007 American Control Conference, New York, NY, USA, 2007; pp. 305–311.
- Kofman, E.; Braslavsky, J.H. Level Crossing Sampling in Feedback Stabilization under Data-Rate Constraints. Proceedings of IEEE Conference on Decision and Control CDC 2006, San Diego, CA, USA, 2006; pp. 4423–4428.
- Vasyutynskyy, V. Send-on-Delta-Abtastung in PID-Regelungen. Technische Universitaet Dresden, Joerg Vogt Verlag, Dresden,. 2009. [Google Scholar]
- Vasyutynskyy, V.; Kabitzsch, K. Deadband Sampling in PID Control. Proceedings of the 5th IEEE International Conference on Industrial Informatics INDIN 2007, Vienna, Austria, 2007; pp. 45–50.
- Vasyutynskyy, V.; Kabitzsch, K. Implementation of PID Controller with Send-On-Delta Sampling. Proceedings of International Control Conference ICC 2006, Glasgow, UK, 2006.
- Cervin, A.; Aström, K.J. On Limit Cycles in Event-Based Control Systems. Proceedings of 46th IEEE Conference on Decision and Control, New Orleans, LA, USA, 2007.
- Zhang, G.; Zheng, W.X. Stability and Bifurcation Analysis of a Class of Networked Dynamical Systems. IEEE Trans. Circuits Syst–II 2009, 56, 664–668. [Google Scholar]
- Miśkowicz, M. Sampling of Signals in Energy Domain. Proceedings of IEEE International Conference on Emerging Technologies and Factory Automation ETFA, Catania, Italy, 2005; pp. 263–266.
- Riesz, F.; Nagy, B. Functional Analysis; Dover Publications, Inc: New York, NY, USA, 1990. [Google Scholar]
- Rudin, W. Real and Complex Analysis, 3rd ed; McGraw-Hill Book: New York, NY, USA, 1987. [Google Scholar]
- Sakul, C. A New CMOS Squaring Circuit Using Voltage/Current Input. Proceedings of the 23rd International Technical Conference on Circuits/Systems, Computers and Communications ITC-CSCC, Shimonoseki City, Japan, 2008; pp. 525–528.
- De Paoli, F.; Tisato, F. On the Complementary Nature of Event-Driven and Time-Driven Models. Contr. Eng. Pract 1996, 4, 847–854. [Google Scholar]
- Miśkowicz, M. Comparison of Intensive and Extensive Sensor Networking Technologies. Int. J. Online Eng 2006, 1, 1–6. [Google Scholar]
- Elson, J.; Estrin, D. An Address-Free Architecture for Dynamic Sensor Networks; Technical Report 00-724; University of Southern California, Computer Science Department: Los Angeles, CA, USA, 2000. [Google Scholar]
- Wang, J.-F.; Li, L.-F.; Christakos, G. Sampling and Kriging Spatial Means: Efficiency and Conditions. Sensors 2009, 9, 5224–5240. [Google Scholar]
- Wang, J.F.; Christakos, G.; Hu, M.G. Modeling Spatial Means of Surfaces with Stratified Non-Homogeneity. IEEE Trans. Geosc. Rem. Sens 2009, 47, 4167–4174. [Google Scholar]
| Sampling resolution (threshold ζ) | Number of samples in energy sampling | Number of samples in periodic sampling | Energy sampling effectiveness |
|---|---|---|---|
| 4E-3 | 4 | 24 | 6 |
| 1E-3 | 7 | 38 | 5.430 |
| 3.3E-5 | 24 | 120 | 5 |
| 1E-5 | 37 | 179 | 4.838 |
| 1E-7 | 173 | 833 | 4.815 |
| 1E-8 | 373 | 1,791 | 4.802 |
| Signal | Step response | Asymptotic effectiveness |
|---|---|---|
| First-order step response | ||
| Differentiation circuit | ||
| Integration circuit | ||
| Second-order critically damped step response | ||
| Second-order overdamped step response | ||
| nth-order critically damped step response | ||
| Second-order underdamped step response (0 < ξ < 1) | Symbolic solution is not available, the numeric solutions for a particular set of parameters can be calculated | |
| x(t) = k(1 − cos ωn t) | Harmonic signal—second-order undamped step response (ξ = 0) |
| Signal | Energy sampling effectiveness | Integral sampling effectiveness | Send-on-delta effectiveness |
|---|---|---|---|
| χ∞(η = 3) = 2,31 where: η = b/T | q∞(η = 3) = 1.93 | p(η = 3) = 3.16 | |
| χ∞(η = 3) = 2,31 where: η = b/T | q∞(η = 3) = 1.93 | p(η = 3) = 3.16 | |
| χ∞(η = 20) = 1.039 where: η = b/T | q∞(η = 20) = 1.032 | p(η = 20) = 1.053 | |
| χ∞(η = 20) = 1.85 where: η = b/T | q∞(η = 20) = 1.46 | p(η = 20) = 1.92 | |
| χ∞(n = 2, λ = 5) = 1,62 where: η = b/T | q∞(n = 2,η = 5) = 1.46 | p(n = 2, λ = 5) = 1,92 | |
| x (t) = x0 (1 − cos ωn t) | χ∞ = 1,402 bωn = πm/2, m = 1,2,… | q∞ = 1.31 | pmin = 1.57 |
| x(t) = kt | χ∞ = 1 | q∞ = 1 | p = 1 |
© 2010 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Miskowicz, M. Efficiency of Event-Based Sampling According to Error Energy Criterion. Sensors 2010, 10, 2242-2261. https://doi.org/10.3390/s100302242
Miskowicz M. Efficiency of Event-Based Sampling According to Error Energy Criterion. Sensors. 2010; 10(3):2242-2261. https://doi.org/10.3390/s100302242
Chicago/Turabian StyleMiskowicz, Marek. 2010. "Efficiency of Event-Based Sampling According to Error Energy Criterion" Sensors 10, no. 3: 2242-2261. https://doi.org/10.3390/s100302242




