This section presents the four central models for our work, namely clustering strategy (Section 2.1.), WSNs from the signal processing viewpoint (Section 2.2.), a model for the observed data (Section 2.3.) and a model for sensor deployment (Section 2.4.)
2.1. Clustering
WSNs present several constraints such as battery capacity, and limited computing capabilities [
1]. Among those constraints, energy limitation is considered as the most important aspect to address in order to improve the network lifetime. Many lifetime-maximizing techniques have been proposed, and each approach provides a certain level of energy saving [
14].
Clustering sensors into groups is a popular strategy to save energy [
15] by exploring correlation present in the data collected by neighbor sensors. This technique is usually performed in three phases: (i) leader election, which aims at choosing one representative for each group, the Cluster Head (CH); (ii) cluster formation, where all other nodes will join only one group represented by its CH; and (iii) data communication, where group members report their data to CH. The CH usually performs data fusion, and delivers the fused data toward to the sink node. Nodes are attached to groups and the ideal number of groups depend on the clustering objective. Abbasi and Younis [
15] describe a taxonomy of WSN clustering techniques, and discuss some clustering objectives.
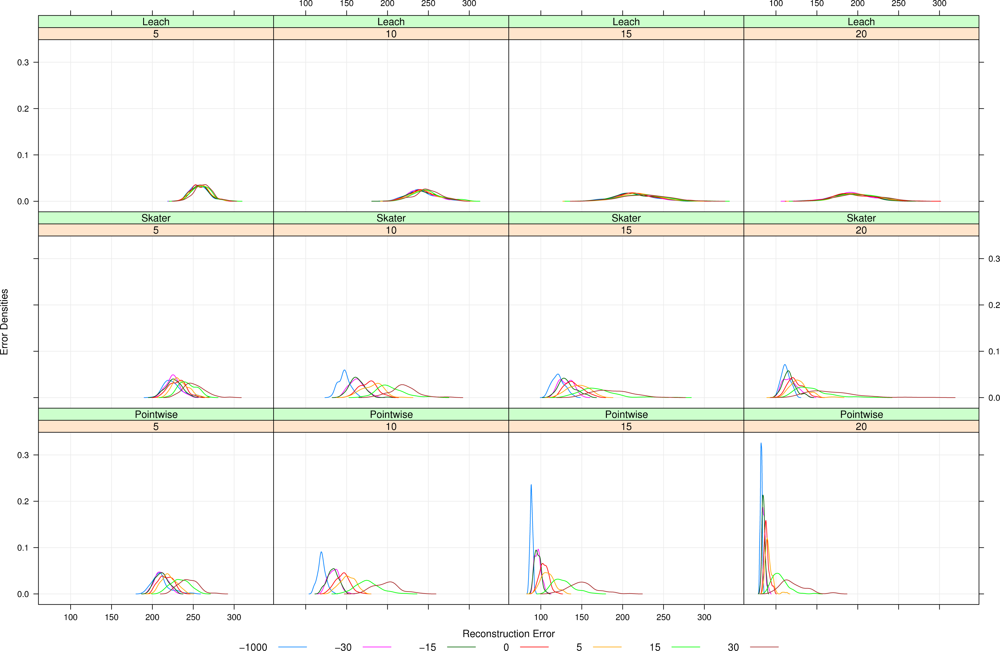
In the following, two clustering approaches are detailed. The former creates clusters based on geographical information, while the later is based on a data-aware clustering technique. These approaches will be assessed in terms of the quality of reconstructed signal in Section 4.
2.1.1. LEACH
LEACH (Low-Energy Adaptive Clustering Hierarchy) [
16] is a popular WSN clustering approach. It executes in rounds, and each round performs the three aforementioned phases. LEACH assumes that all nodes are able to reach the sink node in one hop, and that they are capable of organizing the groups and the communication by power control schemes. Both CHs and group members deliver their data to the sink and to CHs, respectively, directly (single hop).
There are two different versions of LEACH proposed in [
16]: one considers that CHs are elected in a distributed fashion, and the other in a centralized way. Initially (first round), the election occurs randomly, following an uniform law, by a rule tuned to elect
k CHs, in average. In the next rounds, the nodes that were chosen as CHs in the last [
n/k] rounds, being
n the number of nodes and
k the number of clusters, are not eligible. This approach warrants that the CH role will be alternated in order to better distribute the energy consumption. The remaining energy of the nodes may be used to adjust the probability law, and force nodes with more energy to be elected more likely. In the second version, CHs are elected in a centralized fashion (LEACH-C). Each node sends the information about its current location and energy level to the sink node. The problem to find
k optimal clusters and the CHs nodes that minimize the energy consumption is NP-hard and it is solved by the sink applying a simulated annealing solution.
Once the election finishes, CHs inform their role by an advertisement message. Thus, all other nodes receive this message and join only one group represented by the CH that requires the minimum communication energy. LEACH takes this decision based on the received signal strength of the advertisement message from each CH. Note that, typically, this will lead to choosing the closest CH, unless there is an obstacle impeding communication. After clusters are formed, each group member configures its power to reach its corresponding CH. The communication within the group uses a TDMA scheme and, outside the groups, CHs employ a direct-sequence spread spectrum. These schemes attempt to diminish intraand inter-group interferences.
The main goal of our assessment is to analyze the reconstruction error. Thus, questions related to energy consumption were not considered and CHs were chosen randomly in a similar manner of the distributed version of LEACH. The difference is that we forced the CHs to be far from at least r units (in our scenarios, r = 30). This choice makes CHs more equally distributed on the sensor field and diminishes the reconstruction error.
2.1.2. SKATER
LEACH assumes that nearby nodes have correlated data, while SKATER (Spatial ‘K’luster Analysis by Tree Edge Removal) [
17,
18] introduces an additional restriction to produce good quality data summaries. SKATER uses a data-aware clustering procedure that mainly influences the way clusters are formed. Its hypothesis is that data fused on spatially homogeneous clusters will have a better statistical quality (less variability) than those fused on geographical clusters such as LEACH. Apart from the proposals by Kotidis [
19], and Toulone and Madden [
20], data homogeneity is rarely used for sensor clustering.
As spatially homogeneous clusters, SKATER looks for a partition with three properties: (i) nodes of the same group have to be similar to each other in some predefined attributes; (ii) the attributes are different among different groups, and (iii) nodes of the same group must belong to a predefined neighborhood structure.
SKATER works in two steps. First, it creates a minimal spanning tree (MST) from the graph representation for the neighborhood of the geographical structure of the nodes. The cost of the edges represents the similarity of the sensors’ collected data, defined as the euclidian square distance between them (data might be in ℝp). In the second step, SKATER performs a recursive partitioning of the MST to get contiguous clusters. The partitioning method considers the internal homogeneity of the clusters, i.e., it uses the sensors’ data information. Thus, SKATER transforms the regionalization problem into a graph partitioning problem. The partitioning method chooses the edge whose removal leads to more homogeneous clusters, and, recursively, creates a new graph that is a forest. The process is repeated until the forest has k trees (k clusters). This process uses an objective function proportional to the variance of the data collected by the same group sensors.
SKATER is a centralized clustering processing and presents high computational cost due to the exhaustive comparison of all possible values of the objective function. However, SKATER uses a polynomial-time heuristic for fast tree partitioning.
In our work, we used SKATER to build homogeneous clusters. The process is similar to that described in LEACH, but the cluster formation is performed in the same manner as in SKATER. CHs are chosen randomly among cluster members.
2.2. WSNs and signal processing
As presented in Aquino
et al. [
21], and Frery
et al. [
22], a WSN can be conveniently described as sampling/reconstruction processes within the signal processing framework.
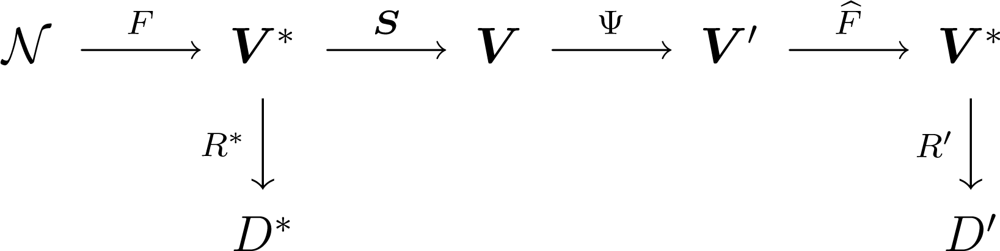
A WSN collecting information can be represented by the diagram shown in
Figure 1, where
denotes the environment and the process to be measured,
F is the phenomenon of interest, with
V* its spatiotemporal domain. A set of ideal rules (
R*) leading to ideal decisions (
D*) could be devised if true, complete and uncorrupted observation of the phenomenon was possible. One has, instead, sensors
S = (
S1, . . .,
Sn), each measuring the phenomenon in a certain position and producing a report in its domain
Vi, 1 ≤
i ≤
n; all possible domain sets are denoted
V = (
V1, . . .,
Vn). From the signal theory viewpoint,
F is the stochastic process that models the signal to be analyzed,
S is the sampling strategy.
Most of the time, collecting all data from every sensor is a waste of resources since there is redundant information. In order to save resources, e.g., energy and, therefore, to extend the network lifetime, information fusion techniques are used [
8]. They are denoted by Ψ and produce values in a reduced subset
V′ ⊂
V. A reconstruction function
F̂ is then applied to these fused data, aiming at restoring the events described by
F as close as possible; this function should be regarded to as an estimator. Using this new information, the sets of rules and decisions become
R′ and
D′, respectively. Ideally,
D′ and
D* are the same.
The class of transformations Ψ we consider here is formed by two different steps: the first is the clustering of nodes, and the second is data aggregation. Aggregated data, with their corresponding locations, are used as input to a reconstruction process that runs in the sink, and then delivered to the user. The data sent to the user, i.e., the reconstructed signal, is compared with the phenomenon of interest by means of a measure of error which we use to assess the impact of sensor placement and data aggregation on the performance of the WSN. This is performed for a number of phenomena of interest.
Besides the already defined clustering techniques, namely, LEACH and SKATER, Pointwise data processing that makes neither clustering nor aggregation is used in this work as a benchmark.
In our study, data aggregation will be done by taking the mean value of the data observed at each cluster; this reduction makes sense when these data can be safely summarized by a single value.
Signal reconstruction is performed with two strategies: Voronoi cells and Kriging. They require the same information, namely sensor position and value, being the latter more computationally intensive.
2.3. The data
Sensors measure a continuously varying function
F describing, for instance, the illumination on the ground of a forest or the air pressure in a room [
18,
23].
Random fields are collections of random variables indexed in a
d-dimensional space [
24,
25]. Such models can be used to describe natural phenomena, such as temperature, moist and gravity. Following Reis
et al. [
18], we use a zero-mean isotropic Gaussian random field for describing the truth being monitored by the WSN,
i.e.,
F in the diagram shown in
Figure 1.
We assume a stable covariance function exp(−
ds), where
d ≥ 0 is the Euclidian distance between sites, and
s > 0, called scale, is the parameter that characterizes this model. The scale is related to the granularity of the process.
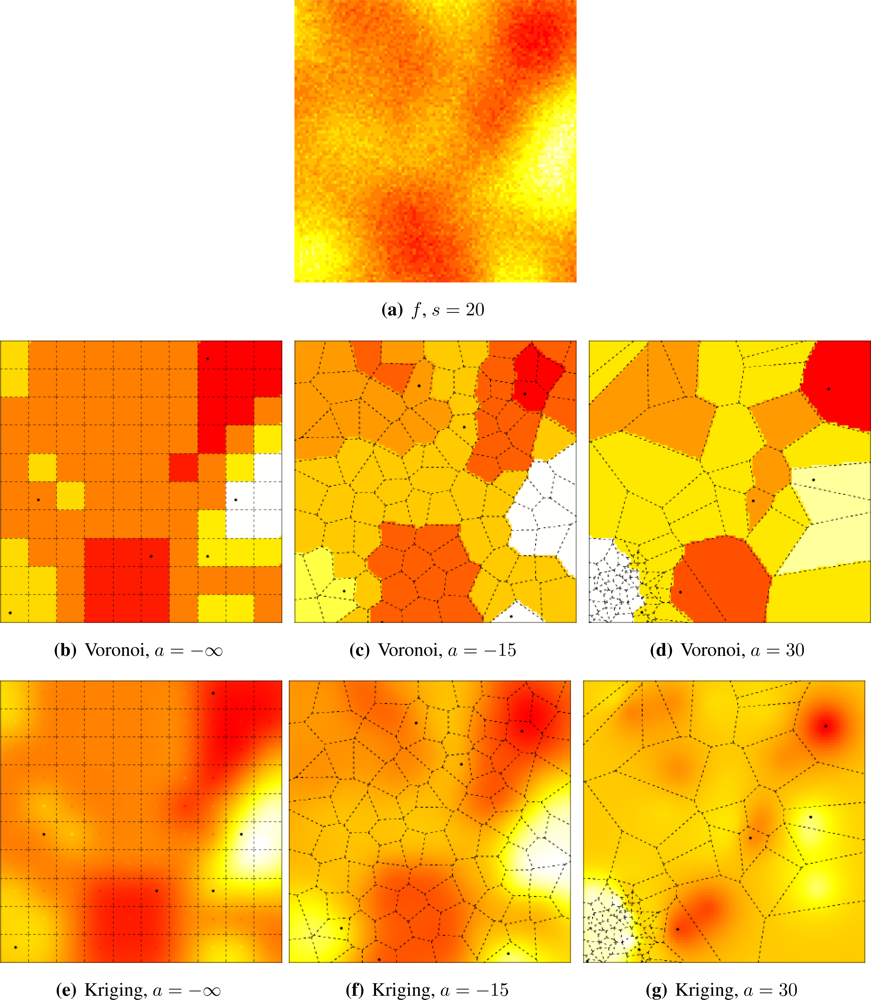
Figure 2 shows four situations, from fine (
s = 5) to coarse (
s = 20) granularity. Samples from this process can be readily obtained using the RandomFields package for R [
25]. We used a red-yellow-white color table in order to enhance the different values.
Sampling outcomes of F will be performed, typically, in irregularly spaced locations, which we describe by means of spatial point processes. The location of those sensors will be described by a stochastic point process, presented in the following section.
2.4. Sensor deployment
Point processes are stochastic models that describe the location of points in space. They are useful in a broad variety of scientific applications such as ecology, medicine, and engineering [
26].
The isotropic stationary Poisson model, also known as fully random or uniformly distributed, is the basic point process. The number of points in the region of interest follows a Poisson law with mean proportional to the area. The location of each point does not have influence on the location of the other points. The other process we will use is a repulsive one, where points cannot lie at less than a specified distance. Using these two processes we build a composed point process able to describe many practical situations.
The Poisson point process over a finite region
W ⊂ ℝ
2 is defined by the following properties:
The probability of observing n ∈ ℕ0 points in any set A ⊂ W follows a Poisson distribution: Pr(NA = n) = e−ημ(A)[ημ (A)]n/n!, where η > 0 is the intensity and μ(A) is the area of A.
Random variables used to describe the number of points in disjoint subsets are independent.
Without loss of generality, in order to draw a sample from a Poisson point process with intensity η > 0 on a squared window W = [0, ℓ] × [0, ℓ], first sample from a Poisson random variable with mean ηℓ2. Assume n was observed. Now obtain 2n samples from independent identically distributed random variables with uniform distribution on [0, ℓ], say x1, . . ., xn, y1, . . ., yn. The n points placed at coordinates (xi, yi)1≤i≤n are an outcome of the Poisson point process on W with intensity η. If n is known beforehand, rather than the outcome of a Poisson random variable, then the n points placed at coordinates (xi, yi)1≤i≤n are an outcome of the Binomial point process on W; this last process is denoted B(n).
The Matérn’s Simple Sequential Inhibition process can be defined iteratively as the procedure that places at most n points in W. The first point is placed uniformly, and until all the n points are placed or the maximum number of iterations tmax is reached, a new location is chosen uniformly on W regardless the previous points. A new point is placed there if the new location is not closer than r to any previous point; otherwise the location is discarded, the iteration counter is increased by one and a new location is chosen uniformly. At the end, there are m ≤ n points in W that lie at least r units from each other. This process describes the distribution of non-overlapping discs of radii r/2 on W; denote it M(n, r).
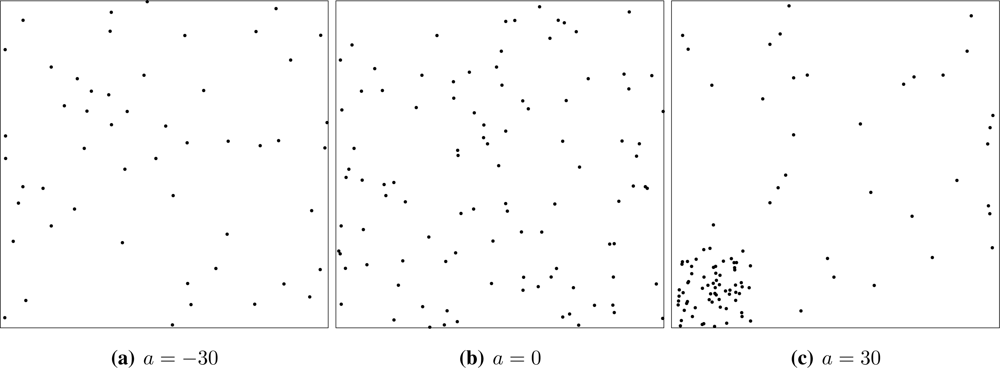
We build an attractive process by merging two Poisson processes with different intensities. A step point process in W′ ⊂ W ⊂ ℝ2 with parameters a, λ > 0 is defined as two independent Point processes: one with parameter λ on W \ W′, and other with parameter aλ on W′. Denote this process S(n, a).
Without loss of generality, we define the compound point process
W = [0, 100]
2,
W′ = [0, 25]
2 and η = 1, denoted by
(
n, a), as
where
rmax is the maximum exclusion distance, which we set to
rmax =
n−1/2. The
(
n, a) point process spans in a seamless manner the repulsive (
a < 0,
Figure 4(a)), full random (
a ∈ [0, 1],
Figure 4(b)) and attractive cases (
a > 0,
Figure 4(c)). For the sake of completeness
(
n, −∞) denotes the deterministic placement of
n regularly spaced sensors on
W at the maximum possible distance among them. Samples from the
process can be easily generated using basic functions from the spatstat package for R [
27].
Repulsive processes are able to describe the intentional, but not completely controlled location of sensors as, for instance, when they are deployed by a helicopter at low altitude. Sensors located by a binomial process could have been deployed from high altitude, so their location is completely random and independent of each other. Attractive situations may arise in practice when sensors cannot be either deployed or function everywhere as, for instance, when they are spread in a swamp: those that fall in a dry spot survive, but if they land on water they may fail to function.
2.5. Signal sampling and reconstruction
Without loss of generality, in the following we consider that the whole process takes place on W = [0, 100]2 and W′ = [0, 25]2 with intensity η = 1, and that there are n = 100 sensors. Once the signal f = F(ω), outcome of the Gaussian random field with parameter s ∈ ℝ presented in Section 2.3., is available, it will be sampled at positions (x1, y1), . . ., (x100, y100), which, in turn, are the outcome of the compound point process (100, a), a ∈ ℝ, defined in Section 2.4..
For each 1 ≤
i ≤ 100, sensor
i, located at (
xi,
yi) ∈
W, captures a portion of
f: the mean value observed within its area of perception
pi,
i.e., it stores the value
vi = ∫
pi f. We chose to work with isotropic homogeneous sensors, where
being
r > 0 the perception radius, which we set to
. If 100 sensors were deployed in regular fashion on
W, their Voronoi cells would have areas of 100 squared units; the same area is produced by circular perception areas of radii
, therefore our choice.
Once every node has its value vi, 1 ≤ i ≤ 100, clustering begins. LEACH groups nearby sensors, while SKATER also employs the values they have stored. Once clusters are formed, the mean of the values stored in the sensors belonging to each cluster are sent to the sink by each CH, along with the information of the position of each node. The next stage begins then, namely, signal reconstruction.
Two reconstruction methodologies were assessed in this work: Voronoi cells and Kriging. The former consists in first determining the Voronoi cell of each sensor,
i.e., the points in
W that are closer to it. Each cluster becomes responsible for the area corresponding to the union of the Voronoi cells that belong to the sensors that form it. Then the reconstructed value at position (
x, y) ∈
W is the mean value returned by the cluster responsible for that point; see
Figure 4. These computations were easily implemented using the deldir package for R.
Kriging is the second reconstruction procedure we employed. It is a geostatistical method, whose simplest version (“simple Kriging”) is equivalent to minimum mean square error prediction under a linear Gaussian model with known parameter values. No parameter was assumed known and, regardless the true covariance model imposed to the Gaussian field, we estimated a general and widely accepted covariance function: the Matérn model given by
where
d > 0 is the distance between points, Γ is the Gamma function,
Kν is the modified Bessel function of second kind and order
ν > 0, and the parameters to be estimated are
ρ > 0, which measures how quickly the correlation decays with distance, and
ν > 0, which is the smoothness parameter. More details about this covariance function, including particular cases, inference and its application, can be seen in [
28].
Given the data and their location, the covariance function is estimated using maximum likelihood. Then, the means are estimated by generalized minimum squares using the covariance as weight: closer values have more influence than distant ones. Notice that such procedure requires the same information needed by Voronoi reconstruction, namely, the sampled data and their position; see
Figure 4.
Ordinary Kriging was used by Yu
et al. [
29] for the simulation of plausible data to be used as the input of sensor network assessment procedures by simulation. For details and related techniques, please refer to Diggle and Ribeiro Jr. [
30].
As a benchmark, the result of applying ordinary Kriging to the original v1, . . ., v100 sampled values without clustering or aggregation is also presented. This approach, which provides the best possible input for any reconstruction procedure, is too costly from the energy consumption viewpoint, but provides a measure of the loss introduced by LEACH, SKATER or any other similar procedure.
Figure 4 presents the general setup and the alternatives we considered.
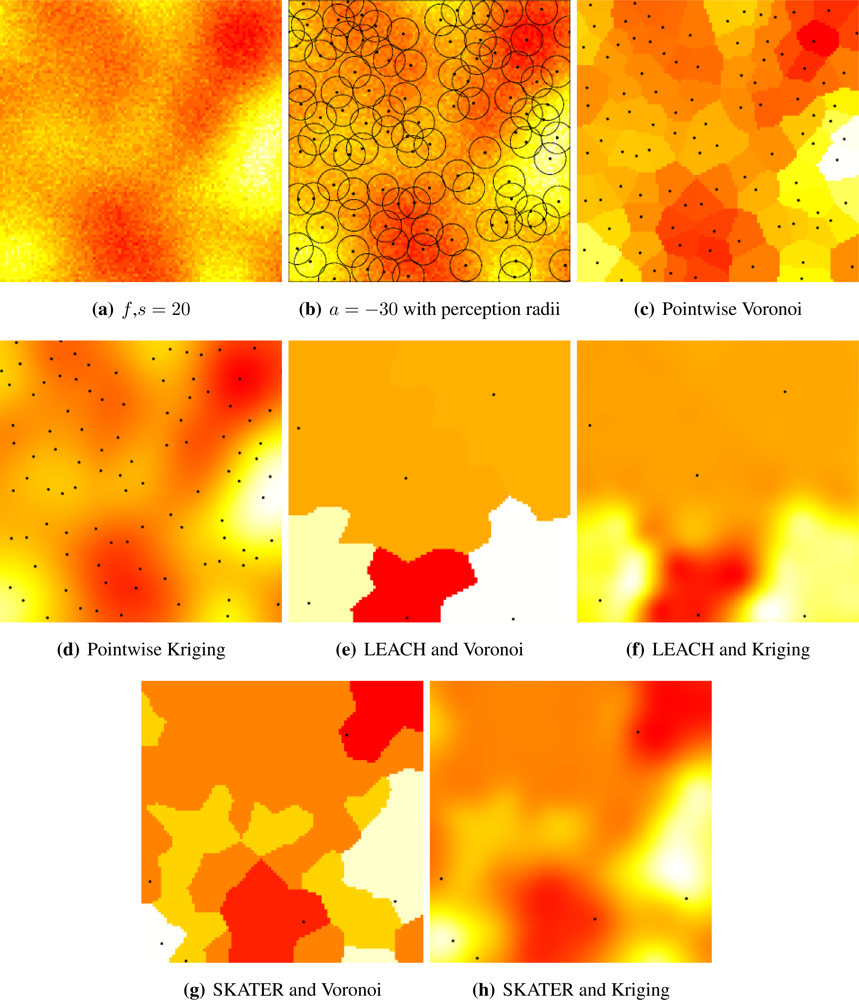
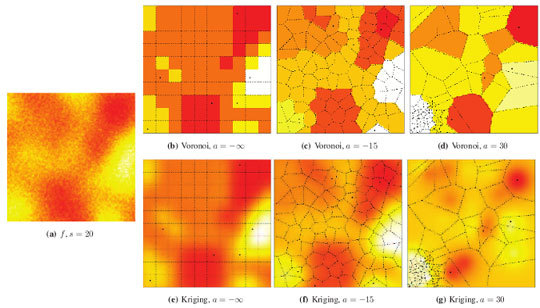
Figure 5(a) shows a sample of the Gaussian random field with coarse granularity,
i.e.,
s = 20.
Figure 5(b) presents the sensors deployed by a repulsive point process (
a = −30) and their radii of perception; notice that they overlap, introducing further correlation among the sampled data.
Figure 5(c) shows the pointwise reconstruction,
i.e., without sensor cluster or data aggregation, using Voronoi cells, while
Figure 5(d) shows the result of using Kriging on the same data. The result of applying LEACH followed by Voronoi reconstruction is shown in
Figure 5(e), while
Figure 5(f) presents the result of using LEACH and Kriging. If SKATER is used as an clustering/aggregation technique, and then Voronoi reconstruction is applied, one obtains the results presented in
Figure 5(g), while if Kriging is employed on those data the reconstructed signal is the one shown in
Figure 5(h). Notice that SKATER better preserves the overall shape of the original data set; this will be quantified in Section 4..
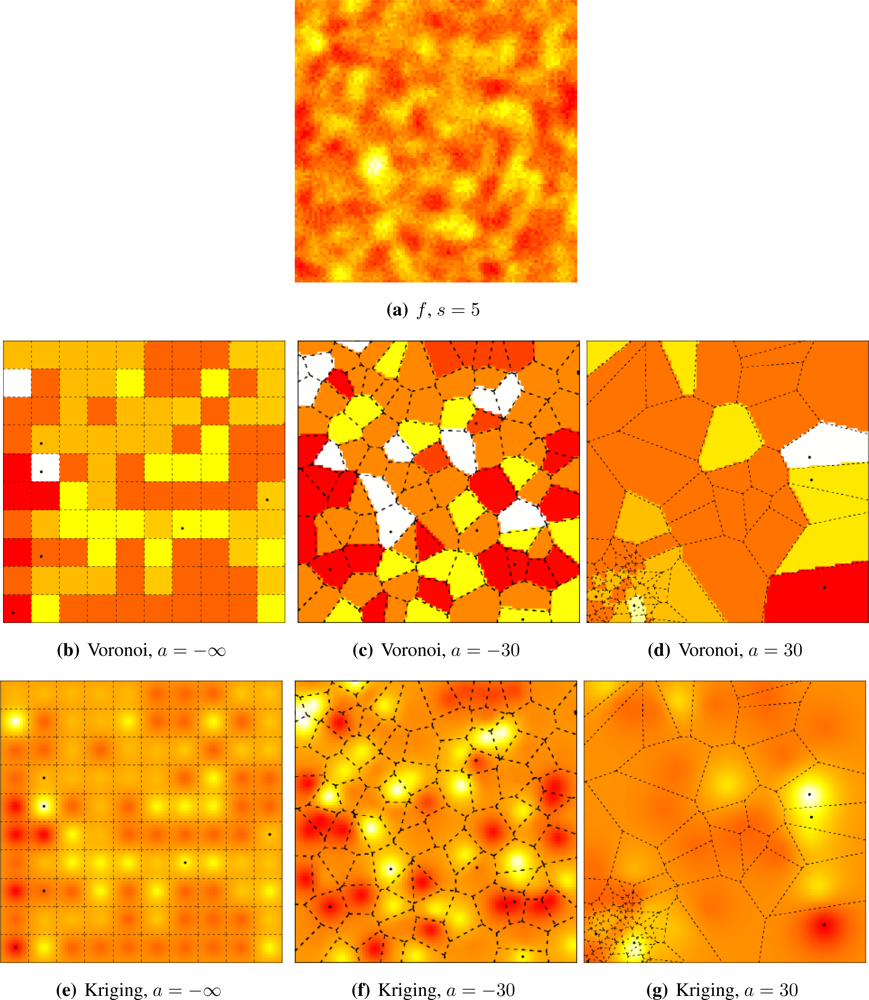
Figures 5 and
6 illustrate the influence of sensor deployment on the Voronoi and Kriging reconstruction approaches for, respectively, coarse (
s = 20) and fine (
s = 5) granularity processes, using SKATER. The dots show the six CHs at time considered.
Figures 5(a) and
6(a) show samples from the coarse and fine processes, respectively. The result of applying SKATER and reconstruction by Voronoi to data obtained from sensors deployed regularly (
a = −∞), and in repulsive (
a = −15) and attractive (
a = 30) manners are presented in
Figures 5(b) and
6(b),
5(c) and
6(c), and in
Figures 5(d) and
6(d). If instead of Voronoi, we used ordinary Kriging, one obtains the results shown in
Figures 5(e) and
6(e),
5(f) and
6(f), and in
Figures 5(g) and
6(g).
It is noticeable that the coarse process is easier to reconstruct, regardless the deployment. Regardless the coarseness of the process and the reconstruction, the more repulsive the deployment the better the reconstruction. Regardless the coarseness and the deployment, ordinary Kriging provides better reconstruction than Voronoi; because of this, only results produced by Kriging are presented in the remainder of this work.