A pedestrian or personal navigation system provides position information about a person indoors or outdoors. For example, if a firefighter carrying a personal navigation system is injured in the line of duty, we can know her/his position from the information transmitted by a pedestrian navigation system. Pedestrian navigation systems using inertial sensors are proposed in [1–6]. The main advantage of inertial sensor-based systems is that they are environment-independent; pedestrian navigation systems using vision or wireless communication require that landmarks or wireless nodes be installed in the environments [7,8].

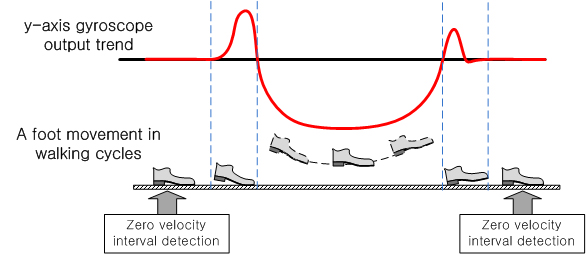
There are many different pedestrian navigation systems using inertial sensors. They use similar inertial navigation algorithms to compute the position [9,10]. Also they all use zero velocity updating algorithms. When an inertial navigation algorithm is used, the position and velocity errors diverge by a few seconds without error resetting. During normal walking cycles, a foot touches the ground almost periodically and stays on the ground for a short time (usually about 0.1∼0.3 s), which is called the zero velocity interval. In the zero velocity updating algorithm, this zero velocity interval is detected and thus the velocity error is reset to zero. Accordingly the position and velocity errors diverge very slowly, and consequently being able to reliably detect this zero velocity interval is an important issue.

Slightly different zero detection algorithms are used in [1–3,5,6]. In [1], the zero velocity interval is determined based on gyroscope and accelerometer output norms. If the outputs are less than some threshold for a predetermined time, the zero velocity interval is decided. In [2,3], similar algorithms are used, where the main difference is which sensor values are used. 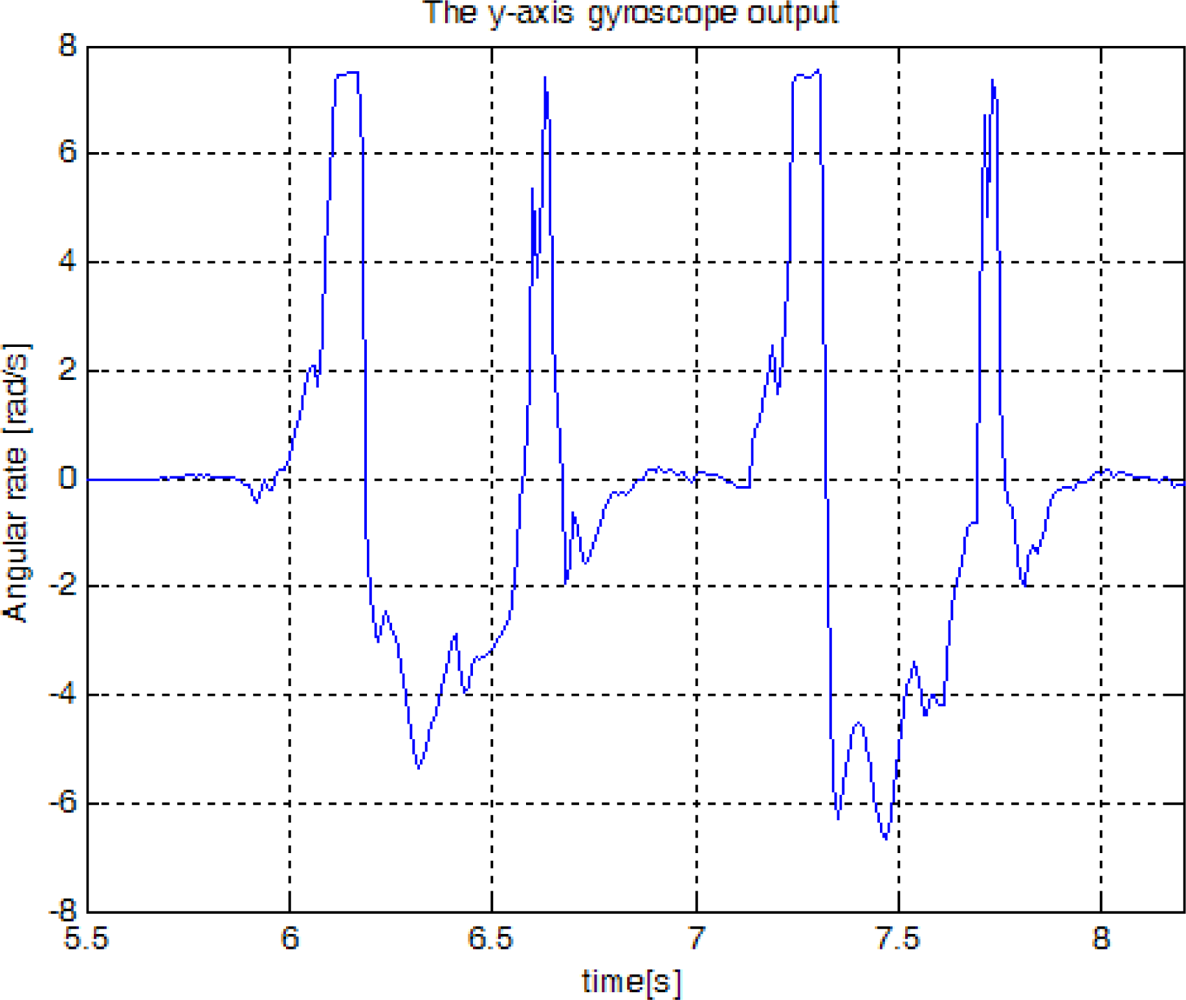In [2], the zero velocity interval is determined based on z-axis accelerometer and y-axis gyroscope outputs (see Figure 1 for the coordinate frame). In [3], the zero velocity interval is determined based on norms of gyroscope outputs. In [5], the zero velocity interval is detected based on the variance of accelerometer values. In [6], the zero velocity interval is detected based on norms of accelerometers and gyroscopes along with variance of accelerometers.

To use the zero velocity algorithms in [1–3,5,6], some threshold values (both for sensor values and time duration) must be assigned. These threshold values could differ significantly when a person is walking and running. The sensor values tend to become large and the interval duration tend to become shorter when a person is running. If we choose the threshold values too small, then we cannot detect zero velocity intervals when a person is running. On the other hand, if the threshold values are too large, then we could detect wrong zero velocity intervals. In general, the methods in [1–3,5,6] are relatively good for walking scenarios, but not for both walking and running.

In this paper, we propose a new zero velocity detection algorithm using a hidden Markov model [11,12]. The most relevant result is [4], where a zero velocity detection algorithm using a hidden Markov model is also used. The main differences are twofold. One is that only one gyroscope value is used in this paper while a foot sensor is also used in [4], which makes the zero detection problem relatively easy. The other difference is that a Markov model is constructed using segmentation of gyroscope outputs instead of using gyroscope outputs directly, which makes the zero velocity detection more reliable.

In inertial sensor-based pedestrian navigation systems, inertial sensors are installed on a shoe, as can be seen in Figure 1. Note that the y-axis is nearly perpendicular to the sagittal plane. Thus, when a person walks or runs, the dominant rotation axis is the y-axis. We use y-axis gyroscope value to determine the zero velocity intervals. The gyroscope measures angular rate of foot rotations, and y-axis gyroscope output in our system has positive values when a foot is rotating clockwise.

Figure 2 shows the y-axis gyroscope output of two walking steps. From experiments, we found that a typical pattern is given as in Figure 3, where the pattern consists of four segments. The pattern starts with the zero value segment and it has two positive value segments and one negative value segment between them. These four segments are related to the foot movement. When a foot is on the ground, the output value is near upon zero. As a foot takes off the ground, the gyroscope output has positive values. And then it has negative values when a foot is swinging. Lastly, gyroscope output has positive values once more when the heel of a foot (or shoe) contacts the ground. This pattern is repeated in walking and running. We assign four states (1,2,3, and 4) to each segment, as in Figure 3. The details are discussed in Section 3.

Figure 3 shows how the y-axis gyroscope value changes during the normal walking cycles. A foot touches the ground almost periodically for a short interval. During this short interval, a foot is fixed on the ground and not moving. These short intervals are called “zero velocity intervals”. Due to sensor noises in the real data, it is not always easy to determine the zero velocity interval. Similar patterns can be observed during running cycles. In the running cycles, the zero velocity interval becomes shorter and it is more difficult to detect the zero velocity interval. We divided the gait pattern into four states based on the features of the y-axis gyroscope output. At this time, the state 1 is zero velocity interval.

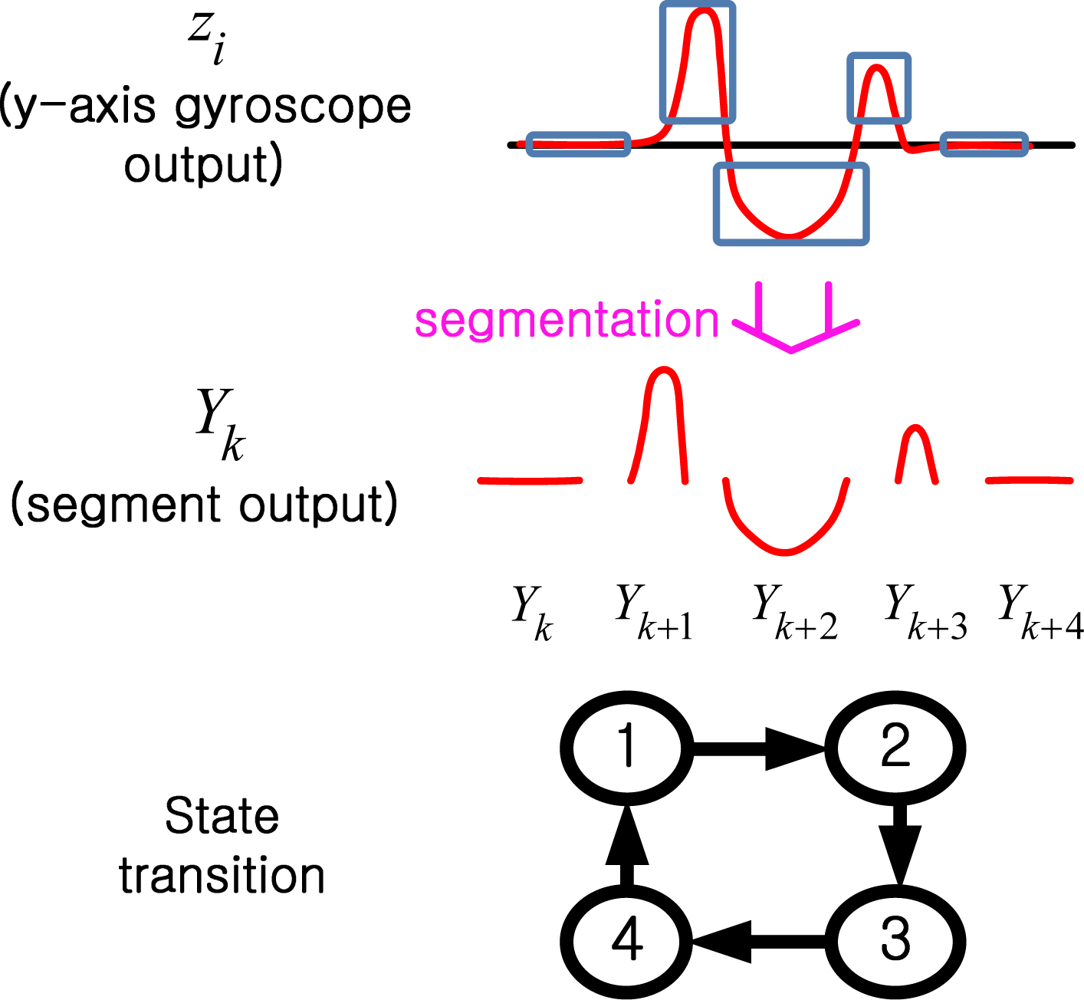
In this section, we introduce a hidden Markov model for the zero velocity detection. The walking states are modeled as a finite state machine (see Figure 4), whose states can be observed through y-axis gyroscope value z_i Instead of using z_i directly as in [4], Y_k (a series of segments derived from z_i) is used as an output in the hidden Markov model.

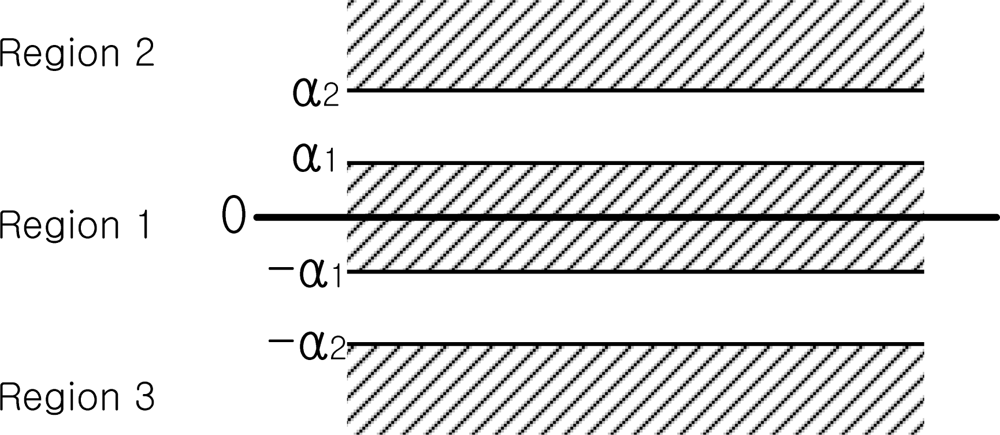
The segmentation of y-axis gyroscope value z_i is explained. First three regions (Region 1, 2, and 3) are defined depending on z_i values (see Figure 5). To formally state this, we define a function f(z_i): (1) f ( z i ) = { 1 , | z i | ≤ α 1 2 , z i > α 2 3 , z i < − α 2 0 , otherwise where   0 < α 1 ≤ α 2   .

If z_i values stay in the region j more than N_j (j = 1,2,3) (that is, at least N_j consecutive z_i values have the same f(z_i)), those z_i values make a segment.

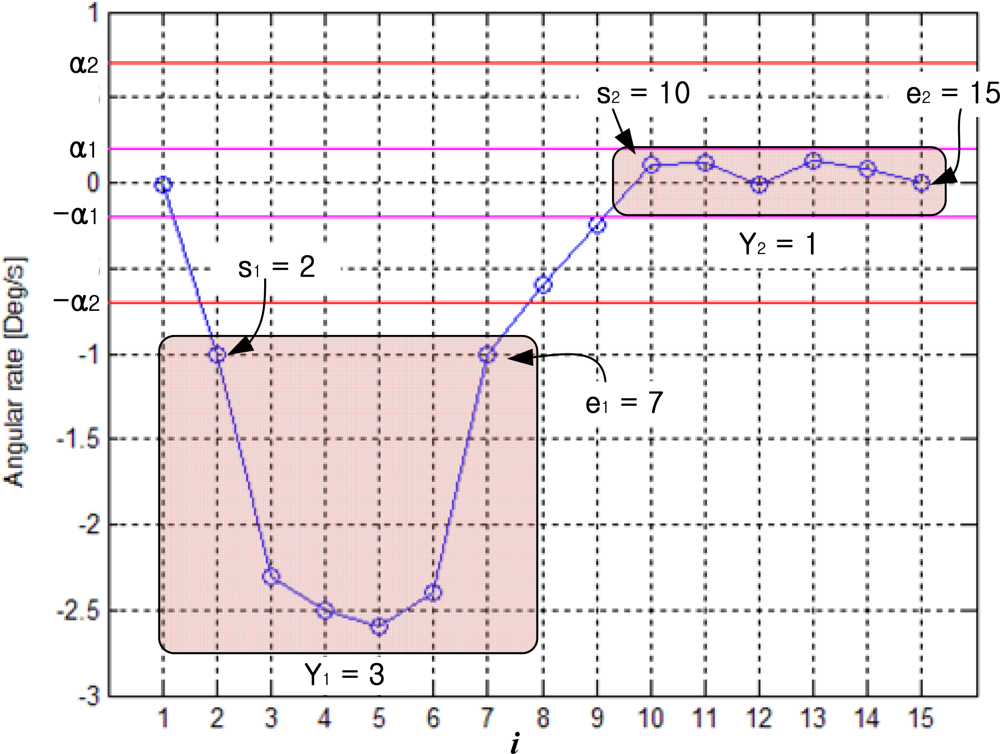
A segmentation example of is given in Figure 6 with N₁=N₂=N₃=3. Since six consecutive z_i (2≤i≤7) values have the same f(z_i) =3 (that is 6≥ N₃ = 3), they form the first segment. We will use Y_k (k is the segment index) to denote the segment value, which is defined by Y_k =f(z_i), where z_i belongs to the k-th segment. In Figure 6, we note that Y₁=3. Similarly, the second segment is Y₂=1. Also note that some z_i values do not belong to any segments. For example, z₈ and z₉ do not belong to any segments and these values are ignored.

In Figure 6, s_k and e_k denote the starting and ending indices of the k-th segment, respectively: note that s₁ = 2, e₁ = 7, s₂ =10 and e₂ =15.

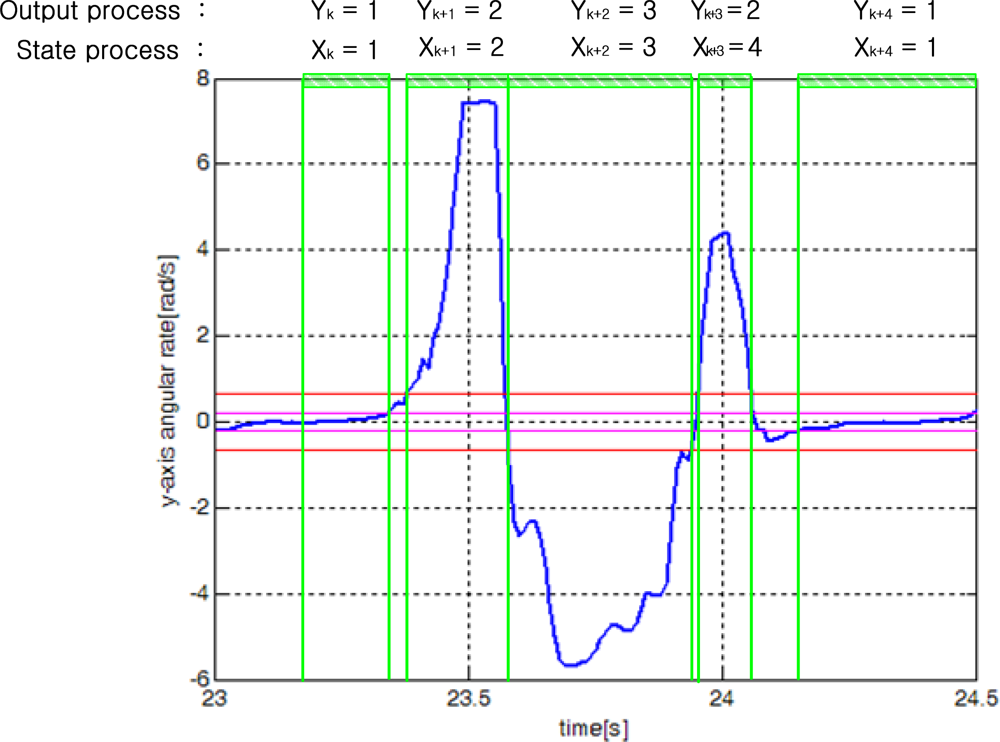
We will identify each segment using the finite state hidden Markov model. We assume that there is a Markov process X_k, which represents four walking states in Figure 3. X_k assumes one of four states: 1, 2, 3, and 4. When a person is walking, a typical state transition is 1→2→3→4→1→…. The Markov process X_k cannot be obtained directly but is estimated through the output Y_k (that is, segment output), which can be observed. An example of state transitions of X_k and output Y_k is given in Figure 7.

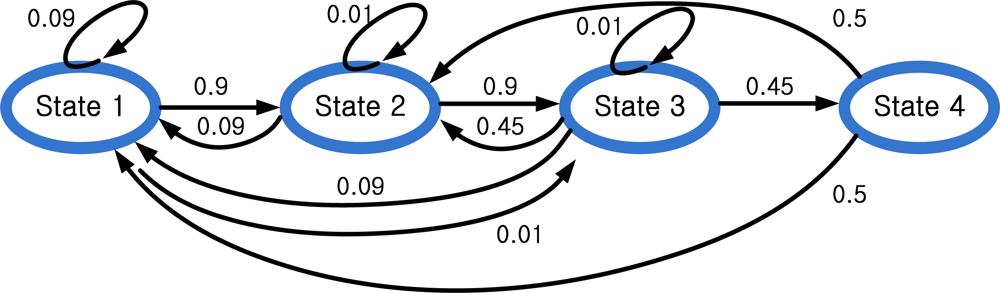
From experimental results, we determined the state transition probability as in Figure 8. A typical state transition is 1→2→3→4→1. However, there are also other possible transition patterns. For example, 4→3→2 transition (state 1 is missing) is possible. In this case, output data corresponding to state 1 is too short to be recognized as Y_k and state 1 is considered to be missing.

From Figure 8, the state transition probability matrix A is given by: (2) A = [ 0.09 0.09 0.09 0.5 0.9 0.01 0.45 0.5 0.01 0.9 0.01 0 0 0 0.45 0 ]where the (m,n) -th element of A is given by: A mn = Pr [ X k + 1 = m | X k = n ] ,       ∑ m = 1 4 A m n = 1.

The determination of A is a trial-and-error process, which is explained in the following. A normal state transition is 1→2→3→4→1→2→3→4. If walking and running cycles consist of only normal transitions, A should be as follows: A = [ 0 0 0 1 1 0 0 0 0 1 0 0 0 0 1 0 ]

However, we found that some states are missing during walking and running. A person walked or ran 30 steps and we examined Y_k. If no state is missing, Y_k should be 1→2→3→2 for one walking or running cycle. If Y_k is 1→2→3→1, then we know state 4 is missing. The results are summarized in Table 1.

From Table 1, we can draw the following conclusions:

- State 1 is sometimes missing (in particular, when a person is running)

Thus we modified A₁ to allow the following state transitions: 1→2→3→1 (state 4 is missing), 1→2→3→4→2 (state 1 is missing), and 1→2→3→2 (state 1 and 4 are missing): A 1 = [ 0 0 0 p 3 1 0 p 1 p 4 0 1 0 0 0 0 p 2 0 ]

If we choose large p₁ (for example p₁= 0.9 and p₂= 0.1), it tends to estimate the transition 1→2→3→4 (normal cycle) as 1→2→3→2 (state 1 and 4 are missing). On the other hand, if we choose small p₁ (for example, p₁ = 0.1 and p₂ = 0.9), it tends to estimate the transition 1→2→3→2 (state 1 and 4 are missing) as 1→2→3→4 (normal cycle). If difference between p₁ and p₂ is not large, the estimation results are similar.

Finally, we added small values for most transitions to allow unusual transitions. For example, when a person is standing and idly moving foot, unusual transitions (such as 2→1) could happen.

We have explained guidelines of how A are determined. Some values (such as 0.01 and 0.09) are determined by changing values and testing the results. We note that the proposed A is by no means an optimal A. As far as we know there is no analytic design procedure to derive the optimal A as stated in [13]. It is possible that extensive tuning of the parameters could produce better results and to derive a better tuning method is one of future topics.

If the output Y_k=1, then we can assume X_k=1 from Figure 7. Also if Y_K=2 then X_k is either 2 or 4. If Y_k= 3, then X_k is 3. This observation is contained in a matrix C, which represents the link between the output process Y_k and the state process X_k. Matrix C is defined by: C mn = Pr [ Y k = m | X k = n ] ,     ∑ m = 1 3 C mn = 1.

In this paper, we use the following C matrix: (3) C = [ 1 0 0 0 0 1 0 1 0 0 1 0 ]

Once A and C are defined, we can estimate X_k from the output Y_k using HMM filters or smoothers [11–14]. Let Π_k|k+l ∈R^4×1 be a probability vector whose i-th element is given by Pr[X_k=i|Y_1,⋯,Y_k+l]. If l=0, then the problem becomes an HMM filter. If l>0, the problem becomes an HMM (fixed-lag) smoother problem. It is known that an HMM smoother gives a more reliable result than an HMM filter [11]. We found an HMM smoother with l=1 gives a significantly much more reliable results in our case (see the experimental results in Table 1). For example, suppose the state 4 and 1 are missing and the state transitions are given by 1→2→3→2→3 (X_k). In the case, the outputs are given by 1→2→3→2→3(Y_k). If we use an HMM filter, the estimated first four states are likely to be 1→2→3→4 (X_k) since it only uses the current outputs 1→2→3→2(Y_k). On the other hand, an HMM smoother gives the correct estimates using the outputs 1→2→3→2→3(Y_k). When an HMM smoother with l=1, we can obtain an estimation result only after the current and the next outputs are available. Thus the estimation result is delayed by the combined duration of the current and next segments: typical delay is 1 second.

After X_k is estimated, the next step is to determine zero velocity intervals. We decide that the time i belongs to zero velocity intervals if |z_i|≤α₃ with anti-chattering algorithm and i satisfies the following conditions: case   1 :   if X k − 1 = 1 , X k = 2 s k − 1 + β 1 ≤ i ≤ e k − 1 − γ 1 case   2 :   if X k − 1 = 4 , X k = 2 s k − 1 + β 2 ≤ i ≤ s k − γ 2 case    3 :   if X k − 1 = 3 , X k = 2 s k − 1 + β 3 ≤ i ≤ s k − γ 3 .

The |z_i|≤α₃ condition is used as a safeguard to prevent false identification of the zero velocity interval.

Case 1 corresponds to the normal walking cycles, where the state transition is 3→4→1→2 (see Figure 7). Since the zero velocity interval belongs to the state 1, the interval is chosen inside state 1. The parameters β₁ and γ₁ are used to discard time intervals near edges of the interval whose state is 1: β 1 = γ 1 = 0.1 ( e k − 1 − s k − 1 )   .

Since a foot is moving before and after state 1, the foot velocity cannot be zero in the edge regions. Thus we cut 10% (corresponding to 0.1) off the interval at both edges. If we choose larger values (for example, 0.2), the chance that a non-zero velocity interval is mistakenly identified as a zero velocity interval is reduced. However, we could obtain narrower zero velocity intervals, which is not desirable.

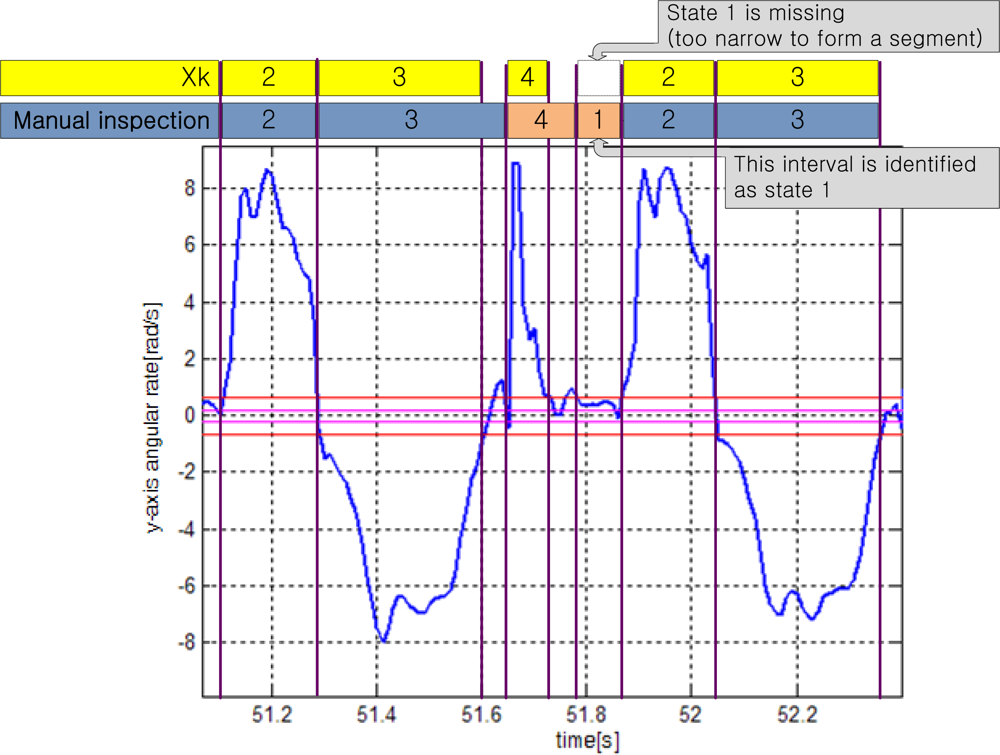
Case 2 and 3 correspond to walking or running cycles, where state 1 and/or state 4 are missing. Case 2 is when state 1 is missing. This could happen if the zero velocity interval is too short to form a segment. For example, state 1 is missing in Figure 9: state transition is 2→3→4→2→3. However, we can identify an interval corresponding to state 1 in Figure 9 by the manual inspection. This interval is identified as state 1 in the manual inspection. Thus the state classifications by the manual inspection and by X_k are different: even if some states are missing in X_k transition, they can be identified in the manual inspection.

We manually inspected the data and found the average duration ratio of each state is given as follows: ( state   1 ,     state   2 ,     state   3 ,     state   4 ) = ( 11.3 % ,   27.4 % ,   42.8 % ,   18.5 % ) .

The ratio was computed from a weighted average of walking (weighting 0.1) and running (weighting 0.9) data. More weighting was given to running since missing states (like in case 2 and 3) are more likely to happen in running.

In case 2, the state 1 is missing. We assume the interval of missing state 1 is (s_k–1+b_k,s_k). Note that the average duration percentage of state 4 and state 1 are 18.5% and 11.3%, respectively. Thus the duration ratio between s_k–1 and s_k is 0.621:0.379. Thus we choose β₂ and γ₂ as follows (see Figure 10): β 2 = 0.621 ( s k − s k − 1 ) ,       γ 2 = 0

In other words, the interval [s_k–1, s_k] is divided into [s_k−1,s_k−1+β₂] and [s_k−1 +β₂,s_k], where the latter is considered as state 1 interval.

Case 3 is when state 4 and 1 are missing. In this case, interval [s_k–1, s_k] includes the state 3 and missing states (4 and 1). Note that the average duration percentage of state 3, 4, and state 1 are 42.8%, 18.5%, and 11.3%, respectively. Thus the duration ratio among state 3:state 4:state 1 is 0.589 : 0.255 : 0.156. Thus we choose β₃ and γ₃ as follows: β 3 = 0.844 ( s k − s k − 1 ) ,     γ 3 = 0

When the interval [s_k–1+β_j, e_k–1−γ_j] is determined, we checked whether z_i, i∈[s_k–1+β_j, e_k–1−γ_j] satisfies |z_i|<α₃ condition. Let U = {i| |z_i| < α₃, i ∈ [s_k−1 + β_j,e_k−1−γ_j]}. If the set U consists of more than one intervals as in Figure 11, the interval whose duration is the largest is chosen as the zero velocity interval.

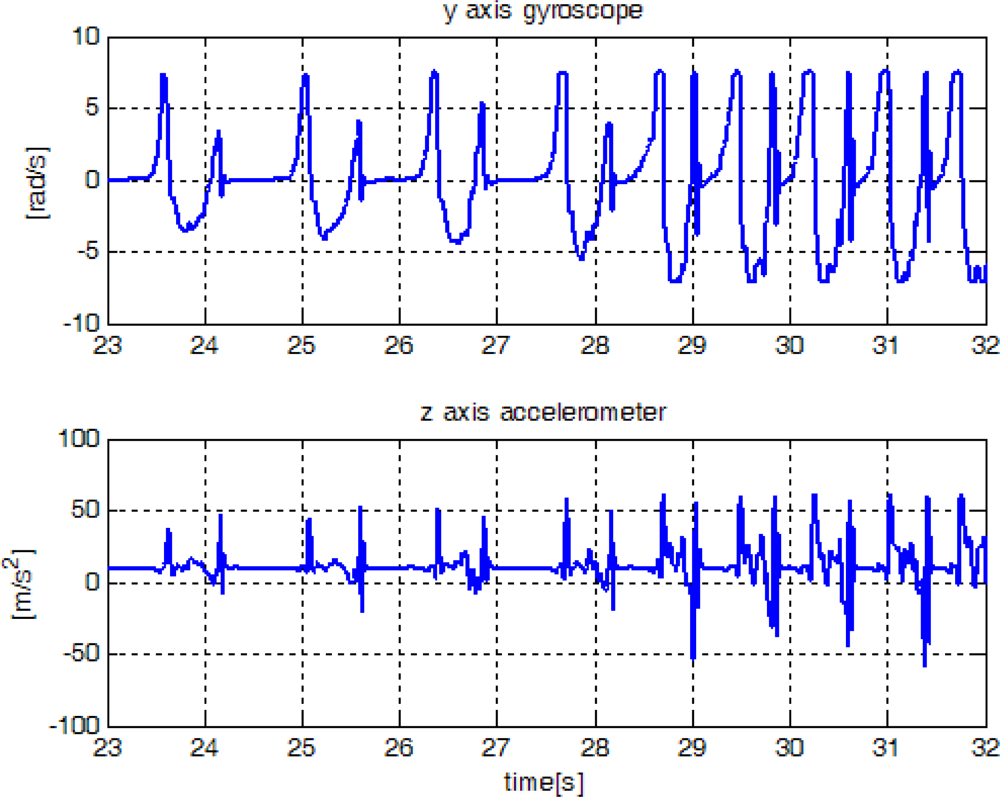
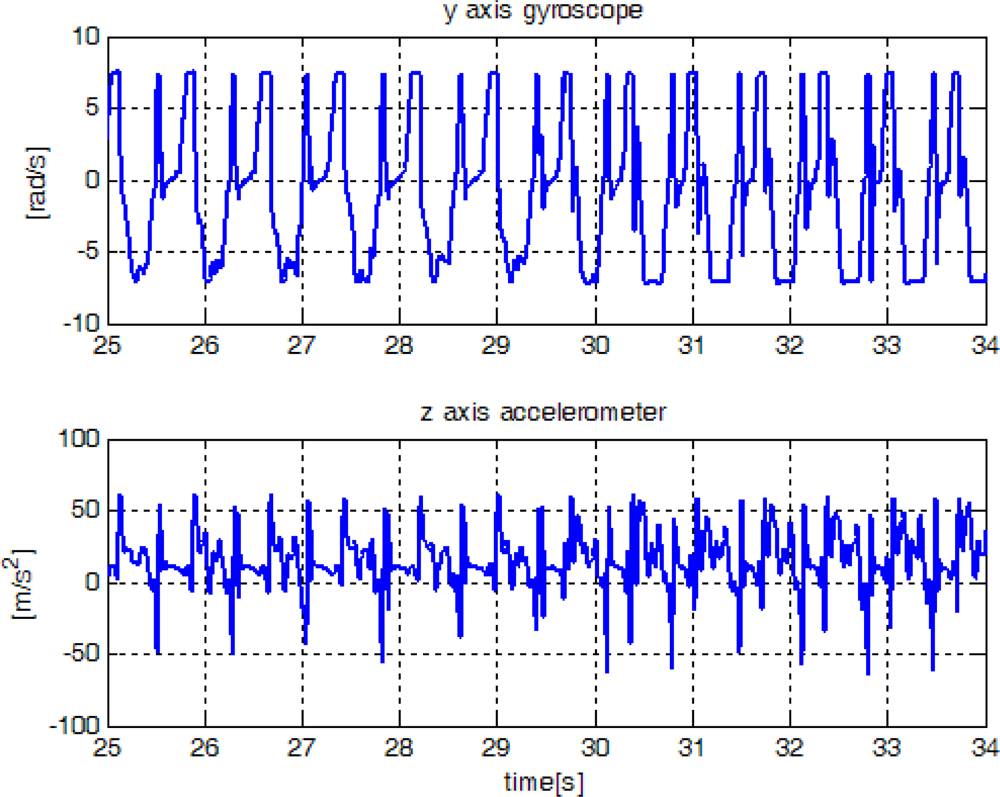
In this section, the proposed method is verified using experiment data, which are obtained from an inertial sensor unit (Xsens Mti) attached on a shoe. The sampling rate is 100 Hz. In Figure 12, sensor outputs are given when a person walked and then ran slowly. We note that only gyroscope output is used in the proposed algorithm. The z-axis accelerometer output is also given since it is used by other existing algorithms. The proposed algorithm along with other existing algorithms [1–3] are applied to the experiment data. The parameters of the proposed algorithm are given by: α 1 = α 2 = α 3 = 0.7 , N 1 = N 2 = 10 , N 3 = 20 , l = 1

The parameters α_j and N_j are determined from the experimental data so that normal walking gives four different states. For example, if we use a smaller α₂ value, it becomes sensitive to noises so that states 2/3/4 could be falsely identified. On the other hand, if we use larger α₂ value, states 2/3/4 could be lost. The parameter N_j is closely related to α_j. For example, smaller N₂ has a similar effect of using smaller α₂ in the sense that state 2/3/4 could be falsely identified.

As a reference, zero velocity interval is determined by manually analyzing gyroscope data. When data are analyzed manually from the plot, the sensor noises and irregularities can be easily spotted and thus we can consider the detected interval as a true zero velocity interval.

The result is given in Figure 13. The algorithm in [1] failed to detect the zero velocity interval when a person is running. The algorithm in [3] is not reliable in the sense that there are false zero velocity detections.

In Figure 14, sensor outputs are given when a person ran slowly and then ran fast. The speeds of “walk”, “run slowly” and “run fast” are about 1.05 m/s, 2.14 m/s, and 3.50 m/s, respectively, which are computed by dividing the distance by the elapsed time. The zero detection results are given in Figure 15. It can be seen that the methods in [1] and [2] cannot detect the zero velocity intervals when a person ran fast. In all cases (Figures 13 and 15), the proposed algorithm reliably detected the zero velocity intervals.

To compare performance of each method quantitatively, a person walked or ran 30 steps at different speed. Since there is one zero velocity interval in each step, 30 zero velocity intervals should be detected. The number of detected zero velocity intervals by different methods is given in Table 2. We can see when a person is walking, all methods give a good result. When a person is running, method 1 and 2 failed to detect the zero velocity intervals most times. The method [3] and the proposed method with an HMM smoother are able to detect all the zero velocity intervals. When counting the number of detected zero velocity intervals, we counted one even if there are more than two detection during the same zero velocity interval. For example, see the two detected zero velocity intervals by the method [3] between 24 and 25 s. These two intervals are counted as one interval. We note that there is a zero velocity interval between the two detected zero velocity intervals, but it is not detected by the method [3]. On the other hand, the proposed method detects almost the whole range of a zero velocity interval. Thus the proposed method can detect the zero velocity intervals more reliably.

We also investigated whether there is false zero velocity detection (an interval is identified as a zero velocity interval while a foot is not in the zero velocity interval). The result is given in Table 3, where the same experiment data were used as in Table 2. It can be seen that the method in [3] sometimes falsely identifies the zero velocity intervals: we found the method in [3] sometimes falsely identifies zero crossing points of gyroscope norm as zero velocity intervals. There was no false zero velocity detection in other methods.

In this paper, we have proposed a new zero velocity detection algorithm, which can be used in inertial sensor based pedestrian navigation systems.

Existing zero detection methods usually work well for normal walking cycles, but the detection is not reliable for running cycles, in particular when the running speed is high. Using a hidden Markov model, the proposed algorithm can analyze both walking and running cycles and the zero velocity interval is thus more reliably detected.

The actual state transition probabilities differ depending on speed of a person. In this paper, we used one averaged transition probability. It is a future work to derive a zero velocity detection algorithm that uses multiple state transition probability matrices.