Lix@C60: Calculations of the Encapsulation Energetics and Thermodynamics
Abstract
:1. Introduction
2. Calculations
3. Results and discussion
4. Conclusions
Acknowledgments
References
- Hebard, RC; Haddon, AF; Rosseinsky, MJ; Murphy, DW; Duclos, SJ; Lyons, KB; Miller, B; Rosamilia, JM; Fleming, RM; Kortan, AR; Glarum, SH; Makhija, AV; Muller, AJ; Eick, RH; Zahurak, SM; Tycko, R; Dabbagh, G; Thiel, FA. Conducting Films of C60 and C70 by Alkali-Metal Doping. Nature 1991, 350, 320–322. [Google Scholar]
- Dunlap, BI; Ballester, JL; Schmidt, PP. Interactions between C60 and Endohedral Alkali Atoms. J. Phys. Chem 1992, 96, 9781–9787. [Google Scholar]
- Joslin, CG; Yang, J; Gray, CG; Goldman, S; Poll, JD. Infrared Rotation and Vibration-Rotation Bands of Endohedral Fullerene Complexes – Absorption Spectrum of Li+@C60 in the Range 1–1000 cm−1. Chem. Phys. Lett 1993, 208, 86–92. [Google Scholar]
- Kaplan, T; Rasolt, M; Karimi, M; Mostoller, M. Numerical Simulation of He+ and Li+ Collisions with C60. J. Phys. Chem 1993, 97, 6124–6126. [Google Scholar]
- Wan, ZM; Christian, JF; Basir, Y; Anderson, SL. Collision of Alkali Ions with C60/C70 – Insertion, Thermionic Emission, and Fragmentation. J. Chem. Phys 1993, 99, 5858–5870. [Google Scholar]
- Joslin, CG; Gray, CG; Goldman, S; Yang, J; Poll, JD. Raman Spectra of Endohedral Fullerenes – Li+@C60. Chem. Phys. Lett 1993, 215, 144–150. [Google Scholar]
- Slanina, Z; Adamowicz, L. MNDO Study of Charged Complexes of Dodecahedron-Shaped C20 with Li. J. Mol. Struct. (Theochem) 1993, 281, 33–37. [Google Scholar]
- Varganov, SA; Avramov, PV; Ovchinnikov, SG. Ab Initio Calculations of Endo- and Exohedral C60 Fullerene Complexes with Li+ Ion and the Endohedral C60 Fullerene Complex with Li2 Dimer. Phys. Solid Stat 2000, 42, 388–392. [Google Scholar]
- Slanina, Z; Lee, S-L. Quantum-Chemical Studies of Superconducting Fullerene Derivatives. Chin. J. Phys 1996, 34, 633–637. [Google Scholar]
- Bol, A; Stott, MJ; Alonso, JA. Density Functional Pseudopotential Study of the Endohedral Complex Li2@C60. Physica B 1997, 240, 154–166. [Google Scholar]
- Kusch, C; Krawez, N; Tellgmann, R; Winter, B; Campbell, EEB. Thermal Desorption Spectroscopy of Fullerene Films Containing Endohedral Li@C60. Appl. Phys. A 1998, 66, 293–298. [Google Scholar]
- Slanina, Z; Uhlík, F; Lee, S-L; Adamowicz, L. Quantum-Chemical Calculations of Model Systems of Interest in Fullerene-Based Superconductivity. J. Low Temp. Phys 2003, 131, 1259–1263. [Google Scholar]
- Gromov, A; Lassesson, A; Jonsson, M; Ostrovskii, DI; Campbell, EEB. IR Spectroscopy Investigation of Purified Endohedral Li@C60 and Li@C70. In Fullerenes, Vol. 12: The Exciting World of Nanocages and Nanotubes, PV 2002-12; Kamat, P, Guldi, D, Kadish, K, Eds.; The Electrochemical Society: Pennington, 2002; pp. 621–629. [Google Scholar]
- Gromov, A; Krawez, N; Lassesson, A; Ostrovskii, DI; Campbell, EEB. Optical Properties of Endohedral Li@C60. Curr. App. Phys 2002, 2, 51–55. [Google Scholar]
- Slanina, Z; Uhlík, F; Chow, TJ. Non-Central Location of Li in Li@C60. In Fullerenes, Vol. 13: Fullerenes and Nanotubes: The Building Blocks of Next Generation Nanodevices, PV 2003-15; Guldi, DM, Kamat, PV, D’Souza, F, Eds.; The Electrochemical Society: Pennington, 2003; pp. 569–574. [Google Scholar]
- Campbell, EEB. Fullerene Collision Reactions; Kluwer Academic Publishers: Dordrecht, 2003. [Google Scholar]
- Popok, VN; Azarko, II; Gromov, AV; Jonsson, M; Lassesson, A; Campbell, EEB. Conductance and EPR Study of the Endohedral Fullerene Li@C60. Sol. Stat. Commun 2005, 133, 499–503. [Google Scholar]
- Lassesson, A; Hansen, K; Jonsson, M; Gromov, A; Campbell, EEB; Boyle, M; Pop, D; Schulz, CP; Hertel, IV; Taninaka, A; Shinohara, H. A Femtosecond Laser Study of the Endohedral Fullerenes Li@C60 and La@C82. Eur. Phys. J. D 2005, 34, 205–209. [Google Scholar]
- Slanina, Z; Uhlík, F; Lee, S-L; Adamowicz, L; Nagase, S. Computations of Endohedral Fullerenes: The Gibbs Energy Treatment. J. Comput. Meth. Sci. Engn 2006, 6, 243–250. [Google Scholar]
- Pavanello, M; Jalbout, AF; Trzaskowski, B; Adamowicz, L. Fullerene as an Electron Buffer: Charge Transfer in Li@C60. Chem. Phys. Lett 2007, 442, 339–343. [Google Scholar]
- Wan, TSM; Zhang, HW; Nakane, T; Xu, ZD; Inakuma, M; Shinohara, H; Kobayashi, K; Nagase, S. Production, Isolation, and Electronic Properties of Missing Fullerenes: Ca@C72 and Ca@C74. J. Am. Chem. Soc 1998, 120, 6806–6807. [Google Scholar]
- Kodama, T; Fujii, R; Miyake, Y; Suzuki, S; Nishikawa, H; Ikemoto, I; Kikuchi, K; Achiba, Y. 13C NMR Study of Ca@C74: The Cage Structure and the Site-Hopping Motion of a Ca Atom Inside the Cage. Chem. Phys. Lett 2004, 399, 94–97. [Google Scholar]
- Haufe, O; Hecht, M; Grupp, A; Mehring, M; Jansen, M. Isolation and Spectroscopic Characterization of New Endohedral Fullerenes in the Size Gap of C74 to C76. Z. Anorg. Allgem. Chem 2005, 631, 126–130. [Google Scholar]
- Reich, A; Panthofer, M; Modrow, H; Wedig, U; Jansen, M. The Structure of Ba@C74. J. Am. Chem. Soc 2004, 126, 14428–14434. [Google Scholar]
- Becke, AD. Density-Functional Thermochemistry. III. The role of exact exchange. J. Chem. Phys 1993, 98, 5648–5652. [Google Scholar]
- Lee, C; Yang, W; Parr, RG. Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar]
- Frisch, MJ; Trucks, GW; Schlegel, HB; Scuseria, GE; Robb, MA; Cheeseman, JR; Montgomery, JA, Jr; Vreven, T; Kudin, KN; Burant, JC; Millam, JM; Iyengar, SS; Tomasi, J; Barone, V; Mennucci, B; Cossi, M; Scalmani, G; Rega, N; Petersson, GA; Nakatsuji, H; Hada, M; Ehara, M; Toyota, K; Fukuda, R; Hasegawa, J; Ishida, M; Nakajima, T; Honda, Y; Kitao, O; Nakai, H; Klene, M; Li, X; Knox, JE; Hratchian, HP; Cross, JB; Adamo, C; Jaramillo, J; Gomperts, R; Stratmann, RE; Yazyev, O; Austin, AJ; Cammi, R; Pomelli, C; Ochterski, JW; Ayala, PY; Morokuma, K; Voth, GA; Salvador, P; Dannenberg, JJ; Zakrzewski, VG; Dapprich, S; Daniels, AD; Strain, MC; Farkas, O; Malick, DK; Rabuck, AD; Raghavachari, K; Foresman, JB; Ortiz, JV; Cui, Q; Baboul, AG; Clifford, S; Cioslowski, J; Stefanov, BB; Liu, G; Liashenko, A; Piskorz, P; Komaromi, I; Martin, RL; Fox, DJ; Keith, T; Al-Laham, MA; Peng, CY; Nanayakkara, A; Challacombe, M; Gill, PMW; Johnson, B; Chen, W; Wong, MW; Gonzalez, C; Pople, JA. Gaussian 03, Revision C.01; Gaussian, Inc: Wallingford, CT, 2004. [Google Scholar]
- Hehre, WJ; Radom, L; Schleyer, PvR; Pople, JA. Ab Initio Molecular Orbital Theory; J. Wiley Inc: New York, 1986. [Google Scholar]
- Logan, RA; Cote, RE; Kusch, P. The Sign of the Quadrupole Interaction Energy in Diatomic Molecules. Phys. Rev 1952, 86, 280–287. [Google Scholar]
- Brooks, RA; Anderson, CH; Ramsey, NF. Rotational Magnetic Moments of Diatomic Alkalis. Phys. Rev. Lett 1963, 10, 441–443. [Google Scholar]
- Huber, KP; Herzberg, G. Molecular Spectra and Molecular Structure, IV. Constants of Diatomic Molecules; Van Nostrand Reinhold Company: New York, 1979. [Google Scholar]
- Blanc, J; Broyer, M; Chevaleyre, J; Dugourd, P; Kuhling, H; Labastie, P; Ulbricht, M; Wolf, JP; Wöste, L. High Resolution Spectroscopy of Small Metal Clusters. Z. Phys. D 1991, 19, 7–12. [Google Scholar]
- Kawai, R; Tombrello, JF; Weare, JH. Li5 as a Pseudorotating Planar Cluster. Phys. Rev. A 1994, 49, 4236–4239. [Google Scholar]
- Slanina, Z; Rudziński, JM; Togasi, M; Ōsawa, E. Quantum-Chemically Supported Vibrational Analysis of Giant Molecules: The C60 and C70 Clusters. J. Mol. Struct. (Theochem) 1989, 202, 169–176. [Google Scholar]
- Nagase, S; Kobayashi, K; Akasaka, T. Recent Progress in Endohedral Dimetallofullerenes. J. Mol. Struct. (Theochem) 1997, 398/399, 221–227. [Google Scholar]
- Kobayashi, K; Nagase, S. Bonding Features in Endohedral Metallofullerenes. Topological Analysis of the Electron Density Distribution. Chem. Phys. Lett 1999, 302, 312–316. [Google Scholar]
- Bader, RFW. A Quantum Theory of Molecular Structure and its Applications. Chem. Rev 1991, 91, 893–928. [Google Scholar]
- Bader, RFW. A Bond Path: A Universal Indicator of Bonded Interactions. J. Phys. Chem. A 1998, 102, 7314–7323. [Google Scholar]
- Alcock, CB; Itkin, VP; Horrigan, MK. Vapor Pressure Equations for the Metallic Elements: 298 – 2500 K. Can. Metallurg. Quart 1984, 23, 309–313. [Google Scholar]
- Slanina, Z. Temperature Development of Homo- and Hetero-Clustering in Saturated Vapors. J. Cluster Sci 2004, 15, 3–11. [Google Scholar]
- Slanina, Z; Uhlík, F; Lee, S-L; Adamowicz, L; Nagase, S. Enhancement of Fullerene Stabilities from Excited Electronic States. Comput. Lett 2005, 1, 304–312. [Google Scholar]
- Kobayashi, K; Nagase, S. Structures and Electronic Properties of Endohedral Metallofullerenes; Theory and experiment. In Endofullerenes – A New Family of Carbon Clusters; Akasaka, T, Nagase, S, Eds.; Kluwer Academic Publishers: Dordrecht, 2002; pp. 99–119. [Google Scholar]
- Kobayashi, K; Nagase, S; Maeda, Y; Wakahara, T; Akasaka, T. La2@C80: Is the Circular Motion of Two La Atoms Controllable by Exohedral Addition? Chem. Phys. Lett 2003, 374, 562–566. [Google Scholar]
- Slanina, Z; Lee, S-L; Uhlík, F; Adamowicz, L; Nagase, S. Computing Relative Stabilities of Metallofullerenes by Gibbs Energy Treatments. Theor. Chem. Acc 2007, 117, 315–322. [Google Scholar]
- Gurin, VS. Ab Initio Calculation of Endohedral Fullerenes with Copper and Silver Clusters. Fulleren. Nanotub. Carb. Nanostruct 2005, 13(Suppl. 1), 3–11. [Google Scholar]
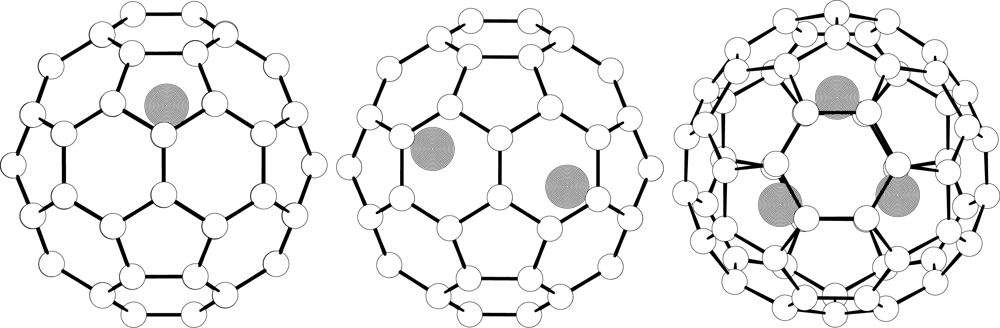
| Species | ΔEYx@Cn | ΔEYx@Cn/x |
|---|---|---|
| Li@C60 | −28.4 | −28.4 |
| Li2@C60 | −51.1 | −25.6 |
| Li3@C60 | −71.0 | −23.7 |
| T (K) | KYx@Cn,p (atm−x) | pY,sat (atm) | ||
|---|---|---|---|---|
| Li@C60 | ||||
| 298.15 | 6.62×1017 | 3.52×10−23 | 2.33×10−5 | 1.0 |
| 1000 | 3.47×102 | 9.72×10−4 | 0.337 | 1.0 |
| 1500 | 3.05 | 0.467 | 1.42 | 1.0 |
| 2000
| 0.305
| 10.1
| 3.08
| 1.0
|
| Li2@C60 | ||||
| 298.15 | 2.62×1027 | 3.52×10−23 | 3.24×10−18 | 1.39×10−13 |
| 1000 | 3.30 | 9.72×10−4 | 3.11×10−6 | 9.24×10−6 |
| 1500 | 7.47×10−4 | 0.467 | 1.63×10−4 | 1.15×10−4 |
| 2000
| 1.26×10−5 | 10.1
| 1.29×10−3 | 4.18×10−4 |
| Li3@C60 | ||||
| 298.15 | 2.42×1036 | 3.52×10−23 | 1.05×10−31 | 4.52×10−27 |
| 1000 | 0.282 | 9.72×10−4 | 2.58×10−10 | 7.67×10−10 |
| 1500 | 2.72×10−6 | 0.467 | 2.77×10−7 | 1.95×10−7 |
| 2000 | 9.90×10−9 | 10.1 | 1.02×10−5 | 3.31×10−6 |
© 2008 by MDPI This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Slanina, Z.; Uhlík, F.; Lee, S.-L.; Adamowicz, L.; Nagase, S. Lix@C60: Calculations of the Encapsulation Energetics and Thermodynamics. Int. J. Mol. Sci. 2008, 9, 1841-1850. https://doi.org/10.3390/ijms9091841
Slanina Z, Uhlík F, Lee S-L, Adamowicz L, Nagase S. Lix@C60: Calculations of the Encapsulation Energetics and Thermodynamics. International Journal of Molecular Sciences. 2008; 9(9):1841-1850. https://doi.org/10.3390/ijms9091841
Chicago/Turabian StyleSlanina, Zdeněk, Filip Uhlík, Shyi-Long Lee, Ludwik Adamowicz, and Shigeru Nagase. 2008. "Lix@C60: Calculations of the Encapsulation Energetics and Thermodynamics" International Journal of Molecular Sciences 9, no. 9: 1841-1850. https://doi.org/10.3390/ijms9091841




