ijms International Journal of Molecular Sciences Int. J. Mol. Sci. 1422-0067 Molecular Diversity Preservation International (MDPI) ijms-09-00131 Full Research Paper Computing the Szeged and PI Indices of VC5C7[p,q] and HC5C7[p,q] Nanotubes IranmaneshAli1* AlizadehYaser1 TaherkhaniBahman2 Department of Mathematics, Tarbiat Modares University, P. O. Box: 14115-137, Tehran, Iran; E-mail: yalizadeh@modares.ac.ir Department of Mathematics, Payame Noor University, Takestan/Gazvin, 3481699445 Iran; E-mail: bahman.taherkhani@pnu.ac.ir Author to whom correspondence should be addressed; E-mail: iranmana@modares.ac.ir. 5 2 2008 2 2008 9 2 131 144 27 8 2007 21 9 2007 15 10 2007 © 2008 by MDPI 2008

In this paper we give a GAP program for computing the Szeged and the PI indices of any graph. Also we compute the Szeged and PI indices of VC5C7 [ p,q] and HC5C7 [ p,q] nanotubes by this program.

 Szeged index PI-index nanotubes Gap programming 1. Introduction

One of the main distinctive characteristics of modern chemistry is the use of theoretical tools for the molecular modeling of physicochemical processes, chemical reaction, medicinal and toxicological events, etc., in which chemicals are involved. The success of the molecular modeling is judged by the insights that it offers on the nature of the processes studied, which permit better comprehension and a their rational modification. These properties, measured experimentally, are almost invariably expressed in quantitative terms, for instance boiling point, refraction index, transition state energy, percentage of inhibition of some enzymatic activity, lethal dose, and so forth. The paradigm for the modeling of such properties is the relationship that exists between them and the molecular structure of chemical. This fact highlights the first challenge for molecular modeling: the properties are expressed as number while the molecular structure is not. The way to solve this problem is by using molecular descriptors, which are numbers representing information about different molecular features, to describe quantitatively the properties under study. These models are known as quantitative structure-property (QSPR) and quantitative structure-activity relationships (QSAR), depending on the physicochemical or biological nature of the properties studied, respectively.

Topological indices of nanotubes are numerical descriptors that are derived from graphs of chemical compounds. Such indices based on the distances in a graph are widely used for establishing relationships between the structure of nanotubes and their physicochemical properties. Usage of topological indices in biology and chemistry began in 1947, when the chemist Harold Wiener [1] introduced the so-called Wiener index to demonstrate correlations between physicochemical properties of organic compounds and the index of their molecular graphs. Wiener originally defined his index (W) on trees and studied its use for correlations of physicochemical properties of alkanes, alcohols, amines and their analogous compounds [2]. Starting from the middle of the 1970s, the Wiener index gained much popularity and, since then, new results related to it are constantly being reported. For a review, historical details and further bibliography on the chemical applications of the Wiener index see [3–5]. Another topological index was introduced by Gutman and called the Szeged index, abbreviated as Sz [2]. Let G be a connected graph. The vertex-set and edge-set of G denoted by V(G) and E(G) respectively. The distance between the vertices u and v, d(u,v), in a graph is the number of edges in a shortest path connecting them. Two graph vertices are adjacent if they are joined by a graph edge. Let e be an edge of a graph G connecting the vertices u and v. Two sets N1 (e|G) and N2 (e|G) are defined as follows:

N 1 ( e | G ) = { x ∈ V  ( G ) | d ( x , u ) < d ( x , v ) }  and  N 2 ( e | G ) = { x ∈ V ( G ) | d ( x , v ) < d ( x , u ) } .

The number of elements of N1 (e| G) and N2 (e|G) are denoted by n1(e|G) and n2 (e|G) respectively.

The Szeged index of the graph G is defined as S z  ( G ) = ∑ e ∈ E ( G ) n 1 ( e | G ) . n 2 ( e | G ).

For the reason of the coincidence of Wiener and Szeged indices in case of trees the authors in [6] and [7] introduced another Szeged/Wiener-like topological index and named it the Padmakar-Ivan index, abbreviated as PI. In fact the PI index of the graph G is denoted by PI(G) and defined as follows:

P I ( G ) = ∑ e ∈ E ( G ) n 1 ( e | G ) + n 2 ( e | G ) .

Applications of the PI index to QSRP/QSAR were studied in [8]. The index was mostly compared with the Wiener and the Szeged indices. It turned out that the PI index has similar discriminating power as the other two indices and in many cases (for instance to model ¢max, the so called difference in doublet of deformation mode, of unbranched cycloalkanes) it gives better results. As we already mentioned, The Szeged index incorporates the distribution of vertices of a molecular graph, while the PI index does this job for the edges. Hence it seems that a combination of both could give good results in QSRP/QSAR studies. Indeed, the combination of the PI index and the Szeged index is the best for modeling polychlorinated biphenyls (PCBs) in environment among the three possible pairs of indices selected from the PI index, the Szeged index, and the Wiener index [8]. For the Wiener and the Szeged indices such studies were previously done in [9,10]. The Szeged and PI indices of some nanotubes were computed in [11–14].

The computation of Szeged and PI indices seems straightforward, but this is not entirely true. For computing the Szeged (or PI) index of any graph, we must obtain n1 (e|G) and n2 (e|G) for any edge in the graph and this takes very long time. Up to now, many papers have been published in the international scientific literature which computed the Szeged index (or PI index) of some nanotubes by the above explanation [11–22]. In our paper, we obtain an algorithm which is faster than the direct implementation. Also, since up to now, not give any algorithm for computing these indexes, it is the best algorithm by GAP program and therefore, our paper is the first paper in this subject which give an algorithm for computation of Szeged and PI indices of any graph.

 2. An algorithm for the computation of the Szeged and PI indices for an arbitrary graph

In this section, we give an algorithm that enables us to compute the Szeged and PI indices of any graph. For this purpose, the following algorithm is presented:

1-We assign one number to any vertex.

2-We determine all of adjacent vertices set of the vertex i, i∈V (G) and this set is denoted by N(i).

The set of vertices that their distance to vertex i is equal to t (t ≥ 0) is denoted by D i, t and considering Di, 0 = {i}.Let e = ij be an edge connecting the vertices i and j, then we have the following result:

V = ∪t≥0 Di,t, i ∈ V (G).

(Di,t \ Dj,t) ⊆ (Dj,t−1 ∪ Dj,t +1), t ≥1.

(Di,t ∩Dj,t−1) ⊆ N 2 (e|G) and Di.t ∩D j,t+1⊆N1 (e|G) t ≥1.

(Di,1 ∪{i}) \ (Dj,1 ∪{ j}) ⊆ N1 (e/G) and (D j,1 ∪{ j}) \ (Di,1 ∪{i}) ⊆ N2 (e|G).

According to the above relations, by determining Di,t,t ≥ 1, we can obtain N1 (e|G) and N2 (e|G) for each edge e and therefore the Szeged and PI indices of the graph G is computed. In the following section we obtain the Di,t, t ≥ 1, for each vertex i

3- The distance between vertex i and its adjacent vertices is equal to 1, therefore Di,1 = N(i). For each j ∈ Di,t,t ≥1, the distance between each vertex of set N(j) \ (Di,t ∪ Di,t−1) and the vertex i is equal to t +1, thus we have

D i , t + 1 = ∪ j ∈ D t , t ( N ( j ) \ ( D i , t ∪ D i , t − 1 ) , t ≥ 1.

According to the above equation we can obtain Di,t t ≥ 2 for each i ∈V (G).

4- At the start of program we set SZ and PI equal to zero and T equal to empty set. At the end of program the values SZ and PI are equal to the Szeged and PI indices of the graph G respectively. For each vertex i, 1≤i≤ n, and each vertex j in N(i), we determine N1 (e|G) and N2 (e|G) for edge e =ij,then add the values of n1 (e|G).n2 (e|G) and n1 (e|G) +n2 (e|G) to S Z and PI respectively. Since the edge j i is equal to ij, we add the vertex i to T and continue this step for the vertex i+1 and for each vertex in N(i +1) \ T.

GAP stands for Groups, Algorithms and Programming [23]. The name was chosen to reflect the aim of the system, which is group theoretical software for solving computational problems in group theory. The last years have seen a rapid spread of interest in the understanding, design and even implementation of group theoretical algorithms. GAP software was constructed by GAP's team in Aachen. We encourage the reader to consult Refs. [24] and [25] for background materials and computational techniques related to applications of GAP in solving some problems in chemistry and biology. 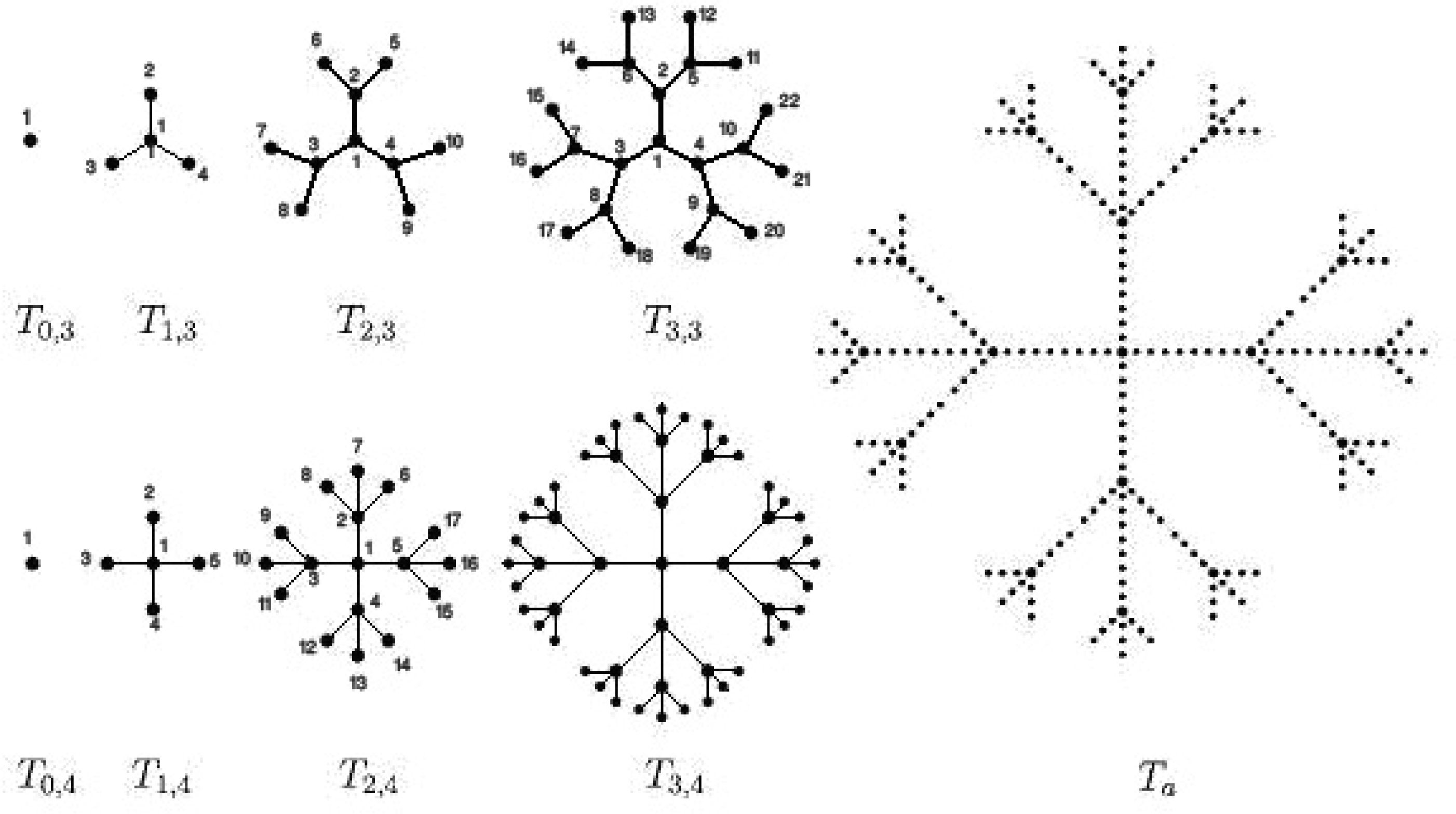According to the above algorithm, we prepared a GAP program to compute the Szeged and PI indices of dendrimersTk ,d.

2.1. Example

The Wiener index of tree dendrimers T k,d, k≥1, d≥3, is computed in [26,27]. Since the Wiener and Szeged index coincide on trees [28,29], thus the Szeged index of Tk ,d is equal to its Wiener index.

The following results are obtained in [26,27].

For every d≥3, the tree T k ,d has order

n ( T k , d ) = 1 + d d − 2 [ ( d − 1 ) k − 1 ]

and its Szeged index is equal to Wiener index, i.e.

S z ( T k , d ) = W   ( T k , d ) = 1 ( d − 2 ) 3 [ ( d − 1 ) 2 k [ k d 3 − 2 ( k + 1 ) d 2 + d ] + 2 d 2 ( d − 1 ) k − d ] .

For computation of the Szeged and PI indices of T k, d by the above program, at first we assign to any vertex one number (See figure 1); according to this numbering, the set of adjacent vertices to each vertex, 1≤i≤n, is obtained by the following program (part 1). In fact part 1 of the program is the presentation of the graph. We use part 2 for compute the Szeged and PI indices of the graph.

The following program computes the Szeged and PI indices of the Tk,d for arbitrary values of d and k.

d:=3; k:=3;#(For example)

n:=1+(d/(d-2))*((d-1)^k - 1);

N:=[];

K1:=[2..d+1];

N[1]:=K1;

for i in K1 do

 if k=1 then N[i]:=[1];

 else

 N[i]:=[(d-1)*i+4-d..(d-1)*i+2];

 Add(N[i],1);fi;

od;

K2:=[d+2..1+(d/(d-2))*((d-1)^(k-1) - 1)];

for i in K2 do

 N[i]:=[(d-1)*i+4-d..(d-1)*i+2];

 Add(N[i],Int((i-4+d)/(d-1)));

od;

K3:=[2+(d/(d-2))*((d-1)^(k-1) - 1)..n];

for i in K3 do

 if k=1 then N[i]:=[1];

  else

 N[i]:=[Int((i-4+d)/(d-1))]; fi;

od;

# (Part2)

D:=[];

for i in [1..n] do

   D[i]:=[];

   u:=[i];

   D[i][1]:=N[i];

   u:=Union(u,D[i][1]);

   s:=1;

   t:=1;

   while s<>0 do

    D[i][t+1]:=[];

    for j in D[i][t] do

     for m in Difference(N[j],u) do

      AddSet(D[i][t+1],m);

     od;

    od;

   u:=Union(u,D[i][t+1]);

     if D[i][t+1]=[] then

    s:=0;

   fi;

   t:=t+1;

   od;

od;

T:=[];

sz:=0;

pi:=0;

for i in [1..n-1] do

N1:=[];

 for j in Difference(N[i],T) do

N2:=[];

  N1[j]:=Union(Difference(N[i],Union([j],N[j])),[i]);

  N2[i]:=Union(Difference(N[j],Union([i],N[i])),[j]);

  for t in [2..Size(D[i])-1] do

   for x in Difference(D[i][t],Union(D[j][t],[j])) do

    if not x in D[j][t-1] then

      AddSet(N1[j],x);

     elif x in D[j][t-1] then

      AddSet(N2[i],x);

    fi;

    od;

 od;

  sz:=sz+Size(N1[j])*Size(N2[i]);

  pi:=pi+Size(N1[j])+Size(N2[i]);

  od;

  Add(T,i);

 od;

sz;# (The value of sz is equal to Szeged index of the graph)

pi; # (The value of pi is equal to PI index of the graph)

 3. Computation of the Szeged and PI indices of <italic>VC</italic><italic><sub>5</sub></italic><italic>C</italic><italic><sub>7</sub></italic><italic>[p,q]</italic> nanotubes with the GAP program

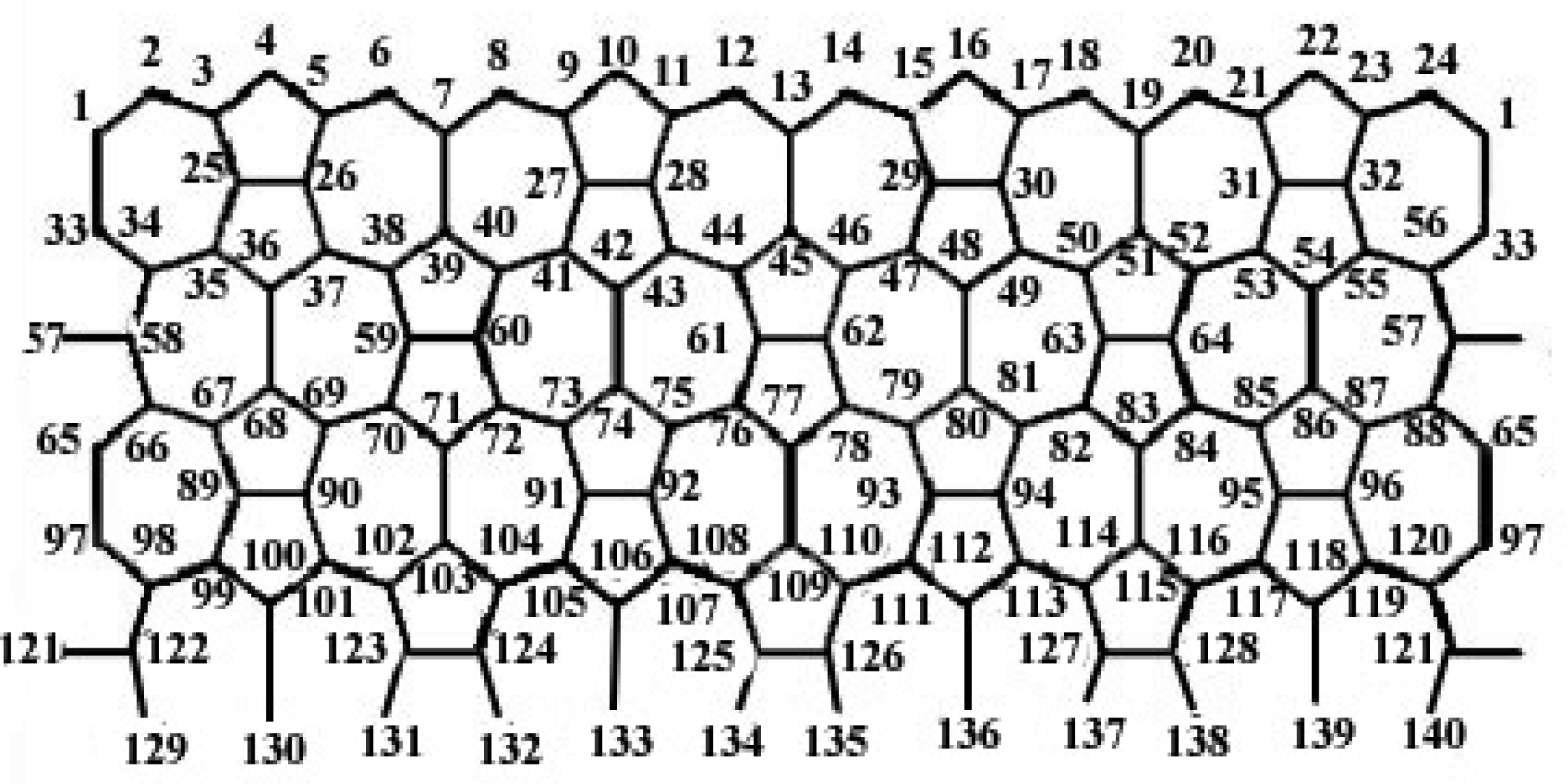
A C5C7 net is a trivalent decoration made by alternating C5 and C7. It can cover either a cylinder or a torus. In this section we compute the Szeged and PI indices of VC5C7[p,q] nanotubes by GAP program.

We denote the number of pentagons in the first row by p, in this nanotube the four first rows of vertices and edges are repeated alternatively, we denote the number of this repetition by q. In each period there are 16 p vertices and 3p vertices which are joined to the end of the graph and hence the number of vertices in this nanotube is equal to16 pq +3p.

We partition the vertices of the graph to the following sets:

K1

The vertices of the first row whose number is 6 p.

 K2

The vertices of the first row in each period except the first one whose number is 6 p(q − 1).

 K3

The vertices of the second rows in each period whose number is 2 pq.

 K4

The vertices of the third row in each period whose number is 6 pq.

 K5

The vertices of the fourth row in each period whose number is 2 pq.

 K6

The last vertices of the graph whose number is3p.

We write a program to obtain the adjacent vertices set to each vertex in the sets Ki, i=1…6. We can obtain the adjacent vertices set to each vertex by the join of these programs. In this program, the value of x is the assign number of vertex i in that row.

The following program computes the Szeged and PI indices of VC5C7[p,q] nanotubes for arbitrary values p and q.

p:=4; q:=2; # (for example)

n:=16*p*q+3*p;

N:=[];

K1:=[1..6*p];

V1:=[2..6*p -1];

for i in V1 do

 if i mod 6=1 then N[i]:=[i-1,i+1,i+8*p];

  elif i mod 6 in [0,2,4] then N[i]:=[i-1,i+1];

   elif i mod 6=3 then N[i]:=[i-1,i+1,(1/3)*(i-3)+6*p+1];

    elif i mod 6=5 then N[i]:=[i-1,i+1,(1/3)*(i-5)+6*p +2];fi;

 N[1]:=[2,6*p,8*p+1];

 N[6*p]:=[6*p-1,1];

od;

K:=[6*p+1..16*p*q];

K2:=Filtered(K,i->i mod (16*p) in [1..6*p]);

for i in K2 do

 x:= i mod (16*p);

 if x mod 6=1 then N[i]:=[i-1,i+1,i+8*p];

  elif x mod 6=2 then N[i]:=[i-1,i+1,(1/3)*(x-2)+2+i-x-2*p];

   elif x mod 6=3 then N[i]:=[i-1,i+1,(1/3)*(x-3)+1+i-x+6*p];

    elif x mod 6=4 then N[i]:=[i-1,i+1,i-8*p];

     elif x mod 6=5 then N[i]:=[i-1,i+1,(1/3)*(x-5) +2+i-x+6*p];

      elif x mod 6=0 then N[i]:=[i-1,i+1,(1/3)*x +1+i-x-2*p];fi;

 if x=1 then N[i]:=[i+1,i-1+6*p,i+8*p];fi;

 if x=6*p then N[i]:=[i-1,i- 6*p+1,i- 8*p+1];fi;

od;

K3:=Filtered(K,i->i mod (16*p) in [6*p+1..8*p]);

for i in K3 do

 x:=(i-6*p) mod (16*p);

 if x mod 2=0 then N[i]:=[i-1,3*(x-2)+5+i-x- 6*p,3*(x-2)+5+i-x+2*p];

  else N[i]:=[i+1,2*x+i- 6*p,2*x+i+2*p];fi;

od;

K4:=Filtered(K,i->i mod (16*p) in [8*p+1..14*p]);

for i in K4 do

x:=(i- 8*p) mod (16*p);

if x mod 6=1 then N[i]:=[i-1,i+1,i- 8*p];

 elif x mod 6=2 then N[i]:=[i-1,i+1,(1/3)*(x-2)+2+i-x+6*p];

  elif x mod 6=3 then N[i]:=[i-1,i+1,(1/3)*(x-3)+1+i-x-2*p];

   elif x mod 6=4 then N[i]:=[i-1,i+1,i+8*p];

    elif x mod 6=5 then N[i]:=[i-1,i+1,(1/3)*(x-5)+2+i-x- 2*p];

     elif x mod 6=0 then N[i]:=[i-1,i+1,(1/3)*x+1+i-x+6*p];fi;

 if x=1 then N[i]:=[i-8*p,i+1,i+6*p-1];fi;

 if x=6*p then N[i]:=[i-1,i-6*p+1,i+1];fi;

od;

K5:=Filtered(K,i->i mod (16*p) in Union([14*p+1..16*p-1],[0]));

for i in K5 do

 x:=(i-14*p) mod (16*p);

 if x mod 2=1 then N[i]:=[i+1,3*(x-1)+i-x-6*p,3*(x-1)+i-x+2*p];

  else N[i]:=[i-1,3*(x-2)+2+i-x-6*p,3*(x-2)+2+i-x+2*p];fi;

 if x=1 then N[i]:=[i+1,i-1,i-1+8*p];fi;

 if x=2*p then N[i]:=[i-1,3*(x-2)+2+i-x-6*p,3*(x-2)+2+i-x+2*p];fi;

od;

K6:=[16*p*q+1..n];

for i in K6 do

 x:=i mod (16*p);

 if x mod 3=1 then y:= (2/3)*(x-1)+2+i-x- 2*p;

  elif x mod 3=2 then y:=i+x- 8*p;

   elif x mod 3=0 then y:=(2/3)*(x- 3)+3+i-x-2*p;fi;

if x=3*p then y:=i- 5*p+1;fi;

 N[i]:=[y];

 N[y][3]:=i;

od;

D:=[];

for i in [1..n] do

  D[i]:=[];

  u:=[i];

  D[i][1]:=N[i];

  u:=Union(u,D[i][1]);

  s:=1;

  t:=1;

  while s<>0 do

   D[i][t+1]:=[];

   for j in D[i][t] do

    for m in Difference(N[j],u) do

     AddSet(D[i][t+1],m);

    od;

   od;

  u:=Union(u,D[i][t+1]);

    if D[i][t+1]=[] then

   s:=0;

  fi;

  t:=t+1;

  od;

od;

T:=[];

sz:=0;

pi:=0;

for i in [1..n-1] do

N1:=[];

  for j in Difference(N[i],T) do

N2:=[];

   N1[j]:=Union(Difference(N[i],Union([j],N[j])),[i]);

   N2[i]:=Union(Difference(N[j],Union([i],N[i])),[j]);

    for t in [2..Size(D[i])-1] do

     for x in Difference(D[i][t],Union(D[j][t],[j])) do

      if not x in D[j][t-1] then

        AddSet(N1[j],x);

       elif x in D[j][t-1] then

        AddSet(N2[i],x);

    fi;

    od;

   od;

  sz:=sz+ Size(N1[j])*Size(N2[i]);

  pi:=pi+ Size(N1[j])+Size(N2[i]);

  od;

  Add(T,i);

od;

sz; # (The value of sz is equal to Szeged index of the graph)

pi; # (The value of pi is equal to PI index of the graph)

 4. Computation of the Szeged and PI indices of <italic>HC</italic><italic><sub>5</sub></italic><italic>C</italic><italic><sub>7</sub></italic><italic>[p,q]</italic> nanotubes with the GAP program

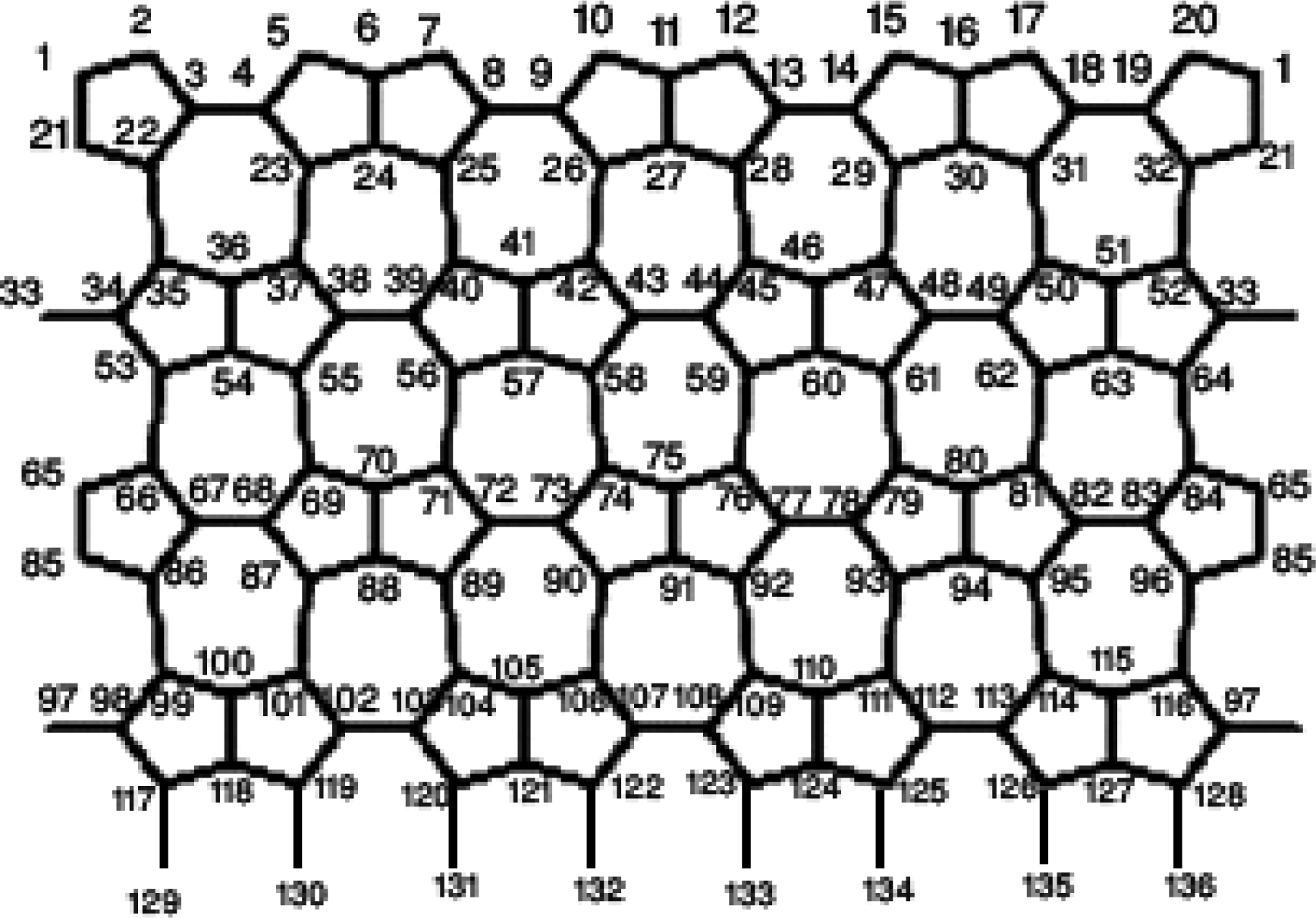
In this section we compute the Szeged and PI indices of HC5C7[p,q] nanotubes similar to the previous section. HC5C7[p,q] nanotubes consists of heptagon and pentagon nets as seen below:

We denote the number of heptagons in the first row by p. In this nanotube the four first rows of vertices and edges are repeated alternatively; we denote the number of this repetition by q. In each period there are 16p vertices and 2p vertices are joined to the end of the graph, and hence the number of vertices in this nanotube is equal to 16pq + 2p.

The following program is the same as the last program. In this program, value of x is the number of vertex i in a row.

p:=6;q:=7;# (for example)

n:=16*p*q+2*p;

N:=[];

for i in [1..5*p] do

 if i mod 5=1 then N[i]:=[i-1,i+1,(3/5)*(i-1)+1+5*p];

  elif i mod 5 in [0,2] then N[i]:=[i-1,i+1];

   elif i mod 5=3 then N[i]:=[i-1,i+1,(3/5)*(i-3)+2+5*p];

    elif i mod 5=4 then N[i]:=[i-1,i+1,(3/5)*(i-4)+3+5*p];fi;

 N[1]:=[2,5*p,5*p+1];

 N[5*p]:=[1,5*p-1];

od;

K:=[5*p+1..16*p*q];

K1:=Filtered(K,i->i mod (16*p) in [1..5*p]);

for i in K1 do

 x:=(i) mod (16*p);

 if x mod 5=1 then N[i]:=[i-1,i+1,(3/5)*(x-1)+1+i-x+5*p];

  elif x mod 5=2 then N[i]:=[i-1,i+1,(3/5)*(x-2)+1+i-x-3*p];

   elif x mod 5=3 then N[i]:=[i-1,i+1,(3/5)*(x-3)+2+i-x+5*p];

    elif x mod 5=4 then N[i]:=[i-1,i+1,(3/5)*(x-4)+3+i-x+5*p];

     elif x mod 5=0 then N[i]:=[i-1,i+1,(3/5)*x+i-x-3*p];fi;

 if x=1 then N[i]:=[i+1,i-1+5*p,i+(5*p)];fi;

 if x=5*p then N[i]:=[i-1,i-5*p,i+1-5*p];fi;

od;

K2:=Filtered(K,i->i mod (16*p) in[5*p+1..8*p]);

for i in K2 do

 x:=(i- 5*p) mod (16*p);

 if x mod 3 =1 then N[i]:=[i-1,i+1,(5/3)*(x-1)+1+i-x- 5*p];

  elif x mod 3 =2 then N[i]:=[i-1,(5/3)*(x-2)+3+i-x- 5*p,(5/3)*(x-2)+3+i-x+3*p];

   elif x mod 3 =0 then N[i]:=[i+1,(5/3)*x-1+i-x- 5*p,(5/3)*x +i-x+3*p];fi;

  if x=3*p then N[i]:=[i-3*p+1,(5/3)*x-1+i-x- 5*p,(5/3)*x +i-x+3*p];fi;

  if x=1 then N[i]:=[i-5*p,i+1,i-1+3*p];fi;

od;

K3:=Filtered(K,i->i mod (16*p) in [8*p+1..13*p]);

for i in K3 do

 x:=(i- 8*p) mod (16*p);

 if x mod 5=1 then N[i]:=[i-1,i+1,(3/5)*(x-1) +i-x+5*p];

  elif x mod 5=2 then N[i]:=[i-1,i+1,(3/5)*(x-2)+1+i-x+5*p];

   elif x mod 5=3 then N[i]:=[i-1,i+1,(3/5)*(x-3)+2+i-x-3*p];

    elif x mod 5=4 then N[i]:=[i-1,i+1,(3/5)*(x-4)+2+i-x+5*p];

     elif x mod 5=0 then N[i]:=[i-1,i+1,(3/5)*x +i-x-3*p];fi;

 if x=1 then N[i]:=[i+1,i-1+5*p,i-1+8*p];fi;

 if x=5*p then N[i]:=[i-1,i-5*p,i+1-5*p];fi;

od;

K4:=Filtered(K,i->i mod (16*p) in Union([13*p+1..16*p-1],[0]));

for i in K4 do

 x:=(i-13*p) mod (16*p);

 if x mod 3=1 then N[i]:=[i+1,(5/3)*(x-1)+2+i-x-5*p,(5/3)*(x-1)+2+i-x+3*p];

  elif x mod 3=2 then N[i]:=[i-1,i+1,(5/3)*(x-2)+4+i-x-5*p];

   elif x mod 3=0 then N[i]:=[i-1,(5/3)*x+1+i-x-5*p,(5/3)*x+i-x+3*p];fi;

 if x=3*p then N[i]:=[i-1,i+1-8*p,(5/3)*x+i-x+3*p]; fi;

od;

K5:=[16*p*q+1..n];

for i in K5 do

 x:=i mod(16*p);

 if x mod 2=0 then y:=(3/2)*x+i-x-3*p;

  else y:=(3/2)*(x-1)+1+i-x-3*p;fi;

 N[i]:=[y];

 N[y][3]:=i;

od;

D:=[];

for i in [1..n] do

   D[i]:=[];

   u:=[i];

   D[i][1]:=N[i];

   u:=Union(u,D[i][1]);

   s:=1;

   t:=1;

   while s<>0 do

    D[i][t+1]:=[];

    for j in D[i][t] do

     for m in Difference(N[j],u) do

      AddSet(D[i][t+1],m);

     od;

    od;

   u:=Union(u,D[i][t+1]);

    if D[i][t+1]=[] then

     s:=0;

   fi;

   t:=t+1;

   od;

od;

T:=[];

sz:=0;

pi:=0;

for i in [1..n-1] do

N1:=[];

 for j in Difference(N[i],T) do

N2:=[];

  N1[j]:=Union(Difference(N[i],Union([j],N[j])),[i]);

  N2[i]:=Union(Difference(N[j],Union([i],N[i])),[j]);

   for t in [2..Size(D[i])-1] do

    for x in Difference(D[i][t],Union(D[j][t],[j])) do

     if not x in D[j][t-1] then

      AddSet(N1[j],x);

     elif x in D[j][t-1] then

      AddSet(N2[i],x);

    fi;

   od;

  od;

 sz:=sz+Size(N1[j])*Size(N2[i]);

 pi:=pi+Size(N1[j])+Size(N2[i]);

 od;

 Add(T,i);

od;

sz;# (The value of sz is equal to Szeged index of the graph)

pi;# (The value of pi is equal to PI index of the graph)

 Conclusions

It takes a long time to compute the Szeged and PI indices of a graph theoretically, especially when the graph has many vertices. According to the algorithm presented in this paper and using the GAP program, we can write a program to compute these indices quickly. This method has been used here for the first time. We teste the algorithm to calculate the Szeged and PI indices of denderimers Tk,d that were computed in [26,27]. In addition we compute these indices for HC5C7 [ p,q] and VC5C7 [ p,q] nanotubes.

 Acknowledgments

This research is supported by Payame Noor University.

 References and Notes WienerHStructural determination of paraffin boiling pointsJ Am Chem Soc194769172010.1021/ja01193a00520291038 KhadikarPVKarmarkarSOn the Estimation of PI index of PolyacenesActa Chim Slov200249755771 NikoliSTrinajstiNMihaliZThe Wiener index: developments and applicationsCroat Chem Acta199568105129 GutmanIYehYNLeeSLLuoYLSome recent results in the theory of the Wiener numberIndian J Chem199332A651661 GutmanIPotgieterJHWiener index and intermolecular forcesJ Serb Chem Soc199762185192 KhadikarPVOn a novel structural descriptorPL Nat Acad Sci Lett200023113118 KhadikarPVKarmarkarSAgrawalVKRelationships and relative correlation potential of the Wiener, Szeged and PI indicesNat Acad Sci Lett200023165170 KhadikarPVKarmarkarSAgrawalVKA novel PI index and its applications to QSPR/QSAR studiesJ Chem Inf Comput Sci20014193494910.1021/ci000309211500110 KhadikarPPDeshpandeNVKalePPDobryninAAGutmanIDomotorGThe Szeged Index and an Analogy with the Wiener IndexJ Chem Inf Comput Sci199535545550 MathurKCSinghSMathurSKhadikarPVModeling polychlorinated biphenyls (PBCs) in environmentPoll Res199918405409 IranmaneshAKhormaliOPI index of HAC5C7 nanotubeJ Comput Theor Nanosci(In press) IranmaneshAKhormaliOSzeged index of HAC5C7 nanotubesJ Comput Theor Nanosci(In press) IranmaneshASoleimaniBPI Index of TUC4C8(R) NanotubesMATCH Commun Math Comput Chem200757251262 IranmaneshASoleimaniBAhmadiASzeged Index of TUC4C8(R) NanotubeJ Comput Theor Nanosci20044147151 AshrafiARLoghmanAPI Index of Zig-Zag Polyhex NanotubesMATCH Commun Math Comput Chem200655447452 AshrafiARLoghmanAPadmakar-Ivan Index of TUC4C8(S) NanotubesJ Comput Theor Nanosci20063378381 AshrafiARRezaeiFPI Index of Polyhex NanotoriMATCH Commun Math Comput Chem200657243250 AshrafiARLoghmanAPI Index of Armchair Polyhex NanotubesArs Combin200680193196 YousefiHBahramiAYazdaniJAshrafiARPI Index of V-Phenylenic Nanotubes and NanotoriJ Comput Theor Nanosci20073604605 AshrafiARSaatiHPI and Szeged Indices of One Pentagonal Carbon NanoconesJ Comput Theor Nanosci20074761763 HeydariATaeriBSzeged index of TUC4C8(R) nanotubesMATCH Commun Math Comput Chem200757463477 EliasiMTaeriBSzeged and Balaban indices of zigzag polyhex nanotubesMATCH Commun Math Comput Chem200656383402 SchonertMGAP, Groups, Algorithms and ProgrammingLehrstuhl De fur Mathematik, RWTHAchen1992 DabirianMIranmaneshAThe Full Non-Rigid Group Theory for Trimethylamine-BH3 ComplexMATCH Commun Math Comput Chem2005547588 TrinajsticNChemical Group TheoryCRC PressBoca Roton, FL1992 EntringerRCMeirAJMoonWSzékelyLAThe Wiener index of trees from certain familiesAustralas J Combin199410211224 GutmanIYehYNLeeSLChenJCWiener numbers of dendrimersMATCH Commun Math Comput Chem199430103115 GutmanIA formula for the Wiener number of trees and its extension to graphs containing cycles, Graph Theory Notes of NewYork199427915 KarmarkarSKarmarkarSJoshiSDasAKhadikarPVNovel application of Wiener vis-à-vis Szeged indices in predicting polychlorinated biphenyls in the environmentJ Serb Chem Soc199762227234 Figures

Molecular graphs of dendrimers T k,d

VC5C7 [4, 2] nanotube.

Rows of m-th period.

HC5C7 [4,2] nanotube.