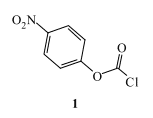
Extended Grunwald-Winstein Analysis - LFER Used to Gauge Solvent Effects in p-Nitrophenyl Chloroformate Solvolysis
Abstract
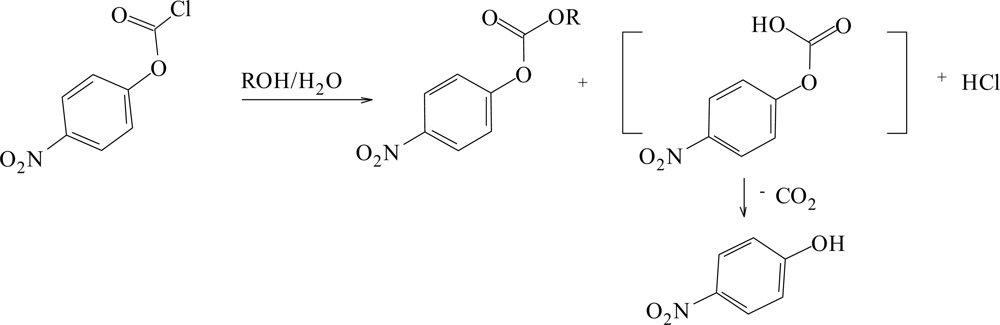
:1. Introduction
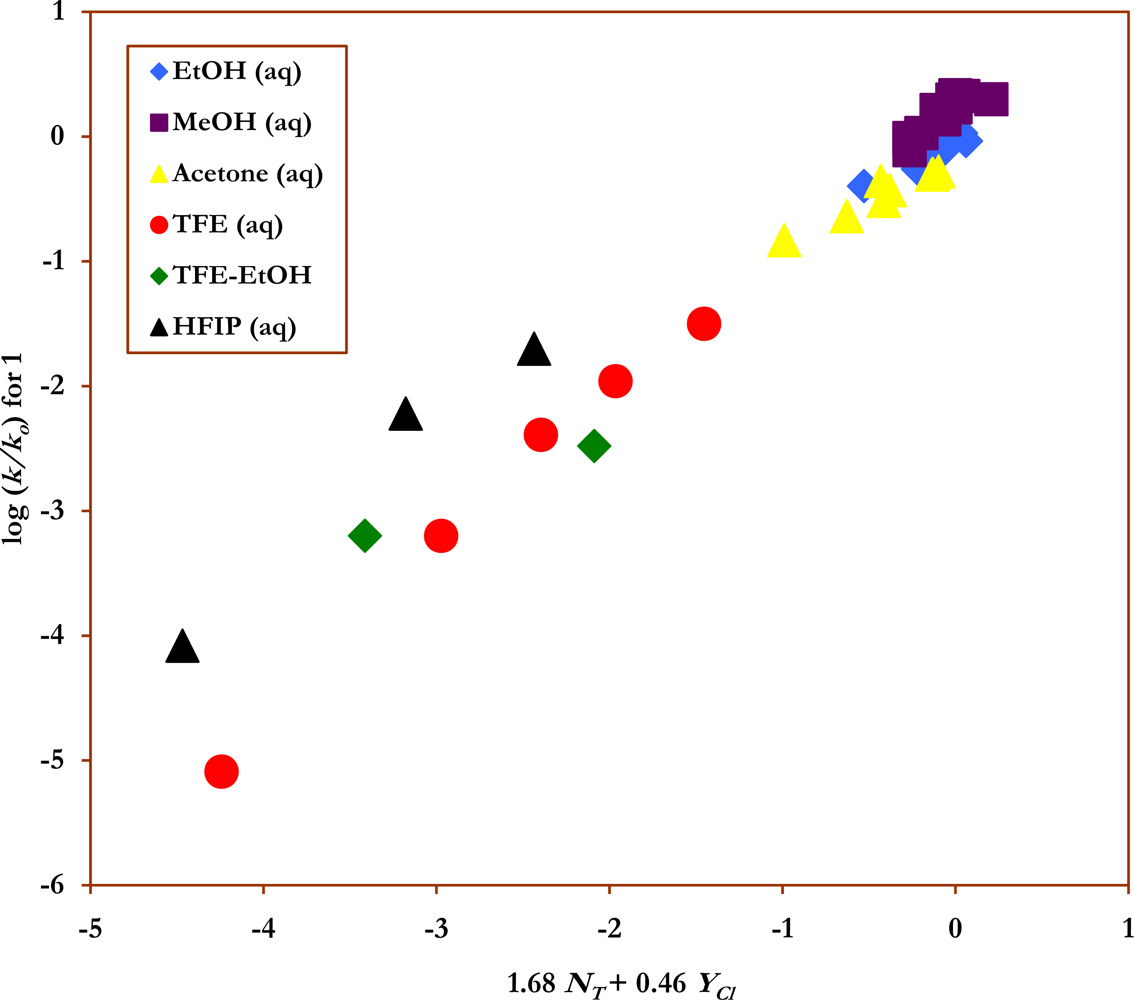
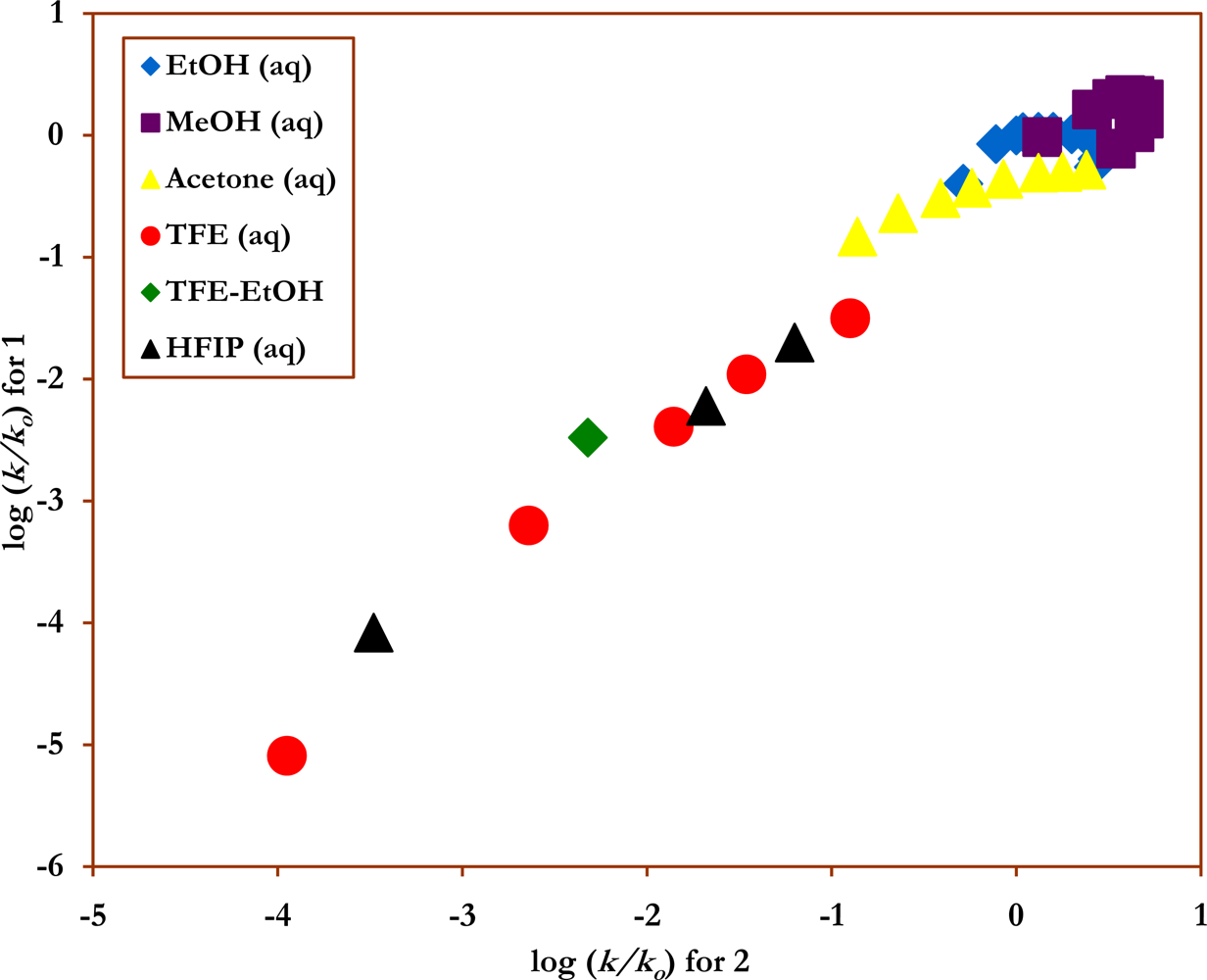
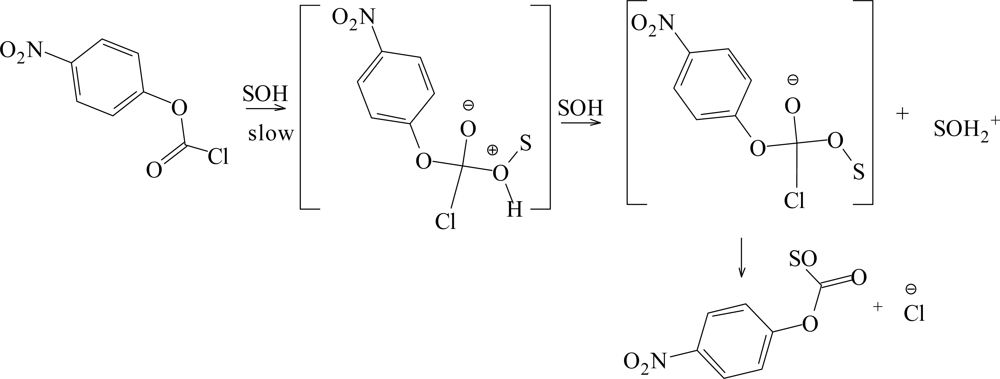
2. Results and Discussion
3. Conclusions
4. Experimental Section
Acknowledgments
References and Notes
- Queen, A. Kinetics of the Hydrolysis of Acyl Chlorides in Pure Water. Can. J. Chem 1967, 45, 1619–1629. [Google Scholar]
- Kivinen, A. The Kinetics of the Solvolysis of Acid Chlorides. Acta Chem. Scand 1965, 19, 845–870. [Google Scholar]
- Bentley, TW; Llewellyn, G; McAlister, JA. SN2 Mechanism for Alcoholysis, Aminolysis, and Hydrolysis of Acetyl Chloride. J. Org. Chem 1996, 61, 7927–7932. [Google Scholar]
- Ryu, ZH; Lim, GT; Bentley, TW. Applications of Third Order Models in Solvolytic Reaction of Aliphatic Substituted Acyl Derivatives in 2,2,2-Trifluoroethanol-Ethanol Systems. Bull. Kor. Chem. Soc 2003, 24, 1293–1302. [Google Scholar]
- Kevill, DN. Choloroformate Esters and Related Compounds. In The Chemistry of the Functional Groups: The Chemistry of Acyl Halides.; Patai, S, Ed.; Wiley: New York, 1972; Chapter 12; pp. 381–453. [Google Scholar]
- Matzner, M; Kurkjy, RP; Cotter, RJ. The Chemistry of Chloroformates. Chem. Rev 1964, 64, 645–687. [Google Scholar]
- Kivinen, A. Mechanisms of Substitution at the COX group. In In The Chemistry of the Functional Groups: The Chemistry of Acyl Halides; Patai, S, Ed.; EdWiley: New York, 1972; Chapter 6pp. 177–230. [Google Scholar]
- Satchell, D. P.N. An Outline of Acylation. Quart. Rev. Chem. Soc 1963, 17, 160–203. [Google Scholar]
- Bentley, TW. Structural Effects on the Solvolytic Reactivity of Carboxylic and Sulfonic Acid Chlorides. Comparisons with Gas-Phase Data for Cation Formation. J. Org. Chem 2008, 73, 6251–6257. [Google Scholar]
- Mikulec, LJ; Puleo, DA. Use of p-Nitrophenyl Chloroformate Chemistry to Immobilize Protein on Orthopedic Biomaterials. J. Biomed. Mater. Res 1996, 32, 203–208. [Google Scholar]
- Grunwald, E; Winstein, S. The Correlation of Solvolysis Rates. J. Am. Chem. Soc 1948, 70, 846–854. [Google Scholar]
- Bentley, TW; Llewellyn, G. Yx Scales of Solvent Ionizing Power. Prog. Phys. Org. Chem 1990, 17, 121–158. [Google Scholar]
- Winstein, S; Grunwald, E; Jones, HW. The Correlation of Solvolyses Rates and the Classification of Solvolysis Reactions into Mechanistic Categories. J. Am. Chem. Soc 1951, 73, 2700–2707. [Google Scholar]
- Schadt, FL; Bentley, TW; Schleyer, P.v.R. The SN2-SN1 Spectrum. 2. Quantitative Treatments of Nucleophilic Solvent Assistance. A Scale of Solvent Nucleophilicities. J. Am. Chem. Soc 1976, 98, 7667–7674. [Google Scholar]
- Kevill, DN; Anderson, SW. An Improved Scale of Solvent Nucleophilicity Based on the Solvolysis of the S-Methyldibenzothiophenium Ion. J. Org. Chem 1991, 56, 1845–1850. [Google Scholar]
- Kevill, DN. Development and Uses of Scales of Solvent Nucleophilicity. In In Advances in Quantitative Structure-Property Relationships; Charton, M, Ed.; EdJAI Press: Greenwich, CT, 1996; Vol. Volume 1, pp. 81–115. [Google Scholar]
- Wells, PR. Linear Free Energy Relationships; Academic Press: New York, 1968; pp. 67–68. [Google Scholar]
- Bentley, TW; Garley, MS. Correlations and Predictions of Solvent Effects on Reactivity: Some Limitations of Multi-Parameter Equations and Comparisons with Similarity Models Based on One Solvent Parameter. J. Phys. Org. Chem 2006, 19, 341–349. [Google Scholar]
- Kevill, DN; D’Souza, MJ. Sixty Years of the Grunwald-Winstein Equation: Development and Recent Applications. J. Chem. Res. 2008, 61–66. [Google Scholar]
- Kevill, DN; Kyong, JB; Weitl, FL. Solvolysis-Decomposition of 1-Adamantyl Chloroformate: Evidence for Ion Pair Return in 1-Adamantyl Chloride Solvolysis. J. Org. Chem 1990, 55, 4304–4311. [Google Scholar]
- Koo, IS; Yang, K; Kang, K; Oh, HK; Lee, I. Stoichiometric Solvation Effects. Product-Rate Correlation for the Solvolyses of Phenyl Chloroformate in Alcohol-Water Mixtures. Bull. Korean Chem. Soc 1996, 17, 520–524. [Google Scholar]
- Kevill, DN; D’Souza, MJ. Concerning the Two Reaction Channels for the Solvolyses of Ethyl Chloroformate and Ethyl Chlorothioformate. J. Org. Chem 1998, 63, 2120–2124. [Google Scholar]
- Kevill, DN; Kim, JC; Kyong, JB. Correlation of the Rates of Methyl Chloroformate with Solvent Properties. J. Chem. Res. Synop. 1999, 150–151. [Google Scholar]
- Kyong, JB; Kim, YG; Kim, DK; Kevill, DN. Dual Pathways in the Solvolyses of Isopropyl Chloroformate. Bull. Korean Chem. Soc 2000, 21, 662–664. [Google Scholar]
- Kevill, DN; D’Souza, MJ. Correlation of the Rates of Solvolyses of n-Octyl Fluoroformate and a Comparison with n-Octyl Chloroformate Solvolyses. J. Chem. Soc. Perkin Trans. 2 2002, 240–243. [Google Scholar]
- Kyong, JB; Yoo, J.–S; Kevill, DN. Solvolysis-Decomposition of 2-Adamantyl Chloroformate: Evidence for Two Reaction Pathways. J. Org. Chem 2003, 68, 3425–3432. [Google Scholar]
- Kyong, JB; Won, H; Kevill, DN. Application of the Extended Grunwald-Winstein Equation to Solvolyses of n-Propyl Chloroformate. Int. J. Mol. Sci 2005, 6, 87–96. [Google Scholar]
- Bentley, TW; Harris, HC; Zoon, H-R; Gui, TL; Dae, DS; Szajda, SR. Mechanisms of Solvolyses of Acid Chlorides and Chloroformates. Chloroacetyl and Phenylacetyl Chloride as Similarity Models. J. Org. Chem 2005, 70, 8963–8970. [Google Scholar]
- Ryu, ZH; Lee, YH; Oh, Y. Stoichiometric Effects. Correlation of the Rates of Solvolysis of Isopropenyl Chloroformate. Bull. Kor. Chem. Soc 2005, 26, 1761–1766. [Google Scholar]
- Kevill, DN; D’Souza, MJ. Correlation of the Rates of Solvolysis of Phenyl Chloroformate. J. Chem. Soc. Perkin Trans. 2 1997, 1721–1724. [Google Scholar]
- Koo, IS; Yang, K; Koo, JC; Park, J.–K; Lee, I. Stoichiometric Solvation Effects. Part 4. Product–rate Correlations for Solvolyses of p-Methoxyphenyl Chloroformate in Alcohol–Water Mixtures. Bull. Korean Chem. Soc 1997, 18, 1017–1021. [Google Scholar]
- Koo, IS; Yang, K; Kang, K; Lee, I; Bentley, TW. Stoichiometric Solvation Effects. Part 3. Product–rate Correlations for Solvolyses of p-Nitrophenyl Chloroformate in Alcohol–Water Mixtures. J. Chem. Soc. Perkin Trans 2 1998, 1179–1183. [Google Scholar]
- Koo, IS; Yang, K; Kang, K; Lee, I. Transition-State Variation in the Solvolyses of para-Substituted Phenyl Chloroformates in Alcohol-Water Mixtures. Bull. Kor. Chem. Soc 1998, 19, 968–973. [Google Scholar]
- Park, KH; Kyong, JB; Kevill, DN. Nucleophilic Substitution Reactions of p-Nitrobenzyl Chloroformate. Bull. Kor. Chem. Soc 2000, 21, 1267–1270. [Google Scholar]
- Kyong, JB; Park, B-C; Kim, C-B; Kevill, DN. Rate and Product Studies with Benzyl and p-Nitrobenzyl Chloroformates under Solvolytic Conditions. J. Org. Chem 2000, 65, 8051–8058. [Google Scholar]
- Kevill, DN; Koyoshi, F; D’Souza, MJ. Correlation of the Specific Rates of Solvolysis of Aromatic Carbamoyl Chlorides, Chloroformates, Chlorothionoformates, and Chlorodithio-formates Revisited. Int. J. Mol. Sci 2007, 8, 346–352. [Google Scholar]
- D’Souza, MJ; Reed, D; Koyoshi, F; Kevill, DN. Consideration of the Factors Influencing the Specific Rates of Solvolysis of p-Methoxyphenyl Chloroformate. Int. J. Mol. Sci 2007, 8, 788–796. [Google Scholar]
- D’Souza, MJ; Ryu, ZH; Park, B-C; Kevill, DN. Correlation of the Rates of Solvolysis of Acetyl Chloride and α-Substituted Derivatives. Can. J. Chem 2008, 86, 359–367. [Google Scholar]
- Castro, EA; Ruiz, MG; Santos, JG. Structure-Reactitvity Correlations in the Aminolysis of Aryl Chloroformates. Int. J. Chem. Kinet. 2001, 281–287. [Google Scholar]
- Kaspi, J; Rappoport, Z. Nucleophilicity and Ionizing Power in Binary Solvent Mixtures. Tetrahedron Lett 1977, 2035. [Google Scholar]
- Kevill, DN; Park, B-C; Park, K-H; D’Souza, MJ; Yaakoubd, L; Mlynarski, SL; Kyong, JB. Rate and Product Studies in the Solvolyses of N, N-Dimethylsulfamoyl and 2-Propanesulfonyl Chlorides. Org. Biomol. Chem 2006, 4, 1580–1586. [Google Scholar]
- Kevill, DN; Ryu, ZH. Additional Solvent Ionizing Power Values for Binary Water – 1,1,1,3,3,3,-Hexafluoro-2-propanol Solvents. Int. J. Mol. Sci 2006, 7, 451–455. [Google Scholar]
- Bentley, TW; Carter, GE. The SN2-SN1 Spectrum. 4. Mechanism for Solvolyses of tert-Butyl Chloride: A Revised Y Scale of Solvent Ionizing Power based on Solvolyses of 1-Adamantyl Chloride. J. Am. Chem. Soc 1982, 104, 5741–5747. [Google Scholar]
- Kevill, DN; D’Souza, MJ. Additional YCl Values and Correlation of the Specific Rates of Solvolysis of tert-Butyl Chloride in Terms of NT and YCl Scales. J. Chem. Res. Synop 1993, 174–175. [Google Scholar]
- Yew, KH; Koh, HJ; Lee, HW; Lee, I. Nucleophilic Substitution Reactions of Phenyl Chloroformates. J. Chem. Soc. Perkin Trans 2 1995, 2263–2268. [Google Scholar]
- Frost, AA; Pearson, RG. Kinetics and Mechanism-a Study of Homogeneous Chemical Reactions 1961, 49–50.
- Kevill, DN; Abduljaber, MH. Correlation of the Rates of Solvolysis of Cyclopropylcarbinyl and Cyclobutyl Bromides Using the Extended Grunwald-Winstein Equation. J. Org. Chem 2000, 65, 2548–2554. [Google Scholar]
| Solvent (%)a | 1; 105k(s−1)b | 2; 105k(s−1)c | 3; 105k(s−1)d | ||
|---|---|---|---|---|---|
| 97% TFE (w/w) | 0.113±0.008 | 0.0570±0.0030 | 0.0300±0.0013 | −3.30 | 2.83 |
| 90% TFE (w/w) | 8.87±0.28 | 1.15±0.08 | 0.825±0.032 | −2.55 | 2.85 |
| 80% TFE (w/w) | 56.8±0.4 | 7.02±0.28 | 8.63±0.24 | −2.22 | 2.90 |
| 70% TFE (w/w) | 153±1.5 | 17.4±1.3 | 15.2±0.6 | −1.98 | 2.96 |
| 50% TFE (w/w) | 438±44 | 63.5±3.0 | 52.6±2.8 | −1.73 | 3.16 |
| 90T-10E (v/v) | 8.82±0.17 | −2.67 | 2.33 | ||
| 80T-20E (v/v) | 45.5±0.7 | 2.43±0.21 | 3.52±0.13 | −1.76 | 1.89 |
| 90%HFIP (w/w) | 1.20±0.06 | 0.166±0.004 | 0.172±0.007 | −3.84 | 4.31 |
| 70%HFIP (w/w) | 83.8±0.9 | 10.5±0.3 | 7.58±0.22 | −2.94 | 3.83 |
| 50%HFIP (w/w) | 277±2 | 31.6±0.6 | 24.9±0.5 | −2.49 | 3.80 |
| Substrate | nb | ℓc | mc | cc | l/m | Rd | Fe |
|---|---|---|---|---|---|---|---|
| 29f | 1.85±0.21 | 0.48±0.05 | 0.14±0.05 | 3.85 | 0.871 | 41 | |
| 1 | 39g | 1.68±0.06 | 0.46±0.04 | 0.074±0.08 | 3.65 | 0.976 | 363 |
| 38h | 1.69±0.07 | 0.46±0.04 | 0.074±0.08 | 3.67 | 0.974 | 323 | |
| 2 | 38h | 1.59±0.07 | 0.54±0.03 | 0.16±0.08 | 2.94 | 0.972 | 299 |
| 3 | 38h | 1.58±0.06 | 0.57±0.04 | 0.17±0.07 | 2.77 | 0.974 | 320 |
© 2008 by MDPI This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
D’Souza, M.J.; Shuman, K.E.; Carter, S.E.; Kevill, D.N. Extended Grunwald-Winstein Analysis - LFER Used to Gauge Solvent Effects in p-Nitrophenyl Chloroformate Solvolysis. Int. J. Mol. Sci. 2008, 9, 2231-2242. https://doi.org/10.3390/ijms9112231
D’Souza MJ, Shuman KE, Carter SE, Kevill DN. Extended Grunwald-Winstein Analysis - LFER Used to Gauge Solvent Effects in p-Nitrophenyl Chloroformate Solvolysis. International Journal of Molecular Sciences. 2008; 9(11):2231-2242. https://doi.org/10.3390/ijms9112231
Chicago/Turabian StyleD’Souza, Malcolm J., Kevin E. Shuman, Shannon E. Carter, and Dennis N. Kevill. 2008. "Extended Grunwald-Winstein Analysis - LFER Used to Gauge Solvent Effects in p-Nitrophenyl Chloroformate Solvolysis" International Journal of Molecular Sciences 9, no. 11: 2231-2242. https://doi.org/10.3390/ijms9112231