Weighted Risk Score-Based Multifactor Dimensionality Reduction to Detect Gene-Gene Interactions in Nasopharyngeal Carcinoma
Abstract
:1. Introduction
2. Results and Discussion
2.1. Comparison of WRSMDR with MDR
| Evaluation Indicator | Two-Locus | Three-Locus | Four-Locus | |||
|---|---|---|---|---|---|---|
| WRSMDR | MDR | WRSMDR | MDR | WRSMDR | MDR | |
| Specific Detection Rate | 0.87 | 0.83 | 0.74 | 0.83 | 0.92 | 0.46 |
| Detection Rate | 1 | 1 | 1 | 1 | 0.97 | 0.56 |
| Error Rate | 0 | 0 | 0 | 0 | 0.01 | 0.44 |
| No Detection Rate | 0 | 0 | 0 | 0 | 0.02 | 0 |
| Evaluation Indicator | Two-Locus | Three-Locus | Four-Locus | |||
|---|---|---|---|---|---|---|
| WRSMDR | MDR | WRSMDR | MDR | WRSMDR | MDR | |
| Specific Detection Rate | 0.96 | 0.61 | 0.57 | 0.66 | 0.94 | 0.68 |
| Detection Rate | 1 | 0.81 | 0.85 | 0.85 | 0.98 | 0.79 |
| Error Rate | 0 | 0.19 | 0.03 | 0.15 | 0.01 | 0.21 |
| No Detection Rate | 0 | 0 | 0.12 | 0 | 0.01 | 0 |
2.2. Application of WRSMDR to NPC Data
| Number of Locus | SNPs | Weighted Risk Score | Consistency | p |
|---|---|---|---|---|
| 2 | rs2860580-rs11865086 | 1.324 | 10 | <0.001 |
| 3 | rs2860580-rs11865086-rs2305806 * | 1.332 | 10 | <0.001 |
| 4 | rs2860580-rs11865086-rs836475-rs4976028 | 1.266 | 4 | <0.001 |
| 5 | rs2860580-rs11865086-rs836475-rs4976028-rs6488297 | 1.236 | 7 | <0.001 |
| Genotype Combination of the Three SNPs a | Disease Probability b | Fold Increase in Risk c | Weight of Genotype d |
|---|---|---|---|
| GG-CC-AG | 0.00077 | 3.07 | 0.03 |
| GG-CC-AA | 0.00045 | 1.78 | 0.03 |
| GG-AC-AA | 0.00038 | 1.51 | 0.09 |
| GG-AC-AG | 0.00037 | 1.49 | 0.11 |
| AG-CC-AG | 0.00036 | 1.43 | 0.03 |
| GG-AA-AA | 0.00034 | 1.36 | 0.08 |
| AG-AC-AA | 0.00032 | 1.29 | 0.09 |
| GG-AA-AG | 0.00031 | 1.24 | 0.08 |
| GG-AA-GG | 0.00031 | 1.23 | 0.02 |
| GG-AC-GG | 0.00027 | 1.07 | 0.03 |
| AG-CC-AA | 0.00026 | 1.03 | 0.02 |
| AG-AC-GG | 0.00019 | 0.77 | 0.03 |
| AG-AC-AG | 0.00019 | 0.77 | 0.09 |
| AG-AA-AG | 0.00017 | 0.67 | 0.07 |
| AG-AA-GG | 0.00016 | 0.66 | 0.02 |
| AG-AA-AA | 0.00016 | 0.62 | 0.08 |
| AA-AC-AG | 0.00013 | 0.52 | 0.02 |
| AA-AC-AA | 0.00010 | 0.39 | 0.02 |
| AA-AA-AG | 0.00008 | 0.33 | 0.01 |
| AA-AA-AA | 0.00006 | 0.26 | 0.01 |
| Number of Locus | SNPs | Prediction Error (%) | Cross-Validation Consistency | p |
|---|---|---|---|---|
| 2 | rs2860580-rs11865086 | 41.65 | 9/10 | <0.001 |
| 3 | rs2860580-rs11865086-rs2305806 * | 40.48 | 10/10 | <0.001 |
| 4 | rs2860580-rs11865086-rs2305806-rs2115485 | 41.31 | 8/10 | <0.001 |
| 5 | rs2860580-rs11865086-rs2305806 -rs2115485-rs7166547 | 45.35 | 5/10 | <0.022 |
2.3. The Advantages and Limitations of WRSMDR
3. Experimental Section
3.1. WRSMDR
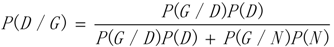
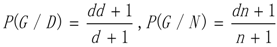
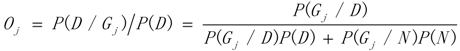
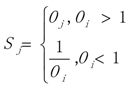
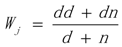
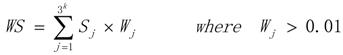
3.2. Data Simulation

| Parameters | Two-Locus Model | Three-Locus Model | Four-Locus Model |
|---|---|---|---|
| Number of predictive SNPs | 2 | 3 | 4 |
| Number of non-predictive SNPs | 8 | 7 | 6 |
| Heritability | 0.05 | 0.05 | 0.05 |
| MAF of predictive SNPs | 0.2 | 0.2 | 0.2 |
| MAF of non-predictive SNPs | (0.01~0.5) | (0.01~0.5) | (0.01~0.5) |
3.3. NPC Data
3.4. Data Analysis
| SNP | Chr. | Locus | MA | Chi-Square Value |
|---|---|---|---|---|
| rs2860580 | 6 | HLA-A | A | 89.95 |
| rs11865086 | 16 | MAPK3 | C | 14.96 |
| rs4976028 | 5 | PIK3R1 | G | 9.98 |
| rs11150675 | 16 | LAT | A | 7.47 |
| rs6488297 | 12 | KLRC1 | A | 7.05 |
| rs941831 | 10 | ITGB1 | G | 5.88 |
| rs836475 | 7 | RAC1 | A | 4.80 |
| rs2733840 | 12 | KLRC4 | G | 3.02 |
| rs2733840 | 12 | KLRC3 | G | 3.02 |
| rs10109834 | 8 | PTK2B | C | 2.71 |
| rs2115485 | 9 | SYK | A | 2.68 |
| rs2305806 | 19 | VAV1 | G | 2.57 |
| rs7166547 | 15 | MAP2K1 | A | 2.35 |
| rs744167 | 12 | PTPN6 | A | 1.97 |
| rs7301582 | 12 | KLRC2 | A | 1.45 |
| rs3019238 | 11 | PAK1 | G | 1.23 |
| rs7645550 | 3 | PIK3CA | A | 0.76 |
| rs11214093 | 11 | IL18 | G | 0.70 |
| rs12310310 | 12 | KLRD1 | A | 0.58 |
| rs4780 | 15 | B2M | G | 0.23 |
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- McKinney, B.A.; Reif, D.M.; Ritchie, M.D; Moore, J.H. Machine Learning for Detecting Gene-Gene Interactions: A Review. Appl. Bioinform. 2006, 5, 77–88. [Google Scholar] [CrossRef]
- Motsinger-Reif, A.A.; Reif, D.M.; Fanelli, T.J.; Ritchie, M.D. A comparison of analytical methods for genetic association studies. Genet. Epidemiol. 2008, 32, 767–778. [Google Scholar] [CrossRef]
- Cordell, H.J. Detecting gene-gene interactions that underlie human diseases. Nat. Rev. Genet. 2009, 10, 392–404. [Google Scholar] [CrossRef]
- Moore, J.H.; Asselbergs, F.W.; Williams, S.M. Bioinformatics challenges for genome-wide association studies. Bioinformatics 2010, 26, 445–455. [Google Scholar]
- Ritchie, M.D.; Hahn, L.W.; Roodi, N.; Bailey, L.R.; Dupont, W.D.; Parl, F.F.; Moore, J.H. Multifactor dimensionality reduction reveals high-order interactions among estrogen metabolism genes in sporadic breast cancer. Am. J. Hum. Genet. 2001, 69, 138–147. [Google Scholar] [CrossRef]
- Ritchie, M.D.; Hahn, L.W.; Mooreet, J.H. Power of multifactor dimensionality reduction for detecting gene-gene interactions in the presence of genotyping error, missing data, phenocopy, and genetic heterogeneity. Genet. Epidemiol. 2003, 24, 150–157. [Google Scholar] [CrossRef]
- Hahn, L.W.; Moore, J.H. Ideal discrimination of discrete clinical end points using multilocus genotypes. In. Silico Biol. 2004, 4, 183–194. [Google Scholar]
- Hahn, L.W.; Ritchie, M.D.; Moore, J.H. Multifactor dimensionality reduction software for detecting gene-gene and gene-environment interactions. Bioinformatics 2003, 19, 376–382. [Google Scholar]
- Moore, J.H.; Gilbert, J.C.; Tsai, C.T.; Chiang, F.T.; Holden, T.; Barney, N.; White, B.C. A flexible computational framework for detecting, characterizing, and interpreting statistical patterns of epistasis in genetic studies of human disease susceptibility. J. Theor. Biol. 2006, 241, 252–261. [Google Scholar] [CrossRef]
- Moore, J.H.; White, B.C. Computational analysis of gene-gene interactions in common human diseases using multifactor dimensionality reduction. Expert Rev. Mol. Diagn. 2004, 4, 795–803. [Google Scholar] [CrossRef]
- Moore, J.H. Genome-wide analysis of epistasis using multifactor dimensionality reduction: Feature selection and construction in the domain of human genetics. In Knowledge Discovery and Data Mining: Challenges and Realities with Real World Data, 1st ed.; Zhu, X.Q., Davidson, I., Eds.; Hershey, IGI Press: New York, NY, USA, 2007; pp. 17–30. [Google Scholar]
- Moore, J.H.; Williams, S.M. Epistasis and its implications for personal genetics. Am. J. Hum. Genet. 2009, 85, 309–320. [Google Scholar] [CrossRef]
- Chung, Y.; Lee, S.Y.; Elston, R.C.; Park, T. Odds ratio based multifactor-dimensionality reduction method for detecting gene-gene interactions. Bioinformatics 2007, 23, 71–76. [Google Scholar] [CrossRef]
- Lee, S.Y.; Chung, Y.; Elston, R.C. Log-linear model-based multifactor dimensionality reduction method to detect gene-gene interactions. Bioinformatics 2007, 23, 2589–2595. [Google Scholar] [CrossRef]
- Lou, X.; Chen, G.B.; Yan, L.; Ma, J.Z.; Zhu, J.; Elston, R.C.; Li, M.D. A generalized combinatorial approach for detecting gene by gene and gene by environment interactions with application to nicotine dependence. Am. J. Hum. Genet. 2007, 80, 1125–1137. [Google Scholar] [CrossRef]
- Velez, D.R.; White, B.C.; Motsinger, A.A.; Bush, W.S.; Ritchie, M.D.; Williams, S.M.; Moore, J.H. A balanced accuracy function for epistasis modeling in imbalanced datasets using multifactor dimensionality reduction. Genet. Epidemol. 2007, 31, 306–315. [Google Scholar] [CrossRef]
- Pattin, K.A.; White, B.C.; Barney, N.; Gui, J.; Nelson, H.H.; Kelsy, K.T.; Andrew, A.S.; Karagas, M.R.; Moore, J.H. A computationally efficient hypothesis testing method for epistasis analysis using multifactor dimensionality reduction. Genet. Epidemiol. 2009, 33, 87–94. [Google Scholar]
- Greene, C.S.; Himmelstein, D.S.; Nelson, H.H.; Kelsey, K.T.; Williams, S.M.; Moore, J.H. Enabling personal genomics with an explicit test of epistasis. Pac. Symp. Biocomput. 2010, 2010, 327–336. [Google Scholar]
- Namkung, J.; Kim, K.; Yi, S.; Chung, W.; Kwon, M.; Park, T. New evaluation measures for multifactor dimensionality reduction classifiers in gene-gene interaction analysis. Bioinformatics 2009, 25, 338–345. [Google Scholar] [CrossRef]
- Bush, W.S.; Dudek, S.M.; Ritchie, M.D. Parallel multifactor dimensionality reduction: A tool for the large-scale analysis of gene-gene interactions. Bioinformatics 2006, 22, 2173–2174. [Google Scholar] [CrossRef]
- Sinnott-Armstrong, N.A.; Greene, C.S.; Cancare, F.; Moore, J.H. Accelerating epistasis analysis in human genetics with consumer graphics hardware. BMC Res. Notes 2009, 2, 149. [Google Scholar] [CrossRef] [Green Version]
- Mei, H.; Cuccaro, M.L.; Martin, E.R. Multifactor dimensionality reduction phonemics: A novel method to capture genetic heterogeneity with use of phenotypic variables. Am. J. Hum. Genet. 2007, 81, 1251–1261. [Google Scholar] [CrossRef]
- Bush, W.S.; Edwards, T.L.; Dudek, S.M.; Mckinney, B.A.; Ritchie, M.D. Alternative contingency table measures improve the power and detection of multifactor dimensionality reduction. BMC Bioinform. 2008, 9, 238–244. [Google Scholar] [CrossRef]
- Gui, J.; Moore, J.H.; Williams, S.C.; Andrews, P.; Hillege, H.L.; Harst, P.; Navis, G.; Asselbergs, F.W.; Diamond, D.G. A Simple and Computationally Efficient Approach to Multifactor Dimensionality Reduction Analysis of Gene-Gene Interactions for Quantitative Traits. PLoS One 2013, 8. [Google Scholar] [CrossRef]
- Yang, C.H.; Lin, Y.D.; Chuang, L.Y.; Chen, J.B.; Chang, H.W. MDR-ER: Balancing functions for adjusting the ratio in risk classes and classification errors for imbalanced cases and controls using multifactor-dimensionality reduction. PLoS One 2013, 8. [Google Scholar] [CrossRef]
- Dai, H.I.; Charnigo, R.J.; Becker, M.L.; Leeder, J.S.; Motsinger-Reif, A.A. Risk score modeling of multiple gene to gene interactions using aggregated-multifactor dimensionality reduction. Biodata Min. 2013, 6, 1. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, J.S. Bayesian inference of epistatic interactions in case-control studies. Nat. Genet. 2007, 9, 1167–1173. [Google Scholar] [CrossRef]
- Wei, W.I.; Sham, J.S. Nasopharyngeal carcinoma. Lancet 2005, 365, 2041–2054. [Google Scholar] [CrossRef]
- Yu, M.C.; Yuan, J.M. Epidemiology of nasopharyngeal carcinoma. Semin. Cancer Biol. 2002, 12, 421–429. [Google Scholar] [CrossRef]
- Hildesheima, A.; Wang, C.P. Genetic predisposition factors and nasopharyngeal carcinoma risk: A review of epidemiological association studies, 2000–2011 Rosetta Stone for NPC: Genetics, viral infection, and other environmental factors. Semin. Cancer Biol. 2012, 22, 107–116. [Google Scholar] [CrossRef]
- Bei, J.X.; Li, Y.; Jia, W.H.; Feng, B.J.; Zhou, A.; Chen, L.Z.; Feng, Q.S.; Low, H.Q.; Zhang, H.X.; He, Z.F.; et al. A genome-wide association study of nasopharyngeal carcinoma identifies three new susceptibility loci. Nat. Genet. 2010, 42, 599–603. [Google Scholar] [CrossRef]
- Tse, K.P.; Su, W.H.; Chang, K.P.; Tsang, N.M.; Yu, C.J.; Tang, P.; See, L.C.; Hsueh, C.; Yang, M.L.; Hao, S.P.; et al. Genome-wide association study reveals multiple nasopharyngeal carcinoma-associated loci within the HLA region at chromosome 6p21.3. Am. J. Hum. Genet. 2009, 85, 194–203. [Google Scholar]
- Ras-Independent Pathway in NK Cell-Mediated Cytotoxicity. Available online: http://www.biocarta.com/pathfiles/h_nkcellspathway.asp (accessed on 5 April 2014).
- Multifactor Dimensionality Reduction Open-Source Software Package. Available online: http://www.multifactordimensionalityreduction.org (accessed on 5 April 2014).
- Kotsiantis, S.; Kanellopoulos, D.; Pintelas, P. Handling imbalanced datasets: A review. GESTS Intern. Transact. Comput. Sci. Eng. 2006, 30, 25–36. [Google Scholar]
- Foster, P. Machine learning from imbalanced data sets 101. In Proceedings of the AAAI’2000 Workshop on Imbalanced Data Sets; New York University: New York, NY, USA, 2000. [Google Scholar]
- Urbanowicz, R.J.; Kiralis, J.; Sinnott-Armstrong, N.A.; Heberling, T.; Fisher, J.M.; Moore, J.H. GAMETES: A fast, direct algorithm for generating pure, strict, epistatic models with random architectures. Biodata Min. 2012, 5, 16. [Google Scholar] [CrossRef]
- Visscher, P.M.; Hill, W.G.; Wray, N.R. Heritability in the genomics era—Concepts and miscon- ceptions. Nat. Rev. Genet. 2008, 9, 255–266. [Google Scholar] [CrossRef]
- Purcell, S.; Neale, B.; Todd-Brown, K.; Thomas, L.; Ferreira, M.A.R.; Bender, D.; Maller, J.; Sklar, P.; Bakker, P.; Daly, M.J. PLINK: A tool set for whole-genome association and population-based linkage analyses. Am. J. Hum. Genet. 2007, 81, 559–575. [Google Scholar] [CrossRef]
- Weighted Risk Score Based Multifactor Dimensionality Reduction. Available online: www.sysucc.org.cn/wrsmdr/index.html (accessed on 5 April 2014).
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Li, C.-F.; Luo, F.-T.; Zeng, Y.-X.; Jia, W.-H. Weighted Risk Score-Based Multifactor Dimensionality Reduction to Detect Gene-Gene Interactions in Nasopharyngeal Carcinoma. Int. J. Mol. Sci. 2014, 15, 10724-10737. https://doi.org/10.3390/ijms150610724
Li C-F, Luo F-T, Zeng Y-X, Jia W-H. Weighted Risk Score-Based Multifactor Dimensionality Reduction to Detect Gene-Gene Interactions in Nasopharyngeal Carcinoma. International Journal of Molecular Sciences. 2014; 15(6):10724-10737. https://doi.org/10.3390/ijms150610724
Chicago/Turabian StyleLi, Chao-Feng, Fu-Tian Luo, Yi-Xin Zeng, and Wei-Hua Jia. 2014. "Weighted Risk Score-Based Multifactor Dimensionality Reduction to Detect Gene-Gene Interactions in Nasopharyngeal Carcinoma" International Journal of Molecular Sciences 15, no. 6: 10724-10737. https://doi.org/10.3390/ijms150610724




