Atomistic Monte Carlo Simulation of Lipid Membranes
Abstract
:1. Introduction
1.1. Membrane Simulations and the Time-Scaling Problem
1.2. Molecular Dynamics Simulation of Lipid Membranes
1.3. Monte Carlo Methods for Atomistic Simulation of Lipids and Other Biomolecules
2. Simulation Details and Analysis of DPPC Structure as Monomer and in the Bilayer
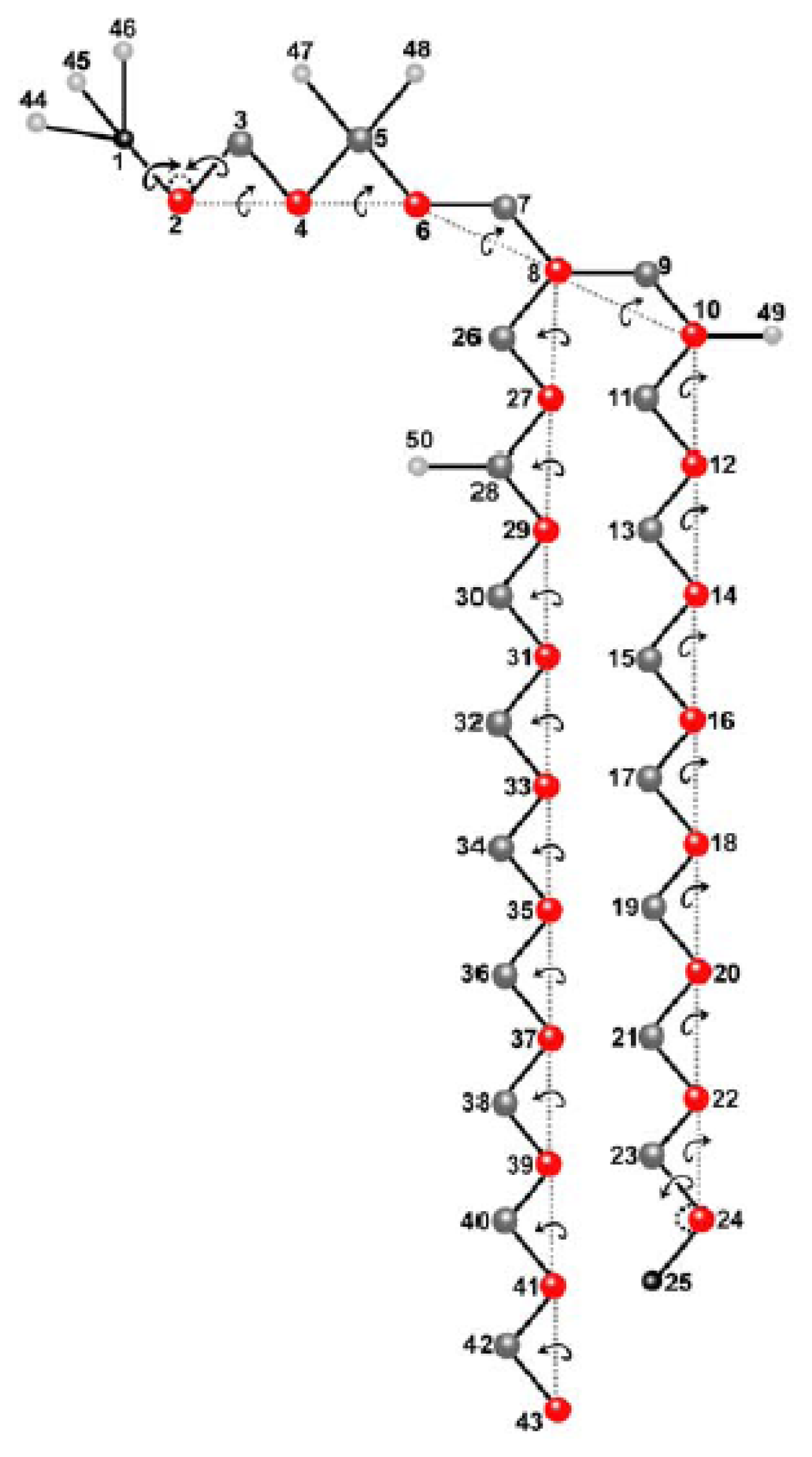
2.1. Molecular Model and Assignment of Moved and Dependent Variables
2.2. Start Configuration, Boundary Conditions, and Solvent Treatment
2.3. Evaluation of DPPC Conformations and Bilayer Structure
3. Results and Discussion
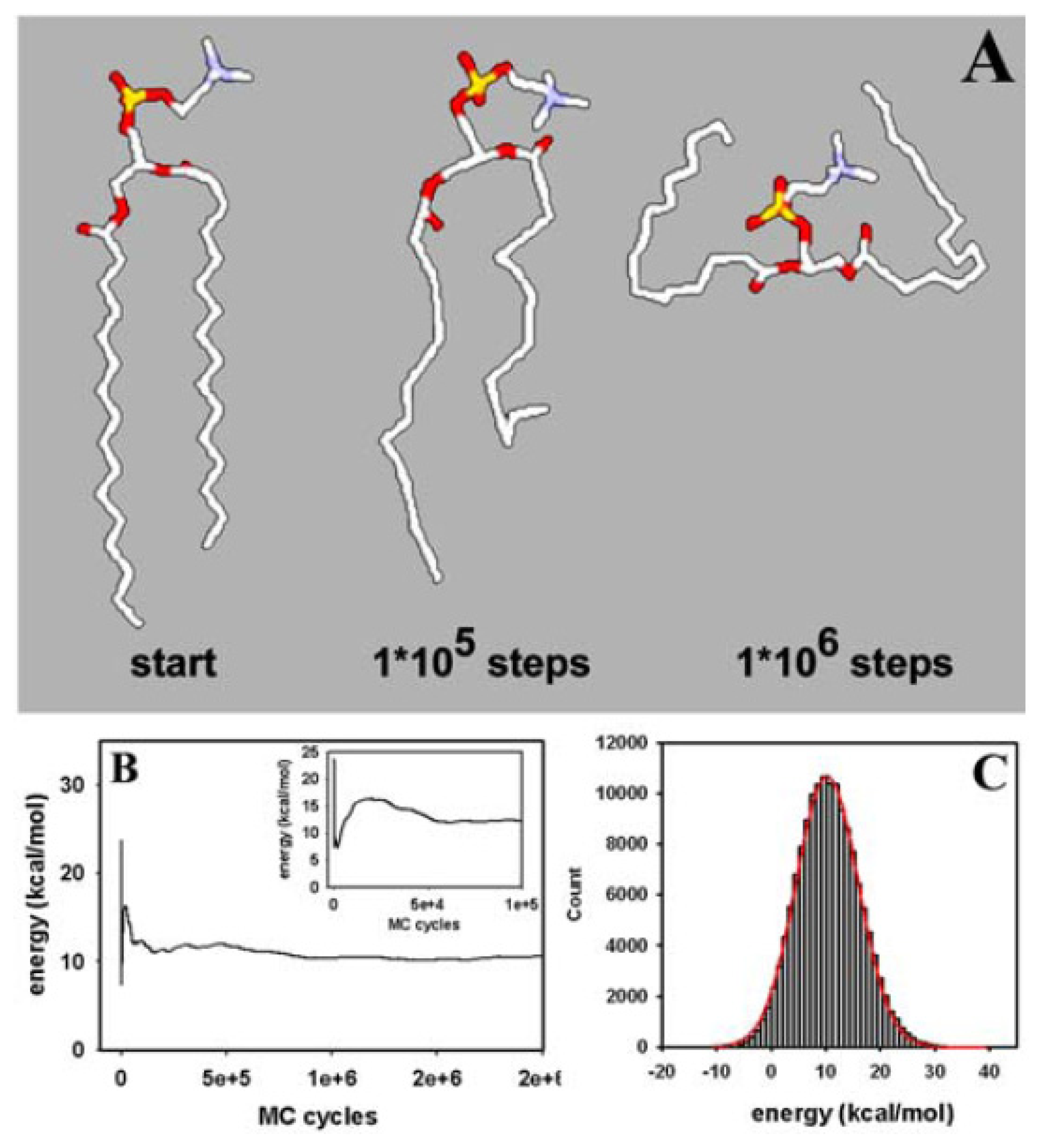
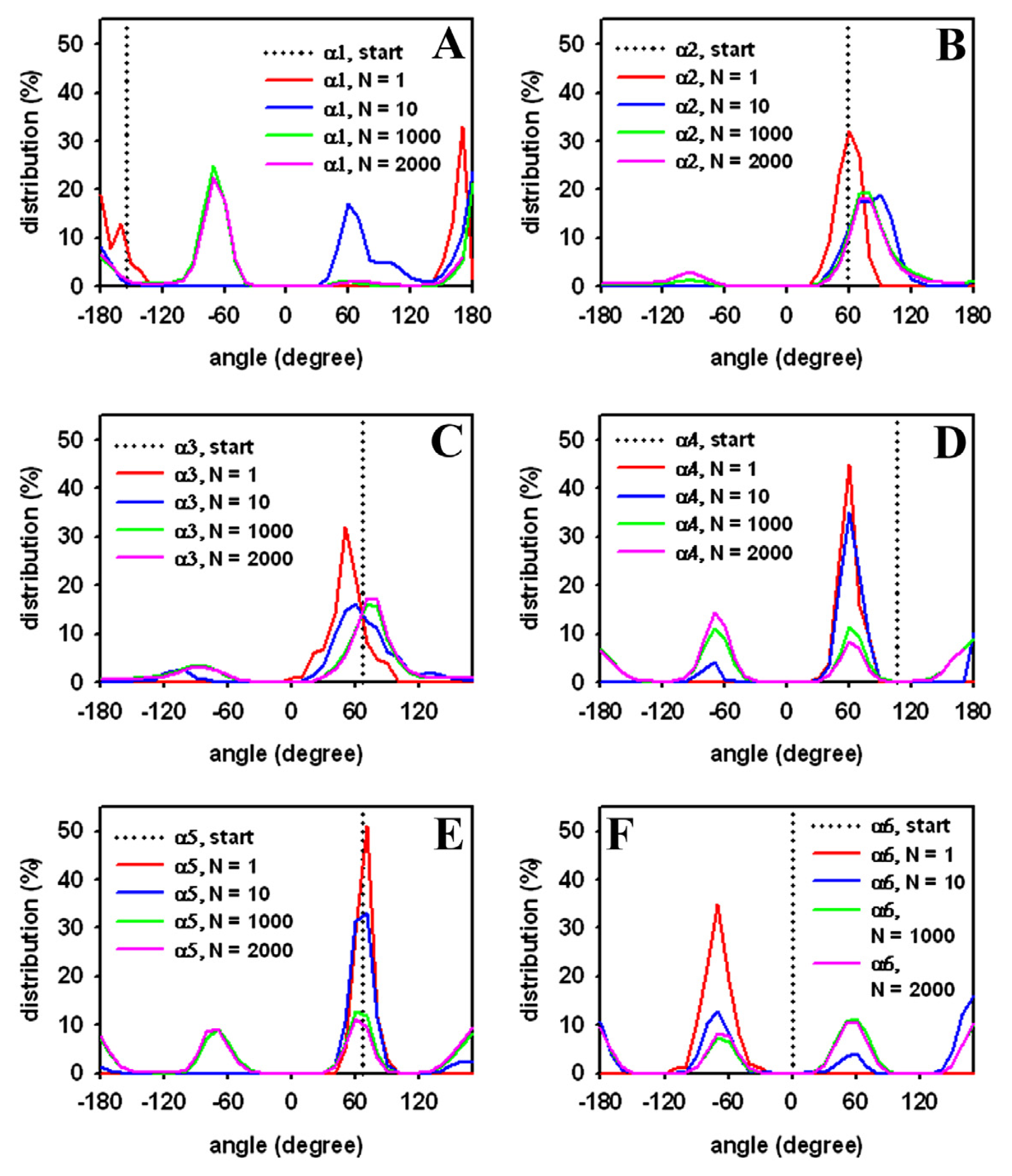
3.1. Efficient Monte Carlo Sampling of Conformations of a Single Lipid Molecule
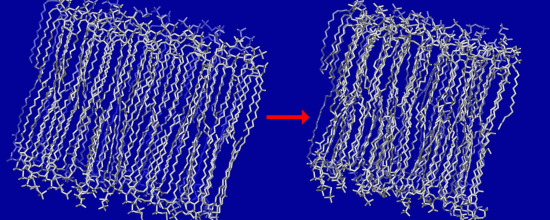
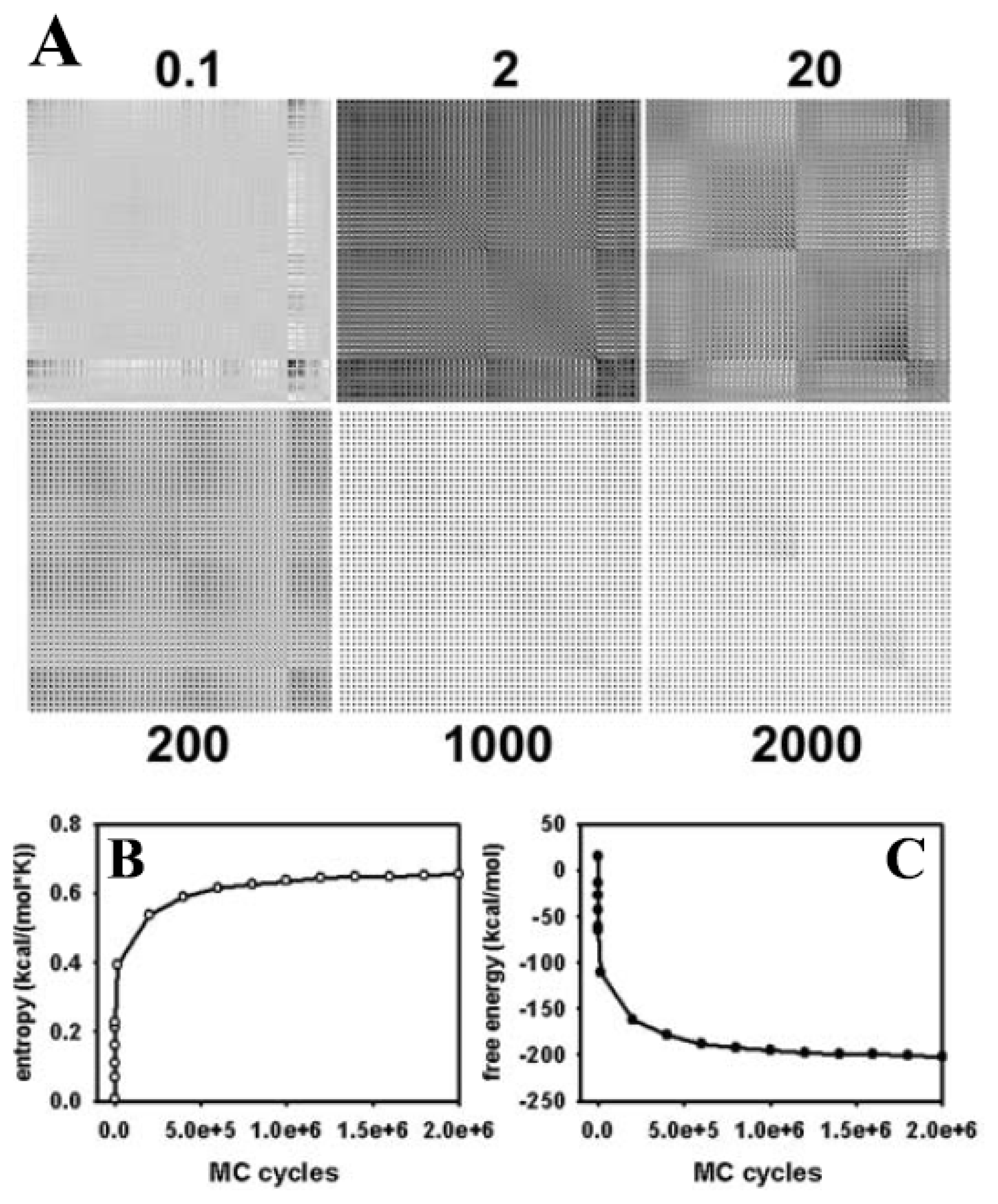
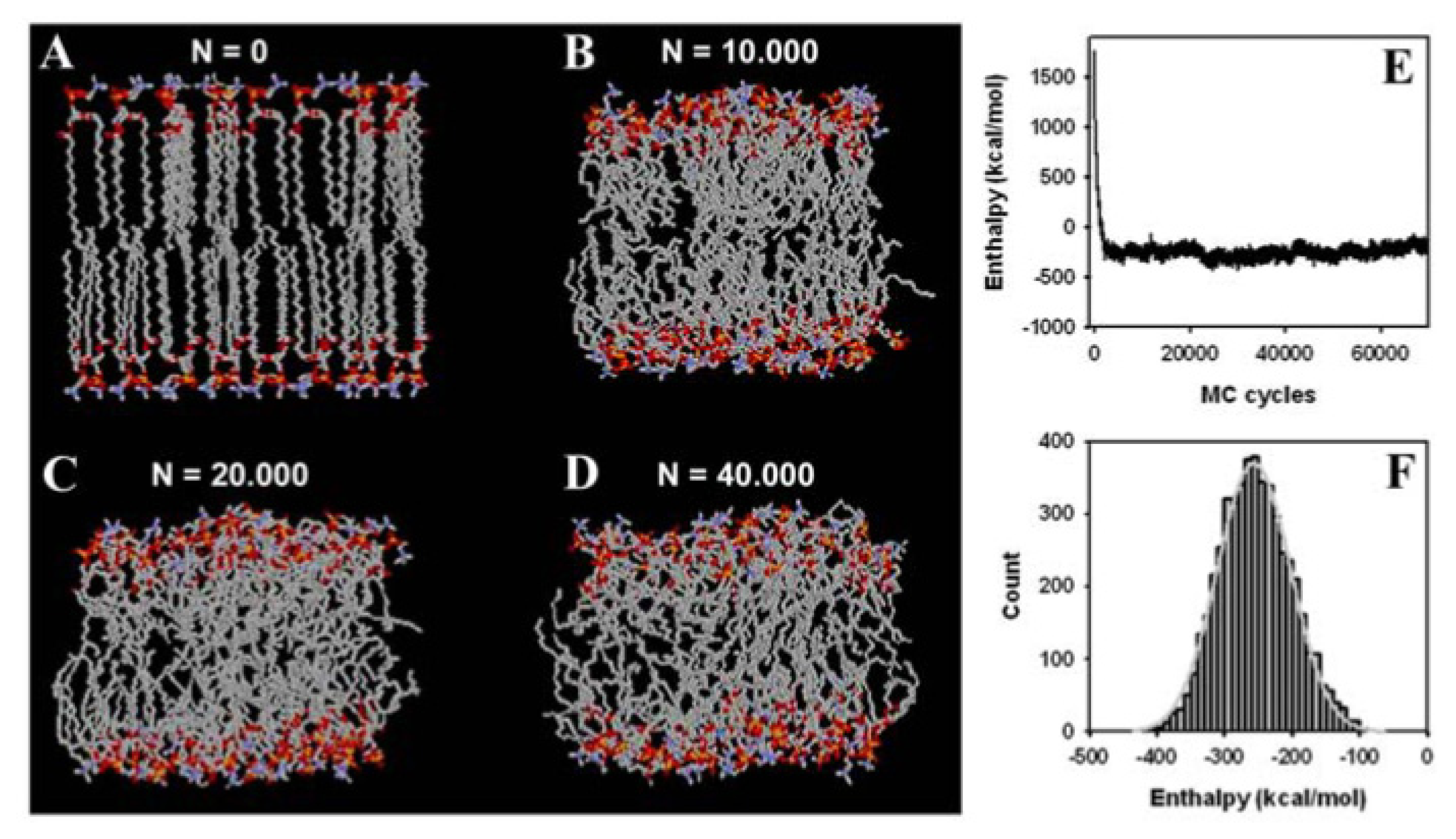
3.2. Large Conformational Moves Mediate the Transition from a Crystalline to a Fluid Bilayer
3.3. Rapid Transition of PC Headgroup Conformations by Local Move Set MC Sampling
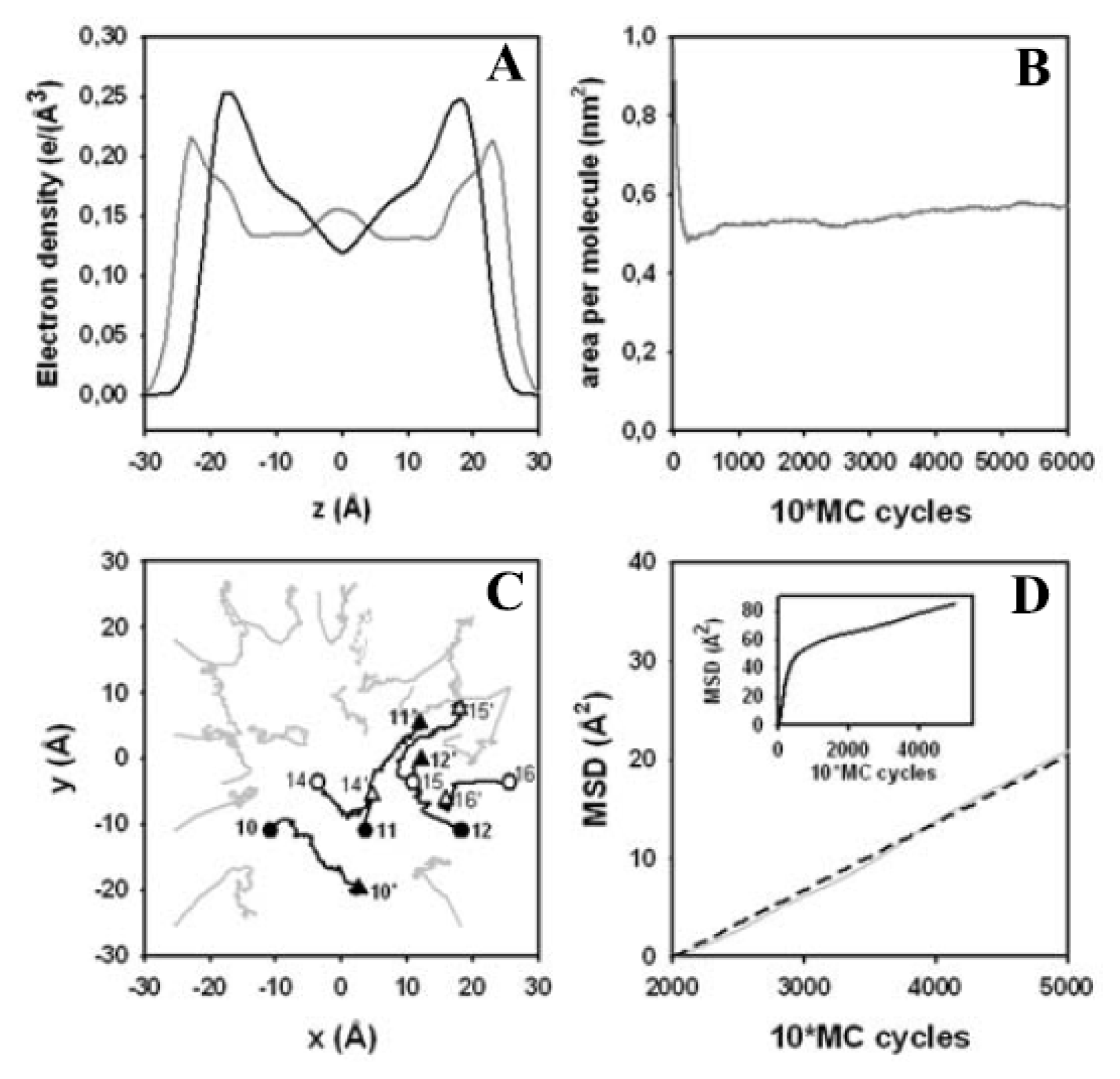
3.4. Electron Density Profile, Area per Lipid and Lateral Displacement of DPPC Molecules
3.5. Impact of the Implicit Solvent on Area per Lipid and Head Group Conformation
4. Summary and Future Improvements of the Presented Local MC Simulation Technique
5. Relationship between Atomistic MC Simulations and Other Membrane Modeling Techniques
5.1. Combination of Atomistic MC and MD Simulations
5.2. Atomistic MC Simulations in Multi-Scale Modeling of Lipid Membranes
Acknowledgments
Conflicts of Interest
References
- Baumgart, T.; Hess, S.T.; Webb, W.W. Imaging coexisting fluid domains in biomembrane models coupling curvature and line tension. Nature 2003, 425, 821–824. [Google Scholar]
- Korlach, J.; Schwille, P.; Webb, W.W.; Feigenson, G.W. Characterization of lipid bilayer phases by confocal microscopy and fluorescence correlation spectroscopy. Proc. Natl. Acad. Sci. USA 1999, 96, 8461–8466. [Google Scholar]
- Gliss, C.; Randel, O.; Casalta, H.; Sackmann, E.; Zorn, R.; Bayerl, T. Anisotropic motion of cholesterol in oriented DPPC bilayers studied by quasielastic neutron scattering: The liquid-ordered phase. Biophys. J 1999, 77, 331–340. [Google Scholar]
- Li, Y.; Ge, M.; Ciani, L.; Kuriakose, G.; Westover, E.J.; Dura, M.; Covey, D.F.; Freed, J.H.; Maxfield, F.R.; Lytton, J.; et al. Enrichment of endoplasmic reticulum with cholesterol inhibits sarcoplasmic-endoplasmic reticulum calcium ATPase-2b activity in parallel with increased order of membrane lipids: Implications for depletion of endoplasmic reticulum calcium stores and apoptosis in cholesterol-loaded macrophages. J. Biol. Chem 2004, 279, 37030–37039. [Google Scholar]
- Oradd, G.; Westerman, P.W.; Lindblom, G. Lateral diffusion coefficients of separate lipid species in a ternary raft-forming bilayer: A Pfg-NMR multinuclear study. Biophys. J 2005, 89, 315–320. [Google Scholar]
- Nagle, J.F.; Tristram-Nagle, S. Structure of lipid bilayers. Biochim. Biophys. Acta 2000, 1469, 159–195. [Google Scholar]
- Tieleman, D.P.; Marrink, S.J.; Berendsen, H.J. A computer perspective of membranes: Molecular dynamics studies of lipid bilayer systems. Biochim. Biophys. Acta 1997, 1331, 235–270. [Google Scholar]
- De Figueiredo, P.; Doody, A.; Polizotto, R.S.; Drecktrah, D.; Wood, S.; Banta, M.; Strang, M.S.; Brown, W.J. Inhibition of transferrin recycling and endosome tubulation by phospholipase A2 antagonists. J. Biol. Chem 2001, 276, 47361–47370. [Google Scholar]
- Sharma, D.K.; Brown, J.C.; Choudhury, A.; Peterson, T.E.; Holicky, E.; Marks, D.L.; Simari, R.; Parton, R.G.; Pagano, R.E. Selective stimulation of caveolar endocytosis by glycosphingolipids and cholesterol. Mol. Biol. Cell 2004, 15, 3114–3122. [Google Scholar]
- Goodwin, J.S.; Drake, K.R.; Remmert, C.L.; Kenworthy, A.K. Ras diffusion is sensitive to plasma membrane viscosity. Biophys. J 2005, 89, 1398–1410. [Google Scholar]
- Mayor, S.; Maxfield, F.R. Insolubility and redistribution of GPI-anchored proteins at the cell surface after detergent treatment. Mol. Biol. Cell 1995, 6, 929–944. [Google Scholar]
- Fujimoto, L.M.; Roth, R.; Heuser, J.E.; Schmid, S.L. Actin assembly plays a variable, but not obligatory role in receptor-mediated endocytosis in mammalian cells. Traffic 2000, 1, 161–171. [Google Scholar]
- Ganguly, S.; Pucadyil, T.J.; Chattopadhyay, A. Actin cytoskeleton-dependent dynamics of the human serotonin(1A) receptor correlates with receptor signaling. Biophys. J 2008, 95, 451–463. [Google Scholar]
- Van Rheenen, J.; Jalink, K. Agonist-induced PIP(2) hydrolysis inhibits cortical actin dynamics: Regulation at a global but not at a micrometer scale. Mol. Biol. Cell 2002, 13, 3257–3267. [Google Scholar]
- Kwik, J.; Boyle, S.; Fooksman, D.; Margolis, L.; Sheetz, M.P.; Edidin, M. Membrane cholesterol, lateral mobility, and the phosphatidylinositol 4,5-bisphosphate-dependent organization of cell actin. Proc. Natl. Acad. Sci. USA 2003, 100, 13964–13969. [Google Scholar]
- Boucrot, E.; Saffarian, S.; Massol, R.; Kirchhausen, T.; Ehrlich, M. Role of lipids and actin in the formation of clathrin-coated pits. Exp. Cell Res 2006, 312, 4036–4048. [Google Scholar]
- Mueller, V.; Ringemann, C.; Honigmann, A.; Schwarzmann, G.; Medda, R.; Leutenegger, M.; Polyakova, S.; Belov, V.N.; Hell, S.W.; Eggeling, C. STED nanoscopy reveals molecular details of cholesterol- and cytoskeleton-modulated lipid interactions in living cells. Biophys. J 2011, 101, 1651–1660. [Google Scholar]
- Kultti, A.; Rilla, K.; Tiihonen, R.; Spicer, A.P.; Tammi, R.H.; Tammi, M. Hyaluronan synthesis induces microvillus-like cell surface protrusions. J. Biol. Chem 2006, 281, 15821–15828. [Google Scholar]
- Pomorski, T.; Holthuis, J.C.; Herrmann, A.; van Meer, G. Tracking down lipid flippases and their biological functions. J. Cell Sci 2004, 117, 805–813. [Google Scholar]
- Imparato, A.; Shillcock, J.C.; Lipowsky, R. Lateral and transverse diffusion in two-component bilayer membranes. Eur. Phys. J. E 2003, 11, 21–28. [Google Scholar]
- Jülicher, F.; Lipowsky, R. Shape transformations of vesicles with intramembrane domains. Phys. Rev. E 1996, 53, 2670–2683. [Google Scholar]
- Zuckermann, M.J.; Ipsen, J.H.; Miao, L.; Mouritsen, O.G.; Nielsen, M.; Polson, J.; Thewalt, J.; Vattulainen, I.; Zhu, H. Modeling lipid-sterol bilayers: Applications to structural evolution, lateral diffusion, and rafts. Methods Enzymol 2004, 383, 198–229. [Google Scholar]
- Ehrig, J.; Petrov, E.P.; Schwille, P. Near-critical fluctuations and cytoskeleton-assisted phase separation lead to subdiffusion in cell membranes. Biophys. J 2011, 100, 80–89. [Google Scholar]
- Roark, M.; Feller, S.E. Molecular dynamics simulation study of correlated motions in phospholipid bilayer membranes. J. Phys. Chem. B 2009, 113, 13229–13234. [Google Scholar]
- Lindahl, E.; Edholm, O. Mesoscopic undulations and thickness fluctuations in lipid bilayers from molecular dynamics simulations. Biophys. J 2000, 79, 426–433. [Google Scholar]
- Falck, E.; Patra, M.; Karttunen, M.; Hyvönen, M.T.; Vattulainen, I. Impact of cholesterol on voids in phospholipid membranes. J. Chem. Phys 2004, 121, 12676–12689. [Google Scholar]
- Böckmann, R.A.; Hac, A.; Heimburg, T.; Grubmüller, H. Effect of sodium chloride on a lipid bilayer. Biophys. J 2003, 85, 1647–1655. [Google Scholar]
- Choubey, A.; Kalia, R.K.; Malmstadt, N.; Nakano, A.; Vashishta, P. Cholesterol translocation in a phospholipid membrane. Biophys. J 2013, 104, 2429–2436. [Google Scholar]
- Voter, A.F. Parallel replica method for dynamics of infrequent events. Phys. Rev. B 1998, 57, 13985–13988. [Google Scholar]
- Hub, J.S.; Aponte-Santamaría, C.; Grubmüller, H.; de Groot, B.L. Voltage-regulated water flux through aquaporin channels in silico. Biophys. J 2010, 99, L97–L99. [Google Scholar]
- Pöyry, S.; Cramariuc, O.; Postila, P.A.; Kaszuba, K.; Sarewicz, M.; Osyczka, A.; Vattulainen, I.; Róg, T. Atomistic simulations indicate cardiolipin to have an integral role in the structure of the cytochrome bc1 complex. Biochim. Biophys. Acta 2013, 1827, 769–778. [Google Scholar]
- Hölttä-Vuori, M.; Uronen, R.L.; Repakova, J.; Salonen, E.; Vattulainen, I.; Panula, P.; Li, Z.; Bittman, R.; Ikonen, E. BODIPY-cholesterol: A new tool to visualize sterol trafficking in living cells and organisms. Traffic 2008, 9, 1839–1849. [Google Scholar]
- Repáková, J.; Holopainen, J.M.; Karttunen, M.; Vattulainen, I. Influence of pyrene-labeling on fluid lipid membranes. J. Phys. Chem. B 2006, 110, 15403–15410. [Google Scholar]
- Niemelä, P.S.; Miettinen, M.S.; Monticelli, L.; Hammaren, H.; Bjelkmar, P.; Murtola, T.; Lindahl, E.; Vattulainen, I. Membrane proteins diffuse as dynamic complexes with lipids. J. Am. Chem. Soc 2010, 132, 7574–7575. [Google Scholar]
- Barucha-Kraszewska, J.; Kraszewski, S.; Jurkiewicz, P.; Ramseyer, C.; Hof, M. Numerical studies of the membrane fluorescent dyes dynamics in ground and excited states. Biochim. Biophys. Acta 2010, 1798, 1724–1734. [Google Scholar]
- Shaw, D.E.; Maragakis, P.; Lindorff-Larsen, K.; Piana, S.; Dror, R.O.; Eastwood, M.P.; Bank, J.A.; Jumper, J.M.; Salmon, J.K.; Yibing, S.; et al. Atomic-level characterization of the structural dynamics of proteins. Science 2010, 330, 341–346. [Google Scholar]
- Jensen, M.Ø.; Jogini, V.; Borhani, D.W.; Leffler, A.E.; Dror, R.O.; Shaw, D.E. Mechanism of voltage gating in potassium channels. Science 2012, 336, 229–233. [Google Scholar]
- Arkhipov, A.; Shan, Y.; Das, R.; Endres, N.F.; Eastwood, M.P.; Wemmer, D.E.; Kuriyan, J.; Shaw, D.E. Architecture and membrane interactions of the EGF receptor. Cell 2013, 152, 557–569. [Google Scholar]
- Periole, X.; Marrink, S.J. The Martini coarse-grained force field. Methods Mol. Biol 2013, 924, 533–565. [Google Scholar]
- Shillcock, J.C. Vesicles and vesicle fusion: Coarse-grained simulations. Methods Mol. Biol 2013, 924, 659–697. [Google Scholar]
- Bennun, S.V.; Hoopes, M.I.; Xing, C.; Faller, R. Coarse-grained modeling of lipids. Chem. Phys. Lipids 2009, 159, 59–66. [Google Scholar]
- Vainio, S.; Jansen, M.; Koivusalo, M.; Rog, T.; Karttunen, M.; Vattulainen, I.; Ikonen, E. Significance of sterol structural specificity. Desmosterol cannot replace cholesterol in lipid rafts. J. Biol. Chem 2006, 281, 348–355. [Google Scholar]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, E. Equation of state calculations by fast computing machines. J. Chem. Phys 1953, 21, 1087–1092. [Google Scholar]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids; Oxford University Press: Oxford, UK, 1987. [Google Scholar]
- Frenkel, D. Introduction to Monte Carlo Methods. In Computational Soft Matter: From Synthetic Polymers to Proteins; Attig, N., Binder, K., Grubmüller, H., Kremer, K., Eds.; NIC Series; Lecture Notes: Jülich, Germany, 2004; Volume 23, pp. 29–60. [Google Scholar]
- Mezei, M.; Swaminathan, S.; Beveridge, D.L. Convergence characteristics of Monte Carlo–Metropolis computer simulations on liquid water. J. Chem. Phys 1979, 71, 3366–3373. [Google Scholar]
- Mezei, M.; Beveridge, D.L. Monte Carlo studies of the structure of dilute aqueous sclutions of Li+, Na+, K+, F−, and Cl−. J. Chem. Phys 1981, 74, 6902–6910. [Google Scholar]
- Rossky, P.J.; Doll, J.D.; Friedman, H.L. Brownian dynamics as smart Monte Carlo simulation. J. Chem. Phys 1978, 69, 4628–4633. [Google Scholar]
- Pangali, C.; Rao, M.; Berne, B.J. On a novel Monte Carlo scheme for simulating water and aqueous solutions. Chem. Phys. Lett 1978, 55, 413–417. [Google Scholar]
- Owicki, J.C.; Scheraga, H.A. Preferential sampling near solutes in Monte Carlo calculations on dilute solutions. Chem. Phys. Lett 1977, 47, 600–602. [Google Scholar]
- Mezei, M. Virial-bias Monte Carlo methods. Efficient sampling in the (T,P,N) ensemble. Mol. Phys 1983, 48, 1075–1082. [Google Scholar]
- Mezei, M.; Bencsath, K.A.; Goldman, S.; Singh, S. The detailed balance energy-scaled displacement Monte Carlo algorithm. Mol. Simul 1987, 1, 87–93. [Google Scholar]
- Mezei, M. Grand-canonical ensemble Monte Carlo study of dense liquids: Lennard-Jones, soft spheres and water. Mol. Phys 1987, 61, 1207–1208. [Google Scholar]
- Mitsutake, A.; Sugita, Y.; Okamoto, Y. Generalized-ensemble algorithms for molecular simulations of biopolymers. Biopolymers 2001, 60, 96–123. [Google Scholar]
- Zuckermann, D.M. Equilibrium sampling in biomolecular simulations. Annu. Rev. Biophys 2011, 40, 41–62. [Google Scholar]
- Mezei, M. On the Potential of Monte Carlo Methods for Simulating Macromolecular Assemblies. In Computational Methods for Macromolecules: Challenges and Applications, Third International Workshop for Methods for Macromolecular Modelling Conference Proceedings; Springer Verlag: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Scott, H.L. Modeling the lipid component of membranes. Curr. Opin. Struct. Biol 2002, 12, 495–502. [Google Scholar]
- Siepmann, J.I.; Frenkel, D. Conflgurational bias Monte Carlo: A new sampling scheme for flexible chains. Mol. Phys 1992, 75, 59–70. [Google Scholar]
- Vacatello, M.; Avitabile, G.; Corradini, P.; Tuzi, A. A computer model of molecular arrangement in a n-paraffinic liquid. J. Chem. Phys 1980, 73, 548–552. [Google Scholar]
- Boyd, R.H. An off-lattice constant-pressure simulation of liquid polymethylene. Macromolecules 1989, 22, 2477–2481. [Google Scholar]
- Uhlherr, A.; Leak, S.J.; Adam, N.E.; Nyberg, P.E.; Doxastakis, M.; Mavrantzas, V.G.; Theodorou, D.N. Large scale atomistic polymer simulations using Monte Carlo methods for parallel vector processors. Comput. Phys. Commun 2002, 144, 1–22. [Google Scholar]
- Karayiannis, N.C.; Mavrantzas, V.G. Advanced Monte Carlo Methods for the Atomistic Simulation of Polymers with a Linear or a Non-Linear Molecular Architecture. In Multiscale Modelling of Polymer Properties; Laso, M., Perpéte, E.A., Eds.; Elsevier: Toronto, ON, Canada, 2006; pp. 31–67. [Google Scholar]
- Mavrantzas, V.G.; Theodorou, D.N. Atomistic simulation of polymer elasticity: Calculation of the free energy of an oriented polymer melt. Macromolecules 1998, 31, 6310–6332. [Google Scholar]
- Scott, H.L.; Jacobsson, E.; Subramanian, S. Simulations of lipid membranes with atomic resolution. Comput. Phys 1998, 12, 328–334. [Google Scholar]
- Chiu, S.W.; Clark, M.M.; Jakobsson, E.J.; Subramanian, S.; Scott, H.L. Application of combined Monte Carlo and Molecular Dynamics method to simulation of dipalmitoylphosphatidylcholine lipid bilayer. J. Comput. Chem 1999, 20, 1153–1164. [Google Scholar]
- Jedlovszky, P.; Mezei, M. Grand canonical ensemble Monte Carlo simulation of a lipid bilayer using extension biased rotations. J. Chem. Phys 1999, 111, 10770–10773. [Google Scholar]
- Jedlovszky, P.; Mezei, M. Orientational order of the water molecules across a fully hydrated DMPC bilayer: A Monte Carlo simulation study. J. Phys. Chem. B 2001, 105, 3614–3623. [Google Scholar]
- Jedlovszky, P.; Mezei, M. Effect of cholesterol on the properties of phospholipid membranes. 2. Free energy profile of small molecules. J. Phys. Chem. B 2003, 107, 5322–5332. [Google Scholar]
- Alinchenko, M.G.; Voloshin, V.P.; Medvedev, N.N.; Mezei, M.; Pártay, L.; Jedlovszky, P. Effect of cholesterol on the properties of phospholipid membranes. 4. Interatomic voids. J. Phys. Chem. B 2005, 109, 16490–16502. [Google Scholar]
- Hoffmann, D.; Knapp, E.W. Polypeptide folding with off-lattice Monte Carlo dynamics: The method. Eur. Biophys. J 1996, 24, 387–403. [Google Scholar]
- Go, N.; Scheraga, H.A. Ring closure and local conformational deformations of chain molecules. Macromolecules 1970, 3, 178–187. [Google Scholar]
- Manocha, D.; Canny, J.F. Efficient inverse kinematics for general 6R manipulators. IEEE Trans. Robot. Autom 1994, 10, 648–657. [Google Scholar]
- Coutsias, E.A.; Seok, C.; Jacobson, M.P.; Dill, K.A. A kinematic view of loop closure. J. Comput. Chem 2004, 25, 510–528. [Google Scholar]
- Wu, M.G.; Deem, M.W. Analytical rebridging Monte Carlo: Application to cis/trans isomerization in proline-containing. J. Chem. Phys 1999, 111, 6625–6632. [Google Scholar]
- Dinner, A.R. Local deformations of polymers with nonplanar rigid main-chain internal coordinates. J. Comp. Chem 2000, 21, 1132–1144. [Google Scholar]
- Dodd, L.R.; Boone, T.D.; Theodorou, D.N. A concerted rotation algorithm for atomistic Monte Carlo simulation of polymer melts and glasses. Mol. Phys 1993, 78, 961–996. [Google Scholar]
- Hoffmann, D.; Knapp, E.W. Folding pathways of a helix-turn-helix model protein. J. Phys. Chem. B 1997, 101, 6734–6740. [Google Scholar]
- Ulmschneider, J.P.; Jorgensen, W.L. Monte Carlo backbone sampling for polypeptides with variable bond and dihedral angles using concerted rotations and a Gaussian bias. J. Chem. Phys 2003, 118, 4261–4271. [Google Scholar]
- Mezei, M. Efficient Monte Carlo sampling for long molecular chains using local moves, tested on a solvated lipid bilayer. J. Chem. Phys 2003, 118, 3874–3879. [Google Scholar]
- Hu, J.; Ma, A.; Dinner, A.R. Monte Carlo simulations of biomolecules: The MC module in CHARMM. J. Comput. Chem 2006, 27, 203–216. [Google Scholar]
- Pant, K.P.V.; Theodorou, D.N. Variable connectivity method for the atomistic Monte Carlo simulation of polydisperse poymer melts. Macromolecules 1995, 28, 7224–7234. [Google Scholar]
- Mavrantzas, V.G.; Boone, T.D.; Zervopoulou, E.; Theodorou, D.N. End-bridging Monte Carlo: A fast algorithm for atomistic simulation of condensed phases og long polymer chains. Macromolecules 1999, 32, 5072–5096. [Google Scholar]
- Uhlherr, A. Monte Carlo conformational sampling of the internal degrees of freedom of chain molecules. Macromolecules 2000, 33, 1351–1360. [Google Scholar]
- Uhlherr, A.; Mavrantzas, V.G.; Doxastakis, M.; Theodorou, D.N. Directed bridging for fast atomistic Monte Carlo simulations of bulk polymers. Macromolecules 2001, 34, 8554–8568. [Google Scholar]
- Bruccoleri, R.E.; Karplus, M. Chain closure with bond angle variations. Macromolecules 1985, 18, 2767–2773. [Google Scholar]
- Ulmschneider, J.P.; Ulmschneider, M.B.; di Nola, A. Monte Carlo vs molecular dynamics for all-atom polypeptide folding simulations. J. Phys. Chem. B 2006, 110, 16733–16742. [Google Scholar]
- Ulmschneider, J.P.; Jorgensen, W.L. Polypeptide folding using Monte Carlo sampling, concerted rotation, and continuum solvation. J. Am. Chem. Soc 2004, 126, 1849–1857. [Google Scholar]
- Betancourt, M.R. Efficient Monte Carlo trial moves for polypeptide simulations. J. Chem. Phys 2005, 123, 174905:1–174905:7. [Google Scholar]
- Okamoto, Y. Generalized-ensemble algorithms: Enhanced sampling techniques for Monte Carlo and molecular dynamics simulations. J. Mol. Graph. Model 2004, 22, 425–439. [Google Scholar]
- Neyts, E.C.; Bogaerts, A. Combining molecular dynamics with Monte Carlo simulations: Implementations and applications. Theor. Chem. Acc 2013, 132, 1320. [Google Scholar] [CrossRef]
- Vitalis, A.; Pappu, R.V. Methods for Monte Carlo simulations of biomacromolecules. Annu. Rep. Comput. Chem 2009, 5, 49–76. [Google Scholar]
- Bottaro, S.; Boomsma, W.; Johansson, K.E.; Andreetta, C.; Hamelryck, T.; Ferkinghoff-Borg, J. Subtle Monte Carlo updates in dense molecular systems. J. Chem. Theory Comput 2012, 8, 695–702. [Google Scholar]
- Boomsma, W.; Frellsen, J.; Harder, T.; Bottaro, S.; Johansson, K.E.; Tian, P.; Stovgaard, K.; Andreetta, C.; Olsson, S.; Valentin, J.B.; et al. PHAISTOS: A framework for Markov Chain Monte Carlo simulation and inference of protein structure. J. Comput. Chem 2013, 34, 1697–1705. [Google Scholar]
- Sklenar, H.; Wüstner, D.; Rohs, R. Using internal and collective variables in Monte Carlo simulations of nucleic acid structures: Chain breakage/closure algorithm and associated Jacobians. J. Comput. Chem 2006, 27, 309–315. [Google Scholar]
- Rohs, R.; Bloch, I.; Sklenar, H.; Shakked, Z. Molecular flexibility in ab initio drug docking to DNA: Binding-site and binding-mode transitions in all-atom Monte Carlo simulations. Nucleic Acids Res 2005, 33, 7048–7057. [Google Scholar]
- Rohs, R.; Sklenar, H.; Shakked, Z. Structural and energetic origins of sequence-specific DNA bending: Monte Carlo simulations of papillomavirus E2-DNA binding sites. Structure 2005, 13, 1499–1509. [Google Scholar]
- Minary, P.; Levitt, M. Conformational optimization with natural degrees of freedom: A novel stochastic chain closure algorithm. J. Comput. Biol 2010, 17, 993–1010. [Google Scholar]
- Sim, A.Y.L.; Minary, P.; Levitt, M. Modeling nucleic acids. Curr. Opin. Struct. Biol 2012, 22, 273–278. [Google Scholar]
- Smondyrev, A.M.; Berkowitz, M.L. United atom force field for phospholipid membranes: Constant pressure molecular dynamics simulation of dipalmitoylphosphatidylcholine/water system. J. Comput. Chem 1999, 20, 531–545. [Google Scholar]
- Ryckaert, J.-P.; Bellemans, A. Molecular dynamics of liquid n-butane near its boiling point. Chem. Phys. Lett 1975, 30, 123–125. [Google Scholar]
- Berger, O.; Edholm, O.; Jähnig, F. Molecular dynamics simulations of a fluid bilayer of dipalmitoylphosphatidylcholine at full hydration, constant pressure, and constant temperature. Biophys. J 1997, 72, 2002–2013. [Google Scholar]
- Manousiouthakis, V.I.; Deem, M.W. Strict detailed balance is unnecessary in Monte Carlo simulation. J. Chem. Phys 1999, 110, 2753–2756. [Google Scholar]
- Vanderkooi, G. Multibilayer structure of dimyristoylphosphatidylcholine dihydrate as determined by energy minimization. Biochemistry 1991, 30, 10760–10768. [Google Scholar]
- Cornell, W.D.; Cieplak, P.; Bayly, C.I.; Gould, I.R.; Merz, K.M., Jr.; Ferguson, D.M.; Spellmeyer, D.C.; Fox, T.; Caldwell, J.W.; Kollman, P.A. A second generation force field for the simulation of proteins, nucleic acids, and organic molecules. J. Am. Chem. Soc 1995, 117, 5179–5197. [Google Scholar]
- Hingerty, B.E.; Ritchie, R.H.; Ferrell, T.L.; Turner, J.E. Dielectric effects in biopolymers: The theory of ionic saturation revisited. Biopolymers 1985, 24, 427–439. [Google Scholar]
- Lavery, R.; Sklenar, H.; Zakrzewska, K.; Pullman, B. The flexibility of the nucleic acids: (II). The calculation of internal energy and applications to mononucleotide repeat DNA. J. Biomol. Struct. Dyn 1986, 3, 989–1014. [Google Scholar]
- Schlitter, J. Estimation of absolute and relative entropies of macromolecules using the covariance matrix. Chem. Phys. Lett 1993, 215, 617–621. [Google Scholar]
- Andricioaei, I.; Karplus, M. On the calculation of entropy from covariance matrices of the atomic fluctuations. J. Chem. Phys 2001, 115, 6289–62812. [Google Scholar]
- Altman, B.; Hughes, C.; Gerstein, M.B. Methods for displaying macromolecular structural uncertainty: Application to the globins. J. Mol. Graph 1995, 13, 142–152. [Google Scholar]
- Tu, K.; Tobias, J.; Klein, M.L. Constant pressure and temperature molecular dynamics simulation of a fully hydrated liquid crystal phase dipalmitoylphosphatidylcholine bilayer. Biophys. J 1995, 69, 2558–2562. [Google Scholar]
- Egberts, E.; Marrink, S.J.; Berendsen, H.J. Molecular dynamics simulation of a phospholipid membrane. Eur. Biophys. J 1994, 22, 423–436. [Google Scholar]
- Greiner, W.; Neise, L.; Stöcker, H. Thermodynamik und Statistische Mechanik; Verlag Harri Deutsch: Frankfurt, Germany, 1993; pp. 297–315. [Google Scholar]
- Edholm, O.; Berendsen, H.J. Entropy estimation from simulation of non-diffusive systems. Mol. Phys 1984, 51, 1011–1028. [Google Scholar]
- Moore, P.B.; Lopez, C.F.; Klein, M.L. Dynamical properties of a hydrated lipid bilayer from a multinanosecond molecular dynamics simulation. Biophys. J 2001, 81, 2484–2494. [Google Scholar]
- Tanford, C. The Hydrophobic Effect. Formation of Micells and Biological Membranes; Wiley: New York, NY, USA, 1980. [Google Scholar]
- Gill, S.J.; Wadsö, I. An equation of state describing hydrophobic interactions. Proc. Natl. Acad. Sci. USA 1976, 73, 2955–2958. [Google Scholar]
- Grabitz, P.; Ivanova, V.P.; Heimburg, T. Relaxation kinetics of lipid membranes and its relation to the heat capacity. Biophys. J 2002, 82, 299–309. [Google Scholar]
- Blume, A. Apparent molar heat capacities of phospholipids in aqueous dispersion. Effects of chain length and head group structure. Biochemistry 1983, 22, 5436–5442. [Google Scholar]
- Wiener, M.C.; Suter, R.M.; Nagle, J.F. Structure of the fully hydrated gel phase of dipalmitoylphosphatidylcholine. Biophys. J 1989, 55, 315–325. [Google Scholar]
- Tu, K.; Tobias, J.; Blasie, K.; Klein, M.L. Molecular dynamics investigation of the structure of a fully hydrated gel-phase dipalmitoylphosphatidylcholine bilayer. Biophys. J 1996, 70, 595–608. [Google Scholar]
- Smondyrev, A.M.; Berkowitz, M.L. Molecular dynamics simulation of DPPC bilayer in DMSO. Biophys. J 1999, 76, 2472–2478. [Google Scholar]
- Seelig, J. Deuterium magnetic resonance: Theory and application to lipid membranes. Q. Rev. Biophys 1977, 10, 353–418. [Google Scholar]
- Lindahl, E.; Edholm, O. Spatial and energetic-entropic decomposition of surface tension in lipid bilayers from molecular dynamics simulations. J. Chem. Phys 2000, 113, 3882–3893. [Google Scholar]
- Ulmschneider, J.P.; Ulmschneider, M.B.; di Nola, A. Monte Carlo folding of trans-membrane helical peptides in an implicit generalized born membrane. Proteins 2007, 69, 297–308. [Google Scholar]
- Patra, M.; Karttunen, M.; Hyvönen, M.T.; Falck, E.; Lindqvist, P.; Vattulainen, I. Molecular dynamics simulations of lipid bilayers: Major artifacts due to truncating electrostatic interactions. Biophys. J 2003, 84, 3636–3645. [Google Scholar]
- Feller, S.E.; Pastor, R.W. On simulating lipid bilayers with an applied surface tension: Periodic boundary conditions and undulations. Biophys. J 1996, 71, 1350–1355. [Google Scholar]
- Anézo, C.; de Vries, A.H.; Höltje, H.D.; Tieleman, D.P.; Marrink, S.J. Methodological issues in lipid bilayer simulations. J. Phys. Chem. B 2003, 107, 9424–9433. [Google Scholar]
- Poger, D.; Mark, A.E. Lipid bilayers: The effect of force field on ordering and dynamics. J. Chem. Theory Comput 2012, 8, 4807–4817. [Google Scholar]
- Smondyrev, A.M.; Berkowitz, M.L. Structure of dipalmitoylphosphatidylcholine/cholesterol bilayer at low and high cholesterol concentrations: Molecular dynamics simulation. Biophys. J 1999, 77, 2075–2089. [Google Scholar]
- Sklenar, H.; Eisenhaber, F.; Poncin, M.; Lavery, R. Including solvent and counterion effects in the force field integrated electrostatic approach (FIESTA). In Theoretical Biochemistry and Molecular Biophysics; Beveridge, D.L., Lavery, R., Eds.; Adenine Press: Schenectady, NY, USA, 1990; pp. 317–335. [Google Scholar]
- Larsson, P.; Lindahl, E. A high-performance parallel-generalized born implementation enabled by tabulated interaction rescaling. J. Comput. Chem 2010, 31, 2593–2600. [Google Scholar]
- Chiu, S.W.; Pandit, S.A.; Scott, H.L.; Jakobsson, E. An improved united atom force field for simulation of mixed lipid bilayers. J. Phys. Chem. B 2009, 113, 2748–2763. [Google Scholar]
- Piggot, T.J.; Pineiro, Á.; Khalid, S. Molecular dynamics simulations of phosphatidylcholine membranes: A comparative force field study. J. Chem.Theory Comput 2012, 8, 4593–4609. [Google Scholar]
- Skjevik, Å.A.; Madej, B.D.; Walker, R.C.; Teigen, K. LIPID11: A modular framework for lipid simulations using amber. J. Phys. Chem. B 2012, 116, 11124–11136. [Google Scholar]
- Wang, Z.J.; Deserno, M. A systematically coarse-grained solvent-free model for quantitative phospholipid bilayer simulations. J. Phys. Chem. B 2010, 114, 11207–11220. [Google Scholar]
- Kofke, D.A. On the acceptance probability of replica-exchange Monte Carlo trials. J. Chem. Phys 2002, 117, 6911–6914. [Google Scholar]
- Gross, J.; Janke, W.; Bachmann, M. Massively parallelized replica-exchange simulations of polymers on GPUs. Comput. Phys. Commun 2011, 182, 1638–1644. [Google Scholar]
- Pawley, G.S.; Bowler, K.C.; Kenway, R.D.; Wallace, D.J. Concurrency and parallelism in MC and MD simulations in physics. Comput. Phys. Commun 1985, 37, 251–260. [Google Scholar]
- Anderson, J.A.; Jankowski, E.; Grubb, T.L.; Engel, M.; Glotzer, S.C. Massively parallel Monte Carlo for many-particle simulations on GPUs. J. Comput. Phys 2013, 254, 27–38. [Google Scholar]
- Pronk, S.; Páll, S.; Schulz, R.; Larsson, P.; Bjelkmar, P.; Apostolov, R.; Shirts, M.R.; Smith, J.C.; Kasson, P.M.; van der Spoel, D.; et al. GROMACS 4.5: A high-throughput and highly parallel open source molecular simulation toolkit. Bioinformatics 2013, 29, 845–854. [Google Scholar]
- Kikuchi, K.; Yoshida, M.; Maekawa, T.; Watanabe, H. Metropolis Monte Carlo method as a numerical technique to solve the Fokker-Planck equation. Chem. Phys. Lett 1991, 185, 335–338. [Google Scholar]
- Tiana, G.; Sutto, L.; Broglia, R.A. Use of the Metropolis algorithm to simulate the dynamics of protein chains. Phys. A 2007, 380, 241–249. [Google Scholar]
- Coppock, P.S.; Kindt, J.T. Atomistic simulations of mixed-lipid bilayers in gel and fluid phases. Langmuir 2009, 25, 352–359. [Google Scholar]
- Chiu, S.W.; Jakobsson, E.; Subramaniam, S.; Scott, H.L. Combined Monte Carlo and molecular dynamics simulation of fully hydrated dioleyl and palmitoyl-oleyl phosphatidylcholine lipid bilayers. Biophys. J 1999, 77, 2462–2469. [Google Scholar]
- Chiu, S.W.; Vasudevan, S.; Jakobsson, E.; Mashl, R.J.; Scott, H.L. Structure of sphingomyelin bilayers: A simulation study. Biophys. J 2003, 85, 3624–3635. [Google Scholar]
- Chiu, S.W.; Jakobsson, E.; Mashl, R.J.; Scott, H.L. Cholesterol-induced modifications in lipid bilayers: A simulation study. Biophys. J 2002, 83, 1842–1853. [Google Scholar]
- De Joannis, J.; Coppock, P.S.; Yin, F.; Mori, M.; Zamorano, A.; Kindt, J.T. Atomistic simulation of cholesterol effects on miscibility of saturated and unsaturated phospholipids: Implications for liquid-ordered/liquid-disordered phase coexistence. J. Am. Chem. Soc 2011, 133, 3625–3634. [Google Scholar]
- Ribeiro, A.S.T.; de Alencastro, R.B. Mixed Monte Carlo/molecular dynamics simulations in explicit solvent. J. Comput. Chem 2012, 33, 901–905. [Google Scholar]
- Timoneva, M.; Groenewegen, J.; Thijsse, B. Modeling diffusion and phase transitions by a uniform-acceptance force-biased Monte Carlo method. Phys. Rev. B 2010, 81, 144107:1–144107:13. [Google Scholar]
- Mees, M.J.; Pourtois, G.; Neyts, E.C.; Thijsse, B.J.; Stesmans, A. Uniform-acceptance force-bias Monte Carlo method with time scale to study solid-state diffusion. Phys. Rev. B 2012, 85, 134301:1–134301:9. [Google Scholar]
- Lyubartsev, A.P.; Laaksonen, A. Calculation of effective potentials from radial distribution fucntions: A reverse Monte Carlo approach. Phys. Rev. E 1995, 52, 3730–3737. [Google Scholar]
- Henderson, R.L. A uniqueness theroem for fluid pair correlation functions. Phys. Lett 1974, 49A, 197–198. [Google Scholar]
- Shelley, J.C.; Selley, M.Y.; Reeder, R.C.; Bandyopadhyay, S.; Moore, P.B.; Klein, M.L. Simulations of phospholipids using a coarse grain model. J. Phys. Chem. B 2001, 105, 9785–9792. [Google Scholar]
- Sodt, A.J.; Head-Gordon, T. An implicit solvent coarse-grained lipid model with correct stress profile. In J. Chem. Phys; 2010; Volume 132, pp. 205103:1–205103:8. [Google Scholar]


© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Wüstner, D.; Sklenar, H. Atomistic Monte Carlo Simulation of Lipid Membranes. Int. J. Mol. Sci. 2014, 15, 1767-1803. https://doi.org/10.3390/ijms15021767
Wüstner D, Sklenar H. Atomistic Monte Carlo Simulation of Lipid Membranes. International Journal of Molecular Sciences. 2014; 15(2):1767-1803. https://doi.org/10.3390/ijms15021767
Chicago/Turabian StyleWüstner, Daniel, and Heinz Sklenar. 2014. "Atomistic Monte Carlo Simulation of Lipid Membranes" International Journal of Molecular Sciences 15, no. 2: 1767-1803. https://doi.org/10.3390/ijms15021767