The Effect of Carbon Monoxide Co-Adsorption on Ni-Catalysed Water Dissociation
Abstract
:1. Introduction
2. Results and Discussion
2.1. Adsorption Sites and Energies
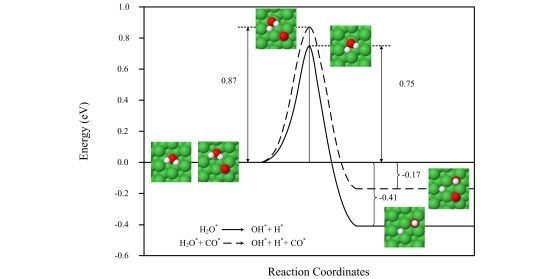
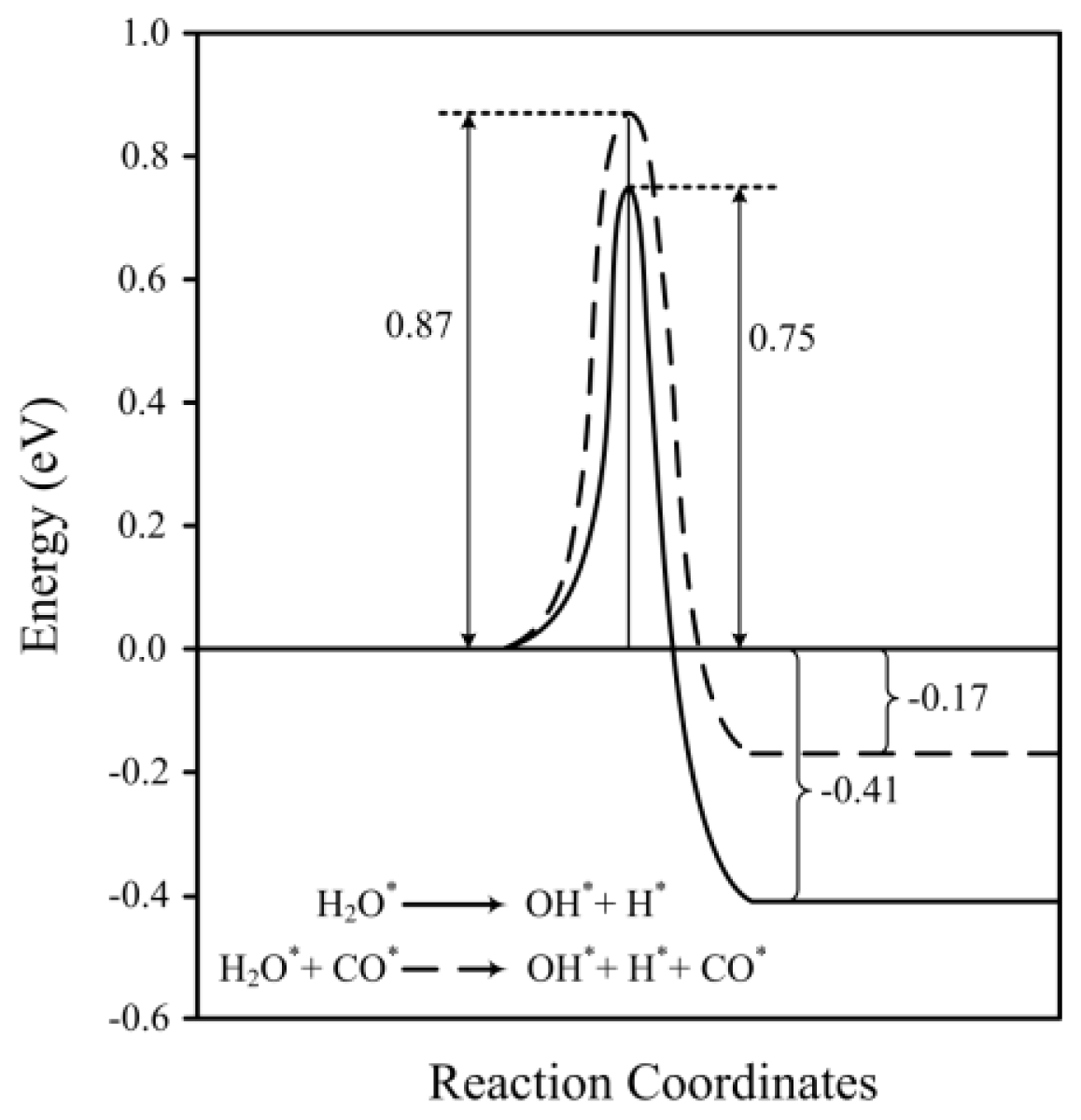
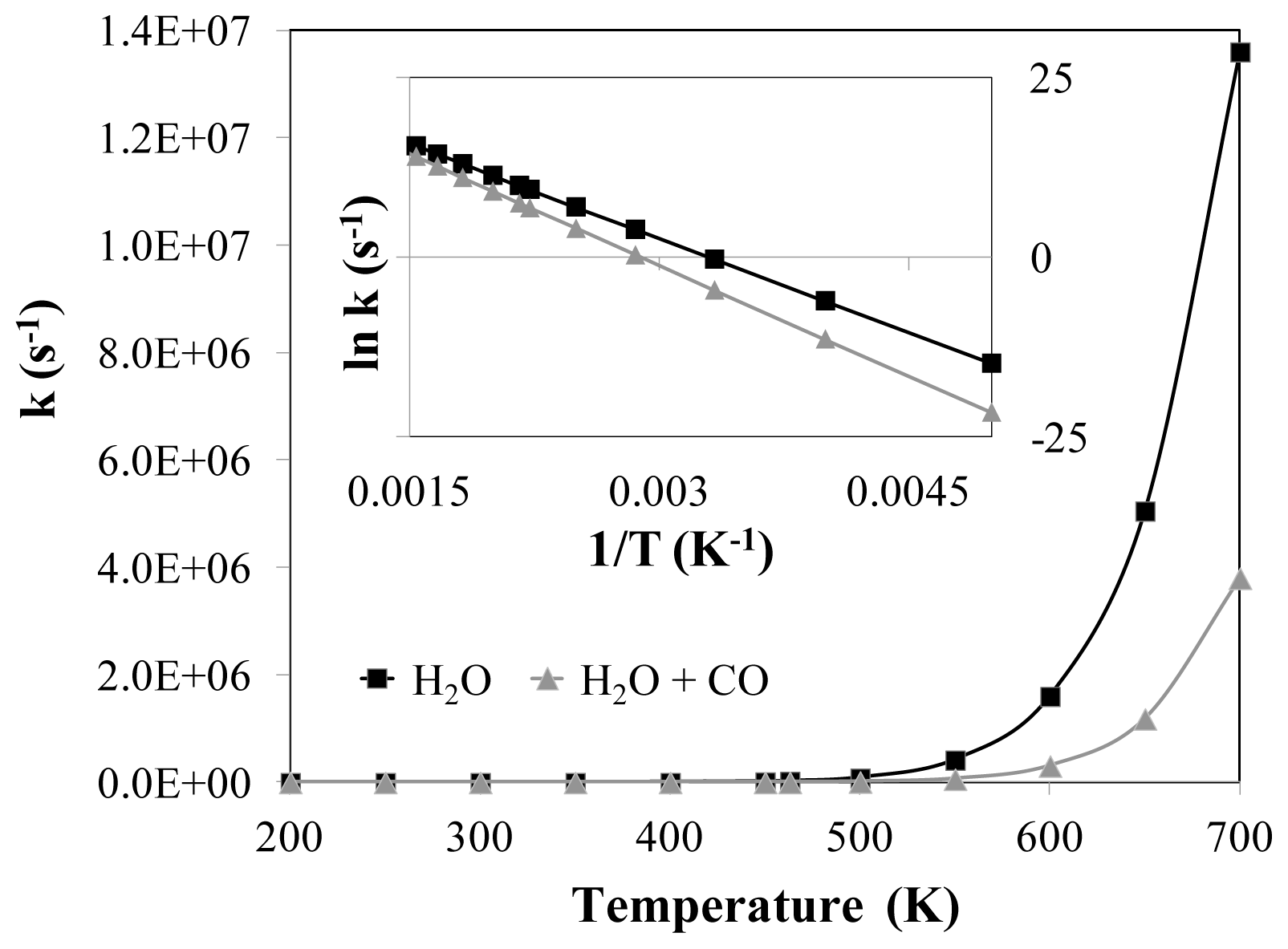
2.2. Transition States and Reaction Energies
3. Methods and Models
4. Conclusions
Acknowledgments
Conflicts of Interest
References
- Higman, C.; van der Burgt, M. Gasification, 2nd ed.; Gulf Professional Publishing: Jordan Hill, Oxford, UK, 2008. [Google Scholar]
- Yu, J.; Tian, F.; Chow, M.; McKenzie, L.; Li, C. Effect of iron on the gasification of Victorian brown coal with steam: Enhancement of hydrogen production. Fuel 2006, 85, 127–133. [Google Scholar]
- Rozovskii, A.; Lin, G. Fundamentals of methanol synthesis and decomposition. Top. Catal 2003, 22, 137–150. [Google Scholar]
- Larrubia Vargas, M.A.; Busca, G.; Costantino, U.; Marmottini, F.; Montanari, T.; Patrono, P.; Pinzari, F.; Ramis, G. An IR study of methanol steam reforming over ex-hydrotalcite Cu–Zn–Al catalysts. J. Mol. Catal. A 2007, 266, 188–197. [Google Scholar]
- Lee, S.H.D.; Applegate, D.V.; Ahmed, S.; Calderone, S.G.; Harvey, T.L. Hydrogen from natural gas: Part I—Autothermal reforming in an integrated fuel processor. Int. J. Hydrogen Energy 2005, 30, 829–842. [Google Scholar]
- Callaghan, C.A. Kinetics and catalysis of the water-gas-shift reaction: A microkinetic and graph theoretic approach. Master’s Thesis, Worcester Polytechnic Institute, Worceste, MA, USA, 2006. [Google Scholar]
- Hwang, K.-R.; Lee, C.-B.; Park, J.-S. Advanced nickel metal catalyst for water-gas shift reaction. J. Power Sources 2011, 196, 1349–1352. [Google Scholar]
- Li, Y.; Fu, Q.; Flytzani-Stephanopoulos, M. Low-temperature water-gas shift reaction over Cu- and Ni-loaded cerium oxide catalysts. Appl. Catal. B 2000, 27, 179–191. [Google Scholar]
- Kim, S.H.; Nam, S.-W.; Lim, T.-H.; Lee, H.-I. Effect of pretreatment on the activity of Ni catalyst for CO removal reaction by water-gas shift and methanation. Appl. Catal. B 2008, 81, 97–104. [Google Scholar]
- Bond, G. Mechanisms of the gold-catalysed water-gas shift. Gold. Bull 2009, 42, 337–342. [Google Scholar]
- Bunluesin, T.; Gorte, R.J.; Graham, G.W. Studies of the water-gas-shift reaction on ceria-supported Pt, Pd, and Rh: Implications for oxygen-storage properties. Appl. Catal. B 1998, 15, 107–114. [Google Scholar]
- Pazmiño, J.H.; Shekhar, M.; Damion Williams, W.; Cem Akatay, M.; Miller, J.T.; Nicholas Delgass, W.; Ribeiro, F.H. Metallic Pt as active sites for the water-gas shift reaction on alkali-promoted supported catalysts. J. Catal 2012, 286, 279–286. [Google Scholar]
- Grabow, L.C.; Gokhale, A.A.; Evans, S.T.; Dumesic, J.A.; Mavrikakis, M. Mechanism of the water gas shift reaction on Pt: First principles, experiments, and microkinetic modeling. J. Phys. Chem. C 2008, 112, 4608–4617. [Google Scholar]
- Fajín, J.L.; Cordeiro, M.; Illas, F.; Gomes, J.R. Influence of step sites in the molecular mechanism of the water gas shift reaction catalyzed by copper. J. Catal 2009, 268, 131–141. [Google Scholar]
- Nakamura, J.; Campbell, J.M.; Campbell, C.T. Kinetics and mechanism of the water-gas shift reaction catalysed by the clean and Cs-promoted Cu (110) surface: A comparison with Cu(111). J. Chem. Soc. Faraday Trans 1990, 86, 2725–2734. [Google Scholar]
- Ovesen, C.; Stoltze, P.; Nørskov, J.; Campbell, C. A kinetic model of the water gas shift reaction. J. Catal 1992, 134, 445–468. [Google Scholar]
- Ovesen, C.; Clausen, B.; Hammershøi, B.; Steffensen, G.; Askgaard, T.; Chorkendorff, I.; Nørskov, J.K.; Rasmussen, P.; Stoltze, P.; Taylor, P. A microkinetic analysis of the water-gas shift reaction under industrial conditions. J. Catal 1996, 158, 170–180. [Google Scholar]
- Campbell, C.T.; Daube, K. A surface science investigation of the water-gas shift reaction on Cu(111). J. Catal 1987, 104, 109–119. [Google Scholar]
- Froment, G.F.; Waugh, K. Dynamics of Surfaces and Reaction Kinetics in Heterogeneous Catalysis; Froment, G.F., Waugh, K.C., Eds.; Elsevier Science: Amsterdam, The Netherlands, 1997; Volume 109. [Google Scholar]
- Waugh, K.C. Prediction of global reaction kinetics by solution of the Arrhenius parameterised component elementary reactions: Microkinetic analysis. Catal. Today 1999, 53, 161–176. [Google Scholar]
- Fishtik, I.; Datta, R. A UBI-QEP microkinetic model for the water-gas shift reaction on Cu(111). Surf. Sci 2002, 512, 229–254. [Google Scholar]
- Rhodes, C.; Hutchings, G.; Ward, A. Water-gas shift reaction: Finding the mechanistic boundary. Catal. Today 1995, 23, 43–58. [Google Scholar]
- Askgaard, T.; Norskov, J.; Ovesen, C.; Stoltze, P. A kinetic model of methanol synthesis. J. Catal 1995, 156, 229–242. [Google Scholar]
- Van Herwijnen, T.; de Jong, W. Kinetics and mechanism of the CO shift on CuZnO: 1. Kinetics of the forward and reverse CO shift reactions. J. Catal 1980, 63, 83–93. [Google Scholar]
- Callaghan, C.; Fishtik, I.; Datta, R.; Carpenter, M.; Chmielewski, M.; Lugo, A. An improved microkinetic model for the water gas shift reaction on copper. Surf. Sci 2003, 541, 21–30. [Google Scholar]
- Lund, C.R. Water-gas shift kinetics over iron oxide catalysts at membrane reactor conditions. Final Rep. Chem. Eng. Dep. Univ. Buffalo 2002, 14260–14200. [Google Scholar]
- Ma, D.; Lund, C.R. Assessing high-temperature water-gas shift membrane reactors. Ind. Eng. Chem. Res 2003, 42, 711–717. [Google Scholar]
- Rodriguez, J.A.; Graciani, J.; Evans, J.; Park, J.B.; Yang, F.; Stacchiola, D.; Senanayake, S.D.; Ma, S.; Pérez, M.; Liu, P. Water-gas shift reaction on a highly active inverse CeOx/Cu(111) catalyst: Unique role of ceria nanoparticles. Angew. Chem 2009, 121, 8191–8194. [Google Scholar]
- Rodriguez, J.; Ma, S.; Liu, P.; Hrbek, J.; Evans, J.; Perez, M. Activity of CeOx and TiOx nanoparticles grown on Au(111) in the water-gas shift reaction. Science 2007, 318, 1757–1760. [Google Scholar]
- Huang, S.-C.; Lin, C.-H.; Wang, J.-H. Trends of water gas shift reaction on close-packed transition metal surfaces. J. Phys. Chem. C 2010, 114, 9826–9834. [Google Scholar]
- Park, J.B.; Graciani, J.; Evans, J.; Stacchiola, D.; Senanayake, S.D.; Barrio, L.; Liu, P.; Sanz, J.F.; Hrbek, J.; Rodriguez, J.A. Gold, copper, and platinum nanoparticles dispersed on CeOx/TiO2(110) surfaces: High water-gas shift activity and the nature of the mixed-metal oxide at the nanometer level. J. Am. Chem. Soc 2009, 132, 356–363. [Google Scholar]
- Gokhale, A.A.; Dumesic, J.A.; Mavrikakis, M. On the mechanism of low-temperature water gas shift reaction on copper. J. Am. Chem. Soc 2008, 130, 1402–1414. [Google Scholar]
- Fajín, J.L.; Cordeiro, M.; Illas, F.; Gomes, J.R. Descriptors controlling the catalytic activity of metallic surfaces toward water splitting. J. Catal 2010, 276, 92–100. [Google Scholar]
- Blaylock, D.W.; Ogura, T.; Green, W.H.; Beran, G.J. Computational investigation of thermochemistry and kinetics of steam methane reforming on Ni(111) under realistic conditions. J. Phys. Chem. C 2009, 113, 4898–4908. [Google Scholar]
- Zhu, T.; van Grootel, P.W.; Filot, I.A.; Sun, S.-G.; van Santen, R.A.; Hensen, E.J. Microkinetics of steam methane reforming on platinum and rhodium metal surfaces. J. Catal 2012, 297, 227–235. [Google Scholar]
- Rostrup-Nielsen, J.R.; Sehested, J.; Nørskov, J.K. Hydrogen and synthesis gas by steam- and CO2 reforming. Adv. Catal 2002, 47, 65–139. [Google Scholar]
- Van Grootel, P.W.; Hensen, E.J.M.; van Santen, R.A. DFT study on H2O activation by stepped and planar Rh surfaces. Surf. Sci 2009, 603, 3275–3281. [Google Scholar]
- Keiser, J.; Hoffbauer, M.; Lin, M. Production of hydroxyl on polycrystalline nickel studied by thermal desorption/laser-induced fluorescence. J. Phys. Chem 1985, 89, 2635–2638. [Google Scholar]
- Phatak, A.A.; Delgass, W.N.; Ribeiro, F.H.; Schneider, W.F. Density functional theory comparison of water dissociation steps on Cu, Au, Ni, Pd, and Pt. J. Phys. Chem. C 2009, 113, 7269–7276. [Google Scholar]
- Henderson, M.A. The interaction of water with solid surfaces: Fundamental aspects revisited. Surf. Sci. Rep 2002, 46, 1–308. [Google Scholar]
- Politano, A.; Chiarello, G. Enhancement of hydrolysis in alkali ultrathin layers on metal substrates in the presence of electron confinement. Chem. Phys. Lett 2010, 494, 84–87. [Google Scholar]
- Liu, K.; Gao, S. Water adsorption on Na/Cu(111): State-specific coupling with quantum well states. J. Phys. Chem. C 2012, 116, 17613–17618. [Google Scholar]
- Meng, S.; Wang, E.; Gao, S. Water adsorption on metal surfaces: A general picture from density functional theory studies. Phys. Rev. B 69, 04.
- Meng, S.; Xu, L.; Wang, E.; Gao, S. Vibrational recognition of hydrogen-bonded water networks on a metal surface. Phys. Rev. Lett 2002, 89, 176104. [Google Scholar]
- Somorjai, G.A.; Li, Y. Introduction to surface chemistry and catalysis, 2nd ed.; Wiley: Hoboken, NJ, USA, 2010. [Google Scholar]
- Morikawa, Y.; Mortensen, J.J.; Hammer, B.; Nørskov, J.K. CO adsorption and dissociation on Pt(111) and Ni(111) surfaces. Surf. Sci 1997, 386, 67–72. [Google Scholar]
- Christmann, K.; Schober, O.; Ertl, G. Adsorption of CO on a Ni(111) surface. J. Chem. Phys 1974, 60, 4719. [Google Scholar]
- Netzer, F.P.; Madey, T.E. The structure of CO on Ni(111). J. Chem. Phys 1982, 76, 710. [Google Scholar]
- Ellis, T.; Kruus, E.; Wang, H. The interaction between water and carbon monoxide coadsorbed onto Ni(100). Surf. Sci 1992, 273, 73–87. [Google Scholar]
- Lin, C.-H.; Chen, C.-L.; Wang, J.-H. Mechanistic studies of water-gas-shift reaction on transition metals. J. Phys. Chem. C 2011, 115, 18582–18588. [Google Scholar]
- Koverga, A.A.; Frank, S.; Koper, M. Density functional theory study of electric field effects on CO and OH adsorption and co-adsorption on gold surfaces. Electrochim. Acta 2013, 101, 244–253. [Google Scholar]
- Politano, A.; Chiarello, G. Vibrational investigation of catalyst surfaces: Change of the adsorption site of CO molecules upon coadsorption. J. Phys. Chem. C 2011, 115, 13541–13553. [Google Scholar]
- Politano, A.; Chiarello, G.; Benedek, G.; Chulkov, E.; Echenique, P. Vibrational spectroscopy and theory of alkali metal adsorption and co-adsorption on single-crystal surfaces. Surf. Sci. Rep 2013, 68, 305–389. [Google Scholar]
- Fleischer, I.; Popolan, D.M.; Krstič, M.; Bonačič-Koutecký, V.; Bernhardt, T.M. Composition dependent selectivity in the coadsorption of H2O and CO on pure and binary silver-gold clusters. Chem. Phys. Lett 2013, 565, 74–79. [Google Scholar]
- Ayastuy, J.; Gutierrez-Ortiz, M.; González-Marcos, J.; Aranzabal, A.; Gonzalez-Velasco, J. Kinetics of the low-temperature WGS reaction over a CuO/ZnO/Al2O3 catalyst. Ind. Eng. Chem. Res 2005, 44, 41–50. [Google Scholar]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558. [Google Scholar]
- Kresse, G.; Hafner, J. Ab initio molecular-dynamics simulation of the liquid-metal-amorphous-semiconductor transition in germanium. Phys. Rev. B 1994, 49, 14251. [Google Scholar]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci 1996, 6, 15–50. [Google Scholar]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett 1996, 77, 3865. [Google Scholar]
- Pan, Y.; Zhang, H.; Shi, D.; Sun, J.; Du, S.; Liu, F.; Gao, H. Highly ordered, millimeter-scale, continuous, single-crystalline graphene monolayer formed on Ru(0001). Adv. Mater 2009, 21, 2777–2780. [Google Scholar]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953. [Google Scholar]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar]
- Nørskov, J.K.; Bligaard, T.; Hvolbæk, B.; Abild-Pedersen, F.; Chorkendorff, I.; Christensen, C.H. The nature of the active site in heterogeneous metal catalysis. Chem. Soc. Rev 2008, 37, 2163–2171. [Google Scholar]
- Pozzo, M.; Carlini, G.; Rosei, R.; Alfè, D. Comparative study of water dissociation on Rh(111) and Ni(111) studied with first principles calculations. J. Chem. Phys 2007, 126, 164706. [Google Scholar]
- Hansen, H.A.; Rossmeisl, J.; Nørskov, J.K. Surface Pourbaix diagrams and oxygen reduction activity of Pt, Ag and Ni(111) surfaces studied by DFT. Phys. Chem. Chem. Phys 2008, 10, 3722–3730. [Google Scholar]
- Remediakis, I.N.; Abild-Pedersen, F.; Nørskov, J.K. DFT study of formaldehyde and methanol synthesis from CO and H2 on Ni(111). J. Phys. Chem. B 2004, 108, 14535–14540. [Google Scholar]
- Mittendorfer, F.; Hafner, J. Hydrogenation of benzene on Ni(111) a DFT study. J. Phys. Chem. B 2002, 106, 13299–13305. [Google Scholar]
- Loffreda, D.; Simon, D.; Sautet, P. Vibrational frequency and chemisorption site: A DFT-periodic study of NO on Pd(111) and Rh(111) surfaces. Chem. Phys. Lett 1998, 291, 15–23. [Google Scholar]
- Henkelman, G.; Uberuaga, B.P.; Jónsson, H. A climbing image nudged elastic band method for finding saddle points and minimum energy paths. J. Chem. Phys 2000, 113, 9901. [Google Scholar]
- Henkelman, G.; Jónsson, H. Improved tangent estimate in the nudged elastic band method for finding minimum energy paths and saddle points. J. Chem. Phys 2000, 113, 9978–9985. [Google Scholar]
- Chorkendorff, I.; Niemantsverdriet, J.W. Concepts of Modern Catalysis and Kinetics, 2nd ed.; Wiley: Weinheim, Germany, 2006. [Google Scholar]
- Van Harrevelt, R.; Honkala, K.; Nørskov, J.K.; Manthe, U. The reaction rate for dissociative adsorption of N on stepped Ru(0001): Six-dimensional quantum calculations. J. Chem. Phys 2005, 122, 234702. [Google Scholar]
- Shannon, R.T.; Prewitt, C.T. Effective ionic radii in oxides and fluorides. Acta Cryst 1969, 25, 925–946. [Google Scholar]



| Species | Adsorption site | Vibrational frequencies | dsurf-molb | Bond length c | ||
|---|---|---|---|---|---|---|
| H2O* | t | −0.36 | −0.27 | 3723, 3612, 1558, 489, 427, 227, 172, 122, 84 | H2O: 2.157 | O–Ha: 0.979; O–Hb: 0.978 |
| OH*+H* | OH: f; H: f | −6.23 | −5.83 | 3712, 1220, 952, 776, 546, 502, 387, 290, 248 | OH: 1.950; H: 1.655 | O–Ha: 0.973 |
| H2O*+CO* | H2O: t; CO: f | −2.38 | −2.32 | 3721, 3412, 1662, 1566, 737, 516, 379, 349, 322, 306, 226, 190, 149, 128, 76 | H2O: 2.114; CO: 1.903 | O–Ha: 0.990; O–Hb: 0.975; C–O: 1.213 |
| OH* + H* + CO* | OH: f; H: f; CO: f | −7.99 | −7.63 | 3704, 1761, 1253, 972, 740, 567, 520, 415, 395, 322, 299, 277, 246, 166, 122 | OH: 1.923; H: 1.646; CO: 1.872 | O–Ha: 0.974; C–O: 1.195 |
| Species | Vibrational modes | k | dO–H | Imaginary frequency | ||||
|---|---|---|---|---|---|---|---|---|
| H2O* → OH* + H* | 0.96 | 0.75 | 3653, 837, 748, 677, 432, 393, 167, 71 | 2.03×104 | −0.30 | −0.41 | 1.559 | 797 |
| H2O* + CO* → OH* + H* + CO* | 1.09 | 0.87 | 3623, 1726, 921, 765, 690, 465, 400, 377, 324, 282, 162, 147, 136, 105 | 1.76×103 | −0.05 | −0.17 | 1.560 | 817 |
© 2013 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Mohsenzadeh, A.; Borjesson, A.; Wang, J.-H.; Richards, T.; Bolton, K. The Effect of Carbon Monoxide Co-Adsorption on Ni-Catalysed Water Dissociation. Int. J. Mol. Sci. 2013, 14, 23301-23314. https://doi.org/10.3390/ijms141223301
Mohsenzadeh A, Borjesson A, Wang J-H, Richards T, Bolton K. The Effect of Carbon Monoxide Co-Adsorption on Ni-Catalysed Water Dissociation. International Journal of Molecular Sciences. 2013; 14(12):23301-23314. https://doi.org/10.3390/ijms141223301
Chicago/Turabian StyleMohsenzadeh, Abas, Anders Borjesson, Jeng-Han Wang, Tobias Richards, and Kim Bolton. 2013. "The Effect of Carbon Monoxide Co-Adsorption on Ni-Catalysed Water Dissociation" International Journal of Molecular Sciences 14, no. 12: 23301-23314. https://doi.org/10.3390/ijms141223301