Medium Optimization for Exopolysaccharide Production in Liquid Culture of Endophytic Fungus Berkleasmium sp. Dzf12
Abstract
:1. Introduction
2. Results and Discussion
2.1. FFD Experiments and Statistical Analyses
2.2. Single-Factor Experiments and Analyses
2.3. CCD Experiments, Model Building and Statistical Analysis
2.4. Response Surface and Contour Plots Analyses
2.5. Optimization of the Variables and Verification of the Model
3. Experimental Section
3.1. Cultivation of the Endophytic Fungus Berkleasmium sp. Dzf12
3.2. Preparation of the Exopolysaccharide
3.3. Procedure Optimization and Experimental Design
4. Conclusions
Acknowledgments
References
- Wang, H.X.; Ng, T.B.; Liu, W.K.; Ooi, V.E.C.; Chang, S.T. Polysaccharide-Peptide complexes from the cultured mycelia of the mushroom Coriolus versicolor and their culture medium activate mouse lymphocytes and macrophages. Int. J. Biochem. Cell Biol 1996, 28, 601–607. [Google Scholar]
- Lee, J.S.; Cho, J.Y.; Hong, E.K. Study on macrophage activation and structural characteristics of purified polysaccharides from the liquid culture broth of Hericium erinaceus. Carbohydr. Polym 2009, 78, 162–168. [Google Scholar]
- Li, S.P.; Zhao, K.J.; Ji, Z.N.; Song, Z.H.; Dong, T.T.X.; Lo, C.K.; Cheung, J.K.H.; Zhu, S.Q.; Tsim, K.W.K. A polysaccharide isolated from Cordyceps sinensis, a traditional Chinese medicine, protects PC12 cells against hydrogen peroxide-induced injury. Life Sci 2003, 73, 2503–2513. [Google Scholar]
- Chen, J.; Zhang, W.; Lu, T.; Li, J.; Zheng, Y.; Kong, L. Morphological and genetic characterization of a cultivated Cordyceps sinensis fungus and its polysaccharide component possessing antioxidant property in H22 tumor-bearing mice. Life Sci 2006, 78, 2742–2748. [Google Scholar]
- Leung, P.H.; Zhao, S.; Ho, K.P.; Wu, J.Y. Chemical properties and antioxidant activity of exopolysaccharides from mycelial culture of Cordyceps sinensis fungus Cs-HK1. Food Chem 2009, 114, 1251–1256. [Google Scholar]
- Li, P.; Luo, C.; Sun, W.; Lu, S.; Mou, Y.; Peng, Y.; Zhou, L. In vitro antioxidant activities of polysaccharides from endophytic fungus Fusarium oxysporum Dzf17. Afr. J. Microbiol. Res 2011, 5, 5990–5993. [Google Scholar]
- Chen, Y.; Mao, W.; Yang, Y.; Teng, X.; Zhu, W.; Qi, X.; Chen, Y.; Zhao, C.; Hou, Y.; Wang, C.; et al. Structure and antioxidant activity of an extracellular polysaccharide from coral-associated fungus, Aspergillus versicolor LCJ-5-4. Carbohydr. Polym 2012, 87, 218–226. [Google Scholar]
- Peng, Y.; Zhang, L.; Zeng, F.; Kennedy, J.F. Structure and antitumor activities of the water-soluble polysaccharides from Ganoderma tsugae mycelium. Carbohydr. Polym 2005, 59, 385–392. [Google Scholar]
- Gan, D.; Ma, L.; Jiang, C.; Xu, R.; Zeng, X. Production, preliminary characterization and antitumor activity in vitro of polysaccharides from the mycelium of Pholiota dinghuensis Bi. Carbohydr. Polym 2011, 84, 997–1003. [Google Scholar]
- Cheng, J.-J.; Lin, C.-Y.; Lur, H.-S.; Chen, H.-P.; Lu, M.-K. Properties and biological functions of polysaccharides and ethanolic extracts isolated from medicinal fungus, Fomitopsis pinicola. Process Biochem 2008, 43, 829–834. [Google Scholar]
- Cardozo, F.T.G.S.; Camelini, C.M.; Mascarello, A.; Rossi, M.J.; Nunes, R.J.; Barardi, C.R.M.; Mendonca, M.M.; Simoes, C.M.O. Antiherpetic activity of a sulfated polysaccharide from Agaricus brasiliensis mycelia. Antivir. Res 2011, 92, 108–114. [Google Scholar]
- Cheng, J.-J.; Lu, M.-K.; Lin, C.-Y.; Chang, C.-C. Characterization and functional elucidation of a fucosylated 1,6-α-d-mannogalactan polysaccharide from Antrodia cinnamomea. Carbohydr. Polym 2011, 83, 545–553. [Google Scholar]
- Telles, C.B.S.; Sabry, D.A.; Almeida-Lima, J.; Costa, M.S.S.P.; Melo-Silveira, R.F.; Trindade, E.S.; Sassaki, G.L.; Wisbeck, E.; Furlan, S.A.; Leite, E.L.; et al. Sulfation of the extracellular polysaccharide produced by the edible mushroom Pleurotus sajor-caju alters its antioxidant, anticoagulant and antiproliferative properties in vitro. Carbohydr. Polym 2011, 85, 514–521. [Google Scholar]
- Li, P.; Mou, Y.; Shan, T.; Xu, J.; Li, Y.; Lu, S.; Zhou, L. Effects of polysaccharide elicitors from endophytic Fusarium oxysporium Dzf17 on the growth and diosgenin production in cell suspension culture of Dioscorea zingiberensis. Molecules 2011, 16, 9003–9016. [Google Scholar]
- Li, P.; Lu, S.; Shan, T.; Mou, Y.; Li, Y.; Sun, W.; Zhou, L. Extraction optimization of water-extracted mycelial polysaccharide from endophytic fungus Fusarium oxysporum Dzf17 by response surface methodology. Int. J. Mol. Sci 2012, 13, 5441–5453. [Google Scholar]
- Backman, P.A.; Sikora, R.A. Endophytes: An emerging tool for biological control. Biol. Control 2008, 46, 1–3. [Google Scholar]
- Schulz, B.; Boyle, C.; Draeger, S.; Rommert, A.-K.; Krohn, K. Endophytic fungi: A source of novel biologically active secondary metabolites. Mycol. Res 2002, 106, 996–1004. [Google Scholar]
- Aly, A.H.; Debbab, A.; Kjer, J.; Proksch, P. Fungal endophytes from higher plants: A prolific source of phytochemicals and other bioactive natural products. Fungal Divers 2010, 41, 1–16. [Google Scholar]
- Zhao, J.; Shan, T.; Mou, Y.; Zhou, L. Plant-Derived bioactive compounds produced by endophytic fungi. Mini Rev. Med. Chem 2011, 11, 159–168. [Google Scholar]
- Zhou, L.; Zhao, J.; Shan, T.; Cai, X.; Peng, Y. Spirobisnaphthalenes from fungi and their biological activities. Mini Rev. Med. Chem 2010, 10, 977–989. [Google Scholar]
- Kharwar, R.N.; Mishra, A.; Gong, S.K.; Stierle, A.; Stierle, D. Anticancer compounds derived from fungal endophytes: Their importance and future challenges. Nat. Prod. Rep 2011, 28, 1208–1228. [Google Scholar]
- Strobel, G.; Daisy, B.; Castillo, U.; Harper, J. Natural products from endophytic microorganisms. J. Nat. Prod 2004, 67, 257–268. [Google Scholar]
- Zhang, H.W.; Song, Y.C.; Tan, R.X. Biology and chemistry of endophytes. Nat. Prod. Rep 2006, 23, 753–771. [Google Scholar]
- Wasser, S.P.; Weis, A. Therapeutic effects of substances occurring in higher basidiomycetes mushrooms, a modern perspective (review). Crit. Rev. Immunol 1999, 19, 65–96. [Google Scholar]
- Wasser, S.P. Medicinal mushrooms as a source of antitumor and immunomodulating polysaccharides. Appl. Microbiol. Biotechnol 2002, 60, 258–274. [Google Scholar]
- Li, P.; Sun, W.; Luo, C.; Shan, T.; Mou, Y.; Mao, Z.; Zhou, L. In vitro evaluation of antioxidant activities of polysaccharides from the endophytic fungus Berkleasmium sp. Dzf12. Afr. J. Microbiol. Res 2012, 6, 471–477. [Google Scholar]
- Zhang, R.; Li, P.; Zhao, J.; Yin, C.; Zhou, L. Endophytic fungi from Dioscorea zingiberensis and their effects on the growth and diosgenin production of the host plant cultures. Nat. Prod. Res. Dev 2010, 22, 11–15. [Google Scholar]
- Cai, X.; Shan, T.; Li, P.; Huang, Y.; Xu, L.; Zhou, L.; Wang, M.; Jiang, W. Spirobisnaphthalenes from the endophytic fungus Dzf12 of Dioscorea zingiberensis and their antimicrobial activities. Nat. Prod. Commun 2009, 4, 1469–1472. [Google Scholar]
- Zhao, J.; Zheng, B.; Li, Y.; Shan, T.; Mou, Y.; Lu, S.; Li, P.; Zhou, L. Enhancement of diepoxin ζ production by yeast extract and its fractions in liquid culture of Berkleasmium-like endophytic fungus Dzf12 from Dioscorea zingiberensis. Molecules 2011, 16, 847–856. [Google Scholar]
- Zhao, J.; Li, Y.; Shan, T.; Mou, Y.; Zhou, L. Enhancement of diepoxin ζ production with in situ resin adsorption in mycelial liquid culture of the endophytic fungus Berkleasmium sp. Dzf12 from Dioscorea zingiberensis. World J. Microbiol. Biotechnol 2011, 27, 2753–2758. [Google Scholar]
- Li, Y.; Li, P.; Mou, Y.; Zhao, J.; Shan, T.; Ding, C.; Zhou, L. Enhancement of diepoxin ζ production in liquid culture of endophytic fungus Berkleasmium sp. Dzf12 by polysaccharides from its host plant Dioscorea zingiberensis. World J. Microbiol. Biotechnol 2012, 28, 1407–1413. [Google Scholar]
- Li, Y.; Shan, T.; Mou, Y.; Li, P.; Zhao, J.; Zhao, W.; Peng, Y.; Zhou, L.; Ding, C. Enhancement of palmarumycin C12 and C13 production in liquid culture of endophytic fungus Berkleasmium sp. Dzf12 by oligosaccharides from its host plant Dioscorea zingiberensis. Molecules 2012, 17, 3761–3773. [Google Scholar]
- Zhu, Y.; Knol, W.; Smits, J.P.; Bol, J. Medium optimization for nuclease Pl production by Penicillium citrinum in solid-state fermentation using polyurethane foam as inert carrier. Enzyme Microb. Technol 1996, 18, 108–112. [Google Scholar]
- Vaidya, R.; Vyas, P.; Chhatpar, H.S. Statistical optimization of medium components for the production of chitinase by Alcaligenes xylosoxydans. Enzyme Microb. Technol 2003, 33, 92–96. [Google Scholar]
- Wang, Y.-H.; Yang, B.; Dong, M.-L.; Liang, D.; Xu, A.-L. Optimization of medium composition for the production of clavulanic acid by Streptomyces clavuligerus. Process Biochem 2005, 40, 1161–1166. [Google Scholar]
- Luo, J.; Liu, J.; Ke, C.; Qiao, D.; Ye, H.; Sun, Y.; Zeng, X. Optimization of medium composition for the production of exopolysaccharides from Phellinus baumii Pilát in submerged culture and the immuno-stimulating activity of exopolysaccharides. Carbohydr. Polym 2009, 78, 409–415. [Google Scholar]
- Yin, Y.; Gao, Q.; Zhang, F.; Li, Z. Medium optimization for the high yield production of single (+)-terrein by Aspergillus terreus strain PF26 derived from marine sponge Phakellia fusca. Process Biochem 2012, 47, 887–891. [Google Scholar]
- Rao, K.J.; Kim, C.-H.; Rhee, S.-K. Statistical optimization of medium for the production of recombinant hirudin from Saccharomyces cerevisiae using response surface methodology. Process Biochem 2000, 35, 639–647. [Google Scholar]
- Box, G.E.P.; Hunter, W.G.; Hunter, J.S. Statistics for Experimenters; John Wiley & Sons, Inc: Hoboken, NJ, USA, 1978; pp. 510–539. [Google Scholar]
- Ibrahim, H.M.; Yusoff, W.M.W.; Hamid, A.A.; Illias, R.M.; Hassan, O.; Omar, O. Optimization of medium for the production of β-cyclodextrin glucanotransferase using central composite design (CCD). Process Biochem 2005, 40, 753–758. [Google Scholar]
- Nikerel, I.E.; Oner, E.; Kirdar, B.; Yildirim, R. Optimization of medium composition for biomass production of recombinant Escherichia coli cells using response surface methodology. Biochem. Eng. J 2006, 32, 1–6. [Google Scholar]
- Zhang, T.; Wen, S.; Tan, T. Optimization of the medium for glutathione production in Saccharomyces cerevisiae. Process Biochem 2007, 42, 454–458. [Google Scholar]
- Liu, J.; Luo, J.; Ye, H.; Sun, Y.; Lu, Z.; Zeng, X. Medium optimization and structural characterization of exopolysaccharides from endophytic bacterium Paenibacillus polymyxa EJS-3. Carbohydr. Polym 2010, 79, 206–213. [Google Scholar]
- Pujari, V.; Chandra, T.S. Statistical optimization of medium components for enhanced riboflavin production by a UV-mutant of Eremothecium ashbyii. Process Biochem 2000, 36, 31–37. [Google Scholar]
- Gao, H.; Gu, W.-Y. Optimization of polysaccharide and ergosterol production from Agaricus brasiliensis by fermentation process. Biochem. Eng. J 2007, 33, 202–210. [Google Scholar]
- Liu, J.-Z.; Weng, L.-P.; Zhan, Q.-L.; Xu, H.; Ji, L.N. Optimization of glucose oxidase production by Aspergillus niger in a benchtop bioreactor using response surface methodology. World J. Microbiol. Biotechnol 2003, 19, 317–323. [Google Scholar]
- Murthy, M.S.R.C.; Swaminathan, T.; Rakshit, S.K.; Kosugi, Y. Statistical optimization of lipase catalyzed hydrolysis of methyloleate by response surface methodology. Bioprocess Eng 2000, 22, 35–39. [Google Scholar]
- Box, G.E.P.; Wilson, K.B. On the experimental attainment of optimum conditions. J. Roy. Stat. Soc. B 1951, 13, 1–45. [Google Scholar]
- Kiran, B.; Kaushik, A.; Kaushik, C.P. Response surface methodological approach for optimizing removal of Cr (VI) from aqueous solution using immobilized cyanobacterium. Chem. Eng. J 2007, 126, 147–153. [Google Scholar]
- Muralidhar, R.V.; Chirumamila, R.R.; Marchant, R.; Nigam, P. A response surface approach for the comparison of lipase production by Candida cylindracea using two different carbon sources. Biochem. Eng. J 2001, 9, 17–23. [Google Scholar]
- Wu, Y.; Cui, S.W.; Tang, J.; Gu, X. Optimization of extraction process of crude polysaccharides from boat-fruited sterculia seeds by response surface methodology. Food Chem 2007, 105, 1599–1605. [Google Scholar]
- Wang, Z.J.; Luo, D.H.; Ena, C. Optimization of polysaccharides extraction from Gynostemma pentaphyllum Makino using uniform design. Carbohydr. Polym 2007, 69, 311–317. [Google Scholar]
- Jiao, Y.; Chen, Q.; Zhou, J.; Zhang, H.; Chen, H. Improvement of exo-polysaccharides production and modeling kinetics by Armillaria luteo-virens Sacc. In submerged cultivation. LWT Food Sci. Technol 2008, 41, 1694–1700. [Google Scholar]
- Zhuang, Y.P.; Chen, B.; Chu, J.; Zhang, S. Medium optimization for meilingmycin production by Streptomyces nanchangensis using response surface methodology. Process Biochem 2006, 41, 405–409. [Google Scholar]
- Yatsyshyn, V.Y.; Fedorovych, D.V.; Sibirny, A.A. Medium optimization for production of flavin mononucleotide by the recombinant strain of the yeast Candida famata using statistical designs. Biochem. Eng. J 2010, 49, 52–60. [Google Scholar]
- Soto-Cruz, O.; Saucedo-Castaneda, G.; Pablos-Hach, J.L.; Gutierrez-Rojas, M.; Favela-Torres, E. Effect of substrate composition on the mycelial growth of Pleurotus ostreatus. an analysis by mixture and response surface methodologies. Process Biochem 1999, 35, 127–133. [Google Scholar]
- Triveni, R.; Shamala, T.R.; Rastogi, N.K. Optimized production and utilization of exopolysaccharide from Agrobacterium radiobacter. Process Biochem 2001, 36, 787–795. [Google Scholar]
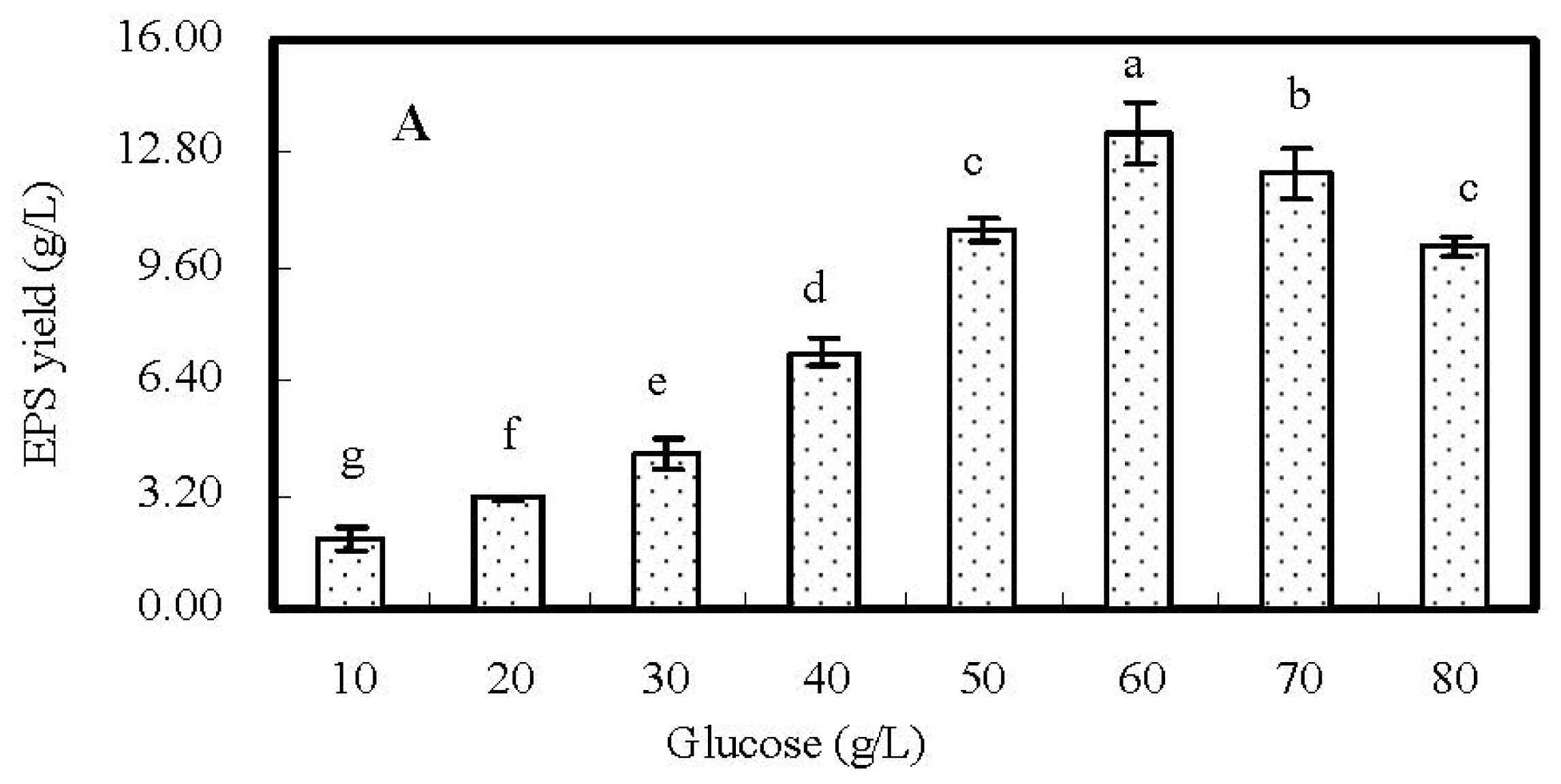
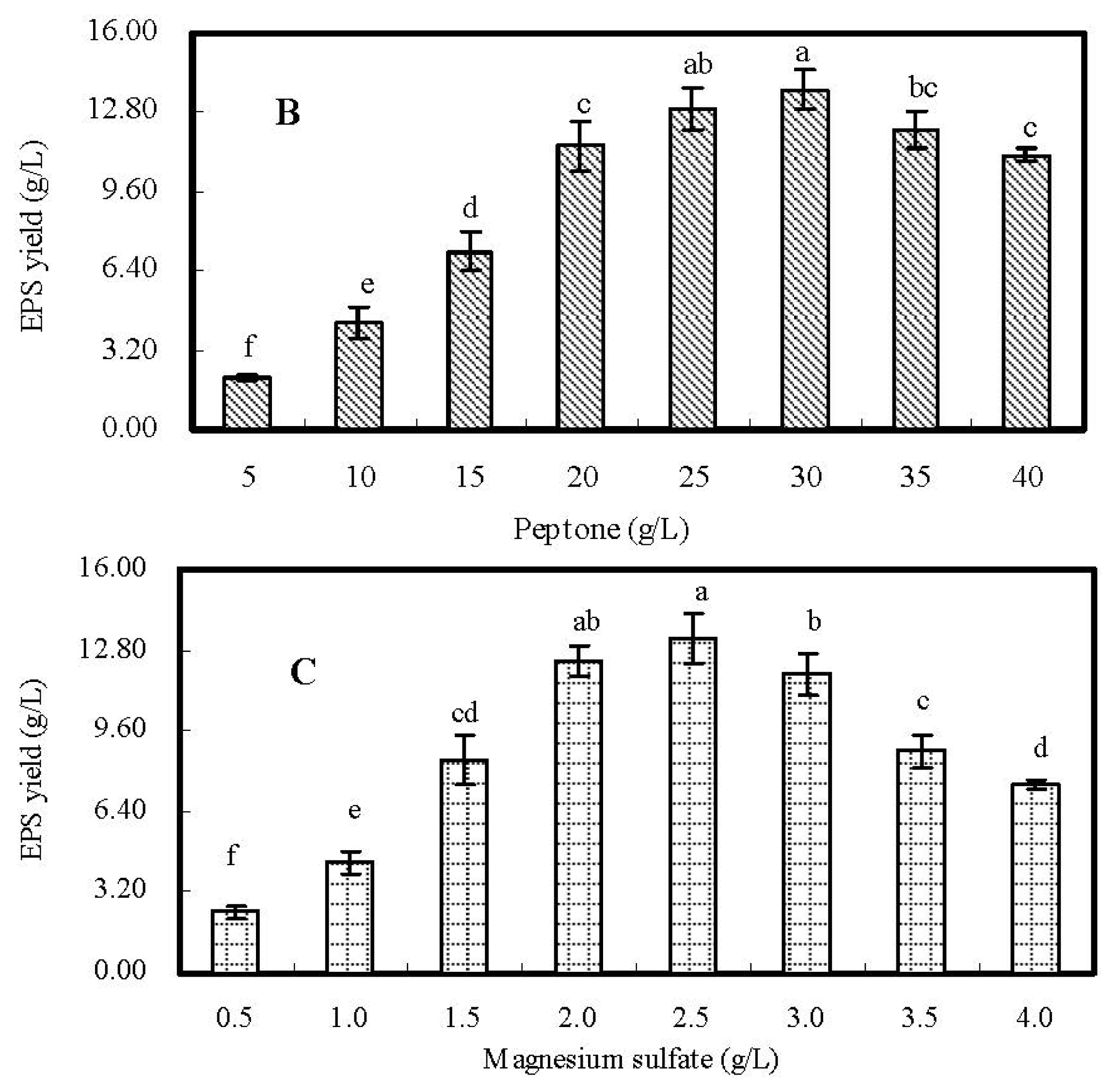

| Run | Glucose (g/L) | Peptone (g/L) | KH2PO4 (g/L) | MgSO4·7H2O (g/L) | FeSO4·7H2O (g/L) | EPS Yield (g/L) |
|---|---|---|---|---|---|---|
| 1 | 30 | 10 | 0.5 | 0.5 | 0.05 | 1.20 |
| 2 | 60 | 10 | 0.5 | 0.5 | 0.01 | 1.42 |
| 3 | 30 | 20 | 0.5 | 0.5 | 0.01 | 2.80 |
| 4 | 60 | 20 | 0.5 | 0.5 | 0.05 | 3.67 |
| 5 | 30 | 10 | 2.0 | 0.5 | 0.01 | 1.12 |
| 6 | 60 | 10 | 2.0 | 0.5 | 0.05 | 2.36 |
| 7 | 30 | 20 | 2.0 | 0.5 | 0.05 | 3.85 |
| 8 | 60 | 20 | 2.0 | 0.5 | 0.01 | 6.62 |
| 9 | 30 | 10 | 0.5 | 2.0 | 0.05 | 2.82 |
| 10 | 60 | 10 | 0.5 | 2.0 | 0.01 | 5.37 |
| 11 | 30 | 20 | 0.5 | 2.0 | 0.01 | 5.08 |
| 12 | 60 | 20 | 0.5 | 2.0 | 0.05 | 13.63 |
| 13 | 30 | 10 | 2.0 | 2.0 | 0.01 | 2.97 |
| 14 | 60 | 10 | 2.0 | 2.0 | 0.05 | 6.84 |
| 15 | 30 | 20 | 2.0 | 2.0 | 0.05 | 5.57 |
| 16 | 60 | 20 | 2.0 | 2.0 | 0.01 | 10.89 |
| Source | Sum of squares | d.f. | F Value | p-Value p > F | Significance |
|---|---|---|---|---|---|
| Glucose | 40.29 | 1 | 12.67 | 0.0052 | ** |
| Peptone | 49.04 | 1 | 15.42 | 0.0028 | ** |
| KH2PO4 | 1.12 | 1 | 0.35 | 0.5664 | |
| MgSO4·7H2O | 56.74 | 1 | 17.84 | 0.0018 | ** |
| FeSO4·7H2O | 1.84 | 1 | 0.58 | 0.4641 |
| Variable (g/L) | Symbol | Coded level | |||||
|---|---|---|---|---|---|---|---|
| Uncoded | Coded | −1.682 | −1 | 0 | 1 | +1.682 | |
| Glucose | X1 | x1 | 43.18 | 50 | 60 | 70 | 76.82 |
| Peptone | X2 | x2 | 21.59 | 25 | 30 | 35 | 38.41 |
| MgSO4·7H2O | X3 | x3 | 1.66 | 2 | 2.5 | 3 | 3.34 |
| EPS Yield (g/L) | ||||||
|---|---|---|---|---|---|---|
| Run | x1 | x2 | x3 | Experimental Ye | Predicted Yp | Ye − Yp |
| 1 | 0 | −1.682 | 0 | 6.07 | 6.23 | −0.17 |
| 2 | 0 | 0 | 1.682 | 9.30 | 9.59 | −0.29 |
| 3 | 0 | 1.682 | 0 | 10.22 | 9.99 | 0.23 |
| 4 | −1 | −1 | −1 | 2.71 | 2.45 | 0.26 |
| 5 | −1 | 1 | 1 | 7.89 | 7.52 | 0.36 |
| 6 | −1 | 1 | −1 | 7.32 | 7.81 | −0.49 |
| 7 | 1 | 1 | 1 | 10.01 | 10.31 | −0.30 |
| 8 | 0 | 0 | 0 | 13.43 | 12.52 | 0.91 |
| 9 | 0 | 0 | 0 | 11.95 | 12.52 | −0.57 |
| 10 | 1 | −1 | −1 | 4.47 | 4.88 | −0.41 |
| 11 | 1 | 1 | −1 | 6.01 | 6.00 | 0.01 |
| 12 | 0 | 0 | −1 | 4.87 | 4.52 | 0.35 |
| 13 | 1.682 | 0 | 0 | 8.51 | 8.39 | 0.13 |
| 14 | −1 | −1 | 1 | 4.12 | 4.18 | −0.06 |
| 15 | 0 | 0 | 0 | 12.09 | 12.52 | −0.43 |
| 16 | 0 | 0 | 0 | 12.73 | 12.52 | 0.21 |
| 17 | −1.682 | 0 | 0 | 3.94 | 4.00 | −0.06 |
| 18 | 1 | −1 | 1 | 11.64 | 11.20 | 0.44 |
| 19 | 0 | 0 | 0 | 13.02 | 12.52 | 0.50 |
| 20 | 0 | 0 | 0 | 11.89 | 12.52 | −0.43 |
| Source | Sum of squares | d.f. | Mean square | F Value | Probability p > F |
|---|---|---|---|---|---|
| Model | 228.02 | 9 | 25.34 | 78.46 | <0.0001 |
| Lack of fit | 1.20 | 5 | 0.24 | 0.59 | 0.71 |
| Pure error | 2.03 | 5 | 0.41 | ||
| Corrected total | 231.25 | 19 |
| Model term | Coefficient estimate | Standard error | Sum of squares | d.f. | Mean square | F Value | Probability p > F |
|---|---|---|---|---|---|---|---|
| Intercept | 12.52 | 0.23 | |||||
| x1 | 1.30 | 0.15 | 23.18 | 1 | 23.18 | 71.79 | <0.0001 |
| x2 | 1.12 | 0.15 | 17.06 | 1 | 17.06 | 52.83 | <0.0001 |
| x3 | 1.51 | 0.15 | 31.12 | 1 | 31.12 | 96.36 | <0.0001 |
| x1x2 | −1.06 | 0.20 | 8.96 | 1 | 8.96 | 27.75 | <0.0001 |
| x1x3 | 1.15 | 0.20 | 10.58 | 1 | 10.58 | 32.76 | 0.0004 |
| x2x3 | −0.50 | 0.20 | 2.01 | 1 | 2.01 | 6.24 | 0.0002 |
| x12 | −2.24 | 0.15 | 72.04 | 1 | 72.04 | 223.09 | 0.0316 |
| x22 | −1.56 | 0.15 | 34.99 | 1 | 34.99 | 108.36 | <0.0001 |
| x32 | −1.93 | 0.15 | 53.80 | 1 | 53.80 | 166.61 | <0.0001 |
| Variable (g/L) | Level | |
|---|---|---|
| −1 | +1 | |
| Glucose | 30 | 60 |
| Peptone | 10 | 20 |
| KH2PO4 | 0.5 | 2.0 |
| MgSO4·7H2O | 0.5 | 2.0 |
| FeSO4·7H2O | 0.01 | 0.05 |
© 2012 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Li, P.; Xu, L.; Mou, Y.; Shan, T.; Mao, Z.; Lu, S.; Peng, Y.; Zhou, L. Medium Optimization for Exopolysaccharide Production in Liquid Culture of Endophytic Fungus Berkleasmium sp. Dzf12. Int. J. Mol. Sci. 2012, 13, 11411-11426. https://doi.org/10.3390/ijms130911411
Li P, Xu L, Mou Y, Shan T, Mao Z, Lu S, Peng Y, Zhou L. Medium Optimization for Exopolysaccharide Production in Liquid Culture of Endophytic Fungus Berkleasmium sp. Dzf12. International Journal of Molecular Sciences. 2012; 13(9):11411-11426. https://doi.org/10.3390/ijms130911411
Chicago/Turabian StyleLi, Peiqin, Liang Xu, Yan Mou, Tijiang Shan, Ziling Mao, Shiqiong Lu, Youliang Peng, and Ligang Zhou. 2012. "Medium Optimization for Exopolysaccharide Production in Liquid Culture of Endophytic Fungus Berkleasmium sp. Dzf12" International Journal of Molecular Sciences 13, no. 9: 11411-11426. https://doi.org/10.3390/ijms130911411





