Vibrational Stark Effect of the Electric-Field Reporter 4-Mercaptobenzonitrile as a Tool for Investigating Electrostatics at Electrode/SAM/Solution Interfaces
Abstract
:1. Introduction
2. Results and Discussion
2.1. The Nitrile Stretching Modes of MBN in SAM Coated Ag and Au Surfaces
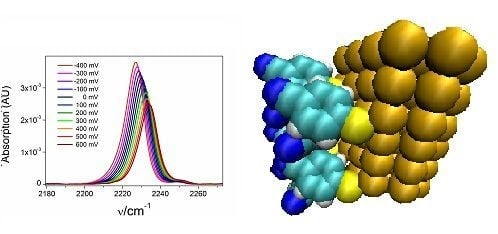
2.2. Potential-Dependent Measurements of MBN-SAMs on Ag and Au Surfaces
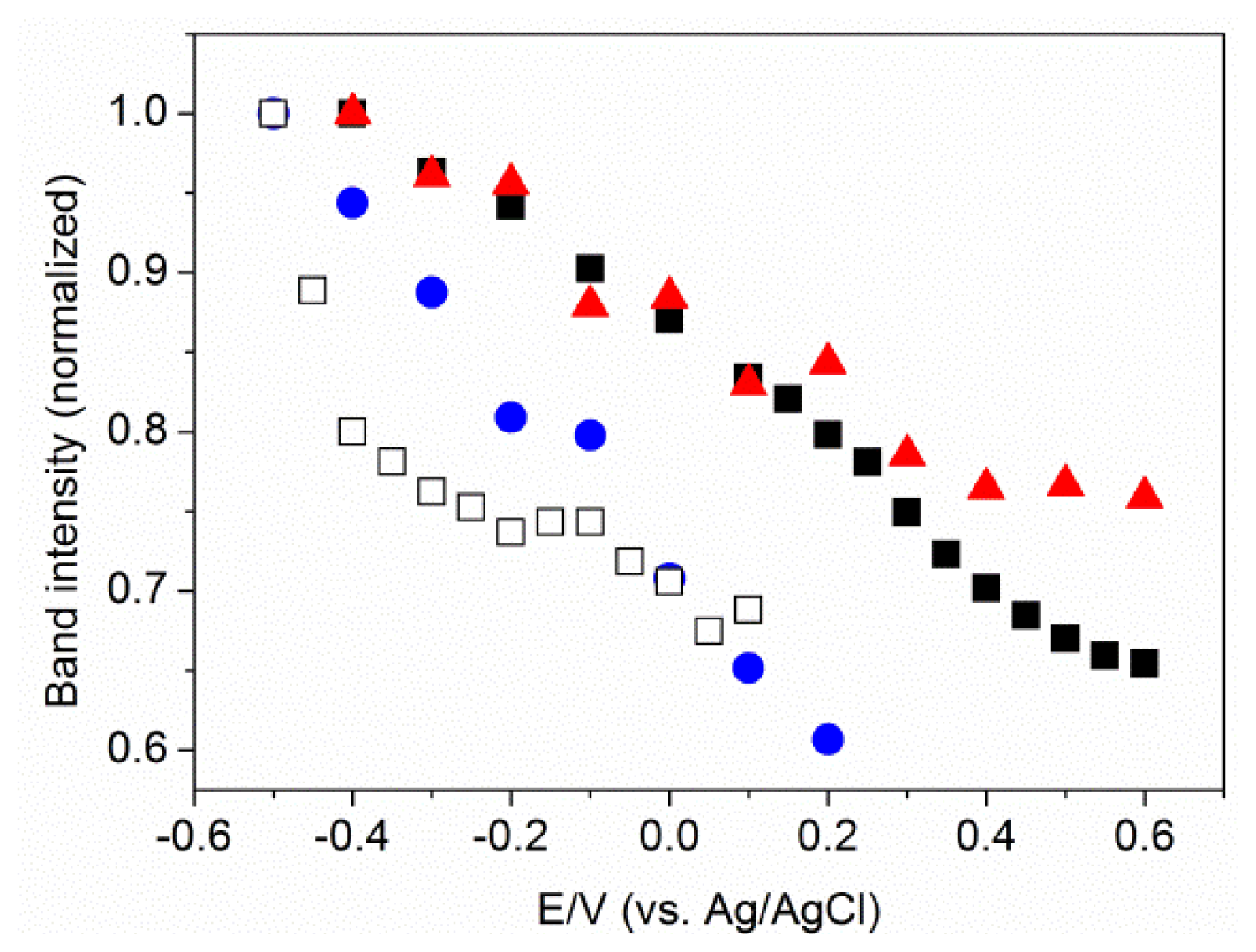
2.3. MBN in Mixed SAMs on Au Electrodes
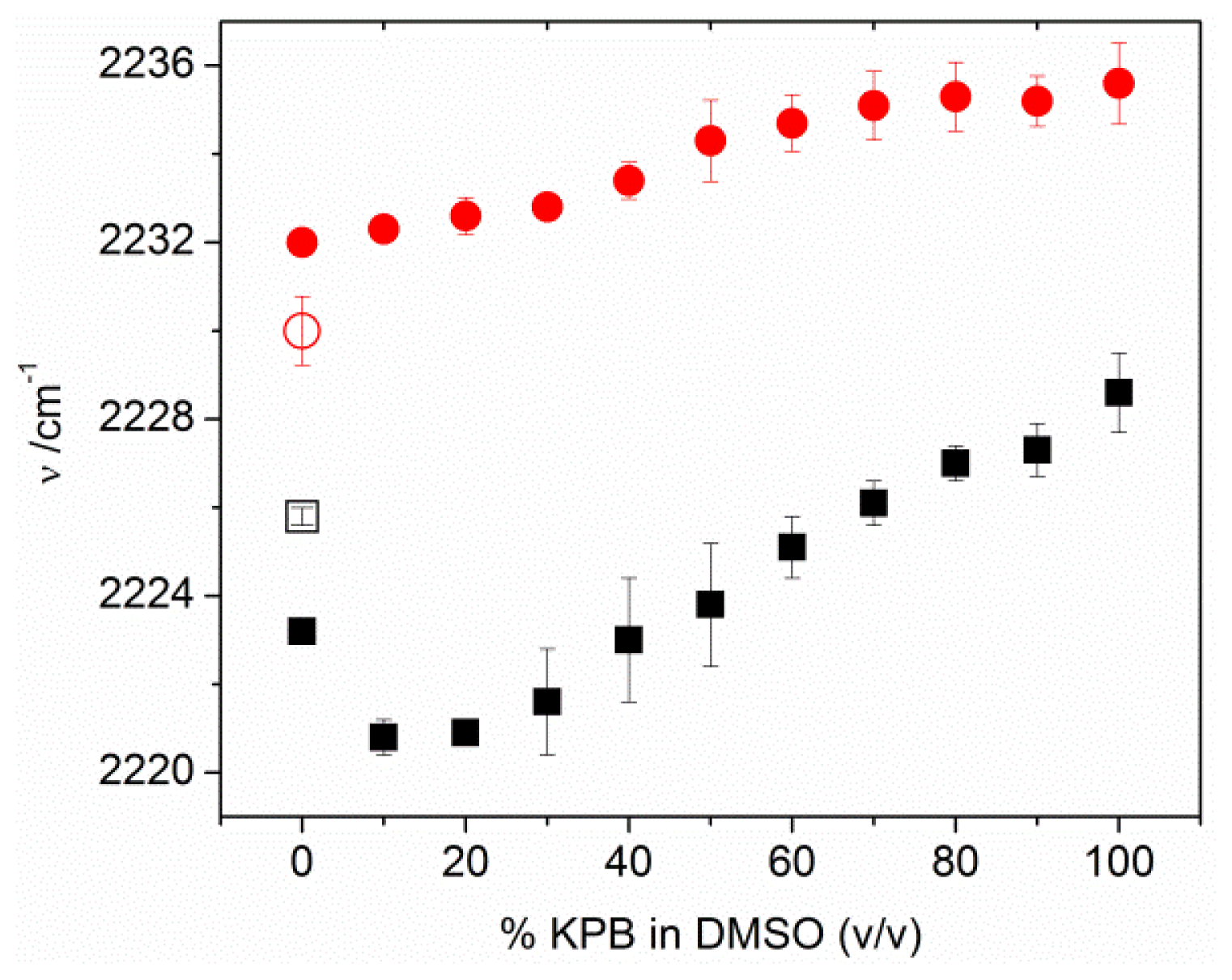
2.4. Factors Controlling the Zero-Field Nitrile Stretching Frequency
2.5. Electrostatic Model
2.6. The Effective Potential of Zero Charge
3. Experimental Section
3.1. Materials
3.2. SAM Preparation
3.3. Spectro-Electrochemical Measurements
4. Conclusions
Supplementary Information
ijms-13-07466-s001.pdfAcknowledgments
References
- Love, J.C.; Estroff, L.A.; Kriebel, J.K.; Nuzzo, R.G.; Whitesides, G.M. Self-assembled monolayers of thiolates on metals as a form of nanotechnology. Chem. Rev 2005, 105, 1103–1169. [Google Scholar]
- Samanta, D.; Sarkar, A. Immobilization of bio-macromolecules on self-assembled monolayers: Methods and sensor applications. Chem. Soc. Rev 2011, 40, 2567–2592. [Google Scholar]
- Mbindyo, J.K.N.; Mallouk, T.E.; Mattzela, J.B.; Kratochvilova, I.; Razavi, B.; Jackson, T.N.; Mayer, T.S. Template synthesis of metal nanowires containing monolayer molecular junctions. J. Am. Chem. Soc 2002, 124, 4020–4026. [Google Scholar]
- Smith, C.P.; White, H.S. Theory of the interfacial potential distribution and reversible voltammetric response of electrodes coated with electroactive molecular films. Anal. Chem 1992, 64, 2398–2405. [Google Scholar]
- Ramírez, P.; Granero, A.; Andreu, R.; Cuest, A.; Mulder, W.H.; Calvente, J.J. Potential of zero charge as a sensitive probe for the titration of ionizable self-assembled monolayers. Electrochem. Commun 2008, 10, 1548–1550. [Google Scholar]
- Oklejas, V.; Sjostrom, C.; Harris, J.M. SERS detection of the vibrational stark effect from nitrile-terminated SAMs to probe electric fields in the diffuse double-layer. J. Am. Chem. Soc 2002, 124, 2408–2409. [Google Scholar]
- Oklejas, V.; Harris, J.M. In-situ investigation of binary-component self-assembled monolayers: A SERS-based spectroelectrochemical study of the effects of monolayer composition on interfacial structure. Langmuir 2003, 19, 5794–5801. [Google Scholar]
- Suydam, I.T.; Snow, C.D.; Pande, V.S.; Boxer, S.G. Electric fields at the active site of an enzyme: Direct comparison of experiment with theory. Science 2006, 313, 200–204. [Google Scholar]
- Fafarman, A.T.; Sigala, P.A.; Herschlag, D.; Boxer, S.G. Nitrile bonds as infrared probes of electrostatics in ribonuclease S. J. Am. Chem. Soc 2010, 132, 12811–12813. [Google Scholar]
- Jo, H.; Culik, R.M.; Korendovych, I.V.; DeGrado, W.F.; Gai, F. Selective incorporation of nitrile-based infrared probes into proteins via cysteine alkylation. Biochemistry 2010, 49, 10354–10356. [Google Scholar]
- Schkolnik, G.; Utesch, T.; Salewski, J.; Tenger, K.; Millo, D.; Kranich, A.; Zebger, I.; Schulz, C.; Zimányi, L.; Rákhely, G.; et al. Mapping local electric fields in proteins at biomimetic interfaces. Chem. Commun 2012, 48, 70–72. [Google Scholar]
- Aschaffenburg, D.J.; Moog, R.S. Probing hydrogen bonding environments: Solvatochromic effects on the CN vibration of benzonitrile. J. Phys. Chem. B 2009, 113, 12736–12743. [Google Scholar]
- Ghosh, A.; Remorino, A.; Tucker, M.J.; Hochstrasser, R.M. 2D IR photon echo spectroscopy reveals hydrogen bond dynamics of aromatic nitriles. Chem. Phys. Lett 2009, 469, 325–330. [Google Scholar]
- Murgida, D.H.; Hildebrandt, P. Electron-transfer processes of cytochrome c at interfaces. New insights by surface-enhanced resonance raman spectroscopy. J. Phys. Chem. B 2001, 105, 1578–1586. [Google Scholar]
- Lecomte, S.; Hildebrandt, P.; Soulimane, T. Dynamics of the heterogeneous electron-transfer reaction of cytochrome c552 from thermus thermophilus. A time-resolved surface-enhanced resonance raman spectroscopic study. J. Phys. Chem. B 1999, 103, 10053–10064. [Google Scholar]
- Fafarman, A.T.; Sigala, P.A.; Schwans, J.P.; Fenn, T.D.; Herschlag, D.; Boxer, S.G. Quantitative, directional measurement of electric field heterogeneity in the active site of ketosteroid isomerase. Proc. Natl. Acad. Sci. USA 2012, 109, E299–E308. [Google Scholar]
- Stein, S.E. Infrared Spectra. NIST Chemistry WebBook, NIST Standard Reference Database Number 69; Linstrom, P.J., Mallard, W.G., Eds.; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2003. Available online: http://webbook.nist.gov accessed on 6 May 2012.
- Suydam, I.T.; Snow, C.D.; Pande, V.S.; Boxer, S.G. Electric fields at the active site of an enzyme: Direct comparison of experiment with theory. Science 2006, 313, 200–204. [Google Scholar]
- Natan, A.; Kuritz, N.; Kronik, L. Polarizability, susceptibility, and dielectric constant of nanometer-scale molecular films: A microscopic view. Adv. Funct. Mater 2010, 20, 2077–2084. [Google Scholar]
- Trasatti, S. Work function, electronegativity, and electrochemical behaviour of metals. J. Electroanal. Chem 1971, 33, 351–378. [Google Scholar]
- Valette, G. Hydrophilicity of metal surfaces, silver, gold and copper electrodes. J. Electroanal. Chem 1982, 139, 285–301. [Google Scholar]
- Wang, L.; Rangger, G.M.; Romaner, L.; Heimel, G.; Bučko, T.; Ma, Z.; Li, Q.; Shuai, Z.; Zojer, E. Electronic structure of self-assembled monolayers on Au(111) surfaces: The impact of backbone polarizability. Adv. Funct. Mater 2009, 19, 3766–3775. [Google Scholar]
- Heimel, G.; Romaner, L.; Zojer, E.; Brédas, J.L. Toward control of the metal-organic interfacial electronic structure in molecular electronics: A first-principles study on self-assembled monolayers of π-conjugated molecules on noble metals. Nano Lett 2007, 7, 932–940. [Google Scholar]
- Ballav, N.; Schüpbach, B.; Dethloff, O.; Feulner, P.; Terfort, A.; Zharnikov, M. Direct probing molecular twist and tilt in aromatic self-assembled monolayers. J. Am. Chem. Soc 2007, 129, 15416–15417. [Google Scholar]
- Frey, S.; Stadler, V.; Heister, K.; Eck, W.; Zharnikov, M.; Grunze, M. Structure of thioaromatic self-assembled monolayers on gold and silver. Langmuir 2001, 17, 2408–2415. [Google Scholar]
- Käfer, D.; Bashir, A.; Witte, G. Interplay of anchoring and ordering in aromatic self-assembled monolayers. J. Phys. Chem. C 2007, 111, 10546–10551. [Google Scholar]
- Han, S.W.; Lee, S.J.; Kim, K. Self-assembled monolayers of aromatic thiol and selenol on silver: Comparative study of adsorptivity and stability. Langmuir 2001, 17, 6981–6987. [Google Scholar]
- Schalnat, M.C.; Pemberton, J.E. Comparison of a fluorinated aryl thiol self-assembled monolayer with its hydrogenated counterpart on polycrystalline Ag substrates. Langmuir 2010, 26, 11862–11869. [Google Scholar]
- Shaw, S.K.; Lagutchev, A.; Dlott, D.D.; Gewirth, A.A. Sum-frequency spectroscopy of molecular adsorbates on low-index Ag surfaces: Effects of azimuthal rotation. Anal. Chem 2009, 81, 1154–1161. [Google Scholar]
- Akinaga, Y.; Nakajima, T.; Hirao, K. A density functional study on the adsorption of methanethiolate on the (111) surfaces of noble metals. J. Chem. Phys 2001, 114, 8555–8564. [Google Scholar]
- Ehler, T.T.; Malmberg, N.; Noe, L.J. Characterization of self-assembled alkanethiol monolayers on silver and gold using surface plasmon spectroscopy. J. Phys. Chem. B 1997, 101, 1268–1272. [Google Scholar]
- Gershevitz, O.; Sukenik, C.N. In situ FTIR-ATR analysis and titration of carboxylic acid-terminated SAMs. J. Am. Chem. Soc 2004, 126, 482–483. [Google Scholar]
- Burris, S.C.; Zhou, Y.; Maupin, W.A.; Ebelhar, A.J.; Daugherty, M.W. The effect of surface preparation on apparent surface pKa’s of ω-mercaptocarboxylic acid self-assembled monolayers on polycrystalline gold. J. Phys. Chem. C 2008, 112, 6811–6815. [Google Scholar]
- Emets, V.V.; Damaski, B.B. The relation between the potential of zero charge and work function for sp-metals. Russ. J. Electrochem 2009, 45, 45–57. [Google Scholar]
- Trasatti, S. The concept and physical meaning of absolute electrode potential: A reassessment. J. Electroanal. Chem 1982, 172, 1–13. [Google Scholar]
- Heimel, G.; Romaner, L.; Zojer, E.; Bredas, J.L. The interface energetics of self-assembled monolayers on metals. Acc. Chem. Res 2008, 41, 721–729. [Google Scholar]
- Natan, A.; Kronik, L.; Haick, H.; Tung, R.T. Electrostatic properties of ideal and non-ideal polar organic monolayers: Implications for electronic devices. Adv. Mater 2007, 19, 4103–4117. [Google Scholar]
- Alloway, D.M.; Graham, A.L.; Yang, X.; Mudalige, A.; Colorado, R., Jr; Wysocki, V.H.; Pemberton, J.E.; Lee, T.R.; Wysocki, R.J.; Armstrong, N.R. Tuning the effective work function of gold and silver using ω-functionalized alkanethiols: Varying surface composition through dilution and choice of terminal groups. J. Phys. Chem C 2009, 113, 20328–20334. [Google Scholar]
- Wisitruangsakul, N.; Zebger, I.; Ly, K.H.; Murgida, D.H.; Egkasit, S.; Hildebrandt, P. Redox-linked protein dynamics of cytochrome C probed by time-resolved surface enhanced infrared absorption spectroscopy. Phys. Chem. Chem. Phys 2008, 10, 5276–5286. [Google Scholar]
- Wackerbarth, H.; Klar, U.; Gunther, W.; Hildebrandt, P. Novel time-resolved surface-enhanced (resonance) raman spectroscopic technique for studying the dynamics of interfacial processes: Application to the electron transfer reaction of cytochrome c at a silver electrode. Appl. Spectrosc 1999, 53, 283–291. [Google Scholar]
- Ly, K.H.; Wisitruangsakul, N.; Sezer, M.; Feng, J.J.; Kranich, A.; Weidinger, I.; Zebger, I.; Murgida, D.H.; Hildebrandt, P. Electric field effects on the interfacial electron transfer and protein dynamics of cytochrome c. J. Electroanal. Chem. 2011, 660, 367–376. [Google Scholar]
- Murgida, D.H.; Hildebrandt, P. Redox and redox-coupled processes of heme proteins and enzymes at electrochemical interfaces. Phys. Chem. Chem. Phys 2005, 7, 3773–3784. [Google Scholar]
- Ly, H.K.; Sezer, M.; Wisitruangsakul, N.; Feng, J.J.; Kranich, A.; Millo, D.; Weidinger, I.M.; Zebger, I.; Murgida, D.H.; Hildebrandt, P. Surface-enhanced vibrational spectroscopy for probing transient interactions of proteins with biomimetic interfaces: Electric field effects on structure, dynamics and function of cytochrome c. FEBS J 2011, 278, 1382–1390. [Google Scholar]



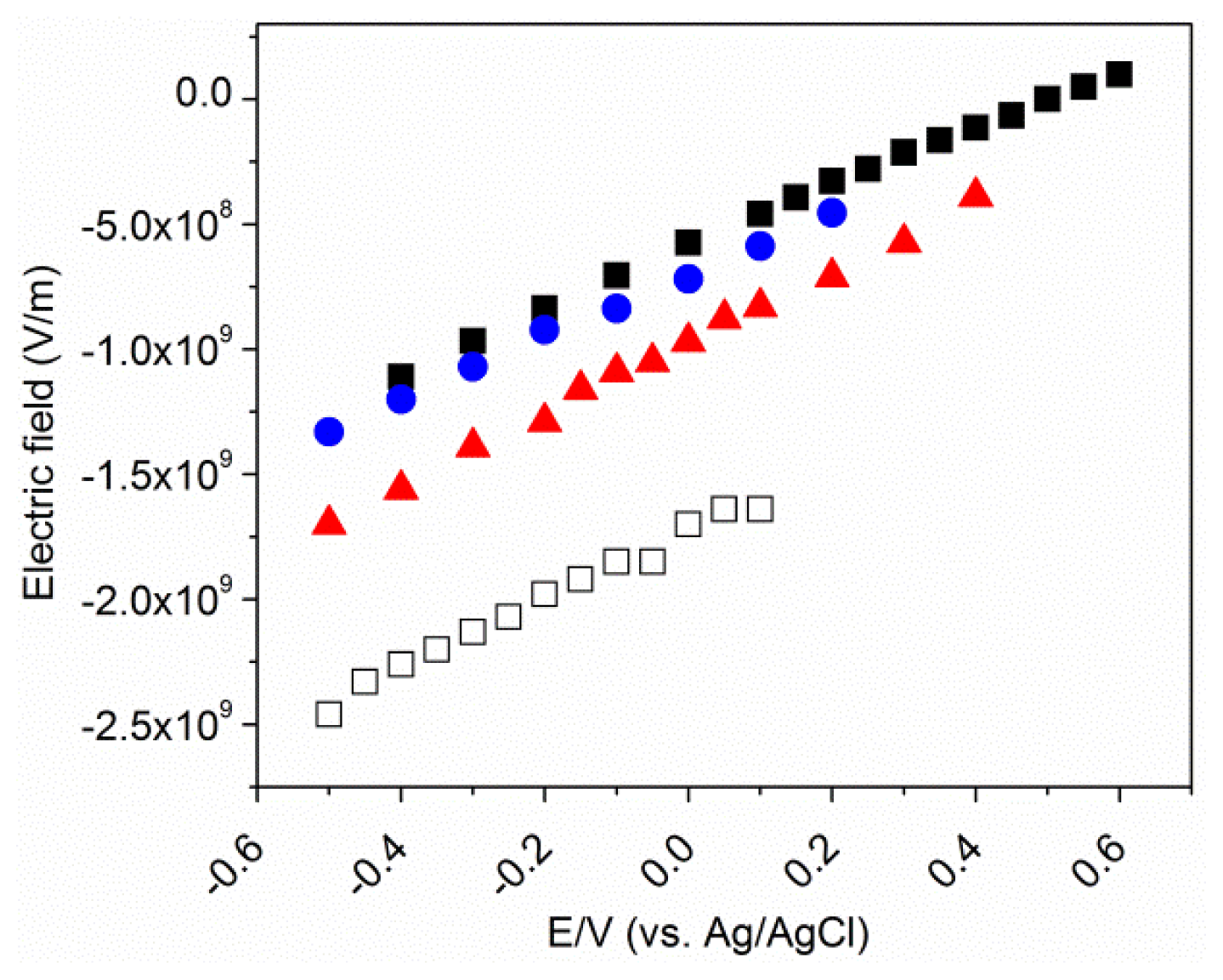
| Slope b (cm−1/V) | Intercept b (cm−1) | k c (CV−1m−2) | E0, exp. c (V) | σ0 c (Cm−2) | E0, calc. d (V) | E0, calc. e (V) | |
|---|---|---|---|---|---|---|---|
| Ag/MBN | 8.3 | 2227 | −0.117 | 1.277 | 1.005 | 1.685 | 1.936 |
| Au/MBN | 8.0 | 2230 | −0.186 | 0.425 | 0.199 | 0.215 | 0.402 |
| Au/TP f/MBN | 7.5 | 2229 | −0.153 | 0.587 | 0.267 | - | - |
| Au/MHA/MBN | 8.7 | 2228 | −0.232 | 0.621 | 0.330 | - | - |
© 2012 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Schkolnik, G.; Salewski, J.; Millo, D.; Zebger, I.; Franzen, S.; Hildebrandt, P. Vibrational Stark Effect of the Electric-Field Reporter 4-Mercaptobenzonitrile as a Tool for Investigating Electrostatics at Electrode/SAM/Solution Interfaces. Int. J. Mol. Sci. 2012, 13, 7466-7482. https://doi.org/10.3390/ijms13067466
Schkolnik G, Salewski J, Millo D, Zebger I, Franzen S, Hildebrandt P. Vibrational Stark Effect of the Electric-Field Reporter 4-Mercaptobenzonitrile as a Tool for Investigating Electrostatics at Electrode/SAM/Solution Interfaces. International Journal of Molecular Sciences. 2012; 13(6):7466-7482. https://doi.org/10.3390/ijms13067466
Chicago/Turabian StyleSchkolnik, Gal, Johannes Salewski, Diego Millo, Ingo Zebger, Stefan Franzen, and Peter Hildebrandt. 2012. "Vibrational Stark Effect of the Electric-Field Reporter 4-Mercaptobenzonitrile as a Tool for Investigating Electrostatics at Electrode/SAM/Solution Interfaces" International Journal of Molecular Sciences 13, no. 6: 7466-7482. https://doi.org/10.3390/ijms13067466