Target Molecular Simulations of RecA Family Protein Filaments
Abstract
:1. Introduction
2. Results and Discussion
2.1. Homology Models Construction and Evaluation
2.2. TMD Conformational Calculations
3. Experimental Section
3.1. Homology Modeling and Refinement of the Models
3.2. TMD Simulations
4. Conclusions
Acknowledgment
References
- Seitz, E.M.; Brockman, J.P.; Sandler, S.J.; Clark, A.J.; Kowalczykowski, S.C. RadA protein is an archaeal RecA protein homolog that catalyzes DNA strand exchange. Genes Dev 1998, 12, 1248–1253. [Google Scholar]
- Kowalczykowski, S.C.; Dixon, D.A.; Eggleston, A.K.; Lauder, S.D.; Rehrauer, W.M. Biochemistry of homologous recombination in Escherichia coli. Microbiol. Rev 1994, 58, 401–465. [Google Scholar]
- Roca, A.I.; Cox, M.M. RecA protein: Structure, function, and role in recombinational DNA repair. Prog. Nucleic Acid Res. Mol. Biol 1997, 56, 129–223. [Google Scholar]
- DiRuggiero, J.; Santangelo, N.; Nackerdien, Z.; Ravel, J.; Robb, F.T. Repair of extensive ionizing-radiation DNA damage at 95 degrees C in the hyperthermophilic archaeon Pyrococcus furiosus. J. Bacteriol 1997, 179, 4643–4645. [Google Scholar]
- Kil, Y.V.; Glazunov, E.A.; Lanzov, V.A. Characteristic thermodependence of the RadA recombinase from the hyperthermophilic archaeon Desulfurococcus amylolyticus. J. Bacteriol 2005, 187, 2555–2557. [Google Scholar]
- Kowalczykowski, S.C.; Eggleston, A.K. Homologous pairing and DNA strand-exchange proteins. Annu. Rev. Biochem 1994, 63, 991–1043. [Google Scholar]
- West, S.C. Molecular views of recombination proteins and their control. Nat. Rev. Mol. Cell Biol 2003, 4, 435–445. [Google Scholar]
- Cox, M.M. The bacterial reca protein as a motor protein. Annu. Rev. Microbiol 2003, 57, 551–577. [Google Scholar]
- Aihara, H.; Ito, Y.; Kurumizaka, H.; Yokoyama, S.; Shibata, T. The N-terminal domain of the human Rad51 protein binds DNA: Structure and a DNA binding surface as revealed by NMR. J. Mol. Biol 1999, 290, 495–504. [Google Scholar]
- Kinebuchi, T.; Kagawa, W.; Kurumizaka, H.; Yokoyama, S. Role of the N-terminal domain of the human DMC1 protein in octamer formation and DNA binding. J. Biol. Chem 2005, 280, 28382–28387. [Google Scholar]
- Eggler, A.L.; Lusetti, S.L.; Cox, M.M. The C terminus of the Escherichia coli RecA protein modulates the DNA binding competition with single-stranded DNA-binding protein. J. Biol. Chem 2003, 278, 16389–16396. [Google Scholar]
- Wu, Y.; He, Y.; Moya, I.A.; Qian, X.; Luo, Y. Crystal structure of archaeal recombinase RadA: A snapshot of its extended conformation. Mol. Cell 2004, 15, 423–435. [Google Scholar]
- Ariza, A.; Richard, D.J.; White, M.F.; Bond, C.S. Conformational flexibility revealed by the crystal structure of a crenarchaeal RadA. Nucleic Acids Res 2005, 33, 1465–1473. [Google Scholar]
- Yang, S.; Yu, X.; Seitz, E.M.; Kowalczykowski, S.C.; Egelman, E.H. Archaeal RadA protein binds DNA as both helical filaments and octameric rings. J. Mol. Biol 2001, 314, 1077–1085. [Google Scholar]
- McIlwraith, M.J.; Hall, D.R.; Stasiak, A.Z.; Stasiak, A.; Wigley, D.B.; West, S.C. RadA protein from Archaeoglobus fulgidus forms rings, nucleoprotein filaments and catalyses homologous recombination. Nucleic Acids Res 2001, 29, 4509–4517. [Google Scholar]
- Lee, M.-H.; Leng, C.-H.; Chang, Y.-C.; Chou, C.-C.; Chen, Y.-K.; Hsu, F.-F.; Chang, C.-S.; Wang, A.H.J.; Wang, T.-F. Self-polymerization of archaeal RadA protein into long and fine helical filaments. Biochem. Biophys. Res. Commun 2004, 323, 845–851. [Google Scholar]
- Chen, L.-T.; Ko, T.-P.; Chang, Y.-C.; Lin, K.-A.; Chang, C.-S.; Wang, A.H.J.; Wang, T.-F. Crystal structure of the left-handed archaeal RadA helical filament: Identification of a functional motif for controlling quaternary structures and enzymatic functions of RecA family proteins. Nucleic Acids Res 2007, 35, 1787–1801. [Google Scholar]
- Schlitter, J.; Engels, M.; Krüger, P.; Jacoby, E.; Wollmer, A. Targeted molecular dynamics simulation of conformational change: Application to the T↔R transition in insulin. Mol. Simul 1993, 10, 291–308. [Google Scholar]
- Ma, J.; Karplus, M. Molecular switch in signal transduction: Reaction paths of the conformational changes in ras p21. Proc. Natl. Acad. Sci. USA 1997, 94, 11905–11910. [Google Scholar]
- Ferrara, P.; Apostolakis, J.; Caflisch, A. Targeted molecular dynamics simulations of protein unfolding. J. Phys. Chem 2000, 104, 4511–4518. [Google Scholar]
- Wang, Y.-T.; Liao, J.-M.; Chen, C.-L.; Su, Z.-Y.; Chen, C.-H.; Hu, J.-J. Potential of mean force for human lysozyme-camelid vhh hl6 antibody interaction studies. Chem. Phys. Lett 2008, 455, 284–288. [Google Scholar]
- Wang, Y.-T.; Su, Z.-Y.; Chen, C.-L. Potential of mean force of the hepatitis C virus core protein-monoclonal 19D9D6 antibody interaction. Biophys. Chem 2009, 145, 86–90. [Google Scholar]
- Wang, Y.-T.; Su, Z.-Y.; Liao, J.-M.; Chen, C.-L. Potential of mean force for Syrian hamster prion epitope protein—Monoclonal fab 3f4 antibody interaction studies. Eur. J. Med. Chem 2009, 44, 3504–3508. [Google Scholar]
- Liu, J.; Bradley, R.; Eckmann, D.M.; Ayyaswamy, P.S.; Radhakrishnan, R. Multiscale modeling of functionalized nanocarriers in targeted drug delivery. Curr. Nanosci 2011, 7, 727–735. [Google Scholar]
- Liu, J.; Weller, G.E.R.; Zern, B.; Ayyaswamy, P.S.; Eckmann, D.M.; Muzykantov, V.R.; Radhakrishnan, R. Computational model for nanocarrier binding to endothelium validated using in vivo, in vitro, and atomic force microscopy experiments. Proc. Natl. Acad. Sci. USA 2010, 107, 16530–16535. [Google Scholar]
- Bahar, I.; Erman, B.; Monnerie, L. Kinematics of polymer chains with freely rotating bonds in a restrictive environment. 2. Conformational and orientational correlations. Macromolecules 1992, 25, 6315–6321. [Google Scholar]
- Smith, C.A.; Kortemme, T. backrub-like backbone simulation recapitulates natural protein conformational variability and improves mutant side-chain prediction. J. Mol. Biol 2008, 380, 742–756. [Google Scholar]
- Gunasekaran, K.; Gomathi, L.; Ramakrishnan, C.; Chandrasekhar, J.; Balaram, P. Conformational interconversions in peptide β-turns: Analysis of turns in proteins and computational estimates of barriers. J. Mol. Biol 1998, 284, 1505–1516. [Google Scholar]
- Ariza, A.; Richard, D.J.; White, M.F.; Bond, C.S. Conformational flexibility revealed by the crystal structure of a crenarchaeal RadA. Nucleic Acids Res 2005, 33, 1465–1473. [Google Scholar]
- Shin, D.S.; Pellegrini, L.; Daniels, D.S.; Yelent, B.; Craig, L.; Bates, D.; Yu, D.S.; Shivji, M.K.; Hitomi, C.; Arvai, A.S.; et al. Full-length archaeal Rad51 structure and mutants: Mechanisms for RAD51 assembly and control by BRCA2. EMBO J 2003, 22, 4566–4576. [Google Scholar]
- Thompson, J.D.; Gibson, T.J.; Plewniak, F.; Jeanmougin, F.; Higgins, D.G. The CLUSTAL_X windows interface: Flexible strategies for multiple sequence alignment aided by quality analysis tools. Nucleic Acids Res 1997, 25, 4876–4882. [Google Scholar]
- Fiser, A.; Do, R.K.G.; Šali, A. Modeling of loops in protein structures. Protein Sci 2000, 9, 1753–1773. [Google Scholar]
- Wu, Y.; Qian, X.; He, Y.; Moya, I.A.; Luo, Y. Crystal structure of an ATPase-active form of Rad51 homolog from methanococcus voltae. J. Biol. Chem 2005, 280, 722–728. [Google Scholar]
- Case, D.A.; Cheatham, T.E.; Darden, T.; Gohlke, H.; Luo, R.; Merz, K.M.; Onufriev, A.; Simmerling, C.; Wang, B.; Woods, R.J. The Amber biomolecular simulation programs. J. Comput. Chem 2005, 26, 1668–1688. [Google Scholar]
- Laskowski, R.A.; Macarthur, M.W.; Moss, D.S.; Thornton, J.M. PROCHECK: A program to check the stereochemical quality of protein structures. J. Appl. Cryst 1993, 26, 283–291. [Google Scholar]
- Wiederstein, M.; Sippl, M.J. ProSA-web: Interactive web service for the recognition of errors in three-dimensional structures of proteins. Nucleic Acids Res 2007, 35, W407–W410. [Google Scholar]
- Jiang, W.; Hardy, D.J.; Phillips, J.C.; MacKerell, A.D.; Schulten, K.; Roux, B.T. High-performance scalable molecular dynamics simulations of a polarizable force field based on classical drude oscillators in NAMD. J. Phys. Chem. Lett 1997, 2, 87–92. [Google Scholar]
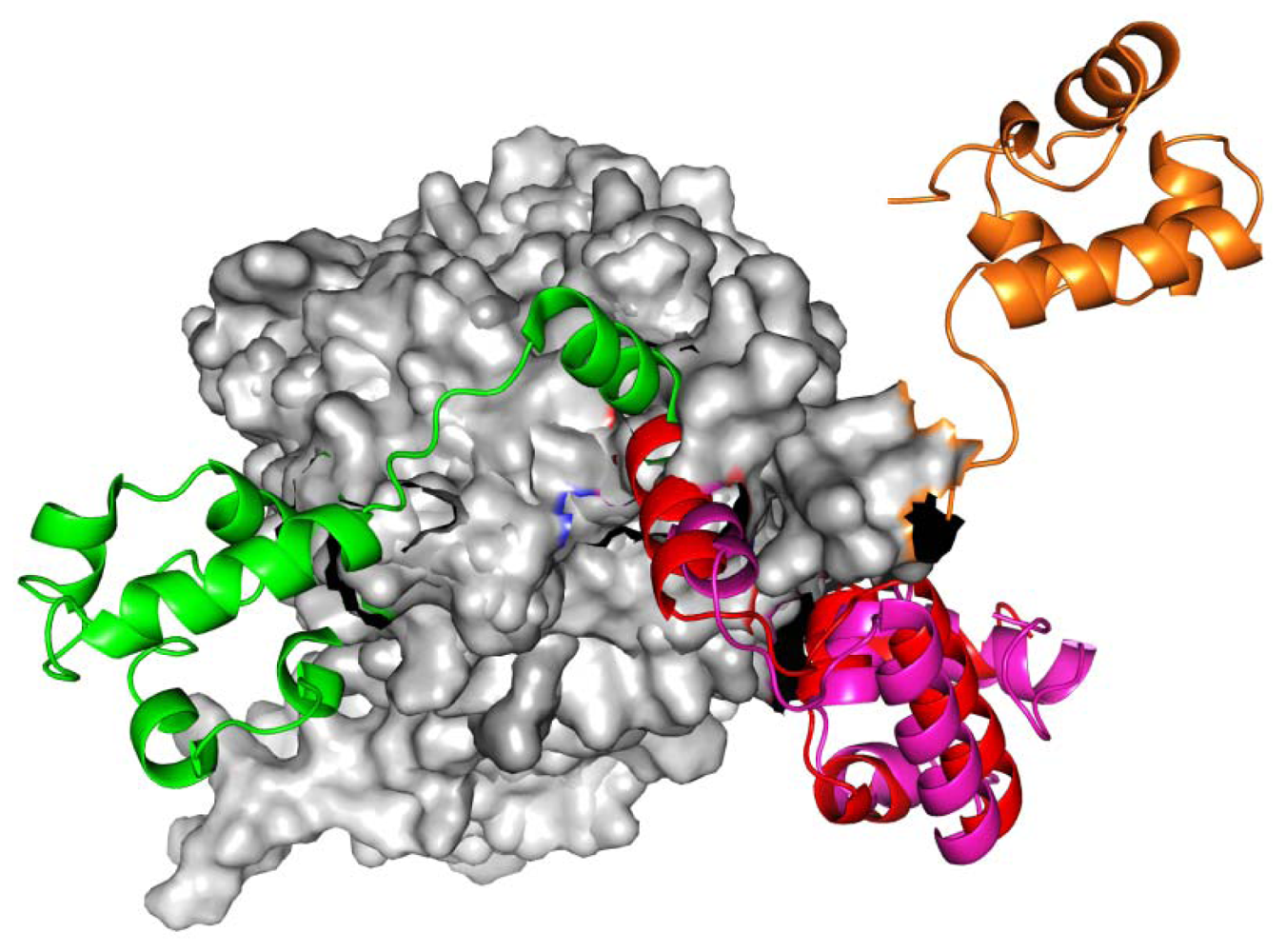


 , Left-hand RadA filaments;
, Left-hand RadA filaments;
 , Close-ring RadA filaments;
, Close-ring RadA filaments;
 , MvRadA filaments;
, MvRadA filaments;
 , Right-hand RadA filaments.
, Right-hand RadA filaments.
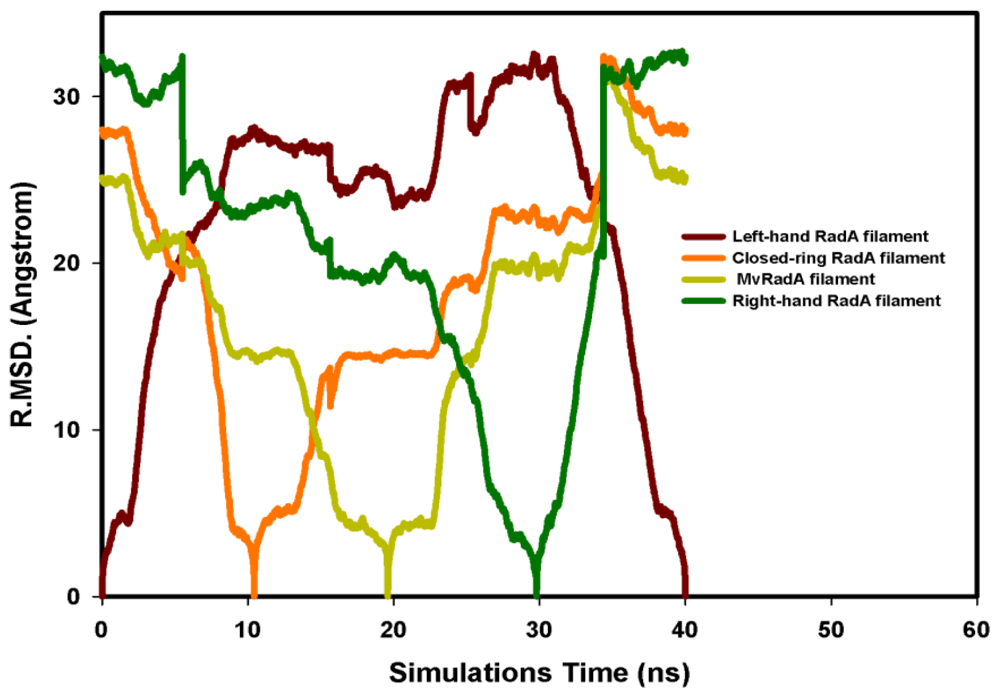
 , Left-hand RadA filaments;
, Left-hand RadA filaments;
 , Close-ring RadA filaments;
, Close-ring RadA filaments;
 , MvRadA filaments;
, MvRadA filaments;
 , Right-hand RadA filaments.
, Right-hand RadA filaments.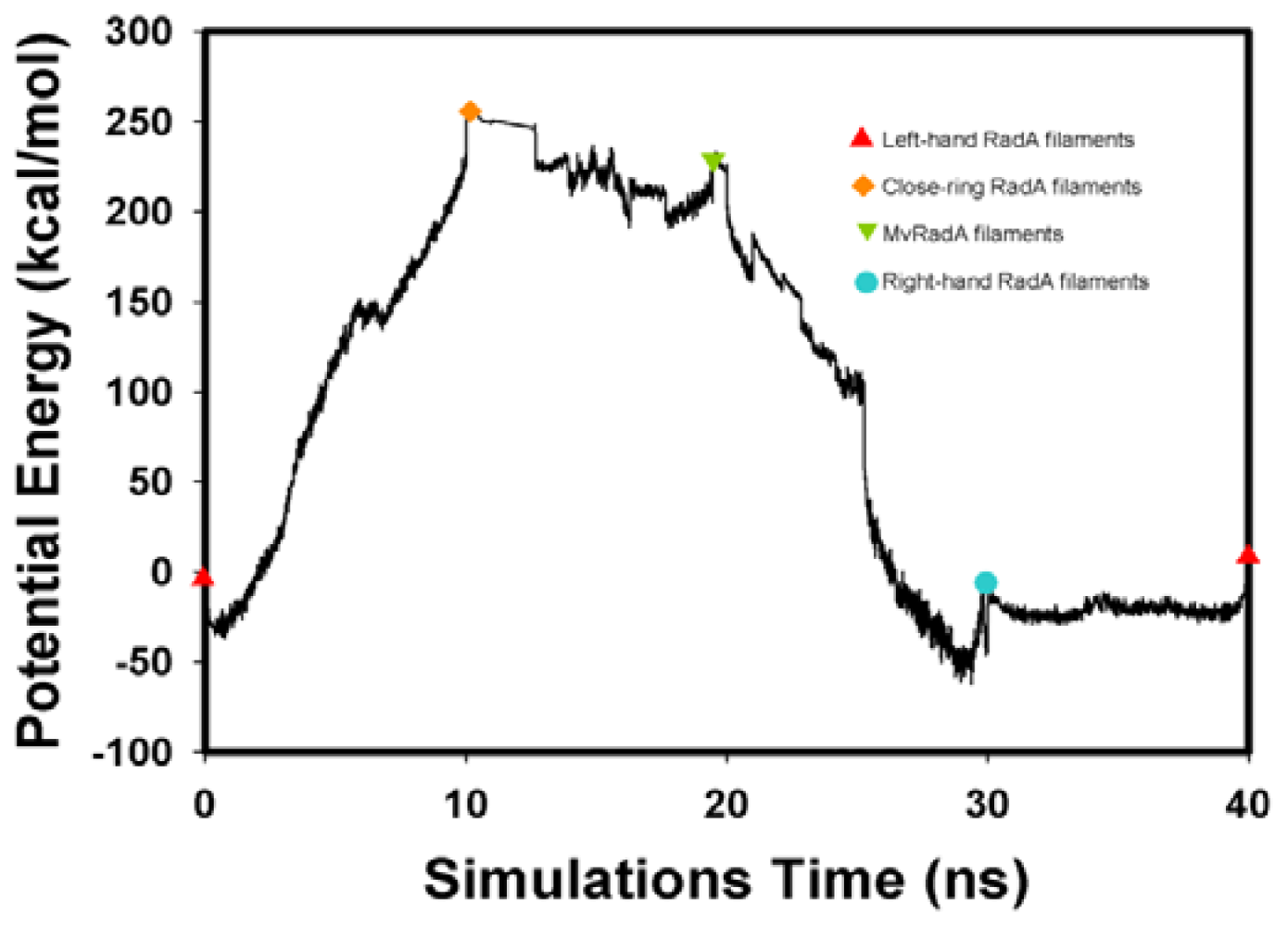
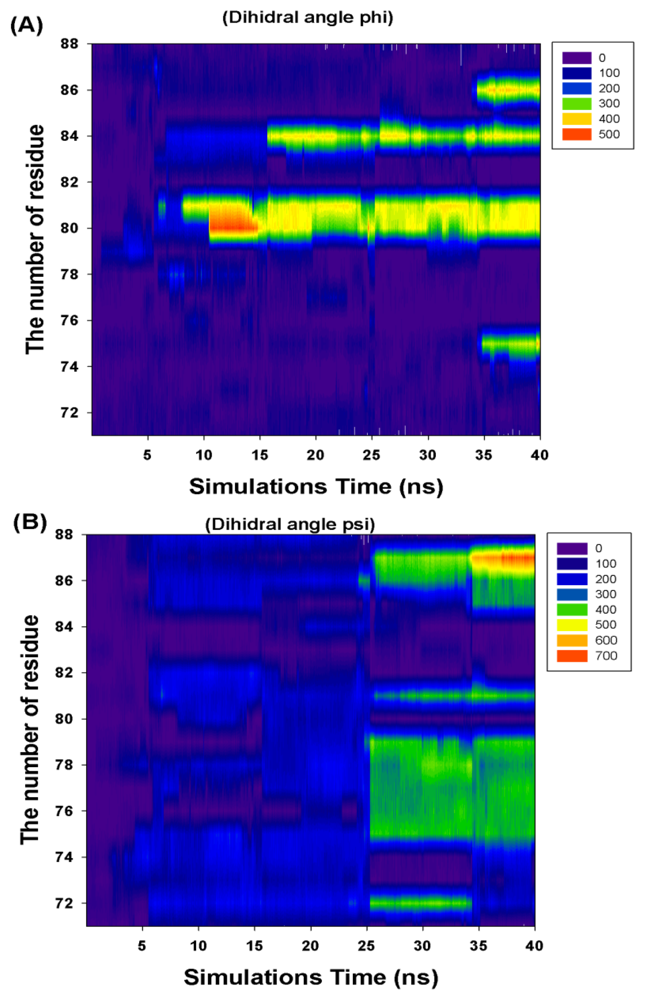
| Residue Number | Cumulate Changed Dihedral Angles | |
|---|---|---|
| Phi (Φ) | Psi (Ψ) | |
| I71 | 0 | 0 |
| R72 | 0 | 360 |
| F73 | 360 | 0 |
| K74 | 0 | 0 |
| T75 | 360 | 360 |
| A76 | 0 | 360 |
| L77 | 0 | 360 |
| E78 | 0 | 360 |
| V79 | 0 | 360 |
| K80 | 360 | 0 |
| K81 | 360 | 360 |
| E82 | 0 | 0 |
| R83 | 0 | 0 |
| M84 | 360 | 0 |
| N85 | 0 | 360 |
| V86 | 360 | 360 |
| K87 | 0 | 720 |
| K88 | 0 | 0 |
© 2012 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Su, Z.-Y.; Lee, W.-J.; Su, W.-S.; Wang, Y.-T. Target Molecular Simulations of RecA Family Protein Filaments. Int. J. Mol. Sci. 2012, 13, 7138-7148. https://doi.org/10.3390/ijms13067138
Su Z-Y, Lee W-J, Su W-S, Wang Y-T. Target Molecular Simulations of RecA Family Protein Filaments. International Journal of Molecular Sciences. 2012; 13(6):7138-7148. https://doi.org/10.3390/ijms13067138
Chicago/Turabian StyleSu, Zhi-Yuan, Wen-Jay Lee, Wan-Sheng Su, and Yeng-Tseng Wang. 2012. "Target Molecular Simulations of RecA Family Protein Filaments" International Journal of Molecular Sciences 13, no. 6: 7138-7148. https://doi.org/10.3390/ijms13067138




