Extraction Optimization of Water-Extracted Mycelial Polysaccharide from Endophytic Fungus Fusarium oxysporum Dzf17 by Response Surface Methodology
Abstract
:1. Introduction
2. Results and Discussion
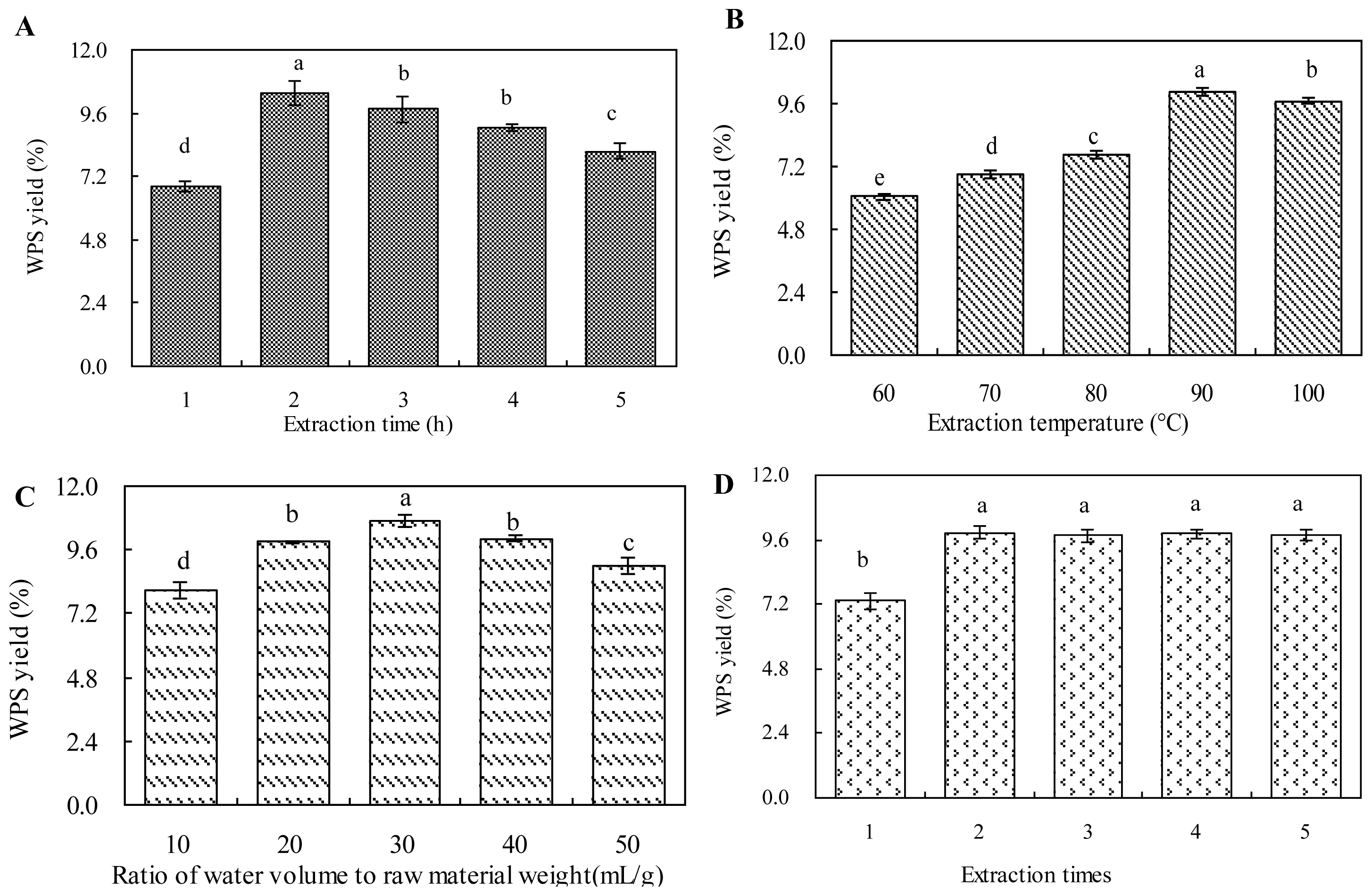
2.1. Effect of Extraction Time on WPS Yield
2.2. Effect of Extraction Temperature on WPS Yield
2.3. Effect of Ratio of Water to Raw Material on WPS Yield
2.4. Effect of Extraction Times on WPS Yield
2.5. Model Building and Statistical Analysis
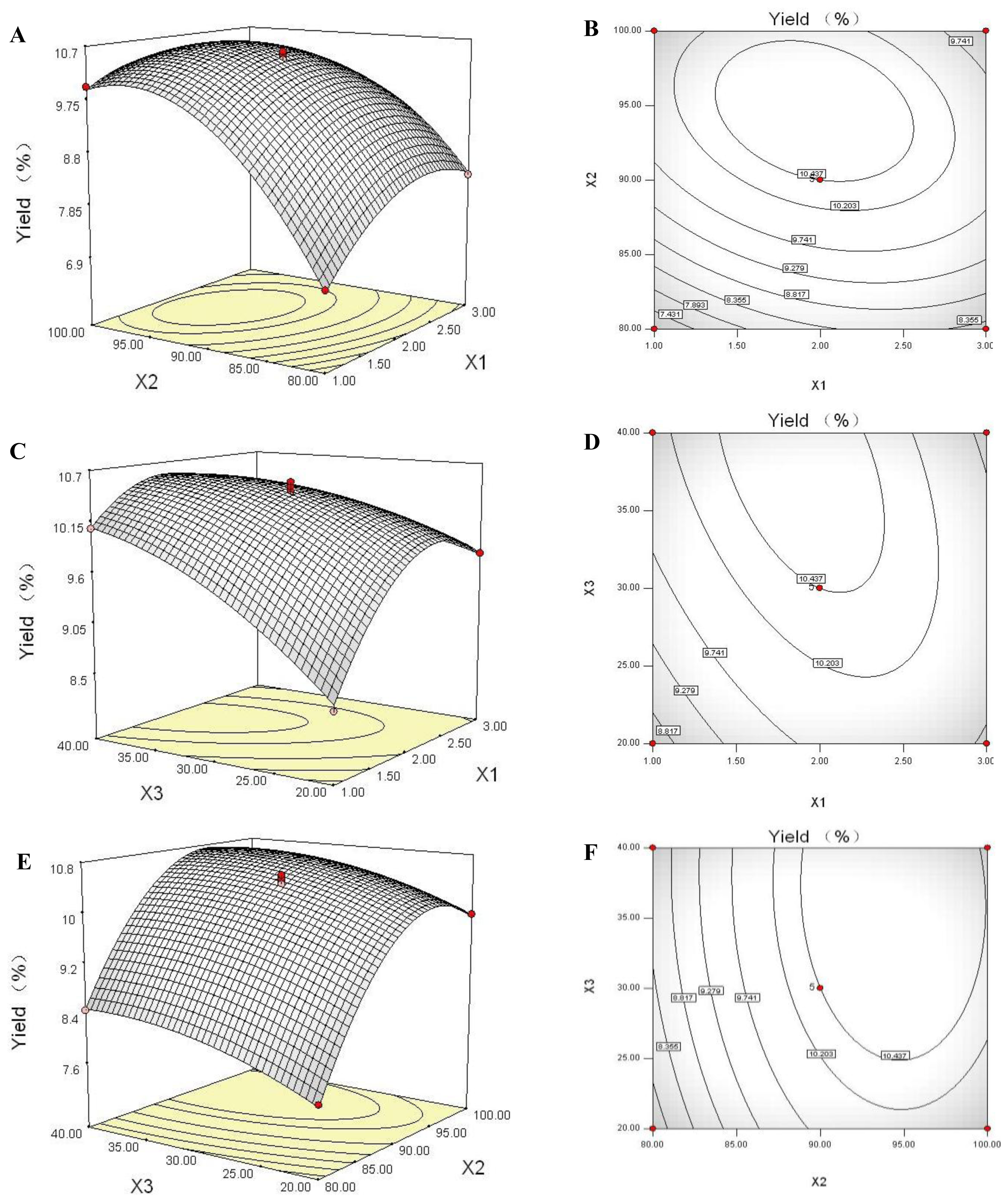
2.6. Response Surface Plot and Contour Plot Analyses
2.7. Optimization of the Extraction Parameters and Validation of the Model
3. Experimental Section
3.1. Cultivation of Fusarium oxysporum Dzf17
3.2. Extraction of WPS
3.3. Experimental Design
4. Conclusions
Acknowledgments
References
- Wilson, D. Endophyte: The evolution of a term, and clarification of its use and definition. Oikos 1995, 73, 274–276. [Google Scholar]
- Strobel, G.A. Harnessing endophytes for industrial microbiology. Curr. Opin. Microbiol 2006, 9, 240–244. [Google Scholar]
- Gimenez, C.; Cabrera, R.; Reina, M.; Gonzalez-Coloma, A. Fungal endophytes and their role in plant protection. Curr. Org. Chem 2007, 11, 707–720. [Google Scholar]
- Li, C.; Gao, J.; Nan, Z. Interactions of Neotyphodium gansuense, Achnatherum inebrians, and plant-pathogenic fungi. Mycol. Res 2007, 111, 1220–1227. [Google Scholar]
- Berg, G. Plant-microbe interactions promoting plant growth and health: Perspectives for controlled use of microorganisms in agriculture. Appl. Microbiol. Biotechnol 2009, 84, 11–18. [Google Scholar]
- Kharwar, R.N.; Mishra, A.; Gond, S.K.; Stierle, A.; Stierle, D. Anticancer compounds derived from fungal endophytes: Their importance and future challenges. Nat. Prod. Rep 2011, 28, 1208–1228. [Google Scholar]
- Zhao, J.; Shan, T.; Mou, Y.; Zhou, L. Plant-derived bioactive compounds produced by endophytic fungi. Mini-Rev. Med. Chem 2011, 11, 159–168. [Google Scholar]
- Wang, J.; Zhang, Z.; Tan, R. Stimulation of artemisinin produciton in Artemisia annua hairy roots by the elicitor from the endophytic Colletotrichum sp. Biotechnol. Lett 2001, 23, 857–860. [Google Scholar]
- Zhang, R.; Li, P.; Xu, L.; Chen, Y.; Sui, P.; Zhou, L.; Li, J. Enhancement of diosgenin production in Dioscorea zingiberensis cell culture by oligosaccharide elicitor from its endophytic fungus Fusarium oxysporum Dzf17. Nat. Prod. Commun 2009, 4, 1459–1462. [Google Scholar]
- Li, P.; Mou, Y.; Shan, T.; Xu, J.; Li, Y.; Lu, S.; Zhou, L. Effects of polysaccharide elicitors from endophytic Fusarium oxysporium Dzf17 on the growth and diosgenin production in cell suspension culture of Dioscorea zingiberensis. Molecules 2011, 16, 9003–9016. [Google Scholar]
- Li, P.; Mao, Z.; Lou, J.; Li, Y.; Mou, Y.; Lu, S.; Peng, Y.; Zhou, L. Enhancement of diosgenin production in Dioscorea zingiberensis cell cultures by oligosaccharides from its endophytic fungus Fusarium oxysporum Dzf17. Molecules 2011, 16, 10631–10644. [Google Scholar]
- Li, N.; Ni, J. Treatment of wastewater from Dioscorea zingiberensis tubes used for producing steroid hormones in a microbial fuel cell. Bioresour. Technol 2011, 102, 2731–2735. [Google Scholar]
- Liu, W.; Huang, W.; Sun, W.L.; Zhu, Y.L.; Ni, J.R. Production of diosgenin from yellow ginger (Dioscorea zingiberensis C. H. Wright) saponins by commercial cellulase. World J. Microbiol. Biotechnol 2010, 26, 1171–1180. [Google Scholar]
- Li, P.; Luo, C.; Sun, W.; Lu, S.; Mou, Y.; Peng, Y.; Zhou, L. In vitro antioxidant activities of polysaccharides from endophytic fungus Fusarium oxysporum Dzf17. Afr. J. Microbiol. Res 2011, 5, 5990–5993. [Google Scholar]
- Bezerra, M.A.; Santelli, R.E.; Oliveira, E.P.; Villar, L.S.; Escaleira, L.A. Response surface methodology (RSM) as a tool for optimization in analytical chemistry. Talanta 2008, 76, 965–977. [Google Scholar]
- Dahiya, S.; Singh, N.; Rana, J.S. Optimization of growth parameters of phytase producing fungus using RSM. J. Sci. Ind. Res 2009, 68, 955–959. [Google Scholar]
- Ferreira, S.L.C.; Bruns, R.E.; Ferreira, H.S.; Matos, G.D.; David, J.M.; Brandao, G.C.; da Silva, E.G.P.; Portugal, L.A.; dos Reis, P.S.; Souza, A.S.; et al. Box-Behnken design: An alternative for the optimization of analytical methods. Anal. Chim. Acta 2007, 597, 179–186. [Google Scholar]
- Dong, C.-H.; Xie, X.-Q.; Wang, X.-L.; Zhan, Y.; Yao, Y.-J. Application of Box-Behnken design in optimisation for polysaccharides extraction from cultured mycelium of Cordyceps sinensis. Food Bioprod. Process 2009, 87, 139–144. [Google Scholar]
- Renjie, L. Optimization of extraction process of Glycyrrhiza glabra polysaccharides by response surface methodology. Carbohydr. Polym 2008, 74, 858–861. [Google Scholar]
- Zhongdong, L.; Guohua, W.; Yunchang, G.; Kennedy, J.F. Image study of pectin extraction from orange skin assisted by microwave. Carbohydr. Polym 2006, 64, 548–552. [Google Scholar]
- Cai, W.; Gu, X.; Tang, J. Extraction, purification, and characterization of the polysaccharides from Opuntia milpa Alta. Carbohydr. Polym 2008, 71, 403–410. [Google Scholar]
- Oosterveld, A.; Beldman, G.; Schols, H.A.; Voragen, A.G.J. Arabinose and ferulic acid rich pectic polysaccharides extracted from sugar beet pulp. Carbohydr. Res 1996, 288, 143–153. [Google Scholar]
- Vinogradov, E.V.; Brade, L.; Brade, H.; Holst, O. Structural and serological characterization of the O-antigenic polysaccharide of the lipopolysaccharide from Acinetobacter baumannii strain 24. Carbohydr. Res 2003, 338, 2751–2756. [Google Scholar]
- Govender, S.; Pillay, V.; Chetty, D.J.; Essack, S.Y.; Dangor, C.M.; Govender, T. Optimisation and characterisation of bioadhesive controlled release tetracycline microspheres. Int. J. Pharmaceut 2005, 306, 24–40. [Google Scholar]
- Volpi, N. Application of high-performance capillary electrophoresis to the purification process of Escherichia coli K4 polysaccharide. J. Chromatogr. B 2004, 811, 253–256. [Google Scholar]
- Ray, B. Polysaccharides from Enteromorpha compressa: Isolation, purification and structural features. Carbohydr. Polym 2006, 66, 408–416. [Google Scholar]
- Bendahou, A.; Dufresne, A.; Kaddami, H.; Habibi, Y. Isolation and structural characterization of hemicellulose from palm of Phoenix dactylifera L. Carbohydr. Polym 2007, 68, 601–608. [Google Scholar]
- Box, G.E.P.; Hunter, W.G.; Hunter, J.S. Statistics for Experimenters; John Wiley & Sons, Inc: Hoboken, NJ, USA, 1978; pp. 510–539. [Google Scholar]
- Pujari, V.; Chandra, T.S. Statistical optimization of medium components for enhanced riboflavin production by a UV-mutant of Eremothecium ashbyii. Process Biochem 2000, 36, 31–37. [Google Scholar]
- Liu, J.-Z.; Weng, L.-P.; Zhang, Q.-L.; Xu, H.; Ji, L.-N. Optimization of glucose oxidase production by Aspergillus niger in a benchtop bioreactor using response surface methodology. World J. Microbiol. Biotechnol 2003, 19, 317–323. [Google Scholar]
- Muralidhar, R.V.; Chirumamila, R.R.; Marchant, R.; Nigam, P. A response surface approach for the comparison of lipase production by Candida cylindracea using two different carbon sources. Biochem. Eng. J 2001, 9, 17–23. [Google Scholar]
- Wang, R.; Chen, P.; Jia, F.; Tang, J.; Ma, F. Optimization of polysaccharides from Panax japonicus C.A. Meyer by RSM and its anti-oxidant activity. Int. J. Biol. Macromol 2012, 50, 331–336. [Google Scholar]
- Liu, J.; Miao, S.; Wen, X.; Sun, Y. Optimization of polysaccharides (ABP) extraction from the fruiting bodies of Agaricus blazei Murill using response surface methodology (RSM). Carbohydr. Polym 2009, 78, 704–709. [Google Scholar]
- Yin, G.; Dang, Y. Optimization of extraction technology of the Lycium barbarum polysaccharides by Box-Behnken statistical design. Carbohydr. Polym 2008, 74, 603–610. [Google Scholar]
- Ye, C.; Jiang, C. Optimization of extraction process of crude polysaccharides from Plantago asiatica L. by response surface methodology. Carbohydr. Polym 2011, 84, 495–502. [Google Scholar]
- Wang, Z.J.; Luo, D.H.; Ena, C. Optimization of polysaccharides extraction from Gynostemma pentaphyllum Makino using uniform design. Carbohydr. Polym 2007, 69, 311–317. [Google Scholar]
- Triveni, R.; Shamala, T.R.; Rastogi, N.K. Optimized production and utilization of exopolysaccharide from Agrobacterium radiobacter. Process Biochem 2001, 36, 787–795. [Google Scholar]
- Soto-Cruz, O.; Saucedo-Castaneda, G.; Pablos-Hach, J.L.; Gutierrez-Rojas, M.; Favela-Torres, E. Effect of substrate composition on the mycelial growth of Pleurotus ostreatus. An analysis by mixture and response surface methodologies. Process Biochem 1999, 35, 127–133. [Google Scholar]
| Run | x1 | x2 | x3 | WPS Yield (%) | ||
|---|---|---|---|---|---|---|
| Experimental Ye | Predicted Y | Ye – Y | ||||
| 1 | 1 | −1 | 0 | 8.162 | 8.207 | −0.045 |
| 2 | 0 | −1 | −1 | 7.649 | 7.615 | 0.034 |
| 3 | −1 | −1 | 0 | 7.027 | 6.933 | 0.094 |
| 4 | 1 | 1 | 0 | 9.318 | 9.352 | −0.034 |
| 5 | 0 | 1 | −1 | 9.826 | 9.803 | 0.023 |
| 6 | −1 | 0 | −1 | 8.511 | 8.579 | −0.068 |
| 7 | 1 | 0 | −1 | 9.695 | 9.684 | 0.011 |
| 8 | 1 | 0 | 1 | 9.684 | 9.616 | 0.068 |
| 9 | −1 | 1 | 0 | 9.978 | 9.933 | 0.045 |
| 10 | −1 | 0 | 1 | 10.077 | 10.088 | −0.011 |
| 11 | 0 | 1 | 1 | 10.344 | 10.378 | −0.034 |
| 12 | 0 | −1 | 1 | 8.456 | 8.480 | −0.024 |
| 13 | 0 | 0 | 0 | 10.437 | 10.437 | 0.000 |
| 14 | 0 | 0 | 0 | 10.535 | 10.437 | 0.098 |
| 15 | 0 | 0 | 0 | 10.339 | 10.437 | −0.098 |
| 16 | 0 | 0 | 0 | 10.388 | 10.437 | −0.049 |
| 17 | 0 | 0 | 0 | 10.486 | 10.437 | 0.049 |
| Source | Sum of Squares | d.f. | Mean Square | F-Value | Probability (p) > F |
|---|---|---|---|---|---|
| Model | 19.24 | 9 | 2.14 | 345.32 | <0.0001 |
| Lack of fit | 0.019 | 3 | 6.44 × 10−3 | 1.07 | 0.4549 |
| Pure error | 0.024 | 4 | 6.00 × 10−3 | ||
| Corrected total | 19.28 | 16 | |||
| R2 = 0.9978 | R2 adj = 0.9949 | CV (%) = 0.83 |
| Model Term | Coefficient Estimate | Standard Error | Sum of Squares | Mean Square | F-Value | Probability (p) > F |
|---|---|---|---|---|---|---|
| Intercept | 10.44 | 0.035 | ||||
| x1 | 0.16 | 0.028 | 0.20 | 0.20 | 32.37 | 0.0007 |
| x2 | 1.02 | 0.028 | 8.35 | 8.35 | 1348.73 | <0.0001 |
| x3 | 0.36 | 0.360 | 1.04 | 1.04 | 167.52 | <0.0001 |
| x1x2 | −0.45 | 0.039 | 0.81 | 0.81 | 130.15 | <0.0001 |
| x1x3 | −0.39 | 0.039 | 0.62 | 0.62 | 100.45 | <0.0001 |
| x2x3 | −0.07 | 0.039 | 0.02 | 0.02 | 3.37 | 0.1089 |
| x1 2 | −0.70 | 0.038 | 2.04 | 2.04 | 329.90 | <0.0001 |
| x2 2 | −1.12 | 0.038 | 5.28 | 5.28 | 852.41 | <0.0001 |
| x3 2 | −0.25 | 0.038 | 0.26 | 0.26 | 42.14 | 0.0003 |
| Variable | Symbol | Coded Level | |||
|---|---|---|---|---|---|
| Uncoded | Coded | −1 | 0 | 1 | |
| Extraction time (h) | X1 | x1 | 1 | 2 | 3 |
| Extraction temperature (°C) | X2 | x2 | 80 | 90 | 100 |
| Ratio (v/w) of water volume (mL) to material weight (g) | X3 | x3 | 20 | 30 | 40 |
© 2012 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Li, P.; Lu, S.; Shan, T.; Mou, Y.; Li, Y.; Sun, W.; Zhou, L. Extraction Optimization of Water-Extracted Mycelial Polysaccharide from Endophytic Fungus Fusarium oxysporum Dzf17 by Response Surface Methodology. Int. J. Mol. Sci. 2012, 13, 5441-5453. https://doi.org/10.3390/ijms13055441
Li P, Lu S, Shan T, Mou Y, Li Y, Sun W, Zhou L. Extraction Optimization of Water-Extracted Mycelial Polysaccharide from Endophytic Fungus Fusarium oxysporum Dzf17 by Response Surface Methodology. International Journal of Molecular Sciences. 2012; 13(5):5441-5453. https://doi.org/10.3390/ijms13055441
Chicago/Turabian StyleLi, Peiqin, Shiqiong Lu, Tijiang Shan, Yan Mou, Yan Li, Weibo Sun, and Ligang Zhou. 2012. "Extraction Optimization of Water-Extracted Mycelial Polysaccharide from Endophytic Fungus Fusarium oxysporum Dzf17 by Response Surface Methodology" International Journal of Molecular Sciences 13, no. 5: 5441-5453. https://doi.org/10.3390/ijms13055441






