Förster Resonance Energy Transfer (FRET) between Heterogeneously Distributed Probes: Application to Lipid Nanodomains and Pores
Abstract
:1. Introduction
2. Results and Discussion
2.1. Limitations of FRET in the Detection of Nanodomains and Cylindrical Pores
2.2. Searching for the Size of the Liquid-Ordered Domains
3. Experimental Section
3.1. FRET Modeling of Uniformly Distributed Probes
3.2. Handling the Lack of Analytical Models for Heterogeneous Probe Distributions
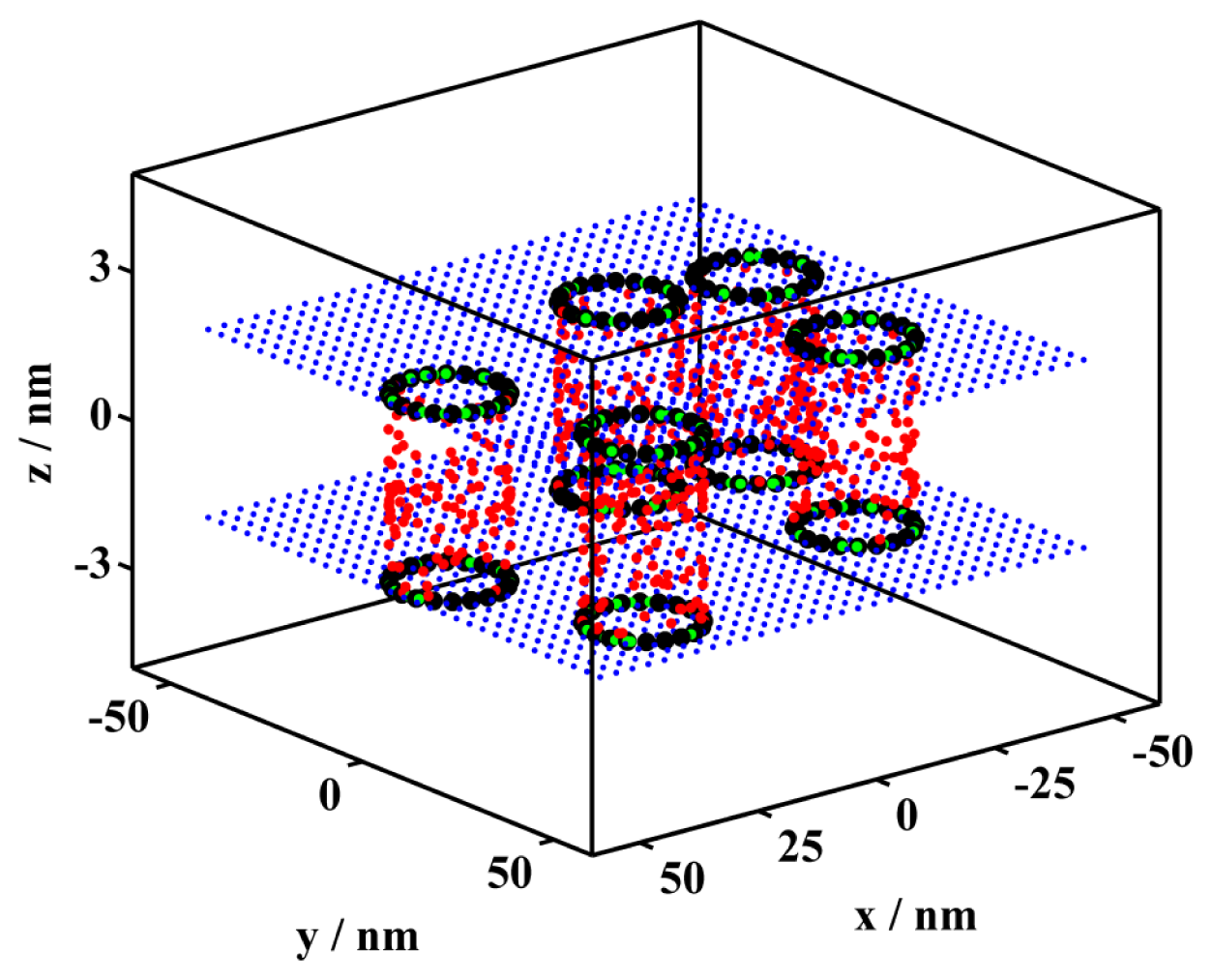
3.2.1. Monte Carlo Simulations
4. Conclusions
Acknowledgments
- Conflict of InterestThe authors declare no conflict of interest.
Abbreviations
| Ar | area fraction of the Lo domains |
| B-F | Baumann-Fayer |
| C2 | reduced surface concentration |
| Chol | cholesterol |
| CTxB | cholera toxin |
| DDEM | donor-donor energy migration |
| DOPC | dioleoylphosphatidylcholine |
| DOPG | dioleoylphosphatidylglycerol |
| FRET | Förster resonance energy transfer |
| Gs(t) | the excitation probability of the initially excited donor |
| GM1 | monosialotetrahexosylganglioside |
| MC | Monte Carlo |
| Ld | liquid disordered phase |
| Lo | liquid ordered phase |
| Ki (i = D or A) | partition coefficient of donors (i = D) or acceptors (i = A) |
| R | radius of a lipid domain or a pore |
| Rpore | radius of a pore |
| R0 | Förster radius |
| SS | steady-state |
| Sph | sphingomyelin |
| TRF | time-resolved fluorescence |
| κ | the angular dependence of dipole-dipole coupling |
| τD | the fluorescence lifetime of the donor |
References
- Brown, D.A. Lipid rafts, detergent-resistant membranes, and raft targeting signals. Physiology 2006, 21, 430–439. [Google Scholar]
- Brogden, K.A. Antimicrobial peptides: Pore formers or metabolic inhibitors in bacteria? Nat. Rev. Microbiol 2005, 3, 238–250. [Google Scholar]
- Simons, K.; Ikonen, E. Functional rafts in cell membranes. Nature 1997, 387, 569–572. [Google Scholar]
- Almeida, P.F.F. Thermodynamics of lipid interactions in complex bilayers. Biochim. Biophys. Acta Biomembr 2009, 1788, 72–85. [Google Scholar]
- Garcia-Saez, A.J.; Chiantia, S.; Schwille, P. Effect of line tension on the lateral organization of lipid membranes. J. Biol. Chem 2007, 282, 33537–33544. [Google Scholar]
- Lundquist, A.; Wessman, P.; Rennie, A.R.; Edwards, K. Melittin-lipid interaction: A comparative study using liposomes, micelles and bilayer disks. Biochim. Biophys. Acta Biomembr 2008, 1778, 2210–2216. [Google Scholar]
- Štefl, M.; Šachl, R.; Humpolíčková, J.; Cebecauer, M.; Macháň, R.; Johansson, L.B.-Å.; Hof, M. Dynamics and size of crosslinking-induced lipid nanodomains in model membranes. Biophys. J. 2012, 102, 2104–2113. [Google Scholar]
- Eggeling, C.; Ringemann, C.; Medda, R.; Schwarzmann, G.; Sandhoff, K.; Polyakova, S.; Belov, V.N.; Hein, B.; von Middendorff, C.; Schonle, A.; et al. Direct observation of the nanoscale dynamics of membrane lipids in a living cell. Nature 2009, 457, U1159–U1121. [Google Scholar]
- Lakowicz, J.R. Principles of Fluorescence Spectroscopy, 3rd ed; Springer: Singapore; p. 2006.
- Valeur, B. Molecular Fluorescence Principles and Applications; Wiley-VCH Verlag GmbH: Weinheim, Germany; p. 2001.
- Chiantia, S.; Ries, J.; Kahya, N.; Schwille, P. Combined afm and two-focus sfcs study of raft-exhibiting model membranes. ChemPhysChem 2006, 7, 2409–2418. [Google Scholar]
- De Almeida, R.F.M.; Loura, L.M.S.; Fedorov, A.; Prieto, M. Lipid rafts have different sizes depending on membrane composition: A time-resolved fluorescence resonance energy transfer study. J. Mol. Biol 2005, 346, 1109–1120. [Google Scholar]
- Šachl, R.; Humpolíčková, J.; Štefl, M.; Johansson, L.B.-Å.; Hof, M. Limitations of energy tranfer in the determination of lipid nanodomain sizes. Biophys. J. 2011, 101, L60–L62. [Google Scholar]
- Baumann, J.; Fayer, M.D. Excitation transfer in dissordered two-dimensional and anisotropic 3-dimensional systems—effects of spatial geometry on time-resolved observables. J. Chem. Phys 1986, 85, 4087–4107. [Google Scholar]
- Bechinger, B. The structure, dynamics and orientation of antimicrobial peptides in membranes by multidimensional solid-state nmr spectroscopy. Biochim. Biophys. Acta Biomembr 1999, 1462, 157–183. [Google Scholar]
- Matsuzaki, K.; Sugishita, K.; Ishibe, N.; Ueha, M.; Nakata, S.; Miyajima, K.; Epand, R.M. Relationship of membrane curvature to the formation of pores by magainin 2. Biochemistry 1998, 37, 11856–11863. [Google Scholar]
- Ludtke, S.J.; He, K.; Heller, W.T.; Harroun, T.A.; Yang, L.; Huang, H.W. Membrane pores induced by magainin. Biochemistry 1996, 35, 13723–13728. [Google Scholar]
- He, K.; Ludtke, S.J.; Huang, H.W.; Worcester, D.L. Antimicrobial peptide pores in membranes detected by neutron inplane scattering. Biochemistry 1995, 34, 15614–15618. [Google Scholar]
- Yang, L.; Harroun, T.A.; Weiss, T.M.; Ding, L.; Huang, H.W. Barrel-stave model or toroidal model? A case study on melittin pores. Biophys. J 2001, 81, 1475–1485. [Google Scholar]
- Schlesinger, P.H.; Saito, M. The bax pore in liposomes, biophysics. Cell Death Differ 2006, 13, 1403–1408. [Google Scholar]
- Qian, S.; Wang, W.C.; Yang, L.; Huang, H.W. Structure of transmembrane pore induced by bax-derived peptide: Evidence for lipidic pores. Proc. Natl. Acad. Sci. USA 2008, 105, 17379–17383. [Google Scholar]
- Song, L.Z.; Hobaugh, M.R.; Shustak, C.; Cheley, S.; Bayley, H.; Gouaux, J.E. Structure of staphylococcal alpha-hemolysin, a heptameric transmembrane pore. Science 1996, 274, 1859–1866. [Google Scholar]
- Baumgart, T.; Hunt, G.; Farkas, E.R.; Webb, W.W.; Feigenson, G.W. Fluorescence probe partitioning between l-O/l-D phases in lipid membranes. Biochim. Biophys. Acta Biomembr 2007, 1768, 2182–2194. [Google Scholar]
- Risselada, H.J.; Marrink, S.J. The molecular face of lipid rafts in model membranes. Proc. Natl. Acad. Sci. USA 2008, 105, 17367–17372. [Google Scholar]
- Blumen, A.; Manz, J. Concentration and time-dependance of the energy-transfer to randomly distributed acceptors. J. Chem. Phys 1979, 71, 4694–4702. [Google Scholar]
- Loura, L.M.S.; Fernandes, F.; Prieto, M. Membrane microheterogeneity: Forster resonance energy transfer characterization of lateral membrane domains. Eur. Biophys. J. Biophys. Lett 2010, 39, 589–607. [Google Scholar]
- Loura, L.M.S.; Fedorov, A.; Prieto, M. Fluid-fluid membrane microheterogeneity: A fluorescence resonance energy transfer study. Biophys. J 2001, 80, 776–788. [Google Scholar]
- Engström, S.; Lindberg, M.; Johansson, L.B.-Å. Monte-carlo simulations of electronic-energy transfer in 3-dimensional systems—a comparison with analytical theories. J. Chem. Phys. 1988, 89, 204–213. [Google Scholar]
- Johansson, L.B.-Å.; Engström, S.; Lindberg, M. Electronic-energy transfer in anisotropic systems. 3. Monte-carlo simulations of energy migration in membranes. J. Chem. Phys. 1992, 96, 3844–3856. [Google Scholar]
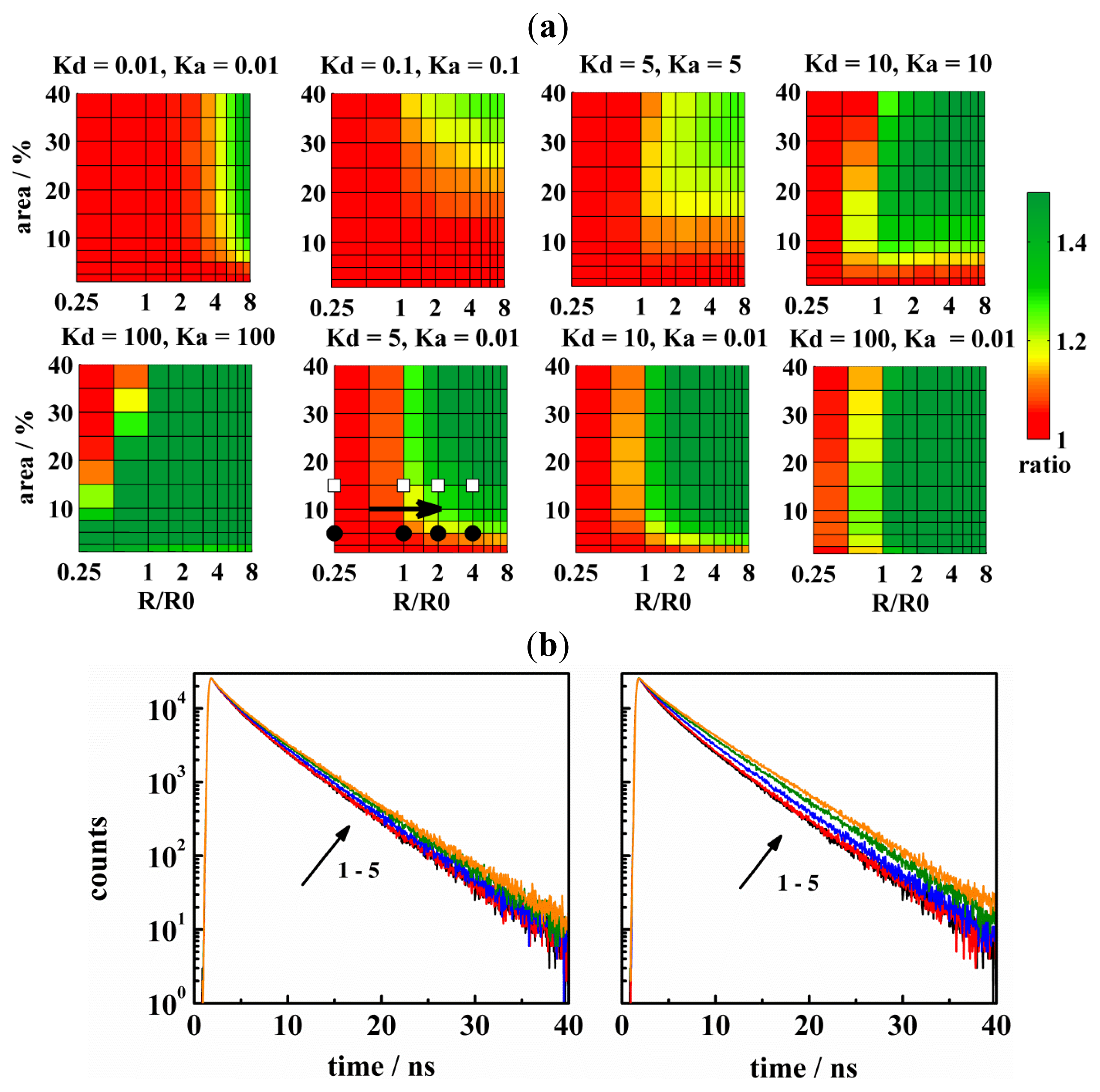
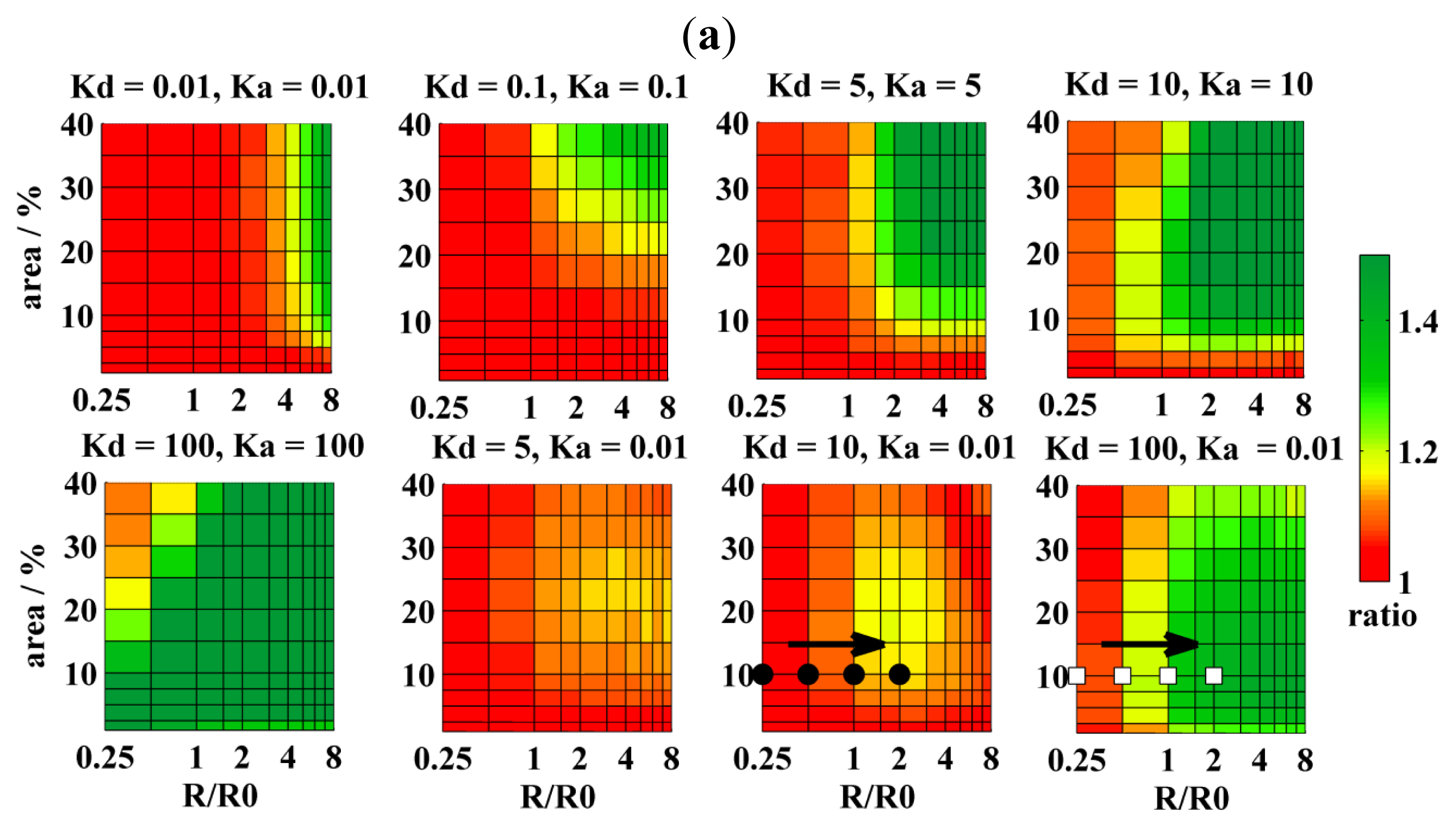
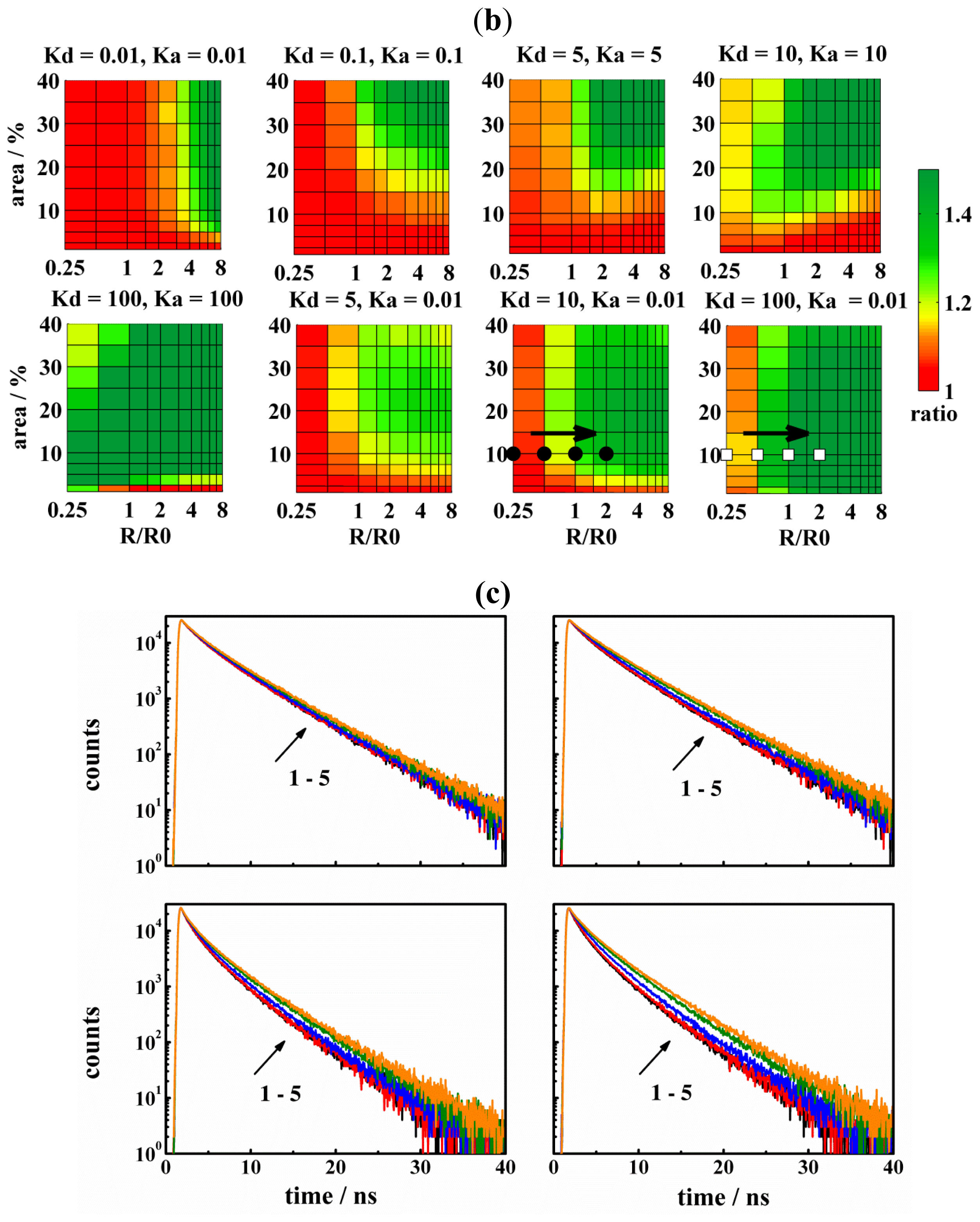

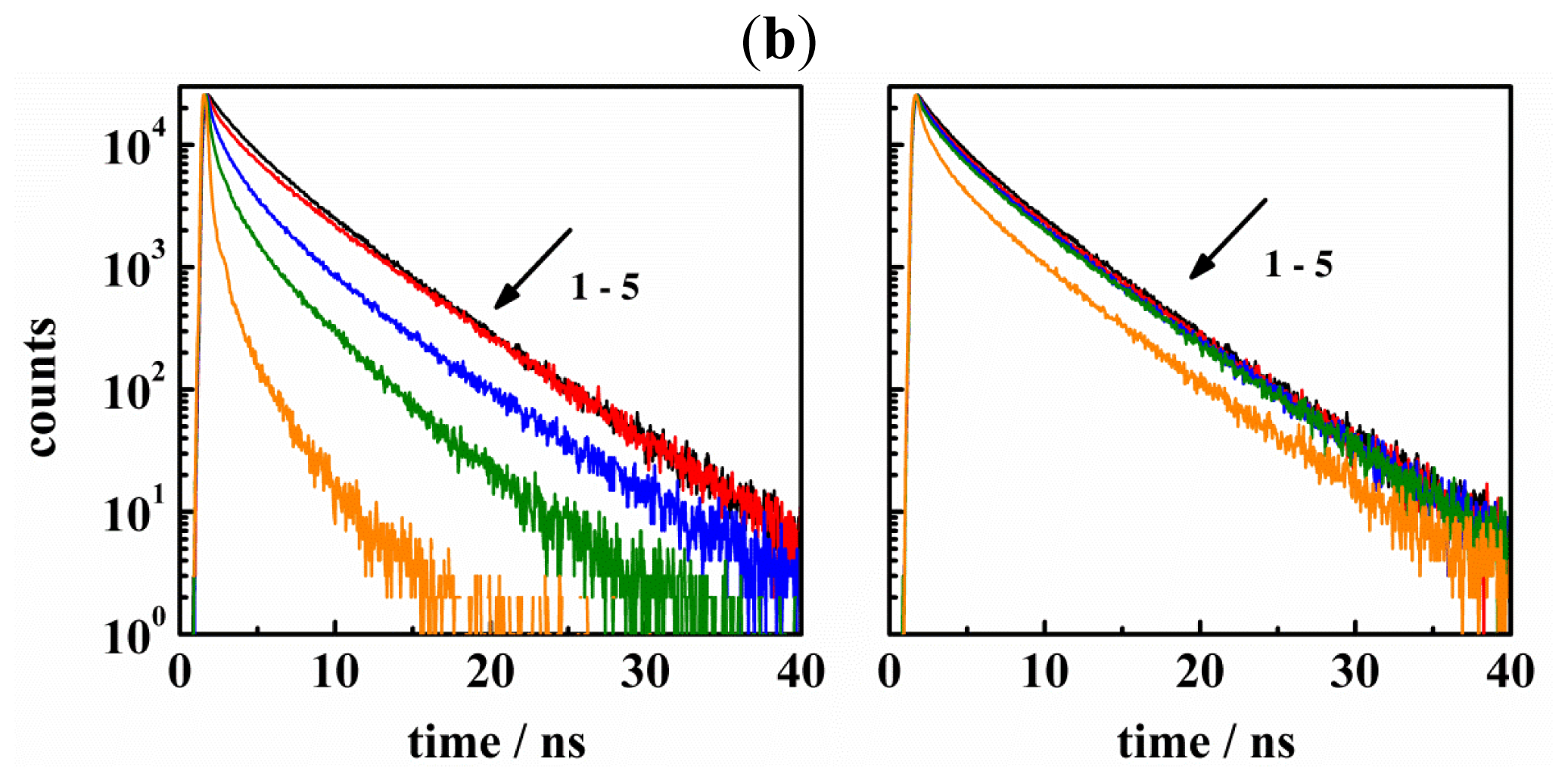
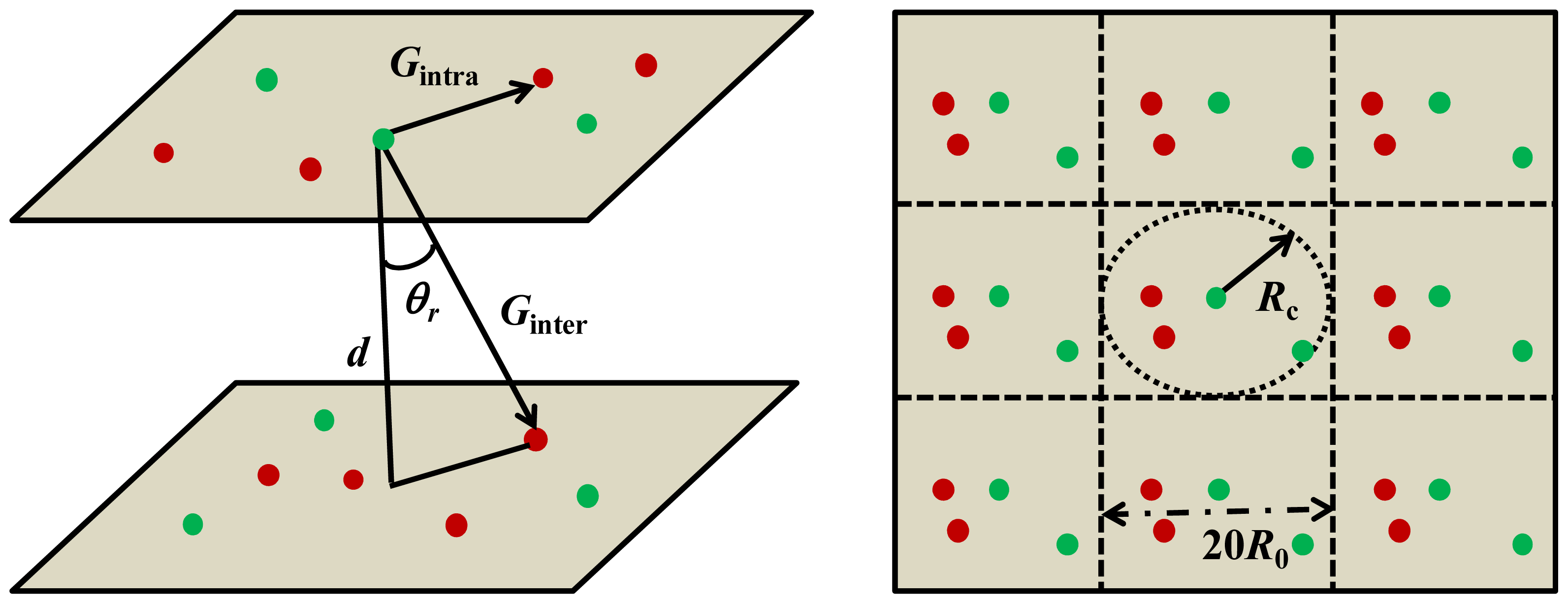
| CA | KD | KA | R/nm | Ar/% | |
|---|---|---|---|---|---|
| reference | 1.52 | 6 | 0.01 | 8 | 6 |
| KD 50% higher | 1.52 | 6 + 3 | 0.01 | 7 | 5 |
| KD 50% lower | 1.52 | 6 − 3 | 0.01 | 8 | 12 |
| CA 10% higher | 1.52 + 0.15 | 6 | 0.01 | 8 | 8 |
| CA 10% lower | 1.52 − 0.15 | 6 | 0.01 | 7 | 7 |
© 2012 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Šachl, R.; Johansson, L.B.-Å.; Hof, M. Förster Resonance Energy Transfer (FRET) between Heterogeneously Distributed Probes: Application to Lipid Nanodomains and Pores. Int. J. Mol. Sci. 2012, 13, 16141-16156. https://doi.org/10.3390/ijms131216141
Šachl R, Johansson LB-Å, Hof M. Förster Resonance Energy Transfer (FRET) between Heterogeneously Distributed Probes: Application to Lipid Nanodomains and Pores. International Journal of Molecular Sciences. 2012; 13(12):16141-16156. https://doi.org/10.3390/ijms131216141
Chicago/Turabian StyleŠachl, Radek, Lennart B.-Å. Johansson, and Martin Hof. 2012. "Förster Resonance Energy Transfer (FRET) between Heterogeneously Distributed Probes: Application to Lipid Nanodomains and Pores" International Journal of Molecular Sciences 13, no. 12: 16141-16156. https://doi.org/10.3390/ijms131216141





