Computational Molecular Nanoscience Study of the Properties of Copper Complexes for Dye-Sensitized Solar Cells
Abstract
:1. Introduction
2. Results and Discussion
3. Experimental Section
4. Conclusions
Acknowledgments
References
- Bobicki, E.R.; Liu, Q.; Xu, Z.; Zeng, H. Carbon capture and storage using alkaline industrial wastes. Prog. Energy Combust. Sci 2012, 38, 302–320. [Google Scholar]
- Canadell, J.G.; Le Quéré, C.; Raupach, M.R.; Field, C.B.; Buitenhuis, E.T.; Ciais, P.; Conway, T.J.; Gillett, N.P.; Houghton, R.A.; Marland, G. Contributions to accelerating atmospheric CO2 growth from economic activity, carbon intensity, and efficiency of natural sinks. Proc. Natl. Acad. Sci. USA 2007, 104, 18866–18870. [Google Scholar]
- Heintz, A. Solar energy combined with chemical reactive systems for the production and storage of sustainable energy: A review of thermodynamic principles. J. Chem. Thermodyn 2012, 46, 99–108. [Google Scholar]
- Hoevenaars, E.J.; Crawford, C.A. Implications of temporal resolution for modeling renewables-based power systems. Renew. Energy 2012, 41, 285–293. [Google Scholar]
- Song, Y.; Wang, J.; Dai, Y.; Zhou, E. Thermodynamic analysis of a transcritical CO2 power cycle driven by solar energy with liquified natural gas as its heat sink. Appl. Energy 2012, 92, 194–203. [Google Scholar]
- Chu, H.-C.; Sahu, D.; Hsu, Y.-C.; Padhy, H.; Patra, D.; Lin, J.-T.S.; Bhattacharya, D.; Lu, K.-L.; Wei, K.-H.; Lin, H.-C. Structural planarity and conjugation effects of novel symmetrical acceptor–donor–acceptor organic sensitizers on dye-sensitized solar cells. Dyes Pigment 2012, 93, 1488–1497. [Google Scholar]
- O’Regan, B.; Gratzel, M. A low-cost, high-efficiency solar cell based on dye-sensitized colloidal TiO2 films. Nature 1991, 353, 737–740. [Google Scholar]
- Gratzel, M. Photoelectrochemical cells. Nature 2001, 414, 338–344. [Google Scholar]
- Wang, P.; Zakeeruddin, S.M.; Moser, J.E.; Nazeeruddin, M.K.; Sekiguchi, T.; Gratzel, M. A stable quasi-solid-state dye-sensitized solar cell with an amphiphilic ruthenium sensitizer and polymer gel electrolyte. Nat. Mater 2003, 2, 402–407. [Google Scholar]
- Cheng, X.; Sun, S.; Liang, M.; Shi, Y.; Sun, Z.; Xue, S. Organic dyes incorporating the cyclopentadithiophene moiety for efficient dye-sensitized solar cells. Dyes Pigment 2012, 92, 1292–1299. [Google Scholar]
- Saito, Y.; Fukuri, N.; Senadeera, R.; Kitamura, T.; Wada, Y.; Yanagida, S. Solid state dye sensitized solar cells using in situ polymerized PEDOTs as hole conductor. Electrochem. Commun 2004, 6, 71–74. [Google Scholar]
- Qiu, F.L.; Fisher, A.C.; Walker, A.B.; Peter, L.M. The distribution of photoinjected electrons a dye-sensitized nanocrystalline TiO2 solar cell modelled by a boundary element method. Electrochem. Commun 2003, 5, 711–716. [Google Scholar]
- Asbury, J.B.; Ellingson, R.J.; Ghosh, H.N.; Ferrere, S.; Nozik, A.J.; Lian, T. Femtosecond IR study of excited-state relaxation and electron-injection dynamics of Ru(dcbpy)2(NCS)2 in solution and on nanocrystalline TiO2 and Al2O3 thin films. J. Phys. Chem. B 1999, 103, 3110–3119. [Google Scholar]
- Chen, J.G.; Chen, C.Y.; Wu, S.J.; Li, J.Y.; Wu, C.G.; Ho, K.C. On the photophysical and electrochemical studies of dye-sensitized solar cells with the new dye CYC-B1. Sol. Energy Mater. Sol. Cells 2008, 92, 1723–1727. [Google Scholar]
- Heimer, T.A.; Heilweil, E.J.; Bignozzi, C.A.; Meyer, G.J. Electron injection, recombination, and halide oxidation dynamics at dye-sensitized metal oxide interfaces. J. Phys. Chem. A 2000, 104, 4256–4262. [Google Scholar]
- Figgemeier, E.; Hagfeldt, A. Are dye-sensitized nano-structured solar cells stable? An overview of device testing and component analyses. Int. J. Photoenergy 2004, 6, 127–140. [Google Scholar]
- Grätzel, M. Nanocrystalline Electronic Junctions. In Studies in Surface Science and Catalysis; Prashant, V.K., Dan, M., Eds.; Elsevier: Amsterdam, The Netherlands, 1997; Volume 103, pp. 353–375. [Google Scholar]
- Grätzel, M. Dye-sensitized solar cells. J. Photochem. Photobiol. C 2003, 4, 145–153. [Google Scholar]
- Kamat, P.V.; Haria, M.; Hotchandani, S. C60 Cluster as an electron shuttle in a Ru(II)-polypyridyl sensitizer-based photochemical solar cell. J. Phys. Chem. B 2004, 108, 5166–5170. [Google Scholar]
- Cao, J.; Sun, J.Z.; Hong, J.; Yang, X.G.; Chen, H.Z.; Wang, M. Direct observation of microscopic photoinduced charge redistribution on TiO2 film sensitized by chloroaluminum phthalocyanine and perylenediimide. Appl. Phys. Lett 2003, 83, 1896–1898. [Google Scholar]
- Zhang, C.-R.; Liu, Z.-J.; Chen, Y.-H.; Chen, H.-S.; Wu, Y.-Z.; Yuan, L.-H. DFT and TDDFT study on organic dye sensitizers D5, DST and DSS for solar cells. J. Mol. Struct. Theochem 2009, 899, 86–93. [Google Scholar]
- Ham, H.W.; Kim, Y.S. Theoretical study of indoline dyes for dye-sensitized solar cells. Thin Solid Films 2010, 518, 6558–6563. [Google Scholar]
- Zhang, C.R.; Liu, Z.J.; Chen, Y.H.; Chen, H.S.; Wu, Y.Z.; Feng, W.; Wang, D.B. DFT and TD-DFT study on structure and properties of organic dye sensitizer TA-St-CA. Curr. Appl. Phys 2010, 10, 77–83. [Google Scholar]
- De Angelis, F. Direct vs. indirect injection mechanisms in perylene dye-sensitized solar cells: A DFT/TDDFT investigation. Chem. Phys. Lett 2010, 493, 323–327. [Google Scholar]
- Zhao, J.; Ji, S.; Wu, W.; Wu, W.; Guo, H.; Sun, J.; Sun, H.; Liu, Y.; Li, Q.; Huang, L. Transition metal complexes with strong absorption of visible light and long-lived triplet excited states: From molecular design to applications. RSC Adv 2012, 2, 1712–1728. [Google Scholar]
- Li, G.; Ray, L.; Glass, E.N.; Kovnir, K.; Khoroshutin, A.; Gorelsky, S.I.; Shatruk, M. Synthesis of panchromatic Ru(II) thienyl-dipyrrin complexes and evaluation of their light-harvesting capacity. Inorg. Chem 2012, 51, 1614–1624. [Google Scholar]
- Vougioukalakis, G.C.; Philippopoulos, A.I.; Stergiopoulos, T.; Falaras, P. Contributions to the development of ruthenium-based sensitizers for dye-sensitized solar cells. Coord. Chem. Rev 2011, 255, 2602–2621. [Google Scholar]
- Alonso-Vante, N.; Nierengarten, J.F.; Sauvage, J.P. Spectral sensitization of large-band-gap semiconductors (thin films and ceramics) by a carboxylated bis(1,10-phenanthroline)copper(I) complex. J. Chem. Soc. Dalton Trans. 1994, 1649–1654. [Google Scholar] [CrossRef]
- Deng, J.; Xiu, Q.; Guo, L.; Zhang, L.; Wen, G.; Zhong, C. Branched chain polymeric metal complexes containing Co(II) or Ni(II) complexes with a donor–π–acceptor architecture: Synthesis, characterization, and photovoltaic applications. J. Mater. Sci 2012, 47, 3383–3390. [Google Scholar]
- Barrientos, L.; Araneda, C.; Loeb, B.; Crivelli, I.G. Synthesis, spectroscopic and electrochemical characterization of copper(I) complexes with functionalized pyrazino[2,3-f]-1,10-phenanthroline. Polyhedron 2008, 27, 1287–1295. [Google Scholar]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev 1964, 136, B864–B871. [Google Scholar]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev 1965, 140, A1133–A1138. [Google Scholar]
- Parr, R.G.; Yang, W. Density-Functional Theory of Atoms and Molecules; Oxford University Press: New York, NY, USA, 1989. [Google Scholar]
- Burke, K.; Werschnik, J.; Gross, E.K.U. Time-dependent density functional theory: Past, present, and future. J. Chem. Phys 2005, 123, 062206. [Google Scholar]
- Stratmann, R.E.; Scuseria, G.E.; Frisch, M.J. An efficient implementation of time-dependent density-functional theory for the calculation of excitation energies of large molecules. J. Chem. Phys 1998, 109, 8218–8224. [Google Scholar]
- Bauernschmitt, R.; Ahlrichs, R. Treatment of electronic excitations within the adiabatic approximation of time dependent density functional theory. Chem. Phys. Lett 1996, 256, 454–464. [Google Scholar]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision A.02; Gaussian Inc: Wallingford, CT, USA; p. 2009.
- Hernández Redondo, A. Copper(I) Polypyridine Complexes: The Sensitizers of the Future for Dye-Sensitized Solar Cells (DSSCs). Ph.D. Thesis, University of Basel, 2009. [Google Scholar]
- Green, M.A. Solar Cells: Operating Principles, Technology and Systems Applications; Prentice-Hall, Inc: Englewood Cliffs, NJ, USA; p. 1982.
- Lu, X.; Wu, C.-M.L.; Wei, S.; Guo, W. DFT/TD-DFT investigation of electronic structures and spectra properties of Cu-based dye sensitizers. J. Phys. Chem A 2010, 114, 1178–1184. [Google Scholar]
- Bessho, T.; Constable, E.C.; Graetzel, M.; Hernandez Redondo, A.; Housecroft, C.E.; Kylberg, W.; Nazeeruddin, M.K.; Neuburger, M.; Schaffner, S. An element of surprise-efficient copper-functionalized dye-sensitized solar cells. Chem. Commun. 2008, 3717–3719. [Google Scholar] [CrossRef]
- Bozic-Weber, B.; Constable, E.C.; Housecroft, C.E.; Neuburger, M.; Price, J.R. Sticky complexes: Carboxylic acid-functionalized N-phenylpyridin-2-ylmethanimine ligands as anchoring domains for copper and ruthenium dye-sensitized solar cells. Dalton Trans 2010, 39, 3585–3594. [Google Scholar]
- Lu, X.; Wei, S.; Wu, C.-M.L.; Li, S.; Guo, W. Can polypyridyl Cu(I)-based complexes provide promising sensitizers for dye-sensitized solar cells? A theoretical insight into Cu(I) versus Ru(II) sensitizers. J. Phys. Chem. C 2011, 115, 3753–3761. [Google Scholar]
- De Angelis, F.; Fantacci, S.; Sgamellotti, A. An integrated computational tool for the study of the optical properties of nanoscale devices: Application to solar cells and molecular wires. Theor. Chem. Acc 2007, 117, 1093–1104. [Google Scholar]
- Weng, Y.-X.; Wang, Y.-Q.; Asbury, J.B.; Ghosh, H.N.; Lian, T. Back electron transfer from TiO2 nanoparticles to FeIII(CN)6 3−: Origin of non-single-exponential and particle size independent dynamics. J. Phys. Chem. B 1999, 104, 93–104. [Google Scholar]
- Sharma, S.K.; Inamdar, A.I.; Im, H.; Kim, B.G.; Patil, P.S. Morphology dependent dye-sensitized solar cell properties of nanocrystalline zinc oxide thin films. J. Alloy. Compd 2011, 509, 2127–2131. [Google Scholar]
- Zhao, Y.; Truhlar, D.G. A new local density functional for main-group thermochemistry, transition metal bonding, thermochemical kinetics, and noncovalent interactions. J. Chem. Phys 2006, 125, 194101–194118. [Google Scholar]
- Zhao, Y.; Truhlar, D.G. Density functional for spectroscopy: No long-range self-interaction error, good performance for rydberg and charge-transfer states, and better performance on average than B3LYP for ground states. J. Phys. Chem. A 2006, 110, 13126–13130. [Google Scholar]
- Zhao, Y.; Truhlar, D. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc 2008, 120, 215–241. [Google Scholar]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys 1993, 98, 5648–5652. [Google Scholar]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar]
- Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys 1999, 110, 6158–6170. [Google Scholar]
- Godbout, N.; Salahub, D.R.; Andzelm, J.; Wimmer, E. Optimization of Gaussian-type basis sets for local spin density functional calculations. Part I. Boron through neon, optimization technique and validation. Can. J. Chem 1992, 70, 560–571. [Google Scholar]
- Sosa, C.; Andzelm, J.; Elkin, B.C.; Wimmer, E.; Dobbs, K.D.; Dixon, D.A. A local density functional study of the structure and vibrational frequencies of molecular transition-metal compounds. J. Chem. Phys 1992, 96, 6630–6636. [Google Scholar]
- Dunning, T.H., Jr.; Hay, P.J. Methods of Electronic Structure Theory; Plenum: New York, NY, USA, 1976; Volume 3. [Google Scholar]
- Hay, P.J.; Wadt, W.R. Ab initio effective core potentials for molecular calculations. Potentials for the transition metal atoms Sc to Hg. J. Chem. Phys 1985, 82, 270–283. [Google Scholar]
- Wadt, W.R.; Hay, P.J. Ab initio effective core potentials for molecular calculations. Potentials for main group elements Na to Bi. J. Chem. Phys 1985, 82, 284–298. [Google Scholar]
- Hay, P.J.; Wadt, W.R. Ab initio effective core potentials for molecular calculations. Potentials for K to Au including the outermost core orbitals. J. Chem. Phys 1985, 82, 299–310. [Google Scholar]
- Francl, M.M.; Pietro, W.J.; Hehre, W.J.; Binkley, J.S.; Gordon, M.S.; DeFrees, D.J.; Pople, J.A. Self-consistent molecular orbital methods. XXIII. A polarization-type basis set for second-row elements. J. Chem. Phys 1982, 77, 3654–3665. [Google Scholar]
- Tomasi, J.; Mennucci, B.; Cammi, R. Quantum Mechanical Continuum Solvation Models. Chem. Rev 2005, 105, 2999–3094. [Google Scholar]
- Cossi, M.; Barone, V. Time-dependent density functional theory for molecules in liquid solutions. J. Chem. Phys 2001, 115, 4708–4717. [Google Scholar]
- Gorelsky, S.I. SWizard program. Available online: http://www.sg-chem.net/ accessed on 30 April 2012.
- Gorelsky, S.I.; Lever, A.B.P. Electronic structure and spectra of ruthenium diimine complexes by density functional theory and INDO/S. Comparison of the two methods. J. Organomet. Chem 2001, 635, 187–196. [Google Scholar]

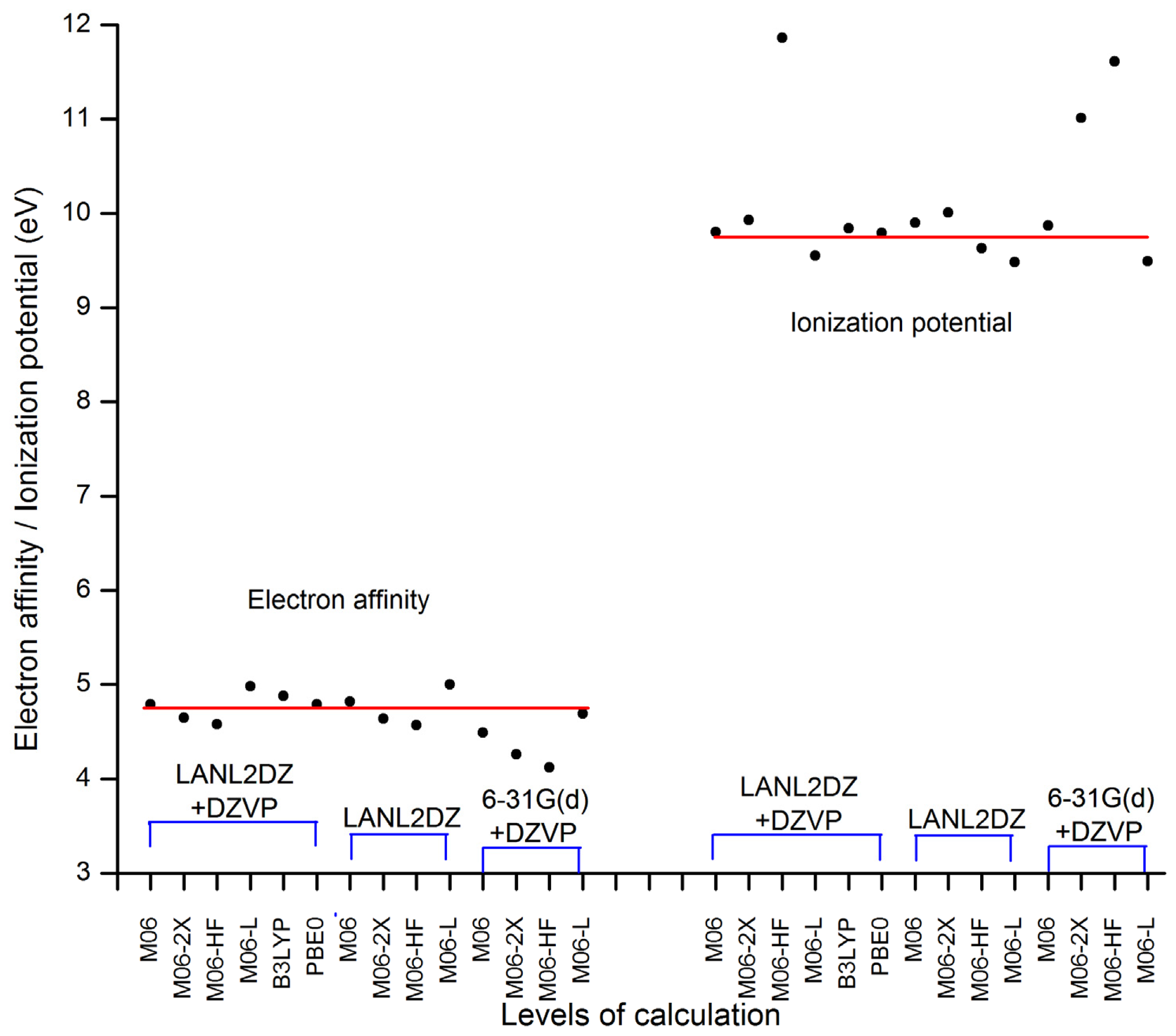
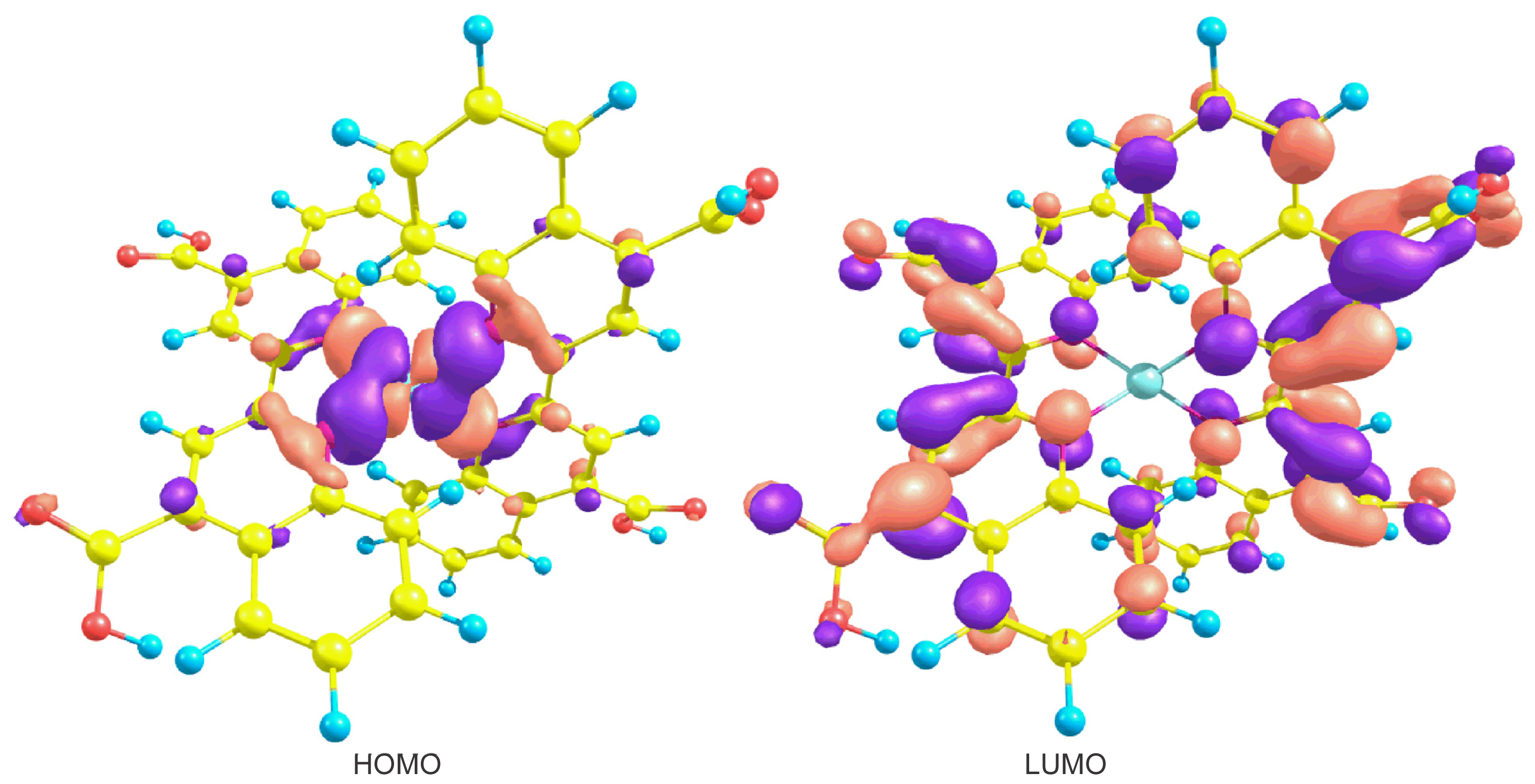
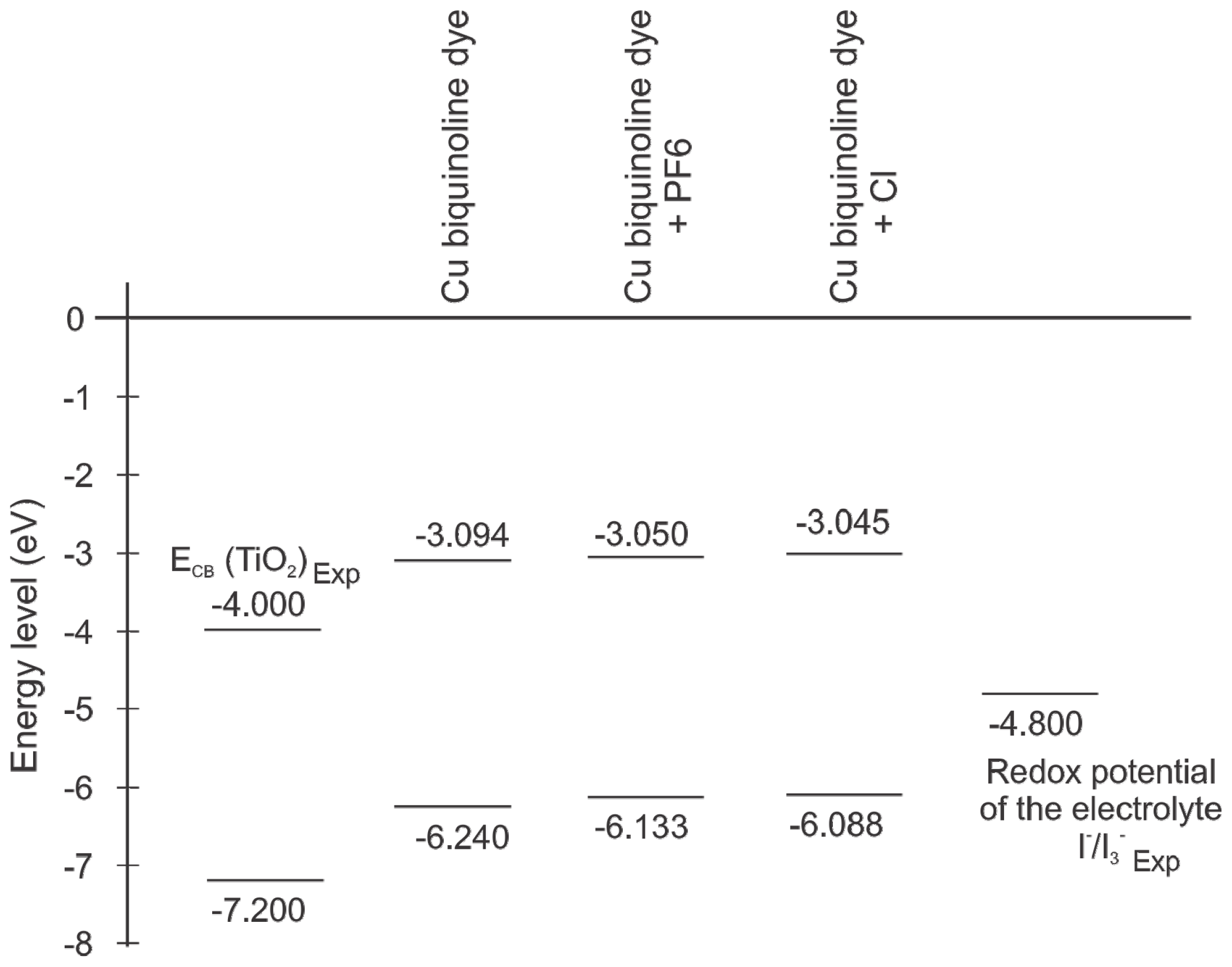
| Basis set | Functional | Electron affinity (eV) | Ionization potential (eV) |
|---|---|---|---|
| LANL2DZ + DZVP | M06 | 4.79 | 9.80 |
| M06-2X | 4.65 | 9.93 | |
| M06-HF | 4.58 | 11.86 | |
| M06-L | 4.98 | 9.55 | |
| B3LYP | 4.88 | 9.84 | |
| PBE0 | 4.79 | 9.79 | |
| LANL2DZ | M06 | 4.82 | 9.90 |
| M06-2X | 4.64 | 10.01 | |
| M06-HF | 4.57 | 9.63 | |
| M06-L | 5.00 | 9.48 | |
| 6–31G(d) + DZVP | M06 | 4.49 | 9.87 |
| M06-2X | 4.26 | 11.01 | |
| M06-HF | 4.12 | 11.61 | |
| M06-L | 4.69 | 9.49 |
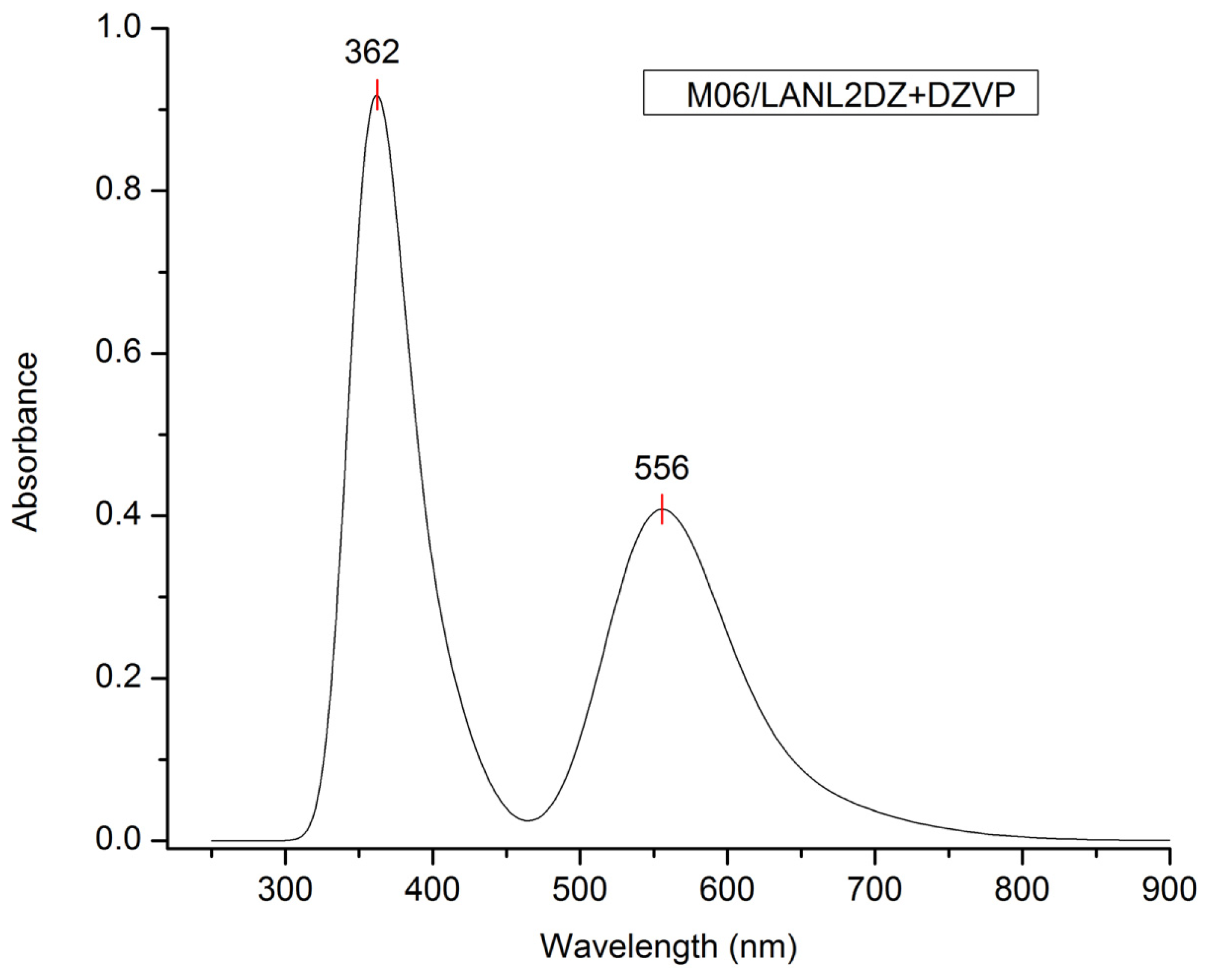
| Model chemistry | λmax (nm) | Model chemistry | λmax (nm) |
|---|---|---|---|
| M06/LANL2DZ + DZVP | 556 | M06-HF/LANL2DZ | 282 |
| M06-2X/LANL2DZ + DZVP | 386 | M06/LANL2DZ | 543 |
| M06-HF/LANL2DZ + DZVP | 279 | M06-2X/LANL2DZ | 378 |
| M06-L/LANL2DZ + DZVP | 641 | M06-L/6–31G(d) + DZVP | 645 |
| B3LYP/LANL2DZ + DZVP | 614 | M06-HF/6–31G(d) + DZVP | 279 |
| PBE0/LANL2DZ + DZVP | 578 | M06/6–31G(d) + DZVP | 488 |
| M06-L/LANL2DZ | 629 | M06-2X/6–31G(d) + DZVP | 328 |
| λ (nm) | E (eV) | Oscillator strength | Assignment; H = HOMO, L = LUMO, L + 1 = LUMO + 1, etc. |
|---|---|---|---|
| 556.0 | 2.25 | 0.1652 | H-1→L + 1(50%) H-0→L + 0(26%) H-1→L + 0(19%) |
| 373.3 | 3.32 | 0.0308 | H-3→L + 0(76%) H-2→L + 0(8%) H-4→L + 0(6%) |
| 362.0 | 3.40 | 0.0372 | H-3→L + 1(54%) H-2→L + 1(9%) H-5→L + 1(8%) |
| H-4→L + 1(7%) H-1→L + 3(5%) | |||
| 358.7 | 3.46 | 0.0225 | H-6→L + 0(43%) H-10→L + 0(16%) H-2→L + 0(13%) |
| H-9→L + 0(8%) H-5→L + 0(8%) | |||
| 355.3 | 3.49 | 0.0295 | H-5→L + 1(67%) H-5→L + 0(11%) H-3→L + 1(10%) |
| 351.6 | 3.53 | 0.0392 | H-6→L + 0(39%) H-10→L + 0(23%) H-9→L + 0(15%) |
| H-2→L + 0(9%) |
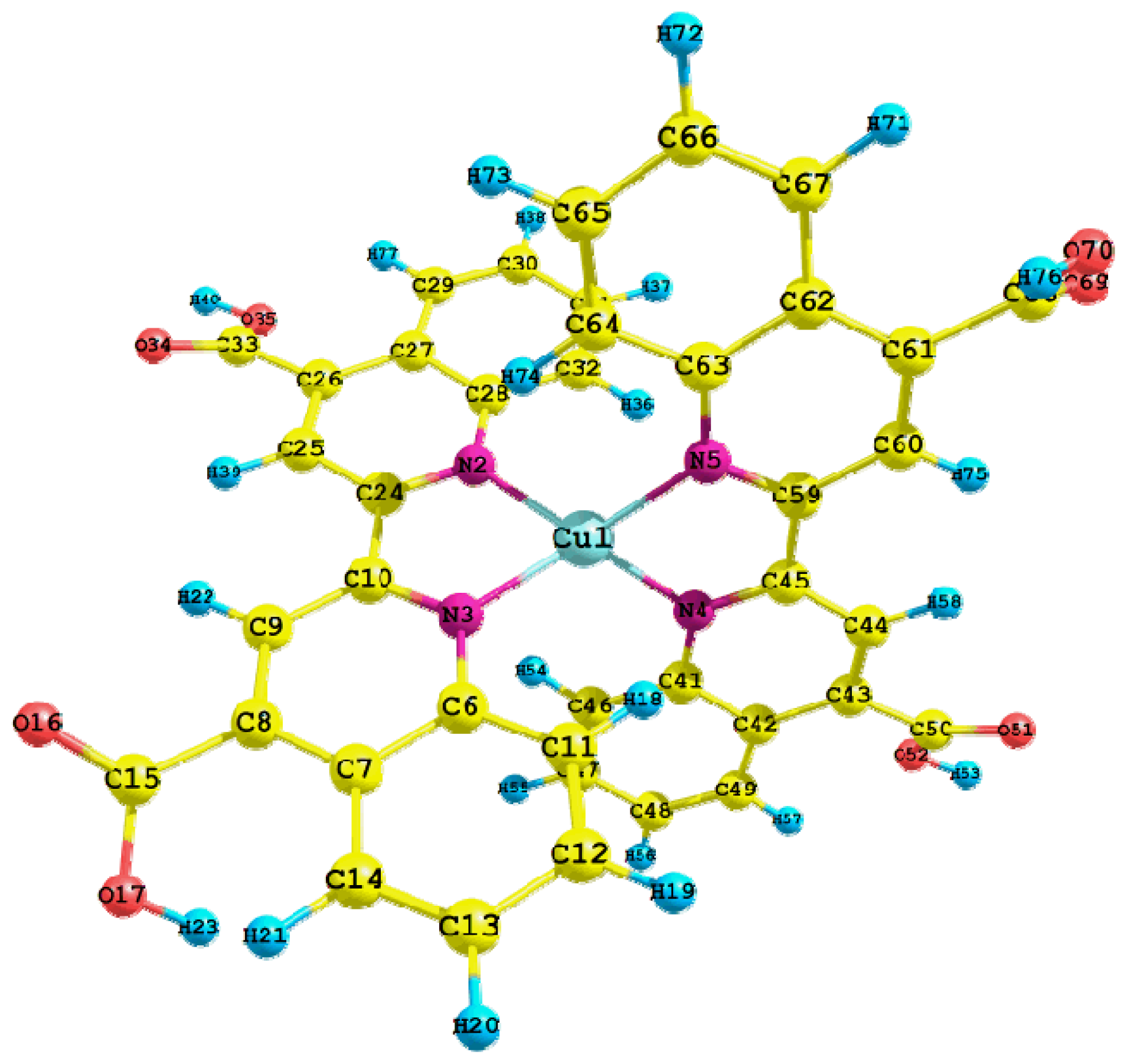
| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Cu1-N2 | 2.024 | C50-O52 | 1.349 |
| Cu1-N3 | 2.023 | O52-H53 | 1.034 |
| Cu1-N4 | 2.022 | Cu1-N2-C28 | 126.0 |
| Cu1-N5 | 2.025 | Cu1-N2-C24 | 113.4 |
| N4-C45 | 1.342 | N2-Cu1-N5 | 121.4 |
| N4-C41 | 1.374 | N2-Cu1-N3 | 81.6 |
| C45-C59 | 1.477 | N2-Cu1-N4 | 128.5 |
| C41-C42 | 1.437 | N3-Cu1-N4 | 122.0 |
| C44-H58 | 1.089 | N3-Cu1-N5 | 128.2 |
| C50-O51 | 1.245 | N4-Cu1-N5 | 81.6 |
| Basis set | Atoms | |
|---|---|---|
| Approach 1 | LANL2DZ | C, H, O and N |
| DZVP | Cu | |
| Approach | 2 LANL2DZ | C, H, O, N, and Cu |
| Approach 3 | 6–31G(d) | C, H, O and N |
| DZVP | Cu | |
© 2012 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Baldenebro-López, J.; Castorena-González, J.; Flores-Holguín, N.; Almaral-Sánchez, J.; Glossman-Mitnik, D. Computational Molecular Nanoscience Study of the Properties of Copper Complexes for Dye-Sensitized Solar Cells. Int. J. Mol. Sci. 2012, 13, 16005-16019. https://doi.org/10.3390/ijms131216005
Baldenebro-López J, Castorena-González J, Flores-Holguín N, Almaral-Sánchez J, Glossman-Mitnik D. Computational Molecular Nanoscience Study of the Properties of Copper Complexes for Dye-Sensitized Solar Cells. International Journal of Molecular Sciences. 2012; 13(12):16005-16019. https://doi.org/10.3390/ijms131216005
Chicago/Turabian StyleBaldenebro-López, Jesús, José Castorena-González, Norma Flores-Holguín, Jorge Almaral-Sánchez, and Daniel Glossman-Mitnik. 2012. "Computational Molecular Nanoscience Study of the Properties of Copper Complexes for Dye-Sensitized Solar Cells" International Journal of Molecular Sciences 13, no. 12: 16005-16019. https://doi.org/10.3390/ijms131216005







