Nitrogen Substituted Phenothiazine Derivatives: Modelling of Molecular Self-Assembling
Abstract
:1. Introduction
2. Computational Details
3. Results and Discussion
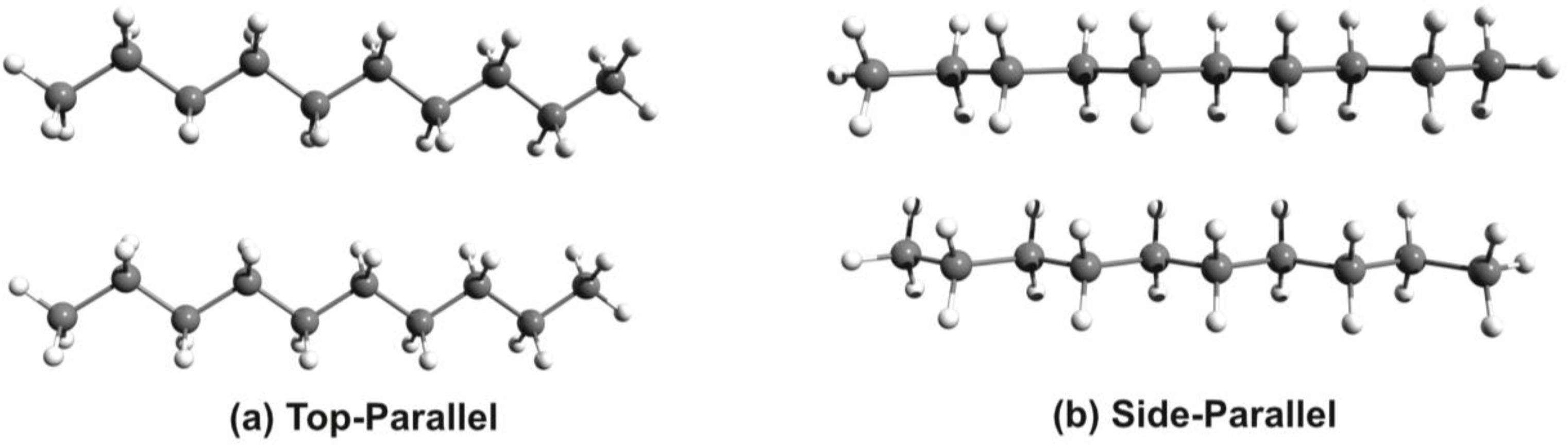
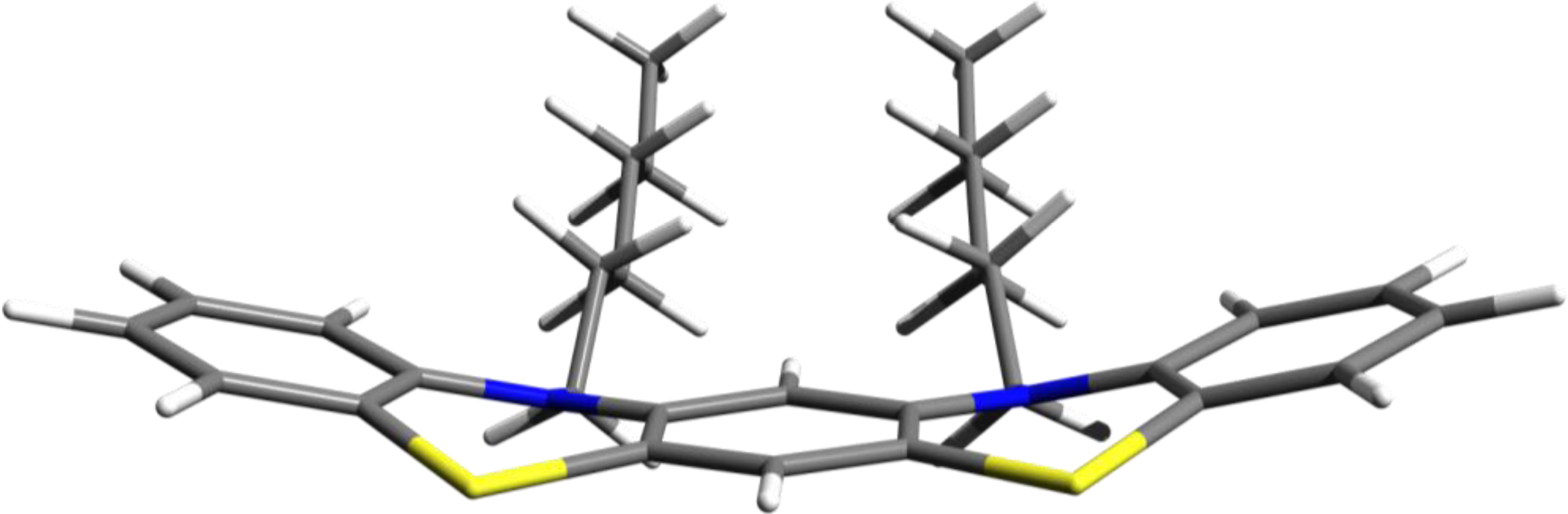
3.1. Phenothiazine Dimers
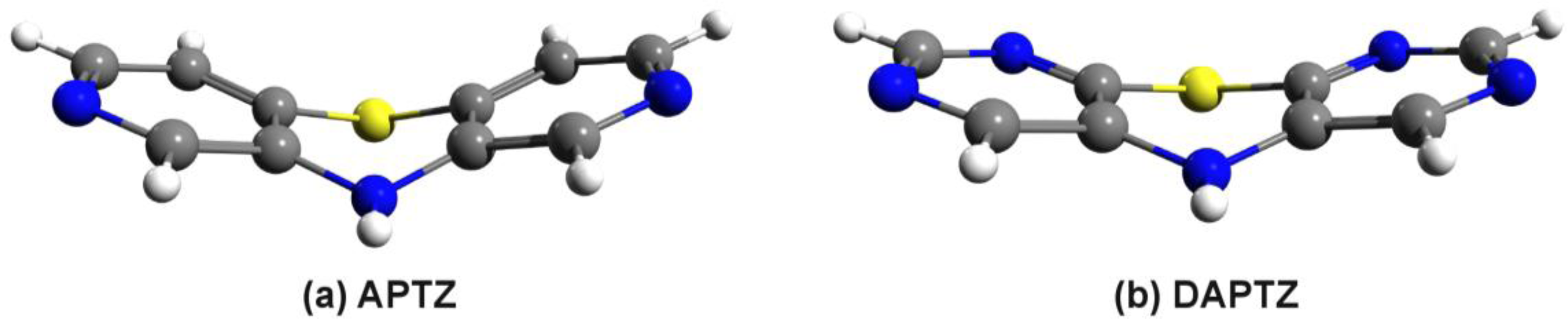
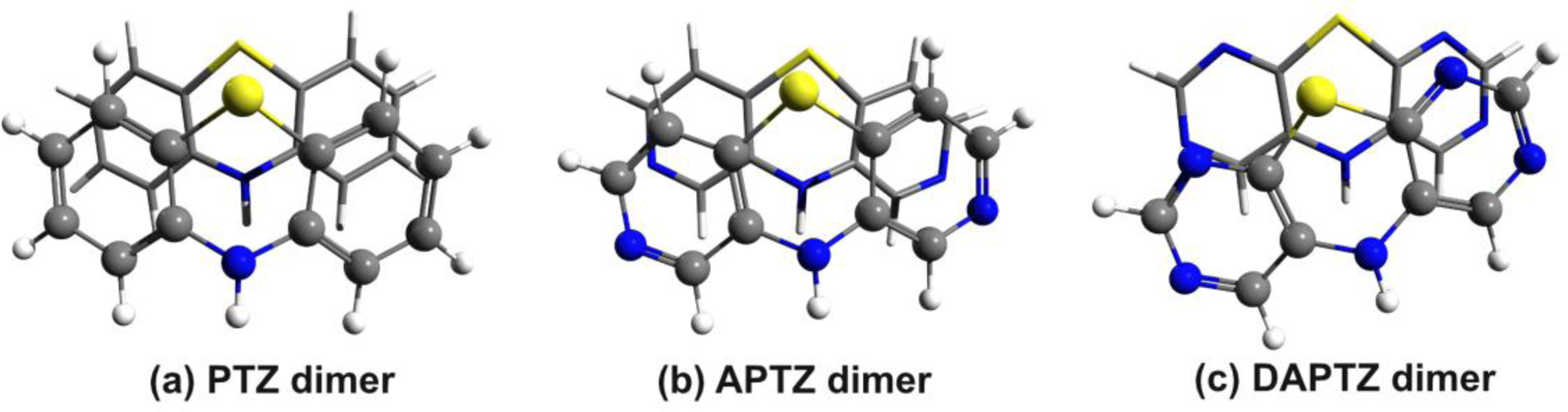
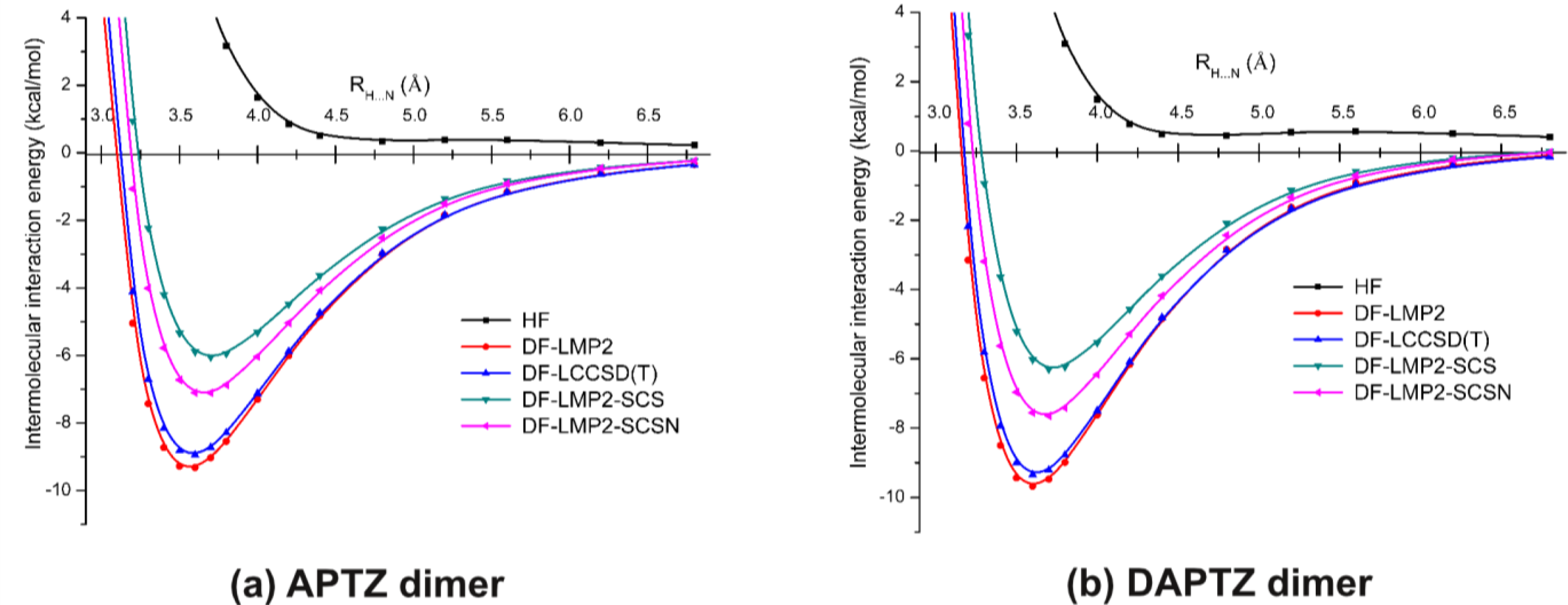
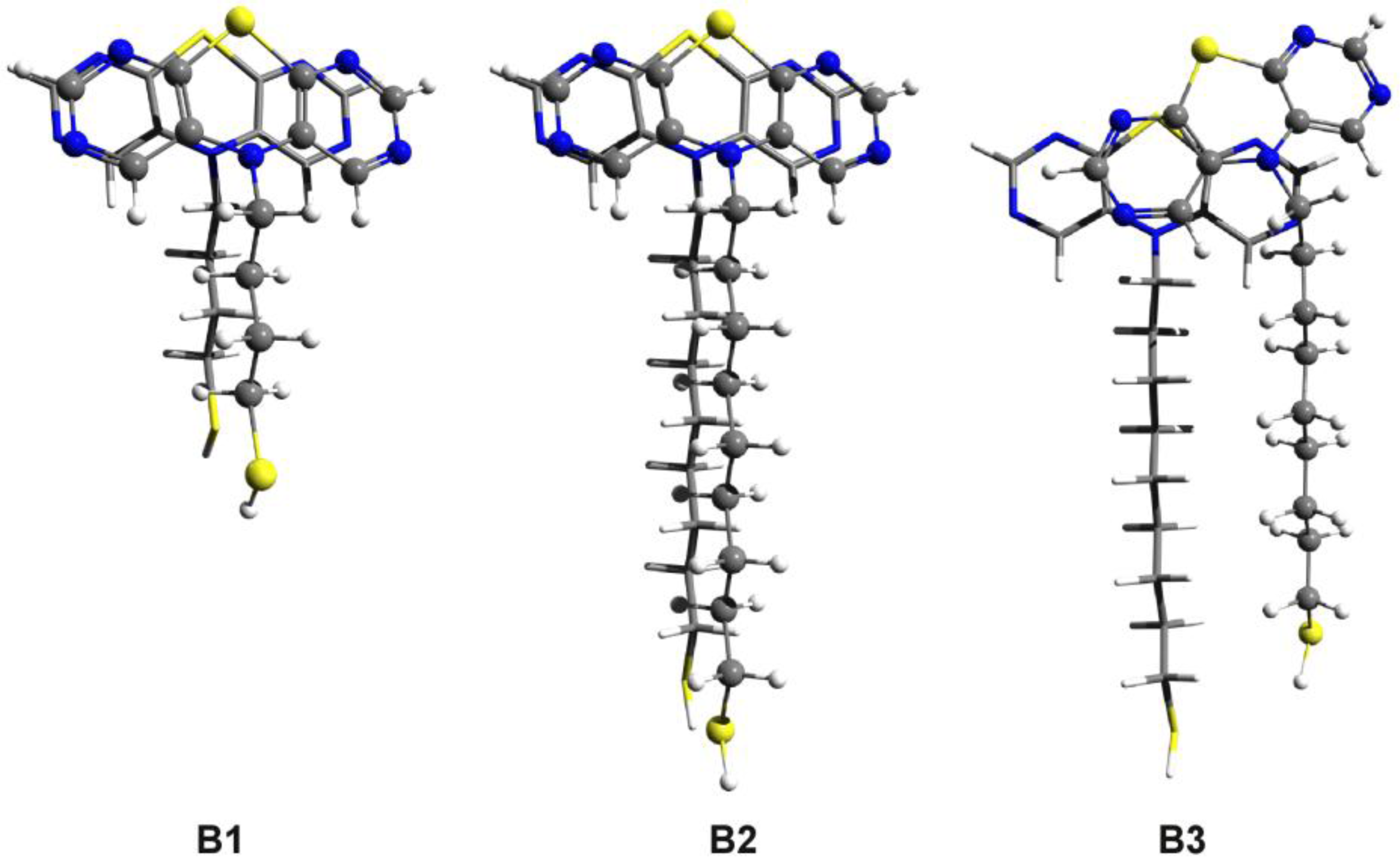
3.2. Nitrogen-Substituted Phenothiazine Dimers
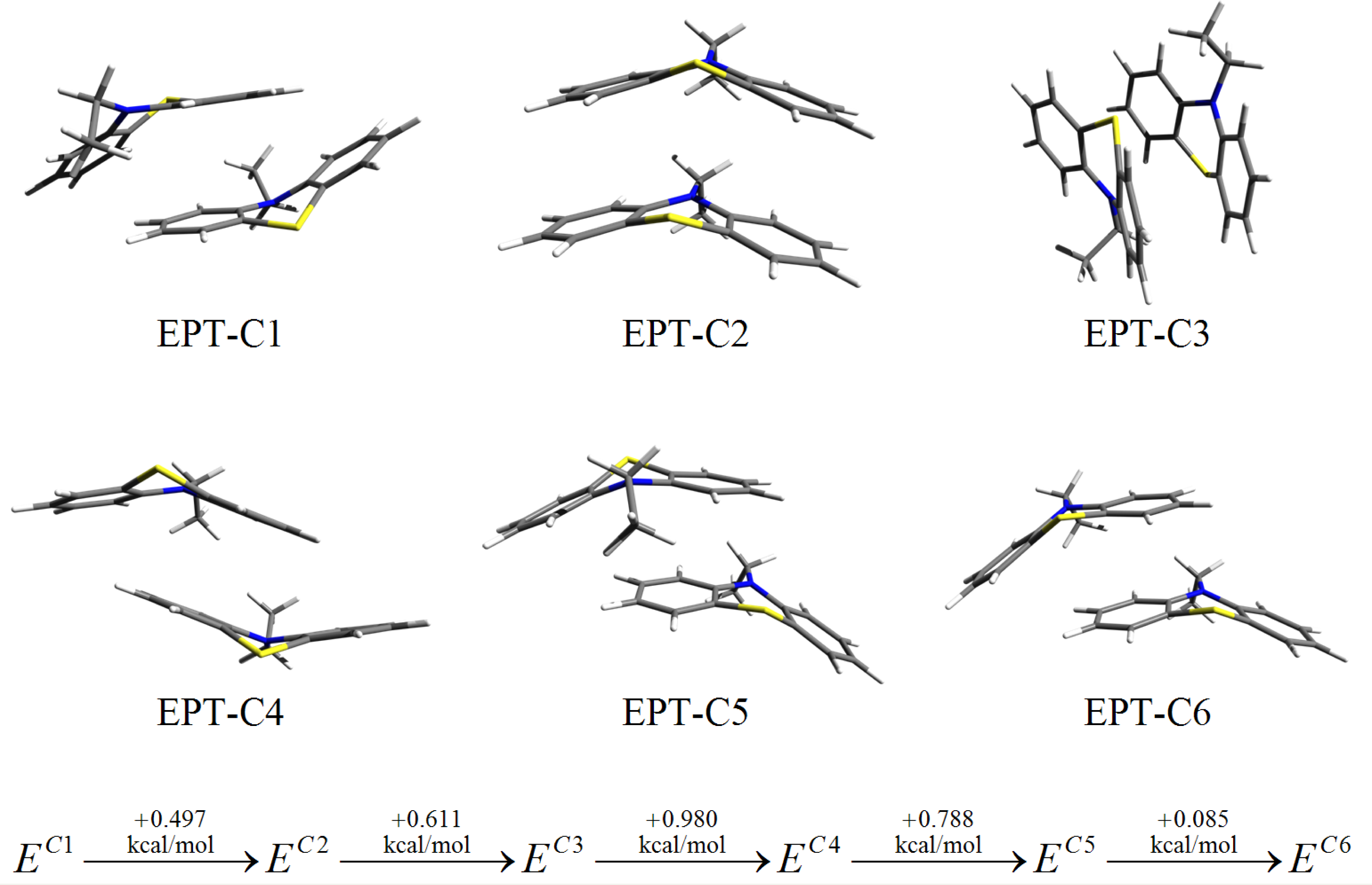
3.3. SCC-DFTB Results
4. Conclusions
Acknowledgments
References
- Hollingsworth, MD. Crystal Engineering: from Structure to Function. Science 2002, 295, 2410–2413. [Google Scholar]
- Leininger, S; Olenyuk, B; Stang, PJ. Self-Assembly of Discrete Cyclic Nanostructures Mediated by Transition Metals. Chem. Rev 2000, 100, 853–908. [Google Scholar]
- Venkataramanan, B; Saifudin, M-A; Jagadese, VJ; Suresh, V. Self-assembly of methacrylamides assisted by an interplay of N–H···O, C–H···O, C–H···π and π–π interactions. Cryst. Eng. Commun 2004, 6, 284–289. [Google Scholar]
- Colquhoun, HM; Zhu, Z; Cardin, CJ; Gan, Y; Drew, MGB. Sterically Controlled Recognition of Macromolecular Sequence Information by Molecular Tweezers. J. Am. Chem. Soc 2007, 129, 16163–16174. [Google Scholar]
- Burley, SK; Petsko, GA. Aromatic-aromatic interaction: A mechanism of protein structure stabilization. Science 1985, 229, 23–28. [Google Scholar]
- Loakes, D. The applications of universal DNA base analogues. Nucleic Acids Res 2001, 29, 2437–2447. [Google Scholar]
- Rutledge, LR; Campbell-Verduyn, LS; Wetmore, SD. Characterization of the stacking interactions between DNA or RNA nucleobases and the aromatic amino acids. Chem. Phys. Lett 2007, 444, 167–175. [Google Scholar]
- Hunter, CA; Sanders, KM. The nature of π–π interactions. J. Am. Chem. Soc 1990, 112, 5525–5534. [Google Scholar]
- Járai-Szabó, F; Aştilean, S; Néda, Z. Understanding self-assembled nanosphere patterns. Chem. Phys. Lett 2005, 408, 241–246. [Google Scholar]
- Love, JC; Estroff, LA; Kriebel, JK; Nuzzo, RG; Witheside, GM. Self-Assembled Monolayers of Thiolates on Metals as a Form of Nanotechnology. Chem. Rev 2005, 105, 1103–1170. [Google Scholar]
- Bende, A; Grosu, I; Turcu, I. Molecular modeling of phenothiazine derivatives: Self-assembling properties. J. Phys. Chem. A 2010, 114, 12479–12489. [Google Scholar]
- Wang, W; Hobza, P. Theoretical Study on the Complexes of Benzene with Isoelectronic Nitrogen-Containing Heterocycles. ChemPhysChem 2008, 9, 1003–1009. [Google Scholar]
- Mignon, P; Loverix, S; Steyaert, J; Geerlings, P. Influence of the π–π interaction on the hydrogen bonding capacity of stacked DNA/RNA bases. Nucl. Acid. Res 2005, 33, 1779–1789. [Google Scholar]
- Mignon, P; Loverix, S; de Proft, F; Geerlings, P. Influence of Stacking on Hydrogen Bonding: Quantum Chemical Study on Pyridine-Benzene Model Complexes. J. Phys. Chem. A 2004, 108, 6038–6044. [Google Scholar]
- Mishra, BK; Arey, JS; Sathyamurthy, N. Stacking and Spreading Interaction in N-Heteroaromatic Systems. J. Phys. Chem. A 2010, 114, 9606–9616. [Google Scholar]
- Główka, ML; Martynowski, D; Kozłowska, K. Stacking of six-membered aromatic rings in crystals. J. Mol. Struct 1999, 474, 81–89. [Google Scholar]
- Wheaton, CA; Dobrowolski, SL; Millen, AL; Wetmore, SD. Nitrosubstituted aromatic molecules as universal nucleobases: Computational analysis of stacking interactions. Chem. Phys. Lett 2006, 428, 157–166. [Google Scholar]
- Pulay, P. Localizability of dynamic electron correlation. Chem. Phys. Lett 1983, 100, 151–154. [Google Scholar]
- Saebo, S; Pulay, P. Local Treatment of Electron Correlation. Annu. Rev. Phys. Chem 1993, 44, 213–236. [Google Scholar]
- Hampel, C; Werner, H-J. Local treatment of electron correlation in coupled cluster theory. J. Chem. Phys 1996, 104, 6286–6297. [Google Scholar]
- Hetzer, G; Schütz, M; Stoll, H; Werner, H-J. Low-order scaling local correlation methods II: Splitting the Coulomb operator in linear scaling local second-order MøllerPlesset perturbation theory. J. Chem. Phys 2000, 113, 9443–9455. [Google Scholar]
- Schütz, M. Low-order scaling local electron correlation methods. III. Linear scaling local perturbative triples correction (T). J. Chem. Phys 2000, 113, 9986–10001. [Google Scholar]
- Schütz, M; Werner, H-J. Low-order scaling local electron correlation methods. IV. Linear scaling local coupled-cluster (LCCSD). J. Chem. Phys 2001, 114, 661–681. [Google Scholar]
- Vahtras, O; Almlöf, J; Feyereisen, MW. Integral approximations for LCAO-SCF calculations. Chem. Phys. Lett 1993, 213, 514–518. [Google Scholar]
- Schütz, M; Rauhut, G; Werner, HJ. Local Treatment of Electron Correlation in Molecular Clusters: Structures and Stabilities of (H2O)n, n = 2–4. J. Phys. Chem. A 1998, 102, 5997–6003. [Google Scholar]
- Hill, JG; Platts, JA; Werner, H-J. Calculation of intermolecular interactions in the benzene dimer using coupled-cluster and local electron correlation methods. Phys. Chem. Chem. Phys 2006, 8, 4072–4078. [Google Scholar]
- Grimme, S. Improved second-order Møller-Plesset perturbation theory by separate scaling of parallel and antiparallel-spin pair correlation energies. J. Chem. Phys 2003, 118, 9095–10002. [Google Scholar]
- Hill, JG; Platts, JA. Spin-Component Scaling Methods for Weak and Stacking Interactions. J. Chem. Theory Comput 2007, 3, 80–85. [Google Scholar]
- Jurečka, P; Šponer, J; Černý, J; Hobza, P. Benchmark database of accurate (MP2 and CCSD(T) complete basis set limit) interaction energies of small model complexes, DNA base pairs, and amino acid pairs. Phys. Chem. Chem. Phys 2006, 8, 1985–1993. [Google Scholar]
- Distasio, RA, Jr; Head-Gordon, M. Optimized spin-component scaled second-order Møller-Plesset perturbation theory for intermolecular interaction energies. Mol. Phys 2007, 105, 1073–1083. [Google Scholar]
- Grimme, S. Semiempiricall GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem 2006, 27, 1787–1799. [Google Scholar]
- Elstner, M; Porezag, D; Jungnickel, G; Elsner, J; Haugk, M; Frauenheim, T; Suhai, S; Seifert, G. Self-consistent-charge density-functional tight-binding method for simulations of complex materials properties. Phys. Rev. B 1998, 58, 7260–7268. [Google Scholar]
- Elstner, M; Jalkanen, KJ; Knapp-Mohammady, M; Frauenheim, T; Suhai, S. DFT studies on helix formation in N-acetyl-(l-alanyl)n-N’-methylamide for n = 1–20. Chem. Phys 2000, 256, 15–27. [Google Scholar]
- Elstner, M; Jalkanen, KJ; Knapp-Mohammady, M; Frauenheim, T; Suhai, S. Energetics and structure of glycine and alanine based model peptides: Approximate SCC-DFTB, AM1 and PM3 methods in comparison with DFT, HF and MP2 calculations. Chem. Phys 2001, 263, 203–219. [Google Scholar]
- Elstner, M; Hobza, P; Frauenheim, T; Suhai, S; Kaxiras, E. Hydrogen bonding and stacking interactions of nucleic acid base pairs: A density-functional-theory based treatment. J. Chem. Phys 2001, 114, 5149–5155. [Google Scholar]
- Liu, HY; Elstner, M; Kaxiras, E; Frauenheim, T; Hermans, J; Yang, WT. Quantum mechanics simulation of protein dynamics on long timescale. Proteins: Struct. Funct., Bioinf 2001, 44, 484–489. [Google Scholar]
- Kubař, T; Jurečka, P; Černý, J; Řezáč, J; Otyepka, M; Valdés, H; Hobza, P. Density-Functional, Density-Functional Tight-Binding, and Wave Function Calculations on Biomolecular Systems. J. Phys. Chem. A 2007, 111, 5642–5647. [Google Scholar]
- Werner, H-J; Knowles, PJ; Lindh, R; Manby, FR; Schütz, M; Celani, P; Korona, T; Mitrushenkov, A; Rauhut, G; Adler, TB; et al. MOLPRO, a Package of ab initio Programs, version 2009.1. Available online: http://www.molpro.net (accessed on 11 May 2011).
- Dunning, TH, Jr. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys 1989, 90, 1007–1023. [Google Scholar]
- Kendall, RA; Dunning, TH, Jr; Harrison, RJ. Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions. J. Chem. Phys 1992, 96, 6796–6806. [Google Scholar]
- Pipek, J; Mezey, PG. A fast intrinsic localization procedure applicable for ab initio and semiempirical linear combination of atomic orbital wave functions. J. Chem. Phys 1989, 90, 4916–4926. [Google Scholar]
- Allouche, AR. Gabedit—A graphical user interface for computational chemistry softwares. J. Comput. Chem 2010, 32, 174–182. [Google Scholar]
- Korth, M; Pitoňák, M; Řezáč, J; Hobza, P. A Transferable H-Bonding Correction for Semiempirical Quantum-Chemical Methods. J. Chem. Theory Comput 2010, 6, 344–352. [Google Scholar]
- Allinger, NL; Lii, J-H. Molecular mechanics. The MM3 force field for hydrocarbons. 3. The van der Waals’ potentials and crystal data for aliphatic and aromatic hydrocarbons. J. Am. Chem. Soc 1989, 111, 8576–8582. [Google Scholar]



| ΔEHF (kcal/mol) | ΔEDF-LMP2 (kcal/mol) | ECorr. (kcal/mol) | EDisp. (kcal/mol) | EIon. (kcal/mol) | |
|---|---|---|---|---|---|
| APTZ | |||||
| cc-pVDZ | +7.056 | −9.343 | −16.399 | −13.854 | −3.462 |
| cc-pVTZ | +9.307 | −12.322 | −21.629 | −17.741 | −5.312 |
| aug-cc-pVDZ | +7.136 | −15.245 | −22.381 | −19.777 | −6.723 |
| aug-cc-pVTZ | +10.024 | −15.138 | −25.162 | −20.378 | −6.117 |
| DAPTZ | |||||
| cc-pVDZ | +6.445 | −9.696 | −16.141 | −14.044 | −3.625 |
| cc-pVTZ | +8.992 | −12.338 | −21.330 | −17.806 | −5.485 |
| aug-cc-pVDZ | +7.616 | −14.714 | −22.330 | −19.807 | −6.926 |
| aug-cc-pVTZ | +9.887 | −14.947 | −24.834 | −20.397 | −6.232 |
| LMP2 | LCCSD(T) | LMP2-SCS | LMP2-SCSN | |
|---|---|---|---|---|
| APTZ | ||||
| Re (Å) | 3.564 | 3.585 | 3.700 | 3.656 |
| Ee (kcal/mol) | −9.287 | −8.888 | −5.999 | −7.097 |
| DAPTZ | ||||
| Re (Å) | 3.605 | 3.622 | 3.728 | 3.680 |
| Ee (kcal/mol) | −9.606 | −9.277 | −6.257 | −7.603 |
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Bende, A.; Turcu, I. Nitrogen Substituted Phenothiazine Derivatives: Modelling of Molecular Self-Assembling. Int. J. Mol. Sci. 2011, 12, 3102-3116. https://doi.org/10.3390/ijms12053102
Bende A, Turcu I. Nitrogen Substituted Phenothiazine Derivatives: Modelling of Molecular Self-Assembling. International Journal of Molecular Sciences. 2011; 12(5):3102-3116. https://doi.org/10.3390/ijms12053102
Chicago/Turabian StyleBende, Attila, and Ioan Turcu. 2011. "Nitrogen Substituted Phenothiazine Derivatives: Modelling of Molecular Self-Assembling" International Journal of Molecular Sciences 12, no. 5: 3102-3116. https://doi.org/10.3390/ijms12053102






